文章信息
- 赵俭辉, 董婷, 蔡波
- ZHAO Jianhui, DONG Ting, CAI Bo
- 基于时空优化长短期记忆网络与烟花算法的AQI预测
- AQI Prediction Based on Long Short-Term Memory Model with Spatial-Temporal Optimizations and Fireworks Algorithm
- 武汉大学学报(理学版), 2019, 65(3): 250-262
- Journal of Wuhan University(Natural Science Edition), 2019, 65(3): 250-262
- http://dx.doi.org/10.14188/j.1671-8836.2019.03.004
-
文章历史
- 收稿日期:2018-09-21

2. 武汉大学 国家网络安全学院,湖北 武汉 430079
2. School of Cyber Science and Engineering, Wuhan University, Wuhan 430079, Hubei, China
空气污染危害人类健康[1, 2],目前评测空气质量的指标是空气质量指数(air quality index,AQI)。AQI主要考虑6项污染物:细颗粒物/PM2.5、可吸入颗粒物/PM10、二氧化硫/SO2、二氧化氮/NO2、臭氧/ O3、一氧化碳/CO。空气质量包括6级:优、良、轻度污染、中度污染、重度污染、严重污染;与之相应,AQI范围划分为:0~50,51~100,101~150,151~ 200,201~300,> 300。AQI指数越大,表示空气受污染的程度越严重。
针对空气污染预测,国内外开展了长期研究,目前采用的主要方法是数值预报和统计模型[3]。数值方法旨在利用污染源排放和气象数据,依据大气动力学、大气化学公式建立物质守恒方程组,通过高算力计算机求解得到污染物的时空分布。数值预报系统十分庞大且复杂,完全模拟大气环境有一定的困难,同时污染源排放数据的获取具有极强的复杂性和不确定性,并且数值模型的计算量巨大,这些原因导致数值预报在实际应用中受到限制。统计预报则不需要考虑大气反应过程,而是以统计学为基础,通过大量的历史数据,建立气象因子与空气质量之间的输入输出模型。这类模型建模便捷,且具有很大的性能提升空间,因此在国内外学者中颇受青睐。目前很多天气领域的研究机构和商业公司,都在基于统计模型对空气质量进行更加精准的预测。
传统的统计预测模型包括时间序列分析、多元回归、灰色系统等。但在实际应用中,单独使用上述数学模型预测空气质量时精度并不是很高。近年来,神经网络技术的研究发展迅速,相较于传统回归模型,将该技术应用于空气污染预测问题取得了更好的结果。Azid等[4]基于主成分分析与神经网络的组合,建立了新模型预测马来西亚空气污染指数。Mishra等[5]对印度德里的PM2.5值进行预测,分别测试了人工神经网络和多元线性回归分析这两种方法,实验结果证明了神经网络模型的预测精度更高。目前,源于人工神经网络的深度学习理论得到了广泛研究[6~8],并开始用于空气质量预测。尹文君等[9]建立深度信念网络(deep belief network,DBN),借助限制玻尔兹曼机预测空气质量指数,且通过实验证明了DBN能够有效预报空气污染。文献[10]采用堆栈降噪自编码器(stacked denoising auto-encoder,SDAE)和网格搜索超参数优化方法建立了AQI等级预测模型,得到了更好的预测效果。目前,在空气质量预测领域基于深度学习的应用仍然很少,深度学习的潜力尚待挖掘。
为了对空气质量进行更加准确高效的预测,本文借助深度学习技术,建立了一种基于长短期记忆(long short-term memory,LSTM)网络的空气质量指数即AQI预测模型;为了避免超参数选取的经验性和随机性,采用具有全局收敛性和高效性的烟花算法(fireworks algorithm,FWA)进行超参数组合寻优;考虑到空气质量的时空相关性,采用时间、空间、时空3种优化策略对模型输入进行优化。通过对网络结构、超参数选取、模型输入3个角度的研究,期望建立一个高性能的AQI预测模型。
1 基于LSTM和FWA的AQI预测模型在传统深度神经网络(deep neural network)中,每一层神经元信号只能往更高层传播,因此只能对输入数据的整体或局部提取特征,但无法模拟时间序列上的变化。本文的研究目标是预测空气质量,而时间相关信息是训练模型的重要依据。所以在建立模型时,需要选用一种能够学习输入数据在时间上相关性的网络结构。
1.1 LSTM模型结构普通神经网络结构为:相邻层神经元之间相互连接,但同一层神经元之间不存在连接。这种网络结构存在劣势,即无法对输入数据提取其时间相关的特征。而递归神经网络(recurrent neural network,RNN)[11, 12]的出现解决了这个问题,RNN中的循环结构可以帮助实现信息持久化。相比于传统神经网络,RNN的最大特点是引入了时序概念,即上一时刻的神经网络状态能直接对下一时刻产生影响。
RNN能学习输入数据在时间上的变化特征,但随着输入AQI数据天数的增加,梯度在反向传播过程中的连乘效应逐渐积累,会使RNN出现梯度爆炸或梯度消失等问题。因此本文使用长短期记忆网络[13, 14]替代RNN建立空气质量预测模型,通过借助LSTM信息持续化存储单元中的输入门、输出门和遗忘门结构的协同作用,选择性记忆信息并进行误差反馈,以解决随AQI数据天数增加造成的长期依赖问题。
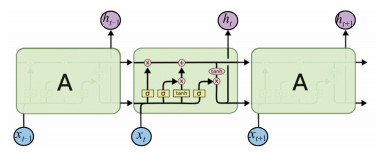
LSTM模块的内部结构比只用一个正切函数tan h 作为激活函数的RNN要复杂很多,如图 1所示。图 1中黑色的线和箭头表示向量序列的流动和方向,箭头分开和聚合表示信息的分流复制与合并,位于LSTM基本模块A(为显示内部结构,中间模块未标注A)内部的圆圈表示向量的逻辑门操作,矩形结构表示学习到的神经网络层,σ 表示Sigmoid函数。在LSTM模块内部,主信息流类似于一条传送带,传送过程中,之前时刻的一部分有用数据经过门结构加入到主数据流中,而主数据流中的一部分信息通过门结构也会进入下一时刻,如此反复形成了循环结构。信息在进入LSTM之后,第一步是通过遗忘门从主信息流中丢弃一些无用信息;第二步是决定哪些信息需要被更新以及更新为何值;第三步开始更新LSTM的单元状态;最后一步则通过输出门确定输出的信息。
|
| 图 1 LSTM模块内部结构示意图 Fig. 1 The inner structure of LSTM unit |
可见,LSTM在RNN的基础上,增加了判断信息是否有用的结构,即记忆块。借助这种结构,使得不符合要求的信息能够通过遗忘门被遗忘,符合要求的信息则通过输出门输出,因此可以解决长期依赖的问题。RNN在每个时间步长内重写自己的记忆,而LSTM通过专门的学习机制对新信息进行记忆、更新和重点聚集,从而能够以极其精确的方式改变记忆的效果,有利于长时间跟踪信息。
1.2 基于FWA的超参数优化如何选择适当的深度神经网络超参数,直接关系到模型的性能,但目前还没有通用且科学的超参数确定方法。基于现有文献,可以发现超参数的选定一般采用经验法。为了减少随意性和盲目性,文献[10]基于多维网格的二次搜索,提出了超参数寻优的新方法,实际上是以一种网格遍历的方式依次尝试每种超参数组合。网格搜索法(GS)虽有不错的寻优能力,但也存在很多问题:首先,网格搜索需要人工设置不同参数的步长,因此无法选取相邻步长之间的超参数组合,容易陷入局部最优;其次,这种网格搜索法效率比较低,无论是否找到了最优超参数组合,都需要匹配完所有组合才能结束遍历过程。对于网格搜索来说,搜索越多解空间的组合,就越容易得到更优解,但是在实际应用中,这种方法因过于耗时而不可取,尤其当超参数个数增多时,遍历海量的参数组合变得不可行,也就是说网格搜索法还不够智能。
对于以LSTM为基础建立的AQI预测模型,其超参数较多且解空间范围较大,为了在合适的解空间内进行更细粒度的搜索,需要引入性能更好的优化算法。考虑到种群的多样性和并发性,为进一步提高超参数寻优的精度和效率,更快的找到全局最优解,本文将烟花算法应用到超参数组合优化问题中。
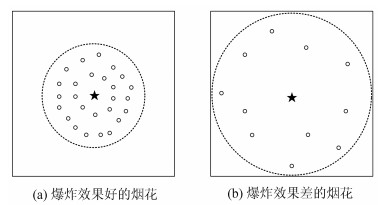
作为群体智能优化算法,烟花算法[15~17]利用爆炸搜索机制获取全局最优解。该算法采用了与烟花爆炸时画面类似的行为方式对目标问题的解空间进行高效搜索,求解复杂优化问题时在性能与效率方面都有着不错的表现。通过对夜空中烟花爆炸过程的观察,发现烟花爆炸时有两种结果:第一种是爆炸效果好的烟花,在爆炸时会产生较多的火花,而且产生的火花位置集中于爆炸中心点;另一种是爆炸效果差的烟花,这类烟花所产生的火花数量稀少,而且零星散落在离爆炸中心较远的位置。图 2显示了这两种爆炸过程。
|
| 图 2 不同爆炸效果的烟花爆炸半径和产生火花数 Fig. 2 The exploded fire radius and generated fireworks from different explosion effects |
从参数寻优的算法角度来看,每个烟花好比搜索空间的一组超参数,本文用模型的预测性能作为评价烟花爆炸效果的标准,即AQI预测模型预测性能好,表示这组超参数的爆炸效果好,该组超参数附近有很大可能存在其他较优的超参数组合,此时该超参数组合周围较近解空间内会产生较多的超参数组火花,用来搜索附近区域以提高局部搜索能力。相比于爆炸效果好的烟花,坏的烟花表示该组超参数的预测性能较差,所以附近存在较优超参数组合的可能性较少,因此爆炸产生的超参数组火花数较少,且距离该组超参数的中心较远,位置也比较分散,可在解空间其他位置搜寻潜在的爆炸效果好的超参数组合,从而提高全局搜索能力。被选中的超参数组火花进入下一轮迭代后,会成为新的超参数组合。
假设有n 个超参数组合,其中Xi=x1,x2,…,xd表示搜索空间内的一组d 维超参数组合,f(Xi)表示在Xi位置处适应度函数的值,即空气质量预测模型的预测误差,该值越小,表示适应度越好。通过以下公式获得每个超参数组合Xi产生的超参数组火花个数
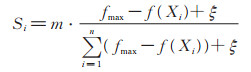
|
(1) |
其中,参数m 用来控制n 个超参数组合产生超参数组火花的总数;ξ 是一个接近0的最小值,避免出现除零错误;fmax是n 个超参数组合中爆炸效果最差的超参数组合的预测误差,即:
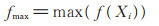
|
(2) |
为了避免效果好的超参数组合周围产生太多的超参数组火花而陷入局部最优,或者效果太差的超参数组合周围产生过少的超参数组火花而错过全局最优,特定义两个边界常量参数a 和b(其中0 < a < b < 1),通过这种限定,超参数组合Xi产生的超参数组火花数量Si '在Si的基础上被修正为:

|
(3) |
相比于爆炸效果差的超参数组合,效果好的超参数组合除了产生的超参数组火花数量较多之外,产生的位置也靠近爆炸中心点。对于超参数组合Xi,其爆炸位移幅度Ai,有如下定义:
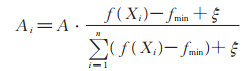
|
(4) |
其中,A 是提前预设的最大爆炸振幅,fmin是n 个超参数组合中爆炸效果最好的适应度函数值,即:
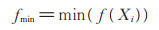
|
(5) |
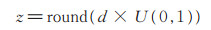
|
(6) |
其中,U(0,1)表示[0, 1]区间上服从均匀分布的随机数。对于d 维超参数组合Xi来说,其通过普通爆炸产生的超参数组火花Xj的位置可由算法1计算得到。
为了保证超参数组合的多样性,在之前的爆炸方式基础上,增加了另外一种变异方式——高斯变异。通过这种方式产生的高斯变异超参数组火花位置与爆炸点位置之间的系数服从期望为1、方差为1的高斯分布。对于d 维超参数组合Xi来说,其通过高斯变异产生的超参数组合Xj的位置可由算法2计算得到。
烟花算法在初始时随机选择n 个位置作为超参数组合进行爆炸,爆炸后的超参数组合与得到的超参数组火花组成集合M。预测效果最好的超参数组合总会被选择进入下一次迭代,其余n-1个超参数组合的选择策略为:依靠该超参数组合(或超参数组火花)与M 中其他超参数组合及超参数组火花之间的距离,为了保证超参数组合的多样性,一般选择距离远的超参数组合(或超参数组火花)进入下一次迭代。超参数组合(或超参数组火花)Xi与M中其他超参数组合(或超参数组火花)的距离为:
| 算法1 普通爆炸超参数组火花位置计算 |
| 1. 初始化超参数组合位置,Xj=Xi |
| 2. 随机确定受爆炸影响的维度z,z=round(d×U(0, 1)) |
| 3. 随机选择超参数组合Xj中受爆炸影响的z维,记为集合D |
| 4. 计算爆炸幅度,h=Ai×U(-1, 1) |
| 5. for each xk in D |
| 6. xk=h+xk |
| 7. if xk不在潜在空间 |
| 8. 把xk映射到解空间 |
| 9. end if |
| 10. end for |
| 算法2 高斯变异超参数组火花位置计算 |
| 1. 初始化超参数组合位置,Xj=Xi |
| 2. 随机确定受爆炸影响的维度z,z=round(d×U(0, 1)) |
| 3. 随机选择超参数组合Xj中受爆炸影响的z维, 记为集合D |
| 4. 计算高斯变异系数g=Gaussian(1, 1) |
| 5. for each xk in D |
| 6. xk=g+xk |
| 7. if xk不在潜在空间 |
| 8. 把xk映射到解空间 |
| 9. end if |
| 10. end for |
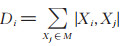
|
(7) |
某个超参数组合或超参数组火花Xi被选择进入下次迭代的概率为:
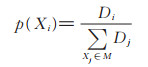
|
(8) |
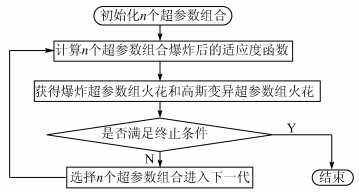
基于烟花算法的超参数寻优流程如图 3所示。具体步骤如下:
|
| 图 3 基于烟花算法的超参数寻优流程图 Fig. 3 Flow chart of super-parameters optimization with fireworks algorithm |
1)在解空间中随机选择n 个位置,每个位置被称为1个烟花,代表 1个超参数组合。
2)对于每一个超参数组合,计算其适应度值,即模型的预测误差,适应度值越小,表示该超参数组合质量越好。
3)根据超参数组合的好坏,确定其爆炸产生超参数组火花数量和爆炸幅度,越好的超参数组合爆炸半径越小且产生的超参数组火花数越多。同时为保证种群多样性,引入了高斯变异算子,以产生一定数量的高斯变异超参数组火花。
4)从所有超参数组合种群、爆炸超参数组火花种群、高斯超参数组火花种群中选择适应度最好的一个直接进入下一代,其余n-1个超参数组合通过选择策略进行获取。
5)判断当前情况是否满足终止条件(即迭代达到烟花算法预设次数如50次,或者预测效果足够理想即预测误差足够小),如果满足则结束迭代,若不满足则重复第2~4步,直至满足终止条件。
在超参数组合优化问题上,烟花算法找到符合要求的解或者达到设定条件之后就能够结束迭代,比类似遍历的网格搜索法更为高效。相比于遗传算法、粒子群算法等其他智能优化算法,烟花算法特有的爆炸机制和选择策略可以保证每一代产生的种群更具多样性,因此更容易收敛到全局最优。除此之外,烟花算法的运作方式还具有分布并行性和高适应性的特点。相比于其他智能优化算法,FWA在本文AQI预测模型超参数组合优化问题上具有更强的适应性和更良好的性能。
1.3 LSTM-FWA的AQI预测模型LSTM在时间序列建模过程中可以保持信息持久化存储,在空气质量预测问题方面,相比于SDAE[10]等神经网络模型,LSTM更适合处理时间相关的AQI数据。因此,本文将结合LSTM与FWA,建立深度学习模型LSTM-FWA,对空气质量进行预测。该模型输入数据为目标城市在预测日前一天的空气质量数据、气象数据以及第二天的气象预报数据,输出数据为预测出的第二天的AQI值。以下表为例,武汉市在预测日前一天的空气质量数据(共8项)如表 1所示;气象数据(共18项)如表 2所示。因此模型输入维度为44,即预测日前一天的8项空气质量数据、18项气象数据,第二天的18项气象数据。
| 空气质量参数 | 值 |
| AQI | 86 |
| 质量等级 | 2 |
| PM2.5/μg·m-3 | 45.9 |
| PM10/μg·m-3 | 119.1 |
| SO2/μg·m-3 | 40.8 |
| CO/μg·m-3 | 1.062 |
| NO2/μg·m-3 | 58 |
| O3/μg·m-3 | 68 |
| 气象参数 | 值 |
| 最高温度/℃ | 9 |
| 平均温度/℃ | 3 |
| 最低温度/℃ | -3 |
| 最高露点/℃ | -4 |
| 平均露点/℃ | -9 |
| 最低露点/℃ | -14 |
| 最大湿度/% | 83 |
| 平均湿度/% | 42 |
| 最小湿度/% | 9 |
| 最大气压/Pa | 1 037 |
| 平均气压/Pa | 1 034 |
| 最小气压/Pa | 1 031 |
| 最大能见度/km | 18 |
| 平均能见度/km | 14 |
| 最小能见度/km | 6 |
| 最大风速/m·s-1 | 11 |
| 最小风速/m·s-1 | 6 |
| 降水量/mm | 0 |
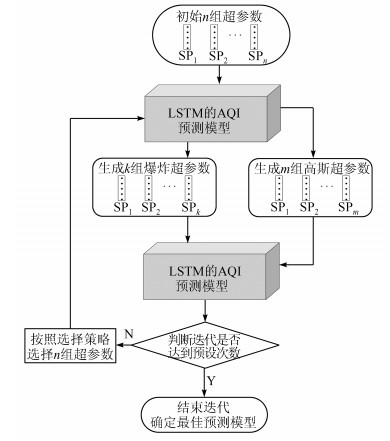
基于上述内容,本文建立了如图 4所示的LSTMFWA预测模型,该模型对应的超参数寻优算法如算法3所示。
|
| 图 4 LSTM-FWA预测模型流程 Fig. 4 Flow chart of LSTM-FWA prediction model |
显然,使用烟花算法进行深度神经网络超参数寻优需要多次训练LSTM模型,整个算法的运算量很大。但在实际应用中,图 4所示的烟花算法超参数寻优只需要做一次,完成后即可得到具有最优参数组合的训练好的LSTM模型,然后基于得到的最佳预测模型,直接进行AQI预测。
本文基于Keras深度学习库,搭建用于多变量序列预测的LSTM空气质量预测模型。该模型包含两层LSTM,首层LSTM的输入维度为44,输出维度定义为超参数;第二层LSTM的输入维度与第一层LSTM输出维度相同,输出维度定义为超参数。为了避免过拟合,在每个LSTM层后加入Dropout层,模型最后接入一个全连接层Dense,并输出一维数据作为预测的AQI值。LSTM-FWA空气质量预测模型(如图 4)的深度学习网络结构如图 5所示,时间步长(输入的AQI数据与气象数据对应的天数)为m,LSTM层数为n(图中展示了2层)。

|
| 图 5 基于LSTM的AQI预测模型 Fig. 5 AQI prediction model based on LSTM |
| 算法3 LSTM⁃FWA超参数寻优算法 |
| 1. 在解空间中随机初始化n个超参数组合的位置; |
| 2. while停止准则==false |
| 3. n个超参数组合分别爆炸,计算对应的适应度函数值,即将各个超参数组合分别应用到基于LSTM的AQI预测模型中进行训练、测试,选取AQI预测值与观测值之间的平均绝对误差MAE作为适应度函数: |
| 4. for每个超参数组合Xi |
| 5. 根据(1)式和(3)式计算该超参数组合爆炸产生的超参数组火花数目Si'; |
| 6. 根据(4)式和(6)式获取该超参数组合Si'个超参数组火花的爆炸位移; |
| 7. 根据算法1获取超参数组合Xi的Si'个超参数组火花的位置; |
| 8. end for |
| 9. for each j in [1 :高斯变异超参数组火花数目] |
| 10. 随机选择一个超参数组合Xj; |
| 11. 使用算法2获取超参数组合Xj的一个高斯超参数组火花的位置; |
| 12. end for |
| 13. 将当前超参数组合、爆炸超参数组火花和高斯变异超参数组火花构成的新候选种群按适应度函数值从小到大排序,从中挑选出适应度函数最优的一个超参数组合; |
| 14. if当前最优超参数组合对应的模型预测性能达到要求 |
| 15. 以当前最优超参数组合作为最终模型的超参数组合并保存模型; |
| 16. 停止准则==true; |
| 17. else |
| 18. 当前最优超参数组进入下一代 |
| 19. 为保证种群多样性,根据(7)式和(8)式计算种群中其他超参数组合进入下一代的概率; |
| 20. 选择其中前n-1个概率最大的超参数组合进入下一代; |
| 21. end while |
输入数据在网络中,主要经历以下4个处理步骤:
1)原始AQI预测训练输入数据在进入模型LSTM层之前,需要被重新构建为形如(nb_samples,timesteps,output_dim)的三维张量,其中nb_samples表示样本数据,加入nb_samples这个维度是为了实现一次训练多个样本,求出平均梯度以更新权重;timesteps为时间步长,在预测AQI时预设该值,根据前timesteps天的数据预测未来一天的AQI,一个时间步长即为样本中的一个观察点;output_dim表示一个时间步长观察到的特征维度。
2)通过第一个LSTM层的映射变换,将原始数据中L1维(AQI预测模型中L1相当于输入数据的维度,即44)的特征映射为L2维,此时返回整个输出序列,因此输出是三维张量,即m 个(nb_samples,L2)二维张量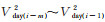
3)以此类推,直到n 个LSTM层结束后,返回输出序列中的最后一个Ln维向量,即下一时刻AQI的特征信息,此时最后一个LSTM层只输出形如(nb_samples,output_dim)的二维张量,在结构图中用灰色信息点表示该输出,即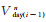
4)在网络顶层添加一个全连接Dense层,将预测的AQI特征信息转化为AQI预测值。
2 时空优化策略考虑到AQI数据具有时间与空间的关联性,本文提出3种策略,分别从时间、空间、时空的角度对输入数据进行优化,提供更多信息用于深度神经网络学习。
2.1 基于时间的优化空气污染是一个连续变化的过程,当前时刻的AQI数据与过去一段时间的数据有关。影响时间的范围取决于污染物扩散条件,扩散条件较差时,时间影响范围变大,但时间范围过大有可能引入无效数据。因此,应该调整时间粒度以得到更丰富的有用特征。上文建立的LSTM - FWA预测模型基于测量日前一天的数据,在此基础上,本文建立了时间属性分别为2天和3天的模型,并且经过试验验证了以2天为时间粒度的模型得到的预测误差最小。这样,以合适的时间粒度对预测模型的输入数据加以时间方面的优化调整,实现了基于时间的优化(temporal optimization,TO),建立了时间优化预测模型,即TO-LSTM-FWA模型。
在时间优化策略下,预测目标城市武汉某一天的空气质量时,模型输入数据为:
1)该天的气象预报数据;
2)过去2天的AQI和气象数据。
2.2 基于空间的优化现有空气质量预测模型基本只从时间角度进行预测,而没考虑污染物在空间中的互相影响。受气象条件的影响,空气污染物具有扩散性,因此目标城市的空气质量会受到周边区域的影响。如果目标城市周边地区发生了高污染事件,经过一段时间传播后,目标城市空气质量会受到影响,监测到的AQI值也会随之升高。上文建立的LSTM-FWA预测模型仅基于一个城市的数据,存在明显的局限性。本文对模型进行空间方面的优化,即同时考虑武汉周边城市的数据。受数据来源限制,本文只能选择南昌、长沙、合肥、郑州等省会城市,并按距离排序为1、2、3、4。空间粒度定义为参与预测的周边城市的个数,并且通过试验验证了以3为空间粒度的模型得到的预测误差最小。这样,以合适的空间粒度对预测模型的输入数据加以空间方面的优化调整,实现了基于空间的优化(spatial optimization,SO),建立了空间优化预测模型,即SO-LSTM-FWA模型。
在空间优化策略下,预测目标城市武汉某一天的空气质量时,模型输入数据为:
1)该天的气象预报数据;
2)过去1天的AQI和气象数据;
3)武汉附近城市(南昌、长沙、合肥)过去1天的AQI数据和气象数据。
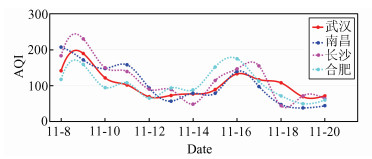
随机截取一段实验数据,以2017年11月8日至2017年11月20日为例,武汉与南昌、长沙、合肥的AQI变化趋势对比如图 6所示。可以看出,相邻城市之间的空气质量指数确实存在一定相关性。将目标周边城市的数据传入SO-LSTM -FWA模型中,有望通过深度学习强大的学习能力挖掘到影响AQI的空间关系特征。
|
| 图 6 武汉与周边城市某时间段的AQI变化趋势 Fig. 6 AQI changing trends of Wuhan and neighboring cities |
通过分析前两种优化策略,我们可以猜测目标城市第二天的空气质量不仅与该城市之前一段时间的历史污染物和气象条件有关,还与该城市周边地区过去一段时间的污染物及气象状况有关。因此将时间信息和空间信息叠加使用,有可能进一步提高预测模型的性能。基于时间优化预测模型与空间优化预测模型,本文从时空结合方向进一步优化预测模型,实现了基于时空的优化(spatiotemporal optimization,STO),建立了时空优化预测模型,即STO-LSTMFWA。在此模型中,以2天为时间粒度,以3为空间粒度,即时间与空间预测模型各自的最优粒度。
在时空优化策略下,预测目标城市武汉某一天的空气质量时,模型输入数据为:
1)该天的气象预报数据;
2)过去2天的AQI和气象数据;
3)武汉附近城市(南昌、长沙、合肥)过去2天的AQI数据和气象数据。
3 实验数据与性能指标 3.1 数据获取本文对武汉市及其周边城市2013年12月—2017年12月这4年间的相关数据进行收集,包括如表 1所示的日均空气质量数据和如表 2所示的气象数据。以2013年12月—2016年12月三年间的1 095条数据为训练集,用于深度神经网络模型的学习;以另外的365条数据为测试集,用于预测模型的测试。本文实验中用到的每日空气质量数据获取自中国空气质量在线监测分析平台(https://www.aqistudy.cn/historydata/index. php);每日气象相关数据的获取自全国历史天气查询平台(http://www.tianqihoubao. com /lishi/index.htm)。
3.2 空缺数据插值数据对于建立与训练模型来说是重中之重,然而在实际应用中,由于各种原因,数据缺失问题不可避免。如果采用不恰当的插值算法,相当于引入了大量噪声,会对数据造成污染。本文收集的原始数据中,同样存在一定数量的数据缺失,针对不同情况的数据缺失,设计了不同的处理方法:对于连续3天以上的数据缺失,直接将这段时间丢弃,否则会在训练数据中引入过多噪声干扰;对于连续缺失数据在3天及以下的情况,采用三次样条插值法(cubic spline interpolation)进行缺失数据插值。
三次样条曲线的原理如下:
对于n+1个样本点(xi,yi)(i = 0,1,…,n),其中a=x0 < x1 < … < xn=b,共有n 个子区间[xi,xi+1](其中xi < xi+1,i = 0,1,…,n- 1),样条函数S(x)是在不同区间内分段定义的公式,该函数满足以下3个条件:
1)插值条件。这是最基本的条件,即S(xi)=yi。
2)连续条件。在整个区间[a,b]上,函数S(x)的一阶导数和二阶导数都必须连续,也就是说S(x)曲线是光滑的,即对xi+(1i=0,1,…,n-2),有:
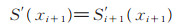
|
(9) |

|
(10) |
3)三次多项式条件。在每个分段区间[xi,xi+1](i = 0,1,…,n-1)上,S(x)都是三次多项式。
例如在数据收集过程中,对于由5个时间节点组成的时间段x=[15 16 20 21 22],获取对应的PM2.5值y=[88 98 126 105 160],而时间节点17、18、19处对应的PM2.5值连续缺失,利用三次样条插值法进行插值。图 7展示了缺失数据的插值效果,根据插值曲线,即可获得缺失的数据值,即虚线对应的PM2.5值。

|
| 图 7 三次样条插值效果 Fig. 7 The effect of cubic spline interpolation |
如表 1和表 2所示,空气质量的影响因子很多,而且其物理性质和单位量纲互不相同,因此无法直接将这些数据用于分析。本文使用归一化方法对原始数据做预处理,使得不同影响因子的取值范围具有同一数量级,从而能够更加合理地进行数据分析。本文采用简单有效的Min-Max标准化模型,通过原始数据的线性变换使数据归一化在[0, 1]范围,归一化函数如下所示:
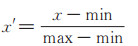
|
(11) |
其中,x 是原始数据,x′是归一化处理后的结果,min和max分别是相应影响因子的最小值和最大值。
为了确保测试集与训练集的一致性,在对训练数据做标准化处理后,也要对测试数据做同样处理,使得所有数据同比例缩放。AQI数据和气象数据的取值范围很大,因此测试集中某影响因子的min值与max值,可能与该影响因子在训练集中的最小值和最大值不同。对个别小于min值或大于max值的测试数据,为使其标准化结果位于[0, 1]范围内,针对上式增加了以下处理:
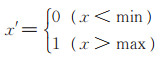
|
(12) |
评价预测模型的性能指标众多,本文在训练阶段使用了平均绝对误差(mean absolute error,MAE);在最终评价模型性能时,还另外使用了均方根误差(root mean squared error,RMSE)以及平均绝对百分误差(mean absolute percentage error,MAPE)对模型预测精度进行整体评估。
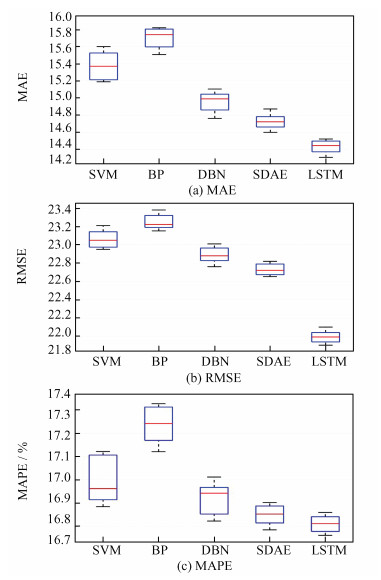
MAE是预测值与实际值的绝对误差的平均值,其计算公式如下:
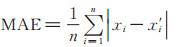
|
(13) |
RMSE为标准误差,是预测值与实际值均方误差MSE的算术平方根,其计算公式如下:

|
(14) |
MAPE是预测值与实际值的相对误差的平均值,其计算公式为:

|
(15) |
(13)~(15)式中,n 表示序列数据的长度,即测试集中测量的天数,xi为第i 天的AQI数据真实值,x'i 为第i 天的AQI数据预测值。3个指标均能反应模型的整体预测性能,其值越小表示预测误差越小,模型的预测性能越优。
4 实验结果与分析 4.1 不同预测模型的性能对比为了分析LSTM模型应用到AQI预测时的性能,在相同样本条件下,将LSTM模型与空气质量预测领域现有的一些传统方法及深度学习方法进行对比,对比模型包括:支持向量机(support vector machine,SVM)[18]、误差反向传播神经网络(back propagation,BP)[19]、深度信念网络(deep belief network,DBN)模型[20]、堆栈降噪自编码(stacked denoising auto-encoder,SDAE)[21]模型。
空气质量除了受到前一天污染物因子和气象条件的影响外,还与预测当天的气象条件有关,因此在本实验中,输入数据由3部分组成:前一天的空气污染物因子(8项)和气象因子(18项),以及预测当天的气象因子(18项),因此输入数据的维度为44,而网络的输出为预测当天的AQI。将模型预测结果与实际污染数据加以比较,可以对算法的预测性能进行评估。
为评价模型的预测性能,本文统计预测值和实际值的差别,利用MAE、RMSE和MAPE作为性能评价标准。由于网格搜索法[10]选出的超参数组合优于经验试凑法,同时为了使对比实验更公平,本文对所有的对比模型均采用网格搜索法选择超参数。为了消除仅对比最优预测结果而导致的偶然性,为每种预测模型选取二维网格搜索结果中预测误差最小的前20组,对比其总体性能分布,得到AQI预测值与观测值之间的MAE、RMSE、MAPE箱形图,如图 8所示。
|
| 图 8 不同模型的AQI误差 Fig. 8 AQI error of different models |
首先,比较所有模型的总体预测性能。由图 8可以看出性能最优的模型是LSTM,其次依次为SDAE、DBN和SVM,而BP的3个性能指标相对来说均最差。由此表明,在AQI预测问题上,LSTM、SDAE、DBN等深度学习模型比SVM具有更强的特征挖掘能力;BP神经网络容易陷入局部最优,而导致训练模型的预测效果较差。
接下来,比较分析所有模型的稳定性。从图 8可以看出,LSTM模型测试产生的前20组最优结果相对比较集中,即模型最为稳定,之后稳定性由强到弱依次为SDAE、DBN、BP,而SVM相对来说最不稳定。
4.2 LSTM的超参数寻优法比较前文介绍了LSTM-FWA空气质量预测模型的结构及工作流程,为验证烟花算法应用于深度学习超参数组合优化问题的可行性并分析其效率,本文设计对比实验,分别建立经验试凑法确定超参数组合的LSTM预测模型和以多维网格二次搜索法为超参数寻优方法的LSTM-GS预测模型,将这两种模型与以烟花算法为超参数寻优方法的LSTMFWA预测模型的结果进行对比。
在基于多维网格二次搜索(GS)和烟花算法的超参数寻优方法中,将LSTM模型中两层LSTM隐含层的维度数、随机舍弃神经元的概率(Dropout)、批训练的数据块大小(batch_size)以及训练轮数(nb_epoch)定义为超参数,每个参数在多维网格二次搜索法中的范围如表 3第3列所示,在烟花算法中的取值范围如表 3第4列所示。由表 3可知,网格搜索法以若干步长为搜索单位,而FWA在整个参数取值范围内搜索。
| 超参数 | 描述 | GS范围 | FWA范围 |
| Layer1 | 第一层LSTM 隐含层维度数 |
{10, 50, 100, 200} | [10,200] |
| Layer2 | 第二层LSTM 隐含层维度数 |
{10, 50, 100, 200} | [10,200] |
| Dropout | 隐含层某些神经 元被关闭的概率 |
{0, 0.1, 0.5, 0.6} | [0, 0.6] |
| batch_size | 批训练数据块 大小 |
{1, 5, 10, 20} | [1,30] |
| nb_epoch | 训练轮数 | {100, 200, 300, 400} | [50,500] |
烟花算法的迭代次数设置为50次,为了综合考虑算法的搜索精度和收敛速度,本文对烟花算法各实验参数的设置如表 4所示。
| 参数 | 对应值 |
| 初始烟花数量(n) | 5 |
| 烟花种群大小(M) | 50 |
| 高斯变异火花数(m) | 5 |
| 爆炸位移幅度调节常数(A) | 40 |
| 爆炸下界常量参数(a) | 0.04 |
| 爆炸上界常量参数(b) | 0.8 |
利用不同预测模型,在相同的数据集上进行对比实验,预测结果如表 5所示。由表 5可以看出,采用了超参数寻优算法的两种预测模型LSTM - FWA和LSTM-GS的预测精度明显高于采用试凑法确定超参数组合的LSTM模型。LSTM - FWA预测模型性能优于LSTM - GS预测模型性能。相比于多维网格二次搜索法,烟花算法在超参数寻优中表现出了更加良好的性能,更容易收敛到全局最优。因此可以得出结论:相较于多维网格二次搜索法,烟花算法应用于深度学习超参数组合优化问题能够得到更优的超参数组合。
| Method | MAE | RMSE | MAPE/% |
| LSTM | 15.373 5 | 22.349 1 | 17.862 5 |
| LSTM⁃GS | 14.305 2 | 21.904 3 | 16.760 5 |
| LSTM⁃FWA | 14.021 1 | 21.732 0 | 15.037 8 |
为了分析LSTM-FWA模型在时间、空间、时空输入优化策略下的性能,建立了对应的3种预测模型:TO-LSTM-FWA模型、SO-LSTM-FWA模型、STO-LSTM-FWA模型。在相同数据集上进行实验,并且与优化之前的LSTM-FWA模型预测结果进行对比,每种模型的预测值与观测值如图 9所示。图 9中散点沿着对角线的聚集程度,能够体现出预测模型的稳定性与准确性。显然,STO- LSTM-FWA模型的散点聚集程度最高,表明其预测值和实际值之间有最强的一致性,或者说该模型得到的AQI预测结果最为可靠。
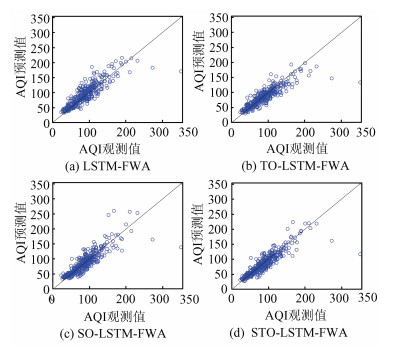
|
| 图 9 LSTM-FWA在不同输入优化策略下的预测散点图 Fig. 9 Prediction scatter diagrams of LSTM-FWA with different strategies of input optimization |
为了更直观地展示在不同输入优化策略下各模型的预测性能,给出了LSTM-FWA及其3种优化模型的误差评价指标柱状图(如图 10)。由图 10可以看出,与优化前的LSTM - FWA模型相比,STO- LSTM- FWA模型性能提升最大,TO - LSTM- FWA模型次之,SO- LSTM- FWA模型性能提升最小。实验结果证实了LSTM - FWA对时空优化数据具有最强的建模能力。

|
| 图 10 LSTM-FWA预测模型在未优化及不同输入优化策略情况下的性能 Fig. 10 Performances of LSTM-FWA prediction model without optimization and with different input optimizations |
现有文献中,只有文献[10]同样采用了深度学习模型与超参数优化,即SDAE-GS。因此,将本文模型与SDAE-GS在不同输入优化策略下的预测性能进行对比。表 6中列出了两种模型分别在输入优化前以及时间优化、空间优化、时空优化策略下的3种性能评价指标。
| 模型 | 优化前 | 时间优化 | 空间优化 | 时空优化 | |||||||||||
| MAE | RMSE | MAPE/% | MAE | RMSE | MAPE/% | MAE | RMSE | MAPE/% | MAE | RMSE | MAPE/% | ||||
| SDAEGS | 14.599 8 | 22.653 5 | 16.784 1 | 14.332 0 | 22.381 6 | 16.406 7 | 12.823 1 | 21.474 5 | 14.223 3 | 13.251 4 | 21.698 9 | 15.399 6 | |||
| LSTMFWA | 14.021 1 | 21.732 0 | 15.037 8 | 12.091 4 | 19.899 0 | 13.504 7 | 13.364 9 | 21.724 9 | 14.633 2 | 11.431 6 | 19.420 2 | 13.248 2 | |||
对表 6进行横向对比,可以看出SDAE-GS模型在空间优化策略下的误差指标比其他两种优化策略都低,即性能最优;时空优化策略下性能较优,时间优化策略下的性能较差,较优化前提升不大。这说明SDAE-GS模型更适合从空间角度进行输入优化,而不适合从时间角度进行优化,因为SDAE网络结构隐含层之间不存在连接,无法对时间进行建模。而LSTM - FWA模型在时空优化策略下的预测误差指标最优,时间优化策略下次之,空间优化策略下性能较优化前提升幅度最小,这说明LSTM - FWA内部的循环结构可以学习输入数据在时间上的变化特征,因此更适合进行时间及时空角度的优化。
对表 6进行纵向对比,可以看出时间优化策略下LSTM-FWA的预测性能更好,空间优化策略下SDAE - GS的预测性能略好,时空优化策略下LSTM-FWA的预测性能明显优于SDAE-GS。这进一步说明:LSTM的循环结构能够对时间特征进行建模,所以在时间相关优化策略下表现更为出众;而SDAE在空间优化策略下提取的特征具有更强的适应性。
根据以上分析,本文确定了时空优化策略下的LSTM-FWA为最佳空气质量预测模型。从3种误差评价指标值看,该模型的预测精度最好,MAE为11.431 6,RMSE为19.420 2,MAPE为13.248 2%。为了更形象地展示STO- LSTM- FWA模型对空气质量指数的预测效果,利用散点连线图展示了365条测试数据的AQI预测值与实际值间的差异(如图 11)。由图 11可以看出本文建立的模型在绝大部分情况下均能对AQI做出较为准确的预测。但对于小概率事件如相邻日期AQI值剧烈变化的情况,预测模型的效果仍然不理想。从深度学习的角度而言,出现这种现象的原因在于这种极端情况的样本数据太少,影响了深度学习网络模型的性能。

|
| 图 11 LSTM-FWA模型预测值与观测值对比 Fig. 11 Comparison of true data and prediction value from LSTM-FWA model |
本文实验基于目前能找到的1 095组数据,将来随着样本数据越来越多,小概率情况的样本数据也会增加,针对小概率事件的预测性能也会相应提高。
5 结论为了解决传统深度学习AQI预测模型难以从时间角度进行建模的问题,本文提出一种基于LSTM和FWA的AQI预测模型LSTM-FWA。该模型的网络结构采用了能够学习时间关联性并具有时间记忆功能的LSTM。同时,为了解决深度神经网络模型的超参数优化问题,提出使用烟花算法进行超参数寻优。另外,还从输入数据角度,建立了时间、空间、时空的优化策略,用于表达AQI数据的时空关联性。预测模型通过训练学习,建立AQI与污染物因子浓度、气象数据之间的关系模型,进而实现AQI值的预测。本文以武汉市空气质量数据为例进行分析,经过实验与比较,得到如下结论:
1)基于LSTM的AQI预测模型能够得到比已有SVM、BP、DBN、SDAE方法更精确、更稳定的预测结果;
2)相比已有的经验试凑法与网格搜索法,烟花算法在深度神经网络模型的超参数寻优问题上具有更好的性能;
3)基于输入优化的LSTM-FWA预测模型与优化前相比,预测性能均得到提高,其中基于时空优化策略的模型具有最优性能,时间优化次之,空间优化性能提升相对较小;
4)比较LSTM-FWA模型与SDAE-GS模型在时间、空间、时空策略下的性能,发现空间优化策略下SDAE-GS模型表现良好,而时间优化策略下和时空优化策略下LSTM - FWA模型表现更为突出。通过综合分析,确定了时空优化策略下的STO-LSTM-FWA为最佳AQI预测模型。
尽管本文的预测模型得到了较好的实验结果,但真正应用到实际预报领域中时,仍然存在问题:由于我国用AQI取代API的时间不长,因此缺乏历史数据,本文模型在训练过程中的学习信息不够充分;其次,由于数据来源的限制,本文实验所用的空气质量数据和气象数据都是日均数据,在时间上跨度比较大,更理想的情况应选用以小时为单位发布的数据进行建模;在空间优化策略中,同样因为数据获取的困难,选择的周边城市均为省会城市,在空间上跨度也较大,更理想的情况应选择周围更近的毗邻城市。随着今后更多监测数据的积累,可以得到更充足的学习样本,使得本文模型能够学习到更好的数据特征,从而对各种空气污染情况做出更准确的预测。
| [1] |
KELLY F J, FUSSELL J C. Air pollution and public health:Emerging hazards and improved understanding of risk[J]. Environmental Geochemistry and Health, 2015, 37(4): 631-649. DOI:10.1007/s10653-015-9720-1 |
| [2] |
SALMOND J, SABEL C E, VARDOULAKIS S. Towards the integrated study of urban climate, air pollution, and public health[J]. Climate, 2018, 6(1): 1-4. DOI:10.3390/cli6010014 |
| [3] |
P REZ V A, ARASA R, CODINA B, et al. Enhancing air quality forecasts over Catalonia (Spain) using model output statics[J]. Journal of Geoscience & Environment Protection, 2015, 3(8): 9-22. DOI:10.4236/gep.2015.38002 |
| [4] |
AZID A, JUAHIR H, TORIMAN M E, et al. Prediction of the level of air pollution using principal component analysis and artificial neural network techniques:A case study in Malaysia[J]. Water, Air, & Soil Pollution, 2014, 225(8): 2063-1. DOI:10.1007/s11270-014-2063-1 |
| [5] |
MISHRA D, GOYAL P, UPADHYAY A. Artificial intelligence based approach to forecast PM2.5 during haze episodes:A case study of Delhi, India[J]. Atmospheric Environment, 2015, 102: 239-248. DOI:10.1016/j.atmosenv.2014.11.050 |
| [6] |
HE K, ZHANG X Y, REN S Q, et al. Deep residual learning for image recognition[C]//2016IEEE Conferenceon Computer Vision and Pattern Recognition(CVPR). New York: IEEE Press, 2016: 770-778. DOI: 10.1109/CVPR.2016.90.
|
| [7] |
LITJENS G, KOOI T, BEJNORDI B E, et al. A survey on deep learning in medical image analysis[J]. Medical Image Analysis, 2017, 42(9): 60-88. DOI:10.1016/j.media.2017.07.005 |
| [8] |
TELLO G, AL-JARRAH O Y, YOO P D, et al. Deepstructured machine learning model for the recognition of mixeddefect patterns in semiconductor fabrication processes[J]. IEEE Transactions on Semiconductor Manufacturing, 2018, 31(2): 315-322. DOI:10.1109/TSM.2018.2825482 |
| [9] |
尹文君, 张大伟, 闫京海. 基于深度学习的大数据空气污染预报[J]. 中国环境管理, 2015, 7(6): 46-52. YI W J, ZHANG D W, YAN J H. Deep learning based air pollutant forecasting with big data[J]. Environmental Conformity Assessment, 2015, 7(6): 46-52. DOI:10.3969/j.issn.1674-6252.2015.06.011 (Ch). |
| [10] |
董婷, 赵俭辉, 胡勇. 基于时空优化深度神经网络的AQI等级预测[J]. 计算机工程与应用, 2017, 53(21): 7-23. DONG T, ZHAO J H, HU Y. AQI levels prediction based on deep neural network with spatial and temporal optimizations[J]. Computer Engineering and Applications, 2017, 53(21): 7-23. DOI:10.3778/j.issn.1002-8331.1705-0420 (Ch). |
| [11] |
AL-MOLEGI A, JABREEL M, GHALEB B. STFRNN: Space time featuresbased recurrent neural network for predicting people next location[C]//IEEE Sym -posium Series on Computational Intelligence (SSCI). New York: IEEE Press, 2017: 1-7. DOI: 10.1109/SSCI.2016.7849919.
|
| [12] |
CHANDRA R, ZHANG M J. Competition and collaboration in cooperative coevolution of Elman recurrent neural networks for timeseries prediction[J]. IEEE Transactions on Neural Networks & Learning Systems, 2015, 26(12): 3123-3136. DOI:10.1109/tnnls.2015.2404823 |
| [13] |
ZHAO J L, QU H, ZHAO J H, et al. Towards traffic matrix prediction with LSTM recurrent neural networks[J]. Electronics Letters, 2018, 54(9): 566-568. DOI:10.1049/el.2018.0336 |
| [14] |
ZHANG Q, WANG H, DONG J Y, et al. Prediction of sea surface temperature using long shortterm memory[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(10): 1745-1749. DOI:10.1109/LGRS.2017.2733548 |
| [15] |
TAN Y, ZHU Y C. Fireworks algorithm for optimization[C]//International Conference in Swarm Intelligence. Heidelberg: Springer, 2010: 355-364. DOI: 10.1007/978-3-642-13495-1_44.
|
| [16] |
ZHANG B, ZHENG Y J, ZHANG M X, et al. Fireworks algorithm with enhanced fireworks interaction[J]. IEEE/ACM Transactions on Computational Biology & Bioinformatics, 2017, 14(1): 42-45. DOI:10.1109/TCBB.2015.2446487 |
| [17] |
HUANG X B, LI H B, ZHU Y C. Shortterm ice accretion forecasting model for transmission lines with modified timeseries analysis by fireworks algorithm[J]. IET Generation Transmission & Distribution, 2018, 12(5): 1074-1080. DOI:10.1049/ietgtd.2017.0619 |
| [18] |
AHMAD I, BASHERI M, IQBAL M J, et al. Performance comparison of support vector machine, random forest, and extreme learning machine for intrusion detection[J]. IEEE Access, 2018, 6: 33789-33795. DOI:10.1109/ACCESS.2018.2841987 |
| [19] |
LIU Y D, LIU S T, WANG Y Z, et al. A stochastic computational multilayer perceptron with backward propagation[J]. IEEE Transactions on Computers, 2018, 67(9): 1273-1286. DOI:10.1109/TC.2018.2817237 |
| [20] |
TRAN S N, GARCEZ A S A. Deep logic networks:Inserting and extracting knowledge from deep belief networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(2): 246-258. DOI:10.1109/TNNLS.2016.2603784 |
| [21] |
JIA C C, SHAO M, LI S, et al. Stacked denoising tensor autoencoder for action recognition with spatiotemporal corruptions[J]. IEEE Transactions on Image Processing, 2018, 27(4): 1878-1887. DOI:10.1109/TIP.2017.2781299 |
 2019, Vol. 65
2019, Vol. 65





