文章信息
- 张海洋, 杜学绘, 任志宇, 陈宇涵
- ZHANG Haiyang, DU Xuehui, REN Zhiyu, CHEN Yuhan
- 基于通用可重构处理器的反馈移位寄存器优化设计研究
- Optimal Design of the Feedback Shift Register Based on the General-Purpose Reconfigurable Processor
- 武汉大学学报(理学版), 2017, 63(2): 133-141
- Journal of Wuhan University(Natural Science Edition), 2017, 63(2): 133-141
- http://dx.doi.org/10.14188/j.1671-8836.2017.02.006
-
文章历史
- 收稿日期:2016-09-18

2. 数学工程与先进计算国家重点实验室,河南 郑州 450001
2. State Key Laboratory of Methematical Engineering and Advanced Computing, Zhengzhou 450001, Henan, China
在当今的信息化时代,序列密码因其实现简单、加解密效率高、密文传输中的错误不会在明文中扩散等特点,得以在军事、外交等专用和保密机构中大量应用.如今,其在商业领域中也得到了很大的发展,如RC4被用于IEEE 802.11 WLAN的加密;欧洲GSM系统的加密采用A5算法[1],短距离无线通信技术标准中的蓝牙技术采用了E0算法[2]作为其安全体系的核心算法.通过研究发现,当前序列密码算法的结构普遍是以反馈移位寄存器 (feedback shift register,FSR) 为基础的[3],FSR的性能直接影响了序列密码算法的处理性能.因此,如何提高FSR的性能已经成为序列密码算法性能提升的关键因素.目前,实现FSR主要有4种方式:1) 采用专用集成电路实现方式.性能能够达到很好的效果,但由于其电路结构固定,导致灵活性与复用性差;2) 采用通用CPU实现方式.具有灵活性高,易于扩展等优点,但由于通用处理器指令系统的局限性,FSR达不到最佳性能;3) 依托组合逻辑的可编程与-异或结构实现方式[4, 5].这种方法具有一定的可重构特性,往往能够通过模式切换实现固定几种密码算法的功能,但随之带来电路网络设计复杂体积庞大,硬件资源往往得不到有效利用,且需紧密结合大量的配置信息为前提;4) 利用FPGA及可重构硬件单元协同计算模型实现方式[6].其输出模式有限,无法达到灵活配置的效果.由此可见,寻求一种兼顾灵活性和高效性的FSR实现方式将是一个具有现实意义的课题.
可重构处理器[7, 8]是近些年发展起来的一个新的计算研究领域.它是由通用处理器和可重构阵列 (RCA, reconfigurable cell array) 组成,这种架构将软件的灵活性和硬件的高效性结合在一起,同时又不会因为过于复杂的电路网络而造成资源浪费.因此,借鉴可重构的设计思想来完成对FSR的设计与实现,既具有高度的灵活性与可扩展性,又保证了高效性.
本文基于文献[9, 10],将通用可重构处理器 (GReP, general-purpose reconfigurable processor) 技术与传统序列密码算法相结合,研究在新型平台下序列密码算法使用的高效性和通用性.从并行化、流水化及资源节约化等方面重点解决序列密码算法存在的执行效率低、并行度不高及通用性差等问题.
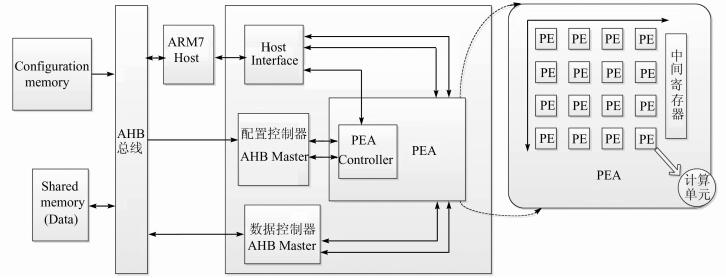
1 GReP通用可重构处理器通用可重构处理器GReP是清华大学为863项目--可重构处理器的研究与设计而自主研发的一款通用性、灵活性与处理能力都较强的软硬件结合的新型可重构平台.核心是由一个串行运算单元 (ARM7) 和一组并行运算阵列 (processing element array, PEA) 组成,每一个并行运算阵列PEA内部是由4×4排列的并行计算单元 (processing element, PE) 组成,计算单元间共享存储 (shared memory),ARM7和PEA之间通过全局寄存器堆 (global register, GR) 交换数据,PEA内部各个PE之间通过Router交换数据.这种架构通过可编程方式动态编写和配置运算规则来实现程序的并行化、流水化.其优点是一次配置多次使用,将软件的灵活性和硬件的高效性结合在一起,既保证了程序运行的可靠性,又通过可编程方式兼顾到硬件通用性,为实现通用性和可编程提供良好硬件基础,架构设计如图 1所示.
|
| 图 1 GReP通用可重构处理器架构 Figure 1 GReP architecture |
GReP通用可重构处理器主要由以下组件及对应指令规则组成:
主控ARM (ARM7 Host):将处理单元阵列配置字 (configtration word, CW) 及部分PEA计算过程中需要的来自主控ARM的数据 (最多15个) 通过指令写入全局寄存器堆中,将PEA计算过程中的数据写入配置控制器的主控接口 (host interface, HI) 的寄存器堆中.配置控制器的主控接口在接受到ARM7 Host写配置字之后使能配置控制器,同时将配置信息的地址和长度交给配置控制器.
配置控制器:从主存中搬运配置包 (configur-ation pack, CP),并解析配置包中每一行对应的PE编号.然后将配置包及每行对应的PE编号交给PEA,由PEA将配置信息分发给各个PE.
PEA Controller:在配置配置控制器和主控均就位后,使能PEA和数据控制器根据配置包执行计算.PEA是可重构阵列内的计算载体 (图 1中虚线所指的部分),它是由16个PE组成的4×4阵列,以及PE间的互连线组成,一个PE可以通过Router访问相邻PE在上一个机器周期的计算结果.在C语言等编写的计算任务中,计算单元PE的管理是由编译器后端来完成的,这个过程对计算任务是隐式管理的.每个PE有一个算数逻辑运算单元ALU (arithmetic logic unit),以及一个私有的用来保存PE 32-bit计算结果的寄存器堆.ALU为可重构设计提供了丰富的计算功能,包含有符号加法、有符号减法、有符号乘法、与、或、异或、绝对值减法、选择操作、逻辑左移、逻辑右移、算术右移、无符号加法、无符号减法等.
数据控制器:负责PEA和Shared memory之间的数据交互.数据控制器可以自动发现访存中的广播行为,并将得到的数据广播给各个PE.
本文后面所做的实验即是遵循这一套指令规则.在C语言实现算法的基础上,人工干预下手动编写编译器后端配置包及初始化数据映射文件,完成算法的可重构映射实现,从而达到对算法的实现与优化.
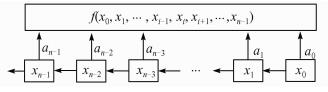
2 FSR特征分析及基于GReP优化设计 2.1 FSR介绍及特征分析FSR实现原理如图 2所示.
|
| 图 2 FSR原理图 Figure 2 FSR schematic diagram |
每个移位寄存器的级数可抽象表示成 (x0, x1, …, xn-1) 形式,其中n为寄存器的级数,xi∈{0, 1},0≤i≤n-1.a0, a1, …, an-1表示为反馈系数,ai∈{0, 1},0≤i≤n-1.f (x0, x1, …, xn-1) 为反馈函数.当反馈系数ai=1时,对应的寄存器级数xi作为反馈函数的一个变量参与运算,即f=f(x0, x1, …, xi-1, xi, xi+1, …, xn-1);相反,当反馈系数ai=0时,对应的寄存器级数xi不参与反馈函数运算,即f=f(x0, x1, …, xi-1, xi+1, …, xn-1).因此,反馈函数可由布尔表达式表示出来:f(x0, x1, …, xn-1)=a0x0⊕a1x1⊕a2x2⊕…⊕an-1xn-1,也即,根据反馈系数ai的取值为0或1来决定移位寄存器对应级数xi是否参与反馈位计算.
FSR的工作步骤主要有:1) 反馈函数计算.在时钟控制下,t0时刻,反馈函数布尔表达式抽取反馈系数ai=1的寄存器对应xi级的固定1-bit数据参与异或运算得到反馈位;2) 移位寄存器进位.在紧接着时钟周期t1时刻,寄存器逐级移位 (右移或左移,视不同算法而定),将t0时刻产生的反馈位补至低位,完成移位操作.
通过对序列密码中FSR的原理介绍,可知其主要由反馈函数和移位寄存器组成.本文研究了公开序列密码算法中的多种FSR.从移位寄存器特征和反馈函数表达式特征两个方面进行分析和归纳,如表 1所示.
| 序列密码算法 | 移存器个数 /级数 |
变量个数 | 线性/非线 性项个数 |
| Grain-80 | 1/80 | 14 | 12/11 |
| Grain-128 | 1/128 | 20 | 6/7 |
| Achterbahn-80 | 11/22~32 | 18 | 8/16 |
| Achterbahn-128 | 13/21~33 | 18 | 8/16 |
| Trivium | 3/9;384;109 | 5 | 3/1 |
| A5/1 | 3/19;22;23 | 10 | 3/1 |
在不同的序列密码算法中,移位寄存器的级数与个数具有很大差异性,即使在同一密码算法中,也存在级数各异的移存器相组合的情况;而反馈函数的特点是其成员变量的不确定性,且存在线性和非线性两种不同的组合形式.通过以上分析,总结出以下两个主要特征:1) FSR个数和级数互不相同,组合形式各异;2) 反馈函数成员变量个数较少,但任意性高,且组合形式无规律可循.
2.2 基于GReP的掩码抽位式反馈函数计算模型从上节的分析可知FSR中存在大量的布尔函数运算及相应的移位操作,在一个移位周期内,按照反馈多项式每一项多次抽取移位寄存器对应位置1-bit数据并逐一异或操作,生成1-bit反馈位.移位寄存器经逐级移位操作后将此1-bit反馈位补至最低位.这种操作在各类算法中大量存在,贯穿算法始终.
而GReP的ALU算数运算单元在执行运算时提供两个32-bit粗粒度和一个1-bit细粒度作为输入参数,运算输出则为一个32-bit粗粒度输出和一个1-bit细粒度.这种独特的计算结构为FSR这种粗粒度输入细粒度输出计算类型提供了运算新方法.如表 2中列举GReP部分指令域命令中,异或操作 (/Xor) 的细粒度输出位执行的操作实际上是将粗粒度输出位Out1逐位异或,即:
| 操作 | 功能 | Operation | Out1 | Out2 |
| \Add | 加法 | T=in1+in2+in3 | Out1=T[31:0] | Out2=T[31] |
| \Sub | 减法 | T=in1-in2-in3 | Out1=T[31:0] | Out2=T[31] |
| \Or | 或 | T[31:0]=in1|in2|{31{1‘b0}, in3} | Out1=T[31:0] | Out2=|T[31:0] |
| \Xor | 异或 | T[31:0]=in1^in2^{31{1‘b0}, in3} | Out1=T[31:0] | Out2=^T[31:0] |

|
具有类似特性的还有其他种类命令,这里就不一一列举.
针对此特性,本文引入掩码的概念,提出掩码抽位式反馈函数计算模型,定义如下.
定义1 在GReP运算结构下,以给定的反馈函数为对象,衍生出反馈抽取掩码M,在时钟周期t1,寄存器R状态值r与掩码值m执行异或运算,在下一时钟周期t2计算得出1-bit细粒度输出Out2即为反馈位.
以A5算法为对象作模型分析说明,A5算法结构将在下节中作详细介绍.算法中移位寄存器R1的反馈函数如下:
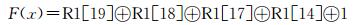
|
(1) |
反馈函数F(x) 抽取移位寄存器R1中固定位14、17、18、19级1-bit数据组成线性布尔函数,最终与1模2加生成1-bit反馈位.
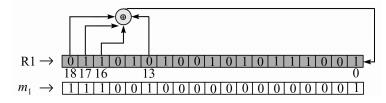
(1) 式掩码抽位式反馈函数计算模型如图 3所示,图中m1记为反馈抽取掩码,将反馈函数选定的抽取项置1,其余项置0,得到二进制掩码值m1=1110010000000000001B.
|
| 图 3 A5算法掩码抽位式反馈函数计算模型 Figure 3 A5 algorithm masking digitized feedback function calculation model |
反馈抽取掩码m1与R1作为ALU运算粗粒度输入参与异或运算,取1-bit细粒度输出F(x) 为最终结果,如下式
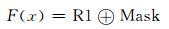
|
(2) |
经指令执行后,仅在1个时钟周期内就可得到反馈函数1-bit反馈位.使用C语言实现代码如下:
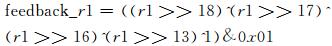
|
(3) |
上式表示一次反馈位计算,即移位寄存器经一次移位操作后的状态.已知通用CPU完成一个二元运算至少消耗一个时钟周期,在不考虑数据存取延时等情况下,通用CPU处理一次反馈位计算至少需要9个时钟周期.因此通过对比,在大量移位操作情况下,通过可重构处理器执行效率理论上可提高9倍.
掩码抽位式计算模型突破传统的软件实现方法,从ALU运算单元上寻找优化点,从而大大节约计算成本,使计算更加简便.在不同密码算法中,各类FSR及反馈函数差异性很大,采用此模型时可将反馈抽取掩码置为立即数等形式提前预置于代码中,无需重新设计硬件单元且软件代码修改量小,具有充分的可重构特性.
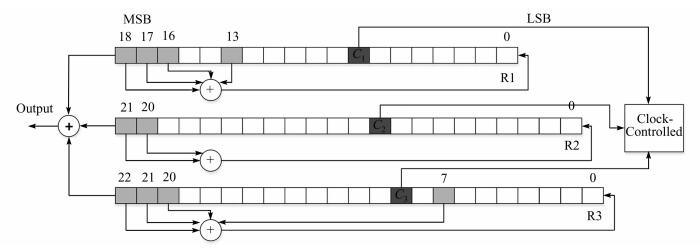
2.3 A5算法并行+流水优化设计 2.3.1 A5算法原理A5加密算法广泛应用于欧洲数字蜂窝移动电话系统GSM中,用于保护手机和基站之间的通信.算法实现是由长度为19-bit、22-bit、23-bit的3个FSR完成,以钟控方式完成加密,密文按序输出,结构如图 4所示.
|
| 图 4 A5算法模型 Figure 4 A5 algorithm model |
设移位寄存器分别为R1, R2, R3,在钟控作用下3个移位寄存器同步加密.钟控抽取位分别是3个寄存器的第8、10、10位,记为C1=R1[8]、C2=R2[10]、C3=R3[10].钟控表达式如下:
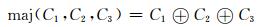
|
(4) |
移位规则为,在时钟周期Ti时刻,设S=C1⊕maj (C1, C2, C3),若S=1,则寄存器R1左移一位实现步进反馈位补至最低位,否则此时刻不变.这种进位规则保证了在Ti时刻,至少有两个移位寄存器实现移位,移位表达式如下,
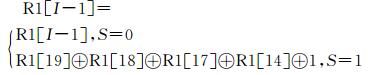
|
(5) |
其中I为寄存器长度.同理, 寄存器R2、R3移位表达式分别为:
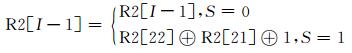
|
(6) |
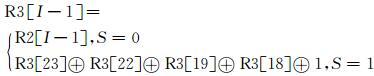
|
(7) |
A5算法密钥流数据生成主要分为以下几步:
Step 1 将移位寄存器组初态设为全零向量.
Step 2 (密钥参与)3个移位寄存器都规则动作64次,将密钥从FSR最低级注入.每次动作1步.在第i步动作时,3个FSR的反馈内容都首先与密钥的第i个比特模2加,并将模2加的结果作为FSR反馈的内容.
Step 3 (帧序号参与)3个FSR都规则动作22次,将帧序号从FSR最低级注入.每次动作1步.在第i步动作时,3个FSR的反馈内容都首先与密钥的第i个比特模2加,并将模2加的结果作为FSR反馈的内容.
此步骤完成后,3个FSR的状态合称为A5算法的初态.
Step 4 (钟控无输出)3个FSR以钟控的方式连续动作100次,但不输出数据.
Step 5 (生成密钥流)3个FSR以钟控的方式连续动作228次,在每次动作后,3个FSR都将最高位寄存器中的值输出,将这3个比特的模2加作为密钥流输出.共输出228位用于加密.
2.3.2 基于GReP架构的A5算法并行+流水优化针对A5算法原理及步骤,本文基于掩码抽位式反馈函数计算模型对FSR整体结构进行优化,利用GReP独特的并行计算单元PEA阵列,将原本串行的FSR实现并行优化,在同一时钟周期中尽可能将计算过程分布到4×4的PE阵列中并行计算,并通过精确时钟控制实现流水化,大大节约时间成本.
代码1为以软件的方式实现上节Step 2的C代码片段.该代码通过一组循环,将64位密钥规则插入用无符号整数的二进制形式表示而成的SFR中.3组移位寄存器彼此独立,但在移位时需同步执行.

|
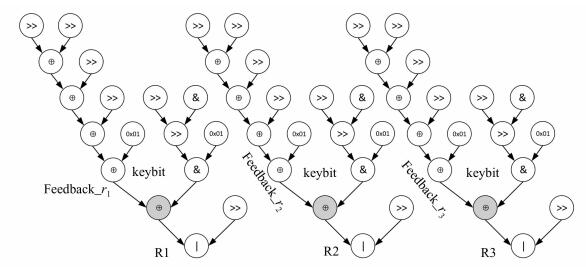
为便于描述,将上述代码拆解为DAG图 (direct acyclic graph,有向无环图),如图 5所示.
|
| 图 5 A5算法Step 2 DAG图 Figure 5 A5 algorithm Step 2 DAG diagram |
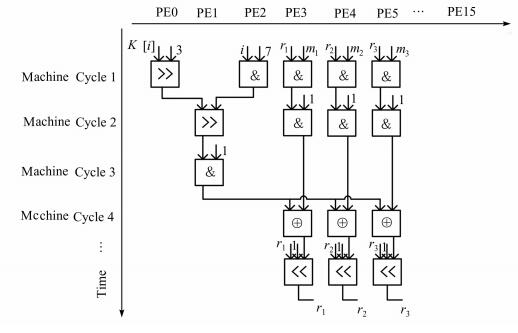
经分析可知,产生密钥bit流输出 (代码中的keybit表示) 与3组移位寄存器R1、R2、R3只在最终移位时产生依赖关系,如图中阴影节点所示.由此可将3组FSR的反馈移位运算与bit流输出放在PE阵列并行执行,并使用上节提出的掩码抽位式反馈函数计算模型完成代码的并行映射.将DAG图拆解映射到GReP并行运算阵列中,如图 6所示,横坐标表示算法所使用的PE并行个数,纵坐标表示时钟周期 (machine cycle).
|
| 图 6 GReP并行化算法映射 Figure 6 GReP parallelization algorithm mapping |
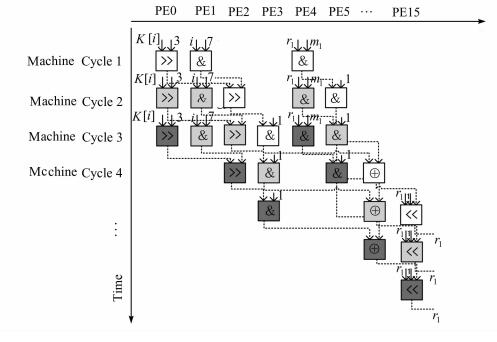
由图 6可看出,计算过程中最多同时用到6个PE,仅用时5个时钟周期.在PEA计算阵列顶层设定循环64次即可完成将64位密钥规则插入LSFR.上述方法仅在一次循环内实现并行运算,并没有将GReP并行特点完全发挥出来.因而进一步将指令流水化,在流水过程中每个PE完成同样的功能,避免了重复配置带来的系统额外开销.如图 7所示,图中不同的阴影代表不同次的流水.
|
| 图 7 GReP流水化算法映射 Figure 7 GReP pipelining algorithm mapping |
理想情况下,GReP设计完成3组密钥参与的加密过程只需要64×5+2=322个时钟周期.而在同等数据量情况下,C语言实现需时钟周期个数可由下式计算:
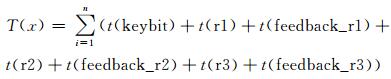
|
(8) |
经计算,完成3组n=64轮循环,最终需要T(x)=7 680个时钟周期.GReP并行流水实现执行效率是它的23.9倍,且随着循环次数的增多,执行效率将被进一步放大.由于篇幅所限,仅以A5中具有代表性的步骤或代码进行解释说明,其他步骤可参照上述方法进行类似优化设计.
3 实验与分析本文在GReP通用可重构平台上对A5算法进行仿真实验.为达到实验效果,在GReP模拟器上编写C语言算法文件,并通过编译器提供的接口在后端编译对应的配置文件完成算法功能映射.部分实验过程已在上一节有所介绍,实验主要步骤如下:
Step 1 按照A5算法步骤,将算法整体分成4个执行步骤,分别编写配置文件.
Step 2 每个配置文件中,首先将初始数据写入对应文件中.如,在InitGlobalReg.txt文件中写入全局寄存器信息,在InitMemoryMap.txt中写入Shared Memory内存信息.
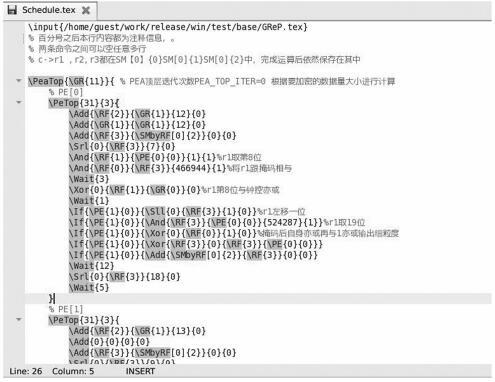
Step 3 按照算法规则编写每个时钟周期下每个PE所完成的指令功能;最终完成各级循环指令控制.由于篇幅所限,截取部分配置文件代码,如图 8所示.
|
| 图 8 PE映射配置文件 Figure 8 PE mapping configuration file |
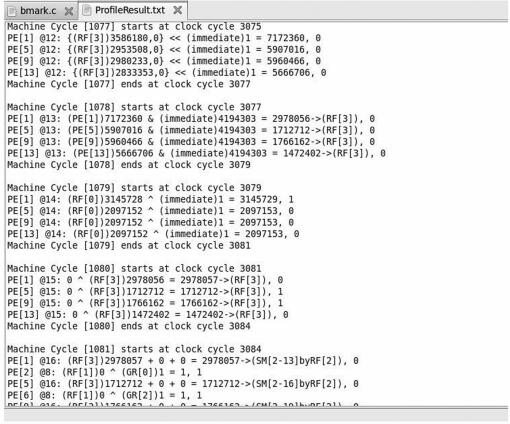
Step 4 使用编译器提供的指令编译配置包,可在ProfileResult.txt文件中查看本配置文件执行结果,部分执行结果如图 9所示.
|
| 图 9 配置文件执行详细过程 Figure 9 The configuration file execution process |
Step 5 利用接口函数在串行程序中调用GReP处理器执行算法.
50 MB数据量与200 MB数据量两种情况下在GReP通用可重构平台与Intel Atom 230处理器平台执行结果,如表 3所示.
| 实现方法 | 处理器性 能/GHz |
数据量 /MB |
吞吐量/ MBs-1 |
执行时 间/s |
| Intel Atom 230 | 1.6 | 50 | 1.51 | 33.12 |
| GReP算法映射 | 0.2 | 50 | 3.27 | 15.29 |
| Intel Atom 230 | 1.6 | 200 | 1.70 | 117.64 |
| GReP算法映射 | 0.2 | 200 | 3.38 | 59.17 |
表 3显示,基于Intel Atom 230的串行加解密平均吞吐量为1.61 MB/s,基于GReP的加密算法平均吞吐量达到3.33 MB/s.GReP处理器实际数据吞吐量约为Intel Atom 230处理器的2.07倍;而Intel Atom 230处理器为单核处理器,其主频为1.6 GHz,由于GReP现在只处于实验阶段,其PEA阵列主频只有0.2 GHz,因此GReP的实际处理能力约为Atom 230的1/8.因此,在相同频率下,GReP加解密速度实际上可达到Intel Atom 230的16.56倍 (2.07×8),执行效率更高.具有执行效率高、可重构性等特点,能够为种类繁多、结构复杂的FSR提供高性能的可重构实现.
4 结论本文通过对基于FSR序列密码算法的特征进行分析,总结出该类密码算法所具有的特征及存在可优化的方面.提出掩码抽位式反馈函数计算模型,并以A5算法为例,基于GReP可重构处理器PEA阵列实现算法的并行化、流水化设计.最终实验结果表明,可重构处理器在处理序列密码算法过程中具有高可行性和高效性,为今后通用可重构处理器在序列密码算法处理中的研究提供了依据和支撑.
| [1] | BIHAM E, DUNKELMAN O. Cryptanalysis of the A5 GSM stream cipher[C]//Progress in Cryptology-INDOCRYPT 2000. Berlin: Springer-Verlag, 2002: 43-51. DOI: 10.100713-540-44495-5-5. |
| [2] | LUETOOTH S I G. Bluetooth specification version 1.1[DB/OL].[2016-05-02]. http://www.bluetooth.com |
| [3] | 刘运毅, 覃团发, 倪皖荪, 等. 简评ECRYPT的候选流密码算法 (下)[J]. 信息安全与通信保密, 2006(9) : 17–21. LIU Y Y, QIN T F, NI W S, et al. Brief evaluations of the candidates to the ECRYPT stream ciphers[J]. Information Security and Communications Privacy, 2006(9) : 17–21(Ch). |
| [4] | 陈韬, 杨萱, 戴紫彬, 等. 面向序列密码的非线性反馈移位寄存器可重构并行化设计[J]. 上海交通大学学报, 2013, 47(1) : 28–32. CHEN T, YANG X, DAI Z B, et al. Design of a reconfigurable parallel nonlinear feedback shift register structure targeted at stream cipher[J]. Journal of Shanghai Jiaotong University, 2013, 47(1) : 28–32(Ch). |
| [5] | 徐光明, 徐金甫, 常忠祥, 等. 序列密码非线性反馈移存器的可重构研究[J]. 计算机应用研究, 2015, 32(9) : 2823–2826. XU G M, XU J F, CHANG Z X, et al. Reconfigurability study on nonlinear feedback shift registers in stream cipher[J]. Application Research of Computers, 2015, 32(9) : 2823–2826(Ch). |
| [6] | 潘光华, 来金梅, 陈利光, 等. FPGA可编程逻辑单元时序功能的设计实现[J]. 电子学报, 2008, 36(8) : 1480–1484. PAN G H, LAI J M, CHEN L G, et al. The design and implementation of sequential circuits in FPGA configurable logic block[J]. Chinese Journal of Electronics, 2008, 36(8) : 1480–1484(Ch). |
| [7] | ZHU M, LIU L, YIN S, et al. A reconfigurable multi-processor SoC for media applications[C/OL].[ 2016-02-23]. http://ieeexplore.ieee.org/document/5537147/. |
| [8] | YAN L, WU B, WEN Y, et al. A reconfigurable processor architecture combining multi-core and reconfigurable processing unit[C/OL].[ 2016-01-23].https://www.researchgate.net/publication/221194123. |
| [9] | 于苏东, 刘雷波, 魏少军. 基于循环映射的可重构处理器设计[J]. 北京邮电大学学报, 2009, 32(4) : 10–14. YU S D, LIU L B, WEI S J. Design of reconfigurable processor based on the loop mapping[J]. Journal of Beijing University of Posts and Telecommunications, 2009, 32(4) : 10–14(Ch). |
| [10] | 魏少军, 刘雷波, 尹首一. 可重构计算处理器技术[J]. 中国科学:信息科学, 2013, 42(12) : 1559–1576. WEI S J, LIU L B, YIN S Y. Key techniques of reconfigurable computing processor[J]. Science China Information Sciences, 2013, 42(12) : 1559–1576(Ch). |
 2017, Vol. 63
2017, Vol. 63





