0 引言

概率密度分布图是一项通过一系列的基于独立的离散事件来产生概率密度从而预测发生此类事件的可能区域的技术^[1].对于一系列给定了时间空间坐标的离散数据，我们可以构造一个概率密度来估计离散事件发生在一个区域的可能性.

常用的进行密度估计的方法是核密度估计法^[2]，它通过求核函数的和来逼近真实密度.高斯分布核函数是最常用的核函数，它具有光滑、空间对称以及非紧支撑的特点.其他概率密度估计方法有紧弦法、log-样条法和总变差最大罚似然估计模型等.但是，这些模型当中均未采用客观的地理信息，从而导致密度估计在无效区域存在有非零的事件发生概率，与客观实际不符合.如离散犯罪事件中入室盗窃和其他类似的犯罪不应当出现在海洋，山脉等无效区域.理想情况下，我们希望能确保概率密度被限制在有效区域当中.所以应当将地理信息有关的数据纳入概率密度估计模型之中.

本文提出新的模型和算法，引入了地理信息，将概率密度估计支撑限定在有效区域内以保证事件发生的真实性.该模型是以最大惩罚项似然估计法为基础的演化方法.密度估计由预设的能量函数最小值计算得出.本文提出的方法中的能量函数是关于有效区域显式独立的，使密度估计遵循我们对于其支撑所提出的假设.

1 最大罚似然估计

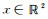
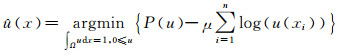
假设u(x)是关于的概率密度分布.已知事件的发生地点为x₁, x₂, …, x_n.最大罚似然估计法(maximum penalized likelihood estimation，MPLE)^[3]由下式给出

(1)

(1) 式由两项组成，惩罚项P(u)和最大似然项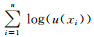，惩罚项是为了让概率密度估计图光滑.参数μ决定了最大似然项在公式中相对于惩罚项的权重大小.

现阶段被提出的惩罚项函数已经有很多，例如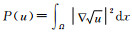和P(u)=∫_Ω|∇³log(u)|²dx等.最近，总变差函数的变形P(u)=∫_Ω|∇u|dx被提出运用到了最大罚似然估计中^[4~7].虽然其中一些方法适用于多种域，但是这些方法并不显式地将预先给定的空间地理信息纳入其中.总变差具有保持梯度的作用，连续区域的边界不必与图像中的边界相一致.传统的TV(total variation)-MPLE模型在离散数据非常稀疏的情况下通常也表现得很差，因为概率密度分布被过度光滑，以至于几乎在各个地方都相等.除此之外, 传统的TV-MPLE方法并没有加入对地理因素的考虑，可能导致预测事件发生在无效区域.

2 修正的总变差MPLE模型

为了加入地理信息，从而区分出有效与无效区域，我们对近几年最大罚似然估计模型的研究成果^[8~10]进行了拓展，提出了新的修正的最大罚似然估计方法(modified total variation MPLE，MTV-MPLE).MTV-MPLE针对地理信息做了改进，引入一个依赖于无效区域的惩罚项函数，使无效区域可由地理图像或者其他预设的地理信息数据来表示.

传统的TV-MPLE方法如下所示

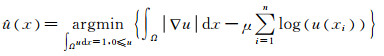
(2)

对于一个设定好的有效区域，希望密度函数u的等高线在有效区域的边缘处对齐.TV-MPLE法允许其最小解不连续的情况出现.

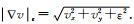
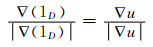
通过使等高线在有效区域的边缘处对齐，在此处产生不连续的情况从而保证密度估计不会因为演化过程而光滑进无效区域.∇(u)/|∇u|表示u的水平曲线的归一化向量，为了避免出现分母为0的情况，有θ=∇(1_D)/|∇(1_D)|_ε，区域D包含有空间信息数据.(1_D)是有效区域边界的符号函数，在无效区域内为1，在有效区域内为0.为了引入地理信息，在(2) 式中加入如下条件

(3)

或要求∫_Ω|∇u|-θ·∇udx=∫_Ω|∇u|+u∇·θdx最小化.将∫_Ω|∇u|+u∇·θdx项包含在(2) 式中，从而得到MTV-MPLE能量函数

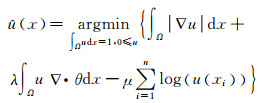
(4)

3 模型求解

MTV-MPLE是一个约束优化问题，有两个约束条件必须要满足:0≤u(x)来保证概率本身为正；∫_Ωu(x)dx=1来保证u(x)本身是一个概率密度估计.常用的求解方法是约束用罚函数形式来表述，增加一个L₂惩罚项得到一个新的极小化问题^[9]

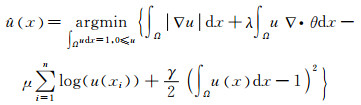
(5)

但是常用的求解方法存在不足，该方法的L₂惩罚项的系数γ如果过大，会影响求解的数值稳定性；若γ取值较小，虽然能保证数值稳定性，但是约束较弱以至于不能保证∫_Ωu(x)dx=1.因此，我们采用梯度投影下降方法来对约束优化问题求解^{[10, 11]}.

对于(4) 式中求解极小问题，令

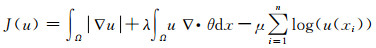
(6)

通过梯度下降和投影交替迭代求解

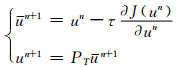
(7)

先进行梯度下降，τ为下降步长，对J(u)求微分

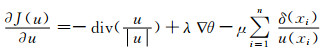
(8)

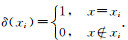
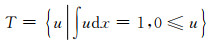
其中对梯度下降得到的uⁿ⁺¹在T上做投影得到uⁿ⁺¹，T为约束所限制的区域

(9)

我们通过不断的梯度下降与投影来迭代求解uⁿ⁺¹的解.实践中为了保证解收敛并且有一个好的实验结果，选取下降步长τ为8E-6, 参数λ选择1.0到1.2之间效果较好.μ选取与u有关，m为矩阵的行数，n为矩阵的列数.μ为1/(mn).

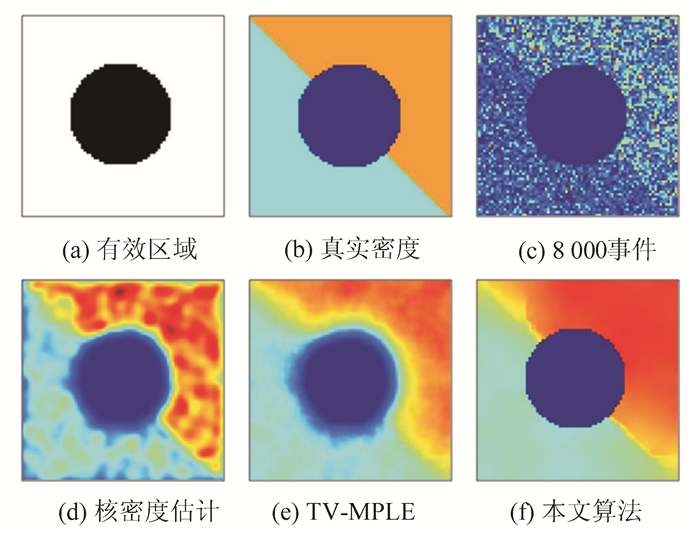
4 数值实验 4.1 模拟数据实验

为了证实我们的模型切实可行，我们预先定义了一个有着尖锐梯度的概率分布图，并根据其在区域内随机产生8 000个离散事件.这8 000个离散事件中，有6 000个发生在区域对角线的右上方，其余2 000个发生在区域对角线左下方，无效区域内没有离散事件.之后依靠MTV-MPLE来得到概率密度分布图并与核密度估计方法和传统的MPLE方法相比较.如图 1所示.

图 1(a)，(b)，(c)是密度估计的先验，(d)，(e)，(f)是针对先验数据的估计结果.其中，有效区域如图 1(a)所示.真实密度和8 000个离散事件在图 1(b)及图 1(c)中所示.同时，我们也给出了核密度估计法以及TV-MPLE法的结果.核密度估计的变量σ=2.结果在图 1(d)及图 1(e)中.MTV-MPLE的结果在图 1(f)中所示.由于引入了地理信息，我们的方法保持了无效区域的边界，并且和预设的真实的解十分接近.而核密度估计法和传统的TV-MPLE法在无效区域内均有概率密度存在.此外，在密度估计过程中，该方法还保持了概率密度边缘尖锐的梯度.表 1中为这三种方法的L₂误差.L₂误差的定义为(∫_Ω u(x)dx-1)², 用来刻画求解结果u是否满足前文提出的第二个约束.

误差越小表示算法收敛性越好，预测结果更契合实际.比较表 1中的3种方法计算效果的L₂误差可以看出，在模拟的4 000个或8 000个离散数据的情况下，MTV-MPLE均比核密度估计法以及传统的TV-MPLE法收敛性好.说明其对约束条件满足得更好.

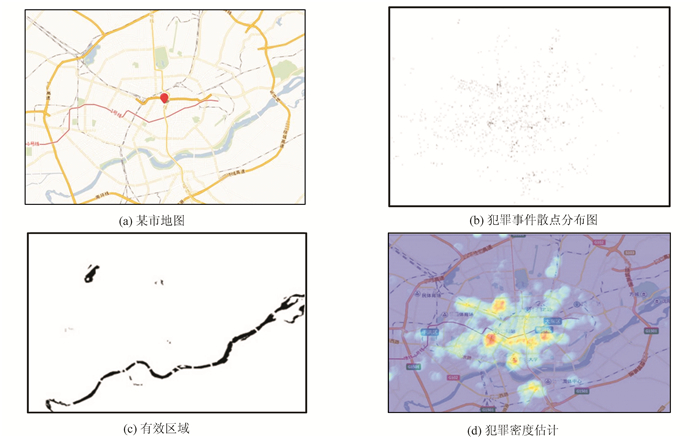
4.2 某城市犯罪事件概率密度估计实验

运用真实的数据测试新方法的效果.实验选取2013年到2015年6月的某市区及其周边区域的犯罪数据，一共1 273个符合条件的犯罪事件.每个犯罪事件均有发生时间与犯罪地点的经纬度坐标.该市及周边地区的地理信息可以由公开的地图数据得到，由地图所示，河流内部及西北方的湖泊为无效区域.用MTV-MPLE进行密度估计，实验结果如图 2所示.

实验选取的区域的地图如2(a)所示，包括该市区以及其周边区域.图 2(b)为犯罪事件的散点分布图.图 2(c)为有效区域，如图所示，在贯穿该市的河流中是没有犯罪事件发生的.图 2(d)为MTV-MPLE估计的概率密度分布图.将犯罪密度分布和实际的地图相对应，比较直观.图像的尺寸为450×650.

从实验结果来看，该市的犯罪密度集中分布在火车站及其周围的街道以及该市一所高校附近.地图上有一条横贯城区的河，其为无效区域，在迭代演化过程中，概率密度具有光滑性且有效区域的边界也得到了很好的保持.该城市的河湖等无效区域也没有概率密度分布.改进的概率密度估计方法在面对实际数据的检验时取得良好的效果，已经在实际应用中对警方布控起到了指导作用.

犯罪事件的发生地点是警方用GPS定位的.测定离散事件的空间信息时受制于GPS设备定位精度的影响，测量过程存在细微的误差.比如有少量离散事件发生在有效区域和无效区域的边缘，由于测量误差的存在会被认为发生在无效区域中.但实验表明，新算法在测量存在误差的实际数据中取得了和模拟数据一样的良好效果.主要是因为(4) 式所定义的TV-MPLE能量函数中λ∫_Ω u∇·θdx能够保证概率密度分布在无效区域中为0，能量函数关于有效区域是显式独立的.这说明新的方法对实际数据有很好的适用性.

5 结论

本文主要研究了如何将地理信息引入概率密度估计的方法.传统的根据离散事件生成概率密度分布图的方法并不考虑地理信息，从而可能会导致预测的概率密度出现在根本不可能发生事件的无效区域.

以解决此类问题为目的，我们提出了修正的TV-MPLE模型和算法.与传统的方法相比较，该方法既能依据地理信息区分有效区域与无效区域，又能确保概率密度的支撑.根据实际地理信息.在无效区域中，对事件的发生概率的估计为0.在模拟数据实验中，修正的TV-MPLE法的收敛性要优于核密度估计方法与传统的MPLE方法.

本文将该方法用于构建基于地理信息的某城市犯罪概率密度分布图，估计效果直观且符合实际.在湖泊、河流等无效区域内，犯罪事件的概率密度为0.相关方法已经被用于警用软件的开发，用于为各地警方布控提供更合理的参考.