文章信息
- 冯孝周, 史柯楠, 安晓敏
- FENG Xiaozhou, SHI Kenan, AN Xiaomin
- 具有Holing-Ⅲ反应项的捕食系统的平衡态共存解
- Coexistence Solution on the Steady-State of a Predator-Prey System with Holing-Ⅲ Functional Response
- 武汉大学学报(理学版), 2018, 64(6): 525-532
- Journal of Wuhan University(Natural Science Edition), 2018, 64(6): 525-532
- http://dx.doi.org/10.14188/j.1671-8836.2018.06.007
-
文章历史
- 收稿日期:2017-11-20

生态系统中相互作用物种关于空间和时间的动力学行为是生态学的一个中心问题.具有多物种相互作用的反应扩散模型成为许多学者研究的焦点.特别地,关于种群系统解的共存性、持续性及稳定性已成为该领域研究的热门课题.当物种空间均匀分布时, 一般通过常微分方程系统的正解来刻画.而物种在空间不均匀的情况下, 通常利用非线性反应扩散方程的共存解来刻画物种的演变规律.关于非线性偏微分方程模型的动力学行为的研究在种群生态学中具有重要意义.近几十年来, 学者们广泛地研究了由非线性反应扩散导出的具有空间项的捕食模型, 得到了许多重要研究成果(参见文献[1~9]).
在文献[9]中,我们研究了具有Holling-Ⅲ反应项的捕食系统在Neumann条件下的正平衡态解的局部分歧与全局分歧解的存在性.而在本文中, 考虑以下具有Holling-Ⅲ功能性反应项捕食系统在齐次Dirichlet边界条件下的平衡态模型:
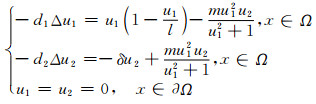
|
(1) |
其中Ω是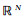
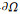
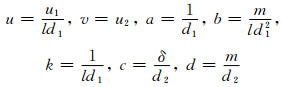
|
因此, 参数a, b, c, d, k均为正常数,故系统(1)可以转化如下形式:
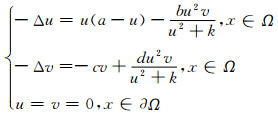
|
(2) |
本文考虑系统(2)的更一般的情况, 即参数a, b, d, k为正常数和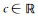
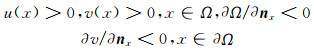
|
其中nx表示单位外法线方向向量,则称(u, v)为系统(2)的共存解.
为了得到主要结果, 我们首先引入一些符号[10].对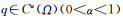
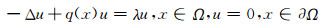
|
(3) |
并简记λ1(0)为λ1, 易知λ1(q)是严格增加的,即当q1(x)≤q2(x)且q1(x)≠q2(x)时,λ1(q1)<λ1(q2)(参见文献[5, 7]).
定义Θ(p(x))为下面方程的惟一解,
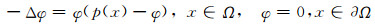
|
(4) |
且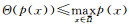
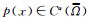
为了简化运算, 记Θ(a)为Θ.在本文中, 我们首先建立系统(2)共存态解存在的充分必要条件,主要结果如定理1.
定理1 系统(2)存在一个共存态解的充分必要条件是a>λ1且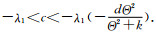
第1节给出了一些预备知识;第2节利用比较原理,Leray-Schauder度理论及不动点指标可加性,给出了定理1的证明;第3节利用数值模拟的方法研究了系统(2)一维方程的平衡态解,验证了理论结果的正确性.
1 预备知识在本节中, 我们主要给出一些本文后面证明所需要的基本定理.
定理2[11, 15] 设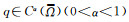
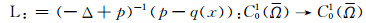
|
r(L)表示算子L的谱半径.则下列结论成立:
(ⅰ) λ1(q)>0⇔r(L)<1;
(ⅱ) λ1(q)<0⇔r(L)>1;
(ⅲ) λ1(q)=0⇔r(L)=1.
从定理2, 可以推导出以下定理,参见文献[3, 11, 12, 14].
定理3 设q(x)∈L∞(Ω), φ≥0, φ≠0, x∈Ω且φ=0, 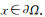
(ⅰ)若0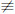
(ⅱ)若0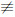
(ⅲ)若-Δφ+q(x)φ≡0, 则λ1(q)=0.
考虑下面单个方程:
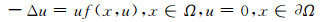
|
(5) |
其中Ω是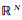
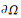
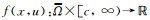
(H1) f(x, u)是关于x的Cα函数, 其中0<α<1;
(H2) f(x, u)为C′函数, 且关于u, fu(x, u)<0,(x, u)∈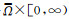
(H3) 对于某个正常数C, 在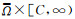
(ⅰ)系统(5)的非负解u(x)满足u(x)≤C, 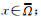
(ⅱ)若λ1(-f(x, 0))≥0, 则系统(5)没有正解,且平凡解u(x)=0是全局渐近稳定的;
(ⅲ)若λ1(-f(x, 0))<0, 则系统(5)具有惟一的全局渐近稳定的正解,且u(x)=0的平凡解是不稳定的.
为了利用不动点指标理论, 下面给出不动点指标理论基本框架, 这也是后续证明的基本理论.
设E为Banach空间, 且为闭凸集.若对所有γ≥0, λW⊂W, 且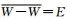
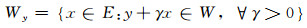
|
且
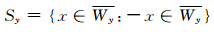
|
故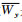
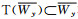
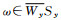
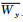
(ⅰ)若L在Wy上具有性质α, 则indexW(A, y)=0;
(ⅱ)若L在Wy上不具有性质α, 则
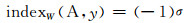
|
其中σ是L在W的所有大于1的特征值的代数重数之和.
注1 由定理4(ⅱ)可知, 当c>-λ1时, 系统(2)没有形如(0, v)的半平凡解.
2 系统(2)共存态解本节主要利用第1节中的理论成果证明定理1.首先给出一个关于系统(2)具有共存解的必要条件.
定理6 若系统(2)具有共存态解, 则a>λ1且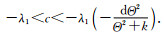
证 假设(u, v)是系统(2)的一个共存态解.那么a>λ1和0<u<Θ.由于(u, v)满足:
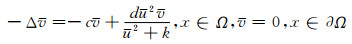
|
所以,
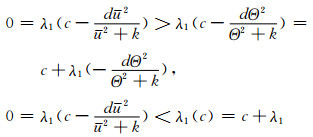
|
故a>λ1且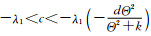
为了证明a>λ1和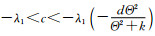
定理7 假定c>-λ1, 那么系统(2)的任何共存态解(u, v)都有如下先验边界:
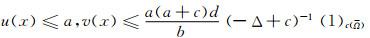
|
(6) |
证 由系统(2)第一个方程可知, u满足:
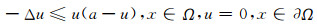
|
(7) |
因此, 根据极大值原理知, u(x)≤a.通过直接计算, 由系统(2)的两个方程可知:
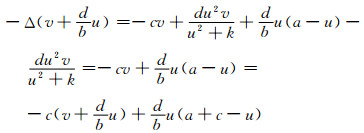
|
因此,
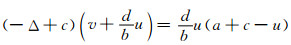
|
故a+c>0,否则,若a+c≤0,则可导出
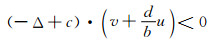
|
从而
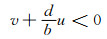
|
所以矛盾.因此, a+c>0是系统(2)存在共存态解的必要条件.在这种情况下
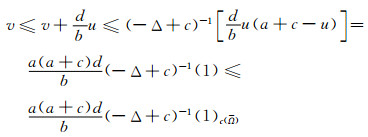
|
定理7得证.
下面引入以下符号
E=C01(Ω)×C01(Ω)
W=K×K, K={φ∈C01(Ω):φ≥0, x∈Ω}
D={(u, v)∈W:u≤a+1, v≤Q+1}
其中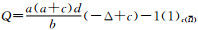
由定理7可知, 系统(2)的非负解必在D中.取充分大正常数p,p>max{a+bQ/k, c}, 使得u(a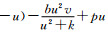
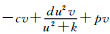
定义一个正紧算子A:E→E,具体如下:
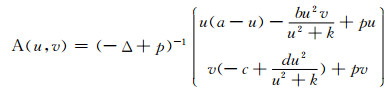
|
注2 由椭圆方程的正则性[12]知, 系统(2)等价于(u, v)=A(u, v).故, 证明A在D中具有正不动点等价于证明系统(2)具有正解.若A在D中有一个正不动点(u, v), 则(u, v)是系统(2)的一个共存态解.
引理1 假设a>λ1和c>-λ1, 那么
(ⅰ) degW(I-A, D)=1;
(ⅱ) indexW(A0, (0, 0))=0.
证 (ⅰ)显然, A在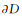
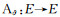
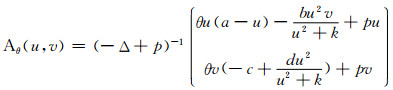
|
则A1=A.对于每个θ, Aθ的一个不动点是下面问题的解:

|
(8) |
类似于定理7的证明可知, 对每个θ∈[0, 1], Aθ的不动点(u, v)满足u≤a和v≤Q.因此, Aθ在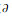
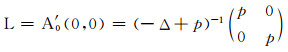
|
假设L(ξ1, ξ2)=(ξ1, ξ2), 对某些(ξ1, ξ2)∈W(0, 0)=K×K,显然(ξ1, ξ2)=(0, 0).因此I-L在W(0, 0)上是可逆的.由于λ1>0, 根据定理2知,r(L)<1.故L没有性质α.从而由定理5可得:
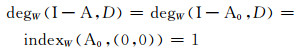
|
(ⅱ)注意到A(0, 0)=(0, 0).令
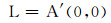
|
则
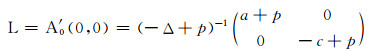
|
假设对某个(ξ1, ξ2)∈W(0, 0), L(ξ1, ξ2)=(ξ1, ξ2), 则

|
(9) |
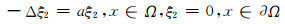
|
(10) |
若ξ1≠0, 则a=λ1,这与λ1<a矛盾.同样, 由于c>λ1, 易知ξ2=0.故(ξ1, ξ2)=(0, 0).因此, I-L在W(0, 0)中是可逆的.由于a>λ1, 根据定理2可知, ra[(-Δ+p)-1(a+p)]>1是算子(-Δ+p)-1(a+p)的主要特征值,且对应的特征函数φa>0.由于S(0, 0)={(0, 0)}, 故(φa, 0)∈W(0, 0)S(0, 0).令ta=ra-1, 则(I-taL)(φa, 0)=(0, 0)∈S(0, 0).故L具有性质α.因此, 由定理5知, indexW(A0, (0, 0))=0.定理得证.
接下来, 我们计算系统(2)的半平凡解的指标数.
引理2 假设a>λ1和c>-λ1, 那么下面结论成立:
(ⅰ)若indexW(A0, (0, 0))=0, 则indexW(A0, (Θ, 0))=0;
(ⅱ)若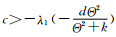
证 由定理6和引理1直接得到(ⅱ)的结果.事实上, 由定理6知, 如果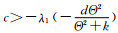
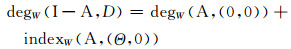
|
(11) |
由引理1知,
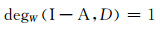
|
且

|
则由(11)知,
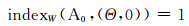
|
接下来, 给出(ⅰ)的证明.观察A(Θ, 0)=(Θ, 0).令L=A′(Θ, 0), 则
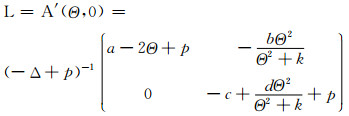
|
假设对某个(ξ1, ξ2)∈W(Θ, 0)=C01×K有L(ξ1, ξ2)=(ξ1, ξ2), 则
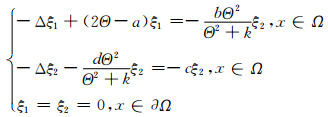
|
(12) |
考虑到ξ2∈K, 由定理3知, 当ξ2≠0时, 由(12)式的第二个方程得出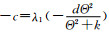
这与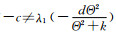
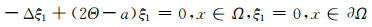
|
(13) |
由定理3知,若ξ1≠0, 则λ1(2Θ-a)=0.而另一方面, λ1(2Θ-a)>λ1(Θ-a)=0, 故两者矛盾.因此(ξ1, ξ2)=(0, 0), I-L在W(Θ, 0)上是可逆的.
下证L在W(Θ, 0)具有性质α.事实上, 令
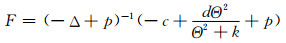
|
(14) |
由于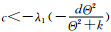
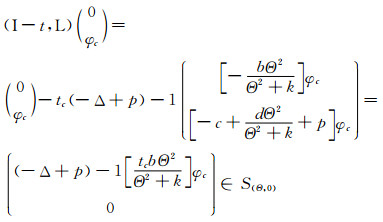
|
于是证明了L具有性质α.
故indexW(A0, (Θ, 0))=0.引理2得证.
下面证明a>λ1和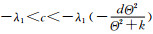
定理8 若a>λ1且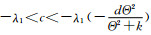
证 如果a>λ1和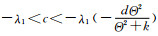
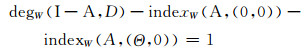
|
因此由Kronecker存在定理[14],系统(2)至少有一个共存态解.定理8的证明完成.
注3 由定理6和定理8显然可证明,系统(2)具有共存态解充分必要条件是a>λ1和-λ1<c<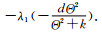
本节运用MATLAB软件对系统(2)进行数值模拟.为了研究方便,不失一般性,我们给出平衡态方程的正解在一维情况下的数值解图像(图 1~图 6).通过数值计算得到的图像可直观验证前面定理的正确性.系统(2)对应的一维系统形式如下:
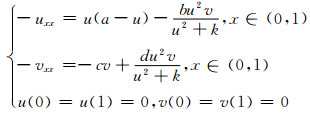
|
(15) |
|
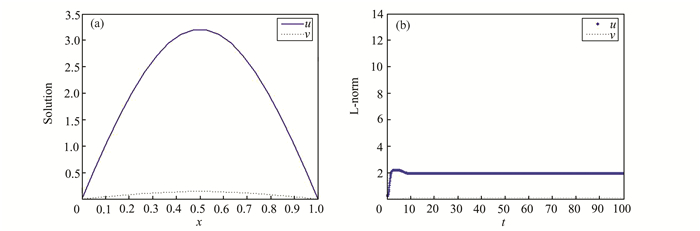
| 图 1 当a=13>λ1时u, v的共存解(a)及长时变化趋势(b) Figure 1 Coexistence solution (a) and long time change trend of (b) u, v when a=13 > λ1 |
|
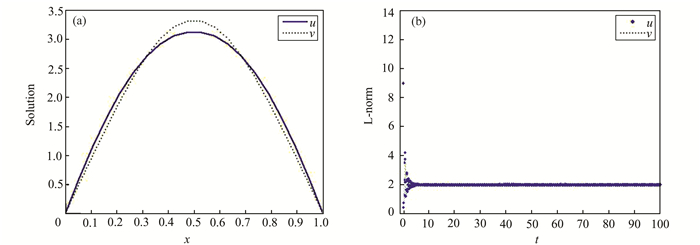
| 图 2 当a=21>λ1时,u, v的共存解(a)及长时变化趋势(b) Figure 2 Coexistence solution (a) and long time change trend (b) of u, v when a=21 > λ1 |
|
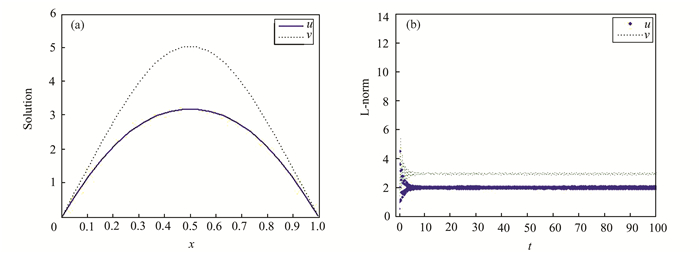
| 图 3 当a=25>λ1时,u, v的共存解(a)及长时变化趋势(b) Figure 3 Coexistence solution (a) and long time change trend (b) of u, v when a=25 > λ1 |
|
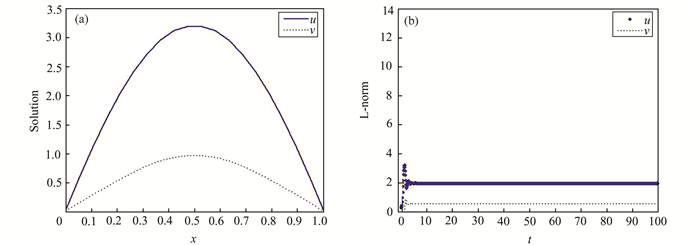
| 图 4 当a=20, c=-15时,u, v的共存解(a)及长时变化趋势(b) Figure 4 Coexistence solution (a) and long time change trend (b) of u, v when a=20, c=-15 |
|
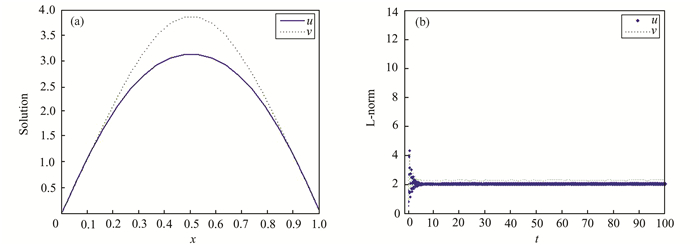
| 图 5 当a=20, c=-10时,u, v的共存解(a)及长时变化趋势(b) Figure 5 Coexistence solution (a) and long time change trend (b) of u, v when a=20, c=-10 |
|
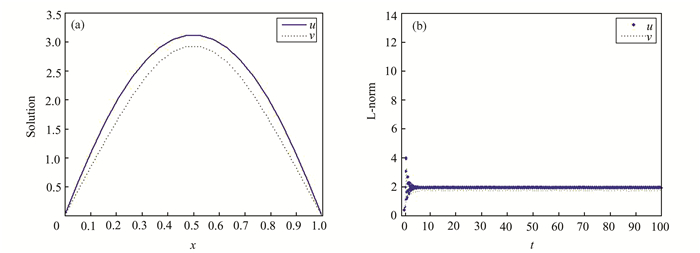
| 图 6 当a=20, c=-3时,u, v的共存解(a)及长时变化趋势(b) Figure 6 Coexistence solution (a) and long time change trend (b) of u, v when a=20, c=-3 |
系统(15)平衡态方程中的参数满足充分必要条件:a>λ1和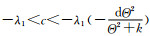
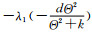
利用比较原理、Leray Schauder度理论及不动点指标可加性,研究了一类具有Holling-Ⅲ反应项的捕食模型中参数不同取值对系统在Dirichlet边界条件下平衡态解的共存解存在性的影响,得到了具有Holling-Ⅲ反应项的捕食模型共存解存在的充分必要条件,如定理1,定理6与定理7.利用数值模拟的方法研究了一维方程的平衡态解的变化规律,验证了理论结果的正确性,也实现了该模型解的可视化.研究表明该捕食系统中参数满足一定的条件时,两种生物种群可以共同生存的生态现象.
| [1] |
CHEN J P. The qualitative analysis of two species predator-prey model with Holling type Ⅲ functional response[J]. Applied Mathematics & Mechanics, 1986, 7(1): 77-86. |
| [2] |
HOLLING C S. The functional response of predators to prey density and its role in mimicry and populations regulation[J]. Memoirs of the Entomological Society of Canada, 1965, 97(45): 53-60. |
| [3] |
CANO-CASANOVA S, LÓPEZ-GÓMEZ J. Properties of the principle eigenvalues of a general class if non-classical mixed boundary value problems[J]. Journal Differential Equations, 2002, 178(1): 123-211. DOI:10.1006/jdeq.2000.4003 |
| [4] |
CASAL A, EELBECK J C, LÓPEZ-GÓMEZ J. Existence and uniqueness of coexistence states for a predator-prey model with diffusion[J]. Differential Integral Equations, 1994, 7(2): 411-439. |
| [5] |
DU Y H, LOU Y. Some uniqueness and exact multiplicity results for a predator-prey model[J]. Transactions of the American Mathematical Societ, 1997, 349(6): 2443-2475. DOI:10.1090/S0002-9947-97-01842-4 |
| [6] |
DU Y H, LOU Y. S-shaped global bifurcation curve and Hopf bifurcation of positive solution to a predator-prey model[J]. J Differential Equations, 1998, 144(2): 390-440. DOI:10.1006/jdeq.1997.3394 |
| [7] |
冯孝周, 李艳玲, 聂华. 具有功能反应项的捕食模型解的定性分析[J]. 西北师范大学学报(自然科学版), 2011, 47(5): 9-16. FENG X Z, LI Y L, NIE H. Qualitative analysis of solutions of predator-prey model with functional responses[J]. Journal of Northwest Normal University (Natural Science), 2011, 47(5): 9-16 (Ch). DOI:10.3969/j.issn.1001-988X.2011.05.003 |
| [8] |
冯孝周, 吴建华. 具有饱和与竞争项的捕食系统的全局分歧及稳定性[J]. 系统科学与数学, 2010, 30(7): 979-989. FENG X Z, WU J H. Global bifurcation and stability for prey-predator model with predator saturation and competition[J]. Journal of Systems Science and Mathematical Sciences, 2010, 30(7): 979-989 (Ch). |
| [9] |
冯孝周, 李畅通. 具有Holling Type Ⅲ反应项的捕食系统正平衡态解的存在性[J]. 安徽大学学报(自然科学版), 2013, 37(3): 16-21. FENG X Z, LI C T. Existence of positive steady-state for prey-predator system with Holling Type Ⅲ response[J]. Journal of Anhui University (Natural Science Edition), 2013, 37(3): 16-21 (Ch). DOI:10.3969/j.issn.1000-2162.2013.03.003 |
| [10] |
CRANDALLM G, RABINOWITZ P H. Bifurcation from simple eigenvalues[J]. Journal of Functional Analysis, 1971, 8: 321-340. DOI:10.1016/0022-1236(71)90015-2 |
| [11] |
DANCER E N. On positive solutions of some pairs of differential equations[J]. Transactions of the American Mathematical Society, 1984, 284(2): 729-743. DOI:10.1090/S0002-9947-1984-0743741-4 |
| [12] |
DANCER E N. On positive solutions of some pairs of differential equations, Ⅱ[J]. Journal of Differential Equations, 1985, 60(2): 236-258. DOI:10.1016/0022-0396(85)90115-9 |
| [13] |
DANCER E N. On the indices of fixed points of mapping in cones and applications[J]. Journal of Mathematical Analysis and Applications, 1983, 91: 131-151. DOI:10.1016/0022-247X(83)90098-7 |
| [14] |
PAO C V. Nonlinear Parabolic and Elliptic Equations[M]. New York: Plenum Press, 1992.
|
| [15] |
LI L. Coexistence theorems of steady states for predator-prey interacting systems[J]. Transactions of the American Mathematical Society, 1988, 305(1): 143-166. DOI:10.1090/S0002-9947-1988-0920151-1 |
| [16] |
RUAN W H, FENG W. On the fixed point index and multiple steady states of reaction-diffusion system[J]. Differential Integral Equations, 1995, 8(2): 371-391. |
| [17] |
SMOLLER J. Shock Waves and Reaction-Diffusion Equations[M]. New York: Spring-Verlag, 1994.
|
 2018, Vol. 64
2018, Vol. 64