文章信息
- 陈林, 张帅伟, 钟卫东, 杨晓元, 刘文超
- CHEN Lin, ZHANG Shuaiwei, ZHONG Weidong, YANG Xiaoyuan, LIU Wenchao
- 基于粒子群优化算法的多S盒相关性能量分析方法
- Correlation Power Analysis Method for Multiple S-Boxes Based on Particle Swarm Optimization Algorithm
- 武汉大学学报(理学版), 2019, 65(3): 309-315
- Journal of Wuhan University(Natural Science Edition), 2019, 65(3): 309-315
- http://dx.doi.org/10.14188/j.1671-8836.2019.03.012
-
文章历史
- 收稿日期:2018-08-19

相关性能量分析(correlation power analysis,CPA)是Brier等[1]于2004年提出的一种密码攻击方法。该攻击技术利用统计学中的皮尔逊相关系数[2]进行密钥恢复,达到攻击的效果。相比于其他密钥恢复技术,该技术具有更强的攻击性和解密效率。在相关性能量分析攻击中,攻击者通过猜测不同密钥,进行虚拟能量消耗的计算,模拟密码设备在真实情况下的工作状态。2004年,ÖRS等[3]阐述了针对AES硬件实现能量分析攻击的可行性,展示了如何建立一个可靠的测量装置和如何改进相关系数。2007年,Mulder等[4]在椭圆曲线密码系统的硬件实现上进行了能量分析攻击。2017年,Lo等[5]提出通过对设备使用汉明权值,建立相关的能量分析方法,对密码算法进行破译。
数据加密标准(data encryption standard,DES)[6]是一种使用密钥加密的分组密码算法,在非密级政府通信中使用,适用范围广且其加密安全性较高。S盒是DES算法中惟一的非线性部分,具有混淆的作用,它的密码强度决定了整个密码算法的安全强度。传统侧信道能量分析[7]方法研究方面,Kocher等[8]对能量曲线的区分仅仅依靠于单个S盒的单比特信息;Mayer-sommer [9]通过使用单个S盒的多比特信息,对能量曲线进行分类;Brier等[1]对单个S盒的所有比特信息加以利用,进一步增强了能量曲线的分类效果。传统能量分析方法每次仅利用单个S盒的比特信息进行分析对比,造成能量曲线与密钥的相关性较差,从而影响破解密钥的效率和准确率。因此,若要增强能量曲线与密钥之间的联系,可将多个S盒视为一个整体,对其进行并行攻击。但在DES算法中,密钥是56位,这就意味着如果想用暴力破解的方式对密钥进行一次性恢复,需要进行256次尝试,计算次数为指数级别[10]。此时所猜测的密钥数量过大,计算困难,因此需要对其猜测密钥能力进行强化。
为提高能量曲线与DES密钥之间的相关性,解决传统能量分析方法在攻击多个S盒对应轮密钥过程中,猜测密钥数目成指数增长所造成的计算量过大的问题,考虑到粒子群优化(particle swarm optimization,PSO)算法极高的计算效率和较强的可靠性,本文提出了一种基于PSO算法的多S盒相关性能量分析方法。以DES算法加密的数据作为实验对象,进行参数优化和性能分析实验,验证本文方法的高效性和可靠性。
1 预备知识 1.1 CPA攻击原理CPA攻击是一种极为有效的密码攻击方法[11]。该方法对密码设备实施攻击时,攻击者不需要对该设备进行详细的研究,通常只需知道设备加密时应用的是何种加密算法即可。密码设备在执行加解密算法过程中所产生的功耗变化形成了实测能量曲线。CPA攻击通过分析能量曲线与密钥之间的相关性,进行密码恢复工作。
CPA的攻击策略包含3个步骤:
第1步:选择M组不同的明文,在设备上进行加解密运算,记录每一组明文采用真实密钥进行加解密时产生的实测能量曲线。
第2步:将S盒输入作为攻击点,利用相应的汉明距离或者汉明重量模型进行CPA攻击,并根据猜测密钥,计算S盒输入的中间值确定中间值矩阵[12]。
第3步:将中间值映射为猜测密钥的能量消耗矩阵。计算由猜测密钥所产生的能量曲线与采用真实密钥获得的实测能量曲线的皮尔逊相关系数[13],计算方法如下:
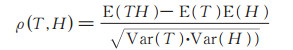
|
(1) |
其中,H是通过猜测密钥计算得出的能量曲线集合;T是实测能量曲线集合;Var()表示能量曲线集合的协方差;E()表示能量曲线集合的数学期望。当该线性相关系数达到最大时,可以认为此时对应的猜测密钥即为正确密钥。
1.2 PSO算法PSO算法是1995年由Kennedy和Eberhart等[14]提出的一种进化算法。它通过对鸟群飞行觅食的模拟,快速计算得到问题的最优解[15]。该算法概念简明、实现方便、收敛快、参数设置少、易编程。类比鸟群寻找食物的过程,种群中的个体会遵循以下原则:
1)避免与相邻的个体发生碰撞、冲突;
2)尽量与自己周围的个体在速度上保持协调一致;
3)尽量试图向自己所认为的群体最优位置靠近。
在PSO算法中,设搜索空间为D维,总粒子数即种群规模为n [16]。id代表d维空间第i个粒子,1 ≤ i ≤ n,1 ≤ d ≤ D。第i个粒子的位置表示为向量Xi=(xi1,xi2,…,xiD);第i个粒子“飞行”历史中的过去最优位置为Pi=(pi1,pi2,…,piD),其中第g个粒子的过去最优位置Pg为所有Pi中的最优位置;第i个粒子的位置变化率(速度)为向量Vi,Vi=(vi1,vi2,…,viD)。每个粒子的位置按(2)式和(3)式进行变化:
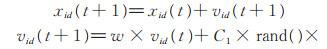
|
(2) |
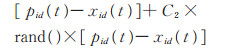
|
(3) |
其中,t为当前进化代数;C1、C2为加速因子;rand()为[0, 1]之间的随机数;w为惯性权重,w较大时,PSO算法适用于对解空间进行大范围搜索,w较小时,PSO算法适用于对解空间进行小范围搜索。第d维的位置变化范围为[−Xmaxd,Xmaxd],速度变化范围为[−Vmaxd,Vmaxd],迭代中若位置和速度超过边界范围则取边界值。粒子群初始位置和速度随机产生,然后按(2)式和(3)式进行迭代,直至找到最优解。本文利用改进的粒子群算法[17]将全体粒子群(global)分成若干个有部分粒子重叠的相邻子群,通过邻域决定群体历史最优位置,邻域决定了单个粒子如何与其他粒子相连。邻域随迭代次数的增大线性变大,最终邻域扩散到整个粒子群,每个粒子根据子群内过去最优位置Pg调整位置。
2 本文方法本文提出的基于PSO算法的多S盒相关性能量分析方法是在分析多S盒汉明重量的基础上,将CPA攻击中恢复密钥的过程转化为PSO算法中鸟群搜寻食物的过程,将密钥空间转换为进行迭代个体所处的位置,并选择合适的适用度函数比较个体所处位置的优劣情况,确定最优解。该方法可通过以下5个步骤进行构建。
步骤1:对轮密钥进行编码。将DES中48位轮密钥分成8份,轮密钥以二进制字符串进行编码,每份有6位密钥。表 1显示了一个48位轮密钥进行编码的过程,rki为第i个S盒的轮密钥输入,Key为S盒的十进制密钥,Particle为密钥的二进制编码。
| 编码方式 | rk1 | rk2 | rk3 | rk4 | rk5 | rk6 | rk7 | rk8 |
| Key(十进制) | 8 | 16 | 7 | 34 | 58 | 30 | 19 | 1 |
| Particle(二进制) | 001000 | 010000 | 000111 | 100010 | 111010 | 011110 | 010011 | 000001 |
步骤2:种群初始化。在对轮密钥进行编码后,需要对粒子群进行初始化,确定初始种群的大小和规模。初始种群中的每个个体相当于随机猜测的密钥。在初始化种群的过程中,如果初始种群数量过小,可能会影响最终解的效果,出现局部最优解;如果种群数量过多,会降低种群的汇集速度及求解速度。因此种群参数的选择需要针对具体问题,进行具体设定。表 2是数量为m的种群个体初始化结果,即猜测密钥的二进制编码。
| 序号 | K1 | K2 | K3 | K4 | K5 | K6 | K7 | K8 |
| 1 | 101100 | 010111 | 011100 | 101010 | 010101 | 111100 | 010001 | 101100 |
| 2 | 011110 | 010110 | 101100 | 010111 | 000111 | 001101 | 101100 | 110010 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| m | 111010 | 010111 | 010001 | 111110 | 001010 | 011001 | 101001 | 001111 |
步骤3:确定适用度函数,通过计算数据经S盒加密后产生的汉明重量与能量曲线之间的适用度值,对粒子群中的个体位置进行优化。适用度函数F作为对粒子群中个体优先级大小评判的惟一标准,担当挑选优秀个体的职能。在每一次种群迭代中,通过比较F的大小,选择最接近正确密钥的随机密钥,并使这些猜测密钥向正确密钥方向移动。本文采用下式计算适用度函数:
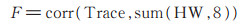
|
(4) |
其中,corr为相关系数,HW为S盒输入输出值的汉明重量,sum (HW,8)为8个S盒输入输出值的汉明重量值的和,Trace为实测能量曲线。F越大代表适用度越高,说明当前猜测密钥能够更好地向代表正确密钥的位置移动。通过计算多个S盒的汉明重量,建立基于PSO算法的多S盒CPA方法。通过求解每次迭代过程中群体中每一个个体位置的适用度值,对其进行排序,然后选择适用度值高的个体位置,利用粒子速度和邻域定义,更新历史最佳位置(pbest)和全局最佳位置(gbest)。
步骤4:调整PSO算法的移动速度和搜索范围。在每一次迭代过程中,都需要对粒子速度和邻域进行调整,以便更好地找出合理的个体。粒子的速度更新主要由3部分组成:前次迭代中自身的速度wvt;自我认知部分C1r1 (pbestid - xidt - 1),表示粒子本身的选择,即粒子i当前位置与自己历史最佳位置之间的距离;社会经验部分C2r2 (gbestid - xidt - 1),表示粒子间的信息共享与合作,即粒子i当前位置与群体历史最佳位置之间的距离。
每次迭代过程中,在对群体进行速度和邻域调整之后,每个粒子会在区域最佳解和全域最佳解影响下,同惯性向量相互作用产生一个运动向量,让粒子向最优位置移动,进一步求解正确密钥。
步骤5:对比相关系数大小[18]。经过一定的迭代次数后,对相关系数进行观察,若相关系数达到最高且不再明显变化,则得出最佳位置,也就恢复了正确的密钥。否则,返回步骤3,再次对个体进行优化。
本文方法中,个体适用度的大小决定个体位置的优先级别。因此,对每一次迭代过程中个体适用度大小排序,以此进行位置变换,代表部分正确S盒密钥的个体会一步步向代表正确密钥的最优位置靠近。在运动过程中,PSO算法将确保在多S盒能量分析过程中代表猜测密钥的整体向正确密钥的方向进行移动。随着粒子运动的速度和邻域的变化,代表密钥的位置编码逐步优化为全局最优解。因此,可以从庞大的密钥空间中,求解得到正确密钥。
3 数值模拟实验针对本文方法,进行参数优化实验以及性能分析实验,以选择最优参数并验证本文方法的高效性和可靠性。实验仪器包括MSO5204型示波器(泰克公司,带宽1 GHz,采样率5 GSa/s),自主设计的能量采集电路板和能量采集分析系统。
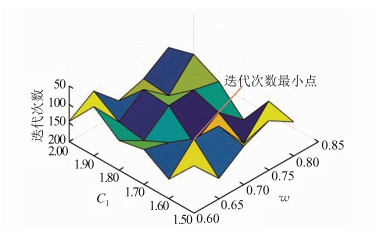
3.1 参数优化为使本文方法调整至最优水平,需对PSO算法的相关参数进行优化。在PSO算法中,惯性权重w与加速因子C1、C2对算法性能影响最大。参照文献[19],本文将种群个数设置为90,对w、C1、C2这3个参数进行了测试,如图 1所示。由于C1=C2,故图 1中未标注C2。
|
| 图 1 惯性权重与加速因子对迭代次数的影响 Fig. 1 The influence of inertia weight and acceleration factor on iteration times |
由图 1可知,在初始种群固定的前提下,w和C1、C2的变化都会影响恢复密钥所需的迭代次数。在种群个数为90的前提下,当w为0.65,C1、C2均为1.60时,种群迭代次数最少,只需迭代95次即可恢复全部密钥,使PSO算法达到最佳优化效果,进而提高本文方法的计算效率。
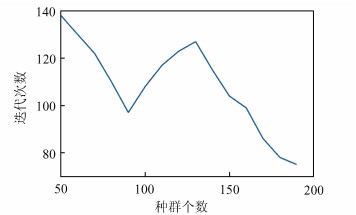
在确定参数w、C1、C2后,通过实验选取最优种群个数。图 2为惯性权重w为0.65,加速因子C1、C2均为1.60时,不同种群数量情况下,恢复正确密钥所需迭代次数。在种群数量取每种数值时,均重复进行10次密钥恢复实验,然后求取不同种群数量情况下恢复密钥所需的平均迭代次数。
|
| 图 2 迭代次数随种群个数的变化 Fig. 2 The iteration times varies with population size |
如图 2所示,随着种群数量的增多,种群迭代次数先减少后增加再减少。这是因为在不同种群个数情况下,种群结构自身的特性对粒子群中信息的传递及种群的多样性变化具有较大影响[20]。通过实验可以得出,种群个数为90时,本文方法恢复正确密钥所需种群数量和迭代次数都相对较少。因此,本文设置种群个数为90,w为0.65,C1、C2均为1.60。
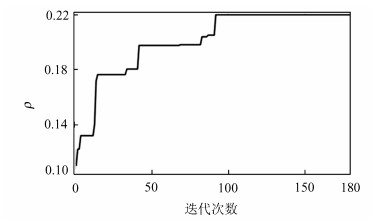
图 3所示为利用本文方法进行能量分析时,求解过程即密钥恢复过程中,相关系数随迭代次数的变化。由图 3可知,随着迭代次数的增加,相关系数ρ不断变化,直至相关系数保持平稳达到最高值0.22,即恢复出正确密钥。
|
| 图 3 相关系数随迭代次数的变化 Fig. 3 Variation of correlation coefficient with iteration times |
为验证本文方法的可靠性和高效性,对FPGA(field-programmable gate array)中的DES算法进行攻击。
3.2.1 相关性分析首先对不同轮密钥对应的能量曲线与实测能量曲线进行模拟实验。根据正确轮密钥与其他猜测错误的轮密钥的区分结果,验证相比于传统能量分析方法利用本文方法破解DES算法密钥时,能量曲线与密钥的相关性优势。
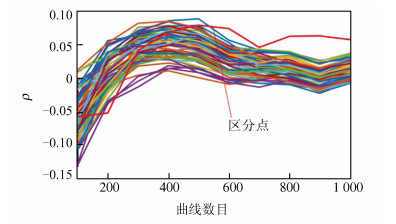
图 4和图 5是通过传统能量分析方法和本文方法,分别利用DES的1个S盒和8个S盒对汉明重量进行分析,获得相关系数与能量曲线数量之间的关系。其中,曲线数目为采集到的实测能量曲线条数。从图 4和图 5可以看出,随着能量曲线数目的不断增加,代表正确密钥的相关系数曲线会与代表错误密钥的相关系数曲线逐渐分离。
|
| 图 4 利用传统能量分析方法对1个S盒进行攻击的结果 Fig. 4 Results of attacking an S⁃box using traditional power analysis method |
|
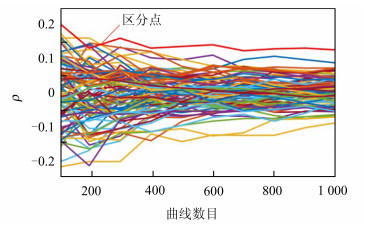
| 图 5 利用本文方法对8个S盒进行攻击的结果 Fig. 5 Results of attacking 8 S⁃boxes using the proposed method |
通过图 4可以得出,对1个S盒进行传统能量分析时,密钥为6个比特位,一共有64种情况,因此产生64条相关系数曲线。分离出的红色曲线代表该S盒正确轮密钥的相关系数曲线,其余63种曲线为该S盒非正确轮密钥的相关系数曲线。通过实验可以得出,在能量曲线数目大约为550条这一区分点(正确轮密钥的相关系数曲线与其余轮密钥的相关系数曲线分离且后续不再重合)处,正确轮密钥与错误轮密钥区分完毕。
在图 5中,因为是以8个S盒作为一个整体进行攻击,此时轮密钥为48比特位,一共有248种可能,所产生的猜测密钥数量过多,因此图 5只显示了代表正确轮密钥的相关系数曲线(红色曲线)以及部分错误的猜测轮密钥的相关系数曲线。通过实验中的区分点可知本文方法在利用8个S盒对DES算法进行能量分析攻击时,仅仅需要250条能量曲线便可区分正确密钥与错误密钥。
通过上述对比实验可知,相比于传统能量分析方法,利用本文方法破解DES算法密钥时,能量曲线与密钥的相关性优势更大,对能量信息的利用率更高。与传统相关性能量分析方法相比,本文方法将正确密钥与错误密钥区分所需的实测能量曲线数量大幅减少,对能量信息的利用率提高约55%。
采用本文方法对DES算法进行能量分析攻击既避免了其余S盒能量信息变为噪声,又可以增强能量信息与密钥之间的联系。这就表明,通过对多个S盒的并行攻击,可显著提高信噪比[21],更好地利用每一个S盒的能量泄露信息。
3.2.2 正确率分析为对比在获取实测能量曲线数目有限的条件下,传统能量分析方法与本文方法的正确率,本节主要进行了以下对比实验:利用传统能量分析方法对DES算法的S盒逐个进行能量分析,恢复DES密钥;利用本文提出的基于PSO算法的多S盒相关性能量分析方法同时对DES算法的8个S盒进行能量分析,恢复DES密钥。正确率=相同位数/密钥总位数× 100%,其中相同位数是指通过攻击获取的密钥从第一位至最后一位与正确密钥对应位置匹配正确的总数量。本小节实验,DES正确密钥不参与计算和优化过程,仅作为猜测密钥正确率计算的标准。为使本文提出的基于PSO算法的相关性能量分析方法达到最佳优化效果,基于上述参数选择实验,设置PSO算法的惯性权重w为0.65,加速因子C1、C2均为1.60,种群个数为90。
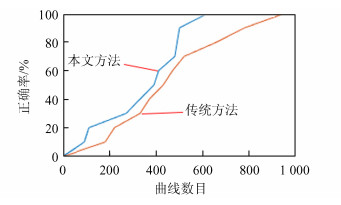
图 6所示为采用DES算法对数据进行加密后,利用本文方法以及传统方法进行相关性能量分析时,恢复DES密钥所需的实测能量曲线数量与正确率之间的关系。从图 6中可以看出,当实测能量曲线为600条时,本文方法的密钥恢复正确率已经达到100%,而传统能量分析方法正确率仅为70%,正确率提高约30%。
|
| 图 6 正确率随能量曲线数量的变化 Fig. 6 Accuracy varies with the number of power curves |
由此可得出,与传统能量分析方法相比,本文提出的能量分析方法,利用PSO算法实现方便、收敛快、参数设置少,同时对多个S盒进行能量分析攻击,增强了信噪比,能快速求解正确密钥。在恢复密钥的过程中,本文提出的能量分析方法能够更好地利用能量信息,增强能量曲线与密钥之间的相关性,从而在曲线数目有限(600条)的情况下,大幅度提高密钥恢复正确率。
4 结语本文提出一种基于PSO算法的多S盒相关性能量分析方法。该方法将CPA攻击中恢复密钥的过程转化为PSO算法中鸟群搜寻食物的过程,利用PSO算法搜索速度快、效率高的特点,解决同时对多个S盒进行能量分析所带来的密钥空间急剧扩增的问题,极大地提高了密钥恢复速度和正确率。与传统的相关性能量分析方法相比,本文提出的能量分析方法使得密钥与实测能量曲线的相关性更为紧密。通过本文方法与传统的单S盒能量分析方法的对比实验可知,在DES算法密钥恢复过程中,本文方法有效增强了信号的信噪比,对能量信息的利用率提高约55%;在实测能量曲线数目有限(600条)的情况下,密钥恢复正确率提高约30%。验证了本文提出的能量分析方法能够更高效准确地恢复出正确密钥,完成对DES算法的攻击。
| [1] |
BRIER E, CLAVIER C, OLIVIER F.Correlation power analysis with a leakage model[C]//International Workshop on Cryptographic Hardware and Embedded Systems-CHES 2004(LNCS 3165).Heidelberg: Springer, 2004: 16-29.DOI: 10.1007/978-3-540-28632-5_2.
|
| [2] |
李宏彬, 赫光中, 果秋婷. 基于皮尔逊相关系数的有机质谱相似性检索方法[J]. 化学分析计量, 2015, 24(3): 3337. LI H B, HE G Z, GUO Q T. Organic mass spectrometry similarity retrieval method based on Pearson correlation coefficient[J]. Chemical Analysis and Meterage, 2015, 24(3): 33-37. DOI:10.3969/j.issn.1008-6145.2015.03.009 (Ch). |
| [3] |
ÖRS S B, GÜRKAYNAK F, OSWALD E, et al.Poweranalysis attack on an ASIC AES implementation[C]// International Conference on Information Technology: Coding and Computing.New York: IEEE Press, 2004: 546552.DOI: 10.1109/ITCC.2004.1286711.
|
| [4] |
MULDER E D, ÖRS S B, PRENEEL B, et al. Differential power and electromagnetic attacks on a FPGA implementation of elliptic curve cryptosystems[J]. Computers & Electrical Engineering, 2007, 33(5-6): 367-382. DOI:10.1016/j.compeleceng.2007.05.009 |
| [5] |
LO O, BUCHANAN W J, CARSON D. Power analysis attacks on the AES-128 S-box using differential power analysis (DPA) and correlation power analysis (CPA)[J]. Journal of Cyber Security Technology, 2017, 1(2): 88-107. DOI:10.1080/23742917.2016.1231523 |
| [6] |
徐洪波, 李颖华. DES加密算法在保护文件传输中数据安全的应用[J]. 信息网络安全, 2009, 9(6): 24-26. XU H B, LI Y H. Application of DES encryption algorithms in protecting data security in file transfer[J]. Information Network Security, 2009, 9(6): 24-26. DOI:10.3969/j.issn.1671-1122.2009.06.009 (Ch). |
| [7] |
MIZUNO H, IWAI K, TANAKA H, et al.A correlation power analysis countermeasure for enocoro-128 v2 using random switching logic[C]//International Conference on Networking & Computing.New York: IEEE Press, 2012: 326-328.DOI: 10.1109/ICNC.2012.62.
|
| [8] |
KOCHER P C, JAFFE J, JUN B.Differential power analysis[C]// CRYPTO ' 99 Proceedings of the 19th Annual International Cryptology Conference on Advances in Cryptology.Heidelberg: Springer, 1999: 388-397.
|
| [9] |
MAYER-SOMMER R.Smartly analyzing the simplicity and the power of simple power analysis on smartcards [C]// Cryptographic Hardware and Embedded Systems. Heidelberg: Springer, 2000: 78-92.DOI: 10.1007/3-54044499-8_6.
|
| [10] |
邱伟星, 肖克芝, 倪昉, 等. 一种DES密钥延长方法[J]. 计算机工程, 2011, 37(5): 167-168+171. QIU W X, XIAO K Z, NI F, et al. A DES key extension method[J]. Computer Engineering, 2011, 37(5): 167-168+ 171. DOI:10.3969/j.issn.1000-3428.2011.05.056 (Ch). |
| [11] |
ZHANG H L, ZHOU Y B, FENG D G. Theoretical and practical aspects of multiple samples correlation power analysis[J]. Security & Communication Networks, 2016, 9(18): 56-60. DOI:10.1002/sec.1686 |
| [12] |
张琪, 吴震, 王敏, 等. SM4算法S盒输入的相关性能量攻击的研究[J]. 计算机应用与软件, 2015, 32(12): 290-293+333. ZHANG Q, WU Z, WANG M, et al. SM4 algorithm Sbox input correlation energy attack research[J]. Computer Applications and Software, 2015, 32(12): 290-293+333. DOI:10.3969/j.issn.1000-386x.2015.12.068 (Ch). |
| [13] |
樊海锋, 徐金甫, 严迎建. 针对AES密码芯片的CPA攻击[J]. 计算机工程与设计, 2010, 31(1): 37-40. FAN H F, XU J F, YAN Y J. CPA attacks against AES cryptographic chips[J]. Computer Engineering and Design, 2010, 31(1): 37-40. (Ch). |
| [14] |
KENNEDY J, EBERHART R C.Particle swarm optimization[C]// Proceedings of IEEE International Conference on Neural Networks.New York: IEEE, 1995: 1942-1948.DOI: 10.1109/ICNN.1995.488968.
|
| [15] |
VIMAL K P, AMIT K S, RAMANPREET S, et al. A modified algorithm of particle swarm optimization for form error evaluation[J]. Technisches Messen, 2017, 84(4): 272-292. DOI:10.1515/teme-2016-0040 |
| [16] |
梅东晖, 李红灵. 基于多目标混合粒子群算法的虚拟机负载均衡研究[J]. 信息网络安全, 2018, 18(2): 78-83. MEI D H, LI H L. Load balancing of virtual machines based on multi-objective hybrid particle swarm optimization[J]. Information Network Security, 2018, 18(2): 78-83. DOI:10.3969/j.issn.1671-1122.2018.02.011 (Ch). |
| [17] |
KENNEDY J, EBERHART R C.A discrete binary version of the particle swarm algorithm[C]//IEEE International Conference on Systems, Man, and Cybernetics. New York: IEEE, 1997: 4104-4108.DOI: 10.1109/ICSMC.1997.637339.
|
| [18] |
LOPEZ-MARTINEZ C, FABREGAS X. Polarimetric SAR speckle noise model[J]. IEEE Transactions on Geoscience and Remote Sensing, 2003, 41(10): 2232-2242. DOI:10.1109/TGRS.2003.815240 |
| [19] |
王东风, 孟丽. 粒子群优化算法的性能分析和参数选择[J]. 自动化学报, 2016, 42(10): 1552-1561. WANG D F, MENG L. Performance analysis and parameter selection of particle swarm optimization algorithm[J]. Journal of Automation, 2016, 42(10): 1552-1561. (Ch). |
| [20] |
段晓东, 高红霞, 张学东, 等. 粒子群算法种群结构与种群多样性的关系研究[J]. 计算机科学, 2007, 34(11): 164-166+177. DUAN X D, GAO H X, ZHANG X D, et al. Study on the relationship between population structure and population diversity of particle swarm optimization[J]. Computer Science, 2007, 34(11): 164-166+177. DOI:10.3969/j.issn.1002-137X.2007.11.044 (Ch). |
| [21] |
PAN Q, ZHANG L, DAI G Z, et al. Two denoising methods by wavelet transform[J]. IEEE Transactions on Signal Processing, 1999, 47(12): 3401-3406. DOI:10.1109/78.806084 |
 2019, Vol. 65
2019, Vol. 65





