文章信息
- 焦儒旺, 曾三友, 李晰, 李长河
- JIAO Ruwang, ZENG Sanyou, LI Xi, LI Changhe
- 基于学习的动态多目标方法求解约束优化问题
- Constrained Optimization by Solving Equivalent Dynamic Constrained Multi-Objective Based on Learning
- 武汉大学学报(理学版), 2017, 63(2): 177-183
- Journal of Wuhan University(Natural Science Edition), 2017, 63(2): 177-183
- http://dx.doi.org/10.14188/j.1671-8836.2017.02.012
-
文章历史
- 收稿日期:2016-05-16

2. 中国地质大学 机械与电子信息学院,湖北 武汉430074;
3. 河北地质大学 信息工程学院,河北 石家庄 050031
2. School of Mechanical Engineering and Electronic Information, China University of Geosciences, Wuhan 430074, Hubei, China;
3. School of Information Engineering, Hebei GEO University, Shijiazhuang 050031, Hebei, China
约束优化问题 (constrained optimization problem, COP) 是广泛存在于现实世界的问题,由于约束条件限制,可行域变得复杂多样,这给问题求解带来一定的困难,因此它也是优化领域较难处理的问题.常用的约束处理技术有惩罚函数法[1, 2],可行解优先法[3, 4]、ε约束法[5]、随机排序法[6, 7]和多目标法[8~13]等.
近些年来,利用多目标方法求解约束优化问题取得了不小进展. Coello等[8]将每个约束作为一个目标,然后采用Pareto排序来定义个体的等级,使可行个体的等级总是优于不可行个体,接着依照个体等级构造适应度函数,以确保可行个体更容易进入下一代种群. Venkatraman等[9]提出了两阶段的策略求解约束优化问题,第一阶段以个体的约束违反值来进行排序,其目标是至少找到一个可行解;第二阶段将约束优化问题转化为两目标优化问题,并以Pareto占优关系来进行排序. Wang等[10]提出了结合多目标技术的混合约束优化演化算法,该算法采用全局搜索和局部搜索结合的形式,在全局搜索和局部搜索中均以个体之间的Pareto支配关系进行优劣比较和选择. Wang等[11]采用多目标技术在求解约束优化问题时,将种群分别分为可行种群、不可行种群和半可行种群,并根据不同种群来采取不同的比较准则选择个体. Gao等[12]提出了双种群的协同演化算法,借助多目标思想,将种群分为两个子种群:可行种群和不可行种群,可行种群负责优化目标,不可行种群负责优化违约值.閤大海等[13]提出一种基于适应排序的分组选择方法,将种群分为精英组与普通组,对精英组个体使用随机选择方式,对普通组个体使用适应排序选择方式,以此加快多目标与差分进化结合算法的收敛速度.
以上提到的工作都是将约束优化问题转化为不等价的多目标优化问题,然后采用结合Pareto占优、Pareto排序以及其他多目标技术的演化算法来求解约束优化问题,而不是求解多目标优化问题.针对上述问题,本文提出将约束优化问题转化为等价的动态约束多目标优化问题 (dynamic constrained multi-objective optimization problem,DCMOP),然后采用动态约束多目标演化算法来求解动态约束多目标优化问题,并引进基于学习的机制自适应的控制差分演化算法的杂交概率和缩放因子,以提高算法效率.
1 约束优化问题转化为约束多目标优化问题定义1 约束优化问题 (COP):一个约束优化问题通常包括n个决策变量,1个目标函数,m个约束条件,目标函数和约束条件是决策变量的函数.约束优化问题可描述为:
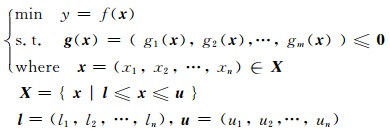
|
(1) |
x为决策向量,X表示决策空间,l和u分别为下界和上界,g(x)≤0是约束条件,0代表约束边界.
当包含等式约束h(x)=0时, 将其转化为不等式约束|h(x)|-ε≤0. ε是一个接近于0的正实数,本文ε=0.000 1.
个体x违反第i个约束条件程度定义为
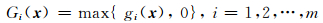
|
(2) |
一个个体标准化后所有违反约束程度的平均值定义为该个体的违约目标.
定义2 违约目标
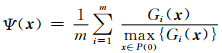
|
(3) |
本文首先构造一种同约束优化问题等价的多目标优化问题,违约目标Ψ(x) 作为另一目标加入到约束优化问题中.约束多目标优化问题 (constrained multi-objective optimization problems,CMOPs) 模型如下:
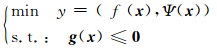
|
(4) |
在多目标优化中,评价两个个体关系常使用Pareto占优准则[14].但是Pareto占优准则只适合在可行域中使用,在整个搜索空间中则使用约束Pareto占优:
定义3 约束Pareto占优
1) 如果两个都是可行个体,采用Pareto占优准则;
2) 如果一个是可行个体,另一个是不可行个体,则可行个体胜出;
3) 如果两个都是不可行个体,则约束违反程度小的胜出.
(4) 式中约束多目标优化问题的Pareto最优解集是单个解的集合.单个解其实是 (1) 式中约束优化问题的最优解.这样,约束多目标优化问题就等价于约束优化问题 (CMOP≅COP).然后可采用约束多目标演化算法求解约束多目标优化问题,这也意味着解决了约束优化问题.然而,这样做并没有丢弃约束条件,约束多目标演化算法同样面临着约束处理难题.
2 约束多目标优化问题转化为动态约束多目标优化问题约束多目标演化算法同约束演化算法面临着相同的约束处理难题.然而,一旦种群是可行的,约束多目标演化算法就可成功应用于求解约束多目标优化问题.这是因为无约束多目标演化算法可以有效求解无约束多目标优化问题,当种群是可行种群时,约束多目标演化算法就等价于无约束多目标演化算法.对于约束多目标演化算法,关键是确保种群是可行的.
通常来讲,不可能在整个搜索过程中始终保持种群是可行的.因此,保持种群中的大多数个体是可行个体,约束多目标演化算法性能就不会显著下降.本文构造一种动态控制可行域的方法.其主要思想是在搜索过程的起始,构造一个较宽的初始约束边界e,这样就可产生一个较大的可行域.接着,逐渐收缩适当小的边界来确保种群中大多数个体仍是可行个体.动态约束多目标优化问题表示如下:
定义4 动态约束多目标优化问题 (DCMOP)
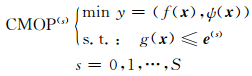
|
(5) |
其中,
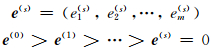
|
S为最终环境状态,s为环境状态,e(s)为s状态下动态约束边界.当一个解满足g(x)≤e时,称该解为e可行解,否则为e不可行解.
(1) 式中的初始约束优化问题与 (5) 式中的动态约束多目标优化问题的关系如下:CMOP(s-1)的可行集包含CMOP(s)(s=1, 2,…, S) 的可行集.所有CMOP(s)(s=1,2,…,S) 的Pareto最优集包含初始约束优化问题的最优解.在最终环境状态s=S时,e(s)=0,ψ(x)=0.这样 (5) 式的动态约束多目标优化问题在最终环境状态s=S下 (CMOP(S)) 可以简化为
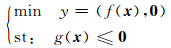
|
(6) |
最终环境状态CMOP(S)的Pareto最优集是一个解的集合,也就是 (1) 式中初始约束优化问题的最优解.这样,可以称动态约束优化问题等价于约束优化问题 (DCMOP≅COP).
动态约束边界模型如下:
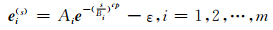
|
(7) |
ε是给定的接近于0的正实数,p控制环境状态变化的程度 (本文ε=0.000 1,p=2). Ai和Bi是常量.
为了使初始种群满足e可行,在环境状态s=0时,将最大的违反约束值作为ei(0)初始约束边界,即ei(0)=max{Gi(x)}.当达到最终状态s=S时,约束边界收缩到0,即ei(S)=0.根据e(0)和e(S)可求得Ai和Bi:
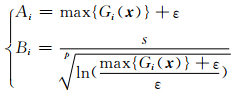
|
(8) |
本文将经典的多目标演化算法NSGA-Ⅱ[15]加入到动态约束多目标演化算法框架中作为实例化的动态约束多目标演化算法,将NSGA-Ⅱ的杂交和变异算子换成差分演化算法[16]的杂交和变异, 记为DCNSGAII-DE.
针对无约束的问题,该算法采用基于Pareto占优准则进行个体间比较.对于动态约束多目标优化问题,采用e约束Pareto占优替代Pareto占优.
定义5 e约束Pareto占优
1) 如果两个都是e可行个体,则采用Pareto占优;
2) 如果一个是e可行个体,另一个是e不可行个体,则e可行个体胜出;
3) 如果两个都是e不可行个体,则违约目标更小的个体胜出.
3.2 基于学习的参数自适应本文将差分演化算法 (differential evolution,DE)[16]作为搜索引擎.在差分演化算法中,参数的设置对算法性能有很大的影响.为了选择最合适的缩放因子和交叉概率,结合文献[5]和[17],提出了基于学习的自适应参数设置策略.差分演化算法的两个参数比例因子和交叉概率由成功的操作动态决定.成功的操作定义为:父代种群与新产生的子代种群合并,进行非劣排序后,子代种群个体作为下一代父代种群中的个体则视为成功的操作.缩放因子F和杂交概率Cr分别由其平均值uF和uCr产生,并赋予一定的扰动ω,rand (-0.5, 0.5) 是-0.5至0.5之间的随机数,这样做可避免F和Cr不稳定, 发生太大变动.
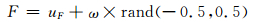
|
(9) |
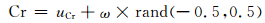
|
(10) |
uF和uCr由成功操作的次数SN、成功操作的缩放因子总和SF、成功操作的交叉概率总和SC来更新:
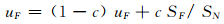
|
(11) |
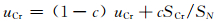
|
(12) |
c是属于[0, 1]之间的常量 (建议值c=0.1).随着种群不断演化,好的个体的F和Cr随着学习过程不断趋向最优值,从而增强算法的局部搜索能力.同时,为了避免算法陷入局部最优,每隔T代,将平均值uF和uCr重新初始化为F0和Cr0.
引入学习机制的DCNSGAII-DE算法称为DCNSGAII-DE-BL.
3.3 DCNSGAII-DE-BL算法框架步骤1 初始化
a. 初始化父代种群;
b. 动态约束边界e=e(0),环境状态s=0,演化代数t=0;
c. uF=F0, uCr=Cr0,
SF=SCr=SN=0.
步骤2
a. t=t + 1;
b. 若种群e可行,则收缩边界e=e(s+1),更新e可行率,将精英个体作为下一代初始种群,s=s+1.
步骤3
a. 由 (9) 式产生缩放因子F,并将F截断至[0.4, 0.9];
b. 由 (10) 式产生交叉概率Cr,并将Cr截断至[0, 1];
c. 由差分算法的杂交和变异算子产生子代种群,并利用非劣排序选择下一代父代种群.
步骤4
a. 若子代个体进入下一代父代种群的个数为SN,则由 (11) 和 (12) 式更新uF和uCr.
步骤5
a. 若t% T=0,则uF=F0, uCr=Cr0;
b. 若达到最终环境状态
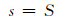
|
或达到最大异常停机代数
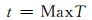
|
则算法终止并输出最优解;否则转至步骤2.
算法步骤1中父代种群的初始化、步骤3中子代种群的产生可以参见DE[16],步骤3中下一代父代种群的选择可以参见NSGA-Ⅱ[15].
4 实验与分析为测试DCNSGAII-DE-BL的有效性,采用cec2010[18]国际标准测试函数,同4个较为先进的约束处理算法:CMODE[11]、εADE[5]、MS-ECHT-DE[19]和AIS[20]进行数值实验比较. CMODE在多目标处理方面与本文类似,εADE在约束边界动态化方面与本方法类似.而AIS和MS-ECHT-DE为最近提出的比较有效的典型算法.
本文算法参数设置为:种群大小为100;每个问题运行25次.初始化比例因子F0=0.5,交叉概率Cr0=0.9.每隔T代重新初始化F0和Cr0,T=100.最大环境状态S=6 000.对于每一环境状态的变化,算法将演化至少1代来实现种群e可行.所以每个问题每运行一次,算法将会演化至少6 000代 (约600 000次函数评估).若一个问题没有可行解或算法找不到可行解,设置最大异常停机代数MaxT=10 000.
4.1 性能评价指标为了评价比较不同算法性能的显著性,将Wilcoxon符号秩和检验和Friedman检验结果作为算法的性能评价指标.
Wilcoxon符号秩和检验:该方法是在成对观测数据的符号检验基础上发展起来的,比传统的单独用正负号的检验更加有效,是非参数的统计测试方法.R+与R-分别代表正秩总和与负秩总和.将第一个算法对比第二个算法,如果R+值大于R-值则代表第一个算法优于第二个算法.
Friedman检验:Friedman检验是对若干个算法进行秩排序,一个算法的秩值越小则表明该算法越优.
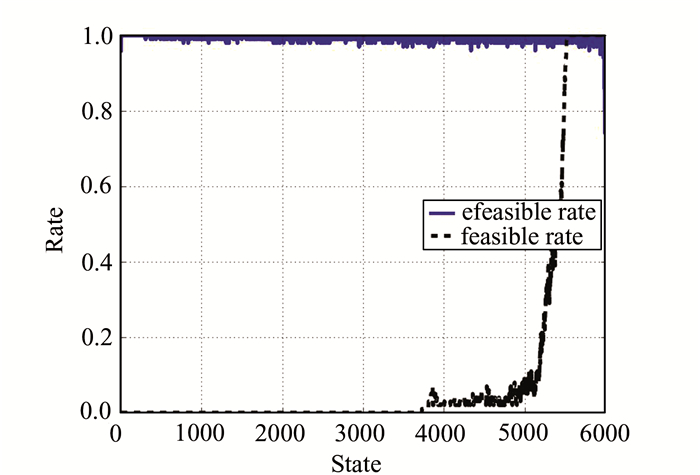
4.2 可行率与e可行率的变化图 1展示了对于测试问题C04,DCNSGAII-DE-BL随着环境状态的改变,可行率与e可行率的变化.从图 1中可以明显看出,在整个搜索过程中,DCNSGAII-DE-BL的可行率较低,但是e可行率始终接近于100%,这也验证了DCNSGAII-DE-BL可以始终在可行域中搜索,如同无约束多目标演化算法求解无约束多目标优化问题.
|
| 图 1 C04的可行率与e可行率变化 Figure 1 Feasible rates and e-feasible rates of C04 |
由于篇幅限制,表 1只给出了30维的cec2010标准测试函数的实验结果以及Friedman检验结果.通过表 1中的Friedman检验,可以看出DCNSGAII-DE-BL的秩序优于DCNSGAII-DE,同样在表 2中,DCNSGAII-DE-BL对比DCNSGAII-DE的R+值大于R-值,说明学习机制很好地增强了算法的寻优能力,提高了算法效率.
| Problem | Criterion | εADE | CMODE | MS-ECHT-DE | AIS | DCNSGAII-DE | DCNSGAII-DE-BL |
| C01 | Mean | -8.192E-01 | -8.208E-01 | -6.982E-01 | -8.201E-01 | -8.194E-01 | -8.206E-01 |
| Std | 2.35E-03 | 1.48E-03 | 7.37E-02 | 3.25E-04 | 9.64E-03 | 2.20E-03 | |
| C02 | Mean | 1.67E+00 | 8.70E-01 | -1.61E+00 | -2.21E+00 | -2.27E+00 | -1.35E+00 |
| Std | 3.95E-01 | 9.20E-01 | 4.91E-01 | 2.84E-03 | 9.89E-03 | 8.90E-01 | |
| C03 | Mean | 2.87E+01 | 2.41E+01 | 3.48E+01 | 6.68E+01 | 6.49E+01 | 2.87E+01 |
| Std | 4.61E-07 | 1.07E+01 | 3.06E+01 | 4.26E+02 | 6.46E+01 | 4.53E-07 | |
| C04 | Mean | 2.29E-02 | 8.38E-04 | 8.01E-02 | 1.98E-03 | 7.39E-06 | 1.42E-04 |
| Std | 1.40E-02 | 4.09E-04 | 2.76E-01 | 1.61E-03 | 3.12E-07 | 1.30E-04 | |
| C05 | Mean | 3.94E+02 | 2.93E+02 | -1.46E+02 | -4.36E+02 | -4.19E+02 | -4.84E+02 |
| Std | 1.09E+02 | 1.94E+02 | 4.87E+01 | 2.51E+01 | 2.25E+02 | 1.86E-09 | |
| C06 | Mean | 4.19E+02 | -4.90E+02 | -1.34E+02 | -4.54E+02 | -5.23E+02 | -5.09E+02 |
| Std | 8.29E+01 | 2.99E+01 | 5.53E+01 | 4.79E+01 | 9.91E+00 | 2.21E+01 | |
| C07 | Mean | 2.47E+01 | 2.37E-04 | 6.38E-01 | 1.07E+00 | 3.79E+01 | 9.83E+00 |
| Std | 2.89E+01 | 2.99E+01 | 1.49E+00 | 1.61E+00 | 2.82E+01 | 1.28E+00 | |
| C08 | Mean | 1.04E+01 | 4.17E-01 | 1.89E+02 | 1.65E+00 | 4.42E+01 | 2.58E+01 |
| Std | 1.06E+01 | 2.93E-01 | 4.27E+02 | 6.41E-01 | 3.12E+01 | 3.21E+01 | |
| C09 | Mean | 4.68E+12 | 1.52E+13 | 5.80E+02 | 1.57E+00 | 5.04E+03 | 1.22E+12 |
| Std | 1.00E+13 | 8.84E+12 | 1.87E+03 | 1.96E+00 | 1.38E+04 | 2.25E+12 | |
| C10 | Mean | 1.43E+13 | 3.87E+13 | 1.96E+03 | 1.78E+01 | 5.79E+12 | 4.15E+11 |
| Std | 1.56E+13 | 1.04E+13 | 4.29E+03 | 1.88E+01 | 1.04E+13 | 1.27E+12 | |
| C11 | Mean | -4.03E-03 | 1.33E-02 | 6.47E-03 | -1.58E-04 | -6.15E-03 | -3.71E-03 |
| Std | 8.51E-02 | 8.74E-03 | 9.34E-03 | 4.67E-05 | 2.14E-02 | 2.20E-03 | |
| C12 | Mean | 1.81E+00 | 1.32E+01 | -1.99E-01 | 4.29E-06 | -1.51E+01 | -3.84E+00 |
| Std | 1.74E+02 | 6.68E+01 | 4.02E-04 | 4.52E-04 | 8.44E+01 | 1.01E+02 | |
| C13 | Mean | -6.75E+01 | -3.83E+01 | -6.03E+01 | -6.62E+01 | -6.84E+01 | -6.40E+01 |
| Std | 3.24E-01 | 2.28E+00 | 2.36E+00 | 2.27E-01 | 2.04E-08 | 1.78E+00 | |
| C14 | Mean | 4.37E+00 | 8.96E+00 | 1.99E+03 | 8.68E-07 | 2.93E+01 | 9.47E+00 |
| Std | 4.73E+00 | 2.55E+00 | 7.03E+03 | 3.14E-07 | 2.88E+01 | 3.92E+00 | |
| C15 | Mean | 2.23E+13 | 1.62E+13 | 5.37E+01 | 3.41E+01 | 3.27E+01 | 2.16E+01 |
| Std | 2.07E+13 | 7.39E+12 | 1.19E+02 | 3.82E+01 | 2.86E+01 | 9.84E-08 | |
| C16 | Mean | 5.92E-01 | 6.63E-02 | 7.68E-03 | 8.21E-02 | 4.13E-03 | 1.77E-04 |
| Std | 3.98E-01 | 2.90E-02 | 2.57E-02 | 1.12E-01 | 1.06E-02 | 1.63E-02 | |
| C17 | Mean | 5.00E+02 | 4.09E+02 | 4.40E-01 | 3.61E+00 | 4.98E-01 | 2.86E-01 |
| Std | 8.27E+02 | 3.35E+02 | 3.28E-01 | 2.54E+00 | 5.31E-01 | 2.30E-01 | |
| C18 | Mean | 1.83E+06 | 7.87E+03 | 1.00E-01 | 4.02E+01 | 1.60E-01 | 0.00E+00 |
| Std | 2.02E+06 | 3.42E+03 | 4.50E-01 | 1.80E+01 | 3.47E-01 | 0.00E+00 | |
| Friedman-Test | 4.64(6) | 4.00(5) | 3.89(4) | 3.11(3) | 2.83(2) | 2.53(1) | |
| 注:括号内的数字为6个算法Friedman-Test由小到大的排序 | |||||||
| Algorithm | R+ | R- | |
| DCNSGAII-DE-BL vs | εADE | 129 | 24 |
| DCNSGAII-DE-BL vs | CMODE | 139 | 32 |
| DCNSGAII-DE-BL vs | MS-ECHT-DE | 118 | 53 |
| DCNSGAII-DE-BL vs | AIS | 94 | 77 |
| DCNSGAII-DE-BL vs | DCNSGAII-DE | 114 | 57 |
与4个当前较为先进的约束处理算法的实验结果对比,可以看出DCNSGAII-DE-BL在几种算法中的Friedman秩序最小,排名第一. 表 2中Wilc-oxon符号秩和检验,DCNSGAII-DE-BL对比εADE、CMODE、MS-ECHT-DE和AIS,其R+都大于R-.因此可以得出结论,所提出的算法在约束处理方面优于所比较的算法.
4.5 计算复杂度分析考虑DCNSGAII-DE-BL在一代中的计算复杂度,则算法的时间复杂度为O(N2),其中N为种群大小.而对于计算违约目标的额外复杂度,则为O(mN),m为约束的个数.因此,DCNSGAII-DE-BL总的时间复杂度为O(mN+N2).这也与大多数约束处理算法在计算复杂度上近似,说明所提出的算法在保持高效率的同时并没有增加额外计算量.
5 结论本文提出了求解约束优化问题的动态约束方法.首先将约束优化问题转化为等价的动态约束多目标优化问题,然后采用动态约束多目标演化算法求解动态约束多目标优化问题,也即解决了约束优化问题.动态技术通过逐渐收缩的动态约束边界实现,约束边界的慢慢收敛,使得种群搜索一直在可行区域中进行.因此在解决约束多目标优化问题上,该算法的性能同多目标演化算法求解无约束多目标优化问题一样有效.同时,引进基于学习的机制自适应调整差分演化的两个参数来提高算法的局部搜索能力.同4个较为先进算法的实验结果比较,表明DCNSGAII-DE-BL在处理约束优化问题上效果更优.
| [1] | XIAO J, XU J, SHAO Z, et al. A genetic algorithm for solving multi-constrained function optimization problems based on KS function[C]//IEEE Congress on Evolutionary Computation (CEC'2007). Washington D C: IEEE, 2007: 4497-4501. http://ieeexplore.ieee.org/abstract/document/4425060/ |
| [2] | DEB K, DATTA R. A fast and accurate solution of constrained optimization problems using a hybrid bi-objective and penalty function approach[C]//IEEE Congress on Evolutionary Computation(CEC'2010). Washington D C: IEEE, 2010: 1-8. http://ieeexplore.ieee.org/abstract/document/5586543/ |
| [3] | HE Q, WANG L. A hybrid particle swarm optimization with a feasibility-based rule for constrained optimization[J]. Applied Mathematics and Computation, 2007, 186(2) : 1407–1422. DOI:10.1016/j.amc.2006.07.134 |
| [4] | RODRIGUES M D, DE LIMA B S, GUIMARAES S, et al. Balanced ranking method for constrained optimization problems using evolutionary algorithms[J]. Information Sciences, 2016, 327(12) : 71–90. |
| [5] | TAKAHAMA T, SAKAI S. Efficient constrained optimization by the ε constrained adaptive differential evolution[C]//IEEE Congress on Evolutionary Computation(CEC'2010). Washington D C: IEEE, 2010: 2052-2059. http://ieeexplore.ieee.org/abstract/document/5586545/ |
| [6] | RUNARSSON T P, YAO X. Stochastic ranking for constrained evolutionary optimization[J]. IEEE Transactions on Evolutionary Computation, 2000, 4(3) : 284–294. DOI:10.1109/4235.873238 |
| [7] | MALLIPEDDI R, SUGANTHAN P N, QU B Y, et al. Diversity enhanced adaptive evolutionary programming for solving single objective constrained problems[C]//IEEE Congress on Evolutionary Computation (CEC'2009). Washington D C: IEEE, 2009: 2106-2113. http://ieeexplore.ieee.org/abstract/document/4983201/ |
| [8] | COELLO C A. Constraint-handling using an evolutionary multiobjective optimization technique[J]. Civil Engineering Systems, 2000, 17(4) : 319–346. DOI:10.1080/02630250008970288 |
| [9] | VENKATRAMAN S, YEN G G. A generic framework for constrained optimization using genetic algorithms[J]. IEEE Transactions on Evolutionary Computation, 2005, 9(4) : 424–435. DOI:10.1109/TEVC.2005.846817 |
| [10] | WANG Y, CAI Z X, GUO G R, et al. Multiobjective optimization and hybrid evolutionary algorithm to solve constrained optimization problems[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 2007, 37(3) : 560–575. DOI:10.1109/TSMCB.2006.886164 |
| [11] | WANG Y, CAI Z X. Combining multiobjective optimization with differential evolution to solve constrained optimization problems[J]. IEEE Transactions on Evolutionary Computation, 2012, 16(1) : 117–134. DOI:10.1109/TEVC.2010.2093582 |
| [12] | GAO W F, YEN G G, LIU S Y. A dual-population differential evolution with coevolution for constrained optimization[J]. IEEE Transactions on Cybernetics, 2015, 45(5) : 1108–1121. |
| [13] | 閤大海, 李元香, 刘伟. 求解约束优化问题的加速CMODE算法[J]. 华中科技大学学报 (自然科学版), 2016, 44(4) : 48–52. XIA D H, LI Y X, LIU W. Accelerated CMODE algorithm for solving constrained optimization problems[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2016, 44(4) : 48–52(Ch). |
| [14] | DEB K. Multi-objective Optimization Using Evolutionary Algorithms[M]. Chichester: John Wiley & Sons, 2001. |
| [15] | DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2) : 182–197. DOI:10.1109/4235.996017 |
| [16] | STORN R, PRICE K V. Differential evolution-A simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4) : 341–359. DOI:10.1023/A:1008202821328 |
| [17] | ZHANG J, SANDERSON A C. JADE: Adaptive differential evolution with optional external archive[J]. IEEE Transactions on Evolutionary Computation, 2009, 13(5) : 945–958. DOI:10.1109/TEVC.2009.2014613 |
| [18] | MALLIPEDDI R, SUGANTHAN P N. Problem Definitions And Evaluation Criteria for the CEC 2010 Competition on Constrained Real-Parameter Optimization[R]. Singapore: Nanyang Technological University, 2010. http://www3.ntu.edu.sg/home/EPNSugan/index_files/CEC10-Const/CEC10-Const.htm |
| [19] | WEI W, WANG J, TAO M. Constrained differential evolution with multiobjective sorting mutation operators for constrained optimization[J]. Applied Soft Computing, 2015, 33(C) : 207–222. |
| [20] | ZHANG W, YEN G G, HE Z, et al. Constrained optimization via artificial immune system[J]. IEEE Transactions on Systems, Man, and Cybernetics, 2014, 44(2) : 185–198. |
 2017, Vol. 63
2017, Vol. 63





