文章信息
- 李焕哲 , 吴志健 , 郭肇禄 . 2016
- LI Huanzhe, WU Zhijian, GUO Zhaolu . 2016
- 两阶段多峰优化算法求解纳什均衡
- Two-Stage Multimodal Optimization Algorithm for Solving Nash Equilibrium
- 武汉大学学报(理学版), 2016, 62(5): 444-450
- Journal of Wuhan University(Natural Science Edition), 2016, 62(5): 444-450
- http://dx.doi.org/10.14188/j.1671-8836.2016.05.007
-
文章历史
- 收稿日期:2015-09-07

2. 河北地质大学 信息工程学院,河北 石家庄 050031 ;
3. 江西理工大学 理学院, 江西 赣州 341000
2. School of Information Engineering, Hebei GEO University, Shijiazhuang 050031, Hebei, China ;
3. School of Science, Jiangxi University of Science and Technology, Ganzhou 341000, Jiangxi, China
纳什均衡(Nash Equilibrium)又被称为非合作博弈均衡,是博弈论中的一个重要研究内容.纳什均衡是一种策略组合,它要求每个参与人的策略对其他参与人的策略均是最优反应.纳什均衡理论被广泛应用于社会、经济、军事、政治、科研等领域.纳什在文献[1, 2]中给出了纳什均衡的定义并证明了纳什均衡解的存在性.实际上,一个博弈可能存在多个纳什均衡,而在有限策略博弈中纳什均衡的计算是一项具有挑战性的任务.求解纳什均衡的算法主要有Lemke-Howson 算法[3]、单纯型剖分算法[4]、全局牛顿算法[5]、同伦算法[6]、函数极小化算法[7]和多矩阵迭代算法[8]等,这些算法大多计算过程复杂难于实现.为了简化求解过程,学者们提出了一系列的算法来解决此问题.例如,禁忌搜索算法[9]、退火回归神经网络极值搜索算法[10]和演化算法[11~13]等.其中演化算法[14, 15]因具有自适应、自组织、内在并行性、易实现等特点,它的寻优过程仅依赖于问题适应度信息,不需要待解问题连续可微,所以演化算法经常用于求解常规优化算法难于处理的非线性的、约束的问题.纳什均衡问题可被转换为带约束的最优化问题,通过演化算法的自动寻优进行问题求解,这为求解纳什均衡问题开辟了一条新途径.
演化算法中多数算法着重研究求解单个纳什均衡点,若想找出博弈中的全部纳什均衡点则需要运行算法多次.本文提出了一种用于求解多峰优化问题的两阶段多峰优化算法,并将该算法应用于求解纳什均衡问题,旨在通过一次算法的运行,尽可能多的求出纳什均衡点,这有利于在多个纳什均衡点中找出精化解.第一阶段运行的NCDE算法[16]是带有邻域变异策略的排挤差分演化算法,实验向量的生成被限制在一定数量的相似个体(个体的相似性通过个体之间的欧氏距离来衡量)之间,这有助于更好的保持种群的多样性.NCDE算法有两个主要优点:其一,它具有很强的全局搜索能力以及良好的保持种群多样性的能力.其二,NCDE是一种隐式小生境技术,在保持种群多样性上对种群的大小要求不高,在极端情况下,甚至每个个体都可以独立保持一个小生境.但是,有利必有失,NCDE这种低选择压力机制无疑会降低它的收敛速度.第二阶段运行的CMA_ES [17]算法克服了一些传统演化算法相关的典型问题,例如在严重缩放和高度不可分问题上的低性能、对大种群的内在需求以及种群的早熟问题.然而,在其本质上,CMA-ES算法是一种局部搜索算法,它具有很强的局部搜索能力,但在全局搜索能力上相对较弱.我们提出的算法,简称为NBC-CMA,正好弥补了NCDE收敛速度慢及CMA-ES全局搜索能力弱的缺点.NBC-CMA算法和另外6个较新的多峰优化算法进行了比较,在比较实验中我们提出的算法表现出了更优的性能.
1 问题描述一个包含有限策略的N人非合作博弈,可形式化定义为Γ=((N,Si,ui),i=1,…,N)[10, 13].其中,N代表参与人的数量;对每个参与人i∈{1,…,N},Si={si1,si2,…,sim}代表参与人i有m个可用策略;S=S1×S2×…×SN代表博弈中所有可能的策略组合的集合.对每个参与人i∈{1,…,N},ui:S→R代表支付函数.
令pij(j=1,…,mi)表示参与人i选择策略sij的概率,其中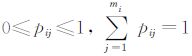
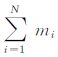
在纯策略的情况下,参与人i的收益ui为纯策略组合s=(s1,…,sN)的函数,表示为ui(s)=ui(s1,…sN).在混合策略纳什均衡中,参与人关心的是给定的纯策略收益组成的期望收益,参与人i的期望支付函数ui(p)有定义域${{\mathbb{R}}^{m}}$,可由公式(1)计算得到.

|
(1) |
其中,实值函数pi:Si→$\mathbb{R}$足公式(2).
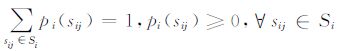
|
(2) |
定义1 一个混合策略组合p*=(p1*,p2*,…,pN*) ∈P是一个纳什均衡,如果对于所有的i∈{1,…,N}满足ui(pi,p-i*)≤ui(p*),pi∈Pi.p-i*为除i之外的所有其他参与人的混合策略组合[12, 13].
寻找一个博弈的纳什均衡问题可被构造为寻找一个实值函数的全部全局最小值问题.这个函数可由x,z,g三个子函数构造,三个子函数定义域均为P.
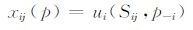
|
(3) |
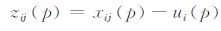
|
(4) |
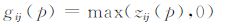
|
(5) |
其中,Sij表示参与人i采取一个纯策略,即选取策略sij的概率pij为1.v:P→$\mathbb{R}$由公式(6)定义.函数v是连续可微的且对于所有的p∈P有v(p)≥0,一个策略组合p*是一个纳什均衡当且仅当v(p*)=0.
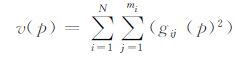
|
(6) |
NBC-CMS算法在第一阶段充分发挥NCDE算法全局搜索能力强的特点进行粗粒度搜索,尽可能多的定位最优解的大概位置.在NCDE演化一定代数之后,调用 DMC (Detect Multimodal Clustering)[18]聚类方法,以识别当前种群中形成的聚类.然后,根据识别出的聚类数量,相同数量的CMA-ES实例被生成,每一个CMA-ES实例对应一个不同的聚类.每个聚类的最好搜索点作为CMA-ES的起始搜索点,每个聚类与其最近相邻聚类欧氏距离的六分之一作为CMA-ES的起始搜索步长,每个实例被独立的运行直到终止条件满足.为了充分地利用剩余的评价次数,算法采用了CMA-ES实例重新初始化和档案存储机制.在算法的运行过程中,为了增强演化初期搜索新峰的能力及保持子种群的稳定性,我们提出搜索点补充策略(search point replenishment strategy,SPRS).
2.1 搜索点补充策略SPRS的主要思想是在演化初期增加小生境间搜索点的迁移,以增强搜索新峰的能力、平衡子种群的大小以及保持子种群的稳定性.为了减少由于搜索点迁移对原小生境的影响,我们对包含搜索点数量最多的小生境,选择其最相似且更差的搜索点进行迁移,把它迁移到包含搜索点数最少的小生境内,并在该小生境半径内随机均匀地重新初始化该搜索点.随演化的进行,这种搜索点迁移会被逐渐减少,以降低对种群结构的破坏.另外,搜索点迁移后的重新初始化半径也会逐渐收缩,以保证种群收敛.在进行搜索点补充前需要对当前种群进行聚类操作,我们采用Preuss提出的Nearest-Better Clustering (NBC)聚类方法[19]进行子种群划分,NBC方法被认为是一个无参数的聚类方法,而且有着优秀的聚类性能.这里之所以没有采用DMC方法进行子种群划分,因为DMC方法依赖于适应度景观上的种群拓扑结构来划分聚类.这种机制会消耗额外的适应度评价次数,不适于被多次调用,但该方法却有更好的聚类性能.SPRS伪代码如算法1所示.
| 算法1 SPRS策略 |
|
输入:MINindi,C,R 1. 从聚类集合C中分别选择包含最多和最少搜索点数量的聚类cmax和cmin 2. 如果cmin中的搜索点数目大于等于MINindi,则算法终止 3. 从聚类cmax中选择一对具有最大相似性(以欧氏距离度量)的搜索点 4. 从被选择的一对搜索点中选择适应度较低的搜索点pk,并把它加入到cmin中 5. 根据公式(7)计算重新初始化半径rreinit 6. 在半径rreinit内均匀随机地初始化搜索点pk 7. 跳转到step 1 |
MINindi是聚类中允许的最少搜索点数量,它可由种群数量除以聚类数目CN求得.聚类集合C和聚类数量CN由NBC方法获得.R用于计算重新初始化半径rreinit.
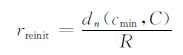
|
(7) |
dn(cmin,C)计算cmin到离它最近的聚类之间的距离(两个聚类中最好搜索点之间的距离),cmin代表包含最少搜索点的聚类.R为收缩因子用于限制重新初始化半径的大小,如果演化代数小于4,R=1,否则R=iter-3,iter为当前演化代数.这样做的目的是保证在算法运行早期有更大的初始化半径,随着演化代数的增加,初始化半径逐渐缩小.
2.2 算法框架在算法的迭代过程中,算法分两个阶段执行.在第一阶段执行NCDE算法进行粗粒度搜索,当满足一定条件时SPRS会被调用.首先,只有当前迭代次数等于阈值α时,SPRS才会被调用.这样做可以使得对SPRS的调用随演化的进行逐渐减少.其次,为了进一步限制对SPRS的调用,如果当前消耗的评价次数大于等于总评价次数的1/5时,则不再调用SPRS.
阈值α的取值如下,其中D为问题维度,
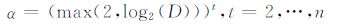
|
(8) |
下面要解决何时转入第二阶段的问题,首先要明确在转入第二阶段前,并不需要精确定位最优值的位置.只要知道最优值的大概位置即可,所以转换的时机并不需要非常准确.根据这一点,我们引入了一个自适应的启发式参数θ:
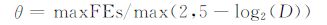
|
(9) |
当已消耗的评价次数大于等于阈值θ时,终止第一阶段并转入第二阶段的准备阶段.公式(9)中的MaxFEs代表允许的最大评价次数.在第二阶段开始前的准备阶段,需要精确的对种群划分聚类,所以此时调用DMC方法进行聚类划分,以期望获得更准确的划分结果.然后和已获得聚类数目相同的CMA-ES实例被生成,每一个CMA-ES实例对应一个聚类并覆盖搜索空间中的一个不同区域.取聚类中的最好搜索点作为CMA-ES实例的起始搜索点,并定义当前实例与它最邻近实例之间欧氏距离的二分之一为覆盖距离,则取覆盖距离的三分之一作为当前实例的起始步长(即用于控制变异强度的标准偏差),这样做的目的在于希望在CMA-ES随机抽取的搜索点中,有99%的搜索点落在覆盖距离之内,可以从统计上避免邻近CMA-ES实例间覆盖范围的相互重叠.为了充分利用剩余的评价次数,引入了CMA-ES实例重新初始化和档案存储机制.重新初始化机制是指当一个实例被终止并且有剩余的评价次数时,该实例会被重新随机初始化并重新启动它.档案存储机制是指实例在重新初始化之前,存储它已找到的最优解.档案的大小不超过种群的数量,若档案被存满时,则采用替换原则,用优质解替换档案中劣质解.整个算法框架的伪代码如算法2所示.
| 算法2 NBC-CMA算法框架 |
|
1. 初始化种群
2. 执行NBC聚类方法识别聚类,执行SPRS进行搜索点补充 3. converged=false,iter=0,t=2 4. while FEs<MaxFEs do a) if not converged then i. 如果iter==α and FEs<MaxFEs/5,则执行NBC聚类算法和SPRS并令t=t+1 ii.执行NCDE算法 iii.如果FEs≥θ,则执行DMC划分聚类并初始化CMA-ES实例,并令converged=true b) else i. 分别执行所有CMA-ES实例 ii. 若条件满足执行档案存储和实例重启 c) iter=iter+1 5. end while |
| FEs代表目前消耗的评价次数. |
从软件GAMBIT(ver. 0.2007.12 .4 )[20]中选择10个不同难度的博弈问题,每个问题都包含多个纳什均衡.博弈问题描述见表 1所示,在GAMBIT文件中给出了所有参与人的支付矩阵.选定的博弈问题可被转化为4维到12维之间的约束优化问题.这些测试问题的纳什均衡即包含纯策略又包含混合策略.其中F6,F7和F10,由于它们包含的可用策略总数多,搜索空间大且计算量大,这给求解造成一定困难.求解纳什均衡问题主要有两个难点:一是计算量大,通常情况下计算量随策略总数(问题维度)的增加急剧增长,博弈F6单次函数评价的计算量大约是F1的37.5倍,是F10的1.88倍;二是对解空间的约束给问题的求解造成困难,生成的实验向量经常不在可行解空间内.为了解决这一问题,通常先在解空间进行搜索生成一个实验向量,然后把这个实验向量映射到可行解空间再进行函数评价,很明显这种映射是满射.映射按下式进行,
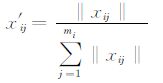
|
(10) |
其中,X=(xij)i=1,…,N;j=1,…,mi代表一个混合策略组合.
3.2 性能评价方法本文使用峰比率和找到的纳什均衡数量的平均值进行算法的性能评价,峰比率(peak ratio,PR)按以下式计算,
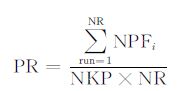
|
(11) |
NPFi代表算法第i次运行结束后找到的纳什均衡数量,NKP是由表 1所列出的已知纳什均衡数量,PR度量在NR次运行中找到已知纳什均衡数量的平均比例.找到的纳什均衡数量的平均值(Mean)计算公式如下
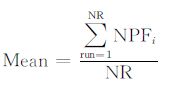
|
(12) |
| 博弈 | 参与人 数量 | 策略数量 | 纳什 均衡 | GAMBIT 文件 |
| F1 | 2 | 2×2 | 3 | coord2.nfg |
| F2 | 2 | 3×3 | 7 | coord3.nfg |
| F3 | 2 | 4×4 | 15 | coord4.nfg |
| F4 | 3 | 2×2×2 | 9 | 2×2×2.nfg |
| F5 | 3 | 3×3×3 | 5 | 3×3×3.nfg |
| F6 | 3 | 5×4×3 | 3 | 5×4×3.nfg |
| F7 | 3 | 8×2×2 | 5 | 8×2×2.nfg |
| F8 | 4 | 2×2×2×2 | 3 | 2×2×2×2.nfg |
| F9 | 4 | 2×2×2×2 | 5 | g3.nfg |
| F10 | 5 | 2×2×2×2×2 | 5 | 2×2×2×2×2.nfg |
本实验中所有算法代码均由Visual C++2012编写,操作系统为Windows 7.为了检验NBC-CMA算法的性能,我们选择了6个对等的算法进行比较.大多数算法是最近提出的新算法,它们在和其他算法的比较实验中都表现出了优秀的性能.它们是NEA[19]、S-CMA[21]、IPOP-CMA-ES[22]、NCDE[16]、LIPS[23]和FERPSO[24].其中IPOP-CMA-ES是基于重启机制、时间上串行运行的算法,这里以它作为一个测试基准,来检验所有算法的性能.
求解精度设置为e=1.0E-8,F1的最大评价次数设置为10 000,F2设置为20 000,F6、F7设置为100 000,其余问题均设置为50 000. 为了保证比较的公平性,所有算法都在不同种群大小下(种群大小从25开始,以步长25递增)被独立执行30次.对于每一个种群大小,所有算法都被独立执行30次,最后计算其PR值及平均找到的纳什均衡数量,然后从所有运行结果中选择最好运行结果作为最终结果参与比较.
我们提出的算法共引入了3个新参数gradations,α和θ.NBC-CMA的参数gradations(DMC聚类中插入点的个数)被设置为固定值8.α和θ是两个自适应参数,不需要设置.对于NCDE算法有3个参数,邻域大小m被设置为种群大小的1/15,收缩因子F设置为0.5,交叉概率Cr设置为0.9(因为纳什均衡问题属于不可分问题,较大的Cr值有利于问题的求解).CMA-ES除了stopTolFun和stStopFitness外均使用默认参数值,stopTolFun设置为1.0E-7,stStopFitness设置为要搜索的最优值.当CMA-ES实例找到最优值或陷入停滞时,CMA-ES实例会被终止以节省评价次数.IPOP-CMA-ES算法的种群增长因子设置为1.1,并保证每次重启种群大小至少增加一个个体.对于NEA和S-CMA算法,它们的最大允许小生境数量设置为要搜索的纳什均衡数量.为了保证和其他CMA算法比较的公平性,在原IPOP-CMA-ES和S-CMA算法的基础上为其增加了档案存储机制.其他算法的参数均取其默认值.
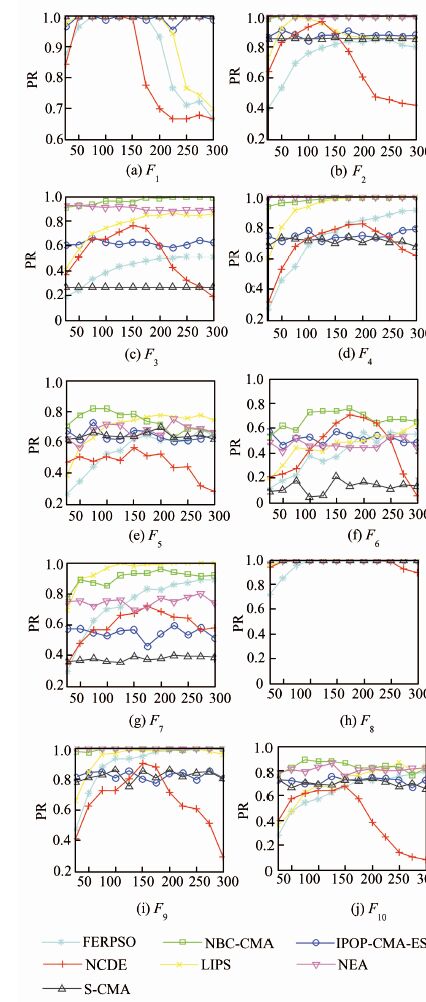
4 实验结果分析图 1给出了在精度要求为e=1.0E-8时,对每个种群大小所有算法都独立运行30次求得PR值的曲线图.图 1的运行结果中,对每个博弈问题计算每种算法在最好种群下找到的纳什均衡点的平均值,其结果如表 2所示.求得的最好结果在表格中用黑体显示,小括号中的数字代表该算法的秩,表格最后一行为算法在所有测试问题上的秩和.F1、F2、F8和F9是相对简单的问题,取得全部均衡点相对容易,其中F2由于评价次数设置得少,大部分算法没能每次运行都取得全部均衡点,仅NBC-CMA和NEA能在多数种群规模下每次都取得全部均衡点.F3和F4由于包含的纳什均衡点较多,求解维度增加,NBC-CMA、NEA和LIPS算法表现出了优于其他算法的性能.F5,F6,F7和F10是较难的问题,尤其F6和F7在所有测试问题中最难求解,不仅问题维数高,而且计算量显著大于其他测试问题.在这4个测试问题上,NBC-CMA在3个问题上是最好的,在F7上劣于LIPS算法,这可能和LIPS算法采用了基于邻域变异的策略有关,领域变异策略具有很好的保持种群多样性的能力,该策略使得算法具有很好的稳定性.在实验结果的总体效果上,NBC-CMA算法最好,LIPS次之.在F2,F3,F5,F6和F10上,NBC-CMA的结果优于所有其他算法.在F1,F4,F8和F9上,NBC-CMA取得了与其他算法相同的结果.
|
| 图 1 所有算法在不同种群大小下求得的PR值曲线图 Figure 1 The graph of PR values achieved under different populations for all algorithms |
| 博弈 | FERPSO | IPOP-CMA | LIPS | NBC-CMA | NCDE | NEA | S-CMA |
| F1 | 3.00(1) | 3.00(1) | 3.00(1) | 3.00(1) | 3.00(1) | 3.00(1) | 3.00(1) |
| F2 | 5.93(7) | 6.40(5) | 6.97(3) | 7.00(1) | 6.77(4) | 7.00(1) | 6.00(6) |
| F3 | 7.73(6) | 10.00(5) | 12.90(3) | 14.93(1) | 11.40(4) | 13.90(2) | 4.00(7) |
| F4 | 8.20(4) | 7.10(6) | 9.00(1) | 9.00(1) | 7.40(5) | 9.00(1) | 6.63(7) |
| F5 | 3.43(6) | 3.67(4) | 3.90(2) | 4.10(1) | 2.83(7) | 3.77(3) | 3.50(5) |
| F6 | 1.70(5) | 1.73(4) | 1.93(3) | 2.30(1) | 2.13(2) | 1.6(6) | 0.63(7) |
| F7 | 4.47(3) | 2.97(6) | 5.00(1) | 4.80(2) | 3.60(5) | 4.00(4) | 2.00(7) |
| F8 | 3.00(1) | 3.00(1) | 3.00(1) | 3.00(1) | 3.00(1) | 3.00(1) | 3.00(1) |
| F9 | 5.00(1) | 4.27(7) | 5.00(1) | 5.00(1) | 4.50(5) | 5.00(1) | 4.30(6) |
| F10 | 4.00(4) | 3.88(5) | 4.40(2) | 4.50(1) | 3.43(7) | 4.37(3) | 3.73(6) |
| 秩和 | 38 | 44 | 18 | 11 | 41 | 23 | 53 |
| 注:小括号中的数字代表该算法的秩,黑体为求得的最好结果 | |||||||
通过把N人非合作博弈的纳什均衡问题转化为带约束的传统优化问题,实现了用多峰优化算法对纳什均衡问题的求解.通过算法的一次运行可求出多个纳什均衡解,这对纳什均衡解的精化提供了方便.实验结果表明我们提出的NBC-CMA多峰优化算法是有效的,尤其在F3,F5,F6和F10这4个较难的博弈问题上表现出了优于其他算法的性能.
将来的研究工作围绕以下两点展开:首先,对NBC-CMA算法进行改进,尝试用其他优秀算法替代NCDE和CMA-ES算法,以期获得更好的性能;其次,把NBC-CMA算法应用于动态环境中的多峰优化问题.
| [1] | NASH J F. Equilibrium points in n-person games[J]. The National Academy of Sciences of the United States of America, , 1950, 36 (1) : 48–49 DOI:10.1073/pnas.36.1.48 |
| [2] | NASH J F. Non-cooperative games[J]. The Annals of Mathematics , 1951, 54 (2) : 286–295 DOI:10.2307/1969529 |
| [3] | LEMKE C E, HOWSON J J T. Equilibrium points of bimatrix games[J]. Journal of the Society for Industrial & Applied Mathematics , 1964, 12 (2) : 413–423 |
| [4] | van Der LAAN G, TALMAN A J J, van HEIJDEN L. Simplicial variable dimension algorithms for solving the nonlinear complementarity problem on a product of unit simplices using a general labelling[J]. Mathematics of Operations Research , 1987, 12 (3) : 377–397 DOI:10.1287/moor.12.3.377 |
| [5] | GOVINDAN S, WILSON R. A global newton method to compute Nash equilibria[J]. Journal of Economic Theory , 2003, 110 (1) : 65–86 DOI:10.1016/S0022-0531(03)00005-X |
| [6] | HERINGS P J, PEETERS R J. A differentiable homotopy to compute Nash equilibria of n-person games[J]. Economic Theory , 2001, 18 (1) : 159–185 DOI:10.1007/PL00004129 |
| [7] | GOVINDAN S, WILSON R. Computing Nash equilibria by iterated polymatrix approximation[J]. Journal of Economic Dynamics and Control , 2004, 28 (7) : 1229–1241 DOI:10.1016/S0165-1889(03)00108-8 |
| [8] | SUREKA A, WURMAN P R. Using Tabu best-response search to find pure strategy Nash equilibria in normal form games[C]//Proceedings of the Fourth International Joint Conference on Autonomous Agents and Multiagent Systems. New York: ACM, 2005. 1023-1029. |
| [9] | 查旭, 左斌, 胡云安. 利用退火回归神经网络极值搜索算法求纳什均衡解[J]. 控制与决策 , 2006, 21 (10) : 1167–1171 ZHA X, ZUO B, HU Y A. Nash equilibrium solution by extremum seeking algorithm based on annealing recurrent neural network[J]. Control and Decision, , 2006, 21 (10) : 1167–1171 |
| [10] | LUNG R, DUMITRESCU D. An evolutionary model for solving multi-player non-cooperative games . . http://www.cs.ubbcluj.ro/~studia-i/2007-kept/314-LungDumitrescu.pdf. |
| [11] | PAVLIDIS N G, PARSOPOULOS K E, VRAHATIS M N. Computing Nash equilibria through computational intelligence methods[J]. Journal of Computational and Applied Mathematics , 2005, 175 (1) : 113–136 DOI:10.1016/j.cam.2004.06.005 |
| [12] | 余谦, 王先甲. 基于粒子群优化求解纳什均衡的演化算法[J]. 武汉大学学报(理学版) , 2006, 52 (1) : 25–29 YU Q, WANG X J. Evolution algorithm for solving Nash Equilibrium based on particle swarm optimization[J]. J Wuhan Univ (Nat Sci Ed) , 2006, 52 (1) : 25–29 |
| [13] | 伍文, 孟相如, 康巧燕, 等. 粒子群算法求解混合战略近似纳什均衡[J]. 计算机应用研究 , 2014, 31 (8) : 2299–2302 WU W, MENG X R, KANG Q Y, et al. New PSO based algorithm for finding mixed strategy approximate Nash equilibrium[J]. Application Research of Computers, , 2014, 31 (8) : 2299–2302 |
| [14] | GUO Z, YUE X, ZHANG K, et al. Enhanced social emotional optimisation algorithm with generalised opposition-based learning[J]. International Journal of Computing Science and Mathematics , 2015, 6 (1) : 59–68 DOI:10.1504/IJCSM.2015.067543 |
| [15] | GUO Z, YUE X, WANG S, et al. Self-adaptive differential evolution with elite opposition-based learning[J]. ICIC Express Letters , 2016, 10 (2) : 405–410 |
| [16] | QU B Y, SUGANTHAN P N, LIANG J J. Differential evolution with neighborhood mutation for multimodal optimization[J]. IEEE Transactions on Evolutionary Computation , 2012, 16 (5) : 601–614 DOI:10.1109/TEVC.2011.2161873 |
| [17] | HANSEN N, OSTERMEIER A. Completely derandomized self-adaptation in evolution strategies[J]. Evolutionary Computation, , 2001, 9 (2) : 159–195 DOI:10.1162/106365601750190398 |
| [18] | STOEAN C, PREUSS M, STOEAN R, et al. Multimodal optimization by means of a topological species conservation algorithm[J]. IEEE Transactions on Evolutionary Computation , 2010, 14 (6) : 842–864 DOI:10.1109/TEVC.2010.2041668 |
| [19] | PREUSS M. Niching the CMA-ES via nearest-better clustering[C]//Proceedings of the 12th Annual Conference Companion on Genetic and Evolutionary Computation.New York: ACM, 2010: 1711-1718. |
| [20] | MCKELVEY R D, MCLENNAN A M, TUROCY T L. Gambit: Software tools for game theory . .http://sourceforge.net/projects/gambit/files/gambit-stable/0.2007:12.04/. |
| [21] | SHIR O M, EMMERICH M, BACK T. Adaptive niche radii and niche shapes approaches for niching with the CMA-ES[J]. Evolutionary Computation , 2010, 18 (1) : 97–126 DOI:10.1162/evco.2010.18.1.18104 |
| [22] | AUGER A, HANSEN N. A restart CMA evolution strategy with increasing population size . . http://ieeexplore.ieee.org/xpls/icp.jsparnumber=1554902. |
| [23] | QU B Y, SUGANTHAN P N, DAS S. Adistance-based locally informed particle swarm model for multimodal optimization[J]. IEEE Transactions on Evolutionary Computation , 2013, 17 (3) : 387–402 DOI:10.1109/TEVC.2012.2203138 |
| [24] | LI X D. Amultimodal particle swarm optimizer based on fitness Euclidean-distance ratio[C]//Proc of the 9th Annual Conference on Genetic and Evolutionary Computation. New York: ACM, 2007: 78-85. |
 2016, Vol. 62
2016, Vol. 62





