文章信息
- 马蓉, 冯盛源, 熊金波, 金彪, 王丽丽
- MA Rong, FENG Shengyuan, XIONG Jinbo, JIN Biao, WANG Lili
- 基于安全博弈模型的隐私保护方法
- Privacy Protection Method Based on Security Game Model
- 武汉大学学报(理学版), 2018, 64(2): 165-174
- Journal of Wuhan University(Natural Science Edition), 2018, 64(2): 165-174
- http://dx.doi.org/10.14188/j.1671-8836.2018.02.010
-
文章历史
- 收稿日期:2017-08-03

2. 福建省网络安全与密码技术重点实验室, 福建 福州, 350007
2. Fujian Provincial Key Laboratory of Network Security and Cryptology, Fujian Normal University, Fuzhou 350007, Fujian, China
随着云计算、大数据技术的快速发展和云服务的广泛普及,人们日常生活的诸多领域也发生着巨大的变化,如在商业、娱乐、医疗和教育等方面.互联网在给人们带来巨大生活便利的同时也带来了日益严重的安全威胁.近几年,各种各样因网络信息不安全而导致严重损失的事件已屡见不鲜,这也说明了网络信息安全的重要性.尤其是网络信息安全问题与国家安全及众多行业紧密相关,如何在社会信息化的进程中正确理解和分析信息安全问题是一个亟需解决的问题.
传统常见的网络安全技术一般采用在遭受攻击后单方面的静态被动安全防御,多数适用在某一个特定的攻击场景或攻击方法,且其解决方案缺少定量分析和决策框架[1, 2].为解决这一问题,博弈论被越来越多的应用于网络安全、隐私保护和无线网络等领域问题的研究中[3~17],为信息安全问题提供了一个数学工具,用以描述和分析网络中复杂的多人竞争行为.彭长根等[7]从博弈论和密码学的共性出发, 综述了密码系统博弈模型及相关概念, 阐述了其在经济学中的机制及其在博弈密码协议设计中的应用及前景.Manshaei等[8]探讨综述了博弈论在网络安全中的应用,认为博弈论在网络安全方面的研究主要集中在6个方面:物理层和MAC层的安全、自组织网络的安全、入侵检测系统、匿名性和隐私、网络安全经济学和密码学.周丹丹等[12]从经典的博弈论模型角度概述博弈论在隐私保护方面的理论、方法和应用,并分别针对4种典型的隐私保护问题给出博弈论解决方案.本文将从信息安全博弈模型这一新的角度对基于博弈论的隐私保护方法进行分类描述.对三类典型的信息安全博弈模型即确定性安全博弈模型、随机安全博弈模型和具有有限信息的安全博弈模型进行描述和形式化定义,对基于三类信息安全博弈模型所提出的隐私保护方法进行分类举例论述,并对此进行比较,讨论其优点和局限性.另外,也指出现有方法所面临挑战以及今后研究方向.
1 安全博弈模型概述本节将对三类安全博弈模型进行概述介绍并给出其形式化定义.通常情况下安全博弈模型由以下几点构成,即博弈双方的参与者、策略、收益[18]和博弈中双方的信息结构.博弈中的信息结构是指在安全博弈中,攻防双方对彼此信息的了解程度.
1.1 确定性安全博弈模型确定性安全博弈模型(或双矩阵安全博弈模型)是信息安全博弈模型研究的起点,它是对在安全博弈中攻防双方对彼此的策略集合及相应收益函数完全了解的情景中的安全问题的建模.该模型的行为集都是有限的离散型行为.在有限静态情况下,每个参与者的收益或损失用矩阵表示,每个矩阵中元素取值代表攻击者和防御者的各自行为的成本和回报.
本文用PA表示攻击者,PD代表防御者,攻击者的攻击行为集合记为AA={a1, …, aNA};防御者的防御行为集合为AD={d1, …, dND}.
博弈模型中GA为攻击者NA×ND维博弈收益矩阵,GD为防御者NA×ND维博弈收益矩阵.矩阵GA和GD中的元素代表博弈参与者成本最小化的值.如果是零和安全博弈的话,GA=-GD,此时称这个博弈为矩阵博弈.在确定性安全博弈中,攻击者PA要最大化其回报,而防御者PD则要付出博弈模型中的矩阵最小化成本.
如果一个安全博弈模型在采用纯策略时得到纳什均衡,则定义pA=[p1, LpNA]为攻击者攻击行为集合AA中相应攻击行为的概率分布,qD=[q1, LqND]为防御者防御行为集合AD中相应防御行为的概率分布,这里0≤pi, qj≤1且∀i,∀j都有∑ipi=∑jqj=1.用(p*, q*)来表示混合策略下的纳什均衡概率分布,并用(vA*, vD*)=(p*GAq*T, p*GDq*T)分别来表示安全博弈攻击者PA和防御者PD在纳什均衡时取得的收益[19].
1.2 随机安全博弈模型随机安全博弈模型(或马尔可夫安全博弈)是对确定性安全博弈框架的扩展,通过利用概率理论对安全问题中的未知和不可控参数进行建模.在随机安全博弈模型的框架内可以更符合现实情况地研究潜在博弈参数、其相互依赖关系和外部因素的动态特性.随机处理的结果使得参与者行为参数化,从而可以基于网络系统属性对参与者的决策效果进行建模分析.
两个参与者(攻击者PA与防御者PD)的零和马尔可夫博弈是在一个有限状态空间中进行的,每个参与者都有一个有限数目的行为选择.网络系统环境被定义为有限的环境状态集合S={s1, s2, …,sNs}.
假设状态是根据离散有限状态马尔可夫链进行演化的,这样就可以利用完善的分析工具来研究这个问题.状态转换参数化是由以下映射决定的:
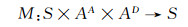
|
(1) |
令pS=[p1, …, pNp]作为状态空间S的概率分布,0≤pS≤1, ∀i并且∑ipiS=1.在离散和有限的情况下,考虑映射M可以用Ns×Ns维的转换(或马尔可夫)矩阵M(a, d)=[Mi, j(a, d)]Ns×Ns进行参数化,a∈AA, d∈AD且
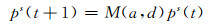
|
(2) |
式中,t≥1表示重复随机安全博弈的不同阶段.
在(1)式中映射M可以通过状态的数量获得尽可能多的零和博弈矩阵G(s)进行有选择地参数化,其中s∈S,矩阵G(s)为NA×ND维矩阵.即在阶段t给定一个状态s(t)∈S参与者的零和博弈为

|
(3) |
例如,如果在状态s3攻击者PA采取行为a4且防御者PD采取行为d2,那么博弈的收益就是G4, 2(3)(攻击者PA为回报,而防御者PD为损失).
参与者的策略依赖于相关的状态并且是1.1节讨论的策略扩展,
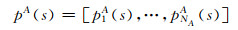
|
(4) |
为攻击者PA策略在行为集合AA以及给定状态s∈S下的概率分布,
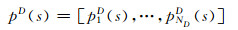
|
(5) |
为防御者PD策略在行为集合AD以及给定状态s∈S下的概率分布,这里0≤piA, piD≤1, ∀i且∑ipiA=∑ipiD=1.在随机安全博弈模型中矩阵博弈的每个阶段并不都存在惟一的纳什均衡[19].
1.3 具有有限信息的安全博弈模型在许多信息安全问题中,防御者与恶意攻击者了解对方的信息都是有限的,主要限制之一是防御者有限的观察能力,这些在有限信息下的博弈被称为具有有限信息的安全博弈(即贝叶斯安全博弈).本文利用概率的方法进行描述参与者的属性信息,在博弈中有一个特殊的自然参与者,它对每个参与者给定一个预先确定的概率分布和类型的组合并构成他们的固定策略.随后参与者根据每个可能的参与者类型组合并按预先确定的概率分布加权从而计算出自己的策略.下面以安全防御系统为例,描述具有有限信息的安全博弈模型.
把一个防御者用来侦测恶意攻击行为的虚拟传感器网络定义为博弈的自然参与者.对攻击者PA和防御者PD都要考虑传感器侦测到入侵的概率,当他们决定自身反应的最优策略时,他们已经有了自身的固定策略.
防御系统通常包括一个虚拟传感器网络以收集信息和检测恶意攻击,它可以作为具有有限信息的安全博弈模型的自然参与者.这里,本文考虑一个分布式传感器网络
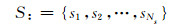
|
(6) |
监控恶意行为现象的防御系统可以表示为以下子系统集合
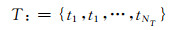
|
(7) |
上述子系统可是攻击者的目标,T中的子系统可能代表操作系统、中间件、应用程序或部分网络以及分布在多个主机上的业务处理过程.将目标系统T的增强攻击行为与检测异常行为定义为
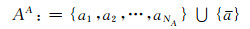
|
(8) |
这里,a表示“没有攻击”.在这种情况下,通常所说的攻击就有两个特定的属性:一个是目标子系统t∈T,另一个是攻击威胁或者检测异常.因此攻击集合AA是威胁集合和检测异常集合的并集.给定一组攻击集合AA,并且定义线性映射关系:P:AA→AA来描述实际攻击和传感器网络S的输出之间的关系.具体来说,用矩阵

|
(9) |
来表示攻击是否被系统正确报告,矩阵元素pij表示将攻击i报告成为攻击j的概率.如果i≠j,那么传感器网络就是一次攻击混淆成了另一次攻击.这种误报对攻击者是很有益的.如果j=a,那么pij就是对于已经发生的攻击行为漏报的概率.类似地,如果i=a且j≠a,那么pij就是对于攻击j进行错误预报的概率.因此矩阵P描述了虚拟传感器网络作为自然参与者所采取的混合策略.
对于以上三类安全博弈模型特征及适用问题的归纳总结如表 1.
| 安全博弈模型 | 模型特征 | 对应均衡 | 适用问题特征 |
| 确定性安全博弈模型 | 静态; 完全信息 |
纳什均衡 | 参与者双方知道彼此收益函数及策略选择 |
| 随机安全博弈模型 | 动态; 完全信息 |
子博弈精炼纳什均衡 | 参与者双方策略选择与状态空间有关 |
| 具有有限信息的安全博弈模型 | 静态; 不完全信息 |
贝叶斯纳什均衡 | 参与者双方对彼此收益函数了解有限 |
博弈模型的基本特征是策略的依存性,而信息安全的隐私保护的抽象特征也恰恰是安全主体之间的策略依存性.在信息安全的隐私保护研究中引入安全博弈模型能够更为直观的用数学和逻辑学的理论方法描述隐私保护问题,为该问题提供定量的决策分析框架,获得的安全博弈及其均衡解可以作为正式决策和算法发展以及预测攻击行为的基础.
2.1 基于确定性安全博弈模型的隐私保护方法在两人非合作的确定性安全博弈中,一个参与者是攻击者,攻击者吸引一个或者多个人恶意攻击防御系统.通过分析确定性安全博弈的博弈矩阵,得出纳什均衡.下面通过简单入侵检测系统中的隐私防护和用户隐私信息投资决策的隐私保护问题,给出基于确定性安全博弈模型的隐私保护方案.
2.1.1 简单入侵检测系统中的隐私防护企业使用信息安全技术来达到对攻击者进行防御的目的,但是作为攻击者,则会通过很多的方式来达到其攻击的目的.通常情况下会通过现有的博弈模型来对其展开研究.近年来在该方面对其进行研究的重心就是以入侵检测系统为中心来开展工作,对于简单入侵检测系统(即不考虑网络状态变化)可用确定性安全博弈模型进行分析.
入侵检测可以被定义为用于监视一个计算机系统或网络中发生的时间以及分析它们遭到入侵的迹象.入侵检测和防御系统(IDPS)由三个主要部分组成:信息源、分析和应对.入侵检测系统下的安全博弈的目标是使这三个部分具体化为决策过程,而且主要侧重于应对部分.下面举例说明确定性安全博弈模型在入侵检测系统中的应用.
在简单的入侵检测博弈模型中(图 1(a)),设定攻击者PA的攻击行为集合为AA={a, a},a表示攻击者对网络发动攻击的行为,而a代表攻击者没有发动攻击.防御者PD的防御行为集合为AD={d, d},d代表防御者加强防御行为,d代表防御者并没有采取加强的防御行为,而是采用的默认防御行为.所以用非零和的博弈形式,则上述的确定性入侵检测博弈模型可以描述为图 1(b)的矩阵形式.
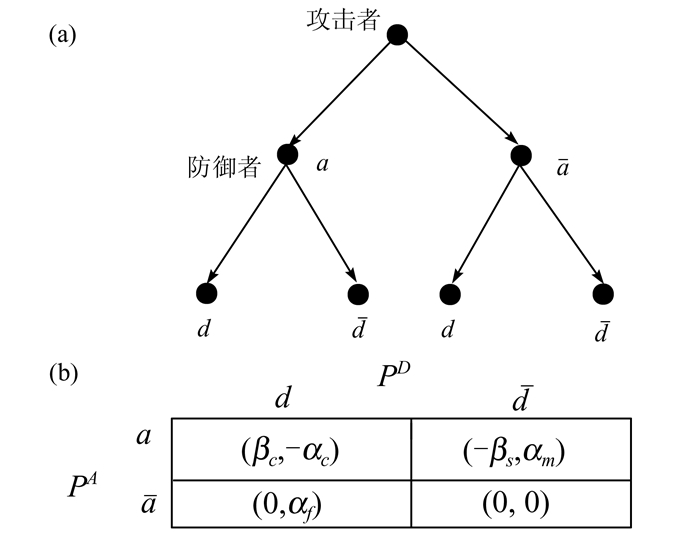
|
| 图 1 简单的入侵检测博弈模型(a)及其矩阵形式(b) Figure 1 A simple intrusion detection game model (a) and its matrix(b) |
其中,α和β都是正数,参数-αc为防御者PD在侦测到攻击者攻击时获得收益,αf是攻击者没有发起攻击而防御者错误地识别出了攻击行为所付出的成本,αm攻击者发起了攻击但是防御者没有发现攻击行为所付出的成本.βc为攻击者PA发起攻击但是被防御者识别检测出来所付出的成本,而-βs则是攻击者发起攻击而防御者没有识别检测出攻击行为而获得的收益.尽管对于防御者来说错误地识别攻击行为也是要付出成本的,但攻击者这时是没有成本的,因此在矩阵中将双方的收益值都设置为0.
在此确定性入侵检测安全博弈模型中没有纯策略纳什均衡解.因此假设0≤p≤1和1-p分别是攻击者PA采取攻击行为a和不采取攻击行为a的概率.相应的,设0≤q≤1和1-q分别是防御者PD加强防御行为d和并没有采取进一步加强的防御行为d的概率,在此安全博弈模型中混合策略(p*, q*)就是纳什均衡解,如果满足下面的不等式
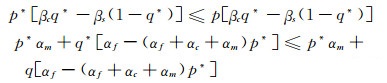
|
(10) |
对(10)式求解,得到该博弈模型惟一的纳什均衡解:
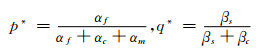
|
攻击者对于网络攻击的概率在纳什均衡时为p*,而p*会随着αf值增加而相应地增加,对于防御者而言一个更小的错误识别攻击行为成本意味着可以使用更多的防御资源进行防御,这就使得攻击者不会轻易地发动攻击.
2.1.2 用户隐私信息投资决策的隐私保护目前人们在使用网络时都需要向网络的服务系统提供使用者的个人信息,以此来当作对提供网络服务的供应商的回报,进而可以使得使用者得到更好的网络服务.但是很多时候使用者的信息都会被泄露出去,这不仅会减少使用者对供应商的信任,而且会给使用者带来隐私隐患或损失.将责任一味地推给供应商有失公正,D’Acquisto等学者提出了使用确定性安全博弈模型来解决诸如此类的问题[20, 21].使用博弈策略的目标就是让使用者在提供极少量隐私的前提下得到最好的服务,供应商则是在投入极少的资金Y*的前提下承担最少的损失,用户的损失用X*来表示.整个过程其实就是能够使博弈的双方得到更大的利益,从而找出双方的纳什均衡策略(X*, Y*).
一般情况下对使用者和供应商的需求是用曲线方程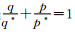

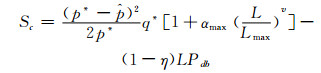
|
(11) |
(11)式中的Lmax指的是L的最大值,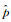
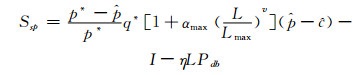
|
(12) |
(12)式中的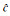
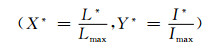
|
在确定性安全博弈模型为攻防双方提供对策与资源分配的指导方针的基础上,越来越多的研究集中在通过概率模型和博弈论方法定量评估操作安全和相应可靠性领域的安全问题.攻击者策略是在很多假设基础上得到的,并且不同的情况会产生不同的纳什均衡和其他的结果.网络随机状态空间模型为网络的安全属性提供了分析基础,基于攻击者策略对于不同的情况状态之间的转换概率是可以计算出来的.因此只要获得网络安全状态的具体示意图,就可以明确地整合攻击者的行为.下面通过入侵检测系统中有关隐私的防护与网络攻防的隐私保护的量化工作进行分析,介绍在随机安全博弈模型的基础上制订具有针对性的隐私保护措施和方案.
2.2.1 入侵检测系统中的隐私防护随机安全博弈模型应用在入侵检测系统中,可以更全面和现实地分析入侵检测系统中的博弈.姜伟等[22]给出了基于随机攻防博弈模型的最优防御策略选取.在入侵检测博弈模型中单个系统的脆弱性可以在网络上被监视并且使用可控的马尔可夫链来进行建模.
考虑一个单独的系统,其状态空间有两种状态:S={v, v}.式中,v代表可以被攻击的系统脆弱性,v代表在给定时间段里系统没有脆弱性,马尔可夫链的状态转移概率由发现影响系统脆弱性的概率以及系统升级的概率或者由于系统打了补丁使得系统相应脆弱性消失的概率决定.这些概率自然都是依赖防御者的行为,如果防御者分配更多的资源用于系统的运行维持,那么系统新的脆弱性发生的概率就会降低,而原有的脆弱性发生的概率就会增加,一个被忽视的系统可能会有更多的脆弱性,被攻击的可能性非常大.
将随机入侵检测博弈模型定义为一个零和的马尔可夫博弈,同样的这里攻击者为PA,防御者为PD.
给定状态空间S={v, v},在特定状态下的概率用下面的向量表示:
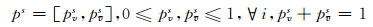
|
状态概率根据下面的式子进行变换
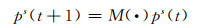
|
(13) |
式中,t≥1代表博弈阶段,状态转移或者马尔可夫矩阵取决于防御者PD的行为d和d,表示为M(n)和M(d),另外类似的随机入侵博弈模型的矩阵取决于状态空间S,可以表示为G(v)和G(v).
随机入侵检测博弈模型运行的环境具有系统脆弱性,因此随机入侵检测博弈模型不同于简单入侵检测博弈模型,它具有动态性的特征.随机入侵检测博弈模型中的参与者不仅要考虑当前成本还要考虑博弈演化带来的未来成本的折现.
2.2.2 网络攻防隐私保护量化分析如今,越来越多新的网络的攻击手段和防御工具不断发展,其中防御工具具有多元化,隐藏性较好,传播速度快等特征,单一的规则很难对其描述.一个攻防模型的建立主要存在两个难点:第一,网络攻击是人为进行的破坏[23, 24],带有很强的设计意图,很难推测出这种设计意图;第二,网络结构极其巨大复杂,对其进行网络安全性分析异常困难.而随机博弈的模型能够较好的描述攻击者的意图,从而更好地为人们选择防范做出贡献,并且,该模型还能详细分析出各种防范安全措施的具体效果.
王元卓等[25]采用随机博弈模型的网络攻防实验整体架构,提出了网络攻防博弈模型的快速建模方法,最终成功生成模型,在平均攻击时间和网络的攻击成功率方面有很大提高,并且在较为脆弱的节点和隐藏的路径方面进行了探讨.
当对SGN(stochastic game net)进行建立时,可以假定每一个理智的参与者都会以自己的利益最大的作为目标.参与博弈攻守双方所表现出的动作的集合的形式分别为Ai={a1, a2, …, ak}与Di={d1, d2, …, dL}.假如攻击者选定在位置pi上进行某一攻击行为,并在达到攻击目标的同时没有被检测出来,那么此时系统将会转移到位置pj上,继续进行博弈,用γkl表示攻守双方动作对(ak, dl)的总输出:
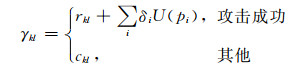
|
(14) |
其中rkl表示攻击者行为是ak且防御者行为是dl时攻击者在pi上的效益.当对其他的一些位置所造成的影响进行整体考虑时,用U(pi)表示在pi的位置上所产生的期望的效用,同时将δi∈[0, 1]用来表示其折扣的系数.同理攻击者可以在pi的位置上建立一个|Ai| × |Di|阶的矩阵:
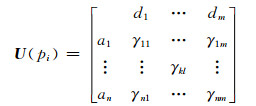
|
(15) |
攻击者目标是最大化自身收益,防御者的目标则是使攻击者所得收益最小.分别用πi1与πi2来表示攻击者与防御者的博弈策略.此时,双方整体在pi上所产生期望效用可进一步表示为:
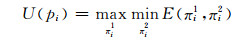
|
(16) |
通过建立随机安全博弈模型来描述网络攻防双方之间的博弈关系并对其均衡解进行求解最重要的目的是对攻击者攻击概率及相应攻击策略进行预测并建立防御者相应的防御策略.这样不但可以清楚地分析攻防过程, 同时也为选择有效的防御策略提供有力的依据.
2.3 基于有限信息的安全博弈模型的隐私保护方法在很多应用中,参与者不能了解彼此的支付函数,他们基于对对手类型的估计或者观察对手的行为来调整他们的策略.然而这些观察结果可能由于参与者沟通渠道不完善而不准确,所以采用贝叶斯博弈方法分析具有有限信息的安全博弈.下面通过无线自组织网络中的信任与隐私权衡和位置隐私保护的问题提出相应的措施和方案.
2.3.1 无线自组织网络中的信任与隐私权衡根据无线自组织网络中相互可通信的结点间所发送信息的真假,将它们分为两类,一类是良性结点,一类是恶意结点.为保证无线自组织网络中的良好通信,需要各个结点依据其余结点所发送的信息进行投票以确定恶意结点位置并将其排除,但在投票过程中会面临隐私泄露问题.
Raya等[26]运用有限信息的安全博弈模型来处理无线自组织网络中的结点参与投票排除恶意结点与投票过程中可能泄露隐私两者间的权衡问题.在投票过程中,泄露自身位置信息和身份隐私信息的风险与此结点在投票过程中的贡献成正比.假设每个结点都是理性参与者,都希望以最小隐私信息泄露为代价来获取服务,此时无线自组织网络中的各个结点将会出现搭便车的现象,没有结点愿意主动做出投票贡献,却想坐享其成.此时将很难通过结点间的信任投票以判断出恶意结点位置并去除.Raya等将每个结点在投票贡献和隐私保护间的权衡看作是一个博弈过程.在此博弈过程中,每个参与博弈的结点对其他结点的信息了解有限,所以采用有限信息的安全博弈模型.下面从宏观角度的博弈GAD来阐述这一问题.
宏观角度是指从整体出发,考虑所有参与博弈的结点可能采取的行为.将博弈参与者分为攻击方A和防守方D,记作P={A, D}.他们在每一次投票过程中有相同的策略集合,即投票S(会泄露自己的隐私信息)或者是不投票W(等待),即SA=SD={W, S}.两者间先由防守方D选择策略,再由攻击方A选择策略,其博弈是动态博弈.vA和vD分别表示两者在此博弈中的得到收益.pA, pD分别表示两者赢得博弈的概率(与每一方的结点数量有关),且pA+pD=1.此动态博弈过程如图 2所示,结点表示博弈参与者,分支代表其相应策略,叶子结点表示两者收益,其中左叶子节点表示防守方的收益,右叶子节点则表示攻击方的收益,参数c表示达到信任等级所泄露的最小化的信息.通过分析图 2可以看出,攻击方与防守方的纳什均衡点的策略组合是(W, W),即双方一直选择等待博弈结束通过其获胜概率pA, pD来决定最终博弈赢家,显然这不是所希望的结果.为改变这一结果,并鼓励博弈参与方积极进行投票,引入一个回报r,当满足r≥c+δ时,策略组合(S, S)为新的纳什均衡点.
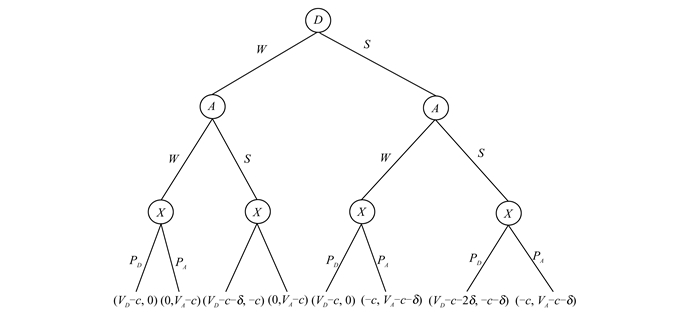
|
| 图 2 扩展博弈树 Figure 2 Extends the game tree |
基于用户所提交的位置信息可为用户提供丰富的应用服务,给生活带来诸多便利.与此同时,也面临着用户位置信息所蕴含的诸多隐私泄露问题.敌手可能通过攻击服务器以获取用户信息,或从用户交互中推断某用户的位置信息.为了保护个人隐私,用户在提交其位置信息时会选择对位置信息进行模糊化处理(例如添加噪声),但也会因此降低用户所获得的服务质量.此时需要在服务质量和隐私泄露风险间做出权衡.
Shokri等[27]采用有限信息的安全博弈模型来应对位置个人隐私的保护,其中博弈参与者为用户,位置服务提供商和敌手,其隐私保护框架如图 3所示.用户与敌手间的博弈过程是动态的,并且两者所能观察到对方的信息是有限的.其过程为先由用户以保证一定位置服务质量的前提下制定其位置信息隐私保护策略,利用合理的隐私保护机制以最大程度降低敌手猜测出用户准确位置信息的准确度,此时若敌手获得了用户的位置信息则视作用户收益遭到损失.
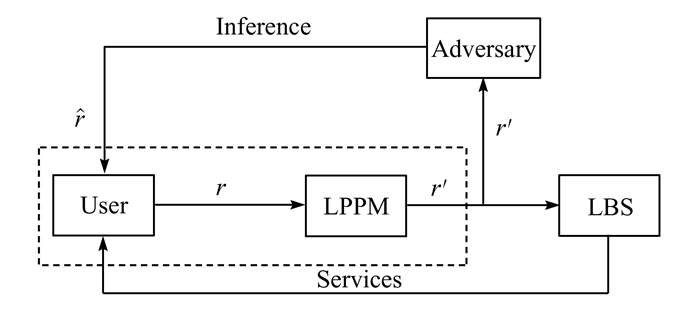
|
| 图 3 位置隐私保护框架 Figure 3 Location privacy protection framework |
位置隐私保护机制LPPM(location privacy protection mechanism)[28~30]可以很好的解决用户在位置服务质量和隐私泄露风险间的权衡问题.LPPM中用户策略为利用某一概率分布φ(r)用其他虚假的位置信息r′去替代用户的真实位置信息r,或者把用户的真实位置信息模糊化处理为r′,记作fake〈r′|r〉,并将fake〈r′|r〉发送给位置服务提供商来得到相关的位置服务.敌手的攻击策略是利用其自身的猜测机制,通过观察到的模糊位置信息r′来猜测此用户位置信息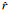
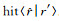
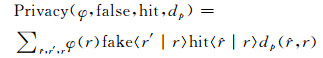
|
(17) |
(17)式中的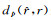
在此博弈中,用户希望最大程度保护其隐私信息,而敌手则希望用户的隐私保护程度最小,以此求解该博弈的纳什均衡,该用户的隐私期望收益为

|
(18) |
敌手的期望收益为:
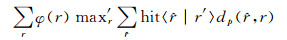
|
(19) |
此纳什均衡点求解过程规约为求解线性规划问题,通过求解得到了该博弈的最优解,即得到用户在位置服务质量和隐私保护权衡间的最佳隐私保护机制和敌手的最好猜测攻击策略.
2.4 综合分析通过对基于三类安全博弈模型的信息安全隐私保护实例进行总结对比分析,可以得到如下结论:
确定性安全博弈模型可以对隐私保护参与者的确定参数进行定量分析从而制定该参与者的相关决策.其博弈均衡解可为隐私保护参与者的正式决策和算法选用提供参考.但在此博弈模型中因为它只能对确定性参数和参与双方了解彼此收益函数的情况进行分析,不具有动态特性.不适用于真实复杂的网络环境.
通过在确定性安全博弈模型基础上进行扩展,随机性安全博弈模型可研究隐私保护中博弈参与者的潜在博弈参数、参数相互依赖关系和外部因素的动态特征,可以用以描述用户与敌手间的攻防策略因时间变化动态调整过程.但在实际网络环境中,由于有限的观察能力,隐私保护参与者双方往往不能完全观察对方的行为和行为潜在的演变.并且每个参与者对于对手的了解为有限的信息.此时,随机性安全博弈模型不再适用.
具有有限信息的安全博弈模型是通过引入特殊自然参与者,利用概率描述隐私保护中博弈参与者的未知属性信息,它适用于大多数真实的网络环境.但仍具有一定的局限性,在真实的网络安全问题中,其状态空间实际上是无限的,但在现有用以隐私保护的博弈模型的研究中,多数是基于假设其为有限的状态空间来进行近似求解,这在分析过程中,就可能得到不满意的结果.
表 2为这三种模型的隐私保护综合分析的对比.
| 安全博弈模型 | 隐私保护目的 | 典型应用场景 | 对应博弈模型 | 优点 | 局限性 |
| 确定性安全博弈 | 制定防御决策 | 网络入侵检测 | 完全信息静态博弈 | 对确定参数定量分析制定决策方案 | 不适用于真实网络环境不具有动态特性 |
| 制定投资方案 | 用户隐私信息投资 | 完全信息静态博弈 | |||
| 随机性安全博弈 | 预测攻击行为 | 动态网络入侵检测 | 完全信息动态博弈 | 可研究动态特征预测敌手行为 可描述策略因时间动态调整过程 |
对参与者未知属性信息无法研究 |
| 量化隐私保护策略 | 网络攻防分析 | 完全信息动态博弈 | |||
| 具有有限信息安全博弈 | 位置隐私保护机制 | 基于位置的服务 | 不完全信息静态博弈 | 用概率描述未知信息 适用于大多数网络环境 |
有限状态空间近似求解 |
| 排除恶意节点 | 无线自组织网络中隐私权衡 | 不完全信息动态博弈 |
采用博弈论方法解决隐私保护问题,通过求解博弈均衡点,找到满足多方利益的解决方案,从而达到平衡隐私保护和服务质量间关系的目的.然而,运用博弈论解决隐私保护问题也面临如下挑战:
1) 对用户隐私的量化问题.隐私量化是用博弈论分析隐私保护问题时必须要解决的问题,但同时也具有很大难度.现有工作对隐私的量化并没有给出统一的形式,仅仅从理论上进行抽象概括,部分工作采用具体数值表示隐私[31~33].
2) 对纳什均衡点的求解问题.在用博弈分析解决隐私保护问题时,为了达到博弈目标即纳什均衡,需要求解隐私博弈的纳什均衡解,而纳什均衡解很难在多项式时间求得.所以纳什均衡的计算复杂性对安全博弈仍是一个巨大挑战.
3) 数据可用性和隐私保护效率权衡问题.不同隐私保护方案对隐私数据信息的保护程度也各不相同,各类隐私保护方法实现隐私保护的效率和最终数据的可用性等方面均有不同,如何利用博弈论分析在保证数据可用性的同时提高隐私保护方法的时空效率也是未来下一步的研究方向.
| [1] |
WANG Y, WANG Y, LIU J, et al. A survey of game theoretic methods for cyber security[C/OL]. [2017-02-22]. https://www.researchgate.net/publication/308173085. DOI: 10.1109/DSC.2016.90.
|
| [2] |
DO C T, TRAN N H, HONG C, et al. Game theory for cyber security and privacy[J]. ACM Computing Surveys (CSUR), 2017, 50(2): 30. |
| [3] |
GOSSNER O. Repeated Games Played by Cryptographically Sophisticated Players[M]. Belgium: Université Catholique de Louvain, 1998: 10-16.
|
| [4] |
ASOKAN N, SHOUP V, WAIDNER M. Optimistic fair exchange of digital signatures[J]. IEEE Journal on Selected Areas in communications, 2000, 18(4): 593-610. DOI:10.1109/49.839935 |
| [5] |
朱建明, RAGHUNATHANS. 基于博弈论的信息安全技术评价模型[J]. 计算机学报, 2009, 32(4): 828-834. ZHU J M, RAGHUNATHAN S. Evaluation model of information security technology based on game theore-tic[J]. Journal of Computers, 2009, 32(4): 828-834. |
| [6] |
田有亮, 马建峰, 彭长根, 等. 秘密共享体制的博弈论分析[J]. 电子学报, 2011, 39(12): 2790-2795. TIAN Y L, MA J F, PENG C G, et al. Game-theoretic analysis of secret sharing scheme[J]. Acta Electronica Sinica, 2011, 39(12): 2790-2795. |
| [7] |
彭长根, 田有亮, 刘海, 等. 密码学与博弈论的交叉研究综述[J]. 密码学报, 2017, 4(1): 1-15. PENG C G, TIAN Y L, LIU H, et al. A survey on the intersection of cryptography and game theory[J]. Journal of Cryptologic Research, 2017, 4(1): 1-15. DOI:10.13868/j.cnki.jcr.000158 |
| [8] |
MANSHAEI M H, ZHU Q, ALPCAN T, et al. Game theory meets network security and privacy[J]. ACM Computing Surveys (CSUR), 2013, 45(3): 25. |
| [9] |
XIANG Y, WANG L. A game-theoretic study of load redistribution attack and defense in power systems[J]. Electric Power Systems Research, 2017, 151: 12-25. DOI:10.1016/j.epsr.2017.05.020 |
| [10] |
FIELDER A, PANAOUSIS E, MALACARIA P, et al. Decision support approaches for cyber security investment[J]. Decision Support Systems, 2016, 86: 13-23. DOI:10.1016/j.dss.2016.02.012 |
| [11] |
DO C T, TRAN N H, HONG C, et al. Game theory for cyber security and privacy[J]. ACM Computing Surveys (CSUR), 2017, 50(2): 30. |
| [12] |
周丹丹, 李威伟, 孙宇清. 博弈论隐私保护方法研究综述[J]. 小型微型计算机系统, 2015, 36(12): 2696-2700. ZHOU D D, LI W W, SUN Y Q. Survey on game theory based on privacy protection[J]. Journal of Chinese Computer Systems, 2015, 36(12): 2696-2700. DOI:10.3969/j.issn.1000-1220.2015.12.015 |
| [13] |
PAWLICK J, ZHU Q. A mean-field stackelberg game approach for obfuscation adoption in empirical risk minimization[EB/OL]. [2017-06-08]. https://arxiv.org/pdf/1706.02693.pdf.
|
| [14] |
FARRAJ A, HAMMAD E, Al D A, et al. A game-theoretic analysis of cyber switching attacks and mitigation in smart grid systems[J]. IEEE Transactions on Smart Grid, 2016, 7(4): 1846-1855. DOI:10.1109/TSG.2015.2440095 |
| [15] |
OROJLOO H, AZGOMI M A. A game-theoretic approach to model and quantify the security of cyber-physical systems[J]. Computers in Industry, 2017, 88: 44-57. DOI:10.1016/j.compind.2017.03.007 |
| [16] |
LASZKA A, JOHNSON B, GROSSKLAGS J. Mitigation of targeted and non-targeted covert attacks as a timing game[C]//Decision and Game Theory for Security. Switzerland: Springer International Publishing, 2013: 175-191. DOI: 10.1007/978-3-319-02786-9_11.
|
| [17] |
MA R, XIONG J B, LIN M W, et al. Privacy Protection-Oriented Mobile Crowdsensing Analysis Based on Game Theory[C/OL]. [2017-03-15]. http://ieeexplore.ieee.org/abstract/document/8029545/. DOI: 10.1109/Trustcom/BigDataSE/ICESS.2017.342.
|
| [18] |
MYERSON R B. Game Theory:Analysis Conflict[M]. Cambridge: Harvard University Press, 2013.
|
| [19] |
BASAR T, OLSDER G J. Dynamic Noncooperative Game Theory[M]. Philadelphia: Society for Industrial and Applied Mathematics, 1998: 265-363.
|
| [20] |
D'ACQUISTO G, FLAMINI M, NALDI M. A game-theoretic formulation of security investment decisions under ex-ante regulation[C]// Information Security and Privacy Research. Berlin: Springer, 2012: 412-423.
|
| [21] |
何建琼, 田有亮, 周凯. 可证明安全的社交网络隐私保护方案[J]. 网络与信息安全学报, 2016, 2(8): 62-67. HE J Q, TIAN Y L, ZHOU K. Provably secure social network privacy-preserving scheme[J]. Chinese Journal of Network and Information Security, 2016, 2(8): 62-67. DOI:10.11959/j.issn.2096-109x.2016.00082 |
| [22] |
姜伟, 方滨兴, 田志宏, 等. 基于攻防博弈模型的网络安全测评和最优主动防御[J]. 计算机学报, 2009, 32(4): 817-827. JIANG W, FANG B X, TIAN Z H, et al. Evaluating network security and optimal active defense based on attack-defense game model[J]. Chinese Journal of Computers, 2009, 32(4): 817-827. |
| [23] |
NICOL D M, SANDERS W H, TRIVEDI K S. Model-based evaluation: from dependability to security[J]. IEEE Transactions on Dependable and Secure Computing, 2004, 1(1): 48-65. DOI:10.1109/TDSC.2004.11 |
| [24] |
AVIZIENIS A, LAPRIE J C, RANDELL B, et al. Basic concepts and taxonomy of dependable and secure computing[J]. IEEE Transactions on Dependable and Secure Computing, 2004, 1(1): 11-33. DOI:10.1109/TDSC.2004.2 |
| [25] |
王元卓, 林闯, 程学旗, 等. 基于随机博弈模型的网络攻防量化分析方法[J]. 计算机学报, 2010, 33(9): 1748-1762. WANG Y Z, LIN C, CHENG X Q, et al. Analysis for network attack-defense based on stochastic game model[J]. Chinese Journal of Computers, 2010, 33(9): 1748-1762. |
| [26] |
RAYA M, SHOKRI R, HUBAUX J P. On the tradeoff between trust and privacy in wireless ad hoc networks[C]//Proceedings of the Third ACM Conference on Wireless Network Security. New York: ACM, 2010: 75-80.
|
| [27] |
SHOKRI R, THEODORAKOPOULOS G, TRONCOSO C, et al. Protecting location privacy: Optimal strategy against localization attacks[C]//Proceedings of the 2012 ACM Conference on Computer and Communications Security. New York: ACM, 2012: 617-627.
|
| [28] |
万盛, 李凤华, 牛犇, 等. 位置隐私保护技术研究进展[J]. 通信学报, 2016, 37(12): 124-141. WAN S, LI F H, NIU B, et al. Research progress of location privacy-preserving techniques[J]. Journal on communications, 2016, 37(12): 124-141. DOI:10.11959/j.issn.1000-436x.2016279 |
| [29] |
吴莎莎, 熊金波, 叶帼华, 等. 移动互联网环境下基于假位置的位置隐私保护研究[J]. 信息网络安全, 2016(10): 54-59. WU S S, XIONG J B, YE G H, et al. Research on location privacy protection based on dummy locations in mobile internet environment[J]. Netinfo Security, 2016(10): 54-59. DOI:10.3969/j.issn.1671-1122.2016.10.009 |
| [30] |
周凯, 彭长根, 何建琼, 等. 可证明安全的LBS中连续查询的轨迹隐私保护方案[J]. 信息网络安全, 2017(1): 007. ZHOU K, PENG C G, HE J Q, et al. Provable secure trajectory privacy preserving scheme for continuous queries in location-based services[J]. Netinfo Security, 2017(1): 43-47. DOI:10.3969/j.issn.1671-1122.2017.01.007 |
| [31] |
朱义杰, 彭长根, 李甲帅, 等. 一种结合查询隐私和位置隐私的LBS隐私度量框架[J]. 信息网络安全, 2016(2): 47-53. ZHU Y J, PENG C G, LI J S, et al. A framework of privacy metric in LBS combining query privacy with location privacy[J]. Netinfo Security, 2016(2): 47-53. DOI:10.3969/j.issn.1671-1122.2016.02.008 |
| [32] |
王彩梅, 郭亚军, 郭艳华. 位置服务中用户轨迹的隐私度量[J]. 软件学报, 2012, 23(2): 352-360. WANG C M, GUO Y J, GUO Y H. Privacy metric for user's trajectory in location-based services[J]. Journal of software, 2012, 23(2): 352-360. |
| [33] |
彭长根, 丁红发, 朱义杰, 等. 隐私保护的信息熵模型及其度量方法[J]. 软件学报, 2016, 27(8): 1891-1903. PENG C G, DING H F, ZHU Y J, et al. Information entropy models and privacy metrics methods for privacy protection[J]. Journal of Software, 2016, 27(8): 1891-1903. |
 2018, Vol. 64
2018, Vol. 64





