文章信息
- 彭冲, 徐鹏, 陈锟山, 岳显昌
- PENG Chong, XU Peng, CHEN Kunshan, YUE Xianchang
- 基于介质模型的城市环境中电磁场的统计分布
- Statistical Distributions of Electromagnetic Fields from Dielectric Rough Surfaces with Urban Buildings
- 武汉大学学报(理学版), 2016, 62(6): 542-546
- Journal of Wuhan University(Natural Science Edition), 2016, 62(6): 542-546
- http://dx.doi.org/10.14188/j.1671-8836.2016.06.009
-
文章历史
- 收稿日期:2015-08-09

2. 中国科学院 遥感与数字地球研究所,北京 100101
2. The Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China
城市居民小区内区的无线通信是一个非常重要的研究课题.由于高频信号在通信中的使用,使得用户接收信号在小范围内就会产生很强的信号变化,并且在波长的尺度范围内,信号的强度也会发生很强的波动.根据测量结果,尽管信号在小区域内随机变化,但进行数据还原分析之后,发现信号的变化规律符合统计学中的一些特性[1].因此,在城市环境中,系统设计人员更多地参考信号的统计分布特性来表达城市环境无线通信中传播信号的信道模型特性.
理论研究中,根据射线追踪、基尔霍夫-惠更斯(Kirchhoff-Huygens)近似等近似方法,以无线电波在平地面上的传播特性为基础,建立了许多城市中信号传播的模型[2~6],得到城市环境中电磁信号的分布,分析信号的距离衰减因子.这些模型在涉及城市建筑的计算时具有很多的局限,特别是在建筑的拐角处,处理过程复杂,计算量大,难以给出拐角处剧烈的电磁幅度和相位的变化.而采用基于Maxwell方程的数值仿真,能够求得精确解,相比于近似方法,具有更高的精度.文献[7]和[8]根据蒙特卡洛的数值模拟方法,研究了理想电导体(PEC)城市建筑物环境,在可变建筑物高度和可变排距下900 MHz通信信号的电磁场统计分布.本文在此基础上,将理想电导体模型延伸到介质模型,900 MHz单频信号延伸为中心频率为900 MHz的宽带信号,使得模拟结果更趋近于真实环境.由于多径效应不仅改变接收信号的幅度,也改变信号的相位分布,本文除研究常规的信号快衰落、慢衰落和距离关系等统计规律外,还拓展了信号相位分布和频率衰落的研究,探讨相位分布与信号多径模型之间的联系.
采用数值方法,会产生巨大的数据量,特别是在使用迭代法求解时,矩阵向量积的计算量和存储量在求解城市大尺度问题时会急剧增大,相对于理想电导体模型,介质模型矩量法计算的内存需求和计算量是前者的4倍.由于城市建筑物表面的大坡度影响,其矩阵方程条件数变得极差,使得其迭代法求解变得更难收敛,以致难以求解.因此,本文采用并行三角(LU)分解法直接求解.
1 积分方程的建立与离散图 1为二维城市环境的介质模型中信号自基站发射到用户接收的示意图.建筑物设定为矩形结构,3层楼高,约为9 m,标准偏差为0.1 m,建筑物的相对介电常数ε1=4(其中空气中相对介电常数ε=1).在建筑物之间的路面考虑为高斯相关随机粗糙面(如插图所示),均方根高度为0.01 m,相关长度为0.3 m,楼间距在15~20 m之间随机分布,为减少电脑存储量和运算量,把建筑物水平地面的坐标设为-4.5 m.由于路面与建筑的相对介电常数相差不大,也记为ε1=4.发射天线(x=0 m处)的信号源为柱面点源,表达式为
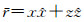

|
| 图 1 二维城市环境电磁场传播的介质模型 Figure 1 Dielectric model of electromagnetic propagation over 2-D urban environment |
考虑一个柱面点源入射到图 1所示的介质城市表面.根据Maxwell方程组,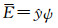


|
(1) |

|
(2) |
其中,



文中采用屋顶基函数和伽辽金法来离散此积分方程,在城市环境的介质模型中,其屋顶基函数的表达式为[7]:

|
(3) |
在建筑物顶部和路面,u=x;在建筑物侧面,u=z.离散之后的阻抗矩阵方程为[10]:

|
(4) |
其中,A(0)、B(0)、A(1)、B(1)代表阻抗矩阵元素;


为了确保采样精度,离散密度为每个波长20个点,采用并行LU分解来求解矩阵方程(4).
通过阻抗矩阵求出城市建筑环境表面的等效电磁流,根据惠更斯原理,得出离地面高1.5 m处散射场,再结合入射场,得出总场,也就是用户接收到的电磁波信号.
2 仿真数值结果及分析模拟仿真是在8核32 GB内存的电脑上运行的,运行平台为Intel Fortran.求解阻抗矩阵的方法采用的是Intel math kernel library里面的LU分解.阻抗矩阵中的未知数N=32 000, 每个模拟实现的完成需要约3.66 h.
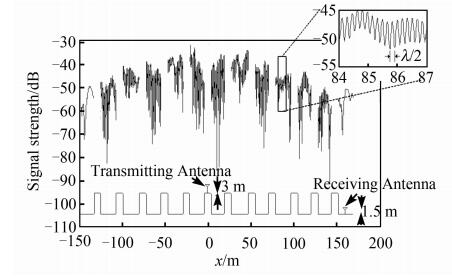
2.1 接收信号的幅度和相位图 2下面的部分为二维城市环境的剖面结构,显示了发射天线对应的位置(x=0 m处)和高度以及接收天线的高度.图 2上面的部分表示TE波入射情况下,城市街道上1.5 m处接收信号的幅值.图 2中放大的部分为水平位置84 m到87 m之间的场分布,显示两个峰值之间的距离为半个波长,相邻峰值间信号的强度发生近20 dB的巨大波动;在短距离内,信号一度达到了30 dB,这些都与文献[1]中的测量结果一致.
|
| 图 2 900 MHz下室外街道1.5 m高处TE波信号幅度 Figure 2 Total field at height of 1.5 m above the ground level for TE case at 900 MHz |
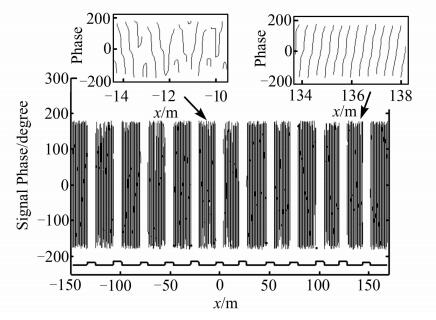
图 3显示电场在相应位置上的相位分布,并给出靠近天线的街道区域(-14~-10 m)以及远离天线的街道区域(134~138 m)的相位分布情况.相位的值域设定在(-π, π)的范围内,由于缺少2 kπ(k=…, -2, -1, 0, 1, 2, …)的相位补偿,有一些相邻两点之间的相位会从π跳到-π.因此,在两点之间出现大于π的相位差的时候截断,然后重新开始另外一个相位从-π到π的循环.如图 3所示,左上图显示楼房的拐角处以及靠近天线的街道,相位分布显现出相当大的波动,这说明在这些区域多路线的干扰显得非常大,多径传播的影响严重.右上图显示其他地方相位基本上呈线性分布.
|
| 图 3 城市环境室外街道上1.5 m高处信号的相位分布 Figure 3 Phase distributions of signal at height of 1.5 m above the ground level |
本文共完成了25次模拟,显示出很好的收敛性.根据这些模拟数据,采用文献[1]和文献[7]中的方法对信号的快衰落、慢衰落、距离关系以及频率衰落进行分析.
图 4的(a)和(b)分别表示TE波和TM波作为发射信号时接收信号的快衰落情况.如图所示,图中描绘3条曲线,分别为瑞利累计分布函数、K=3的Rician累计分布函数(CDF)以及本文统计的106 m到116 m共600个点信号的累计分布函数.对于TE波来说,如图 4(a)所示,模拟的结果跟K=3的Rician分布函数完美的符合,说明小区域信号变化呈Rician分布,这与文献[8]中PEC城市环境下的分布相同.而对于TM波来说,图 4(b)显示,跟TE波类似,符合Rician分布,但Rician分布的参数不同,K=1.5,说明TM波小区域内的接收信号波动更为稳定.

|
| 图 4 模拟结果的累计分布函数与莱斯、瑞利分布的对比(a) TE波; (b) TM波 Figure 4 Cumulative distribution functions of simulation, compared with Rayleigh distribution and Rician distribution (a) For TE case; (b) For TM case |
图 5显示出接收信号慢衰落的累计分布函数.纵坐标为高斯坐标,标准的正态累计分布函数显示为一条直线.模拟结果表明,距离天线85 m和135 m处的信号累计分布函数都趋近于正态分布,相应的电场就是对数正态分布.对于TE波,如图 5(a)所示,在85 m处信号累计分布函数的标准偏差为2.31 dB,在135 m处信号的标准偏差为4.79 dB.但对于TM波,图 5(b)显示,在85 m处信号的标准偏差为3.20 dB,在135 m处信号的标准偏差为6.80 dB,它的标准偏差大于TE波,这同PEC环境下的模拟结果类似.仿真结果显示城市环境中电磁场慢衰落趋近于对数正态分布,在不同的地方,它的分布类似,但参数不一样,离天线越远的地方标准偏差越大,信号的衰减越多.

|
| 图 5 距天线135 m和85 m处慢衰落的累计分布(a) TE波; (b) TM波 Figure 5 Cumulative distribution functions of slow fading at 85 m and 135 m (a) For TE case; (b) For TM case |
图 6表示接收信号随路径损耗的距离依赖关系.图中每个点都表示长4 m区域内的信号平均值.城市环境中的距离衰减因子依赖于基站天线高度,当天线比建筑物高时距离衰减因子小于4[1].天线入射到图 2城市环境下,最小二乘法的拟合结果如图 6所示,TE波和TM波的距离衰减因子n分别为3.70和3.89,其中,拟合的偏差是因为慢衰落的影响大于理想电导体城市模型中TE波(n=3.46)[8]和TM波(n=2.83)[7]的距离衰减因子.由于介质模型中TM波存在Brewster角的影响,相同条件下TM波的距离衰减因子反而比TE波稍大一些,并且更接近于城市蜂窝系统基站天线测量的3.75[1].

|
| 图 6 最小二乘法拟合的距离关系(a) TE波(n=3.70);(b) TM波(n=3.89) Figure 6 Least-square fit straight line of the small-area averages (a) For TE case: The rang index is n=3.70; (b) For TM case: The range index is n=3.89 |
根据多径模型理论,不同长度的射线路径的相位会随着频率的变化而变化,而接收信号幅度也将随着频率变化[1].图 7显示了无线信道与频率之间的关系.图中曲线为同一个城市环境TE波频率从897 MHz变化到903 MHz而产生的信号强度变化曲线,中心频率为900 MHz,频率离散的步长为0.15 MHz.如图所示,最小值之间的频率差接近于1 MHz.在约300 m的路径下,相位发生2π的变化,频率差约为1 MHz[1],这与图中频率最小值之间的间距基本相符合,很好的验证了文献[1]中的结论.

|
| 图 7 距离天线110 m和145 m处,随着中心频率900 MHz变化的场分布图 Figure 7 Fields of 110 m and 145 m away from the transmitting antenna plotted with frequency variation at the center frequency of 900 MHz for the urban environment |
本文基于Maxwell方程组的数值模拟方法,以通信中传播信号对建筑物的响应为基础,从理论上研究了城市环境中微蜂窝无线通信模型的信道传播特征.研究表明不同的极化天线传播的效应相似,但小区域和长距离内的衰减程度不一样,相对于水平极化天线,垂直极化天线发射的信号在小区域内波动稳定,但长距离内衰减更快.在实际通信中,应依所处实际环境和用户体验,选用合适的天线,达到更好的通信效果.频率衰落理论验证了多径效应,信号的相位分布体现在天线附近多径效应的复杂性,借此可选取合适的基站地点.当然,由于真实的城市环境是三维的,解决三维城市环境的大尺度问题是下一步研究的方向.
| [1] | BERTONI H L. Radio Propagation for Modern Wireless Systems.[M] Upper Saddle River: Prentice-Hall, 2000 : 15 -33. |
| [2] | LIU Z Y, GUO L X, FAN T Q. Microcellular propagation prediction model based on an improved ray tracing algorithm[J]. Journal of the Optical Society of America A , 2013, 30 (11) : 2372–2380 DOI:10.1364/JOSAA.30.002372 |
| [3] | HE R S, ZHONG Z D, AI B, et al. Analysis of the relation between Fresnel zone and path loss exponent based on Two-Ray model[J]. IEEE Antennas & Wireless Propagation Letters , 2012, 11 (1) : 208–211 |
| [4] | JANASWAMY R. Path loss predications in the presence of buildings on flat terrain: A 3-D vector parabolic equation approach[J]. IEEE Transactions on Antennas & Propagation , 2003, 51 (8) : 1716–1728 |
| [5] | PEDERSEN K I, MOGENSEN P E, FLEURY B H. A stochastic model of the temporal and azimuthal dispersion seen at the base station in outdoor propagation environments[J]. IEEE Transactions on Vehicular Technology , 2000, 49 (2) : 437–447 DOI:10.1109/25.832975 |
| [6] | HAN C, BICEN A O, AKYILDIZ I F. Multi-ray channel modeling and wideband characterization for wireless communications in the terahertz band[J]. IEEE Transactions on Wireless Communications , 2015, 14 (5) : 2402–2412 DOI:10.1109/TWC.2014.2386335 |
| [7] | XU P, LAM K W, TSANG L, et al. Statistical distributions of fields in urban environment based on Monte Carlo simulations of Maxwell Equations[J]. IEEE Antennas & Wireless Propagation Letters , 2004, 3 (1) : 34–37 |
| [8] | XU P, TSANG L. Propagation over terrain and urban environment using the multilevel UV method and a hybrid UV/SDFMM method[J]. IEEE Antennas & Wireless Propagation Letters , 2004, 3 (1) : 336–339 |
| [9] | TSANG L, KONG J A, DING K H, et al. Scattering of Electromagnetic Waves: Numerical Simulations.[M] New York: Wiley, 2001 : 114 -118. |
| [10] | XU P, TSANG L. Bistatic scattering and emissivities of lossy dielectric surfaces with exponential correlation functions[J]. IEEE Transactions on Geoscience & Remote Sensing , 2007, 45 (1) : 62–72 |
 2016, Vol. 62
2016, Vol. 62





