文章信息
- 李华贞 , 张强 , 顾西辉 , 孙鹏 , 孔冬冬 . 2016
- LI Huazhen, ZHANG Qiang, GU Xihui, SUN Peng, KONG Dongdong . 2016
- 北江流域洪水量级、频率和峰现时间时空特征及影响因子
- Flooding Processes in the North River Basin: Magnitude, Frequency, Timing and Influencing Factors
- 武汉大学学报(理学版), 2016, 62(4): 389-400
- Journal of Wuhan University(Natural Science Edition), 2016, 62(4): 389-400
- http://dx.doi.org/10.14188/j.1671-8836.2016.04.014
-
文章历史
- 收稿日期:2016-02-22

2. 中山大学 华南地区水循环与水安全广东省普通高校重点实验室,广东 广州 510275 ;
3. 中山大学 广东省城市化与地理环境空间模拟重点实验室,广东 广州 510275 ;
4. 安徽师范大学 国土资源与旅游学院,安徽 芜湖 241003
2. Key Laboratory of Water Cycle and Water Security in Southern China of Guangdong High Education Institute, Sun Yat-sen University, Guangzhou 510275, Guangdong, China ;
3. Guangdong Provincial Key Laboratory of Urbanization and Spatial Simulation of Geographical Environment, Sun Yat-sen University, Guangzhou 510275, Guangdong, China ;
4. College of Territorial Resources and Tourism, Anhui Normal University, Wuhu 241003, Anhui, China
在气候变化和人类活动的综合影响下,区域降水[1]及洪涝灾害变化特征[2]均发生较大变异,径流序列的“平稳性”已不复存在[3],基于平稳性假设的方法也不再适用于水文频率分析.近年来,广义可加模型(generalized additive models for location scale and shape,GAMLSS)[4-6]在经济学、医学和生态学等领域已得到广泛应用,而其在水文领域的应用也引起广泛关注.顾西辉等[7]采用GAMLSS模型分析了珠江流域28个测站年最大洪峰流量序列的非平稳性.L’opez等[8]采用GAMLSS模型以气候和水库指标作为解释变量,对1950-2007年西班牙大陆河流的年最大流量序列的非平稳性进行了分析.
北江属珠江水系,是广东省境内一条重要河流,认识北江流域降水径流变化规律,对研究区域水量平衡和合理开发利用水资源都有重要意义[9].李艳等[10]对北江流域水文序列在属性、时间及空间上的变异进行了多角度研究分析,指出1973年可能会是北江流域径流量序列变异的一个分界线.赖成光等[11]评价了北江流域洪灾风险,并与历史发生的大洪水(选取了1915,1949,1982及1994年北江流域典型的4次极端洪水灾害)相比较,明确指出了北江流域洪灾较重及风险较高的区域.王亚雄等[12]采用斯波尔曼和MK法分析了北江下游年径流量变化趋势和变异情况,并在此基础上建立了北江下游年径流量的加权马尔可夫链预测模型.黎坤等[13]对北江天然径流量的变化特征进行了分析,发现1984年后北江流域持续丰水和持续枯水时段开始变长.
上述文献对北江流域径流量研究较多,但多针对单一指标,而未对径流量的非平稳性进行深入定量分析.基于此,本文采用9种洪水指标,从年、季节及POT(超定量采样)等多角度展开北江流域洪水特征研究,为考虑气候变化对水文极值序列一致性的影响,采用GAMLSS模型,将时间和气候指标(采用北大西洋涛动NAO、印度洋偶极子IOD、太平洋年代际振荡PDO 和厄尔尼诺南方涛动ENSO 4种气候指标的年平均值)统一纳入洪水频率分析中,对北江流域年最大洪峰流量序列及超定量洪水发生次数进行拟合分析,以期为科学理解北江流域洪水变化特征、及北江流域防洪减灾与灾害评估提供依据.
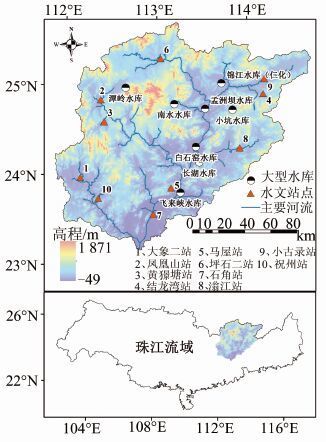
1 研究区域及数据来源北江系珠江流域第二大支流,流域总面积46 710 km2(广东省占流域总面积的92%),干流总长468 km,总落差310m,河道平均坡降为0.26‰,流域内有韶关、清远和佛山3市,大部分是山区和丘陵,地势北高南低[14].该流域至2010年止已建成飞来峡水利枢纽、湾头水利枢纽、南水、孟洲坝、锦江(仁化) 、潭岭、长湖、锦潭、小坑、白石窑和濛里等共11座大型水库[15](图 1),总库容为49.744 亿m3,对北江下游年径流量变化产生重要影响.
|
| 图 1 北江流域以及本文所研究的水文站点与水库在北江流域分布示意图 Figure 1 Locations of the Beijiang River Basin,and the hydrometric stations and dams in Beijiang River Basin studied in this paper |
本文选取北江流域10个代表性水文站点(图 1)的1959-2005年(共47 a)的逐日流量序列资料,数据来源于广东省水文局,经过系统整编,质量可靠.
2 研究方法 2.1 洪水指标采用年最大值抽样和POT采样两种方法对北江流域日流量序列进行抽样处理[16](采用日历年),从中选取9种洪水指标[17](见表 1).前面6种洪水指标(AMF,AMFD,AMFSp,AMFSu,AMFAu,AMFWi)均采用年最大值抽样获得.其中,AMFD即为AMF发生时的对应日期,同时AMF的数值与4个季节AMFSp,AMFSu,AMFAu和AMFWi中的最大值相等.后面3种洪水指标(POT3M,POT3F,MDF)均采用POT抽样获得.其中,POT3F为每年选择的样本数量,POT3M表示每个选出样本的量级,MDF则是用来描述POT序列的发生时间,它是将洪水发生日期向量化的一个定向统计[16].年最大值采样仅选取一年中最大那场洪水,会忽略低于最大那场洪水的其他大洪水信息;而对于一年中没有洪水发生的干旱年份,选取年最大流量值作为洪水信息会影响研究结果的代表性[17].为了弥补年最大值取样的上述缺陷,本文增加了POT采样,扩大样本容量,以增加洪水样本的多样性和代表性[17].本文采用美国水资源协会(USWRC)提出的判别标准[18],对洪峰独立性进行判别.
| 洪水指标 | 定义 |
| AMF | 年最大1日流量 |
| AMFD | 年最大1日流量发生日期 |
| AMFSp | 春季(3-5月)最大1日流量 |
| AMFSu | 夏季(6-8月)最大1日流量 |
| AMFAu | 秋季(9-11月)最大1日流量 |
| AMFWi | 冬季(1,2,12月)最大1日流量 |
| POT3M | 超过阈值的洪峰流量,平均每年2.4~3个洪水样本 |
| POT3F | POT采样,每年选择的样本数量 |
| MDF | POT采样,每年选择的洪水发生的平均日期 |
时间趋势特征主要包含单调趋势变化和变异[17].国际气象组织(WMO)建议使用非参数Mann-Kendall趋势检验法[19].为保证足够长的时间尺度以利于分析研究,本文使用一个21 a的移动窗口,以最大限度地增加每一个窗口的年数和可视窗口的数目[20].
变异点检测方法有多种[21],雷红富等[22]研究发现,秩和检验法在多种变异点检测方法中最优.Killick和Eckley[23]提出的单变异点检测方法(AMOC),可以克服序列正态分布假设的限制.因此,本文选择非参数的秩和检验法和参数的AMOC检验法分别检测变异点,然后综合判定最佳改变时间节点[22-24].
2.3 GAMLSS模型在GAMLSS模型[25]中,假设因变量yi(i=1,2,…,n)相互独立且服从分布函数FY(yi|θi),分布参数向量θi(i=1,2,…,p)[17].记gk(·)为单调连接函数,则分布参数θk与解释变量Xk之间的回归关系如下:
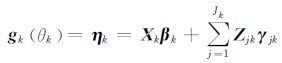
|
(2) |
(2) 式中:ηk和θk均为n维参数向量,βkT={β1k,β2k,…,βJkk}为Jk维线性回归系数向量,Xk为n×Jk阶解释变量矩阵,Zjk为n×qjk阶设计矩阵,γjk为qjk维正态分布的随机效应系数变量.
当解释变量为时间t 时,分布参数与解释变量的函数关系为:

|
(3) |
GAMLSS模型可以同时对各种分布参数建立回归模型,具有很大的灵活性.本文选取5种两参数极值分布(θ1和θ2分别对应均值和方差):Gumbel(GU),Gamma(GA),Logistic(LO),Lognormal(LOGNO)和Weibull(WEI).通过GAMLSS 模型,以时间t和4种气候指标(NAO,IOD,PDO和ENSO)作为解释变量,分别构造参数θ1和θ2与解释变量的线性或非线性函数关系.当分布参数为常量ct时,为平稳性模型Model 0;当分布参数随时间t变化时,为非平稳性模型Model 1;当分布参数随气候指标变化时,为非平稳性模型Model 2.用AIC值(akaike information criterion)选取最优拟合分布及相应函数,用Filliben系数检验模型拟合质量.
3 结果与讨论 3.1 POT采样阈值的确定POT采样阈值的选取需符合3个条件:1) 年平均发生次数AOA在2.4~3之间;2) 样本分散指数DI位于合适的置信区间,从而使POT抽样洪水发生次数服从泊松分布;3) 超定量样本超过部分均值MRL是阈值的线性函数.由以上条件判定大象二站、凤凰山站、黄猄塘站、结龙湾站、马屋站、坪石二站、石角站、滃江站、小古录站、祝州站的阈值分别为:209.5,350.5,175.5,45.45,77.1,712.5,5 350,345,328,138.65 m3/s.
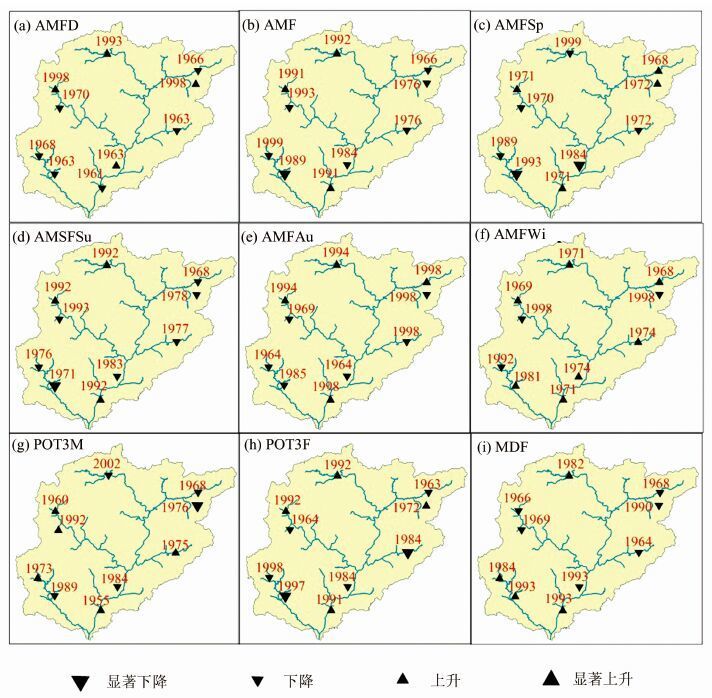
3.2 洪水要素变异和趋势特征图 2为9种洪水指标时间趋势和最佳改变时间点空间分布图.从图 2知,北江流域年最大洪峰流量总体呈下降趋势,其中祝州站呈显著下降趋势;流域中西部地区的站点年最大洪峰流量突变多发生于1980年代中后期,而流域上游的站点年最大流量突变点发生于1960年代中后期到1970年代中期;凤凰山站、结龙湾站、马屋站以及坪石二站的年最大洪峰流量发生日期(图 2(a))出现推迟现象;其他6站年最大洪峰流量发生日期均出现提前现象.
|
| 图 2 北江流域9种洪水指标时间趋势和最佳改变时间点空间分布 Figure 2 Spatial distribution of trends and change points of nine flood indices in the Beijiang River Basin |
北江流域大气环流随季节变化,夏季盛吹东南风和偏南风,冬季常为北风和偏北风,因此其洪水季节性变化较为明显.马屋站和祝州站春季洪水量级均呈显著下降趋势,且在1990年左右发生突变(图 2(c)).北江流域夏季高温湿热,水汽含量大,暴雨集中,洪峰流量一般较大,年最大洪峰流量一般出现在夏季.因此,夏季洪峰流量的趋势和突变特征与年最大洪峰流量基本一致(图 2(b)和(d)).北江流域秋季常有热雷和台风雨,但是只有凤凰山站、坪石二站、石角站和小古录站的秋季最大洪峰流量呈上升趋势,并分别于1994年、1994年、1998年和1998年发生突变;其他6站的秋季最大洪峰流量均呈下降趋势(图 2(e)).北江流域冬季低温,雨量稀少,而从图 2(f)可以看出,只有大象二站、黄猄塘站和结龙湾站冬季洪峰流量呈下降趋势,并分别于1992年、1998年、1998年发生突变;其他7站冬季洪峰流量均呈上升趋势,且洪峰流量突变时间为1960年代末到1970年代初之间(祝州站洪峰流量的突变时间为1981年).这与中国降水季节性变化研究结果相一致,即冬季降水有上升趋势[26].
对于POT采样序列,北江流域西南部地区的站点超定量洪水量级大均呈上升趋势;而北江流域东北部地区的站点超定量洪水量级均呈下降趋势,其中结龙湾站呈显著下降趋势并于1976年发生突变(图 2(g)).北江流域大部分站点洪水发生次数的突变发生于1980年代中期到1990年代,其中滃江站和祝州站均呈显著下降趋势,分别于1984年、1997年发生突变(图 2(h)).北江流域中下游地区各水文站的超定量洪水发生时间均在推迟,而上游地区各水文站的超定量洪水发生时间则均在提前(图 2(i)).
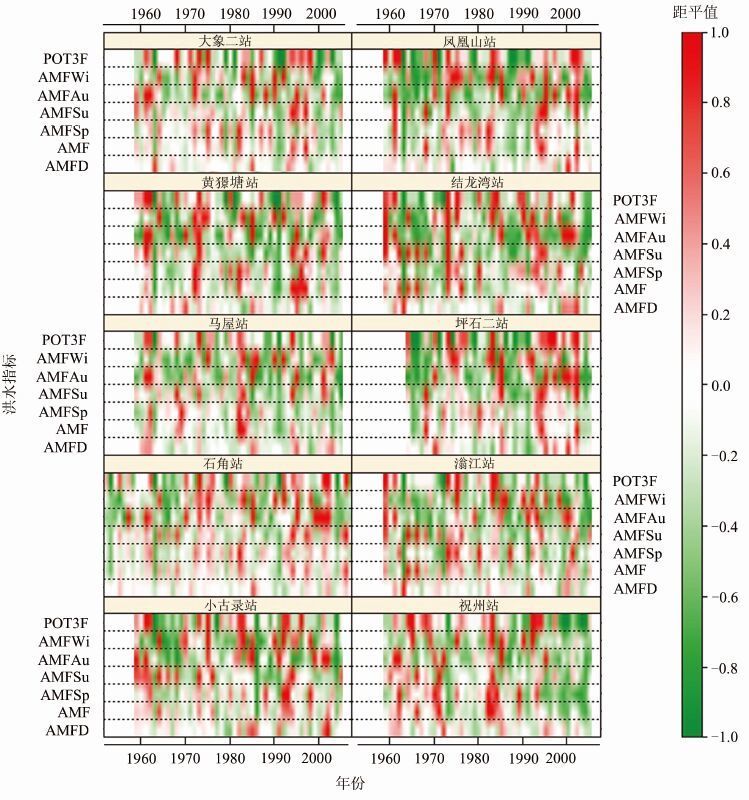
北江流域水文站点7个指标的距平值时间变化特征如图 3所示.从图中可以看出,大象二站和祝州站几乎所有的洪水指标在1990年代中后期以后,均低于均值,说明两站处于洪水逐渐减少的时期;而在1980年代到1990年代中期,几乎所有洪水指标位于均值之上,说明两站处于洪水多发期,这可能是由于该支流上无大型水库的调蓄作用而引起的.北江流域上游(凤凰山站、黄猄塘站、结龙湾站和坪石二站)在1990年代以后,大部分的洪水指标均处于均值之上,洪水较为丰富.尤其是坪石二站,在1990-2003年间几乎所有的洪水指标均处于均值之上.滃江站在1980年代之后,洪水发生次数一直处于均值水平之下,但是冬季洪峰流量却大都高于整个时期的均值.石角站和小古录站在整个研究时期内的各个洪水指标基本上都处于均值之上,说明洪水较为丰富.
|
| 图 3 各水文站点洪水指标距平值时间变化图 注:绿色表示指标低于均值,红色表示指标高于均值 Figure 3 Temporal changes of the differences of flood indices of each hydrological station |
为了更好地反映北江流域不同时期内的洪水特征,采用基于21年时间窗口的滑动Mann-Kendall法进行分析研究,结果见图 4.

|
| 图 4 各水文站点洪水指标滑动MK值时间变化图 Figure 4 The MK variations of flood indices of each hydrological station |
由图 4可知,大象二站春季和冬季洪峰流量由1958年滑动至1968年呈上升或显著上升趋势,1969年滑动至1988年呈下降趋势;而夏季洪峰流量和洪水发生次数由1958年滑动至1975年呈下降或显著下降趋势,1976年滑动至1982年呈上升或显著上升趋势.值得注意的是,大象二站洪水发生的平均时间从1968年起表现为推迟趋势(图 4,大象二站).北江流域上游大部分洪水指标体现出3个阶段:从起始年份滑动至1968年呈显著上升趋势,1969-1975年呈显著下降趋势和1976-1988年呈显著上升趋势(图 4,凤凰山站、黄猄塘站、结龙湾站和坪石二站).马屋站春季和年最大洪峰流量从1958年以后持续处于下降或显著下降趋势;祝州站洪水发生次数从1958年起,持续处于下降或显著下降趋势;值得注意的是,马屋站和祝州站洪水发生的平均时间和年最大洪峰发生的时间从1972年起均表现为推迟趋势(图 4,马屋站和祝州站).滃江站和小古录站的洪水变化特征较为复杂,几乎不存在持续变化的趋势特征;值得注意的是,两站的洪水发生次数自1970年起处于持续下降趋势(图 4,滃江站和小古录站).
图 5为各水文站点的年和各季节量级大于10年一遇[27]及实测以来最大三场洪水的时间和空间分布特征.大象二站年及各季节最大三场洪水集中在1982-1997年,发生洪水的状况愈演愈烈,秋季实测以来最大三场洪水集中发生在1994-1997年(图 5,大象二站).凤凰山站、黄猄塘站、结龙湾站、马屋站、坪石二站、石角站和滃江站7站实测以来最大三场洪水和重现期大于10年的洪水在整个观测期内分布较为均匀,其中凤凰山站、黄猄塘站、坪石二站和石角站4站的洪水发生次数在1992-2002年均较之前有明显增加,这与滑动Mann-Kendall法得出的结论一致;另外,凤凰山站和坪石二站的5种指标在1992-1995年均集中出现了实测以来的最大三场洪水,黄猄塘站的5种指标在1992-1997年集中出现了实测以来的最大三场洪水,结龙湾站和马屋站在2000-2003年集中发生了5场重现期大于10年的洪水,而石角站在2001-2002年集中发生了实测以来的春季最大三场洪水,面临越来越大的春季洪水威胁(图 5,凤凰山站、黄猄塘站、结龙湾站、马屋站、坪石二站、石角站和滃江站).小古录站和祝州站的年最大和季节实测以来最大三场洪水以及重现期大于10 a的洪水都主要集中在1982年以后,其中小古录站实测以来的最大三场洪水集中在1990-1994年,祝州站实测以来的最大三场洪水集中在1982-1985年(图 5,小古录站和祝州站).

|
| 图 5 基于GEV分布的各水文站点年以及季节洪水重现期时间分布图 Figure 5 Temporal variations of the GEV-based return periods of the floods at the annual and seasonal time scales |
各水文站点最大三场洪水均表现为在时间上容易集中在某一时期(例如小古录站集中在1990-1994年,图 5),并且出现在某一年份,多个水文站点同时发生洪水的现象(例如1983年,研究的10个水文站点均爆发了实测以来的冬季最大三场洪水,图 5).
3.3 洪水量级和频率的非平稳性模型用AIC 准则分别确定在Model 0,Model 1和Model 2条件下年最大流量序列的最优拟合分布、最小AIC值及分布参数与解释变量之间的最优函数关系(表 2).总体上看,Lognormal,Weibull和Gamma 分布对北江流域年最大流量序列拟合较好,是3 种模型选择次数最多的分布.对于Model 0,有6个站点的年最大流量序列的最优拟合分布是Lognormal分布.对于Model 1,有5个站点的最优拟合分布是Lognormal分布,有4个站点的最优拟合分布是Weibull分布,大象二站、马屋站、石角站和滃江站的分布参数之一表现出与时间t 的线性依赖关系,马屋站和祝州站的分布参数之一表现出与时间t的非线性依赖关系,而结龙湾站的分布参数θ1和θ2 均表现出与时间t的非线性依赖关系(cs(t)).对于Model 2,其中有6个站点的年最大流量序列的最优拟合分布是Lognormal分布,气候指标IOD是分布参数的最佳解释变量,其中有6个站点的分布参数与气候指标IOD形成线性或非线性的依赖关系,有4个站点的分布参数与气候指标ENSO形成线性或非线性的依赖关系.黎坤等[13]的研究也表明,厄尔尼诺现象对北江有滞后影响,厄尔尼诺现象出现的次年北江年径流量普遍增大.
| 站点 | Model 0 | Model 1 | Model 2 | |||||||
| 最佳分布 | AIC | 最佳分布 | θ1 | θ2 | AIC | 最佳分布 | θ1 | θ2 | AIC | |
| 大象二站 | GA | 604 | WEI | ct | t | 602 | WEI | cs(IOD) | ct | 590 |
| 凤凰山站 | GA | 662 | GA | ct | ct | 662 | LOGNO | ct | IOD+NAO | 649 |
| 黄猄塘站 | LOGNO | 622 | LOGNO | ct | ct | 622 | GA | cs(IOD)+cs(ENSO) | IOD | 599 |
| 结龙湾站 | LOGNO | 513 | WEI | cs(t) | cs(t) | 502 | LOGNO | cs(ENSO) | PDO+ENSO | 503 |
| 马屋站 | LOGNO | 539 | LOGNO | t | cs(t) | 538 | LOGNO | ct | IOD+PDO | 529 |
| 坪石二站 | LOGNO | 637 | LOGNO | ct | ct | 637 | LOGNO | ct | ENSO | 635 |
| 石角站 | WEI | 1 066 | WEI | t | ct | 1 065 | LO | NAO+cs(IOD) | ENSO+NAO | 1 057 |
| 滃江站 | LOGNO | 693 | LOGNO | ct | t | 690 | LOGNO | IOD | PDO | 687 |
| 小古录站 | WEI | 654 | WEI | ct | ct | 654 | WEI | ct | ct | 654 |
| 祝州站 | LOGNO | 606 | LOGNO | cs(t) | ct | 598 | LOGNO | ct | ct | 606 |
| 注:ct表示常量 | ||||||||||
表 3总结了各模型拟合残差的分布矩以及计算的FIlliben系数值,主要用来检验表 2中所选的年最大流量序列最优拟合分布及分布参数与解释变量函数关系的拟合优度,并反映模型是否很好地拟合了数据.从表 3我们可以看出,对于Model 0,Model 1和Model 2,FIlliben系数没有表现出明显偏离正常的残差值,所有模型的Filliben系数均高于0.95,说明模型拟合质量满足分析要求.
| 站点 | Model 0 | Model 1 | Model 2 | ||||||
| Mean | Variance | Filliben | Mean | Variance | Filliben | Mean | Variance | Filliben | |
| 大象二站 | 0.000 | 1.021 | 0.987 | 0.020 | 1.004 | 0.995 | -0.009 | 1.092 | 0.987 |
| 凤凰山站 | 0.000 | 1.022 | 0.986 | -0.008 | 1.017 | 0.988 | 0.003 | 1.022 | 0.989 |
| 黄猄塘站 | 0.000 | 1.022 | 0.988 | 0.000 | 1.022 | 0.994 | 0.004 | 1.026 | 0.991 |
| 结龙湾站 | 0.000 | 1.022 | 0.982 | 0.043 | 0.979 | 0.994 | 0.040 | 1.020 | 0.982 |
| 马屋站 | 0.000 | 1.022 | 0.967 | 0.017 | 1.021 | 0.990 | 0.001 | 1.022 | 0.991 |
| 坪石二站 | 0.000 | 1.024 | 0.986 | 0.000 | 1.024 | 0.987 | 0.027 | 1.024 | 0.986 |
| 石角站 | 0.002 | 0.989 | 0.991 | -0.002 | 1.009 | 0.993 | -0.006 | 0.956 | 0.984 |
| 滃江站 | 0.000 | 1.022 | 0.976 | 0.008 | 1.022 | 0.991 | -0.039 | 1.020 | 0.992 |
| 小古录站 | -0.002 | 1.033 | 0.989 | -0.002 | 1.033 | 0.988 | -0.002 | 1.033 | 0.989 |
| 祝州站 | 0.000 | 1.022 | 0.993 | 0.000 | 1.022 | 0.988 | 0.000 | 1.022 | 0.993 |
| 注:Mean表示均值;Variance表示方差;Filliben表示拟合FIlliben系数值(高于0.95表示拟合精度较高) | |||||||||
分别在Model 0,Model 1 和Model 2 条件下估计北江流域大象二站、坪石二站、石角站和滃江站4 个站点百年一遇设计洪水流量值[27]如图 6所示.Model 0,Model 1和Model 2设计洪水值具有明显不同的变化特征.大象二站Model 0估计的设计值为固定值821 m3/s;Model 1估计的设计值最小为579 m3/s,最大为1 001 m3/s,整个时期内一直呈上升趋势,并且1959-1993 年百年一遇设计洪水值低于Model 0,1993 年之后百年一遇设计洪水值高于Model 0;Model 2估计的设计值最小为553 m3/s,最大为1 224 m3/s,整个时期内基本稳定随机分布在Model 0之下,其中1972、1994和1997年发生了较为明显的突变,表现出洪水特征的不稳定性(图 6,(a)大象二站).坪石二站和石角站Model 0估计的设计值分别为2 852 m3/s和16 915 m3/s;Model 1整个时期内均一直呈线性上升趋势,并且起始年份到1985 年百年一遇设计洪水值均低于Model 0,1985 年之后百年一遇设计洪水值均高于Model 0,这与叶长青等[28]的研究结论一致,即非平稳性洪水设计值随时间由小增大;Model 2整个时期内基本均在Model 0上下范围内稳定随机波动(图 6,(b)坪石二站,(c)石角站).滃江站Model 0估计的设计值为固定值2 428 m3/s;Model 1估计的设计值最小为1 535 m3/s,最大为3 830 m3/s,整个时期内一直呈下降趋势,并且1959-1977 年百年一遇设计洪水值高于Model 0,1977 年之后百年一遇设计洪水值低于Model 0;Model 2估计的设计值最小为1 164 m3/s,最大为5 566 m3/s,整个时期内百年一遇设计洪水值呈随机性变化,1959-1975 年在高于Model 0 的区域内呈现平稳随机波动,1975 年之后突然下降,在低于Model 0的区域内呈平稳随机波动(图 6,(d)滃江站).

|
| 图 6 在Model 0、Model 1和Model 2 条件下百年一遇设计流量值 Figure 6 The 100-years design flow values based on Models 0,1,2 |
用AIC 准则分别确定在Model 1和Model 2下洪水发生次数的Filliben系数值、最小AIC值及分布参数与最佳解释变量之间的最优函数关系(表 4).对于Model 1,黄猄塘站和滃江站的分布参数θ1表现出与时间t 的线性依赖关系,坪石二站和祝州站的分布参数θ1表现出与时间t 的非线性依赖关系.对于Model 2,气候指标IOD和NAO是分布参数的最佳解释变量,其中有6个站点的分布参数分别与气候指标IOD和NAO形成线性的依赖关系,而祝州站的分布参数与气候指标ENSO形成线性的依赖关系.从表 4我们可以看出,对于Model 1和Model 2,FIlliben系数没有表现出明显偏离正常的残差值,所有模型的Filliben系数均高于0.95,说明模型拟合质量满足分析要求.
| 站点 | Model 1 | Model 2 | ||||
| Filliben | θ1 | AIC | Filliben | θ1 | AIC | |
| 大象二站 | 0.993 | ct | 194 | 0.989 | NAO | 193 |
| 凤凰山站 | 0.990 | ct | 186 | 0.990 | ct | 186 |
| 黄猄塘站 | 0.993 | t | 194 | 0.995 | NAO | 192 |
| 结龙湾站 | 0.988 | ct | 185 | 0.982 | IOD | 181 |
| 马屋站 | 0.979 | ct | 179 | 0.987 | ct | 179 |
| 坪石二站 | 0.989 | cs(t) | 164 | 0.992 | NAO | 166 |
| 石角站 | 0.995 | ct | 223 | 0.998 | ct | 223 |
| 滃江站 | 0.984 | t | 183 | 0.973 | IOD | 182 |
| 小古录站 | 0.996 | ct | 185 | 0.991 | IOD | 185 |
| 祝州站 | 0.973 | cs(t) | 197 | 0.991 | ENSO | 203 |
图 7是分别以时间(Model 1) 和气候指标(Model 2) 为解释变量的6个水文站点洪水发生次数拟合效果.Model 1能够初步反映洪水发生次数的时间特征.对于Model 1,黄猄塘站、滃江站和祝州站从1985年左右开始,洪水发生次数有一个阶梯下降的过程,而在1985年前洪水发生次数是一个较为平稳的直线,这与前面图 3结论相一致(图 7(b),(d),(f));坪石二站从1990年左右开始,洪水发生次数有一个阶梯上升的过程,而在1990年前洪水发生次数是一个较为平稳的直线,这与前面图 4结论相一致(图 7(c));大象二站和小古录站在整个时期内的洪水发生次数分位数(5%和95%)是一个较为平稳的直线,无法体现出洪水发生次数的起伏状态.(图 7(a),(e)).将额外的解释变量气候指标纳入到模型中(Model 2) 则能明显改善这种情况,更充分的抓住洪水发生次数的波动和离散特征.

|
| 图 7 基于GAMLSS模型分别以时间(Model 1) 和气候指标(Model 2) 为解释变量拟合各水文站点洪水发生次数序列 Figure 7 Modeled flooding frequency by taking time (Model 1) and climate indices (Model 2) as covariate using GAMLSS |
本文针对北江流域10个代表性水文站点的1959-2005年(共47 a)的逐日流量序列资料,运用滑动秩和检验法和AMOC检验法综合确定样本最佳突变点,采用MK检验法检测时间趋势性,并结GAMLSS模型分别构建洪水量级和频率与影响因子的非平稳性模型,得出如下结论:
1) 由于气候变化和人类活动影响的加剧,北江流域年及季节洪峰流量普遍呈下降或显著下降趋势,并在1990年左右发生突变,与王亚雄等[12]的研究结果一致,即在气候变化和人类活动的综合影响下,北江年径流总量呈减少趋势.同时,王亚雄等[12]对变化环境下北江下游年径流量的加权马尔可夫链预测结果表明,在未来长期过程中,北江下游平水年出现的机会最多.由本文图 2也可以看出,北江流域年最大洪峰流量发生时间和超定量洪水发生时间均呈向前推移的趋势.
2) 大量级洪水(最大三场洪水及重现期大于10 a的洪水)多集中发生在1990年之后,北江流域洪水发生频率、量级及峰现时间均发生了较大改变.各水文站点最大三场洪水均表现为在时间上容易集中在某一时期(例如小古录站集中在1990-1994年,图 5),并且在同一年份同时发生在多个水文站点(例如1983年,研究的10个水文站点均爆发了实测以来的冬季最大三场洪水,图 5).
3) 在GAMLSS模型中,对于年最大洪峰流量序列,LOGNO分布为选择次数最多的最优极值分布,并且通过各种指标(包括Filliben系数)的检验分析,验证了所选分布模型的总体拟合效果较好,并在Model 0,Model 1 和Model 2 条件下估计北江流域4 个站点百年一遇设计洪水流量值,其中,对于Model 1,大象二站、坪石二站和石角站的洪水设计值均随时间逐渐增大,与叶长青等[28]的研究结论一致,即非平稳性洪水设计值随时间由小增大;对于水文站点的洪水发生次数,分别以时间(Model 1) 和气候指标(Model 2) 为解释变量进行模拟分析,充分反映洪水发生次数的随机过程,为区域防洪减灾提供理论依据.
| [1] | GLEICK P H. Climate change, hydrology and water resource GAMLSSs[J]. Reviews of Geophysics, 1989, 27 (3) : 329 –344. |
| [2] | 顾西辉, 张强, 刘剑宇, 等. 变化环境下珠江流域洪水频率变化特征、成因及影响(1951-2010年)[J]. 湖泊科学, 2014 ,26 (5) : 661 –670. GU X H, ZHANG Q, LIU J Y, et al. Characteristics, causes and impacts of flood frequency change in the Pearl River Basin under changing environment (1951-2010) [J]. Journal of Lake Sciences, 2014, 26 (5) : 661 –670. |
| [3] | MILLY P C D, JULIO B, MALIN F, et al. Stationarity IS Dead: Whither Water Management[J]. Science, 2008, 319 (5863) : 573 –574. |
| [4] | 刘昊, 陈浪南. 基于GAMLSS模型的高频流动性指标分布特征[J]. 山西财经大学学报, 2011 ,33 (4) : 25 –33. LIU H, CHEN L N. Non-parametric and non-linear analysis of stock liquidity with high frequency data in China on GAMLSS model[J]. Journal of Shanxi Finance and Economics University, 2011, 33 (4) : 25 –33. |
| [5] | 严恺, 王倩, 姚华, 等. 应用GAMLSS构建基于性别、年龄、身高的新疆7-17 儿童青少年血压参考标准[J]. 中国循证儿科杂志, 2011 ,6 (5) : 343 –348. YAN K, WANG Q, YAO H, et al. Establishment of blood pressure reference centiles modeled by sex, age and height percentiles in children and adolescents aged 7-17 in Xinjiang by GAMLSS program[J]. Chinese Journal of Evidence-based Pediatrics, 2011, 6 (5) : 343 –348. |
| [6] | HERNANDEZ F J, HARE J A. Evaluating diel, ontogenetic and environmental effects on larval fish vertical distribution using generalized additive models for location, scale and shape[J]. Fisheries Oceanography, 2009, 18 (4) : 224 –236. |
| [7] | 顾西辉, 张强, 王宗志. 1951-2010年珠江流域洪水极值序列平稳性特征研究[J]. 自然资源学报, 2015 ,30 (5) : 824 –835. GU X H, ZHANG Q, WANG Z Z. Study on the stability characteristics of flood extreme Series in the Pearl River Basin during 1951-2010[J]. Journal of Natural Resources, 2015, 30 (5) : 824 –835. |
| [8] | L’OPEZ J, FRANC′ES F. Non-stationary flood frequency analysis in continental Spanish rivers, using climate and reservoir indices as external covariates[J]. Hydrology and Earth System Sciences, 2013, 17 : 3189 –3203. |
| [9] | 王乐, 刘德地, 李天元, 等. 基于多变量M-K 检验的北江流域降水趋势分析[J]. 水文, 2015 ,35 (4) : 85 –90. WANG L, LIU D D, LI T Y, et al. Analysis of precipitation trend in Beijiang River Basin Based on multi variable M-K test[J]. Journal of China Hydrology, 2015, 35 (4) : 85 –90. |
| [10] | 李艳, 陈晓宏, 张鹏飞. 北江流域水文特征变异研究[J]. 自然资源学报, 2013 ,28 (5) : 822 –831. LI Y, CHEN X H, ZHANG P F. Study on hydrological characteristic variation in Beijiang River Basin[J]. Journal of Natural Resources, 2013, 28 (5) : 822 –831. |
| [11] | 赖成光, 王兆礼, 宋海娟. 基于BP神经网络的北江流域洪灾风险评价[J]. 水电能源科学, 2011 ,29 (3) : 57 –59. LAI C G, WANG Z L, SONG H J. Evaluation of flood risk in Beijiang River Basin Based on BP neural network[J]. Water Resources and Power, 2011, 29 (3) : 57 –59. |
| [12] | 王亚雄, 黄淑娴, 刘祖发, 等. 变化环境下北江下游年径流量的加权马尔可夫链预测[J]. 生态环境学报, 2011 ,20 (4) : 754 –760. WANG Y X, HUANG S X, LIU Z F, et al. The weighted Markov chain under the changing environment of downstream Beijiang River Runoff Forecast[J]. Ecology and Environmental Sciences, 2011, 20 (4) : 754 –760. |
| [13] | 黎坤, 江涛, 刘德地. 北江天然径流量的变化特征及其影响因素[J]. 水文, 2005 ,25 (3) : 20 –25. LI K, JIANG T, LIU D D. Variation characteristics and its influencing factors of natural runoff in Beijiang River[J]. Journal of China Hydrology, 2005, 25 (3) : 20 –25. |
| [14] | 罗律, 张广存, 吴俊宁. 1965-2010 年广东北江流域汛期降雨量的气候特征分析[J]. 广东气象, 2012 ,34 (3) : 13 –15. LUO L, ZHANGG C, WU J N. The analysis of meteorological characteristics of precipitation during the flood season from 1965 to 2010 in Beijiang River Basin[J]. Guangdong Meteorology, 2012, 34 (3) : 13 –15. |
| [15] | 梁显强. 完善北江流域防洪体系建设的思考[J]. 广东水利水电, 2012 ,3 : 31 –34. LIANG X Q. Thinking about perfecting the construction of Beijiang River Basin flood control system[J]. Guangdong Water Resources and Hydropower, 2012, 3 : 31 –34. |
| [16] | MEDIERO L, SANTILLAN D, GARROTE L, et al. Detection and attribution of trends in magnitude, frequency and timing of floods in Spain[J]. Journal of Hydrology, 2014, 517 : 1072 –1088. |
| [17] | 顾西辉, 张强, 孙鹏, 等. 新疆塔河流域洪水量级、频率及峰现时间变化特征、成因及影响[J]. 地理学报, 2015 ,70 (9) : 1390 –1401. GU X H, ZHANG Q, SUN P, et al. Variation characteristics, causes and effects of flood magnitude, frequency and peak time in Tahe River Basin, Xinjiang[J]. Acta Geographica Sinica, 2015, 70 (9) : 1390 –1401. |
| [18] | LANG M, OUARDAB T B M J, BOBEE B. Towards operational guidelines for over-threshold modeling[J]. Journal of Hydrology, 1999, 255 : 103 –117. |
| [19] | CHEBANA F, OUARDA T, DUONG T. Testing for multivariate trends in hydrological frequency analysis[J]. Journal of Hydrology, 2013, 486 : 519 –530. |
| [20] | WARD P J, EISNER S, FLRKE M, et al. Annual flood sensitivities to El Nio-Southern Oscillation at the global scale[J]. Hydrology and Earth System Sciences, 2014, 18 : 47 –66. |
| [21] | ZHANG Q, GU X H, VIJAY P S, et al. Flood frequency analysis with consideration of hydrological alterations: Changing properties, causes and implications[J]. Journal of Hydrology, 2014, 519 : 803 –813. |
| [22] | 雷红富, 谢平, 陈广才, 等. 水文序列变异点检验方法的性能比较分析[J]. 水电能源科学, 2007 ,25 (4) : 36 –40. LEI H F, XIE P, CHEN G C, et al. Performance comparison and analysis of the test method of hydrological sequence variation points[J]. Water Resources and Power, 2007, 25 (4) : 36 –40. |
| [23] | KILLICK P, ECKLEY I A. Changepoint: An R package for change point analysis[J]. Journal of Statistical Software, 2014, 58 (3) : 1 –19. |
| [24] | ERDMAN C, EMERSON GW. Bcp: An R package for performing a bayesian analysis of change point problems[J]. Journal of Statistical Software, 2007, 23 (3) : 1 –13. |
| [25] | RIGBY R A, STASINOPOULOS D M. Generalized additive models for location, scale and shape (GAMLSS) in R[J]. Applied Statistics, 2005, 54 (3) : 507 –554. |
| [26] | ZHANG Q, XU C Y, CHEN X H, et al. Statistical behaviors of precipitation regimes in China and their links with atmospheric circulation 1960-2005[J]. International Journal of Climatology, 2011, 31 (11) : 1665 –1678. |
| [27] | 刘德地, 杜佩玲. 不同条件下水文要素重现期的计算方法[J]. 水文, 2014 ,34 (5) : 1 –5. LIU D D, DU P L. Methods to calculate return period of hydrological elements under different conditions[J]. Journal of China Hydrology, 2014, 34 (5) : 1 –5. |
| [28] | 叶长青, 陈晓宏, 张家鸣, 等. 不同变化环境背景下非平稳性洪水频率对比研究[J]. 水力发电学报, 2014 ,33 (3) : 1 –9. YE C Q, CHEN X H, ZHANG J M, et al. Comparative study on non-stationary flood frequency analysis in different backgrounds of changing environment[J]. Journal of Hydroelectric Engineering, 2014, 33 (3) : 1 –9. |
 2016, Vol. 62
2016, Vol. 62





