文章信息
- 王泽琪, 刘禄勤
- WANG Zeqi, LIU Luqin
- Power Lindley-Logarithmic分布及其参数估计
- Power Lindley-Logarithmic Distribution and Parameter Estimation
- 武汉大学学报(理学版), 2019, 65(6): 581-592
- Journal of Wuhan University(Natural Science Edition), 2019, 65(6): 581-592
- http://dx.doi.org/10.14188/j.1671-8836.2019.06.008
-
文章历史
- 收稿日期:2018-01-15

寿命分布的研究在科学技术领域中占有重要地位,随着寿命分布理论的逐步发展,人们陆续提出了多种产生寿命分布的机制,为寿命数据的研究提供了便利。1979年,马逢时和刘德辅提出复合极值分布概念[1],将一个连续分布与一个离散分布混合得到一个新的连续型分布,这种产生分布的方法在极值事件的研究中受到重视,其基本思想是设ξ1, ⋯, ξz, ⋯为独立随机变量序列且有相同的分布函数G (x),又设Z是与{ ξz, z =1, 2, ⋯ }相互独立的离散随机变量且其分布律为Pz=P(Z=z),记X=min{ξ1, ξ2, ⋯, ξz},则称X服从由G (x)和Pz复合而成的分布,它表示串联系统的寿命分布。由于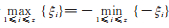
1958年Lindley[9]提出一种以权重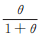
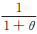
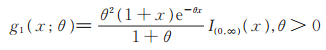
|
Ghitany等[10](2008年)对Lindley分布进行了详细地研究,发现多数情况下Lindley分布具有比指数分布更好的性质,在生存分析与可靠性的研究中意义深远。Ghitany等[11](2013年)对Lindley分布进行推广得到两参数的Power Lindley分布,其密度函数为
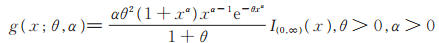
|
(1) |
和Possion分布、几何分布一样,Logarithmic分布是一种离散计数分布,该分布来源于-ln(1 - p)的麦克劳林展开即-ln(1 - p)= p + p2 /2 + p3 /3 + ⋯。Johnson等[12]详细研究了Logarithmic分布作为计数分布的重要性以及其各种性质。该分布在植物以及生物学领域研究中有广泛应用。
本文将Power Lindley(PL)分布与Logarithmic分布进行复合得到一个危险率形式多样的新的三参数寿命分布:Power Lindley-Logarithmic(PLL)分布,研究其相关性质,给出了参数的极大似然估计,并验证了估计的相合性和渐近正态性,给出了求解极大似然估计的EM算法,并进行了Monte Carlo数值模拟。
1 Power Lindley-Logarithmic分布的定义设ξ1,⋯,ξz,⋯为独立同分布的非负随机变量序列,其共同分布是参数为(θ,α)的Power Lindley分布,记为PL(θ,α),其密度函数如(1)式所述,分布函数为
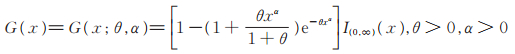
|
(2) |
又设Z是与{ ξz,z = 1,2,⋯}相互独立的随机变量,服从参数为p ∈(0,1)的Logarithmic分布,其分布律为
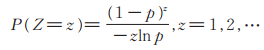
|
(3) |
令X = min { ξ1,ξ2⋯,ξZ},则易见X的分布函数为
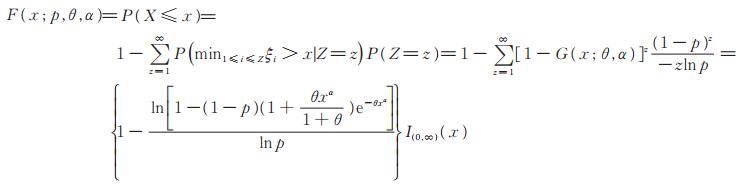
|
(4) |
称此分布为以(p,θ,α)为参数的Power Lindley-Logarithmic分布,记为PLL(p,θ,α),易见其密度函数为
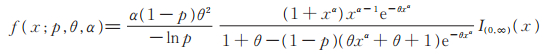
|
(5) |
特别地,当α = 1时,PLL(p,θ,α)就是Liyanage[8]等提出的参数为p,θ的Lindley-Logarithmic分布,简记为LL(p,θ)分布。
2 Power Lindley-Logarithmic分布的性质由(5)式,容易得出:当α > 1且θ ≥ 2α - 1或α = 1且p ≥ θ2时,PLL(p,θ,α)为单峰分布;当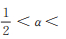
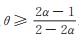
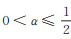
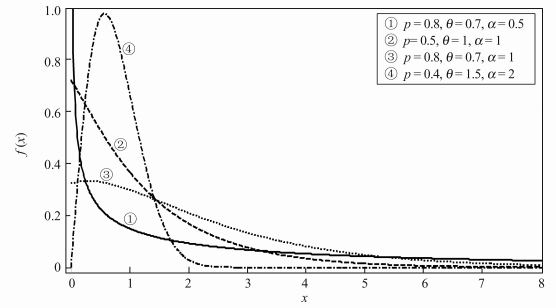
|
| 图 1 不同参数下PLL(p, θ, α)分布的密度函数 Fig. 1 Density of PLL(p, θ, α) distribution under different parameter |
定理1 设0 < u < 1. PLL(p,θ,α)分布的u-分位数为
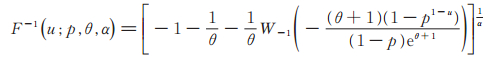
|
其中W-1(·)表示Lambert W函数的负数部分,即方程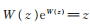
证 令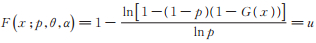

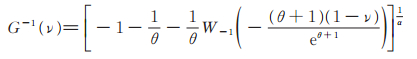
|
故可得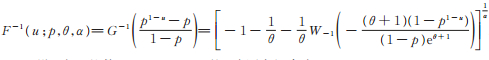
定理2 设r为正整数。PLL(p,θ,α)的r阶原点矩存在,且
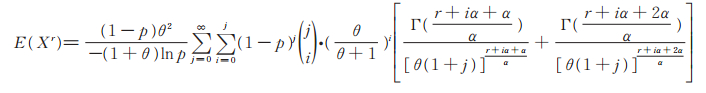
|
证 由(5)式易看出,PLL(p,θ,α)分布的密度函数是与PL(θ,α)分布的分布函数G (x;θ,α)和密度函(x;θ,α)有关的函数,即
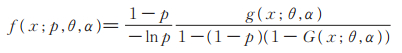
|
又文献[11]证明了PL(θ,α)分布存在有限的各阶矩,故
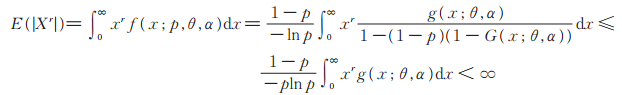
|
所以PLL(p,θ,α)的r阶原点矩存在。又因为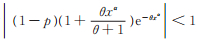
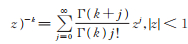
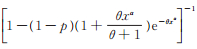
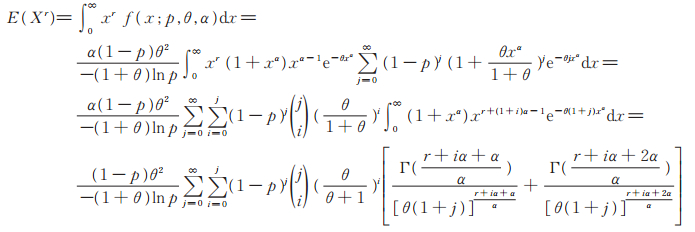
|
下面给出PLL(p,θ,α)分布的危险率函数,先回顾相关定义。非负随机变量X的分布函数为F (x),密度函数为f (x),其生存函数为S (x)= 1 - F (x),危险率函数为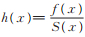
由此得PLL(p,θ,α)分布的生存函数为
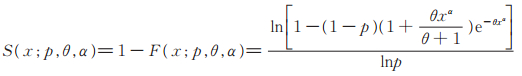
|
(6) |
定理3 若随机变量X~PLL(p,θ,α)分布,则其危险率函数为
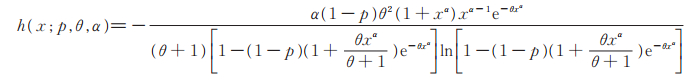
|
(7) |
且
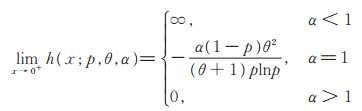
|
(8) |
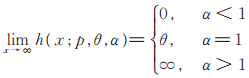
|
(9) |
证由(6)式和危险率函数的定义即得(7)式。(8)式显然成立,利用洛必达法则易得(9)式。证毕。
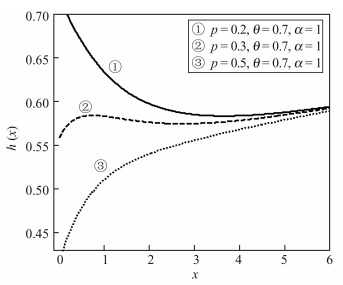
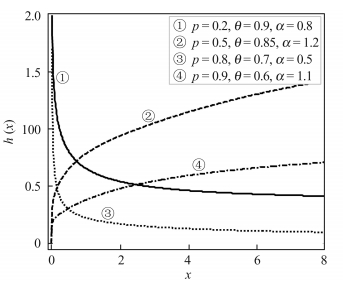
图 2和图 3给出不同参数下PLL(p,θ,α)分布的危险率函数。可见PLL(p,θ,α)分布的危险率函数可以有单调递增型、浴盆型、先单调增再浴盆型、单调递减型四种类型。
|
| 图 2 α = 1时的危险率函数 Fig. 2 The failure rate when α = 1 |
|
| 图 3 α ≠ 1时的危险率函数 Fig. 3 The failure rate when α ≠ 1 |
定理4 设X1,X2,⋯,Xn是来自PLL(p,θ,α)分布的简单随机样本,其分布函数F (·)= F (·;p,θ,α)如(4)式所述,记X(1) = min { X1,X2,⋯,Xn },则有
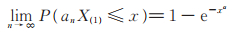
|
其中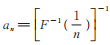
证 记PLL(p,θ,α)分布的密度函数为f (·)= f (·;p,θ,α),由(5)式及洛必达法则有
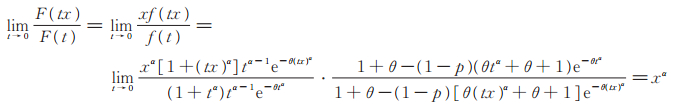
|
再利用文献[14]定理2. 1. 5及定理2. 4. 4即知定理得证。
3 参数的极大似然估计设X1,X2,⋯,Xn是来自PLL(p,θ,α)分布的简单随机样本,样本观测值为x1,x2,⋯,xn,记xobs={ x1,x2,⋯,xn },则由(5)式知对数似然函数为
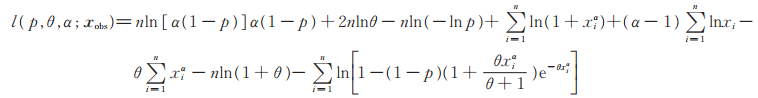
|
为方便,记ϕ=(p,θ,α),其极大似然估计为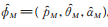
PLL(ϕ)分布的参数空间记为Φ = { ϕ =(p,θ,α):p ∈ (0,1),θ ∈ (0,∞),α ∈ (0,∞) },令
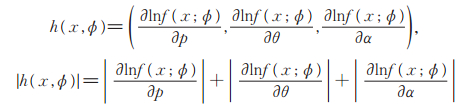
|
则似然方程组可表示为
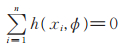
|
(10) |
对任意的ϕ0∈ Φ及充分小的ϵ > 0使得球B(ϕ0,ϵ)={ ϕ:|ϕ - ϕ0| ≤ ϵ }⊂ Φ,记
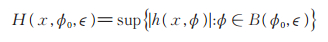
|
定理5 设X1,X2,⋯,Xn是来自PLL(ϕ)分布的简单随机样本,则存在ϕ的一个强相合估计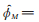
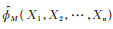

|
证 由(5)式易得
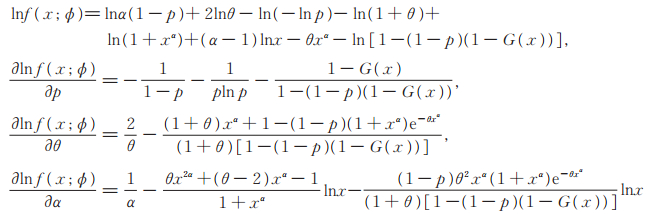
|
根据文献[15]定理4.7,为证MLE的存在性与相合性,只需证明对∀ϕ0 ∈ Φ和充分小的ϵ > 0,有E ϕ0 [H (X,ϕ0,ϵ)] < ∞和Eϕ0 [|lnf (X;ϕ0)|] < ∞。
事实上,h (x,ϕ)作为Φ上的函数在B (ϕ0,ϵ)连续,故存在ϕ1= ϕ1(x)=(p1(x), θ1(x), α1(x))∈ B (ϕ0,ϵ), 使得|h (x,ϕ1)| = H (x,ϕ0,ϵ),为方便,分别将p1 (x),θ1 (x),α1 (x)记为p1,θ1,α1,所以
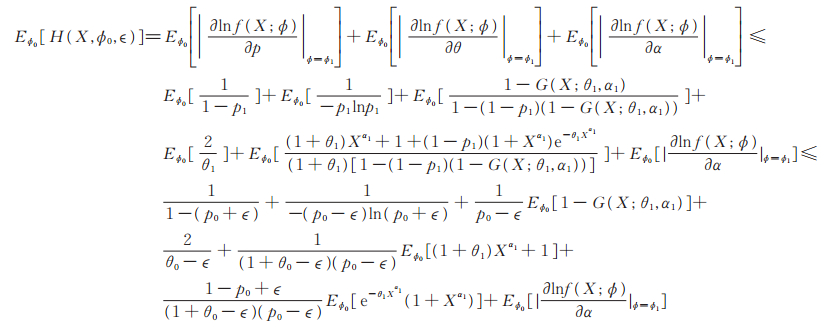
|
显然Eϕ0[1- G (X;θ1,α1)] < ∞。由定理2知Eϕ0[(1 + θ1) X α1+ 1] < ∞和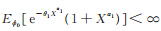
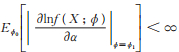
因为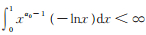
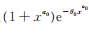
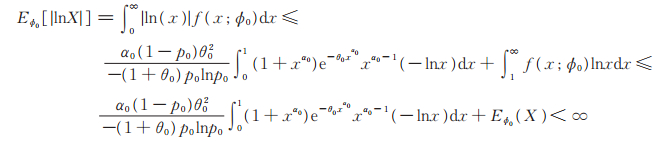
|
又因为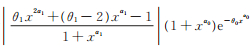
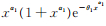
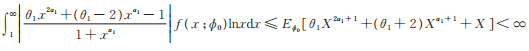
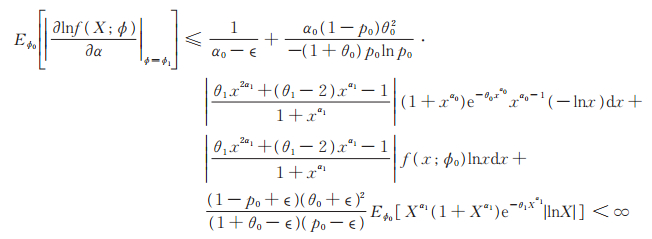
|
从而有Eϕ0[ H (X,ϕ0,ϵ)] < ∞。
又因为
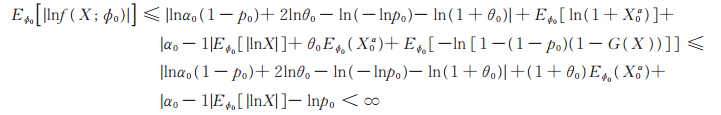
|
证毕。
定理5给出了在n充分大时参数ϕ的极大似然估计的存在性,但并不能保证对任意固定的n,参数ϕ的极大似然估计存在。下面考虑在已知两个参数的情况下,另一个未知参数的极大似然估计的存在性和渐近正态性,将得到类似于文献[3]定理1的结论。由于方法和结论是类似的,我们只考虑当参数θ和α已知时,参数p的极大似然估计。此时关于p的似然方程为
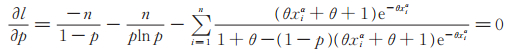
|
(11) |
定理6 设PLL(p,θ,α)分布的参数θ,α已知,p未知。令
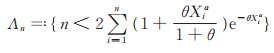
|
则
1)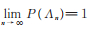
2) ∀n≥ 1, 似然方程(11)在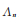
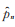
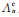
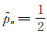
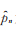
3)记f(x;p)=f(x;p,θ,α), 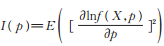
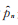
证 1)由(5)式可知
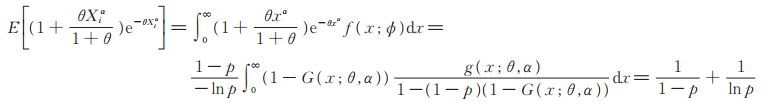
|
因为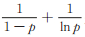
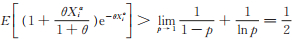
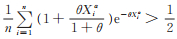
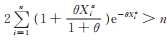
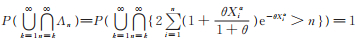
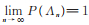
2)由似然方程(11)计算可知
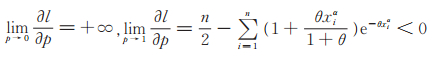
|
故在Λn上方程(10)关于p在(0,1)内至少有一解。
3)仿定理5的证明,将文献[15]定理4. 7用到目前情形,可知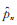
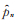
a) 当x > 0时, 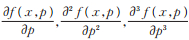
b) 对任意充分小的正数ϵ, 当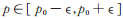
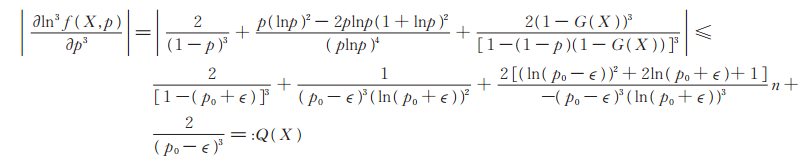
|
易证E (Q (X)) < ∞,从而文献[16]的定理2. 14的条件(2)得到验证;
c)令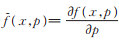
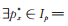
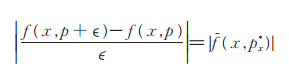
|
因为
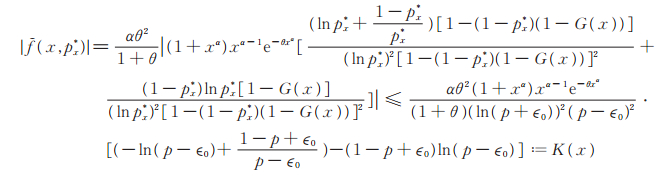
|
易知∫0∞ K (x)dx < ∞,所以由控制收敛定理,对∀p有
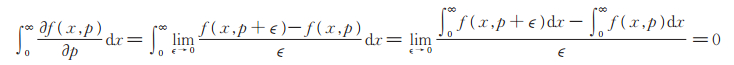
|
同理有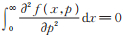
d)Fisher信息量为
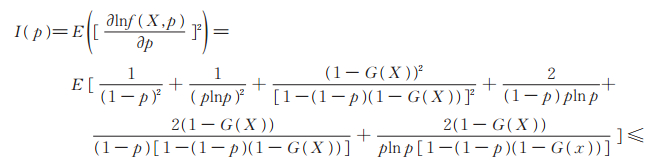
|
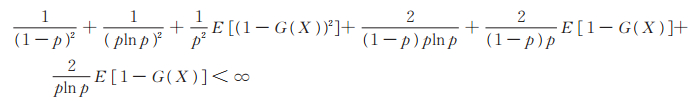
|
又Power Lindley-Logarithmic分布为非退化分布,故I (p) > 0。从而文献[16]的定理2. 14的所有条件均满足,于是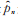
证毕。
4 数值模拟由于PLL(p,θ,α)分布的似然方程组表达式复杂不易求出显式解,因此用EM算法(算法介绍详见文献[17])给出其参数的极大似然估计。
设ξ1,ξ2,⋯,ξz,⋯是来自PL(θ,α)分布的简单随机样本。Z是与ξz(z = 1,2,⋯)相互独立的随机变量,且服从参数为p的Logarithmic分布。令X = min { ξ1,ξ2,⋯,ξZ},易得Z关于X的条件期望为
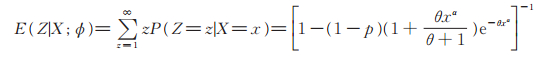
|
记xobs=(x1,x2,⋯,xn)为来自PLL(ϕ)分布的观测数据,z =(z1,z2,⋯,zn)为来自数据Z但不能观测的潜在数据,设ϕ(t)=(p(t),θ(t),α(t))为第t + 1次迭代的初始值,则由EM算法可得
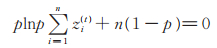
|
(12) |
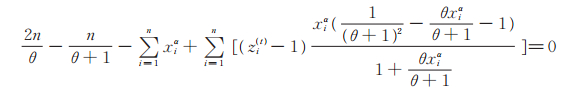
|
(13) |
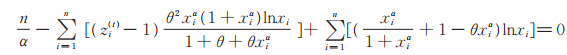
|
(14) |
其中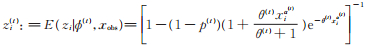
记n为样本容量,则通过以下步骤得到参数ϕ =(p,θ,α)的极大似然估计:
步骤1 产生n个服从U (0,1)分布的随机数,记为u =(u1,u2,⋯,un);
步骤2 将u1,u2,⋯,un分别代入到PLL(ϕ)分布的分位数函数(定理1),计算得到xi = F-1 (ui;ϕ),i=1,2,⋯,n,则xobs =(x1,x2,⋯,xn)为来自PLL(ϕ)分布的容量为n的样本;
步骤3 给定参数的初始值ϕ(0)=(p(0),θ(0),α(0)),设定迭代精度为0. 000 1,用EM算法得到参数ϕ的极大似然估计;
步骤4 重复步骤1~3 1 000次,计算得到的1 000个估计值的均值作为参数ϕ的极大似然估计的最终结果。
假设模拟得到的极大似然估计为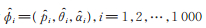
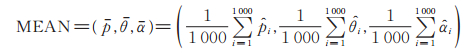
|
样本均方误差为
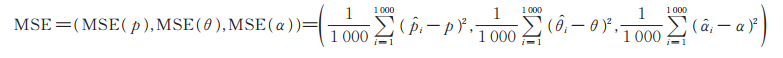
|
样本标准误差为
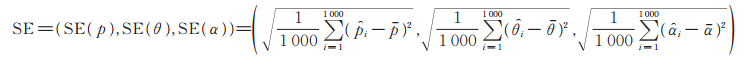
|
表 1给出了在样本容量分别为50,100,500时模拟的结果。
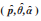
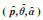
| n | (p, θ, α) | (p(0), θ(0), α(0)) | MEAN | MSE | SE |
| (0. 7, 1. 5, 1. 8) | (0. 5, 1. 7, 2) | (0. 634 5, 1. 465 7, 1. 895 8) | (0. 070 3, 0. 010 0, 0. 066 5) | (0. 257 1, 0. 094 1, 0. 239 5) | |
| 50 | (0. 7, 1, 1. 5) | (0. 5, 1. 3, 2) | (0. 660 0, 0. 966 9, 1. 558 5) | (0. 057 8, 0. 006 5, 0. 028 8) | (0. 237 2, 0. 073 8, 0. 159 4) |
| (0. 4, 0. 8, 2. 5) | (0. 5, 0. 5, 2) | (0. 423 4, 0. 785 6, 2. 585 1) | (0. 051 4, 0. 005 0, 0. 067 3) | (0. 225 7, 0. 069 6, 0. 245 2) | |
| (0. 7, 1. 5, 1. 8) | (0. 9, 1, 1. 5) | (0. 693 5, 1. 483 7, 1. 838 1) | (0. 045 0, 0. 005 0, 0. 024 9) | (0. 212 1, 0. 068 6, 0. 153 1) | |
| 100 | (0. 7, 1, 1. 5) | (0. 4, 1. 3, 2) | (0. 672 2, 0. 981 8, 1. 534 8) | (0. 037 6, 0. 002 9, 0. 013 1) | (0. 192 0, 0. 051 1, 0. 108 9) |
| (0. 4, 0. 8, 2. 5) | (0. 7, 0. 6, 1.5) | (0. 425 1, 0. 798 3, 2. 531 4) | (0. 028 9, 0. 002 7, 0. 032 6) | (0. 168 4, 0. 051 7, 0. 177 8) | |
| (0. 7, 1. 5, 1. 8) | (0. 6, 1, 2) | (0. 677 1, 1. 487 2, 1. 812 6) | (0. 013 1, 0. 001 3, 0. 004 7) | (0. 112 3, 0. 034 4, 0. 067 6) | |
| 500 | (0. 7, 1, 1. 5) | (0. 5, 1. 3, 1.3) | (0. 679 8, 0. 990 4, 1. 506 1) | (0. 010 6, 0. 000 6, 0. 002 3) | (0. 100 8, 0. 022 6, 0. 047 2) |
| (0. 4, 0. 8, 2. 5) | (0. 6, 1, 1) | (0. 416 7, 0. 804 0, 2. 501 1) | (0. 006 6, 0. 000 6, 0. 005 4) | (0. 079 3, 0. 023 3, 0. 073 3) |
从表 1可以看到,用EM算法得到的参数的极大似然估计很好地反映了参数的真值,选取不同的初始值对似然估计值的影响不大,且从整体上来看,随着样本量的增加,估计值越来越高,均方误差和标准误差也越来越小。
下面考虑在两个参数已知情况下,另一参数的极大似然估计及95%渐近置信区间的覆盖率。由于方法类似,我们只考虑当θ和α已知,p未知时的情形。在求解极大似然估计时,同样使用EM算法。
沿用前面的符号,记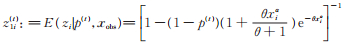
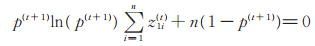
|
(15) |
同方程(12),这里仍用二分法求p( t + 1)。
根据定理6可知固定参数θ和α时,参数p的渐近方差为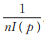
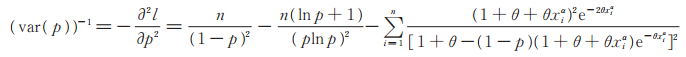
|
记参数p的极大似然估计为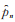
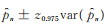
记n为样本容量,则通过以下步骤得到在参数θ,α已知时,未知参数p的极大似然估计:
步骤1 产生n个服从U (0, 1)分布的随机数,记为u =(u1, u2, ⋯, un);
步骤2 将u1,u2,⋯,un分别代入到PLL(ϕ)分布的分位数函数(定理1),计算得到xi = F-1 (ui;ϕ),i=1,2,⋯,n,则xobs =(x1,x2,⋯,xn)为来自PLL(ϕ)分布的容量为n的样本;
步骤3 给定参数的初始值p(0),设定迭代精度为0. 000 1,用EM算法得到参数p的极大似然估计,并判断真值p是否落入95%渐近置信区间;
步骤4 重复步骤1~3 1 000次,计算得到的1 000个估计值的均值作为参数p的极大似然估计的最终结果。
假设模拟得到的极大似然估计为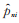
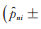
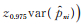
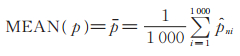
|
样本均方误差为
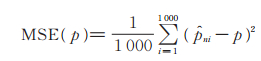
|
样本标准误差为
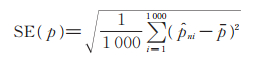
|
参数p的95%置信区间平均长度为
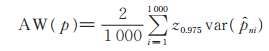
|
95%置信区间的覆盖率为
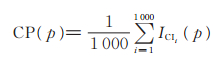
|
通过模拟得到的θ和α已知时,参数p的极大似然估计及渐近置信区间的覆盖率如表 2所示。
| n | (θ, α) | p | p(0) | MEAN(p) | MSE(p) | SSE(p) | AW(p) | CP(p) |
| 100 | (1, 2) | 0. 4 | 0. 8 | 0. 430 8 | 0. 022 4 | 0. 146 7 | 0. 589 1 | 0. 943 |
| (1, 2) | 0. 7 | 0. 5 | 0. 701 2 | 0. 040 3 | 0. 200 9 | 0. 935 1 | 0. 921 | |
| (1.5, 1.8) | 0. 3 | 0. 9 | 0. 325 6 | 0. 014 0 | 0. 115 5 | 0. 446 5 | 0. 943 | |
| (1. 5, 1.8) | 0. 8 | 0. 5 | 0. 791 5 | 0. 036 1 | 0. 190 0 | 1. 040 3 | 0. 935 | |
| 500 | (1, 2) | 0. 4 | 0. 1 | 0. 406 7 | 0. 004 3 | 0. 064 8 | 0. 249 2 | 0. 948 |
| (1, 2) | 0. 7 | 0. 6 | 0. 711 9 | 0. 011 9 | 0. 108 7 | 0. 432 3 | 0. 95 | |
| (1.5, 1.8) | 0. 3 | 0. 6 | 0. 306 3 | 0. 002 4 | 0. 049 0 | 0. 188 4 | 0. 949 | |
| (1. 5, 1.8) | 0. 8 | 0. 2 | 0. 807 1 | 0. 012 9 | 0. 113 5 | 0. 488 2 | 0. 956 | |
| 1 000 | (1, 2) | 0. 4 | 0. 3 | 0. 401 5 | 0. 002 1 | 0. 045 3 | 0. 133 4 | 0. 947 |
| (1, 2) | 0. 7 | 0. 9 | 0. 704 2 | 0. 006 2 | 0. 078 7 | 0. 302 9 | 0. 946 | |
| (1.5, 1.8) | 0. 3 | 0. 4 | 0. 301 8 | 0. 001 2 | 0. 034 2 | 0. 131 1 | 0. 946 | |
| (1.5, 1.8) | 0. 8 | 0. 9 | 0. 803 3 | 0. 007 4 | 0. 086 1 | 0. 345 0 | 0. 958 |
从表 2可以看出,对于相同的固定值θ和α,参数p越小,极大似然估计对p的估计效果越好;选取不同的初始值对p的估计影响不大;随着样本容量n的增大,p的95%渐近置信区间越来越精确;p的95%渐近置信区间的实际覆盖率在0. 95左右,说明当θ和α固定时,p的极大似然估计具有良好的渐近正态性。
| [1] |
马逢时, 刘德辅. 复合极值分布理论及其应用[J]. 应用数学学报, 1979, 34(4): 893-902. MA F S, LIU D F. Theory of compound extreme value distribution and its application[J]. Acta Mathematicae Applicatae Sinia, 1979, 34(4): 893-902. (Ch). |
| [2] |
KUŞ C. A new lifetime distribution[J]. Computational Statistics and Data Analysis, 2007, 51(9): 4497-4509. DOI:10.1016/j.csda.2006.07.017 |
| [3] |
TAHMASBI R, REZAEI S. A two parameter lifetime distribution with decreasing failure rate[J]. Computational Statistics & Data Analysis, 2008, 52(8): 3889-3901. DOI:10.1016/j.csda.2007.12.002 |
| [4] |
LU W B, SHI D M. A new compounding life distribution:The Weibull-Poisson distribution[J]. Journal of Applied Statistics, 2012, 39(1): 21-38. DOI:10.1080/02664763.2011.575126 |
| [5] |
ZAKERZADEH H, MAHMOUDI E. A new two parameter lifetime distribution: Model and properties[EB/OL].[2012-04- 19]. http://cn.arxiv.org/pdf/1204.4248v1.
|
| [6] |
GUI W H, ZHANG S L, LU X M. The Lindley-Poisson distribution in lifetime analysis and its properties[J]. Hacettepe Journal of Mathematics and Statistics, 2014, 43(6): 1063-1077. DOI:10.15672/HJMS.201427453 |
| [7] |
吕晓星, 彭维, 刘禄勤. 一个新的具有单调降失效率的寿命分布[J]. 数学杂志, 2015, 35(5): 1233-1244. LÜ X X, PENG W, LIU L Q. A new lifetime distribution with decreasing failure rate[J]. Journal of Mathematics, 2015, 35(5): 1233-1244. DOI:10.13548/j.sxzz.20140405001 (Ch). |
| [8] |
LIYANAGE G W, PARARAI M. The Lindley power series class of distributions:Model, properties, and applications[J]. Journal of Computations and Modeling, 2015, 5(3): 35-80. |
| [9] |
LINDLEY D V. Fiducial distributions and Bayes'theorem[J]. Journal of the Royal Statistical Society, 1958, 20(1): 102-107. |
| [10] |
GHITANY M E, ATIEH B, NADARAJAH S. Lindley distribution and its application[J]. Mathematics and Computers in Sim- ulation, 2008, 78(4): 493-506. DOI:10.1016/j.matcom.2007.06.007 |
| [11] |
GHITANY M E, AL-MUTAIRI D K, BALAKRISHNAN N, et al. Power Lindley distribution and associated inference[J]. Computational Statistics and Data Analysis, 2013, 64(4): 20-33. DOI:10.1016/j.csda.2013.02.026 |
| [12] |
JOHNSON N L, KEMP A W, KOTZ S. Univariate Discrete Distributions[M]. Hoboken: John Wiley & Sons, 2005: 302-325.
|
| [13] |
JODRÁ P. Computer generation of random variables with Lindley or Poisson-Lindely distribution via the Lambert W function[J]. Mathematics and Computers in Simulation, 2010, 81(4): 851-859. DOI:10.1016/j.matcom.2010.09.006 |
| [14] |
GALAMBOS J. The Asymptotic Theory of Extreme Order Statistics[M]. 2nd Edition. Beijing: China Science Press, 2001: 58-59.
|
| [15] |
陈希孺. 高等数理统计学[M]. 安徽: 中国科学技术大学出版社, 2009: 152-154. CHEN X R. Advanced Mathematical Statistics[M]. Anhui: University of Science and Technology of China Press, 2009: 152-154. (Ch). |
| [16] |
茆诗松, 王静龙, 濮晓龙. 高等数理统计[M]. 第二版.北京: 高等教育出版社, 1998: 120-121. MAO S S, WANG J L, PU X L. Advanced Mathematical Statistics[M]. 2nd Editon. Beijing: Higher Education Press, 1998: 120-121. (Ch). |
| [17] |
MCLACHLAN G, KRISHNAN T. The EM Algorithm and Extensions[M]. Hoboken: John Wiley & Sons, 2007: 18-39.
|
| [18] |
陈晓江, 黄樟灿. 数值分析[M]. 北京: 科学出版社, 2010: 258-260. CHEN X J, HUANG Z C. Numerical Analysis[M]. Beijing: China Science Press, 2010: 258-260. (Ch). |
 2019, Vol. 65
2019, Vol. 65





