文章信息
- 李志慧, 白海艳, 白晨明
- LI Zhihui, BAI Haiyan, BAI Chenming
- 基于量子电路的门限量子秘密共享方案
- Threshold Secret Sharing Scheme Based on Quantum Circuit
- 武汉大学学报(理学版), 2019, 65(2): 200-206
- Journal of Wuhan University(Natural Science Edition), 2019, 65(2): 200-206
- http://dx.doi.org/10.14188/j.1671-8836.2019.02.009
-
文章历史
- 收稿日期:2018-08-17

随着网络信息的快速发展,保密的重要性越来越受到人们的关注。量子计算是通过调控量子信息且遵循量子力学规律的一种新型计算模式,它使得量子比特依次通过不同的量子逻辑门来达到编程的目的,通过组合不同的量子逻辑门可以实现各种量子算法。从计算效率的角度来说由于存在量子力学叠加性,已有某些量子算法在解决问题时比传统的通用计算机速度要快。
在量子密码学领域,安全的量子算法已经开始得到人们的关注,如安全多方计算、盲计算和可验证委托计算[1~10]。最早的量子算法是Deutsch和Jozsa[11]提出,该量子算法表现出经典计算机不具备的计算能力,但却不具有实用性。直到1994年,Shor提出了带有革命性的算法[12],该算法的发现激发了人们对于量子计算机研究的热情,同时也推动了量子密码、量子通信的发展。
1999年,Hillery等人[13]首次提出了一个量子秘密共享方案,该概念的出现为量子态秘密的安全提供了有效的途径。之后,基于量子特点的量子秘密共享方案得到长久的关注和发展[14~21]。所谓(k, n)门限量子秘密共享方案中,一个s位比特的量子态秘密分发给n个参与者,满足任何少于k个参与者密谋合作都不能重建秘密量子态,而任何k个参与者均可重构秘密量子态[22~26]。
在量子电路中,对量子态执行酉变换,其作用相当于在量子态上执行逻辑门后所起的作用。在任意维的Hilbert空间中,如果对应量子态的酉变换都可以通过一个逻辑门组中的元素组合来实现,称这样的逻辑门组为通用量子逻辑门组(universal gate),下文简称通用门。已证明,Toffoli门可实现任意维Hilber空间所有的酉变换[27],但它是三位量子门,从物理实现的角度来说比较困难。然而,不管怎样,像经典计算通用逻辑门组一样,量子计算的通用门有其不同的表现形式,正如文献[28]指出:T门,受控相位门以及Toffoli门中的任意一个与Clifford群门都可以形成一组通用门。而本文考虑的是由Clifford群门和T门组成的通用门。
Ouyang等人[29]提出了一个(n, n)门限量子秘密共享方案,其中n = 4k + 1, k ∈ ℤ+。本文考虑更一般的情形即对任意的正整数n,提出了(n, n)门限量子秘密共享方案,进而利用由离散的Clifford群门和T门组成的量子电路对不诚实参与者攻击进行安全性评估。
1 文献[29]方案回顾1)准备阶段
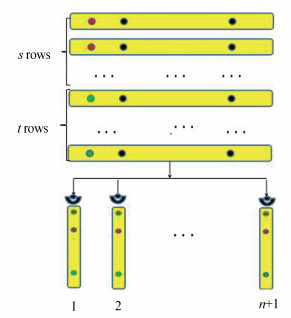
在图 1中,第一列前s位初始化为量子秘密σ,用红色表示;后t位初始化为魔幻态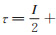
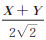
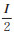
|
| 图 1 n + 1个参与者对应的秘密共享过程 红色表示初始化为量子秘密;绿色表示初始化为魔幻态 Fig. 1 Secret sharing process corresponding to n + 1 participants |
2)加密阶段
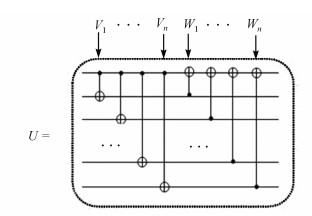
当x ∈ {1, 2, ⋯, N}时,U(见图 2)作用于第x行量子比特,因此U⊗N作用于Nn位量子态,将量子秘密编码成高度混合态。
|
| 图 2 量子电路U示意图 Fig. 2 Schematic diagram of quantum circuit U |
3)共享阶段
U⊗N加密后的n列混合量子态,第y个参与者持第y列混合量子态,其中y ∈ {1, 2, ⋯, n}。
4)解密阶段
(a)收集n个参与者持有的量子态;
(b)用酉阵(U⊗N)†作用于n列共享的混合量子态,丢弃其余列,剩下的第一列含有量子态秘密。
令P= {I, X, Y, Z},当n = 4k + 1, k ∈ ℤ+时,有结论[13]:
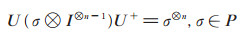
|
(1) |
本文将考虑参与者人数n为任意情形(即不局限于n = 4k + 1,n ∈ ℤ+),并给出新的结论。
2 改进后的量子秘密共享方案 2.1 量子电路及其相关结果本节在文献[29]的基础上进行推广和改进,利用由Clifford群门和T门组成的可证明安全的量子电路图进行分析,给出电路图相应的结论。
在图 1中,第一列量子比特的前s位是将要共享的量子态秘密,后t位是辅助量子态,y表示加密后第y列量子态比特,令N = s + t.用R x表示第x行量子比特,其中:x ∈ {1, 2, ⋯, N},y ∈ {1, 2, ⋯, n + 1}。
在图 2中,当i ∈ {1, 2, ⋯, n }时,Vi表示第i列对应酉阵,令A = VnVn- 1⋯V1; Wi表示第n + i列对应酉阵。
令B = WnWn - 1⋯W1, 则U = BA。
性质1 当σ = I时,有
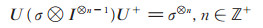
|
(2) |
性质2 当σ = X时,有
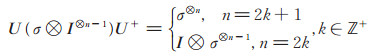
|
(3) |
证 首先证明下式成立
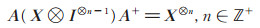
|
(4) |
已知
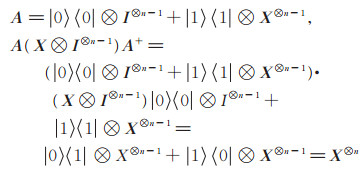
|
当n是奇数时,易知n = 3, 5时,(3)式成立,故归纳假设n = 2k + 1时,(3)式成立。下证n = 2k + 3时,(3)式也成立。由归纳假设和(4)式知:
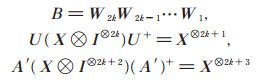
|
当n = 2k + 3时,
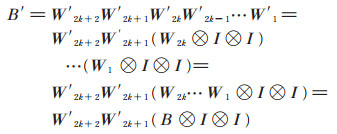
|
其中:
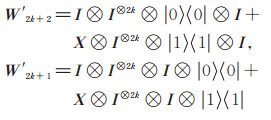
|
则有
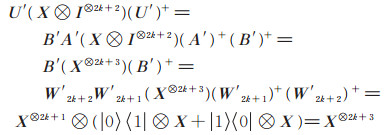
|
当n是偶数时,n = 2, 4时,(3)式成立,归纳假设n = 2k时,(3)式成立。下证n = 2k + 2时,(3)式也成立。由归纳假设和(4)式知:
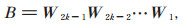
|
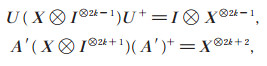
|
当n = 2k + 2时,有
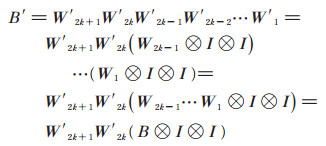
|
其中:
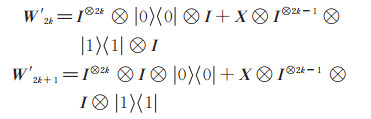
|
则有
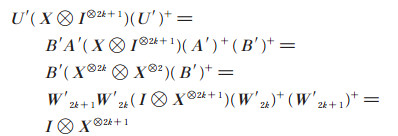
|
由数学归纳法可知(3)式成立。
性质3 当σ = Y时,有
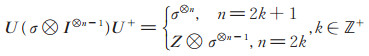
|
(5) |
证 令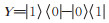
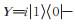
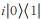
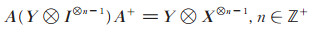
|
(6) |
当n是奇数时,n = 3, 5时,(5)式成立,归纳假设n = 2k + 1时,(5)式成立。下证n = 2k + 3时,(5)式也成立。由归纳假设和(6)式知:
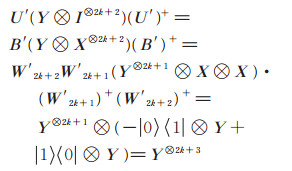
|
当n是偶数时,n = 2, 4时,(5)式成立,归纳假设n = 2k时,(5)式成立。下证n = 2k + 2时,(5)式也成立。由归纳假设和(6)式知:
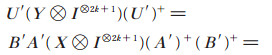
|
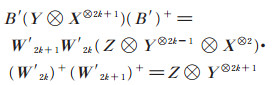
|
由数学归纳法可知(5)式成立。
性质4 当σ = Z时,有
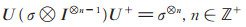
|
(7) |
证 根据计算易知
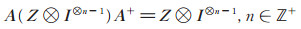
|
(8) |
当n是奇数时,n = 3, 5时,(7)式成立,假设n = 2k + 1时,(7)式成立,下证n = 2k + 3时,(7)式也成立。由假设和(8)式知
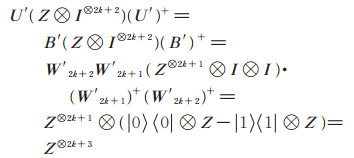
|
当n是偶数时,n = 2, 4时,(7)式成立,假设n = 2k时,(7)式成立,下证n = 2k + 2时,(7)式也成立。由归纳假设和(8)式知
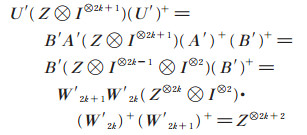
|
由数学归纳法可知(7)式成立。
2.2 量子秘密共享方案1) 准备阶段
第一列前s位初始化为量子秘密,后t位初始化为魔幻态τ, 令N = s + t.其余列初始化为最大混合态
2) 加密阶段
当x ∈ {1, 2, ⋯, N}时,U作用于第x行量子比特,因此U⊗N作用于N (n + 1)位量子态,将量子秘密编码成高度混合态。
3) 共享阶段
U加密后的n + 1列混合量子态,Alice持第1列,第y列量子态分发给第y - 1个参与者,其中y ∈ {2, 3, ⋯, n + 1}。
4) 解密阶段
(a)收集n + 1个参与者的共享态;
(b)用酉阵U†作用于n + 1列共享的混合量子态,丢弃其余列,剩下的第一列含有量子态秘密。
3 共享秘密上的评估为了评估作用在共享秘密上的量子电路,每个参与者只在自己持有的份额上执行量子计算,其计算是在共享和解密阶段之间进行。本文考虑由离散的Clifford门和T门构成的一组通用门集合(当然还有其他组合),其中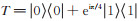
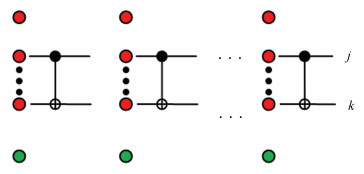
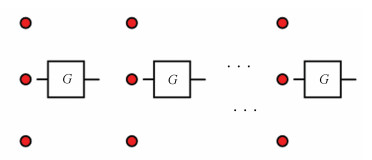
当Ui是Clifford门时,每个参与者在自己持有的一列量子比特子集上执行Ui,因此n + 1方参与者共同实现Ui⊗(n + 1)。Ui是单量子比特Clifford门时如图 3所示(用G来表示Clifford门),Ui是双量子比特CNOT门时如图 4所示。
|
| 图 3 Clifford门作用示意图 Fig. 3 Schematic diagram of Clifford gate action |
|
| 图 4 CONT门作用示意图 Fig. 4 Schematic diagram of CONT gate action |
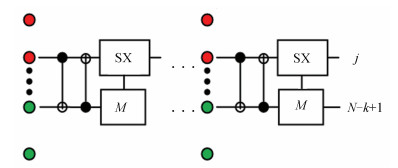
当Ui是T门时,每个参与者在持有的量子秘密上可以执行t个T门,为了实现作用在第j位量子比特上的第k个T门,k ∈ {1, 2, ⋯, t },操作如图 5。
|
| 图 5 第k个T门示意图 Fig. 5 Schematic diagram of the k-th T gate |
其中M框表示测量装置,S= T2。首先计算经过两个受控非门后的量子态:已知第N - k + 1个量子比特为魔幻态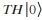
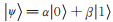
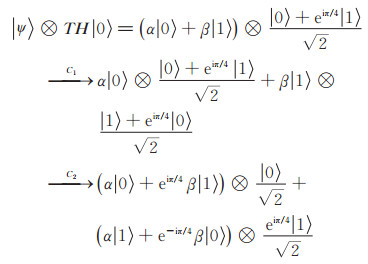
|
其中,C1表示第j位量子比特为控制比特,第N - k + 1位量子比特为目标比特;C2表示第N - k + 1位量子比特为控制比特,第j位量子比特为目标比特。对第N - k + 1位量子比特进行测量,若结果态为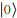
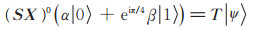
|
若结果态为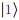
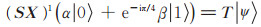
|
因此,最终实现T门作用于第j位量子比特。每评估一个T门就会消耗一个魔幻态[28]。
实例1 n = 4时,假设共享的量子态秘密是σ = X⊗Y⊗Z, t = 2, 则经过本文方案中酉阵U作用后终态为
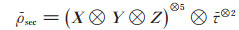
|
其中,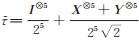
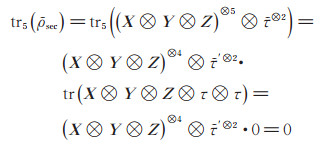
|
其中,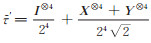
实例2 n = 5时,假设共享的量子态秘密是σ = X⊗Y⊗Z, t = 2, 则经过本文方案中酉阵U作用后终态为
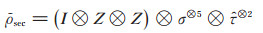
|
其中,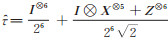
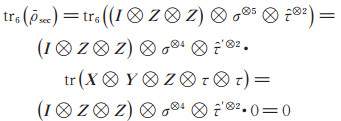
|
其中,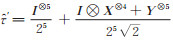
一个方案如果对于内部参与者(比外部参与者拥有更多信息)都是安全的,则这个方案对于其他外部攻击者也是安全的。因此,本文针对不诚实参与者攻击进行分析。
不诚实的参与者攻击:一个(k, n)门限量子秘密共享方案满足两个性质:1)任意k个或者多于k个参与者合作可以完全恢复秘密量子态;2)任意k - 1个或者少于k - 1个参与者合作都不能获得关于秘密量子态的任何信息。当k = n时,第一个性质显然成立,在加密阶段可以看出编码程序是完全可逆的。接下来讨论第二个性质。
加密前量子态秘密为
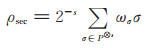
|
(9) |
其中σ = σ1 ⊗ σ2 ⊗ ⋯ ⊗σs,P = {I, X, Y, Z},ωσ是P⊗s中非平凡算子σ对应的系数,当σ是平凡Pauli算子时,ωσ = 1。
当n + 1是奇数时,由上述性质可知,加密后终态为
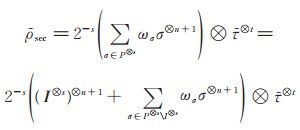
|
其中:
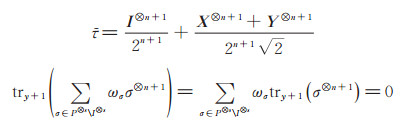
|
则
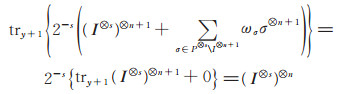
|
假设第y个参与者是诚实的,则其余n - 1个参与者合作得不到关于量子秘密的任何信息。
当n + 1是偶数时,加密后终态为
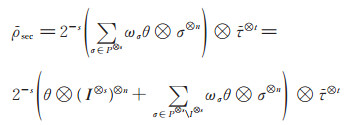
|
其中:
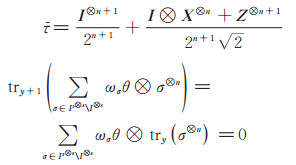
|
则
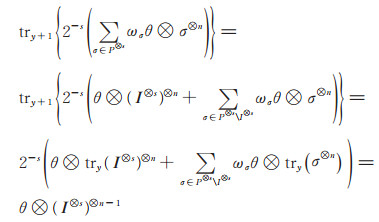
|
θ为Alice持有的第一列量子比特的乘积态。同理假设第y个参与者是诚实的,则其余n - 1个参与者合作得不到关于量子秘密的任何信息。
不论n + 1为偶数还是奇数时,不诚实参与者只能得到高度混合态,得不到关于量子秘密的任何信息。
在共享秘密上门评估也满足第二个性质。假设n个参与者中只有一个是诚实方,而其余n - 1个可以执行任何操作,可证明诚实方公布的结果比特是一致随机的且独立于其他参与者的行为[29]。根据门评估作用效果,得到评估第i个门之后系统状态形式为:
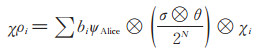
|
(10) |
其中σ ∈ P⊗s, θ ∈ {I, X, Y}⊗t - i, bi是一组标量,ψAlice是Alice持有的一列量子态,χi是不诚实方系统的集合。诚实方与其他系统以乘积态的形式存在,因此其余的n - 1个不诚实的参与者不能恢复秘密,因为诚实方的测量结果没有传递任何有用的信息。
5 结论本文对参与者人数n为任意情形(即不局限于n = 4k + 1)构造了基于量子电路的一个(n, n)门限量子秘密共享方案,且进一步由Clifford群门和T门组成的通用门进行安全性评估。由于通用量子逻辑门有不同的表现形式,因此寻找新型的通用量子逻辑门集合以及考虑其他几类通用门构造的量子电路,并建立基于这些量子电路上的更加安全的量子秘密共享方案,是今后有待研究的问题。
| [1] |
CRÉPEAU C, GOTTESMAN D, SMITH A. Secure Multi-Party Quantum Computing[DB/OL].[2018-05-06]. https://arxiv.org/pdf/quant-ph/0206138.pdf.
|
| [2] |
BROADBENT A, FITZSIMONS J, KASHEFI E. Universal blind quantum computation[C]//Foundations of Compute Science, 2010, 19 (6) : 517-526.DOI: 10.1109/FOCS.2009.36.
|
| [3] |
MORIMAE T, FUJⅡ K. Blind topological measurementbased quantum computation[J]. Nature Communications, 2012, 3(3): 1036. DOI:10.1038/ncomms2043 |
| [4] |
BARZ S, KASHEFI E, BROADBENT A, et al. Demonstration of blind quantum computing[J]. Science, 2011, 335(6066): 303. DOI:10.1126/science.1214707 |
| [5] |
BREZULEANU A. Delegating private quantum computations[J]. Canadian Journal of Physics, 2015, 93(9): 941-946. DOI:10.1139/cjp-2015-0030 |
| [6] |
AHARONOV D, BEN - OR M, EBAN E. Interactive Proofs for Quantum Computations[DB/OL].[2018-06-04]. https://www.researchgate.net/publication/221463088_Interactive_Proofs_For_Quantum_Computations.
|
| [7] |
REICHARDT B W, UNGER F, VAZIRANI U. Classical command of quantum systems[J]. Nature, 2013, 496(7446): 456-460. DOI:10.1038/nature12035 |
| [8] |
FITZSIMONS J F, KASHEFI E. Unconditionally verifiable blind quantum computation[J]. Physical Review A, 2017, 96: 012303. DOI:10.1103/PhysRevA.96.012303 |
| [9] |
MORIMAE T. Verification for measurement-only blind quantum computing[J]. Physical Review A, 2014, 89(6): 4085-4088. DOI:10.1103/PhysRevA.89.060302 |
| [10] |
HAYASHI M, MORIMAE T. Verifiable measurement-only blind quantum computing with stabilizer testing[J]. Physical Review Letters, 2015, 115(22): 220502. DOI:10.1103/PhysRevLett.115.220502 |
| [11] |
DEUTSCH D, JOZSA R. Rapid Solution of Problems by Quantum Computation [R]. Bristol: University of Bristol, 1992. https://royalsocietypublishing.org/doi/abs/10.1098/rspa.1992.0167
|
| [12] |
SHOR P W. Algorithms for quantum computation: Discrete logarithms and factoring[C]//Symposium on Foundations of Computer Science. Washington D C: IEEE Computer Society, 1994: 124 - 134.DOI: 10.1109/SFCS.1994.365700.
|
| [13] |
HILLERY M, BUZEK V, BERTHIAUME A. Quantum secret sharing[J]. Physical Review A, 1999, 59(3): 1829-1834. |
| [14] |
BAI C M, LI Z H, XU T T, et al. A generalized information theoretical model for quantum secret sharing[J]. International Journal of Theoretical Physics, 2016, 55(11): 4972-4986. DOI:10.1007/s10773-016-3121-9 |
| [15] |
DENG F G, GUI L L, ZHOU H Y. An efficient quantum secret sharing scheme with Einstei-Podolsk-Rosen pairs[J]. Physics Letters A, 2006, 340(1): 43-50. DOI:10.1016/j.physleta.2005.04.007 |
| [16] |
BAI C M, LI Z H, LIU C J, et al. Quantum secret sharing using orthogonal multiqudit entangled states[J]. Quantum Information Processing, 2017, 16(12): 304. DOI:10.1007/s11128-017-1739-z |
| [17] |
XIAO L, LONG G L, DENG F G, et al. Efficient multiparty quantum -secret-sharing schemes[J]. Physics, 2004, 69(5): 521-524. DOI:10.1103/PhysRevA.69.052307 |
| [18] |
XU T T, LI Z H, BAI C M, et al. A new improving quantum secret sharing scheme[J]. International Journal of Theoretical Physics, 2017, 56: 1-10. DOI:10.1007/s10773-016-3272-8 |
| [19] |
TITTEL W, ZBINDEN H, GISIN N. Experimental demonstration of quantum secret sharing[J]. Physical Review A, 2001, 63(4): 42301. DOI:10.1103/PhysRevA.63.042301 |
| [20] |
BAI C M, LI Z H, XU T T, et al. Quantum secret sharing using the d-dimensional GHZ state[J]. Quantum Information Processing, 2017, 16(3): 59. DOI:10.1007/s11128-016-1506-6 |
| [21] |
BAI H Y, LI Z H, HAO N. Quantum Security Computation on Shared Secrets[DB/OL].[2018 - 05 - 12]. https://arxiv.org/pdf/1804.03792.pdf. DOI: 10.1007/s10773-018-3905-1.
|
| [22] |
HILLERY M, BUZEK V, BERTHIAUME A. Quantum secret sharing[J]. Physical Review A, 1999, 59(3): 1829-1834. |
| [23] |
CLEVE R, GOTTESMAN D, LO H K. How to share a quantum secret[J]. Physical Review Letters, 1999, 83(3): 648-651. DOI:10.1103/PhysRevLett.83.648 |
| [24] |
GOTTESMAN D. Theory of quantum secret sharing[J]. Physical Review A, 2000, 61(4): 192-193. DOI:10.1103/PhysRevA.61.042311 |
| [25] |
ZHANG Z J, MAN Z X. Multiparty quantum secret sharing of classical messages based on entanglement swapping[J]. Physical Review A, 2005, 72(3): 15-19. DOI:10.1103/PhysRevA.72.022303 |
| [26] |
MARKHAM D, SANDER B C. Graph states for quantum secret sharing[J]. Physical Review A, 2008, 78(4): 042309. DOI:10.1103/PhysRevA.78.042309 |
| [27] |
DEUTSCH D, BARENCO A, EKERT A. Universality in quantum computation[J]. Proceedings Mathematical & Physical Sciences, 1995, 449(1937): 669-677. |
| [28] |
ZHOU X, LEUNG D W, CHUANG I L. Methodology for quantum logic gate constructions[J]. Physical Review A, 2000, 62(5): 052316. DOI:10.1103/PhysRevA.62.052316 |
| [29] |
OUYANG Y, TAN S H, ZHAO L, et al. Computing on quantum shared secrets[DB/OL].[2018 -06 -04]. https://journals.aps.org/pra/pdf/10.1103/PhysRevA.96.052333.
|
 2019, Vol. 65
2019, Vol. 65




