文章信息
- 张艳娟, 秦润兰, 刘红美
- ZHANG Yanjuan, QIN Runlan, LIU Hongmei
- 加强超立方体中条件容错圈
- Cycles in Conditional Faulty Enhanced Hypercube Networks
- 武汉大学学报(理学版), 2016, 62(6): 568-574
- Journal of Wuhan University(Natural Science Edition), 2016, 62(6): 568-574
- http://dx.doi.org/10.14188/j.1671-8836.2016.06.013
-
文章历史
- 收稿日期:2015-09-06

超立方体是现今最著名、最通用, 也是最有效的互连网络的拓扑结构.在高性能计算中尤其在大型工业计算中有着非常重要的作用.因其结构正则、对称以及相对小的传输延迟,许多好的算法易于嵌入等优良性质而受到广泛关注[1].但是超立方体也有它固有的缺点,比如较大的直径,因此设计和维护高维的超立方体网络的复杂度比较高.为了获得比超立方体更优良的性质, 人们提出了超立方体的一系列变型结构, 如广义超立方体, 折叠超立方体, 纽立方体, 增广超立方体以及加强超立方体等等.
在现实网络中,处理器或者处理器连线发生故障是不可避免的,这就要求网络具有一定的容错性.也就是说当网络中一定数目的节点或者连线坏掉时,网络仍然可以有效的工作.在标准容错情况下,故障边的分布不受点的限制.超立方体网络及其变形网络在标准容错条件下已经有许多结论,关于超立方体及其变形结构性质以及点边容错性质,最近文献[2]得到了许多好的结果.例如,文献[2]证明了在超立方体Qn(n≥5)中,当|Fv|+|Fe|≤2n-4, |Fe|≤n-2时,则Qn-Fv-Fe包含一条长度至少为2n-2|Fv|的无故障圈. Du等[3]证明了当|Fv|=2n-3时,则Qn(n≥5)中能嵌入一条长度至少为2n-2|Fv|的无故障圈.由于加强超立方体Qn, k1≤k≤n-1是在n-维超立方体Qn中添加2n-1条的边得到的新结构[4],因此超立方体是加强超立方体的一个支撑子图,那么上述研究结论在加强超立方体Qn, k中均成立.Liu在文献[5]中研究加强超立方体存在大量故障点和故障边时圈的一些性质,即当|Fe|≤n-1且|Fv|+|Fe|≤2n-4时,则Qn, k(n≥4)中能找到一条长为2n-2|Fv|的容错圈. Liu在文献[6]中研究了加强超立方体Qn, k(n≥3, 1≤k≤n-1)的泛圈性问题,证明了当n和k奇偶性不同时,Qn, k中每一条边均在长为n-k+2到2n-1的奇圈上.Zhang[7]证明了当n和k奇偶性相同时,若|Fv|=2,Qn, k中含有长度从4到2n-4的偶圈,而且含有长度从n-k+2到2n-3的所有奇圈.同时文献[7]还证明了当|Fv|≤n-2时,若n和k奇偶性相同,Qn, k中存在长度为2n-2|Fv|的偶圈;若n和k奇偶性不同,Qn, k中存在长度为2n-2|Fv|的偶圈同时有长度为2n-2|Fv|+1的奇圈. Fan[8]证明了在折叠超立方体FQn(n≥4)中,当|Fv|=2n-3,则FQn-Fv中存在一个长度至少为2n-2fv的圈.
然而,由于网络的不同部分可能有不同的可靠性,我们就可以假设在一些部分的某些子集中,这些部分并不是同时坏掉的.Fu[9]提出了条件容错模型,即在网络模型中,所有的点都至少与两条非故障边相连.在这种模型下,也得到了一些结论.例如, Liu[10]证明了在约束条件:1)|Fe|≤2n-3和2)每个节点至少关联两条无故障边时,Qn, k中能找到一条长为2n的容错圈. Liu[11]进一步研究了条件容错模型下若加强超立方体Qn, k满足约束条件:1)|Fe|≤2n-3和2)每个节点至少关联两条无故障边时,当n和k有相同的奇偶性,那么在Qn, k中存在偶长为4到2n的的容错圈;当n和k有不同的奇偶性,那么在Qn, k中存在奇长为n-k+2到2n-1的容错圈.Cao[12]证明了在折叠超立方体FQn(n≥3)中,若|Fe|+|Fv|≤2n-3,|Fe|≥1且每个点至少关联两条非故障边,则在FQn-Fv-Fe中存在一个长度至少为2n-2fv的圈.
本文讨论了加强超立方体网络中存在大量故障点和故障边时圈的一些性质.
1 相关定义及引理G=(V, E)表示一个图,V为点集,E为边集.图中的一条路定义为一个点和边交替出现的序列P=v0e1v1e2v2…eivi…ekvk(1≤i≤k),其中点v1, v2, …, vk互不相同.边ei的端点是vi-1和vi,称P是从v0到vk的一条路或一条(v0, vk)路. k称为路P的长度.在简单图中,P可以由其顶点序列来表示P[v0, vk]=〈v0, v1, v2, …, vk〉.若v0=vk,则称P为圈.圈上所包含的边的数目称为圈长,长为k的圈称为k圈,若k为偶数,则称为偶圈;若k为奇数,则称为奇圈.图G中连接点u和v之间的最短路的长度称为两点间的距离,记为dG(u, v).
超立方体网络Qn=(V(Qn), E(Qn))是n维立方体, 它的图论模型是一个简单的无向图,V(Qn)={x1x2…xn:xi∈{0, 1}, i=1, 2, …, n},超立方体中每个点x都可以用一个长为n的二元位串表示,即x=x1x2…xn,xi=0, 1.设x=x1x2…xi-1xixi+1…xn和y为V(Qn)中两个点,x和y之间有边相连当且仅当y满足:
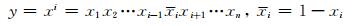
|
Qn中两个顶点x=x1x2…xn和y=y1y2…yn之间的Hamming距离定义为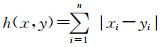
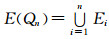
超立方体Qn可以沿着第i(1≤i≤n)-维划分,得到两个子图.分别用Qn-1i0和Qn-1i1表示这两个子图.从划分的定义来看,可知这样得到的两个子图Qn-1i0和Qn-1i1是两个(n-1)-维超立方体子图.一个点x=x1x2…xn是Qn-1i0中的一个点当且仅当此点的第i位为xi=0;类似的,点x是Qn-1i1中的一个点当且仅当此点的第i位为xi=1.
下面给出加强超立方体Qn, k的定义.
定义1 n维加强超立方体记为
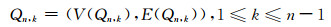
|
其定义如下
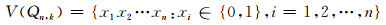
|
设x=x1x2…xi-1xixi+1…xn和y为V(Qn, k)中两个点,x=x1x2…xi-1xixi+1…xn和y之间有边相连当且仅当y满足下列条件之一:
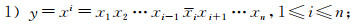
|
或者
2) 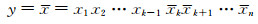
由定义1可知加强超立方体Qn, k是在超立方体Qn中添加2n-1条补边(the complementary edge)后得到的,即V(Qn, k)=V(Qn),E(Qn, k)=Ec∪E(Qn),其中补边集记为
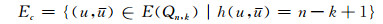
|
边(u, ui)代表Qn, k中的超立方体的i维边,其定义为:
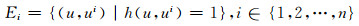
|
在本文中,记Fv为故障点的集合,Fe为故障边的集合,Fec为Qn, k中故障补边的集合,Fei为Qn, k中超立方体的故障i维边的集合,且|Fe|=fe,|Fv|=fv,Fec=Fe∩Ec,Fei=Fe∩Ei,|Fec|=fec,|Fei|=fei.
引理1[5] 在加强超立方体Qn, k中,对任意的j∈{k, k+1, …, n}∪{c},则有Qn, k-Ej同构于Qn.
引理2[5] 在加强超立方体Qn, k(n≥3, 1≤k≤n-1)中,若fe+fv≤2n-4,fe≤n-1,则Qn, k-Fe-Fv中存在一个长度至少为2n-2fv的圈.
引理3[13] 在超立方体Qn(n≥3)中,若fe+fv≤2n-4,fe≤2n-5且Qn中每个点至少关联两条无故障边,则在Qn-Fe-Fv中存在一个长度至少为2n-2fv的圈.
引理4[10] 在加强超立方体Qn, k(n≥3, 1≤k≤n-1)中,若fe≤2n-3且Qn, k中每个点至少关联两条无故障边,则在Qn, k-Fe中存在一个长度为2n的圈.
引理5[6] 在加强超立方体Qn, k(n≥3, 1≤k≤n-1)中,若n和k奇偶性不同,则Qn, k中每一条边均在长为n-k+2到2n-1的奇圈上.
引理6[8] 在折叠超立方体FQn(n≥4)中,若fv=2n-3,则在FQn-Fv中存在一个长度至少为2n-2fv的圈.
引理7[12] 在折叠超立方体FQn(n≥3)中,若fe+fv≤2n-3,fe≥1且FQn中每个点至少关联两条无故障边,则在FQn-Fv-Fe中存在一个长度至少为2n-2fv的圈.
引理8[14] 将加强超立方体Qn, k沿着第i(1≤i≤n)-维划分,可以得到两个子图.我们分别用Qn-1, ki0(Qn-1i0)和Qn-1, ki1(Qn-1i1)来表示这两个子图.当i < k时,得到的两个子图Qn-1, ki0和Qn-1, ki1是两个(n-1)-维的加强超立方体子图;当i≥k时,得到的两个子图Qn-1i0和Qn-1i1是两个(n-1)-维的超立方体子图.一个点x=x1x2…xn是Qn-1, ki0(Qn-1i0)中的一个点当且仅当此点的第i位为xi=0;类似的,此点x是Qn-1, ki1(Qn-1i1)中的一个点当且仅当此点的第i位为xi=1.
引理9[5] 在加强超立方体Qn, k(n≥3, 1≤k≤n-1)中,设u和v为Qn, k中任意两点,若fe+fv≤n-1,则当d(u, v)为奇数时,u和v之间存在一条长为2n-2fv-1的(u, v)路;当d(u, v)为偶数时,u和v之间存在一条长为2n-2fv-2的(u, v)路.
引理10[15] 在超立方体Qn(n≥2)中,设u和v为Qn中任意两点,则u和v之间存在一条长为l的(u, v)路,其中d(x, y)≤l≤2n-1且l与d(x, y)奇偶性相同.
2 条件(2n-4)-点边容错下加强超立方体中容错圈的嵌入若一个点恰好关联了l条无故障边,则称这个点为l-无故障点.
引理11 若fe+fv≤2n-4,则Qn, k中至多存在一个2-无故障点.
证 用反证法证明.假设Qn, k含两个2-无故障点u和v,接下来只需要考虑一种特殊情况即Qn, k中故障元素达到最小值时,即当点u和v有公共邻点,可知Qn, k中故障元素至少为(n-1)+(n-1)-1=2n-3,这与条件fe+fv≤2n-4相矛盾,因此假设不成立,即Qn, k中至多存在一个2-无故障点.
定理1 若Qn, k(n≥4, 1≤k≤n-1)满足约束条件:1) fe+fv≤2n-4和2) Qn, k中每个点至少关联两条无故障边,则Qn, k-Fe-Fv中含一个长度至少为2n-2fv的圈.
证 记Fv为Qn, k中故障点的集合,Fe为Qn, k中故障边的集合,Fec为Qn, k中故障补边的集合,Fei为Qn, k中超立方体故障i-维边的集合,且
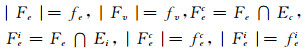
|
由引理2,当fe+fv≤2n-4,fe≤n-1时,Qn, k-Fe-Fv含一个长度至少为2n-2fv的圈.因此,只需要考虑如下情况:fe+fv≤2n-4,fe≥n.由引理11可知Qn, k中至多存在一个2-无故障点,故可以从Qn, k中是否含2-无故障点来分两种情况讨论:
情形1 当加强超立方体Qn, k中恰好存在一个2-无故障点.设u为Qn, k中的2-无故障点,即点u关联恰好两条无故障边,Qn, k-{u}中每个点均为l-无故障点,其中l≥3(若l < 3,这与引理11相矛盾),即Qn, k-{u}中每个点均关联至少3条无故障边.在此情况下,Qn, k中与点u关联的故障边的总数是n-1,故一定存在一个j∈{k, k+1, …, n}∪{c}使得(u, uj)是一条故障边(假设这样的j不存在,则可设(u, ui)为与点u关联的故障边且i∈{1, 2, …, k-1},那么此时可知与点u关联的故障边总数至多为k-1,而k-1≤n-2 < n-1,这与点u关联的故障边的总数是n-1相矛盾,故一定存在这样的j),即fej≥1,j∈{k, k+1, …, n}∪{c}.由引理1知,Qn, k-Ej同构于Qn(j∈{k, k+1, …, n}∪{c}).因为fe+fv≤2n-4且fej≥1,则有
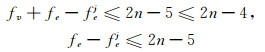
|
又因为Qn, k-{u}中每个点均为l-无故障点,其中l≥3,并且与点u关联的j维边为故障边,所以可知Qn, k-Ej中每个点至少关联两条无故障边,故Qn, k-Ej满足引理3的约束条件,于是由引理3知,在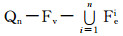
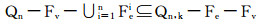
情形2 当加强超立方体Qn, k中不存在2-无故障点.也就是说,Qn, k中每个点均为l-无故障点,其中l≥3,即Qn, k中每个点均关联至少3条无故障边.分以下几种情况讨论:
情形2.1 Fek∪Fek+1∪…∪Fen∪Fec≠∅,在这种情况下,选择一个j-维边(j∈{k, k+1, …, n}∪{c})使得fej≥1.由引理1知,Qn, k-Ej同构于Qn,同情况1中的讨论方法一样,可知此时Qn, k-Ej满足引理3的约束条件,于是可知在Qn, k-Fe-Fv中存在一个长度至少为2n-2fv的圈.
情形2.2 Fek∪Fek+1∪…∪Fen∪Fec=∅,即Qn, k中的故障边全部在集合E1∪E2∪…∪Ek-1中,也就是说Qn, k中的故障边全部分布在Qn, k-Ec(≅Qn)中,即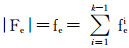
情形2.2.1 fv=0,fe≤2n-4.由于Qn, k中每个点均关联至少两条无故障边且fe≤2n-4≤2n-3,由引理4,Qn, k-Fe中可嵌入一个长度至少为2n的圈.
情形2.2.2 fv≥1,fe≤2n-5.由引理1,Qn, k-Ec同构与Qn,因为Qn, k中每个点均关联至少三条无故障边,故在Qn, k-Ec中每个点关联至少两条无故障边且fe+fv≤2n-4,fe≤2n-5,即Qn, k-Ec满足引理3的约束条件,故由引理3,在Qn-Fv-Fe中存在一个长度至少为2n-2fv的圈,又由于Qn-Fv-Fe⊂Qn, k-Fe-Fv,即在Qn, k-Fe-Fv中能找到一个长度至少为2n-2fv的圈.定理1得证.
3 条件(2n-3)-点边容错下加强超立方体中容错圈的嵌入下面将在定理1的基础上增加故障元素至2n-3来讨论此时加强超立方体中容错圈的嵌入问题,主要证明当Qn, k满足约束条件:1)|Fv|+|Fe|≤2n-3, |Fe|≥k和2)每个节点至少关联两条无故障边时,Qn, k(n≥5)中能嵌入一条长为2n-2|Fv|的容错圈.
引理12 若fe+fv≤2n-3,则Qn, k(n≥4, 1≤k≤n-1)中至多存在两个2-无故障点.
证 用反证法证明.假设Qn, k含三个2-无故障点u,v和w.由引理5可知,当k=n-1时,Qn, k含长度为3的圈.接下来只需要考虑一种特殊情况即Qn, k中故障元素达到最小值时,即三条边(u, v),(v, w)和(w, u)依次连接组成长为3的圈,且三条边(u, v),(v, w)和(w, u)均为故障边,此时,得到故障元素总数至少为
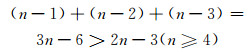
|
这与条件fe+fv≤2n-3相矛盾,因此假设不成立,即Qn, k中至多存在两个2-无故障点.
引理13 若fe+fv≤2n-3,且Qn, k恰好含两个2-无故障点u和v,那么就有d (u, v)=1且uv∈Fe.
证 若d (u, v)>1,那么故障边的总数至少为(n-1)+(n-1)=2n-2>2n-3,与引理条件fe+fv≤2n-3产生矛盾,故d (u, v)=1;若uv∉Fe,那么故障边的总数至少为(n-1)+(n-1)=2n-2>2n-3,与引理条件fe+fv≤2n-3产生矛盾,故uv∈Fe.
定理2 若Qn, k(n≥5)满足约束条件:1) fe+fv≤2n-3,fe≥k和2)每个节点至少关联两条无故障边,则Qn, k-Fe-Fv中能嵌入一条长为2n-2fv的容错圈.
证 记Fv为Qn, k中故障点的集合,Fe为Qn, k中故障边的集合,Fec为Qn, k中故障补边的集合,Fei为Qn, k中故障超立方体的i维边的集合,其中i∈1, 2, …, n,且|Fe|=fe,|Fv|=fv,Fec=Fe∩Ec,|Fec|=fec,|Fei|=fei.由定理1可知,当fe+fv≤2n-4时,Qn, k-Fe-Fv含一个长度至少为2n-2fv的圈.由引理6和引理7可知,当fe+fv=2n-3且k=1时,Qn, 1(=FQn)中含一个长度至少为2n-2fv的圈.由引理4可知,当fv=0, fe=2n-3时,Qn, k中能找到一条长为2n的容错圈.因此,只需要考虑如下情况:当1) fe+fv=2n-3,fv≥1,2≤k≤fe≤2n-4和2)每个节点至少关联两条无故障边时,Qn, k-Fe-Fv(n≥5, k≥2)中能嵌入一条长为2n-2fv的容错圈.由引理11,通过2-无故障点的数量来分三种情况讨论.
情形1 Qn, k不含2-无故障点,也就是说Qn, k中每个点均是l-无故障点,其中l≥3,下面我们分情况讨论:
情形1.1 Fek∪Fek+1∪…∪Fen∪Fec≠∅,在这种情况下,可以找到存在至少一条故障边的一维边j维边,其中j∈{k, k+1, …, n}∪{c},也就是说fej≥1.由引理1可知Qn, k-Ej同构于Qn(即Qn, k-Ej≅Qn).由于fe+fv=2n-3且fv≥1,那么就有fe≤2n-4,fe-fej≤2n-5,fv+fe-fej≤2n-4,又由于Qn, k-Ej个点至少关联两条无故障边,即Qn, k-Ej满足引理3的限制条件,则可知在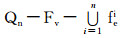
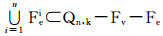
情形1.2 Fek∪Fek+1∪…∪Fen∪Fec≠∅,即所有的故障边均分布在Fe1∪Fe2∪…∪Fek-1中,也就是说所有的故障边均分布在Qn, k-Ec≅Qn中.由于Qn, k中每个点均是l-无故障点,其中l≥3,由引理8可知,对于任意的i∈{1, 2, …, k-1},都有(n-1)-维加强超立方体Qn-1, ki0和Qn-1, ki1中每个点至少关联两条无故障边.设Fvi0Fvi1表示Qn-1, ki0Qn-1, ki1中的故障点集合,Fei0Fei1表示Qn-1, ki0Qn-1, ki1中的故障边集合,令|Fvi0|=fvi0,|Fvi1|=fvi1,|Fei0|=fei0,|Fei1|=fei1.设Fhi为横跨Qn-1, ki0和Qn-1, ki1之间的超立方体的i-维故障边,|Fhi|=fhi.由于fe≥k≥2且所有的故障边均分布在Fe1∪Fe2∪…∪Fek-1中,那么就有max{|Fe1|, |Fe2|, …, |Fek-1|}≥2.
情形1.2.1 max{|Fe1|, |Fe2|, …, |Fek-1|}≥3.
令fhi=max{|Fe1|, |Fe2|, …, |Fek-1|}≥3(i∈1, 2, …, k-1),这样的i-维边确定后,将Qn, k按照i-维边划分得到两个子加强超立方体Qn-1, ki0和Qn-1, ki1.不妨假设fei0+fvi0≤fei1+fvi1,那么则有2(fei0+fvi0)≤fei0+fvi0+fei1+fvi1≤2n-6,故fei0+fvi0≤n-3且fei1+fvi1≤2n-6.由于Qn-1, ki1中每个点至少关联两条无故障边,故由定理1可知,在Qn-1, ki1中存在一个长度至少为2n-1-2fvi1的圈Ch.由于Ch长度为2n-1-2fvi1,即在Ch上至少存在2n-2-fvi1条相互不相交且不同的边.由于n≥5,故2n-2>2n-3,又fv+fe=2n-3,故2n-2-fvi1>fv+fe-fvi1=fei0+fvi0+fei1+fhi>fei0+fvi0+fhi,因此在Ch上至少存在一条边(a, b)使得边(a, ai),(b, bi)和(ai, bi)均为无故障边.令P[a, b]是Ch-{(a, b)}上连接点a和点b的一条路,其长度为2n-1-2fvi1-1.由引理9可知,Qn-1, ki0中点ai和点bi之间存在一条长度至少为2n-1-2fvi0-1的无故障路P[ai, bi],故可以在Qn, k中构造出一个圈为C=P[a, b]⊕(b, bi)⊕P[bi, ai]⊕(ai, a)(用“⊕”来表示路的连接符号,它也可以用来连接边),其长度为2n-1-2fvi0-1+2+2n-1-2fvi1-1=2n-2fv.
情形1.2.2 max{|Fe1|, |Fe2|, …, |Fek-1|}=2,即max{2, k}≤fe≤2(k-1).不失一般性,假设|Fe1|≥|Fe2|≥…≥|Fek-1|,即|Fe1|=2.将Qn, k按照1-维边划分得到两个子加强超立方体Qn-1, k10和Qn-1, k11.不妨假设fe10+fv10≤fe11+fv11,于是就有fe10+fv10≤n-3且fe11+fv11≤2n-5,我们可以分以下几种情况讨论:
情形1.2.2.1 1≤fe10+fv10≤n-3且fe11+fv11≤2n-6,参照情形1.2.1,可以在Qn, k中构造出长度至少为2n-2fv的圈.
情形1.2.2.2 fe10+fv10=0且fe11+fv11=2n-5.由于fv11=fv≥1,设u为Qn-1, k11中的一个故障点,由定理1(假设u为无故障点),则在Qn-1, k11中存在一个不含任何除了u以外的其他故障元素的h-圈Ch,其长度为h=2n-1-2(fv11-1).
情形1.2.2.2.1 若圈Ch含点u,设x和y是点u在圈Ch上的两个邻点,设w (≠u)和z (≠u)分别为点x和y在Ch上的邻点.
情形1.2.2.2.1.1 若(x, x1)和(y, y1)是Qn, k中两条无故障边.由于x和y是点u在圈Ch上的两个邻点,则d (x, y)=2,因此d (x1, y1)=2.由于fe10+fv10=0,即Qn-1, k10是一个无故障加强超立方体,又因为Qn-110⊂Qn-1, k10,由引理10可知,当d (x1, y1)=2时,点x1和y1之间存在一条长度为2n-1-2的路P1=P[x1, y1].由于Ch=P[y, x]⊕(x, y),则C=P[y, x]⊕(x, x1)⊕P[x1, y1]⊕(y1, y)为所求,其长度为2n-2fv.
情形1.2.2.2.1.2 若(x, x1)和(z, z1)是Qn, k中两条无故障边(关于(y, y1)和(w, w1)是Qn, k中两条无故障边的讨论是类似的).由于w (≠u)和z (≠u)分别为点x和y在Ch上的邻点,则d (x, z)=3,因此d (x1, z1)=3.因为Qn-1, k10是无故障加强超立方体,Qn-110⊂Qn-1, k10,故由引理10可知,当d (x1, z1)=3时,点x1和点z1之间存在一条长度为2n-1-1的路P2=P[x1, z1].由于Ch=P[z, x]⊕(x, u)⊕(u, y)⊕(y, z),因此我们需要的圈可以构造为
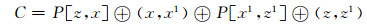
|
其长度为2n-2fv.
情形1.2.2.2.1.3 若(x, x1)和(y, y1)是Qn, k中两条故障边.由于Qn, k中每个点均是l-无故障点,其中l≥3, 故除了点u和边(x, x1)以外,点x在Qn-1, k11中关联至多n-4个故障元素,除了点u和边(y, y1)以外,点y在Qn-1, k11中关联至多n-4个故障元素,因此,在Qn-1, k11中与点x关联的故障元素总数加上与点y关联的故障元素总数之和至多为n-4+n-4+1=2n-7 < 2n-5,故在Qn-1, k11中一定可以找到一个端点不属于{x, y}的故障边(或者一个不与点x关联也不与点y关联的故障点),不妨假设在Qn-1, k11中存在这样的故障边(a, b)(至于存在这样的故障点的情形讨论是一样的),故由定理1(假设(a, b)为无故障边)可知,在Qn-1, k11中存在一个圈C1不含除了(a, b)以外的其他故障元素,其长度为2n-1-2fv11.圈C1不含(a, b)的情况较容易讨论,不妨讨论圈C1含(a, b)的情况.由于故障边(a, b)的端点不属于{x, y},故边(a, a1)和(b, b1)是非故障边.由于d (a, b)=1,d (a, a1)=1,d (b, b1)=1,因此d (a1, b1)=1.由引理10,在超立方体Qn-110中,当d (a1, b1)=1时,点a1和点b1之间存在一条长为2n-1-1的路P[a1, b1].由于圈C1=P[b, a]⊕(a, b), 因此有圈C=P[b, a]⊕(a, a1)⊕P[a1, b1]⊕(b1, b),其长度为2n-1-1+2+2n-1-2fv11-1=2n-2fv.
情形1.2.2.2.1.4 若(x, x1)和(w, w1)是Qn, k中两条故障边(关于(y, y1)和(z, z1)是Qn, k中两条故障边的讨论是类似的).由于Qn, k中每个点均是l-无故障点,其中l≥3, 故除了点u和边(x, x1)以外,点x在Qn-1, k11中关联至多n-4个故障元素,除了边(w, w1)以外,点w在Qn-1, k11中关联至多n-3个故障元素,因此,在Qn-1, k11中与点x关联的故障元素总数加上与点w关联的故障元素总数之和至多为n-3+n-4+1=2n-6 < 2n-5,故在Qn-1, k11中一定可以找到一个不与点x关联也不与点w关联的故障点h (或者一个端点不属于{x, w}的故障边),设m,n为h在Qn-1, k11中的两个邻点,如情形1.2.2.2.1.1的讨论,故可以在Qn, k中找到一个圈C1长度为2n-2fv.
情形1.2.2.2.2 若圈Ch不含点u, 如情况1.2.1的讨论,可知在Qn, k中能找到一个长度为2n-2fv的圈.
情形2 Qn, k恰好含一个2-无故障点,设这个2-无故障点为u,则在Qn, k-{u}中每个点均是l-无故障点,其中l≥3.因为与点u关联的故障边总数为n-1,故一定存在j (∈{k, k+1, …, n, c})-维边使得uuj是一条故障边(假设不存在这样j-维边,即与点u关联的故障边均为(u, ui),其中i∈{1, 2, …, k-1},那么与点u关联的故障边至多为k-1条,而k≤n-1,因此k-1≤n-2 < n-1,这里便产生矛盾,故假设不成立).由引理1知Qn, k-Ej同构于Qn(即Qn, k-Ej≅Qn),与情形1.1的讨论方法一样,可知Qn, k中能构造出长度至少为2n-2fv的圈.
情形3 Qn, k含恰好两个2-无故障点u和点v,由引理13,就有d (u, v)=1且uv∈Fe.
情形3.1 (u, v)∈Fej,其中j∈{k, k+1, …, n, c},由引理1,可知Qn, k-Ej≅Qn,与情况1.1的讨论方法一样,可知Qn, k中能构造出长度至少为2n-2fv的圈.
情形3.2 (u, v)∈Fei,其中i∈{1, 2, …, k-1}.将Qn, k按照i (i < k, 2≤k≤n-1)-维边划分得到两个n-1维的子加强超立方体Qn-1, ki0和Qn-1, ki1使得u∈Qn-1, ki0且v∈Qn-1, ki1.由于点u和点v均为2-无故障点,即在Qn-1, ki0中,与点u关联的故障元素总数为n-2,与点v关联的故障元素总数也为n-2,故fei0+fvi0≥n-2且fei1+fvi1≥n-2,而fe+fv=2n-3且Fei≥1,故fei0+fvi0=n-2, fei1+fvi1=n-2且Fei=1,由定理1,与情况1.2.1的讨论方法一样,可以在Qn, k中构造出长度至少为2n-2fv的圈.
由以上各种情况的分析,完成了此定理的证明.
4 结论互连网络中圈的嵌入问题是一个非常重要的研究课题.网络在实际投入使用时,其处理器和链路同时出现故障是不可避免的,因此,考虑含有故障点和边的网络是非常有必要的.而作为超立方体网络的一种变型结构--加强超立方体中的圈的嵌入问题更是值得我们研究.在本文中,证明了当点边错误元素总数不超过2n-4,且每个节点至少关联两条无故障边时,长度至少为2n-2|Fv|的容错圈可以嵌入到加强超立方体Qn, k中.同时进一步研究了在条件容错模型下(2n-3)-点边容错加强超立方体中容错圈的嵌入,当点边错误元素总数不超过2n-3,错误边数至少k条,且每个节点至少关联两条无故障边时,Qn, k中能嵌入一条长为2n-2|Fv|的容错圈.
| [1] | XU J M. Topological Structure and Analysis of Interconnection Networks.[M] Dordrecht: Kluwer Academic Publishers, 2001 . |
| [2] | TSAI C H. Fault-tolerant cycles embedded in hypercubes with mixed link and node failures[J]. Applied Mathematices Letters , 2008, 21 (8) : 855–860 DOI:10.1016/j.aml.2007.08.012 |
| [3] | DU Z Z, XU J M. A note on cycle embedding in hypercubes with faulty vertices[J]. Information Processing Letters , 2011, 111 (12) : 557–560 DOI:10.1016/j.ipl.2011.03.002 |
| [4] | TZENG N F, WEI S. Enhanced hypercubes[J]. IEEE Transactions on Computers , 1991, 40 (3) : 284–294 DOI:10.1109/12.76405 |
| [5] | LIU M, LIU H M. Path and cycles embedding on faulty enhanced hypercube networks[J]. Acta Mathematica Scientia , 2013, 33B (1) : 227–246 |
| [6] | LIU H M. The structural features of enhanced hypercube networks[DB/OL].[2015-02-03]. http://ieeexplore.ieee.org/stamp/stamp.jsptp=&arnumber=5364139, 2009:345-348. |
| [7] | ZHANG Y J, LIU H M, LIU M. Vertex-fault-tolerant cycles embedding on enhanced hypercube networks[J]. Acta Mathematica Scientia , 2013, 33B (6) : 1–10 |
| [8] | FAN Y H, LIU H M, LIU M. Path and cycles in faulty folded hypercube[J]. Journal of Mathematics , 2013, 33 (3) : 393–400 |
| [9] | FU J S. Longest fault-free paths in hypercubes with vertex faults[J]. Information Science , 2006, 176 (7) : 759–771 DOI:10.1016/j.ins.2005.01.011 |
| [10] | LIU M, LIU H M. Conditional edge-fault-tolerant hamiltonicity of enhanced hypercube[DB/OL].[2015-02-20]. http://ieeexplore.ieee.org/stamp/stamp.jsptp=&arnumber=5974791. |
| [11] | LIU M, LIU H M. Cycles in conditional faulty enhanced hypercube networks[J]. Journal of Communications and Networks , 2012, 14 (2) : 213–221 DOI:10.1109/JCN.2012.6253071 |
| [12] | CAO S L, LIU H M. On constraint fault-free cycles in folded hypercube[J]. International Journal of Applied Mathematics and Statistics , 2013, 42 (12) : 38–44 |
| [13] | DU Z Z, JING J, MA M J, et al. Cycle embedding in hypercubes with faulty vertices and edges[J]. Journal of University of Science and Technology of China , 2008, 38 (9) : 1020–1024 |
| [14] | LIU H M. Properties and performance of enhanced hypercube networks[J]. Journal of Systems Science and Information , 2006, 3 : 251–256 |
| [15] | LI T K, TSAI C H, M J J, et al. Bipanconnectivity and edge-fault-tolerant bipancyclicity of hypercubes[J]. Information Processing Letters , 2003, 87 (2) : 107–110 DOI:10.1016/S0020-0190(03)00258-8 |
 2016, Vol. 62
2016, Vol. 62




