文章信息
- 姜恩华
- JIANG Enhua
- Walsh变换的一种快速并行算法
- A Fast Parallel Algorithm of the Walsh Transform
- 武汉大学学报(理学版), 2019, 65(6): 576-580
- Journal of Wuhan University(Natural Science Edition), 2019, 65(6): 576-580
- http://dx.doi.org/10.14188/j.1671-8836.2019.06.007
-
文章历史
- 收稿日期:2018-03-02

近年来,正交变换的理论和方法引起了科学界和工程界的广泛关注[1~4],在信号处理领域内得到了广泛应用。离散Walsh变换是信号处理领域中应用比较广泛的一种正交变换[1, 5]。变换是信号处理系统的一种数学抽象。在数学上,可将变换看成一种算法或算子。离散正交变换算子的矩阵形式是正交矩阵。由于正交矩阵的逆矩阵的存在性,保证了信号的恢复或重建。另外,由于正交变换满足Parseval定理,保证了信号变换前后能量的守恒。原始信号经过正交变换后得到一组离散系数(谱系数),这组系数通常将原始信号的能量集中在少数系数上,减少了原始信号中各分量的相关性。虽然早在1923年Walsh已提出了完整的Walsh函数的数学理论[6],但Walsh变换真正被人们重视并付诸应用,则是在20世纪60年代快速算法[7]提出以后。它在近代数字逻辑理论和技术中的应用则是在20世纪70年代[8, 9]。目前,Walsh变换的理论和谱技术在计算机科学与技术、通信技术、图像压缩、密码学、近代数字逻辑理论,以及量子可逆逻辑电路等方面均获得了应用[2~4, 10]。由于基函数的排序不同,Walsh变换具有以不同序表示的形式。本文讨论了以Hadamard序表示的离散Walsh变换,或称为Walsh-Hadamard变换,并导出了这种变换的一种并行算法。这种离散正交变换的算子形式可用Hadamard矩阵表示。由于Hadamard矩阵有简单的递推公式,因此这种Walsh变换的应用很广泛。
对于离散Walsh变换的谱系数的计算,虽然有相应的快速算法,但当问题的规模n 增加时,其计算时间将迅速(指数阶)增加,此时应采用并行计算方法来解决此问题。本文将一维Walsh变换转换为二维Walsh变换,并将其用两个一维离散Walsh变换的并行算法计算,导出了离散Walsh变换算法的一种并行算法及其快速并行算法。该算法使计算Walsh谱系数的算法的时间复杂度降低,并且这种算法为实数域上的矩阵运算,适合用高级语言编程实现。
1 布尔函数的分解和Walsh-Hadamard变换的并行算法 1.1 离散Walsh-Hadamard变换像三角函数系一样,Walsh函数系是一个完备的正交函数系[6],其中每个函数只取+1和-1两个值,其波形呈双极性矩形波波形。Hadamard矩阵可以由以Hadamard序排列的Walsh函数WalH (k,θ)的波形对归一化时间θ(θ 不一定是时间)的主值区间[0,1),以N=2n (n 为正整数)等份均匀采样求得。例如,当n=3时,对前8个WalH (k,θ)函数的波形以N=8等份均匀采样,得到以Hadamard序排列的离散Walsh函数为WalH (k,m),其中,k,m = 0,1,⋯,N-1。将它们排列成一个8阶的矩阵,则得一个8阶的Hadamard矩阵H3,利用矩阵的Kronecker乘积运算(也称直积运算),以符号“⊗”表示这种运算,可将它表示为
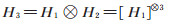
|
式中H1和H2分别为2阶和4阶的Hadamard矩阵。利用递推公式可得2n阶Hadamard矩阵为
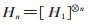
|
(1) |
若把一个离散时间信号f(m),m=0,1,…,2n-1,n 为正整数,看成相应的信号空间的一个点,即一个列向量f= [ f (0),f (1),⋯,f (2n-1)]T,则得该信号的离散Walsh变换和离散Walsh反变换如下
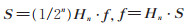
|
(2) |
式中S= [S (0),S (1),⋯,S (2n-1)]T,称为谱系数列向量,其中各分量称为谱系数。
1.2 布尔函数的分解布尔(Boolean)函数即二值逻辑函数,简称逻辑函数,其变量和函数均在布尔集合{0,1}上取值。对于一个定义在变量集合X= {x1,x2,⋯,xn}上的n 变量函数f (X),由Shannon展开定理,可导出它在布尔域上的最小项展开式为
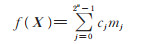
|
(3) |
定义
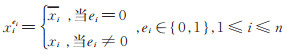
|
(4) |
则得,最小项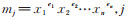
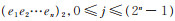
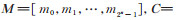
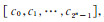
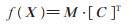
|
(5) |
在变量集合X上取划分

|
(6) |
其中,B1 ∪ B2 = X,B1 ∩ B2 = ∅,以子集合B1和B2中的变量分别组成两组最小项:
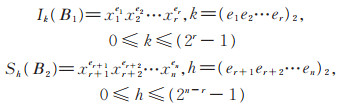
|
并令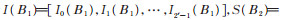
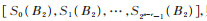
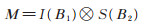
|
(7) |
由(5)式得该函数的最小项展开式为
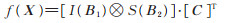
|
(8) |
将矩阵C按划分式(6)重新排序为一个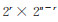
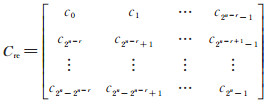
|
(9) |
则得
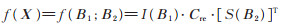
|
(10) |
若令
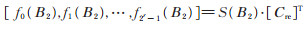
|
(11) |
则得
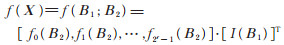
|
(12) |
亦即
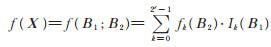
|
(13) |
(13)式即为原函数按照划分式(6)的Shannon展开(分解)式。
1.3 Walsh变换的并行算法在数字信号逻辑处理中,常把一个n 变量布尔函数f (x1,x2,⋯,xn)看作一个数字信号f(m)进行分析、设计或其他处理,其中,m = (x1 x2⋯xn)2,0 ≤ m ≤ (2n - 1)。然而,对于数字逻辑研究领域中所涉及的上述问题,当函数中的变量数目增多时,这些问题在布尔空间直接解决是较困难的,而在Walsh谱空间解决则较有效。当从布尔空间变换到Walsh谱空间时,函数的取值作0 → 1,1 → -1变换,其运算为实数域上的乘法运算和加法运算。将函数f (x1,x2,⋯,xn)之值cm以0 → 1,1 → -1变换,得到相应的值am,m = 0,1,⋯,(2n - 1)。令列向量为F= [a0,a1,⋯,a2n-1]T,则得该布尔函数的离散Walsh变换和离散Walsh反变换如下
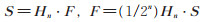
|
(14) |
注意到,上述离散Walsh变换和离散Walsh反变换的矩阵形式是以数字信号的逻辑处理中的形式来定义的,(14)式中2n 阶的Hadamard矩阵Hn 由下式定义:
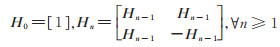
|
(15) |
谱系数列向量S= [S0,Sn,Sn-1,S(n-1) n,Sn-2,⋯, S12⋯n]T。Sj下标的取法如下:当j=0时,Sj= S0;当j ≠ 0时,Sj的一组下标为j = (x1 x2⋯xn - 1xn)2中取值为1的变量的下标组合,例如(x1 x2⋯xn - 1xn)2 = (00⋯01)2表示Sn,(00⋯10)2表示Sn - 1,(00⋯11)2表示S(n- 1) n 等。各阶谱系数的意义如下:S0称为0阶谱系数,它表示f (X)与常量的相关性(相似程度),若S0 =+2n (由于变换矩阵Hn 的正交性,其余的谱系数必均为0),表示f (X)为常量0;若S0 = -2n,表示f (X)为常量1。事实上,S0表示函数f (X)中的常量0的个数与常量1的个数之差。Si称为一阶谱系数,它表示f (X)与相应的变量xi的相关性,若Si= +2n,则表示f (X)= xi;若Si= -2n,则表示f (X)= xi,1 ≤ i ≤ n。其余的谱系数称为高阶谱系数,它们分别表示函数f (X)与相应的异或函数的相关性。例如Sij称为二阶谱系数,i ≠ j,1 ≤ i,j ≤ n,它们表示函数f (X)与相应的异或函数(xi⊕xj)的相关性。又如,S12⋯n 称为n 阶谱系数,它表示函数f (X)与异或函数(x1⊕x2⊕… ⊕xn)的相关性。
为了导出Walsh变换的并行算法,按照划分式(6),将列向量F重新排列为一个2r × 2n-r矩阵为
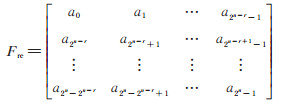
|
(16) |
令各子函数f0 (B2),f1 (B2),⋯,f2r- 1 (B2)的列向量分别为
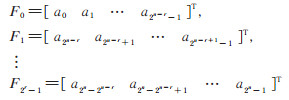
|
(17) |
并令各个子函数f0 (B2),f1 (B2),⋯,f2r- 1 (B2)的Walsh谱系数列向量分别为
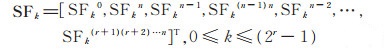
|
(18) |
(18)式中各子函数(0 ≤ k ≤ (2r - 1))的谱系数用上标表示。由Walsh变换的公式,得各子函数的Walsh变换式为
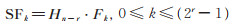
|
(19) |
或以矩阵形式表示为
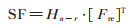
|
(20) |
其中子函数谱系数矩阵SF 为一个2n- r × 2r 矩阵,该矩阵的每一列对应一个子函数的谱系数列向量 SFk。和(8)式相类比,利用Kronecker矩阵乘积的性质,将(14)式中第一式按照划分式(6)表示为
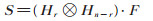
|
(21) |
并且按照划分式(6)将原函数f (X)的谱系数列向量S排列成一个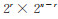
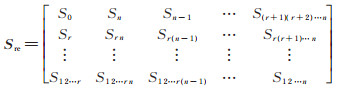
|
(22) |
该矩阵的纵坐标和横坐标分别为(x1 x2⋯xr)2和(xr + 1 xr + 2⋯xn)2,谱系数下标的编码方法如上所述。将(22)式用2r 阶Hadamard逆矩阵[Hr]-1 = (1/2r) ⋅ Hr 相乘,即将B1的变量由谱域反变换到布尔域,作为子函数fk(X)所含原函数最小项的公因子Ik(B1),0 ≤ k ≤ (2r - 1),剩余子函数谱系数矩阵的转置矩阵[SF]T为
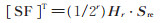
|
(23) |
该转置矩阵[SF]T的每一行对应一个子函数谱系数行向量,即[SFk]T,0 ≤ k ≤ (2r - 1)。将(23)式两边左乘矩阵Hr,则得 Sre = Hr ⋅ [SF]T(24)利用(20)式,则得
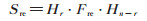
|
(25) |
利用Hadamard矩阵的性质,并利用(20)式及(23)式,即可推得
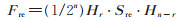
|
(26) |
并且按照划分式(6)将原函数f (X)分解得到各个子函数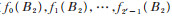
求给定函数的Walsh谱系数的快速并行算法,可以由(20)式和(24)式,分别利用快速Walsh变换并行算法的迭代过程流图[11]通过两步计算实现。
下面以一个简单的例子,说明该快速并行算法的一般步骤。
例1 求4变量布尔函数f (X)= Σ(0, 1, 2, 4, 6, 9, 10, 11, 13)的Walsh谱系数。
计算步骤如下:
1)取划分X= {B1;B2}= {x1,x2;x3,x4 },n= 4,r=2。
2)由函数f (X)的函数值,按照上述划分排列成矩阵Cre,将矩阵Cre的元素值0 → 1,1 → -1变换,得到谱域值矩阵Fre,分别为

|
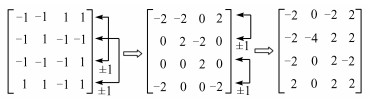
3)计算SF = Hn-r ⋅ [Fre]T。其迭代过程流图如图 1所示。图 1中的连线表示对应的操作是将前行各元素与分别乘以“ +1”(或“-1”)后的后行各元素相加形成新的(迭代后的)前行(或后行)。
|
| 图 1 由[Fre]T计算SF 的迭代过程流图(n=4,r=2) Fig. 1 The iterative process flow diagram of the calculating SF by the [Fre]T |
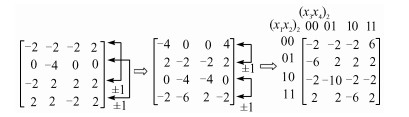
4)计算Sre = Hr ⋅ [SF]T。其迭代过程流图如图 2所示。图 2中,Sre的纵坐标和横坐标分别为(x1 x2)2 = (00,01,10,11)2和(x3 x4)2 = (00,01,10,11)2,在矩阵Sre中各元素的编码方法如上所述。
|
| 图 2 由[SF]T计算Sre的迭代过程流图(n=4,r=2) Fig. 2 The iterative process flow diagram of the calculating Sre by the [SF]T(n=4, r=2) |
将矩阵Sre进行矩阵的拉直运算,即得由(14)式第1式求得的谱系数列向量
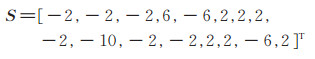
|
设N=2n,n 为变量个数(或问题的规模),计算N=2n 点的Walsh谱系数,需做N2次乘法,N (N - 1)次加法,时间复杂度为
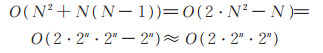
|
计算N=2n 点的Walsh谱系数,需做N log2 N 次加、减法运算,时间复杂度为
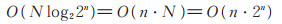
|
设r+q=n,N1=2r,N2=2q,计算N=2n 点的Walsh谱系数,需做(N1 N2
2 + N2 N2
1)次乘法,(N1 N2 (N2 - 1)+ N2 N1 (N1 - 1))次加法。当n 为偶数时,取r=q=n/2,时间复杂度为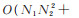
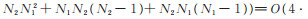
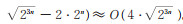
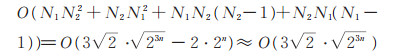
|
当n 为偶数时,取r=q=n/2,计算N =2n 点的Walsh谱系数,需做(2q log2 2q + 2r log2 2r)次向量加、减法运算,时间复杂度为
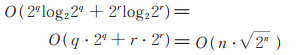
|
当n 为奇数时,取r=(n-1)/2,q=(n+1)/2,计算N=2n 点的Walsh谱系数,时间复杂度为
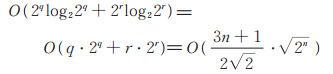
|
已有Walsh变换算法与本文算法计算次数的比较,见表 1。
| 算法 | n | |
| 10 | 20 | |
| Walsh变换 | 2×220 | 2×240 |
| 快速Walsh变换 | 10×210 | 20×220 |
| Walsh变换并行* | 4×215 | 4×230 |
| Walsh变换快速并行* | 10×25 | 20×210 |
| 注: 标注*的算法是本文提出的 | ||
把变换的计算速度定义为每秒完成的计算次数,由表 1可以看出当变量个数n=10时,本文导出的并行算法速度是Walsh变换算法速度的24倍,当n =20时,则为29倍;当变量个数n=10时,本文导出的并行快速算法速度是快速Walsh变换算法速度的25倍,当变量个数n=20时,则为210倍。
3 结语本文基于布尔函数的分解方法,导出了计算Walsh谱系数的一种并行计算方法及其快速并行算法。这两种算法降低了计算的时间复杂度,适用于高级语言编程计算,并且为Walsh变换的并行算法和并行快速算法的硬件实现提供了理论基础。
| [1] |
PARK C S. Recursive algorithm for sliding Walsh Hadamard transform[J]. IEEE Transactions on Signal Processing, 2014, 62(11): 2827-2836. DOI:10.1109/TSP.2014.2316146 |
| [2] |
KARPOVSKY M G, STANKOVIC R S, ASTOLA J T. Spectral Techniques for Design and Testing of Com puter Hardware[DB/OL].[2018-02-01]. http://www.bu.edu/reliable/publications/.
|
| [3] |
MARTINA M, MASERA G. State metric compression techniques for Turbo decoder architectures[J]. IEEE Transactions on Circuits and Systems, 2011, 58(5): 1119-1128. DOI:10.1109/TCSI.2010.2090566 |
| [4] |
PANG S Q, WANG J, WANG X N, et al. Application of orthogonal array and Walsh transform in resilient function[J]. Chinese Journal of Electronics, 2018, 27(2): 281-286. DOI:10.1049/cje.2017.09.011 |
| [5] |
KARPOVSKY M G. Finite Orthogonal Series in the Design of Digital Devices[M]. New York: John Wiley, 1976.
|
| [6] |
WALSH J L. A closed set of orthogonal functions[J]. American Journal of Mathematics, 1923, 45: 5-24. DOI:10.2307/2387224 |
| [7] |
SHANKS J. Computation of the fast Walsh-Fourier transform[J]. IEEE Trans on Computers, 1969, 18(5): 457-459. DOI:10.1109/T-C.1969.222685 |
| [8] |
HURST S L. The Logical Processing of Digital Signals[M]. New York: Grame-Russak, 1978.
|
| [9] |
HURST S L, MILLER D M, MUZIO J C. Spectral Techniques in Digital Logic[M]. London: Academic Press Inc, 1985.
|
| [10] |
MILLER D M. Spectral and Two-place Decomposition Techniques in Reversible Logic[DB/OL].[2018-02-01]. https://ieeexplore.ieee.org/document/1186906/. DOI: 10.1109/MWSCAS.2002.1186906.
|
| [11] |
姜文彬. 利用谱方法的多路选择器树形网络设计[J]. 系统工程与电子技术, 2001, 23(8): 92-97. JIANG W B. Designing of multiplexer tree-type logic networks by spectral means[J]. Systems Engineering and Electronics, 2001, 23(8): 92-97. DOI:10.3321/j.issn:1001-506X.2001.08.028 (Ch). |
 2019, Vol. 65
2019, Vol. 65




