文章信息
- 谢榕, 顾村锋
- XIE Rong, GU Cunfeng
- 一种欧椋鸟群协同算法
- A Starling Swarm Coordination Algorithm
- 武汉大学学报(理学版), 2019, 65(3): 229-237
- Journal of Wuhan University(Natural Science Edition), 2019, 65(3): 229-237
- http://dx.doi.org/10.14188/j.1671-8836.2019.03.001
-
文章历史
- 收稿日期:2018-09-28

2. 上海机电工程研究所,上海 200000
2. Shanghai Electro-Mechanical Engineering Institute, Shanghai 200000, China
许多应用领域,例如无人机集群密集编队、大型公共场所人群应急疏散、工业机器人群体协同作业、疾病传播控制等,均需要大规模智能体共同协同工作[1]。在这些应用系统中,智能体(如传感器、机器人、飞行器等)的个体能力有限,但其群体却能表现出高效的协同合作能力和高级的智能协调水平,即群智能(swarm intelligence)。随着计算机网络、通信通讯、分布计算等技术的不断发展,许多实际应用系统往往变得庞大而复杂,单个智能体因个体的知识能力、计算资源等限制而不能对其进行有效地处理和管理,因而大规模智能群体协同在许多应用中扮演着十分重要的作用。智能群体协同理论的研究一直以来都是人工智能领域群智能研究方向的关键课题,具有十分重要的现实意义,其目的在于研究分散的、自治的智能体如何利用集体行为相互协作,高效地、最大程度地共同完成单个智能体难以完成的复杂任务。
国内外许多学者对协同问题进行了广泛而深入的分析,大多是从群集控制方面开展研究,使群集协作涌现出他们所期望的行为。早期研究源于Reynolds等[2]对鸟群飞行行为的模拟仿真,他们提出了个体应遵循“聚集-分离-对齐”3条简单启发式规则,并构建Boids模型以描述群集行为。该工作实质上是一种无中心控制,通过采用局部规则控制策略达到群体协同的目的。在他们的研究基础上,一些学者提出了大量群集运动模型,较为经典的包括swarm、Cucker- Smale以及Cavagna模型等[3~6]。Kwong等[3]将swarm描述为一些相互作用的个体的集合,对该swarm模型进行群集行为仿真,包括聚集、直线运动、绕圈运动、八字形编队运动等。Wang等[4]则提出一套协调控制法则,并通过增加局部反馈信息对移动自治智能群体进行控制,使其能够产生所需的稳定群体运动。Cucker和Smale[5]采用邻接矩阵描述个体之间相互作用强度,提出了描述个体间速度相互影响的模型。这些方法有一定的局限性,群行为和群模型参数之间的关系往往是未知的,需要通过大量仿真实验确定合适的参数值。Cavagna等[6]尝试建立一般性理论统一群集运动模型,给出群集运动的惯性自旋模型,鸟群飞行时向外传播信息类似于磁性材料中的自旋波。然而群集系统通常高度复杂,群集行为极其多样,通过系统参数调节方法实现对大量群集行为的控制有着不足之处,所以仅仅依靠局部控制策略并不能满足大规模群集系统的有效控制。
近年来,欧椋鸟群集行为这一生物学重要发现为大规模智能群体协同应用提供了一条崭新的思路。一些研究者尝试利用群智能方法解决群体协同问题,并基于传统的粒子群算法进行改进。Cavagna等[7]提出通过极化作用度量欧椋鸟群的整体有序程度,在位移-速度框架下,将这种拓扑相互作用机制引入粒子群算法,使其在具有欧椋鸟飞行特征的同时具有更好的自适应性。Hereford和Blum[8]提出FlockOpt算法,对Boids模型[2]进行了改进,将欧椋鸟群运动模型与群智能算法相结合,解决了单峰搜索空间寻找最优值问题。Netjinda等[9]把欧椋鸟集体反应行为引入粒子群算法,以增加群体多样性,实现更广泛的搜索空间范围,避免次优解决方案。邱华鑫和段海滨[10]把这种鸟群群集飞行机制引入到无人机自主集群编队控制的实际应用中,初步研究成果表明,将该机制与群智能协同研究相互结合具有可行性。但由于欧椋鸟群集飞行的复杂性,当前研究尚没有提出实际的、完整的欧椋鸟群协同算法(starling swarm coordination algorithm,SSCA)的实现方案。
本文提出一种受欧椋鸟群集行为启发的智能群体协同的建模方法。区别于现有遗传算法、粒子群算法、蚁群算法[11~13]等,本文结合欧椋鸟等群集行为动物习性学和计算生物学最新研究成果,解析欧椋鸟生物群集行为机理和内部作用与协调机制,采用无中心自组织思想,利用智能体从其最邻近邻居信息中寻找最优解,并通过智能体之间相互作用的简单行为规则,从局部感知、运动行为、安全规避、适应进化这4个方面构建欧椋鸟群协同算法,实现描述整个群体运动在群体协同问题求解空间中从无序行为到有序行为的演化过程。
1 基本机理定义1(群体协同问题):设智能体(agent)群集的群体规模为N,agent i(i=1,2,…,N)的速度为vi。agent i 通过自适应调整向其周围agent j (j=1,2,…,N-1)聚集,并与其近邻保持一定安全距离。经过时间间隔Δt 后,整个群体的运动方向大致一致,飞行速度大致相同,满足
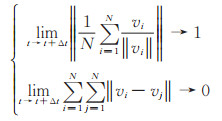
|
表现出整体有序运动状态。
群体协同的实质是大量agent相互作用,在无中心控制情况下所体现出的宏观有序行为,其基本原理包括局部感知、运动行为、安全规避、适应进化4个方面。
1.1 局部感知欧椋鸟群集飞行特点在于每只鸟只留意自己身边6或7只鸟的行为趋向(为方便叙述,下文以7只鸟进行说明),并有能力迅速对近邻鸟的行为作出反应。对应地,agent与其周围7个邻居进行交互,群体运动实际上是每个agent各自按照自己对客观世界的局部理解而产生行为的结果的总和。
agent i 的最邻近7个邻居中的任意一个用agent j 表示。agent j 的速度用vj表示,位置用xj表示。在局部感知下,agent群集表现为各向同性的特征,满足规则1。
规则1(各向同性规则):每个agent周围的邻居分布为各向异性,但其最邻近7个邻居为各向同性,即每个个体运动的方向大致相同。
定义2(拓扑距离):agent i 与从其最邻近的7个邻居中选取的榜样同伴agent j 之间的距离。通过这种拓扑距离(topological distance)[14]决定agent与其所在拓扑空间其他agent之间的相互作用关系。
规则2(拓扑距离规则):agent之间的相互作用取决于拓扑距离。
将拓扑相互作用机制引入群体协同算法,满足规则1和规则2,并对参数进行新的设置,使其在具有欧椋鸟群集飞行特征的同时具有更强的自适应性。如(1)式所示,v_neighbori为agent i 的7个邻居的速度的平均值,即
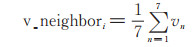
|
(1) |
为了保护自己,也为了提高捕食效率,欧椋鸟通常成群结队地活动,以抱团飞行躲避天敌。对应地,在一定动能作用下,agent产生运动行为,包括随机飞行行为、聚集行为、分散行为和逃逸行为。
agent i 的动能Ei用(2)式进行计算,即
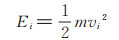
|
(2) |
式中,m 为agent i 的质量(假设agent的质量为单位1),vi为agent i 的速度。
以下描述agent所具有的4种行为包括随机飞行行为、聚集行为、分散行为和逃逸行为。
1)随机飞行行为
设每个agent的感知范围为Rp。当前agent飞行速度用v 表示,位置用x 表示。agent最小、最大飞行速度分别为常量vmin和vmax。当出现入侵者时,agent逃跑速度为ve。以当前agent所在位置为中心,以Rp为半径的一定空间范围内,agent对集合N中每个邻居与自己之间的距离进行比较,选出距离自己最近的7个邻居作为速度变更的参考对象。每个agent根据邻居的速度vj调整自己的速度v。为了防止发生碰撞,将每个agent之间的安全距离设为Re。当两个agent之间的距离小于Re时,agent之间产生排斥作用,自发远离对方。更新后的速度满足规则3。
规则3(速度-位置限定规则):每个agent的速度变化范围限定在[vmin,vmax]内。迭代进化过程中,如果agent以某速度飞行时,其所在位置超出了边界,则将其位置限定为边界值[xmin,xmax]。
2)聚集行为
当agent群体聚集时,设agent i 的当前位置为xi,探索其当前感知范围Rp内最邻近的7个同伴,根据每个对象的位置xj确定一个中心点位置C,di,C表示agent i 与中心点位置C 之间的距离。如果di,C > Re,则agent i 朝同伴的中心位置C 方向,以速度v 飞行一步;否则执行随机飞行行为。对每个agent做如下规定,即尽量向邻近伙伴的中心移动,同时避免过分拥挤。
3)分散行为
当agent群体分散时,设agent i 的当前位置为xi,探索其当前感知范围Rp内最邻近的7个同伴,根据同伴当前群集状态确定一个群集的中心点位置C,然后转向,向着远离C 的方向飞行。
4)逃逸行为
当agent群体逃散时,设agent i 的当前位置为xi,探索其当前感知范围Rp内最邻近的7个同伴,根据同伴当前群集状态确定一个群集的中心点位置C,然后立刻转向,向着远离C 的方向逃走,并且agent i 在逃走过程中逐渐加速,直到达到最大逃跑速度ve为止。
以上4种运动行为在不同条件下可相互转换。根据所要求解问题的性质,agent对当前所处状态进行评价,包括目标函数的变化情况以及伙伴的状态变化情况,从而从随机飞行行为、聚集行为、分散行为和逃逸行为中选择一种行为。评价目标是使所选择的行为为向着最优方向前进的行为,也就是使agent的下一个状态最优的行为。如果下一状态不优于当前状态行为,则采取随机飞行行为。
根据(2)式可以计算每个agent的动能,则群体总动能E 为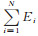
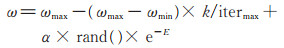
|
(3) |
式中,ωmin、ωmax为权重动态范围,k 为进化代数,itermax为最大进化代数,α 为控制因子,rand()为(0,1)区间的随机数。
1.3 安全规避欧椋鸟群在集体飞行过程中对环境变化具有较强的适应能力,在遇到变化和威胁情况下能够快速一致地进行“三避”,即避让同伴、避开障碍以及躲避入侵。对应地,agent具有避开障碍行为、避让同伴行为以及躲避天敌行为。
1)避开障碍行为。设O 和G 分别表示静态障碍物和目的地。用人工势场[15]进行描述,O 对agent产生排斥力,G 对agent产生吸引力。agent在飞抵目标过程中避开障碍物时,它受到由排斥力和吸引力共同产生的合力影响。
2)避让同伴行为。除了静态障碍物以外,agent还容易与同伴发生相互碰撞,产生追尾避让、拦截避让和迎面避让3种行为。
① 追尾避让行为。agent i 位于agent j 的正前方,两者同向运动时,由于agent j 的速度或加速度大于agent i 的速度,而将发生碰撞时的避让行为。
② 拦截避让行为。agent i 与agent j 的运动方向虽然不同,但在运动过程中相遇时采取的避让行为。
③ 迎面避让行为。agent i 与agent j 相对运动,将发生碰撞时的避让行为。
3)躲避天敌行为。agent i 在运动过程中与入侵者相遇时采取的躲避行为。
一般可以根据传统人工势场法[15],避开静态障碍物以及追尾避让。但传统人工势场方法没有考虑到运动物体的速度与加速度,尽管拦截避让、迎面避让这两种情况可以通过增加排斥力的作用距离或者增大排斥力系数进行规避,但是对于处于较远距离的agent仍然需要进行距离计算,因而造成许多不必要的避碰行为判断,有一定的局限性。因此,本文对传统人工势场法进行改进,提出以下动态人工势场方法进行避让避障。
定义感知半径、排斥半径、保持半径以及吸引半径等参数。
定义3(感知半径):agent搜索空间的最大范围,即视野半径Rp。
定义4(排斥半径):排斥半径Re为agent与同伴之间保持的最小距离,以避免两者发生相互碰撞。
定义5(保持半径):保持半径Rm为agent与其同伴之间的中等距离范围。在该范围内agent之间保持相同的运动方式。
定义6(吸引半径):为了保持整个群体的凝聚力,agent被距离较远的其他同伴所吸引。吸引半径Ra为agent与其搜索空间内吸引它的其他同伴之间的最大距离。
已知agent i 当前时刻t 的速度和加速度,可以预测经过时间间隔Δt 后其位置xi以及群体中其他agent j 的位置xj。如果两个agent在经过Δt 后,xi和xj之间的距离低于安全距离Re,则提前采取避让措施。每个agent在运动过程中体现拓扑距离关系,并遵循经典的“排斥-保持-吸引”3个基本规则,即规则4~6,同时满足规则7。
规则4(排斥规则):agent i 排斥其近距离范围内的其他agent j,即如果di,j < Re,则修改agent i 的飞行方向为远离agent j 的方向。
规则5(保持规则):agent i 紧跟其中等距离范围内的其他agent j,即Re ≤ Rm ≤ Ra。
规则6(吸引规则):agent i 被其较远距离范围内的其他agent j 所吸引,即如果Ra < di,j ≤ Rp,则修改agent i 的飞行方向为agent j 的方向。
规则7(偏离规则):如果di,j > Rp,则agent i 与agent j 之间不发生任何相互作用。
由于两个agent相互预测对方位置并提前采取避让措施,一定程度上可以避免在静态障碍物以及追尾情形这两种情况下的碰撞。如果通过预测发现agent之间的距离大于安全距离,则不需要采取避让措施,一定程度上可避免拦截避让行为。将这种预测方式引入到动态人工势场,可以避免agent之间相互碰撞。
agent i 对障碍物或入侵者等目标O 产生排斥力,并对其视野范围内较近距离的agent j 产生排斥力,遵循规则4;目的地G 对agent i 产生吸引力,agent i 对其视野范围内较远距离的agent j 产生吸引力,遵循规则6。借鉴物理学中势能的概念,根据(4)式,分别得到吸引力函数Fa、排斥力函数Fr和势场PF。
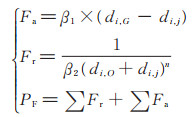
|
(4) |
式中,n 为目标和物体距离的影响因子,一般取n= 2。di,O、di,G、di,j 分别表示agent i 与障碍物或入侵者等目标O、与目的地G 以及与agent j 之间的距离,β1、β2分别表示吸引力系数和排斥力系数。
1.4 适应进化具有进化行为的群集能够像生物一样,通过优胜劣汰的自然选择实现对自身行为的不断调整和演化,产生对环境的自适应能力。对应地,基于进化机制的群集自组织行为,可建立agent自组织框架。
每个agent只关心其一定视野范围内最邻近的7个邻居。根据规则8计算概率后,随机选取其中一个邻居,然后根据规则9计算适应度值,判断该邻居的好坏,好的邻居将成为该agent的“榜样”。
规则8(榜样选择规则):根据pj∼ 1/di,j 原则[8],为agent i 在其周围一定感知半径Rp范围内从最邻近的7个邻居中选择榜样同伴agent j。其中,pj为概率,di,j为agent i 与agent j 之间的距离。距离越小,则选取的概率越大。
遵循规则8,为agent i 选择其榜样同伴agent j。采用转盘赌轮选择机制[11]计算pj,即

|
(5) |
式中,di,q 是agent i 与agent q 之间的距离,di,j 是agent i 与agent j 之间的距离,di,j < Rp,q 是对agent i与其7个邻居的距离求和的计数,取值为1到7。
定义7(适应度函数):对第i 个agent趋向于目标点G 的当前最好位置xi的评价进行度量的函数,用fitness(xi)表示,设定其阈值为fitnessthreshold。
一般根据具体应用问题确定适应度函数。例如,无人机集群应用的适应度函数可定义为无人机与目标之间距离的倒数。
规则9(榜样评价规则):对所选择的榜样同伴agent j 采用fitness(xj)进行评价,以确保选取适应度值较好的同伴。如果fitness(xj) < fitnessthreshold,则适应度值较差,agent j 被淘汰,agent i 保持自己原有的飞行方式;否则agent i 选择agent j 作为自己的榜样同伴。
引入粒子群算法中的pbest变量,即粒子找到的最优位置,采用(6)式进行计算,即
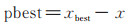
|
(6) |
式中,xbest是agent的历史最好位置,x 是agent的当前位置。
第k+1次迭代进化中,agent i 的当前适应度值为fitnessi(k + 1)
。如果fitnessi(k + 1)
> fitnessi(k)
,k≥0,则更新个体历史最优位置pbesti(k + 1) = pbesti(k) 。其中,pbesti(0) 为agent i 的初始最优位置,即pbesti(0) = xi(0) 。采用适应度函数fitness(xi)计算agent i 最邻近7个邻居的局部最优适应度值fitness local(k + 1) = 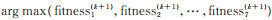
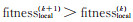
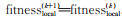
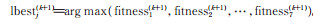
agent i 在k + 1次迭代中的速度更新方程为(7)式。
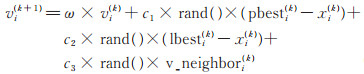
|
(7) |
式中,pbesti 为agent i 所经历的最优位置,lbesti 为agent i 的所有7个邻居所经历的最优位置,为局部极值,即lbesti=max{pbestj} ,j=1,2,…,7。传统的粒子群算法中,位置更新公式采用gbest表示全局最优位置。与传统粒子群算法不同,本文采用“无中心论”思想,即7个邻居局部原则,采用lbesti变量表示agent i 所有7个邻居所经历的最优位置。
c1、c2为加速度常数,设c1=c2 = 2。c3为拓扑作用因子,如(8)式所示,用以保持种群多样性,使得算法能在更大范围内进行搜索。
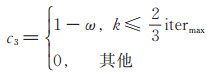
|
(8) |
式中,itermax表示最大进化代数。当ω 减小时,种群逐渐失去多样性,此时补强拓扑作用关系,使agent与其他agent之间的交互得到加强,设置c3=1-ω。这里,默认三分之二代数(即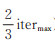
根据更新的速度更新位置,agent i 在k+1次迭代中的位置更新方程如(9)式所示。
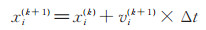
|
(9) |
式中,Δt 为时间间隔,通常设为1。
1.5 整体有序评估欧椋鸟都有从众心理,整个群集向着统一目标方向协调飞行。如果某只鸟偏离群体,它会及时调整自己的飞行方向,与群体保持一致。依靠这种从众心理,欧椋鸟调整自己的个体行为,使得整个群体能保持整齐划一的队形,朝着一致的方向飞行。对应地,开始尚未协同时,整个群体中agent个体按照自己的方向飞行,从整体来看,运动方向是杂乱无章的,表现为各向异性的特征。经过一段时间后,agent都进行自适应调整,最终从整体来看,整个群体的运动方向大致一致,飞行速度大致相同,飞抵目标过程中,表现出宏观有序协调的运动状态。
群体协同效果由极化作用因子ρ 进行评估,由(10)式进行计算,并遵循规则10。
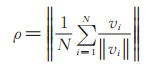
|
(10) |
规则10(极化作用规则):通过极化作用因子ρ度量群体的整体有序程度,反映该群体整体飞行方向的一致程度。当ρ 接近0时,表明群体整体飞行方向杂乱无章;当ρ→ 1时,表明群集整体基本朝向同一方向飞行。
2 本文算法 2.1 基本思想在D 维空间一定群体规模N 的智能个体集合{agent1,agent2,…,agentN}中,每个agent具有一定的飞行速度,并能决定其飞行的方向与距离。agent的位置和速度的初始值随机产生。所有agent都在解空间范围内搜索其周围最邻近的7个邻居。每个agent赋予一定记忆功能,能记住所搜寻到的最优位置。通过适应度函数确定其适应度值,并据此评价其当前位置的优劣。单位时间飞行后,每个agent根据速度更新方程((7)式)、位置更新方程((9)式)动态地调整其飞行方向、速度和位置,下一步将飞向其自身最优位置与7个邻居的局部最优位置的加权中心,并通过极化作用因子评价群集飞行一致性。
2.2 算法框图根据欧椋鸟群协同算法思想,给出如图 1所示的算法框图。
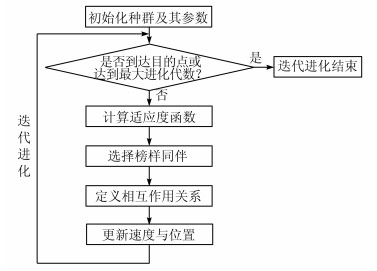
|
| 图 1 欧椋鸟群协同算法框图 Fig. 1 Block diagram of starling swarm coordination algorithm |
欧椋鸟群协同算法的主要步骤如下。
步骤1:初始化种群及其参数。
① 设置群体规模N,最大进化代数itermax,定义进化代数的初始值k = 0,k ≤ itermax。
② 设置最小速度vmin、最大速度vmax,并为每个agent定义初始速度为vi(0) =rand ()× vmax。
③ 定义空间范围为[xmin,xmax],为每个agent定义初始位置为xi(0) = xmin +(xmax - xmin)× rand ()。
④ 为每个agent定义个体历史最优适应度初始值fitnessi(0) = ∞,历史局部适应度初始值fitnesslocal(0) = ∞。初始状态下,所有agent都将它们的初始位置作为其个体最优位置fitnessi 和个体局部最优位置fitnesslocal。
步骤2:计算适应度函数。
① 遵循规则1和规则2,构建拓扑作用机制框架。
② 更新个体历史最优适应度值。在第k+1次迭代进化中,计算agent i 的当前适应度值fitnessi(k + 1)。如果fitnessi(k + 1) > fitnessi(k),则更新个体历史最优位置pbesti(k + 1) = pbesti(k)。
③ 更新局部最优适应度值。计算agent i 最邻近7个邻居的局部最优适应度值fitnesslocal(k + 1)。如果fitnesslocal(k + 1) > fitnesslocal(k),则更新局部最优适应度值fitnesslocal(k + 1)以及局部最优位置lbestj(k + 1) ,计算方法见1.4节。
步骤3:选择榜样同伴。
① 为agent i 获取其周围一定感知半径Rp范围内最邻近7个邻居。
② 遵循规则8进行转盘赌轮选择机制计算,根据概率值为agent选择榜样同伴agent j。然后根据规则9评价这个邻居的好坏,是否能真正成为该agent的“榜样”。
步骤4:定义agent之间的相互作用关系。根据所选择的榜样同伴agent j,确定agent i 与agent j 之间的相互作用关系。
① 定义半径参数,即排斥半径Re、保持半径Rm、吸引半径Ra以及感知半径Rp;
②定义agent之间的拓扑关系。每个agent在运动过程中体现拓扑距离关系,并遵循经典的“排斥-保持-吸引”3个基本规则,即规则4~6,同时满足规则7。
③ 为每个agent计算吸引力、排斥力和势场。
步骤5:更新agent的速度与位置。
① 计算agent的动能。
② 定义速度更新方程、位置更新方程。更新后的速度、位置满足规则3。
③ 引入极化作用因子,对agent群体进行整体有序评估,遵循规则10。
重复以上步骤2~步骤5,进化代数k = k + 1,agent i 选取其最近的7个邻居作为交互对象。经过与相邻个体的速度加权,通过不断地迭代,更新agent的速度和位置,使整个群集行为趋于一致,直至群体到达目的地;或者如果k ≥ itermax,即达到最大进化代数,则终止循环。
3 仿真实验 3.1 仿真方案为了验证欧椋鸟群协同算法的有效性,本文以模拟无人机(unmanned aerial vehicle,UAV)集群协同飞行为例开展仿真实验。为了便于观察,模拟时使用二维平面,没有将高度因素加入模拟软件中。模拟时,给无人机集群布置一个执行抵达目的地的简单任务。程序启动时,无人机集群随机地出现在一片特定区域,初始位置、速度大小和方向随机产生。
初始化参数设置如下。控制因子α 选取为1,惯性权重ω 初始值为1,其动态范围ωmin和ωmax分别取为0.7和1,初始拓扑作用因子c3定义为1,最大迭代次数定义为5 000,单位安全距离阈值Re定义为50。当整个无人机集群全部位于目标地点的单位距离范围500(无量纲)以内,则判定为任务完成。
3.2 仿真结果 3.2.1 协同飞行模拟无人机数量为300时,测试了无人机集群聚合、分散、规避等行为。
1)集群聚合模拟
无人机集群聚合模拟结果如图 2所示,图中x和y 分别表示无人机当前位置的x 坐标和y 坐标。图 2(a)为执行任务过程中聚合前的队形。经过20次、40次、50次迭代之后,队形变化分别如图 2(b)~2(d)所示,无人机集群队形表现出明显的聚集现象。聚合行为中,每个无人机会根据自己以及邻居的状态不断地调整虚拟中心点的位置,但聚合完成后整个集群的队形相对保持不变。
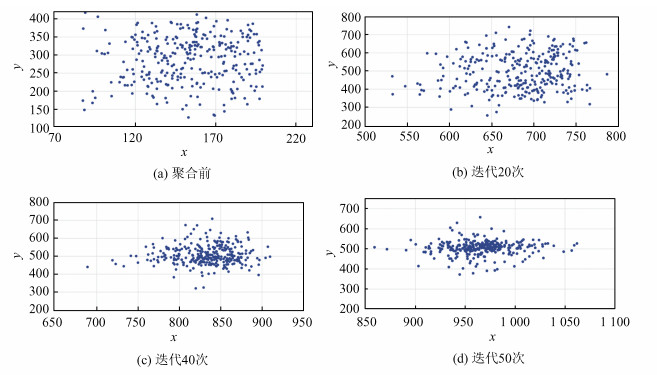
|
| 图 2 无人机集群聚合模拟结果 Fig. 2 Simulation results of UAVs' aggregation |
2)集群分散模拟
无人机集群分散模拟结果如图 3所示。其中,图 3(a)为执行任务过程中集群分散前的队形。经过10次、20次、40次迭代之后,队形变化如图 3(b)~3(d)所示,无人机个体四处散开,整个群体不再保持队形。分散行为中,由于只计算一次中心点,中心点不会发生改变,而呈现出从中心向外扩散的现象。
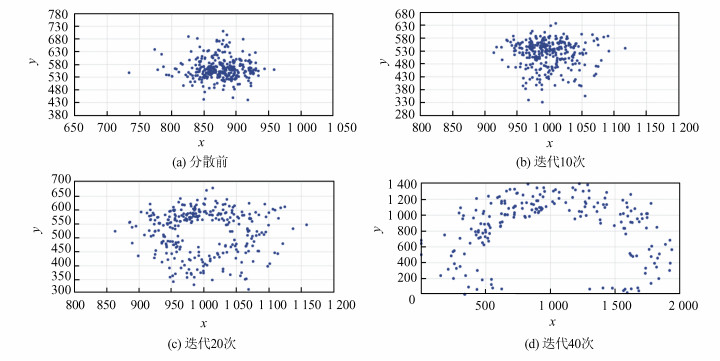
|
| 图 3 无人机集群分散模拟结果 Fig. 3 Simulation results of UAVs'separation |
3)集群规避模拟
无人机集群同伴避让、避开障碍、躲避入侵、抵达目标的模拟结果如图 4所示。图 4中灰色圆代表障碍物,红色目标和黑色目标分别表示入侵者和无人机,蓝色表示目的地。图 4(a)显示集体飞行过程中个体之间保持一定距离,当个体之间距离小于安全距离阈值时,个体之间产生排斥力,使得它们相互之间远离对方。图 4(b)模拟队形避开障碍物区域进行飞行。图 4(c)显示当模拟集群遭遇入侵,入侵者进入无人机集群安全距离范围时,对区域内无人机产生一个较大的排斥力,使得无人机能够躲避入侵者。图 4(d)所示为模拟集群规避后抵达目的地的情形。
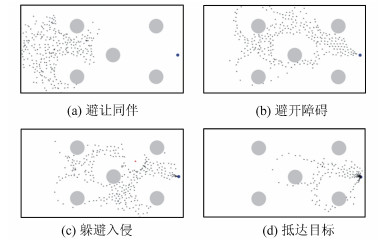
|
| 图 4 无人机集群规避模拟结果 Fig. 4 Simulation results of UAVs'safe avoidance |
在不同无人机数量情况下,分别采用粒子群算法[12]和本文算法,测试无障碍物情况下无人机集群执行抵达目的地任务的效率。无人机数量分别为100、300、500和1 000,分别记录完成任务所需要的迭代次数,以表示执行任务的效率。执行任务效率对比结果如图 5所示。
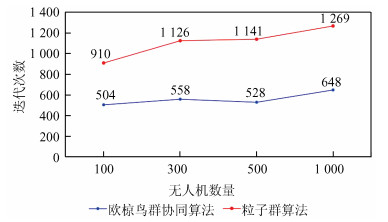
|
| 图 5 无障碍物情况下无人机集群执行协同飞行任务效率对比 Fig. 5 Comparison of efficiency of UAVs'collaborative flight mission under the case of without obstacles |
从对比结果来看,与传统粒子群算法相比,采用欧椋鸟群协同算法进行协同飞行,无人机集群执行任务时的迭代次数明显减少,甚至只有原来的一半,证明在无人机集群协同飞行方面,该方法效果较好,可以大幅减少迭代次数,提高整个集群的工作效率。
4 总结与展望本文提出仿欧椋鸟飞行机制的欧椋鸟群协同算法,从局部感知、运动行为、安全规避、适应进化4个方面构建算法,使算法具有自适应、自组织、自协同的特点。本文主要贡献如下:
1)由于智能群体协同的本质是大量agent在环境的刺激下,共同装载某些相同的行为规则,通过这些规则的反馈作用,呈现某种宏观上的有序现象[16]。因此,本文提出智能群体在协同中应遵循的10条基本简单规则,能较好地体现协同的本质。
2)本文采用无中心自组织协同论思想,智能群体没有全局观点,它只关心其最邻近的7个邻居,在局部中寻找最优值。这种局部感知思想与经典粒子群算法的全局观点是截然不同的。
3)本文提出的思想基于拓扑距离框架,智能群体在数量上可扩展性强,因此可以适用于大规模智能群体的协同应用。
4)进行了模拟无人机集群协同飞行仿真实验。
实验结果表明,与传统粒子群算法相比,加入欧椋鸟群集飞行机制的协同算法,其执行任务的迭代次数明显减少,能大大提高执行任务的效率。
本文从欧椋鸟群密集飞行、相互协调中得到启发,将其群集行为引入到大规模智能群体的协作中,为解决智能个体自适应调控、智能群体无中心自组织协同两大问题提供崭新的研究思路、研究方法和计算模式。
进一步工作将分析欧椋鸟群协同算法各个参数对算法一致性的影响,并研究具有动态拓扑结构的欧椋鸟群协同算法,使之具有信息传播和扩散能力。
致谢: 感谢武汉大学黄王燚、王粤衡、张琳钰为本文所做的算法开发。
| [1] |
WANG Y, GARCIA E, CASBEER D, et al. Cooperative Control of Multiagent Systems:Theory and Applications[M]. New Jersey: Wiley, 2017.
|
| [2] |
REYNOLDS C W. Flocks, herds, and schools:A distributed behavioral model[J]. Computer Graphics, 1987, 21(4): 25-34. DOI:10.1145/37401.37406 |
| [3] |
KWONG H, JACOB C. Evolutionary exploration of dynamic swarm behavior[C]// Proceedings of the IEEE Congress on Evolutionary Computation. New York: IEEE, 2003: 367-374.
|
| [4] |
WANG L, SHI H, CHU T G. Flocking control of groups of mobile autonomous agents via local feedback[C]// Pro- ceedings of the IEEE International Symposium on Intelligent Control. New York: IEEE Press, 2005: 441-446.
|
| [5] |
CUCKER F, SMALE S. Emergent behavior in flocks[J]. IEEE Transactions on Automatic Control, 2007, 52(5): 852-862. DOI:10.1109/TAC.2007.895842 |
| [6] |
CAVAGNA A, GIARDINA I, GRIGERA T S, et al. Silent flocks:Constraints on signal propagation across biological groups[J]. Physical Review Letters, 2015, 114(21): 218101-1. DOI:10.1103/PhysRevLett.114.218101 |
| [7] |
CAVAGNA A, CIMARELLI A, GIARDINA I, et al. Scale-free correlations in starling flocks[J]. Proceedings of the National Academy of Sciences of the United States of America, 2010, 107(26): 11865-11870. DOI:10.1073/pnas.1005766107 |
| [8] |
HEREFORD J, BLUM C. FlockOpt: A new swarm optimization algorithm based on collective behavior of starling birds[C]// Proceedings of 3rd World Congress on Na- ture and Biologically Inspired Computing. New York: IEEE Press, 2011: 17-22.
|
| [9] |
NETJINDA N, ACHALAKU T, SIRINAOVAKU B. Particle swarm optimization inspired by starling flock behavior[J]. Applied Soft Computing, 2015, 35: 411-422. DOI:10.1016/j.asoc.2015.06.052 |
| [10] |
邱华鑫, 段海滨. 从鸟群群集飞行到无人机自主集群编队[J]. 工程科学学报, 2017, 39(3): 317-322. QIU H X, DUAN H B. From collective flight in bird flocks to unmanned aerial vehicle autonomous swarm formation[J]. Chinese Journal of Engineering, 2017, 39(3): 317-322. DOI:10.13374/j.issn2095-9389.2017.03.001 (Ch). |
| [11] |
MITCHELL M. An Introduction to Genetic Algorithms[M]. MA: MIT Press, 1996.
|
| [12] |
KENNEDY J, EBERHART R. Particle Swarm Optimization[C]//Proceedings of IEEE International Conference on Neural Networks. New York: IEEE, 1995: 1942-1948.
|
| [13] |
DORIGO M. Optimization, Learning and Natural Algo- rithms[D]. Milano: Politecnico di Milano, 1992.
|
| [14] |
BALLERINI M, CABIBBO N, CANDELIER R, et al. Interaction ruling animal collective behavior depends on topological rather than metric distance:Evidence from a field study[J]. Proceedings of the National Academy of Sciences of the United States of America, 2008, 105(4): 1232-1237. DOI:10.1073/pnas.0711437105 |
| [15] |
KHATIB O. Real-time obstacle avoidance for manipulators and mobile robots[J]. The International Journal of Robotics Research, 1986, 5(1): 90-98. DOI:10.1109/ROBOT.1985.1087247 |
| [16] |
屈强, 何新华, 刘中晅. 系统涌现的要素和动力学机制[J]. 系统科学学报, 2017, 25(3): 25-29. QU Q, HE X H, LIU Z X. Essential factors and dynamic mechanism of the system emergence[J]. Journal of System Science, 2017, 25(3): 25-29. (Ch). |
 2019, Vol. 65
2019, Vol. 65




