文章信息
- 王丽娜, 史明昊
- WANG Lina, SHI Minghao
- 学生日常行为模式挖掘及差异性分析
- Mining Students' Daily Behavior Patterns and Analyzing Discrepancies
- 武汉大学学报(理学版), 2018, 64(3): 255-261
- Journal of Wuhan University(Natural Science Edition), 2018, 64(3): 255-261
- http://dx.doi.org/10.14188/j.1671-8836.2018.03.009
-
文章历史
- 收稿日期:2017-06-05

在大学生活中,学生的日常行为对学业成绩具有怎样的影响一直是学生、家长关心及科研人员关注和研究的一个重要问题.学生的日常行为模式与学业成绩之间关系的研究,大多数都是基于网上课程以及对学生的问卷调查等数据进行的[1, 2].然而,网上课程和问卷调查数据,难以全面、客观、真实地反映学生的日常行为与学业成绩之间的关系.目前,随着内嵌了各种传感器(如加速计、GPS、陀螺仪等)的智能手机在校园的广泛普及,通过智能手机内嵌的各种传感器,可以从不同维度和不同侧面收集大量反映学生日常行为的上下文数据.使用统计分析、机器学习等方法对这些上下文数据进行深入挖掘,可以客观地推测出与学生日常生活密切相关的日常行为,如学生所处的位置[3]、社交情况[4]、活动状况[5]以及健康状况[6]等,进而可以定量地分析学生行为模式与学业成绩之间的关联关系.例如,文献[7, 8]基于智能手机收集的上下文数据,从整个学期即较长时间跨度上,利用线性回归方法分析了学生行为模式变化与学业成绩的关系.
关联规则分析是数据挖掘中的一个经典方法[9],它通过挖掘数据集中的频繁模式来发现数据之间的相关性和关联关系.然而,传统的关联规则分析并不适用于手机上下文数据中的数值型数据[10].近些年来,模糊集合理论凭借其简单及其类似于人类推理的特点得到广泛应用.如果将模糊集合理论与关联规则方法相融合,并应用于手机上下文数据分析,从而得出“在固定时间内移动时间较多⇒学生在体育馆(或操场)”这样的规则来表达学生的日常行为,这种方法更简洁明了而且便于理解.目前,将模糊集合理论应用于关联规则的挖掘方法可以分为两种:一种是先对数据进行模糊处理,但仍然使用传统关联规则的支持度和置信度[11]概念,另一种则是重新定义模糊关联规则的支持度和置信度[10, 12, 13]概念;在此基础上,采用Apriori挖掘算法[10, 11]和FP-Growth挖掘算法[13]等进行关联规则的挖掘.
本文针对学生行为模式与学业成绩之间的关系展开研究,依据反映学生日常行为的手机上下文数据,提出了一种基于关联规则的行为模式挖掘及行为差异性计算方法.其特点是使用语义化处理方法将数值型的上下文数据转换成具有语义信息的数据,在使用Apriori算法挖掘关联规则的基础上,进一步提取表征学生日常行为模式的特征规则集合,通过定量计算特征关联规则集合之间的非相似性系数,区分不同类型学生行为之间的差异,进而得出学生日常行为与学业成绩之间的关系和影响.最后,在达特茅斯大学StudentLife项目[7]的公开数据集上对该方法的有效性进行了实验验证.
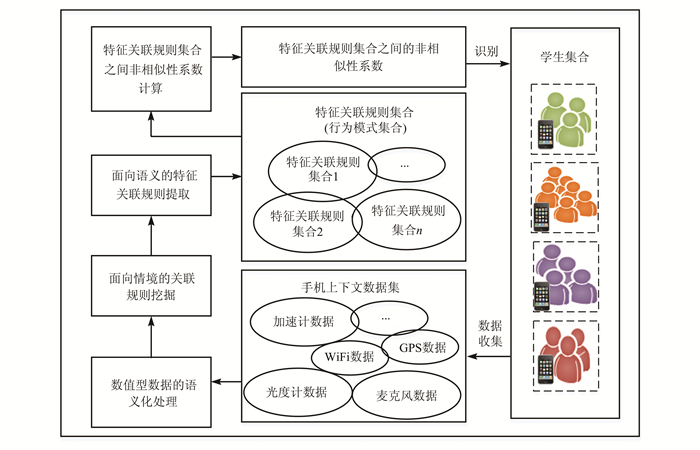
1 模式挖掘及差异性计算方法针对智能手机收集的各种上下文数据的特点,本文提出的一种基于关联规则的行为模式挖掘框架如图 1所示.该框架主要由数值型数据的语义化处理、面向情境的关联规则挖掘、面向语义的特征关联规则提取和非相似性系数计算方法等机制构成.基于该框架,我们提出了一种基于关联规则的行为模式挖掘及差异性计算方法,该方法的核心算法包括以下几个步骤(见算法1):首先,使用语义化处理方法将数值型上下文数据转换成具有语义信息的数据;其次,对原始上下文数据进行预处理,并将学生按照学业成绩进行聚类,分为不同类型的集合;第三,使用Apriori算法挖掘代表不同类型学生日常行为的关联规则集合,对关联规则进行冗余处理和聚类,筛选出表征学生行为的特征关联规则集合(即3~8行);最后,在特征规则集合的基础上,计算不同类型学生行为模式之间的非相似性系数(即9~12行).
|
| 图 1 基于关联规则的行为模式挖掘框架 Figure 1 Behavior pattern mining framework based on association rules |
| 算法1 行为模式挖掘及差异性计算 |
| Algorithm 1 Behavior pattern mining and discrepancy calculation of behavior patterns |
| 输入:记录学生日常行为手机上下文数据 |
| 输出:特征规则集合及非相似性系数 |
| 1. fdata=S-FCM(data) //语义处理 |
| 2.dataSet=Prepare(fdata)//上下文数据预处理 |
| 3. for Di in dataSet do |
| 4. rules=Apriori(Di) |
| 5. rulespruned=Prune(rules) |
| 6. rulesfeature=EFR(rulespruned) |
| 7. add rulesfeature to RulesSet |
| 8. End for |
| 9. for Ri in RulesSet do |
| 10. diff=DBRS(Ri, Ri is not in RulesSet) |
| 11. add diff to DiffSet |
| 12. End for |
该算法可以得到表征和刻画学生行为模式的特征关联规则集合,以及不同类型学生行为模式之间的非相似性系数.通过对这些输出结果进行分析,我们可以进一步计算不同类型学生行为模式之间的差异.下面将对其中的核心机制进行详细地阐述.
1.1 数值型数据的语义化处理数值型数据的语义化处理是指使用相应的语义处理方法,将数值型上下文数据转换为语义型数据,其语义化处理的过程可形式化地表示为f:a→b,f是语义化处理方法,a是范围在0-1之间的某个数值型数据,b是根据相应语义属性的类别数确定的等级信息(如high、middle或者low等).
数值型数据的语义化处理方法S-FCM的核心思想是使用经典的模糊C均值聚类算法—FCM算法[14, 15].FCM的核心是将模糊思想引入到k均值聚类算法中,通过不断迭代优化目标函数,得到每个元素对所有类别的隶属度,从而确定每个元素的隶属关系.然而,由于缺少聚类个数的先验知识,难以准确地设定每个语义属性的类别数量.因此,首先,我们使用组内平方误差和作为评价准则来辅助确定聚类个数,组内平方误差和与聚类个数成反比,当聚类个数增大时,每一类别中样本数量将减小;当组内平方误差和变化值减小时,增加聚类个数并不能增强聚类效果,此时对应的聚类个数是恰当的聚类个数.其次,在获得聚类个数后,将其带入模糊C均值聚类算法FCM中计算出模糊聚类中心,并计算每个数值型数据的隶属度.最后,应用模糊数学的最大隶属原则,完成对数据的语义化处理,即将每个数值型数据都映射为等级信息,从而将数值型数据转化为具有语义信息的数据.比如,某学生在某个时间分片的谈话比为0.8(即conversation=0.8),语义处理后该数据形式为conversation=high,表达含义是该学生在该时间分片中处于谈话较多的状态.
1.2 面向情境的关联规则挖掘在关联规则挖掘算法中,设I={I1, I2, …, Im}是项的集合.给定一组事务集合,其中每个事务T是一个非空项集,使得T⊆I.设A是一个项集,且A⊆T.关联规则是形如A⇒B的蕴涵式,其中A⊂I,B⊂I,A≠Ø,B≠Ø,并且A∩B=Ø [16].采用数据挖掘算法对反映学生日常行为的数据进行挖掘来获取关联规则,所获取的关联规则实际上是对学生日常行为的刻画和描述.因此,挖掘关联规则实际上就是挖掘学生的日常行为模式.
在校园生活中,由于学生的主要任务是上课学习和课后复习,因此,学生的日常生活可以概括地分为上课和非上课两种主要情境;同时,由于受课程作业、测试和考试等方面带来的压力影响,可能导致学生在不同的压力情况下产生不同的行为模式,因此可以从压力大小的角度来区分学生所处的情境.我们将学生的日常生活情境分为上课、非上课、压力很大和压力很小等4种情境.依据这4种情境,我们对收集的移动数据和问卷调查结果进行数据分类,分别提取这4种情境下的所有数据.针对这4种类型的数据集,我们分别使用经典的Apriori算法挖掘出关联规则集合,从而获得4种情境下的关联规则集合,其中置信度和支持度仍沿用传统关联规则中出现的概念和计算方法.例如,在非上课情境下,获取的关联规则的形式为{location type=Library}⇒{conversation=low},即当学生在非上课时所处地点类型为图书馆时,一般较少说话.
1.3 面向语义的特征关联规则提取由于关联规则集合中存在着大量冗余的以及语义非常接近的关联规则,因此,需要对原始的规则集合进行冗余处理,将原始关联规则按照语义层次上的距离进行聚类筛选,进而提取出真正能够精确表征和刻画学生行为模式的特征规则集合.特征关联规则提取算法EFR(如算法2所示)的处理过程如下:根据规则的右部对其进行分类,即右部相同的规则归为一类(即第1行);针对拥有相同右部的每类规则,使用欧式距离计算两两规则间左部的距离,生成距离矩阵(即3~5行).两两规则间的距离(d)计算公式如(1)式所示(其中,ei和ej分别代表规则左部所包含的项,对应项相同时相减结果为0,对应项不同时相减结果为1).
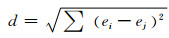
|
(1) |
在获得距离矩阵后,通过层次聚类方法对规则进行聚类(即第6行),之后选取在该类中与每个规则距离之和最小的规则,作为代表该类的特征规则(即第7行);将选取的特征规则合并,形成表征学生行为模式的特征规则集合(即第8行).
| 算法2 特征规则提取算法(EFR) |
| Algorithm 2 Extract Feature Rules |
| 输入:规则集合rules |
| 输出:特征规则集合features |
| 1. clusterrhs=rhsCluster(rules) |
| 2. Features=Ø |
| 3. for ri∈clusterrhs do |
| 4. ruleslhs =getLhs(ri) |
| 5. dist=Distance(ruleslhs) |
| 6. resulthclust=hclust(dist) |
| 7. feature=chooseMinDistance(resulthclust) |
| 8. features=union(features, feature) |
| 9. End for |
| 10. return features |
为直观并且定量地刻画各类学生行为模式的差异性,我们通过计算特征关联规则集合之间的非相似系数的方法,定量地计算学生日常行为的差异性.在不同的生活情境下,非相似性系数越大,说明学生行为模式差别越大,而导致非相似性系数越大的行为模式,则可能是影响学业成绩的主要因素.
特征规则集合之间的非相似性系数计算方法DBRS[17]的核心是计算特征规则集合之间的抽象距离,具体计算过程如下:统计两个特征关联规则集合之间不重复出现的右部个数;对每两个特征规则集合按右部进行分类,依据右部可分为右部相同规则和右部不同规则;先计算两个特征规则集合右部相同规则之间的距离,如果左部完全相同则非相似性系数为0,如果左部有部分不同,使用(1)式累积计算规则之间的距离和;如果存在右部完全不同的规则,则获取拥有不同右部规则的总数,用权值参数展现其差异性.计算特征规则集合之间的距离总和,同时考虑到在确定的时间学生只能有一个确定状态,上述出现的右部均是可能发生的事件,而不是一定发生的事件,因此计算完所有规则的距离和之后,与所有出现的不重复右部个数相除,获得非相似性系数,其计算方法如(2)式所示,dis trhs_same代表右部相同但左部有部分不同规则间距离,dis trhs_diff代表右部不同规则间的距离,n代表不重复的右部个数.
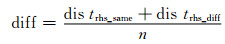
|
(2) |
最后,将结果根据系数的取值范围归一化到0~1区间,即将系数中的最大值置为1,其他值与最大值相除得到0~1区间的系数.通过循环使用非相似性系数计算方法DBRS,最终可以得到m个k×k的非相似性系数矩阵U,m表示生活情境(如上课、非上课、压力很大及压力很小等)的个数,n表示学生类型(如成绩优异、良好、中等及一般等)的个数,即将学生按照某种特征分成k个类型.矩阵U的每个元素uij表示第i个类型学生行为与第j个类型学生行为的非相似性系数,特别地,矩阵 U是一个对称矩阵.因此,通过不同的非相似性系数矩阵U,可以定量地表征在不同生活场景下,不同类型学生行为的非相似性.
2 实验我们选取StudentLife项目[7]的数据集对本文所提出方法的有效性进行实验验证.该项目收集了48名学生持续10周的日常生活状况数据,涵盖了基于智能手机收集的上下文数据、学业成绩数据(30名学生的成绩)以及调查问卷数据等3个方面.其中,手机上下文数据包括GPS、加速度计、Wi-Fi、蓝牙、麦克风、光度计、应用使用情况、通话记录、短信记录、屏幕操作等数据.
2.1 实验结果就语义层次来说,StudentLife数据集中的上下文数据属于原始数据,并不能反映有效的语义信息.故而需要对这些传感器的数据进行处理,将其转变为具有语义信息的数据.首先,利用加速度计判断学生的移动状态,根据GPS、Wi-Fi和蓝牙及其他传感器来获取学生当前的学期周数、星期、时间、学生是否在上课、谈话时间比、环境光亮程度、手机锁定时间比、地点类别、移动时间比、环境噪声比、周围人数、通过问卷的方式获得的压力等级等12个属性.这12个属性中时间、周数、星期、地点、是否上课、压力等级这6个属性已经具有语义含义,因此只需处理数值型属性.其次,使用组内平方误差和确定其中的6个数值型属性的恰当聚类数目,如表 1所示.将属性的聚类数目作为已知条件带入FCM算法中,获取模糊聚类中心和隶属度函数矩阵,应用模糊数学的最大隶属原则完成对数据的语义处理.
| 属性 | 等级个数 |
| 参与者处于移动状态 | 3 |
| 参与者处于谈话状态 | 3 |
| 周围噪声 | 3 |
| 参与者周围人数 | 4 |
| 手机锁屏 | 2 |
| 手机处于昏暗状态 | 2 |
根据学生的GPA成绩,使用K-means聚类算法对30名学生进行聚类,以客观描述该项目学生的成绩分布情况.将30名学生分为4类,如表 2所示.
| 类型 | 人数 | (编号,GPA成绩) |
| 优异 | 6 | (u19,3.947),(u30,3.930),(u22,3.889), (u32,3.826),(u09,3.806),(u43,3.790) |
| 良好 | 12 |
(u27,3.719),(u08,3.705),(u05,3.679), (u10,3.667),(u41,3.652),(u46,3.646), (u49,3.625),(u59,3.519),(u02,3.505), (u17,3.476),(u07,3.474),(u18,3.474) |
| 中等 | 5 | (u57,3.389),(u16,3.373),(u54,3.343), (u14,3.293),(u12,3.245) |
| 一般 | 7 |
(u04,3.029),(u24,2.987),(u01,2.863), (u15,2.815),(u33,2.815),(u25,2.765), (u52,2.400) |
依据上述分类结果,针对上述4种类型的学生进行行为模式挖掘,即进行关联规则挖掘和特征关联规则提取.根据应用的需要和多次实际实验,将挖掘关联规则的支持度设为0.5,置信度设为0.6,挖掘出4个反映4种类型学生的特征关联规则集合,计算它们之间的非相似系数.
2.2 分析讨论本节重点分析讨论学生在上课、非上课、压力很大以及压力较小这4种情境下,4种类型学生行为模式的差异性,如表 3~6所示.
| 类型 | 优异 | 较好 | 中等 | 一般 |
| 优异 | 0.00 | 0.39 | 0.46 | 0.85 |
| 良好 | 0.39 | 0.00 | 0.43 | 0.76 |
| 中等 | 0.46 | 0.43 | 0.00 | 0.59 |
| 一般 | 0.85 | 0.76 | 0.59 | 0.00 |
| 类型 | 优异 | 较好 | 中等 | 一般 |
| 优异 | 0.00 | 0.38 | 0.78 | 0.82 |
| 良好 | 0.38 | 0.00 | 0.68 | 0.76 |
| 中等 | 0.78 | 0.68 | 0.00 | 0.29 |
| 一般 | 0.82 | 0.76 | 0.29 | 0.00 |
| 类型 | 优异 | 较好 | 中等 | 一般 |
| 优异 | 0.00 | 0.36 | 0.60 | 0.47 |
| 良好 | 0.36 | 0.00 | 0.28 | 0.51 |
| 中等 | 0.60 | 0.28 | 0.00 | 0.47 |
| 一般 | 0.47 | 0.51 | 0.47 | 0.00 |
| 类型 | 优异 | 较好 | 中等 | 一般 |
| 优异 | 0.00 | 0.55 | 0.54 | 0.94 |
| 良好 | 0.55 | 0.00 | 0.83 | 1.00 |
| 中等 | 0.54 | 0.83 | 0.00 | 1.00 |
| 一般 | 0.94 | 1.00 | 1.00 | 0.00 |
在上课情境下,一方面,成绩一般的学生与其他3种类型学生行为模式之间的非相似系数都大于0.5,说明成绩一般的学生与其他3种类型学生的行为模式差异性都较大,通过分析发现,成绩一般的学生在课堂上很少谈话,即很少参与课堂讨论;而且,成绩一般的学生使用手机的频率比其他3种类型学生的频率都高,推断上课频繁使用手机给学生的成绩带来负面的影响.另一方面,成绩优异、良好和中等3种类型学生行为模式之间的非相似性系数基本上都小于0.5,说明大多数学生在上课情境下的行为模式基本上是相似的;深入分析成绩优异、良好和中等的学生的具体行为模式,发现他们的谈话频率都较高,即他们都积极参与课堂交流和讨论.因此,在上课情境中,积极参与课堂讨论可能是提高学习成绩的一个重要因素,而在课堂上频繁使用手机可能是影响成绩的一个主要因素.
在非上课情境下,一方面,各类型学生行为模式的非相似性系数基本上都大于0.5,说明大多数学生在该情景下具有不同的行为模式.其中,成绩优异的学生和成绩一般的学生非相似性系数为0.82,是在非上课情境下非相似性系数中最大的,深入分析比较这两类学生的行为模式发现,成绩优异的学生经常处于学习的状态,而成绩一般的学生通常在进行社交活动;成绩一般的学生使用手机的频率比成绩优异的学生更加频繁.另一方面,成绩优异和成绩良好的学生在非上课情境下行为模式较为相似(非相似性系数为0.38);成绩中等和成绩一般的学生在非上课情境下的行为模式较为相似(非相似性系数为0.29).通过具体分析发现,成绩优异和成绩良好学生行为模式的相似性在于他们经常处于学术区域内(比如教学楼、图书馆等)、环境安静、谈话也较少,即他们通常处于认真学习的状态;成绩中等与成绩一般的学生在非上课情境下,经常处于谈话较多的状态,而且手机使用频率较高;同时,成绩中等和成绩一般的学生处于宿舍的时间也比其他类型的学生更多,推断他们经常处于休息状态.
在压力很大的情境下,不同类型学生行为模式之间的非相似性系数基本上小于0.5,说明在该情境下大多数学生的行为模式较为相似.通过进一步分析发现,不同类型的学生大多处于在学术区域、较少移动、环境安静、谈话也较少,即学生们处于努力学习的状态.同时从表 5中可以发现,学习成绩中等和学习成绩优异的学生行为模式差异性最大(非相似性系数为0.60),深入分析发现:中等生的心态常处于比较紧张和消极的状态,而成绩优异的学生手机使用更少,推断成绩优异的学生精力较为集中.
在压力较小的情境下,各类型学生行为模式之间的非相似性系数基本上大于0.5,说明在该情境下不同类型学生之间行为模式的差异较为明显.分析发现:成绩优异的学生与其他学生最明显的区别是手机频率较低,手机经常处于锁屏的状态,推断成绩优异的学生自制力较强,较少受手机的影响;成绩一般的学生最明显的差别是经常在宿舍,周围人较少也较为安静,推断处于睡眠的状态较多;成绩良好的学生和成绩中等的学生手机使用都普遍较多,他们之间的差异在于成绩中等的学生周围环境更安静些,谈话也较少,推断成绩中等的学生更愿意独处;而成绩良好的学生更倾向于留在宿舍且谈话较多,推断成绩良好的学生更喜欢参与宿舍的集体活动.
通过以上4种情境的分析推断,课堂积极参与讨论、在压力较大的时候保持积极放松的心态、在压力较小时减少对手机的依赖以及集中精力学习是积极地提高学习成绩的几种关键行为模式.因此,可以推测课堂参与度、自我控制能力、压力承受能力和手机的使用情况等是影响学生学业成绩的几个主要因素.
3 结论本文针对日常行为与学业成绩关系问题展开研究,提出了一种基于关联规则的学生日常行为模式挖掘及差异性计算方法,通过定量计算学生日常行为之间的非相似性系数,区分出不同类型学生行为模式之间的差异,进而得出学生日常行为与学业成绩之间的关系和影响,并且通过深入分析,推断课堂参与度、自我控制能力、压力承受能力和手机的使用情况等行为模式是影响学生学业成绩的几个主要因素.使用本文所提出的方法,可以较为直观并且有效地分析出不同类型的学生在不同生活情境下的行为模式的差异性,进而可以获得影响学生学业成绩的主要因素.在获取这些与成绩有关的先验知识后,通过手机收集一个时间段中新生日常生活的行为模式数据,通过挖掘计算新生日常行为模式与已知各类型学生行为模式之间的非相似系数,即可发现行为模式的差异性.如果某学生的行为与成绩一般的学生较为相似,便于及时对学生进行预警,同时根据成绩优秀学生的行为模式可以给学生更合理的指导建议.
| [1] |
ROBBINS S B, LAUVER K, LE H, et al. Do psychosocial and study skill factors predict college outcomes? A meta-analysis[J]. Psychological Bulletin, 2004, 130(2): 261. DOI:10.1037/0033-2909.130.2.261 |
| [2] |
WALD A, MUENNIG P A, O'CONNELL K A, et al. Associations between healthy lifestyle behaviors and academic performance in US undergraduates: A secondary analysis of the American college health association's national college health assessment Ⅱ[J]. American Journal of Health Promotion, 2014, 28(5): 298-305. DOI:10.4278/ajhp.120518-QUAN-265 |
| [3] |
CHON J, CHA H. Lifemap: A smartphone-based context provider for location-based services[J]. IEEE Pervasive Computing, 2011(2): 58-67. DOI:10.1109/MPRV.2011.13 |
| [4] |
STOPCZYNSKI A, SEKARA V, SAPIEZYNSKI P, et al. Measuring large-scale social networks with high resolution[J]. Plos One, 2014, 9(4): e95978. DOI:10.1371/journal.pone.0095978 |
| [5] |
LANE N D, PENGYU L, ZHOU L, et al. Connecting personal-scale sensing and networked community behavior to infer human activities[C]//Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing. New York : ACM, 2014: 595-606. DOI: 10.1145/2632048.2636094.
|
| [6] |
SUMIDA M, MIZUMOTO T, YASUMOTO K. Estimating heart rate variation during walking with smartphone [C]//Proceedings of the 2013 ACM International Joint Conference on Pervasive and Ubiquitous Computing. New York: ACM, 2013: 245-254. DOI: 10.1145/2493432.2493491.
|
| [7] |
WANG R, CHEN F, CHEN Z, et al. StudentLife: Assessing mental health, academic performance and behavioral trends of college students using smartphones[C]//Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing. New York: ACM, 2014: 3-14. DOI: 10.1145/2632048.2632054.
|
| [8] |
WANG R, HARARI G, HAO P, et al. SmartGPA: How smartphones can assess and predict academic performance of college students [C]// Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing. New York: ACM, 2015: 1-13. DOI: 10.1145/2750858.2804251.
|
| [9] |
AGRAWAL R, SRIKANT R. Fast algorithms for mining association rules in large databases[C/OL]. [2017-02-03]. http://www.rsrikant.com/papers/vldb94_rj.pdf.
|
| [10] |
ATTILA G. A fuzzy approach for mining quantitative association rules[J]. Acta Cybernetica, 2001, 15(2): 305-320. |
| [11] |
HONG T P, KUO C S, CHI S C. Mining association rules from quantitative data[J]. Intelligent Data Analysis, 1999, 3(5): 363-376. DOI:10.1016/S1088-467X(99)00028-1 |
| [12] |
KUOK C M, FU A, WONG M H. Mining fuzzy association rules in databases[J]. ACM Sigmod Record, 1998, 27(1): 41-46. DOI:10.1145/273244.273257 |
| [13] |
WANG C H, LEE W H, PANG C T. Applying fuzzy FP-Growth to mine fuzzy association rules[J]. World Academy of Science, Engineering and Technology, 2010, 65: 956-962. |
| [14] |
DUNN J C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters[J]. Journal of Cybernetics, 1973, 3: 32-57. DOI:10.1080/01969727308546046 |
| [15] |
BEZDEKJ C. Pattern Recognition with Fuzzy Objective Function Algorithms[M]. New York: Plenum Press, 1981. DOI:10.1007/978-1-4757-0450-1
|
| [16] |
HAN J W, KAMBER M. Data Mining:Concepts and Techniques[M]. 2nd ed. San Francisco: Morgan Kaufmann, 2012.
|
| [17] |
WANG X, HAMILTON H J. DBRS: A density-based spatial clustering method with random sampling [C]// Advances in knowledge and Data Mining(LNCS 2637). Berlin: Springer, 2003: 563-575. DOI: 10.1007/3-540-36175-8-56.
|
 2018, Vol. 64
2018, Vol. 64




