文章信息
- 钟珞, 田蓝, 张开松, 李琳
- ZHONG Luo, TIAN Lan, ZHANG Kaisong, LI Lin
- 面向流数据的演化聚类算法
- Evolving Clustering Method for Stream Data
- 武汉大学学报(理学版), 2017, 63(5): 459-465
- Journal of Wuhan University(Natural Science Edition), 2017, 63(5): 459-465
- http://dx.doi.org/10.14188/j.1671-8836.2017.05.012
-
文章历史
- 收稿日期:2017-03-14

2. 武汉轻工大学 机械工程学院, 湖北 武汉 430023
2. School of Mechanical Engineering, Wuhan Polytechnic University, Wuhan 430023, Hubei, China
聚类分析是将数据集中的样本数据划分为若干个不相交的子集的分析过程,其所要求划分的子集个数通常是未知的.聚类是将数据分类到不同的类的一个过程,使不同类之间的差别尽可能大,同类中的差别尽可能小.聚类分析已应用于众多领域,如市场客户分析、生物基因分类、网络文档归类[1]、图像分割[2].
传统的聚类算法,如K-means[3]、FCM[4]、BIRCH[5]等,处理的是静态数据离线聚类问题.这些算法要求在给定的数据集上尽可能好的进行划分.在聚类分析研究领域里,K-means算法[6]是很典型的基于距离的聚类算法,采用距离作为相似性的评价指标,该算法采用类中样本数据的均值作为聚类中心,算法在聚类过程中多次迭代直到聚类结果的目标函数值达到最小.K-means算法不具有模糊性,不能解决数据重叠问题.模糊C均值算法(FCM)[7]是最常用的使用目标函数值作为聚类准则的模糊聚类算法,该算法在聚类过程中使用隶属度来衡量样本数据属于类的程度.
随着信息技术的发展以及网络上流数据的海量增加,传统的聚类算法难以满足流数据聚类的需求,演化聚类正是适应这一需求而产生的新一类算法.演化聚类算法(ECM)最早是由Song和Kasabov[8, 9]提出的,并将它应用于动态演化神经模糊推理系统(DENFIS)中,创建了模糊推理规则.ECM是一种处理在线数据的聚类算法,数据的分布随时间而变化,每一时刻新数据进入系统,系统要求对新数据做出聚类划分[10].随着输入数据的不断增加,ECM可实时动态地增加聚类个数、调整聚类中心和聚类半径.针对演化数据的聚类,Chakrabarti等[11]研究了数据的时间序列化演化问题,提出了基于时间平滑性框架的演化聚类方法.杜根远等[12]将ECM和FCM[13]相结合,采用ECM确定初始聚类中心,对获得的初始聚类中心采用FCM进行优化,从而完成模糊聚类划分,然后再通过去模糊化转化为确定性分类来实现聚类分割,但是该算法采用FCM优化聚类中心过程属于离线处理过程,优化步骤是在采用ECM处理完所有数据之后进行的,该算法只适用于对已知数量的数据集进行聚类,并不适用于对未知数量的流数据进行聚类.为了解决ECM依赖于预先设置的阈值Dthr和对数据输入秩序敏感性问题,王玲和孙华[14]提出了一种基于自适应学习的演化聚类算法(SALECM),该算法结合分割-融合方法,在无法获取数据先验知识的情况下,无需人为设置参数,可自适应地调整聚类结果,虽然该算法解决了阈值Dthr的问题,但是该算法与文献[12]一样,只适用于对已知数量的数据集进行聚类,并不适用于对未知数量的流数据进行聚类.
为了对未知数量的流数据进行在线聚类,且获得更好的聚类表现,本文在ECM的基础上,改进了ECM的聚类中心和聚类半径更新过程,并且优化了聚类过程中的数据归类准则,提出了一种面向流数据的演化聚类算法(SDECM).SDECM采用类中样本数据的均值作为聚类中心,类中样本数据到其聚类中心的最大距离作为聚类半径,以戴维森保丁指数DBI(Davies-Bouldin Index)[15]作为当前数据的归类准则,通过设置阈值Dthr的值来控制聚类过程中类的最大半径.
1 演化聚类算法ECM是一种快速、一遍扫描的在线聚类算法,用来对流数据进行动态聚类,具有很好的自适应性.该算法是基于距离的聚类处理过程,其聚类中心代表在线模式上的演化节点.针对每个类,该类的所有样本数据与对应的聚类中心的距离均小于或等于预先设置的阈值Dthr,Dthr的取值直接影响最终的聚类结果.
针对在线的聚类过程,样本数据源于在线输入的数据流,算法从空的聚类集合开始,当一个新的类被创建时,当前处理的数据属于该类,采用该数据来初始化聚类中心Cc,并且将该类的聚类半径R初始化为零.随着新数据的不断到来,一些已存在的聚类将会依赖于当前新出现的数据的位置来判定是否更新.针对会被更新的类,通过改变聚类中心的位置和增加聚类半径来进行更新,当聚类半径达到阈值Dthr时,该类的聚类半径不再进行更新[16].
数据经过特征提取后,假定所有的数据对象和聚类中心都保留了q个特征,即是q维数据.两个q维数据样本x={x1, x2, …, xq}和y={y1, y2, …, yq}之间的距离采用归一化欧氏距离公式,定义如下:
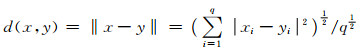
|
(1) |
下面为演化聚类算法ECM的算法描述.
| 算法1 演化聚类算法ECM |
| 输入:数据流中的样本数据xi. |
| 输出:聚类结果C. |
| Step 1:创建第1个聚类C1.将第一个输入的数据点x1作为第1个聚类中心Cc1,并令其初始聚类半径R1=0. |
| Step 2:如果数据流中所有的样本数据都已经被处理了,则算法结束.否则,计算当前输入的数据xi与所有已存在的聚类中心Ccj之间的的距离Dij=‖xi-Ccj‖, j=1, 2, …, k,其中k为已存在的聚类个数. |
Step 3:如果存在某一个距离值Dij满足Dij≤Rj, j=1, 2, …, k,这意味着当前输入的数据xi属于某个已存在的聚类Cm,且满足Dim=‖xi-Ccm‖ 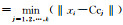 ,在这种情况下,xi∈Cm,既没有新的聚类被创建,也没有任何已存在的聚类中心和聚类半径被更新,返回Step 2,否则进行下一步. ,在这种情况下,xi∈Cm,既没有新的聚类被创建,也没有任何已存在的聚类中心和聚类半径被更新,返回Step 2,否则进行下一步. |
| Step 4:计算当前输入的数据xi与所有已存在的聚类中心Ccj的距离Dij和对应的聚类半径Rj这两项之和,即Sij=Dij+Rj, j=1, 2, …, k.选出一个聚类Ca(对应的聚类中心为Cca,聚类半径为Ra),使其满足Sia=Dia+Ra=min(Sij),其中j=1, 2, …, k. |
| Step 5:如果Sia>2×Dthr(Dthr为预先人为给定的阈值),则xi不属于任何已存在的聚类,采用Step 1的方法创建一个新的聚类,返回Step 2. |
| Step 6:如果Sia≤2×Dthr,则xi∈Ca,聚类Ca通过移动其聚类中心Cca和增加聚类半径Ra进行更新.更新后的聚类半径Ranew=Sia/2,将新的聚类中心Ccanew移动至位于xi与Cca的连线上,使其满足‖Ccanew-xi‖=Ranew,返回Step 2. |
该算法是通过阈值Dthr来决定当前数据是否属于已存在的某一个类,采用最短距离准则来处理当前数据的归类过程.该算法具有较好的自适应性,随着流数据的不断到来,该算法每次只对当前输入的数据进行归类处理,对已经处理过的历史数据将不再进行归类处理,即不再改变历史数据的状态.与传统的聚类算法相比,这一特性使ECM更适合面向流数据聚类.设输入数据流中的样本数据大小为n,聚类个数为k,则该算法的时间复杂度为O(n×k).一般聚类个数k的值都是较小的整数,在n≫k的情况下,可以认为ECM的时间复杂度为T(n)=O(n).
2 引入DBI的流数据演化聚类算法 2.1 戴维森保丁指数聚类中心Ccj, j=1, 2, …, k,即第j个聚类中心,每个聚类中心等于属于该聚类中所有样本的均值,即
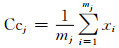
|
(2) |
其中:k为聚类数目,mj为第j个类中样本个数,xi为属于该聚类的样本数据.
聚类半径Rj,j=1, 2, …, k,即第j个聚类半径,表示第j个类的聚类中心与属于该聚类的样本数据间距离的最大值.假设第j个聚类为Cj={xi; i=1, 2, …, mj},聚类中心为Ccj,则聚类半径为
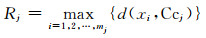
|
(3) |
DBI [15]是由Davies和Bouldin提出的一种基于类内相似性和类间差异性的评估准则.在聚类算法执行过程中,以类间数据对象的相异度高、类内数据对象的相似度高为依据来衡量聚类结果的好坏程度.
xj表示类Ci中的一个样本数据,mi表示类Ci中样本个数,Cci表示类Ci的聚类中心.第i个类的类内相似程度Si表示第i个聚类中样本数据与对应的聚类中心Cci的标准误差,公式如下:
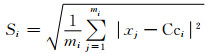
|
(4) |
Si越小表示第i个类的相似程度越高.
戴维森保丁指数的计算公式如下:
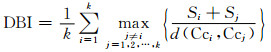
|
(5) |
其中:d(Cci, Ccj)为聚类中心Cci和Ccj之间的距离.
对于聚类结果而言,类内样本相似度越高,Si越小,类间相异度越高,d(Cci, Ccj)越大.因此,DBI越小,聚类质量越好.
2.2 SDECM算法SDECM采用类中样本数据的均值作为聚类中心,类中样本数据到其聚类中心的最大距离作为聚类半径,以DBI作为当前数据的归类准则,通过预先设置阈值Dthr的值来控制聚类过程中类的最大半径.若xi属于已存在的某个类,该算法针对当前输入数据xi的归类过程采用了假设原则,计算xi属于每个类后的聚类结果的DBI值,根据“DBI值越小,聚类性能越好”的评估准则,将DBI值最小的聚类结果作为处理当前输入数据的聚类结果.若xi不属于已存在的某个类,则创建一个新的类,xi属于该新建的类.
下面为面向流数据的演化聚类算法SDECM的算法描述.
| 算法2 面向流数据的演化聚类算法SDECM |
| 输入:数据流中的样本数据xi. |
| 输出:聚类结果C. |
| Step 1和Step 2同ECM |
Step 3:如果存在某一个距离值Dij满足Dij≤Rj, j=1, 2, …, k,这意味着当前输入的数据xi属于某个已存在的聚类Cm,且满足Dim=‖xi-Ccm‖ 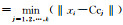 ,在这种情况下,xi∈Cm,既没有新的聚类被创建,也没有任何已存在的聚类半径被更新,根据(2) 式更新Cm的聚类中心,返回Step 2,否则进行下一步. ,在这种情况下,xi∈Cm,既没有新的聚类被创建,也没有任何已存在的聚类半径被更新,根据(2) 式更新Cm的聚类中心,返回Step 2,否则进行下一步. |
| Step 4:如果所有的类都满足Dij>Dthr(Dthr为预先人为设置的阈值),则xi不属于任何已存在的聚类,采用Step 1的方法创建一个新的聚类,返回Step 2. |
| Step 5:如果存在聚类满足Rj<Dij≤Dthr, j=1, 2, …, k,则找出所有满足Rj<Dij≤Dthr的类,并保存所有满足条件的类的下标index,按照(5) 式计算xi归为聚类Cindex后的DBI值,记为DBIindex,若index=argmin(DBIindex),则xi∈Cindex,根据(2) 式更新Cindex的聚类中心,根据(3) 式更新Cindex的聚类半径,返回Step 2. |
SDECM延续了ECM快速处理的优点,随着流数据的不断到来,该算法只对当前输入的数据进行归类处理,对已经处理过的历史数据将不再进行归类处理,即不再改变历史数据的状态.与传统的聚类算法相比,这一特性使SDECM与ECM一样更适合面向流数据聚类,并且解决了传统的聚类算法在不断的迭代过程中数据所属类不断改变的不稳定性.与ECM的区别是,该算法采用DBI评估准则代替ECM中最短距离准则作为聚类过程中数据的归类准则.
设数据流中的样本数据大小为n,聚类个数为k,该算法引入了DBI. DBI计算过程中涉及到第i个聚类中样本数据与对应的聚类中心Cci的标准误差Si,计算Si的平均时间复杂度为O(n/k).单纯计算DBI的时间复杂度为O(k2),在n≫k的情况下,单次计算DBI的时间复杂度为O(n/k).最坏情况下,需要计算k次DBI,因此DBI的整体时间复杂度为O(n/k)×k=O(n).所以SDECM的时间复杂度为T(n)=O(n2).
3 实验结果与分析 3.1 实验环境本文的实验运行环境是Windows 10(64bit)操作系统,实验的处理器是Intel(R) Core(TM) i5-2450 M CPU @2.50 GHz 2.50 GHz,内存为2 GB.算法采用Matlab语言编写,实验软件工具使用MATLAB R2012a.
3.2 实验数据集为了验证SDECM的有效性,本文的实验数据集采用UCI机器学习数据库中的5个标准数据集:Iris, Wine, Seeds, Glass和Breast Cancer,如表 1所示.Iris, Wine, Seeds和Glass均是没有缺失值的数据集,Breast Cancer来源于Breast Cancer Wisconsin(Original)数据集,Breast Cancer Wisconsin(Original)有699个样本实例(其中16个样本实例含有缺失值),Breast Cancer选取了Breast Cancer Wisconsin(Original)中没有缺失值的683个样本实例.表 1中的5个数据集的属性均包含1位类别属性,例如Iris,属性数为5,其中特征属性数为4,类别属性数为1.
| 数据集 | 样本数 | 属性数 | 类别数 |
| Iris | 150 | 5 | 3 |
| Wine | 178 | 14 | 3 |
| Seeds | 210 | 8 | 3 |
| Glass | 214 | 11 | 6 |
| Breast Cancer | 683 | 10 | 2 |
ECM和SDECM都对阈值Dthr敏感,Dthr的取值直接影响着聚类结果的聚类个数和每个类的大小.为了解决阈值Dthr的取值困难问题,Lekova等[17]提出了一种轻量级演化模糊聚类算法LEFCM,该算法采用等步长的方式改变阈值Dthr,在算法寻优过程中获得最佳阈值,本文采用该等步长的方式多次实验获得最佳阈值Dthr.例如,对Iris数据集进行实验过程中,Dthr的取值范围定为[0.1, 10],每次以0.05的长度递增(针对不同的数据集,根据先验知识,Dthr取值范围以及递增长度可以进行调整).表 2显示了不同的阈值Dthr对ECM和SDECM聚类结果的影响.
| 数据集 | Dthr | ECM聚类数 | SDECM聚类数 |
| Iris | 1.05 | 3 | 3 |
| 0.7 | 5 | 4 | |
| 0.6 | 7 | 6 | |
| Wine | 97 | 3 | 3 |
| 80 | 4 | 4 | |
| 50 | 6 | 5 | |
| Seeds | 1.6 | 3 | 3 |
| 1.3 | 4 | 5 | |
| 1.0 | 6 | 6 | |
| Glass | 5.85 | 6 | 6 |
| 5.75 | 7 | 6 | |
| 5.65 | 7 | 7 | |
| Breast Cancer | 4.5 | 2 | 2 |
| 4.0 | 4 | 3 | |
| 3.5 | 5 | 8 |
由表 1可知Iris、Wine, Seeds, Glass和Breast Cancer的实际类别数分别对应为3、3、3、6和2.为了更准确的分析算法的有效性,根据表 2的实验结果分析,Iris, Wine, Seeds, Glass和Breast Cancer数据集在采用ECM和SDECM进行聚类时,Dthr分别取值1.05, 97, 1.6, 5.85和4.5可以得到实际类别数.
3.4 聚类性能评估为了验证SDECM的有效性,本文采用目标函数值J、DBI值、准确率accuracy(A)[18]和纯度purity(P)[19]4个聚类性能度量来评估SDECM和ECM的性能.为了实验的便捷性,采用按行读取数据集中的数据流来模拟流数据.
在聚类分析中,目标函数值J是反映类间相似性或差异性的函数,其计算公式如下:
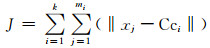
|
(6) |
其中mi表示第i个聚类中样本个数.
准确率是评价聚类结果性能最常用的准则,其计算公式如下:
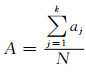
|
(7) |
其中:N表示实验样本数据总数,aj表示聚类结果中的第j个聚类和实际聚类相一致的样本个数.由(7) 式可知,分子部分的aj(j=1, 2, …, k)的值越大表示正确分类的样本数越多,A越大,则聚类结果的准确率越高,聚类质量越好.
另一种评估聚类性能的准则是聚类结果的平均纯度,其计算公式如下:
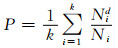
|
(8) |
其中k是聚类数,Ni是第i个类的样本数据个数,Nid是第i个类中主要类别的样本数据个数.
为了方便对聚类结果的效果进行评估,表 1中所有实验数据集的样本数据均保留其类别属性,同一数据集中的样本数据的类别属性相同,表示该样本数据属于同一类.保留每个样本数据的类别属性可以方便对聚类结果的准确率和纯度进行计算.但是类别属性并不是数据的特征属性,该属性的值不但会影响聚类效果,也会影响目标函数值J以及DBI值的计算结果,所以类别属性不应该被涉及到聚类处理、目标函数值J和DBI值的计算过程中.
由于准确率和纯度的计算过程不涉及两个样本数据之间的欧氏距离,而聚类处理、目标函数值J和DBI值的计算过程均涉及两个样本数据之间的欧氏距离,为了消除数据的类别属性对聚类处理、目标函数值J和DBI值的计算结果的影响,本文对实验数据集和欧氏距离进行了以下优化:1) 整理实验数据集,将表 1中的实验数据集的类别属性移到最后一位属性列中;2) 改进(1) 式,改进后的归一化欧氏距离公式如下:
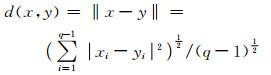
|
(9) |
(9) 式的距离计算公式在计算过程中排除了样本数据的最后一位属性(类别属性),这样处理可以消除类别属性对聚类过程以及目标函数值J和DBI值的影响,又保留了聚类结果的类别属性,为计算准确率和纯度提供了方便.本实验中的距离公式均采用(9) 式计算.
选取表 2中能够得到实际聚类数的阈值Dthr,计算出Iris, Wine, Seeds, Glass和Breast Cancer这5个数据集分别采用ECM和SDECM进行模拟流数据聚类后的聚类结果的目标函数值J、DBI值、准确率和纯度这4个聚类性能度量,实验结果如表 3所示.
| 数据集 | Dthr | 聚类数 | ECM | SDECM | |||||||
| J | DBI | 准确率 | 纯度 | J | DBI | 准确率 | 纯度 | ||||
| Iris | 1.05 | 3 | 57.850 4 | 0.752 5 | 0.733 3 | 0.851 9 | 49.770 9 | 0.8542 | 0.873 3 | 0.908 2 | |
| Wine | 97 | 3 | 7 147.1 | 1.499 2 | 0.612 4 | 0.792 8 | 5 820 | 0.8591 | 0.679 8 | 0.808 2 | |
| Seeds | 1.6 | 3 | 158.024 1 | 0.895 6 | 0.704 8 | 0.843 4 | 131.476 4 | 0.963 8 | 0.838 1 | 0.891 0 | |
| Glass | 5.85 | 6 | 628.132 2 | 1.555 5 | 0.873 8 | 0.873 6 | 623.944 0 | 1.552 9 | 0.873 8 | 0.874 2 | |
| Breast Cancer | 4.5 | 2 | 2 164.5 | 1.428 5 | 0.686 7 | 0.837 4 | 1 072.8 | 1.3449 | 0.916 5 | 0.935 7 | |
表 3的实验结果表明,在选取相同的Dthr值获得实际类别数的前提下,根据“目标函数值J越小,聚类性能越好”、“DBI值越小,聚类性能越好”、“准确率越大,聚类性能越好”和“纯度越大,聚类性能越好”的评估准则分析,在5个实验数据集上SDECM聚类结果的目标函数值比ECM小,纯度比ECM大;在3个实验数据集(Wine,Glass和Breast Cancer)上SDECM聚类结果的DBI值比ECM小;在4个实验数据集(Iris,Wine,Seeds和Breast Cancer)上SDECM的聚类结果的准确率比ECM大.因此,SDECM优于ECM.
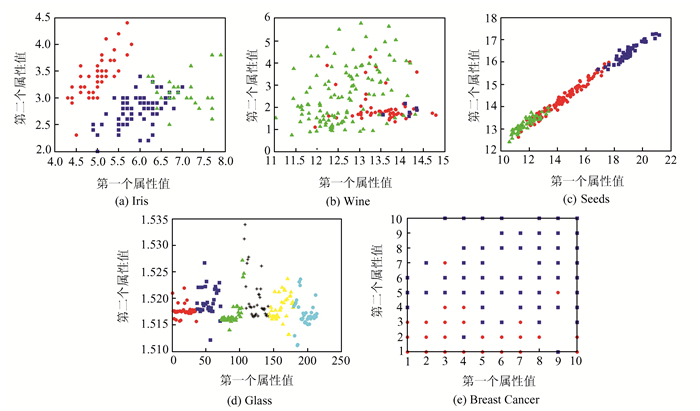
由于本文选用的5个实验数据集都是高维的,难以可视化, 为了更直观的观察聚类效果,采用SDECM分别对5个实验数据集进行聚类,选取聚类结果的每个样本数据的前两个属性进行可视化,分别如图 1中的(a)、(b)、(c)、(d)、(e)所示,其中每个图的横坐标和纵坐标分别表示对应的数据集的第一个属性值和第二个属性值.同一颜色的数据点表示属于同一类,不同颜色的数据点表示属于不同的类,例如图 1(a)横坐标表示Iris的第一个属性值,即花萼长度,纵坐标表示Iris的第二个属性值,即花萼宽度;3种不同的颜色,表示聚类结果的3个分类.
|
| 图 1 SDECM聚类结果 Figure 1 Clustering results of SDECM |
根据图 1可知,SDECM在处理流数据聚类方面具有较好的效果.
4 结论本文在ECM的基础上,提出了一种面向流数据的演化聚类算法SDECM.与传统聚类算法相比,该算法对流数据在线聚类具有更好的适应性.SDECM改进了ECM中的聚类中心和聚类半径更新过程,并且引入DBI作为样本数据归类准则.针对目标函数值J、准确率和纯度这3个聚类性能度量,SDECM的聚类性能均优于ECM.针对DBI值的聚类性能度量,SDECM的聚类性能略优于ECM.实验分析表明,SDECM针对流数据在线聚类具有可行性和有效性.下一步的研究可对参数阈值Dthr进一步优化,并将SDECM应用于其他的研究领域,如图像分割等.
| [1] |
MEI J P, WANG Y, CHEN L, MIAO C.Incremental fuzzy clustering for document categorization[C]//2014 IEEE International Conference on Fuzzy Systems(FUZZ-IEEE). New York:IEEE, 2014:1518-1525.
|
| [2] |
HOU J, LIU W, Xu E, et al. Towards parameter-independent data clustering and image segmentation[J]. Pattern Recognition, 2016, 60: 25-36. DOI:10.1016/j.patcog.2016.04.015 |
| [3] |
HARTIGAN J A, WONG M A. Algorithm AS 136:A K-means clustering algorithm[J]. Applied Statistics, 1979, 28(1): 100-108. DOI:10.2307/2346830 |
| [4] |
TANG J, ZHANG G, WANG Y, et al. A hybrid approach to integrate fuzzy C-means based imputation method with genetic algorithm for missing traffic volume data estimation[J]. Transportation Research Part C Emerging Technologies, 2015, 51: 29-40. DOI:10.1016/j.trc.2014.11.003 |
| [5] |
ZHANG T, RAMAKRISHNAN R, LIVNY M. BIRCH:A new data clustering algorithm and its applications[J]. Data Mining and Knowledge Discovery, 1997, 1(2): 141-182. DOI:10.1023/A:1009783824328 |
| [6] |
ARORAP, DEEPALI D, VARSHNEY S. Analysis of K-means and K-medoids algorithm for big data[J]. Procedia Computer Science, 2016, 78: 507-512. DOI:10.1016/j.procs.2016.02.095 |
| [7] |
MANSOORIE G. FRBC:A fuzzy rule based clustering algorithm[J]. IEEE Transactions on Fuzzy Systems, 2011, 19(5): 960-971. DOI:10.1109/TFUZZ.2011.2158651 |
| [8] |
SONG Q, KASABOV N. ECM-A novel on-line evolving clustering method and its applications[J]. M.i.posner Foundations of Cognitive Science, 2001, 631-682. |
| [9] |
KASABOV N, SONG Q. DENFIS:Dynamic evolving neural-fuzzy inference system and its application for time-series prediction[J]. IEEE Transactions on Fuzzy Systems, 2002, 10(2): 144-154. DOI:10.1109/91.995117 |
| [10] |
张长水, 张见闻. 演化数据的学习[J]. 计算机学报, 2013, 36(2): 310-316. ZHANG C S, ZHANG J W. Learning on time-evolving data[J]. Chinese Journal of Computers, 2013, 36(2): 310-316. DOI:10.3724/SP.J.1016.2013.00310(Ch) |
| [11] |
CHAKRABARTI D, KUMAR R, TOMKINS A. Evolutionary clustering[C]//Proceedings of the 12th ACM SIGKDD International Conference on Know-ledge Discovery and Data Mining. New York:ACM, 2006:554-560.
|
| [12] |
杜根远, 田胜利, 苗放. 结合ECM和FCM聚类的遥感图像分割新方法[J]. 计算机应用研究, 2009, 26(10): 3995-3997. DU G Y, TIAN S L, MIAO F. Remote sensing image segmentation based on evolving clustering and fuzzy C-means[J]. Application Research of Computers, 2009, 26(10): 3995-3997. DOI:10.3969/j.issn.1001-3695.2009.10.115 |
| [13] |
BEZDEK J C, EHRLICH R, FULL W. FCM:The fuzzy C-means clustering algorithm[J]. Computers & Geosciences, 1984, 10(2-3): 191-203. |
| [14] |
王玲, 孙华. 基于自适应学习的演化聚类算法[J]. 控制与决策, 2016, 31(3): 423-428. WANG L, SUN H. Evolving clustering method based on self-adaptive learning[J]. Control and Decision, 2016, 31(3): 423-428. DOI:10.13195/j.kzyjc.2014.1945 |
| [15] |
DAVIES D L, BOULDIN D W. A cluster separation measure[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1979, 1(2): 224-227. |
| [16] |
RAVI V, SRINIVAS E R, KASABOV N K. On-line evolving fuzzy clustering[C]//International Conference on Computational Intelligence and Multimedia Applications. New York:IEEE, 2007, 1:347-351.
|
| [17] |
LEKOVA A K, DIMIYROVA M I. Hand gestures recognition based on lightweight evolving fuzzy clustering method[C]//Proceedings of the 2013 IEEE Second International Conference on Image Information Processing. New York:IEEE, 2013:505-510.
|
| [18] |
SUN Y, ZHU Q M, CHEN Z X. An iterative initial-points refinement algorithm for categorical data clustering[J]. Pattern Recognition Letters, 2002, 23(7): 875-884. DOI:10.1016/S0167-8655(01)00163-5 |
| [19] |
CHEN J Y, HE H H. A fast density-based data stream clustering algorithm with cluster centers self-determined for mixed data[J]. Information Sciences, 2016, 345(C): 271-293. |
 2017, Vol. 63
2017, Vol. 63




