文章信息
- 刘莉君
- LIU Lijun
- 剩余格上几类n-重模糊滤子的系统结构
- Structure of Several Kinds of n-Fold Fuzzy Filter in the Residuated Lattice
- 武汉大学学报(理学版), 2017, 63(6): 538-542
- Journal of Wuhan University(Natural Science Edition), 2017, 63(6): 538-542
- http://dx.doi.org/10.14188/j.1671-8836.2017.06.012
-
文章历史
- 收稿日期:2017-01-02

在非经典逻辑中, Pavelka引入的剩余格是一种非常基本的代数结构, 同时, 作为非经典逻辑系统的语义系统的各种逻辑代数也被广泛研究.目前, 大多数学者都认同剩余格为一种最广泛的逻辑代数结构, 其中格蕴涵代数, BL代数, MV代数, MTL代数等[1, 2]均是剩余格的特殊情况, 而滤子是非经典逻辑代数研究领域的一个重要概念, 它们对各种逻辑系统及与之匹配的逻辑代数的完备性问题的研究发挥着极其重要的作用.近几年学者们已经在各种逻辑代数框架下提出了多种滤子概念, 并获得了许多有价值的研究结果.其中, 文献[3]研究了剩余格上的n-重滤子, 文献[4]研究了剩余格上的广义n-重模糊滤子, 文献[5]在BL代数上引入n-重滤子并研究了它们的性质.因此, 系统地分析各种滤子概念之间的相互关系及层次结构就显得尤为重要, 基于此目的本文在上述工作的基础上, 受文献[6~10]的启发, 将模糊滤子的重理论进一步推广到剩余格上,通过研究剩余格上n-重模糊蕴涵滤子, n-重模糊极滤子和n-重模糊布尔滤子的特征及性质, 获得了剩余格上这几类n-重模糊滤子之间的关系, 以及这几类n-重模糊滤子的若干等价刻画.研究结果不但使剩余格上的模糊滤子理论得到进一步充实和丰富,概念间的层次关系更加的清晰和完善, 而且也能为研究基于剩余格的逻辑系统的结构特征提供理论基础上的支持和保障.
1 定义下面先给出本文将用到的几个定义.
定义1[2] 称(2, 2, 2, 2, 0, 0)-型代数L=(M, ∧, ∨, ⊗, →, 0, 1)为剩余格,若以下条件成立:
1) (M, ∧, ∨,0, 1)是有界格;
2) (M, ⊗,1)是交换的幺半群;
3) 对于任意的x, y, z∈M, x⊗y≤z⇔y≤x→z.
性质1[2] 设L=(M, ∧, ∨, ⊗, →, 0, 1)为剩余格,对于任意的x, y, z∈L, 则以下条件成立:
1) x→y=1当且仅当x≤y;
2) 1→x=x, x→x=1, x→1=1, 0→x=1;
3) x→(y→z)=y→(x→z)=(x⊗y)→z;
4) (x→y)⊗(y→z)≤x→z;
5) y→x≤(z→y)→(z→x),
x→y≤(y→z)→(x→z);
6) 约定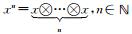
7) ¬x=x→0, x⊗x=0,
¬(x⊗y)=x→¬y=y→¬x,
x∨y≤(y→x)→x;
8) x≤¬x→y, ¬x≤x→y,
x∨y=((x→y)→y)∧((y→x)→x);
9) (x∨y)→z=(x→z)∧(y→z),
x→(y∧z)=(x→y)∧(x→z).
定义2[5] 设L=(M, ∧, ∨, ⊗, →, 0, 1)为剩余格,μ:L→[0, 1]为L上的一个模糊集, 则模糊集μ被称为剩余格L上的模糊滤子, 如果对于任意的x, y∈L, 有
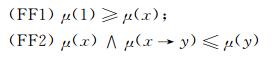
|
性质2[5] 设L=(M, ∧, ∨, ⊗, →, 0, 1)为剩余格,模糊集μ为剩余格L上的模糊滤子, 对于任意的x, y, z∈L, 下列性质成立:
1) 如果x≤y, 则μ(x)≤μ(y), 即μ是保序的;
2) 若μ(x→y)=μ(1), 则μ(x)≤μ(y);
3) μ(x→y)≤μ(y→z)→μ(x→z);
4) μ(y→x)≤μ(z→y)→μ(z→x);
5) μ(y⊗x)=μ(x∧y)=μ(x)∧μ(y);
6) μ((x→y)⊗(y→z))≤μ(x→z).
定义3[6] 设L是剩余格, μ是L上的模糊滤子, 则μ是L上的一个n-重模糊蕴涵滤子(n=1, 2, …), 如果对于任意的x, y, z∈L, 有
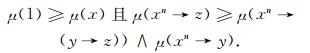
|
定义4[7] 设L是剩余格, μ是L上的模糊滤子, 则μ是L上的一个n-重模糊极滤子(n=1, 2, …), 如果对于任意的x, y, z∈L, 有
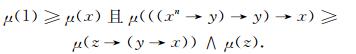
|
定义5[8] 设L是剩余格, μ是L上的模糊滤子, 则μ是L上的一个n-重模糊布尔滤子(n=1, 2, …), 如果对于任意的x∈L, 有μ(1)≥μ(x)且μ(x∨¬xn)=μ(1).
2 主要定理引理1 设L是剩余格, 对于任意的x, y∈L, 则下列等式成立:
1) (x∨y)n→y=xn→y;
2) (x∨¬xn)→(xn→xn+1)=1.
证 1) (x∨y)n→y=(x∨y)n-1→[(x∨y)→y]=(x∨y)n-1→(x→y)=x→[(x∨y)n-1→y]
连续重复n-1次上述过程, 则(x∨y)n→y=xn→y.证毕.
2) 设L是剩余格, 对于任意的x∈L, 由性质1可得
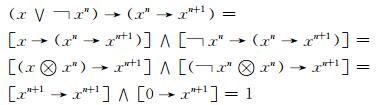
|
引理2 设L是剩余格, μ为L上的n-重模糊蕴涵滤子, 则对于任意的x∈L, 有
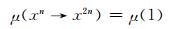
|
证 因为μ为L上的n-重模糊蕴涵滤子, 则对于任意的x∈L, 就有
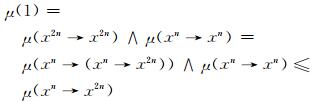
|
即μ(xn→x2n)≥μ(1), 结合(FF1)可知, μ(xn→x2n)=μ(1), 证毕.
定理1 设L是剩余格, μ为L上的模糊集, 则下列条件等价:
1) μ是L上的n-重模糊蕴涵滤子;
2) μ是L上的模糊滤子, 且有
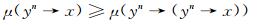
|
证 1)⇒2)
因为模糊集μ是L上的n-重模糊蕴涵滤子, 由定义3可知
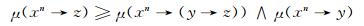
|
在该式中令x=1, 则有
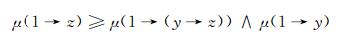
|
即
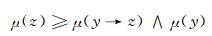
|
故μ是L上的模糊滤子.而另一方面,
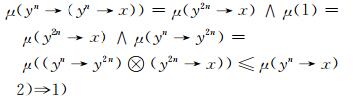
|
对于任意的x, y∈L, 有
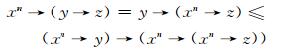
|
则

|
故可得
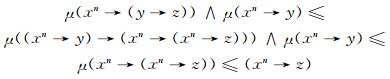
|
综上,由定义3可得μ是L上的n-重模糊蕴涵滤子.证毕.
定理2 设L是剩余格, μ为L上的模糊集, 则下列条件等价:
1) μ是L上的n-重模糊极滤子;
2) μ是L上的模糊滤子, 且对于任意的x, y∈L, 则有μ((xn→y)→y)≤μ(x∨y).
证 1)⇒2)
因为模糊集μ是L上的n-重模糊极滤子, 由定义4可知,
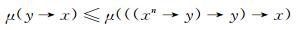
|
在该式中令x=x∨y, 则有
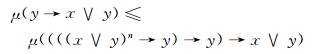
|
又由引理1可得
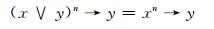
|
且
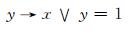
|
从而可得
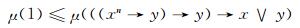
|
再结合(FF1)式μ(1)=μ(((xn→y)→y)→x∨y), 再由性质2可得对于任意的x, y∈L, 有
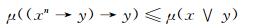
|
2) ⇒1)
对于任意的x, y∈L, 因为
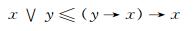
|
则有
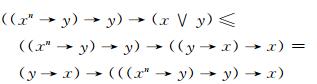
|
即
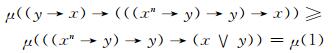
|
再结合(FF1)式
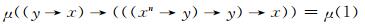
|
即可得
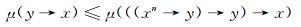
|
综上可知μ是L上的n-重模糊极滤子, 证毕.
定理3 设L是剩余格, μ为L上的模糊滤子, 则下列条件等价:
1) μ是L上的n-重模糊布尔滤子;
2) μ(x∨(xn→y))=μ(1);
3) μ(((xn→y)→x)→x)=μ(1).
证 1)⇒2)
因为μ是L上的n-重模糊布尔滤子, 则对于任意的x, y∈L, 有¬xn≤xn→y, 从而可得
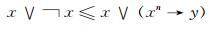
|
即
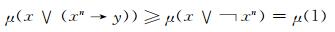
|
再结合(FF1)式可得
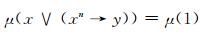
|
2) ⇒3)
对于任意的x, y∈L, 有
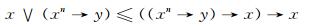
|
因此可得
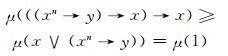
|
结合(FF1)式可得
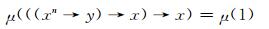
|
3) ⇒1)
因为μ(((xn→y)→x)→x)=μ(1), 在该式中令y=0, 从而就有
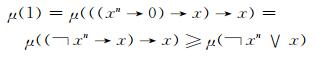
|
结合(FF1)式可得:

|
综上可知μ是L上的n-重模糊布尔滤子, 证毕.
定理4 设L是剩余格, 模糊集μ为L上的模糊滤子, 若μ为剩余格L上的n-重模糊布尔滤子, 则对于任意的x, y∈L, μ也为剩余格L上的n-重模糊极滤子.
证 设模糊集μ为剩余格L上的n-重模糊布尔滤子, 则由定义5知, 对于任意的x∈L, 都有
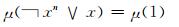
|
又根据性质1和2可得:

|
即
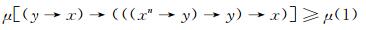
|
再结合(FF1)式可知
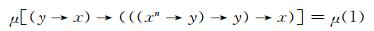
|
由性质2可得:
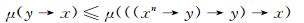
|
即μ(1→(y→x))∧μ(1)≤μ(((xn→y)→y)→x).
由定义4知μ也为剩余格L上的n-重模糊极滤子.证毕.
定理5 设L是剩余格, 模糊集μ为L上的模糊滤子, 若μ为剩余格L上的n-重模糊布尔滤子, 则对于任意的x, y∈L, μ为L上的n-重模糊蕴涵滤子.
证 设L是剩余格, 对于任意的x∈L, 由引理1可知, 在剩余格L上有
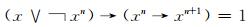
|
因此可得
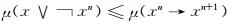
|
又因为μ为剩余格L上的n-重模糊布尔滤子, 即可得

|
从而
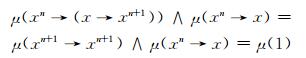
|
则μ(xn→(x→xn+1))∧μ(xn→x)≤μ(xn→xn+1).
综上,由定义3可知模糊滤子μ为L上的n-重模糊蕴涵滤子.证毕.
注 剩余格L上的n-重模糊极滤子与剩余格L上的n-重模糊蕴涵滤子之间没有必然等价关系.
例1 设M1={0, a, b, 1},其中0≤a≤b≤1, 令x∧y=min{x, y}, x∨y=max{x, y}, 且在M中定义二元运算“→”和“⊗”如表 1所示.
| → | 0 | a | b | 1 | ⊗ | 0 | a | b | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| a | 1 | 1 | a | 1 | a | 0 | a | 0 | a |
| b | a | b | a | 1 | b | 0 | 0 | b | b |
| 1 | 0 | a | b | 1 | 1 | 0 | a | b | 1 |
则L=(M1, ∧, ∨, ⊗, →, 0, 1)是一个剩余格, 在L上定义模糊集μ:L→[0, 1]使
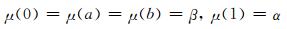
|
其中0≤β<α≤1.可以验证模糊集μ为剩余格L上的n-重模糊极滤子, 但非n-重模糊蕴涵滤子, 这是因为
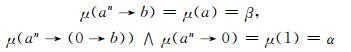
|
显然, μ(an→b)<μ(an→(0→b))∧μ(an→0).
例2 设M2={0, a, b, 1},其中0≤a≤b≤1, 令x∧y=min{x, y}, x∨y=max{x, y}, 且在M中定义二元运算“→”和“⊗”如表 2所示.
| → | 0 | a | b | 1 | ⊗ | 0 | a | b | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| a | 0 | 1 | a | 1 | a | 0 | a | a | a |
| b | 0 | a | 1 | 1 | b | 0 | a | b | b |
| 1 | 0 | a | b | 1 | 1 | 0 | a | b | 1 |
则L=(M2, ∧, ∨, ⊗, →, 0, 1)是一个剩余格, 在L上定义模糊集μ:L→[0, 1]使
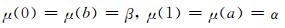
|
其中0≤β<α≤1.可以验证模糊集μ为剩余格L上的n-重模糊蕴涵滤子, 但非n-重模糊极滤子, 这是因为
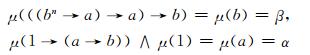
|
显然,
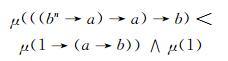
|
定理6 设L是剩余格, 映射μ和δ是L上的模糊滤子, 且满足μ≤δ, μ(1)=δ(1), 若映射μ是L上的n-重模糊蕴涵(极, 布尔)滤子, 则映射δ是L上的n-重模糊蕴涵(极, 布尔)滤子.
证 设L是剩余格, 对于任意的x, y∈L, 令
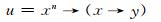
|
则有
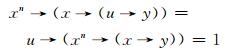
|
因为映射μ是L上的n-重模糊蕴涵滤子, 故由定义3可知:
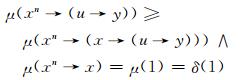
|
又因为μ≤δ, 则有
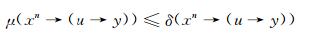
|
即

|
再结合(FF1)式可知:
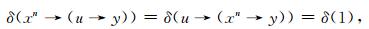
|
因此可得
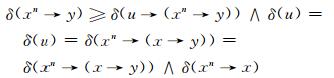
|
综上,由定义3可知映射δ也是L上的n-重模糊蕴涵滤子.
同理可证得映射δ也是L上的n-重模糊极滤子和n-重模糊布尔滤子.证毕.
3 结论在研究剩余格的代数结构中滤子理论起着非常重要的作用.本文在剩余格中引入了n-重模糊蕴涵滤子, n-重模糊极滤子和n-重模糊布尔滤子的概念, 通过研究它们的特征及性质, 系统分析了这几类n-重模糊滤子概念之间的相互关系及其等价刻画.在下一步工作中我们将继续深入研究剩余格上其他的滤子, 为揭示剩余格的代数结构发挥作用.
| [1] |
HAVESHKI M. Some types of filters in BL-algebras[J]. Soft Computing, 2006, 10: 657-664. DOI:10.1007/s00500-005-0534-4 |
| [2] |
周红军. 概率计量逻辑及其应用[M]. 北京: 科学出版社, 2015. ZHOU H J. Probability Measurement Logic and Approximate Reasoning[M]. Beijing: Science Press, 2015. |
| [3] |
KADJI A, LELE C, TONGA M. N-fold filters in residuated lattice[J/OL].[2017-01-03].http://arxiv.org/abs/13081878v1.
|
| [4] |
MA Z M. Some types of generalized fuzzy n-fold filters in residuated lattices[J]. Abstract and Applied Analysis, 2013, 20(3): 1-8. DOI:10.1155/2013/736872 |
| [5] |
孟彪龙, 辛小龙, 杨永伟. BL代数的n-重模糊蕴涵滤子[J]. 计算机工程与应用, 2014, 50(11): 62-65. MENG B L, XIN X L, YANG Y W. N-fold fuzzy filter on BL-algebra[J]. Computer Engineering and Applications, 2014, 50(11): 62-65. DOI:10.3778/j.issn.1002-8331.1311-0073 |
| [6] |
KADJI A, LELE C, NGANOU J B, et al. Folding theory applied to residuated lattice[J]. International Journal of Mathematics and Mathematical Sciences, 2014, 22(5): 1-12. DOI:10.1155/2014/42890 |
| [7] |
BORZOOEI R A. Fuzzy n-fold fantastic filters in BL-algebra[J]. Neural Computing and Application, 2014, 18(3): 378-385. DOI:10.1007/S13370-013-0169-z |
| [8] |
DUMITRU B. Some types of filters in residuated lattices[J]. Soft Comput, 2014, 18(4): 825-837. DOI:10.1007/S00500-013-11846 |
| [9] |
MASOUD H. N-fold filters in BL-algebras[J]. Neural Computing and Application, 2011, 20(6): 461-472. DOI:10.1002/malq.200710029 |
| [10] |
TURUNEN E, TCHIKAPA N. N-fold implicative basic logic is Godel logic[J]. Soft Comput, 2012, 16(4): 177-183. DOI:10.1007/S00500-011-0761-9 |
 2017, Vol. 63
2017, Vol. 63




