文章信息
- 黎栩, 龙鸿健, 高诗剑, 李新强
- LI Xu, LONG Hongjian, GAO Shijian, LI Xinqiang
- 单玻色子交换势模型下对Y(4390)的研究
- Study of Y(4390)in the One-Boson-Exchange Potential Model
- 武汉大学学报(理学版), 2019, 65(5): 495-502
- Journal of Wuhan University(Natural Science Edition), 2019, 65(5): 495-502
- http://dx.doi.org/10.14188/j.1671-8836.2019.05.011
-
文章历史
- 收稿日期:2018-04-08

2016年10月,BESⅢ合作组[1]在e+e- → (hc+π+π-)过程中发现了2个新粒子Y(4390)和Y(4220),并认为它们的量子数很可能均为1--,其中,Y(4390)的质量和宽度分别被确认为M=(4 392±6) MeV,Γ=(140±16) MeV。通过分析Y(4390)的衰变产物,预言它可能是一个包含cc味道的重味矢量强子态。
Y(4390)属于近年来发现的大量奇特强子态之一,这些强子态就是被称为X、Y、Z的类粲偶素或类底偶素态[2~4],其中很多不能用传统的夸克模型进行解释,内部的结构目前也尚无定论。对于这类强子态,常用的研究方法有: QCD求和规则[5]、势模型[6]、格点QCD[7]等。这些方法将奇特强子态解释为强子分子态或多夸克态等。2017年,Wang[8]提出使用QCD求和规则将Y(4390)解释为由一个反介子D1和一个D介子结合形成的D1D的分子态,但是通过该方法计算得到的Y(4390)的质量却比分子态阈值(4 290 MeV)高很多,因此该解释不够合理。2018年,Wang[9]根据数值计算结果提出Y(4390)还可能为矢量四夸克态ccqq。另外,文献[10]中在单玻色子交换模型基础上用BetheSalpeter方程近似的方法进行分析,提出Y(4390)是D1D*的分子态,但是此方法得到的分子态质量为4 384 MeV,仍然比实验上Y(4390)的质量值低一些。目前关于Y(4390)的结构仍无统一且令人满意的解释。
由于Y(4390)与D1D*的阈值很接近,本文尝试从非相对论量子力学的角度出发,将Y(4390)解释为量子数为1--、结构为D1D*/D1D*的强子分子态。D介子是由一个粲夸克和一个轻夸克组成的,可以认为其内在是非相对论的。在非相对论的基础上分析D1D*/D1D*系统,即求解径向薛定谔方程,并使用单玻色子交换势(one-boson-exchange potential,OBEP)模型[11]分析方程中的相互作用势,求解D1D*/D1D*系统的波函数和本征能量,对Y(4390)的性质进行解释和预言。
本文将首先描述OBEP模型的机制,给出标量介子、赝标介子、矢量介子交换势,接着给出模型中的数值计算参数,最后将模型应用到Y(4390)中,对数值结果进行分析。
1 OBEP模型及其在Y(4390)上的应用本节将简要介绍OBEP模型及其相互作用图像并根据Y(4390)在D1D*/D1D*系统下可能交换的玻色子,求出相关玻色子的通用交换势。
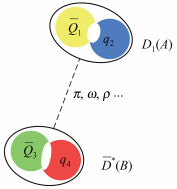
1.1 重味粒子的OBEP模型机制OBEP模型[11]由Yukawa提出的通过单π交换势分析核力的理论[12]基础上发展而来。Yukawa认为质子和中子通过交换π介子结合在一起;Tornqvist [13, 14]也曾用单π交换势解释了氘核束缚态。同样地,在OBEP模型框架下,强子分子态被看作通过交换多种玻色子而形成的束缚态,利用如下方式可得到分子态中介子之间复杂的相互作用:通过考虑π介子的交换可得到长程力,通过考虑σ、ρ、ω、η介子的交换将得到中短程力[11, 13, 14]。但是强子分子态包含4个夸克,单纯求解4个夸克间玻色子的交换作用会使问题变得非常复杂,所以有必要在OBEP模型基础上进行假设和简化。考虑到重味分子态的系统由2个重夸克和2个轻夸克组成,假设各种玻色子的交换主要在轻夸克之间,而重夸克因过重而忽略玻色子交换的影响。因此,自旋算符和同位旋算符等只作用在轻夸克间。下文中为简单起见,用A(Q1q2)、B(Q3q4)分别表示2个重味介子。其中q2、q4分别表示2个轻夸克,Q1、Q3分别表示2个重夸克,Q1和Q3是Q1、Q3的反粒子。重味介子D1和D*间的玻色子交换如图 1。
|
| 图 1 重味介子D1和D*间的玻色子交换 Fig. 1 Bosons exchange between the heavy flavor mesons D1 and D* |
分子系统的量子数限制了能够发生交换的介子种类,下面将对Y(4390)进行分析并推导各介子交换势。
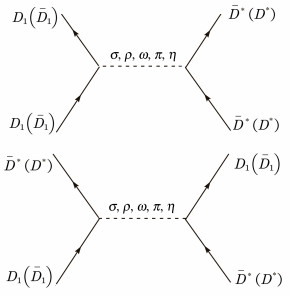
Y(4390)的量子数是JPC=1--,对于量子数为1--的D1D*/D1D*系统,它可能的轨道角动量和宇称是0-和2-,即该分子态的轨道可能处于S波或者D波;D1和D*的宇称分别为+1和-1,则系统的宇称自动满足量子数为-1的要求。在OBEP模型框架下,根据费曼图顶点处的宇称和角动量守恒,可以知道所有可能的交换玻色子[6],相应的费曼图如图 2。
|
| 图 2 D1D*/D1D*系统的玻色子交换费曼图 Fig. 2 Feynman diagrams of bosons exchange in D1D*/D1D* system |
图 2给出了D1和D*散射(及其反粒子散射)之间交换玻色子所有可能的费曼图,并考虑了可能交换的中间玻色子为σ、ρ、ω、π、η。利用费曼规则[14]可分别处理赝标介子(π、η)、标量介子(σ)、矢量介子(ρ、ω)的交换贡献,从而得到它们在动量空间的T矩阵元。由于在玻恩近似下T矩阵等价于相互作用的交换势,因此可得到赝标介子、标量介子、矢量介子的交换势[15]。
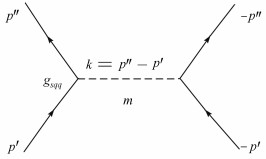
下面以标量介子的交换势为例简要说明推导过程。标量介子的顶点耦合常数是gsqq[16] (gsqq代表标量介子-夸克耦合常数,其中q表示夸克,s表示标量介子),用p'和p″分别表示夸克的入射和出射四动量。交换的标量介子质量为m,四动量为k,对应的费曼图如图 3所示。根据图 3,由费曼规则写出的动量空间的T矩阵元为:
|
| 图 3 交换标量介子的费曼图 Fig. 3 Feynman diagram of exchanging scalar meson |
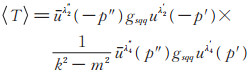
|
(1) |
其中,λ'2、λ″2分别表示入射和出射轻夸克q2的螺旋度,λ'4、λ″4分别表示入射和出射轻夸克q4的螺旋度,uλ(p)、uλ(p)分别表示夸克在定螺旋度λ下对应的狄拉克旋量以及反旋量。
考虑非相对论性约化,将狄拉克旋量近似为:
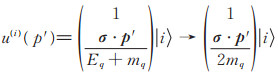
|
(2) |
其中,mq表示夸克质量,σ是泡利自旋矩阵,p'是夸克动量矢量,|i〉表示夸克i的波函数。
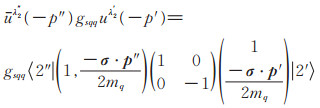
|
(3) |
对于q4也有同样的表达式,再利用介子的动量矢量k=p″-p'和(σ·a)(σ·b)=a·b+iσ·(a×b),对(2)式加以约化,最后可得动量空间下的有效势:
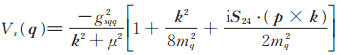
|
(4) |
其中,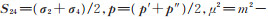
为得到位置空间的有效势需要对(4)式进行傅里叶变换。但当存在交换势如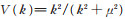
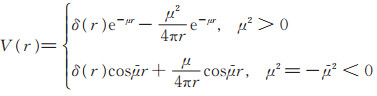
|
(5) |
其中,r表示球坐标系中的半径。
δ函数项出现的原因是直接把强子当作点粒子处理,而没有考虑强子的内部结构。因此需要在费曼图的顶点函数处引入反映强子内部结构的形状因子,其形式为[16~18]:
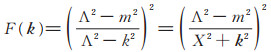
|
(6) |
其中,X2=Λ2-m2,Λ是截断参数,注意k和k分别表示介子的四动量和动量矢量。形状因子考虑了费曼图的高阶贡献,其中涉及到圈图动量的积分,积分动量在趋于无穷大时往往造成积分的发散,所以一般的做法是在某个大动量Λ处对积分进行截断,以压低大动量转移的贡献。大动量意味着短距离,Λ的值和强子的大小(近似为1/Λ)直接相关,在核子-核子相互作用中通常取在0.8~1.5 GeV范围内。由于本文讨论的是重味介子,其半径比核子更小,Λ的取值应该更大一些。同时当截断参数取值变大时,意味着考虑更多的动量交换,分子态间的重味介子吸引力更强,距离更小。当中间态足以形成分子态时,由3.2节可知,分子态的束缚能的确随着截断参数的增加而缓慢增加,均方根半径也随之变小。
本文用修正的顶点函数等效地描述复杂的胶子-夸克过程,在赝标玻色子和矢量玻色子中都引入形状因子的贡献,树图的顶点函数分别为igpqqγ5和
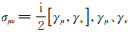
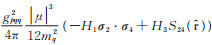

|
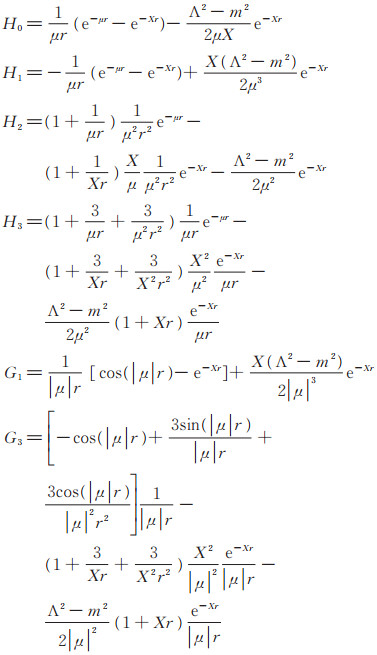
|
其中,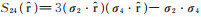
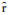
本文采用非相对论薛定谔方程对强子分子态内部的重味介子相互作用进行近似。求解薛定谔方程的关键为势函数的选取,本文将1.2节得到的位置空间OBEP作为势函数的输入,其中OBEP的基本参数输入包括夸克和介子的质量和各耦合常数(如表 1),粒子的质量由实验得到,可采用粒子数据表(particle data group,PDG)所给出的数据[19],而表 1中的fvqq和gpqq,gsqq,gvqq是各个类型的玻色子-夸克耦合常数,目前没有确切的数值,但人们已通过大量实验和唯象模型分析,得到玻色子-核子耦合常数的数值,通过Goldberger-Treiman关系[18, 20]可以推导出这两类耦合常数之间的关系:
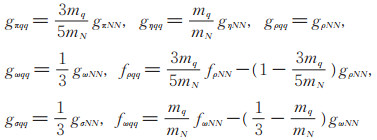
|
(7) |
其中,mN是核子的质量,fωNN、fρNN、gπNN、gηNN、gρNN、gωNN、gσNN均是玻色子-核子耦合常数,fωqq、fρqq、gπqq、gηqq、gρqq、gωqq、gσqq是玻色子-夸克耦合参数。等号右边的耦合常数均是已知的。
3 Y(4390)在D1D*/D1D*系统下的势函数计算本节将考虑Y(4390)的结构,写出其系统波函数;并将1.2节得到的一般OBEP势应用在给定的基矢上,计算势函数的矩阵元,将该势函数代入薛定谔方程中,数值求解该方程。
3.1 OBEP模型机制下对Y(4390)的结构分析对于JPC=1--的Y(4390)粒子,若作为D1D*/D1D*的强子分子态来处理,则它可能处于S波或D波轨道态,同时考虑到组分不带电的D10D*0和组分带正负电的D1+D*-的阈值不同,存在着同位旋破坏,并考虑到电荷共轭变换守恒,可以将D1D*/D1D*系统的波函数写为如下形式[21, 22]:
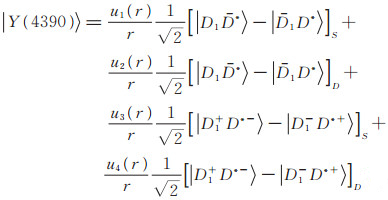
|
(8) |
其中,下标S和D分别表示S波和D波,u1(r)、u2(r)、u3(r)、u4(r)表示对应的空间波函数,相应的基矢为[20]:
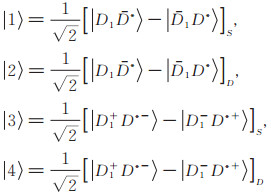
|
(9) |
因为目前实验还没有确定Y(4390)的同位旋量子数,所以在构造(9)式时还考虑到同位旋对称性破缺的可能,如果轨道波函数u1和u3,u2和u4的符号都相同,则系统同位旋I=0主导;如果符号都相反,则同位旋I=1主导。
总的相互作用势V应该是表 1中交换粒子势的总和,同时考虑到介子的G宇称[20],有:
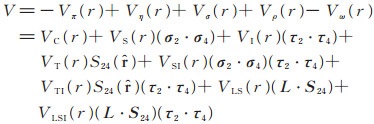
|
(10) |
由此求出相互作用势的矩阵元VY(4390)[20],其中VC表示势能的常数项,VS和VSI分别表示与同位旋无关和相关的由自旋算符σ2·σ4引起的自旋-自旋相互作用项,VI是同位旋作用项,VT和VTI分别是与同位旋无关和相关的张量力项,VLS和VLSI分别表示与同位旋无关和相关的自旋-轨道相互作用。

|
(11) |
在(11)式,位置空间各个有效势V分别是:
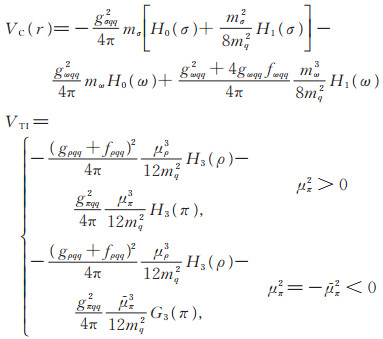
|

|
值得说明的是,μ2=m2-k02中的m、k0作为输入参数,其中k02对应着初态和末态的夸克的静止能差,比如在(11)式的4×4方阵左上角的2×2方块阵中,k02=(mD*0-mD10)2,而其余的方块阵由于同位旋的破缺,D*+D1-会与D*D1存在质量差,k02的取值会有所不同。
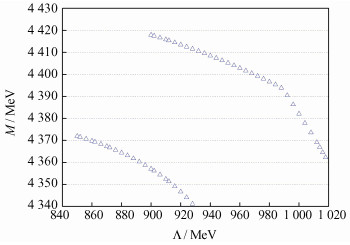
3.2 数值结果和讨论本文将所得到的总的交换玻色子的有效势((11)式),利用FORTRAN程序包FESSDE 2.2,计算四耦合道的径向薛定谔方程[23, 24]的数值解。FESSDE 2.2利用有限元法可以精确求解二阶偏微分方程的本征值问题,将每一个Λ作为程序的参数输入,通过数值求解将得到对应的本征矢和本征能量,即系统的总能量M。二阶偏微分方程的本征解有很多,但由于分子态的势能是负的,本文在D1D*的阈值(4 430 MeV)之下寻找方程的本征值;同时考虑到截断参数应大于最大的中间玻色子质量(mω=782 MeV),以及文献[8]中氘核的Λ取800 MeV,对于重味强子态的Λ应该更大一些,所以本文从850 MeV开始取值,以大约4 MeV的步长,绘制束缚态质量M随Λ变化的趋势(图 4),得到的主要数值解如表 2所示。
|
| 图 4 束缚态质量随截断参数Λ变化关系 Fig. 4 The variation of bound state mass with the cutoff paramater Λ |
| A/MeV | M/MeV | rrms/fm | 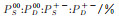 |
| 900 | 4 417.87 | 1.02 | 51.0:1.1:47.2:0.7 |
| 920 | 4 413.80 | 0.88 | 49.1:1.3:49.1:0.5 |
| 950 | 4 405.74 | 0.77 | 49.2:1.1:49.2:0.5 |
| 980 | 4 396.65 | 0.70 | 49.7:0.9:48.8:0.6 |
| 990 | 4 392.46 | 1.41 | 36.4:18.6:26.8:18.2 |
| 992 | 4 390.45 | 1.44 | 32.7:21.0:26.1:20.2 |
图 4绘制了Λ取值为850~1 020 MeV时,在阈值4 430 MeV之下方程的所有根。首先,可以看到,M随Λ的增加基本呈现平缓下降的变化趋势,符合1.2节的预期;其次,在Λ=850 MeV时,方程只有一个根,而在920 MeV左右方程有两个根。图 4左下的那些根对应最低能级,右上的那些根对应第一能级,而两个能级都可能存在束缚态。
对于图 4左下角的最低能级区域,在Λ=920 MeV附近寻找,即M~4 346.7 MeV,可以对应于BaBar合作组[25]发现的质量为4 346 MeV的粒子Y(4360),而实验上已经确认量子数为JPC=1--,符合本文在3.1节对基矢的构造要求。文献[26]也曾用单π交换势模型,将Y(4360)解释为D1D*系统的分子态。
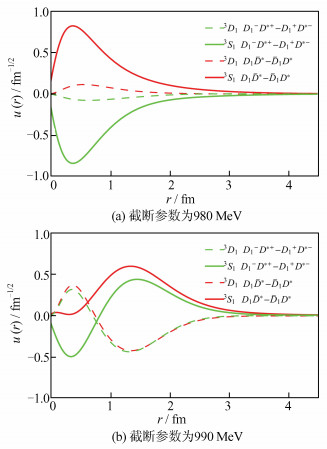
为了找到质量符合Y(4390)的根,本文在表 2中给出了图 4右上角的第一能级M与Λ,以及对应的4个本征轨道波函数的相对占比,并由波函数直接计算出均方根半径(与波函数的平均半径有关)。总体而言,由表 2可知,随Λ的增大,均方根半径变小,符合1.2节的预期。然而Λ取值为990 MeV与980 MeV时,均可以得到质量接近Y(4390)的两个束缚态,但是均方根半径出现很大的不同,Λ为980 MeV时,对应的均方根半径rrms(0.70 fm)比Λ为990 MeV时对应的数值(1.41 fm)更小。Λ为980 MeV时,不同的组分比例中,S波占主要成分,组分|1〉的S波和组分|3〉的S波占据了波函数的98.5%,轨道波函数处于基态,分子态的结合将更稳定更紧密;而Λ为990 MeV的态的均方根半径更大,分子态结合得较为松弛,且有S-D波的大成分混合,即组分|1〉的S波和组分|2〉的D波比例为36.4%:18.6%,组分|3〉的S波和组分|4〉的D波比例为26.8%:18.2%,即它处于激发态。为了更详细地进行观察,图 5给出了当截断参数取980 MeV和990 MeV时,系统各组分的空间波函数的分布。图 5中u(r)表示与4个基矢相关联的轨道波函数,r表示轨道半径;3S1、3D1表示S波和D波函数在总角动量J=1下的轨道态。
|
| 图 5 不同截断参数情况下系统各组分的空间波函数随r的变化 Fig. 5 Variation of spatial wave functions of system components with r under different cutoff parameters |
由图 5可知,当Λ为980 MeV时系统的态主要处于基态,3S1的轨道波函数占主导,且重味介子结合紧密,表现得更稳定,更可能形成强子分子态,符合本文最初的预期;同时结合(8)式可知,3S1的轨道波函数u1和u3,以及3D1的轨道波函数u2和u4具有相反的符号,且u1和u3的占比相近,说明系统处于I=1的同位旋多重态中。而Λ为990 MeV时系统的态不是一个基态,推测是3S1和3D1混合构成的激发态,激发态的粒子在非相对论中往往容易衰变,导致态不够稳定;结合表 2可知,Λ为990 MeV时,均方根半径较大,该束缚态束缚较松;同时u1和u3、u2和u4的符号总体相同,对应系统的I=0部分占主导。综上考虑,本文认为对应截断参数为980 MeV,D1D*/D1D*系统形成的质量约4 396.65 MeV的稳定分子束缚态,将更适合作为Y(4390)的解释。
4 结论本文采用单玻色子交换势模型从非相对论的薛定谔方程近似的角度研究了JPC=1--的D1D*/D1D*系统,并数值求解薛定谔方程,得到系统的束缚态质量和波函数,发现在截断参数Λ为980 MeV时,系统的态质量为4 396.65 MeV,处于轨道3S1态占主导的基态,均方根半径约为0.70 fm,重味介子结合紧密,构成了一个稳定的束缚态,本文希望将这个态用于解释新粒子Y(4390),比文献[13]使用Bethe-Salpeter方程近似得到的质量数值(4 384 MeV)更接近实验峰值。此外,本文还预言该粒子的系统中各组分的轨道波函数所占比等信息,并认为Y(4390)很可能属于同位旋I=1的多重态,是Y(4360)在更高能级下的表现。但是目前没有测量到Y(4390)的同位旋,这些预言有待实验数据的进一步确认。最后,本文得出结论: Y(4390)很可能是量子数为1--的D1D*/D1D*的强子分子态。
| [1] |
ABLIKIM M, ACHASOV M N, AHMED S N A, et al. Evidence of two resonant structures in e+e- → π+π-hc[J]. Physical Review Letters, 2017, 118: 092002-1-092002-8. DOI:10.1103/PhysRevLett.118.092002 |
| [2] |
MIZUK R, CHISTOV R, ADACHI I, et al. Observation of two resonance-like structures in the π+χc1 mass distribution in exclusive B0→K-π+χc1 decays[J]. Physical Review D, 2008, 78: 072004-1-072004-14. DOI:10.1103/PhysRevD.78.072004 |
| [3] |
BONDAR A, GARMASH A, MIVUK R, et al. Observation of two charged bottomonium-like resonances in Y(5S) decays[J]. Physical Review Letters, 2012, 108: 122001-1-122001-6. DOI:10.1103/PhysRevLett.108.122001 |
| [4] |
GARMASH A, BONDAR A, KUZMI A, et al. Amplitude analysis of e+e- → ϒ(nS)π+π-at 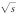 =10.865 GeV[J]. Physical Review D, 2015, 91: 072003-1-072003-16. DOI:10.1103/PhysRevD.91.072003 =10.865 GeV[J]. Physical Review D, 2015, 91: 072003-1-072003-16. DOI:10.1103/PhysRevD.91.072003 |
| [5] |
IOFFE B L. Calculation of baryon masses in quantum chromo-dynamics[J]. Nuclear Physics B, 1981, 188: 317-341. DOI:10.1016/0550-3213(81)90259-5 |
| [6] |
DING G J. Are Y(4260)and Z2+(4250)D1Dor D0D* hadronic molecules?[J]. Physical Review D, 2009, 79: 014001-1-014001-17. DOI:10.1103/PhysRevD.79.014001 |
| [7] |
JAFFE R L. Color non-singlet spectroscopy[J]. Physical Review D, 2005, 72: 074508-1-074508-12. DOI:10.1103/PhysRevD.72.074508 |
| [8] |
WANG Z G. Analysis of the Y(4220)and Y(4390) as molecular states with QCD sum rules[J]. Chinese Physics C, 2017, 41(8): 083103-1-083103-8. DOI:10.1088/1674-1137/41/8/083103 |
| [9] |
WANG Z G. Vector tetraquark state candidates: Y(4260/4220), Y(4360/4320), Y(4390)and Y(4660/4630)[J]. The European Physical Journal C, 2018, 78(6): 518. DOI:10.1140/epjc/s10052-018-5996-5 |
| [10] |
HE J, CHEN D Y. Interpretation of Y(4390)as an isoscalar partner of Z(4430)from D*(2010)D1(2420)interaction[J]. The European Physical Journal C, 2017, 77(6): 398. DOI:10.1140/epjc/s10052-017-4973-8 |
| [11] |
THOMAS C E, CLOSE F E. Is X(3872)a molecule?[J]. Physical Review D, 2008, 78: 034007-1-034007-12. DOI:10.1103/PhysRevD.78.034007 |
| [12] |
YUKAWA H. On the interaction of elementary particles Ⅰ[J]. Supplement of the Progress of Theoretical Physics, 1935, 17: 48-57. DOI:10.1143/PTPS.1.1 |
| [13] |
TORNQVIST N A. Possible large deuteron-like meson meson states bound by pions[J]. Physical Review Letters, 1991, 67(5): 556-559. DOI:10.1103/PhysRevLett.67.556 |
| [14] |
TORNQVIST N A. From the deuteron to deusons, an analysis of deuteron-like meson-meson bound states[J]. Zeitschrift für Physik C Particles and Fields, 1994, 61(3): 525-537. DOI:10.1007/BF01413192 |
| [15] |
SCADRON M D. Advanced Quantum Theory and Its Applications Through Feynmann Diagrams[M]. New York: Springer-Verlag, 1979: 228.
|
| [16] |
MACHLEIDT R, HOLINDE K, ELSTER C. The bonn meson exchange model for the nucleon nucleon interaction[J]. Physics Reports, 1987, 149(1): 1-89. DOI:10.1016/S0370-1573(87)80002-9 |
| [17] |
MACHLEIDT R. The meson theory of nuclear forces and nuclear structure[J]. Advances in Nuclear Physics, 1989, 19: 189-376. |
| [18] |
宁平治. 原子核物理基础:核子与核[M]. 北京: 高等教育出版社, 2003: 224. NING P Z. Fundamental Nuclear Physics: Nucleons and Nuclei[M]. Beijing: Higher Education Press, 2003: 224. (Ch). |
| [19] |
PATRIGNANI C, AGASHE K, AIELLI G, et al. Review of particle physics[J]. Chinese Physics C, 2016, 40(10): 100001-1-100001-5. DOI:10.1088/1674-1137/40/10/100001 |
| [20] |
DING G J, LIU J F, YAN M L. Dynamics of hadronic molecule in one-boson exchange approach and possible heavy flavor[J]. Physical Review D, 2009, 79: 054005-1-054005-18. DOI:10.1103/PhysRevD.79.054005 |
| [21] |
LI M T, WANG W L, DONG Y B. A study of one S-and one P-wave heavy meson interaction in a chiral quark model[J]. Communications in Theoretical Physics, 2015, 63(1): 63-70. DOI:10.1088/0253-6102/63/1/11 |
| [22] |
LI M T, WANG W L, DONG Y B, et al. Zb(10650) and Zb(10610)states in a chiral quark model[J]. Journal of Physics G: Nuclear and Particle Physics, 2013, 40(1): 1-10. DOI:10.1088/0954-3899/40/1/015003 |
| [23] |
ABRASHKEVICH A G, ABRASHKEVICH D G, KASCHIEV M S, et al. Finite-element solution of the coupled-channel Schrodinger equation using high-order accuracy approximations[J]. Computer Physics Communications, 1995, 85: 40-64. DOI:10.1016/0010-4655(94)00106-C |
| [24] |
ABRASHKEVICH A G, ABRASHKEVICH D G, KASCHIEV M S, et al. FESSDE, a program for the finite-element solution of the coupled-channel Schrodinger equation using high-order accuracy approximations[J]. Computer Physics Communications, 1995, 85(1): 65-81. DOI:10.1016/0010-4655(94)00107-D |
| [25] |
AUBERTETB, BARATE R, BONA M, et al. Evidence of a broad structureat an invariant mass of 4.32 GeV/c2 in the reaction e+e- → π+ π-ψ(2S) measured at BaBar[J]. Physical Review Letter, 2007, 98: 212001-1-212001-7. DOI:10.1103/PhysRevLet.98.212001 |
| [26] |
CLOSE F, DOWNUM C, THOMAS C E. Novel charmonium and bottomonium spectroscopies due to deeply bound hadronic molecules from single pion exchange[J]. Physical Review D, 2010, 81: 074033-1-074033-12. DOI:10.1103/PhysRevD.81.074033 |
 2019, Vol. 65
2019, Vol. 65





