文章信息
- 王坤, 黄勃, 曾国辉, 李晓斌
- WANG Kun, HUANG Bo, ZENG Guohui, LI Xiaobin
- 基于改进RRT-Connect的快速路径规划算法
- Faster Path Planning Based on Improved RRT-Connect Algorithm
- 武汉大学学报(理学版), 2019, 65(3): 283-289
- Journal of Wuhan University(Natural Science Edition), 2019, 65(3): 283-289
- http://dx.doi.org/10.14188/j.1671-8836.2019.03.008
-
文章历史
- 收稿日期:2018-07-18

2. 江西省经济犯罪侦查与防控技术协同创新中心, 江西 南昌 330103;
3. 上海应用技术大学 电子与电气工程学院, 上海 200235
2. Center of Economic Crime Detection and Prevention and Control Technology Collaborative Innovation, Nanchang 330103, Jiangxi, China;
3. College of Electrical and Electronic Engineering, Shanghai Institute of Technology, Shanghai 200235, China
路径规划是移动机器人领域的一项热门研究,目前已在自动驾驶[1]、自主探测[2]、计算生物学[3]、图形动画学[4]等领域获得广泛应用。路径规划的最终目的是寻找到一条可以从起始点到目标点的无碰撞路径[5],该路径可以保证移动机器人在移动过程中不会与障碍物发生碰撞,同时这条路径需要满足距离最近、用时最短或耗能最低等指标中的一种或几种。目前在路径规划方面已经出现了众多可行的算法[6~12]。在低维空间中,这些算法尚有一定的优势,但在高维空间中,由于计算的复杂性,其生成路径的效率较低。
为解决高维空间中的路径规划问题,基于采样的路径规划算法被提出并得到发展,其代表算法是LaValle等提出的RRT[13]算法,该算法不需要对环境进行建模,只需要通过随机采样生成随机树的方式来探索整个空间,随机点的选取保证了搜索路径的全局性,从而使算法具有概率完备[14]的特点。由于该算法可以大幅降低高维空间路径规划的计算量,在提出后受到了众多学者的关注。但该算法存在不足:1)由于扩展的随机性,使得算法收敛速度缓慢,路径生成效率低;2)生成的路径只是可行路径,而非最优或次优[15];3)路径生成中没有采用平滑处理,导致生成的路径较为粗糙,不适合机器人的实际移动。
针对RRT算法存在的不足,国内外学者纷纷提出了一系列的改进算法,其中由Kuffner等提出的RRT-Connect算法[16]在规划效率上取得明显进步。该算法通过在起始点和目标点同时生成两棵随机树的方式,用以加速算法的收敛。本文基于RRT- Connect算法,通过在起始点和目标点中间选取第三节点以生成四棵探索树的方式来提高算法的收敛速度,同时在算法扩展过程中,加入启发函数,使随机树在扩展中可以自适应调节步长,并通过引入目标偏置策略,使改进后的算法在无障碍空间中能够以最快速度探索未知区域,增加扩展效率。
1 RRT与RRT-Connect算法RRT算法作为单一查询算法,不需要预先对整个构型空间进行采样与存储,而是通过函数迭代的方式探索整个状态空间[17]。
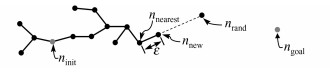
图 1中,ninit、ngoal分别为路径的起始点和目标点,nrand为状态空间
|
| 图 1 RRT算法扩展 Fig. 1 RRT extension |
当随机采样函数通过对空间随机采样获得nrand后,RRT算法便以该点为下一步扩展方向向外扩展,扩展过程中有以下几种情况:1)当nrand与nnearest之间的距离大于ε时,则在nrand与nnearest之间的连线上取一点nnew插入到树中,记为Reached;2)当nrand与nnearest之间的距离小于ε时,则直接将nrand插入到树中,记为Advanced;3)在扩展中遇障,则舍弃原先的扩展方式,并重新生成随机点nrand,记为Trapped。
RRT算法由RRT建树(BU_RRT(ninit))和RRT扩展(EXT(T,nrand))两部分组成。RRT建树过程如下:
| BU_RRT(ninit)//RRT建树 |
| 1 T.init(ninit); |
| 2 for k = 1 to K do |
| 3 nrand←SampleNode(); |
| 4 EXT(T, nrand); |
| 5 Return T |
RRT扩展如下:
| EXT(T,nrand)// RRT扩展 |
| 1 nnearest← NearestNode(nrand,T); |
| 2 if NewNode(nrand,nnearest,nnew) |
| 3 then |
| 4 T.V←nnew; |
| 5 T.E←(nnew,nnearest); |
| 6 if dist(nnew,nnearest)) < ε |
| 7 then |
| 8 nnew←nrand; |
| 9 Return Reached; |
| 10 else |
| 11 Return Advanced; |
| 12 Return Trapped; |
其中,T表示随机树,T.V表示随机树中的节点,T.E表示随机树顶点之间的路径。BU_RRT函数在状态空间中采样随机点,确定扩展方向。通过循环调用EXT函数来扩展未知空间,最终返回生成的搜索树。EXT函数主要用于扩展随机树。根据设定步长判断nnew节点的位置,并将新节点添加到树中。
由于RRT算法在扩展中的随机性,导致其存在收敛速度缓慢,为了提高RRT算法的收敛速度,Kuffner和LaValle提出了RRT-Connect算法[16],该算法分别在起始点和目标点构建两棵并行的随机树,并在每次迭代过程中,使两棵树分别朝着彼此的方向交替扩展,且在扩展中引入了具有贪婪特性的CON函数,实现随机树的快速扩展。
RRT-Connect建树过程如下:
| BU_RRT-Con(ninit, ngoal) |
| 1 T1.init(ninit); T2.init(ngoal); |
| 2 for k = 1 to K do |
| 3 nrand←SampleNode(); |
| 4 if (EXT(T1, nrand) ≠ Trapped) |
| 5 then |
| 6 if (CON(T2, nnew)=Reached) |
| 7 then |
| 8 Return PATH(T1, T2); |
| 9 SWAP(T1, T2); |
| 10 Return Failed; |
其中:T1、T2表示分别从起始点ninit和目标点ngoal生成的随机树:CON函数如下:
该算法首先调用EXT函数,从起始点ninit出发,通过EXT扩展生成节点nnew。此后,T2开始以nnew为方向进行扩展,在T2扩展中,如果没有发生碰撞或者nnew与当前扩展节点之间的距离不小于步长ε时,T2通过调用CON函数来实现快速向nnew扩展,当扩展过程中出现障碍物时,T2停止扩展,T1以当前T2的终止点为目标点开始扩展,通过SWAP函数使两棵树交替扩展,最终相遇并连接。
2 DRRT-Connect算法RRT -Connect算法虽对探索树的扩展速度有很大幅度的提高,但在如防反弹袭击、无人机避障等一些需要高灵敏度的领域仍存在规划效率低的问题。基于上述原因,本文提出的DRRT-Connect,对RRT-Connect算法做出以下两点改进:首先,由于RRT-Connect只能同时生成两棵树,所以DRRT -Connect算法在RRT -Connect算法的基础上引入第三节点,使算法可以同时生成四棵树,以达到加倍扩展RRT-Connect的效果;其次,DRRT-Connect在RRT-Connect算法的基础上加入可自适应调节步长的启发函数,使随机树在探索无障碍空间时的扩展效率更高,同时在算法执行时,引入目标偏置策略,使算法的扩展更具方向性,进一步加速随机树的扩展,减少迭代次数,以下对算法改进原则做详细介绍。
2.1 第三节点选择方式为使DRRT-Connect算法可以实现四棵树同时扩展,需要选择一个第三节点。为提高算法效率,本文以起始点与目标点连线的中心点作为第三节点,假设起始点在构型空间中的坐标为(x1,y1),目标点的坐标为(x2,y2),则求取第三节点ncenter (x3,y3)坐标的公式为:
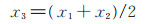
|
(1) |
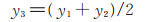
|
(2) |
RRT-Connect算法中步长是给定值,这种给定步长在探索无障碍空间时会限制随机树的扩展速度[18]。本文在DRRT-Connect算法中加入了自适应调节步长的函数,具体为:随机树以初始步长ε探索未知空间,当扩展至新节点时,如在该节点处没有发生碰撞且未与另一棵树相连,则在下一次的扩展中,随机树将在原始步长上增加一个步长ε的宽度继续扩展,以此类推;当扩展中发生碰撞时,则将步长调节为原始步长ε,然后按步长ε进行扩展。
2.3 避障原则由于环境的复杂性,在DRRT-Connect执行过程中会遇到障碍物的情况,所遇障碍物主要包括第三节点生成时遇障与随机树扩展时遇障两种情况。
对于第一种情况,在DRRT-Connect采样第三节点之前,首先进行障碍检测,当第三节点位于障碍物中时,为了提高路径生成效率,则直接选择舍弃第三节点,采用RRT-Connect进行扩展。对于第二种遇障情况,即DRRT-Connect在扩展中遇到障碍物,当此时只有一棵树处于障碍物时,则采用交换扩展顺序的方式开始扩展另一棵树,若在扩展中两棵树同时遇障,此时则调用随机点生成函数,使其在构型空间中随机采样,然后选择较短树以该点为方向向前扩展一步,如脱离障碍物,然后以目标点为方向继续扩展,若该点与目标点仍存在障碍物,则继续调用该函数进行扩展随机树,直至摆脱障碍物。
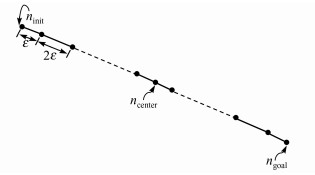
2.4 算法实现基于以上三点原则,DRRT-Connect算法构建过程如图 2所示,首先,算法分别以ninit、ngoal和ncenter为扩展树的起点,然后ninit、ngoal皆以中间点ncenter为目标点,同时并行向目标点扩展,而此时中间点ncenter则分别以ninit、ngoal为目标点开始扩展,四棵树同时并行生长。在扩展中,当第一步扩展没有遇到障碍物,则在下一步将扩展步长增加ε,当在扩展中遇到障碍物时,则将步长恢复至初始状态。
|
| 图 2 DRRT-Connect扩展 Fig. 2 DRRT-Connect extension |
M_EXT函数为改进的随机树扩展函数,该函数主要目的是通过改进原始EXT扩展函数将原先步长固定的扩展方式改为步长随扩展状态的不同进行自适应调节,即当此时扩展状态为Advanced时,在下一次扩展中,算法将在原始步长基础上增加一个ε步长,以此类推。如果下次扩展中返回状态仍为Advanced,则在上次步长基础上继续增加ε,若下次扩展中返回状态为Trapped,说明在扩展中随机树遇到障碍物,则首先将步长还原为原始步长,扩展至再次检测到障碍物。M_EXT函数如下:
| M_EXT(T, nrand) |
| 1 Step←ε; |
| 2 nnearest←NearestNode(nrand, T); |
| 3 if NewNode(nrand, nnearest, nnew) |
| 4 then |
| 5 T. V←nnew; |
| 6 T. E←(nnew, nnearest); |
| 7 if dist(nnew, nnearest) < Step |
| 8 then |
| 9 nnew←nrand; |
| 10 Return Reached; |
| 11 else |
| 12 Step←Step +ε; |
| 13 Return Advanced; |
| 14 Step←ε; |
| 15 Return Trapped; |
BU_DRRT-Con函数为DRRT-Connect算法建树过程,算法首先调用M_EXT函数,分别将从起始点ninit开始的随机树T1和从目标点ngoal开始的随机树T2向外扩展一步,生成nnew1和nnew2。此后,通过引入目标偏置策略,使算法以ncenter为起点,分别以nnew1和nnew2为目标点,向外扩展随机树T3和T4,并调用CON函数,将两树快速扩展,直至在扩展过程中遇到障碍后停止,通过SWAP函数交换扩展顺序,使得T1、T2以T3、T4停止点为目标点进行扩展。如此循环,直至四棵树连接,生成一条完整路径。
| BU_DRRT-Con(ninit, ncenter, ngoal) |
| 1 T1. init(ninit);T2.init(ngoal);T3.init(ncenter);T4.init(ncenter); |
| 2 for k = 1 to K do |
| 3 nrand ← SampleNode(); |
| 4 if(M_EXT(T1,ncenter)≠Trapped,M_EXT(T2,ncenter)≠Trapped) |
| 5 then |
| 6 if(CON(T3,nnew1)=Reached,CON(T4,nnew1)=Reached) |
| 7 then |
| 8 Return PATH(T1,T2,T3,T4); |
| 9 SWAP(T1,T3),SWAP(T2,T4); |
| 10 Return Failed; |
为了对DRRT-Connect算法进行性能比较,本实验对图 3所示的地图进行仿真,地图中空白区域代表无障碍物区,红色区域代表障碍物区。

|
| 图 3 仿真地图 Fig. 3 Simulation map |
仿真所使用的硬件平台为Intel Core(TM)i5- 4200M 2.5GHz CPU,RAM 6GB,算法通过Python编程实现。
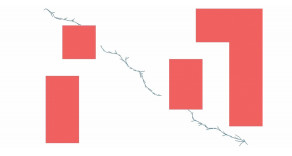
实验中,分别以RRT、RRT* [19]和RRT-Connect作为改进算法的比较对象,通过比较证明DRRT- Connect性能的优越性。图 4为DRRT-Connect算法随机树探索过程,从图 4中可以看出,改进后的算法分别以起始点、目标点以及中间第三节点为起点同时生成四棵随机树,从而加快对未知区域的探索,以加速最终路径生成。
|
| 图 4 DRRT-Connect随机树扩展过程 Fig. 4 Extension process of DRRT-Connect |
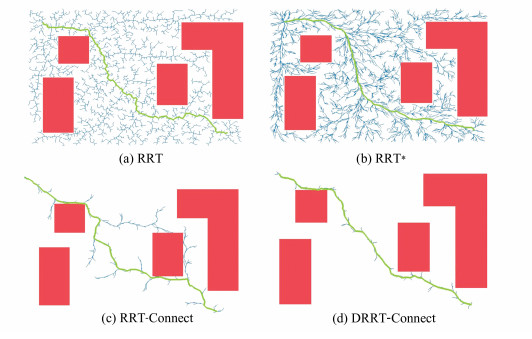
图 5中(a)、(b)、(c)、(d)为DRRT-Connect算法与RRT、RRT*、RRT-Connect三种算法的仿真结果图。从图 5中可以看出,相比于其他三种算法,DRRT -Connect算法所生成的路径具有平滑性好且具有一定的方向性。该结果充分展示出通过四棵树生成的路径在应用到实际场景中时,具有较好的表现。
|
| 图 5 仿真结果对比 Fig. 5 Comparison of simulation results |
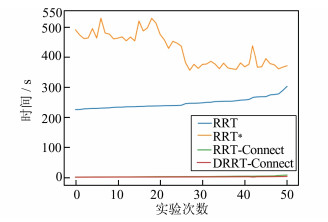
在实验中,分别对每种算法进行50次仿真验证,图 6所示为4种算法寻路时间对比图。从图 6中可以看出,DRRT-Connect算法在50次的仿真实验中耗时远远低于RRT与RRT*算法,相较于RRT- Connect算法而言,由于坐标精度原因,无法明显观测出速度的提升,DRRT-Connect算法平均路径生成时间将在下文分析。
|
| 图 6 寻路时间对比图 Fig. 6 Comparison of pathfinding times |
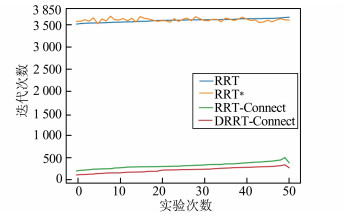
图 7所示为4种算法在生成路径中所需迭代次数示意图,由于自适应步长的加入,DRRT-Connect算法在迭代次数上相较于RRT-Connect算法也有较为明显优势。
|
| 图 7 迭代次数对比图 Fig. 7 Comparison of iteration times |
表 1所示为在50次实验中4种算法的迭代次数、路径长度与生成路径所花费时间的平均值,从数据中可以更为直观的看出,相比于RRT与RRT*算法,DRRT-Connect算法在迭代次数与路径生成时间上都有非常明显的优势;相比于RRT-Connect算法,DRRT-Connect算法在路径规划时间上只需要RRT -Connect算法的50%,在迭代次数上相比RRT-Connect算法降低了32.3%,大大提高了路径的生成效率。
| 算法 | 迭代次数 | 路径长度 | 生成时间/s |
| RRT | 3 591 | 912. 34 | 246. 42 |
| RRT* | 3 604 | 807. 28 | 425. 05 |
| RRT-Connect | 316 | 857. 07 | 2. 92 |
| DRRT-Connect | 214 | 851. 72 | 1. 46 |
在上述实验结果中,改进后的DRRT-Connect算法在迭代次数与路径生成时间上的性能均明显优于改进算法,而在路径长度上相较于RRT*算法不具有明显优势。
迭代次数降低的原因归功于算法中引入的目标偏置策略,该策略使原始RRT算法中使用的随机采样扩展变为具有目标性的扩展方式,将原来每一步扩展都需要首先进行随机采样的方式变为以随机树停止位置作为目标点,直接使算法朝向目标点扩展一步,只有当向目标点扩展时遇到障碍物,才调用随机采样函数,从而使随机树摆脱障碍物,保证算法的概率完备性。
路径生成速度大幅提高的原因主要是DRRT- Connect算法将RRT-Connect算法的两棵随机树扩展方式变为四棵树通过扩展,大幅加速算法生成路径的效率;在无障碍空间中,算法调用自适应步长调节函数,该函数与目标偏置策略相结合,可以使随机树更高效的向目标点进行探索,达到提高路径生成效率的期望。
DRRT-Connect算法在生成路径长度上并未获得提升,主要原因在于DRRT-Connect算法以RRT -Connect算法为基础,并未考虑路径的最优性,而是以提升路径生成效率为目标。通过自适应步长调节函数,可以在一定程度上提高路径的平滑性,但并不能很大幅度降低路径长度。
4 结语本文通过对RRT-Connect算法进行改进,提出了一种可以实现同时生成四棵树并且扩展中步长可自适应调节的DRRT-Connect算法,对改进后算法的原理及实现过程进行了详细分析,通过仿真实验结果,验证了改进后的算法相对于其他算法在路径生成效率及路径平滑性上都具有明显提升。
本文所提算法目前主要用于障碍物较少的简单环境下实现快速路径规划,下一步将尝试针对复杂环境下以及第三节点难以选取的情况进行改进,从而提高算法的泛化性,以便更好地满足工程实践的需要。
| [1] |
李学鋆. 基于UTMD的汽车自动驾驶的路径规划寻优算法[J]. 汽车安全与节能学报, 2018, 9(4): 449-455. LI X Y. Path planning optimization-algorithm for a selfdriving vehicle based on UTMD principle[J]. Journal of Automotive Safety and Energy, 2018, 9(4): 449-455. DOI:10.3969/j.issn.1674-8484 (Ch). |
| [2] |
周光明, 贾梦雷, 陈宗海. 移动机器人未知环境自主探测的一种高效算法[J]. 上海交通大学学报, 2005, 39(6): 936-940. ZHOU G M, JIA M L, CHEN Z H. An efficient algo-rithm for mobile robot's autonomous exploration in un-known environments[J]. Journal of Shanghai Jiaotong University, 2005, 39(6): 936-940. DOI:10.16183/j.cnki.jsjtu.2005.06.022 (Ch). |
| [3] |
CORTES L J, JAILLET L, SIMEON T.Molecular dis-assembly with RRT -like algorithms[C] // IEEE International Conference on Robotics and Automation.Washing-ton D C, IEEE, 2007: 3301–3306.DOI: 10.1109/RO-BOT.2007.363982.
|
| [4] |
LIU Y, BADLER N I.Real-time reach planning for ani-mated characters using hardware acceleration[C] // International Conference on Computer Animation and Social Agents.Washington D C: IEEE, 2003: 86–93.DOI: 10.1109/CASA.2003.1199308.
|
| [5] |
张捍东, 陈阳, 吴玉秀. 未知环境下移动机器人实时路径规划[J]. 计算机工程与应用, 2018, 54(19): 140-146. ZHANG H D, CHEN Y, WU Y X. Real time path plan-ning for mobile robot in unknown environment[J]. Computer Engineering and Applications, 2018, 54(19): 140-146. DOI:10.3778/j.issn.1002-8331.1706-0225 (Ch). |
| [6] |
SINGH Y, SHARMA S, SUTTON R, et al.Towards use of Dijkstra algorithm for optimal navigation of an un-manned surface vehicle in a real-time marine environment with results from artificial potential field[J] // The International Journal on Marine Navigation and Safety of Sea Transportation, 2018, 12(1): 125-131.DOI: 10.12716/1001.12.01.14.
|
| [7] |
ANH V L, VEERAJAGADHESWAR P, VINU S, et al. Modified a star algorithm for efficient coverage path planning in tetris inspired self-reconfigurable robot with in-tegrated laser sensor[J]. Sensors, 2018, 18(8): 1-27. DOI:10.3390/s18082585 |
| [8] |
CAO Q, HUANG Y, ZHOU J.An evolutionary artificial potential field algorithm for dynamic path planning of mo-bile robot[C] // IEEE / RSJ International Conference on Intelligent Robots and Systems.Washington D C: IEEE, 2007: 3331-3336.DOI: 10.1109/IR-OS.2006.282508.
|
| [9] |
周凌云, 丁立新, 邹桢苹. 多启发式信息蚁群优化算法求解取样送检路径规划问题[J]. 武汉大学学报(理学版), 2017, 63(5): 439-447. ZHOU L Y, DING L X, ZOU Z P. Ant colony optimiza-tion with multi-heuristic information for sampling inspec-tion path planning problem[J]. Journal of Wuhan University(Natural Science Edition), 2017, 63(5): 439-447. DOI:10.14188/j.1671-8836.2017.05.009 (Ch). |
| [10] |
WANG X, ZHANG G, ZHAO J, et al. A modified membrane-inspired algorithm based on particle swarm optimization for mobile robot path planning[J]. International Journal of Computers Communications and Control, 2015, 10: 732-745. DOI:10.15837/ijccc.2015.5.2030 |
| [11] |
MOHAMED E, ALAA T, ABOUL E H. Bezier curve based path planning in a dynamic field using modified ge-netic algorithm[J]. Journal of Computational Science, 2018(25): 339-350. DOI:10.1016/j.jocs.2017.08.004 |
| [12] |
KURDI M M, DADYKIN A K, ELZEIN I, et al.Proposed system of artificial neural network for positioning and navi-gation of UAV-UGV[C] // 2018 Electric Electronics, Computer Science, Biomedical Engineerings' Meeting(EBBT).Washington D C: IEEE, 2018: 1-6.DOI: 10.1109/EBBT.2018.8391459
|
| [13] |
LAVALLE S M, KUFFNER J J.Randomized kinody-namic planning[C] // Proceedings 1999 IEEE International Conference on Robotics and Automation.Washing-ton D C: IEEE, 2001: 378-400.DOI: 10.1109/RO-BOT.1999.770022.
|
| [14] |
MATTHEW J, ALEJANDRO P. Optimal bidirectional rapidly-exploring random trees[J]. Robotics and Autonomous Systems, 2015(68): 1-11. DOI:10.1016/j.robot.2015.02.007 |
| [15] |
ISLAM F, NASIR J, MALIK U, et al.RRT* -Smart: Rapid convergence implementation of RRT* towards opti-mal solution[C] // IEEE International Conference on Mechatronics and Automation.Washington D C: IEEE, 2012: 1651-1656.DOI: 10.1109/ICMA.2012.6284384.
|
| [16] |
KUFFNER J J, LAVALLE S M.RRT-connect: An effi-cient approach to single-query path planning[C] // Proceedings 2000 IEEE International Conference on Robotics and Automation.Washington D C: IEEE, 2000: 995-1001.DOI: 10.1109/ROBOT.2000.844730.
|
| [17] |
OLZHASl A, HUSEYIN A V.A novel RRT*-Based al-gorithm for motion planning in dynamic environments [C] // IEEE International Conference on Mechatronics and Automation.Washington D C: IEEE, 2017: 1416-1421.DOI: 10.1109/ICMA.2017.8016024.
|
| [18] |
AN B, KIM J, PARK F C. An adaptive stepsize RRT planning algorithm for open-chain robots[J]. IEEE Robotics and Automation Letters, 2018, 3(1): 312-319. DOI:10.1109/lra.2017.2745542 |
| [19] |
KARAMAN S, FRAZZOLI E. Sampling based algorithms for optimal motion planning[J]. The International Journal of Robotics Research, 2011, 30(7): 846-894. DOI:10.1177/0278364911406761 |
 2019, Vol. 65
2019, Vol. 65





