Domain adaptive Takagi-Sugeno-Kang fuzzy classifier based on pseudo-label refinement
-
摘要: Takagi-Sugeno-Kang (TSK)模糊分类器由于其良好的分类性能和可解释性在多个领域有着广泛的应用。针对训练样本和测试样本分布差异所导致的TSK模糊分类器泛化性能下降问题提出了一种基于伪标签细化的域适应TSK模糊分类器。该分类器使用模糊规则前件的非线性映射和后件的线性映射能力构建源域和目标域数据的模糊共享特征空间，并在模糊共享特征空间采用基于图随机游走和标签过滤细化两种策略来提升目标域伪标签质量来更好地进行域对齐。通过在多个公开数据集上的广泛实验，验证了所提出的域适应TSK模糊分类器不仅具备可靠的分类性能，还具有良好的可解释性。Abstract: The Takagi-Sugeno-Kang (TSK) fuzzy classifier (FC) has been widely applied to various fields owing to its excellent classification performance and interpretability. To address the degradation of the generalization performance of this TSK TSK FC caused by the differences in the distributions of the training and test samples, a domain adaptive (DA) pseudo-label refinement (PLR)-based TSK FC (DA-TSK-PLR-FC) is proposed. This classifier leverages the nonlinear and linear mapping capabilities of the antecedent and consequent parts in fuzzy rules to construct a fuzzy shared feature space for source and target domain data. In this fuzzy shared feature space, graph-based random walking and label filtering refinement were applied to enhance the pseudo-label quality in the target domain, thereby enhancing the effectiveness of the domain alignment. Further, extensive experiments using multiple public datasets reveal that the proposed DA-TSK-PLR-FC achieves reliable classification performance and good interpretability.
-
域适应[1-2]是迁移学习的一个重要分支，主要用于解决在训练数据（源域）和测试数据（目标域）分布不一致情况下如何提高模型的泛化能力。根据目标域数据标签是否可以获取，域适应方法可以分为半监督域适应(semi-supervised domain adaptation, SSDA)[3]和无监督域适应(unsupervised domain adaptation, UDA)[4]。相比SSDA，UDA应用更为广泛。现有的UDA研究中域对齐主要采用两种方式，即子空间学习[5-7]和分布对齐[8-9]。子空间学习通过子空间变换对齐不同域的子空间，以获得更好的数据表示。分布对齐旨在减少域之间数据的边缘或条件概率分布差异。最初，Pan等[8]引入核函数，将源域和目标域数据映射到高维空间，并通过最小化最大均值差异(maximum mean discrepancy, MMD)来降低两域的数据边缘分布差异。在此基础上，Long等[9]进一步设计了条件概率分布最小化策略。此后，在学习共享特征空间时，核函数成为将原始数据映射到高维空间的常用技术，而MMD成为最常用的距离度量方法。然而，核函数的映射缺乏可解释性，其选择需要从数据性质、问题复杂度等多方面进行考量。
TSK模糊分类器[10]基于“IF-THEN”模糊规则解释输入和输出结果，具有良好的线性逼近能力和可解释性，目前众多学者将其和迁移学习结合，以解决小样本训练问题。例如，Yang等[11]提出了一种基于直推式迁移学习的TSK模糊逻辑系统，将最终输出视为新特征空间中的线性模型结果。Feng等[12]结合联合分布适应与TSK模糊逻辑系统。此外，Xu等[13]提出一种通过TSK模糊规则学习共享特征空间的迁移表示学习方法。基于此，本研究设想将TSK模糊规则整合到UDA框架中，以替代核函数进行特征映射，从而增强UDA方法的可解释性。此外，在采用最小化MMD进行域对齐时，基于目标域生成的伪标签质量对于域对齐的效果有着非常重要的影响。目前，大多数方法依赖基于源域标记数据训练的分类器来生成目标域的伪标签，但往往忽略了对伪标签质量的评估[14]。
为了克服现有工作存在的缺点，本研究提出一种基于伪标签细化的域适应TSK模糊分类器(domain adaptive takagi-sugeno-kang fuzzy classifier via pseudo label refinement, DA-TSK-PLR-FC)，具有3个优点：
1)利用模糊规则前件的非线性映射和后件的线性映射能力构建源域和目标域数据的模糊共享特征空间，提高数据特征表达能力；
2)在模糊特征空间使用基于图的随机游走策略进行伪标签预测，有助于保留数据中可能存在的几何结构特性；
3)不直接使用通过随机游走所得的伪标签，而是采用软标签和硬标签组合编码的方法，自适应地优化伪标签质量。
1. TSK模糊规则与特征学习
TSK模糊分类器是一种由“IF-THEN”模糊规则驱动的分类器，具有高度的可解释性[15]。以一阶单输出TSK模糊分类器为例，模糊规则形式为
$$ \begin{gathered} {\text{If: }}{x_1}{\text{ is }}\zeta _1^k \wedge {x_2}{\text{ is }}\zeta _2^k \wedge \cdots \wedge {x_d}{\text{ is }}\zeta _d^k, \\ {\text{Then: }} l_k \left( {\boldsymbol{x}} \right) = p_0^k + p_1^k{x_1} + p_2^k{x_2} + \cdots + p_d^k{x_d} \\ {\text{ }}k = 1,2,\cdots,K \end{gathered} $$ (1) 式中：
${x_i}(i = 1,2, \cdots ,d)$ 表示输入变量的第$i$ 维度，$d$ 是输入样本的维数。$\zeta _i^k$ 表示模糊集合，“$ \wedge $ ”代表模糊合操作符。$K$ 为模糊规则数，则$ l_k \left( {\boldsymbol{x}} \right) $ 表示第$k$ 条规则的输出。$ p_0^k , p_1^k , \cdots , p_d^k $ 为后件参数。那么，TSK模糊分类器的输出为$$ y = \sum\limits_{k = 1}^K {\frac{{ \varphi ^k ({\boldsymbol{x}}) l_k \left( {\boldsymbol{x}} \right)}}{{\displaystyle\sum\limits_{ k^{'} = 1}^K { \varphi ^{ k^{'} } ({\boldsymbol{x}})} }}} = \sum\limits_{k = 1}^K { {\tilde \varphi }^k ({\boldsymbol{x}})} l_k \left( {\boldsymbol{x}} \right) $$ (2) 其中
$$ \varphi ^k ({\boldsymbol{x}}) = \prod_{i = 1}^d {{\varphi _{\zeta _i^k}}\left( {{{\boldsymbol{x}}_i}} \right)} $$ (3) 式中：
$ \varphi ^k ({\boldsymbol{x}}) $ 为模糊隶属度，经过归一化后得到$ {\tilde \varphi }^k ({\boldsymbol{x}}) $ 。由于高斯模糊隶属度函数具有最佳近似性质[16]，模糊集合
$\zeta _i^k$ 通常采用它进行模糊化处理：$$ \varphi_{i_{i}^{k}}\left({\boldsymbol{x}}_{i}\right)=\exp \left(-\frac{1}{2}\left(\frac{x_{i}-c_{i}^{k}}{\delta_{i}^{k}}\right)\right)^{2} $$ (4) 式中：
$c_i^k$ 是高斯隶属度函数的中心，$\delta _i^k$ 是方差，分别称为中心前件参数和宽度前件参数，可以通过模糊C均值聚类(fuzzy C-means, FCM)评估[17]，计算公式为$$ c_i^k = \frac{{\displaystyle\sum_{j = 1}^n {r_{jk}}{x_{ji}}}}{{\displaystyle\sum_{j = 1}^N {r_{jk}}}} $$ (5) $$ \delta _i^k = h \cdot \frac{{\displaystyle\sum_{j = 1}^n {r_{jk}}{{\left( {{x_{ji}} - c_i^k} \right)}^2}}}{{\displaystyle\sum_{j = 1}^N {r_{jk}}}} $$ (6) 式中：
${r_{jk}}$ 是输入向量${{\boldsymbol{x}}_j}$ 对于第$k$ 类的模糊隶属度，$h$ 是一个可调的尺度参数，$n$ 是输入训练样本的个数。对于通过模糊规则的前件映射得到的特征向量
$ {\boldsymbol{x}}_{\mathrm{g}} \in {{\bf{R}}^{K\left( {d + 1} \right) \times 1}}$ 和所有模糊规则的后件参数的组合向量$ {\boldsymbol{p}}_{\mathrm{g}} \in {{\bf{R}}^{K\left( {d + 1} \right) \times 1}}$ ，可以作出定义：$$ {\boldsymbol{x}}_{\mathrm{e}} = {(1, {\boldsymbol{x}}^{\rm T} )}^{\rm T} $$ $$ {{{\tilde {\boldsymbol x}}}}^k = { {\tilde \varphi }^k ({\boldsymbol{x}}){\boldsymbol{x}}}_{\mathrm{e}} $$ $$ {\boldsymbol{x}}_{\rm g} = {( {( {{{\tilde {\boldsymbol x}}}}^1 )}^{\rm T} , {( {{{\tilde {\boldsymbol x}}}}^2 )}^{\rm T} , \cdots , {( {{{\tilde {\boldsymbol x}}}}^K )}^{\rm T} )}^{\rm T} $$ $$ {\boldsymbol{p}}^k = {( p_0^k , p_1^k , \cdots , p_d^k )}^{\rm T} $$ $$ {\boldsymbol{p}}_{\rm g} = {( {( {\boldsymbol{p}}^1 )}^{\rm T} , {( {\boldsymbol{p}}^2 )}^{\rm T} , \cdots , {( {\boldsymbol{p}}^K )}^{\rm T} )}^{\rm T} $$ 因此，式(2)的输出可以改写为模糊规则后件的线性形式：
$$ y = {\boldsymbol{p}}_{\rm g}^{\rm T} {\boldsymbol{x}}_{\rm g} $$ (7) 在多输出TSK模糊分类器中，单个模糊规则具有多组后件参数，则m维输出的后件参数
${\boldsymbol{P}} \in {{\bf{R}}^{K\left( {d + 1} \right) \times m}}$ 表示为$$ {\boldsymbol{P}} = \left[ {{\boldsymbol{p}}_{\text{g}}^1 \quad {\boldsymbol{p}}_{\text{g}}^2 \quad \cdots \quad {\boldsymbol{p}}_{\text{g}}^m} \right] $$ 将多输出TSK视为特征变换的映射函数
$ \varPsi $ [13]，以实现特征学习，并将式(7)转换为$$ \varPsi ({q_i}) = {\boldsymbol{P}}^{\rm T} {{\boldsymbol{g}}_{{q_i}}} $$ (8) 式中，
$ {{\boldsymbol{g}}_{ q_i }} \in {{\bf{R}}^{K\left( {d + 1} \right) \times 1}} $ 为数据集合${{q}}$ 中的任意实例$ q_i $ 经由前件映射得到的特征向量，定义为$$ {{\boldsymbol{g}}_{{q_i}}} = {\left[ {{{\left( {{\tilde{\boldsymbol x}}_{{q_i}}^1} \right)}^{\rm T}} \quad {{\left( {{\tilde{\boldsymbol x}}_{{q_i}}^2} \right)}^{\text{T}}} \quad \cdots \quad {{\left( {{\tilde{\boldsymbol x}}_{{q_i}}^K} \right)}^{\rm T}}} \right]^{\rm T}} $$ 2. DA-TSK-PLR-FC
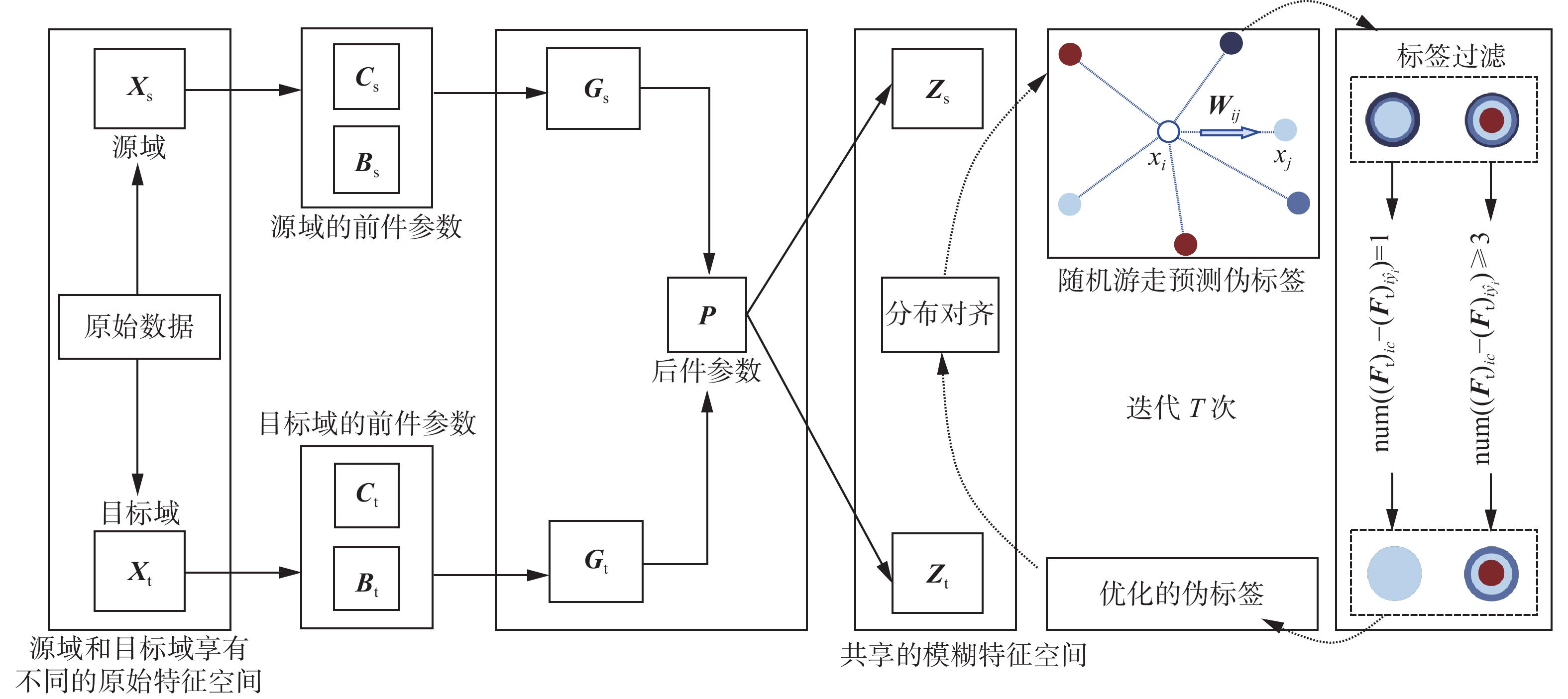
如图1所示，DA-TSK-PLR-FC框架主要由3个构件组成：1）基于模糊规则的源域和目标域模糊共享特征空间构建；2）基于图随机游走的目标域伪标签生成和自适应伪标签过滤；3）基于模糊特征空间的域对齐。
图 1 DA-TSK-PLR-FC框架Fig. 1 Framework of DA-TSK-PLR-FC
下载:
全尺寸图片
2.1 问题定义
在UDA中，给定一个有标签的源域
$ {\boldsymbol{D}}_{\rm s} = \{ {\boldsymbol{X}}_{\rm s} , {\boldsymbol{Y}}_{\rm s} \} $ ，其中$ {\boldsymbol{X}}_{\rm s} = {\left\{ { {\boldsymbol{x}}_{{\rm s}_i} } \right\}}_{i = 1}^{ n_{\rm s} } $ ，$ {\boldsymbol{X}}_{\rm s} $ 为含有$d$ 特征维度的源域数据集合，$ {\boldsymbol{Y}}_{\rm s} = {\left\{ { y_{{\rm s}_i} } \right\}}_{i = 1}^{ n_{\rm s} } $ 是属于$c$ 类别的源域标签集合。给定一个无标签的目标域$ D_{\rm t} = \{ {\boldsymbol{X}}_{\rm t} \} $ ，其中$ {\boldsymbol{X}}_{\rm t} = {\left\{ { {\boldsymbol{x}}_{{\rm t}_i} } \right\}}_{i = 1}^{ n_{\rm t} } $ ，$ {\boldsymbol{X}}_{\rm s} $ 为同样含有$d$ 特征维度的目标域数据集合。令$ P_{\rm s} ( {\boldsymbol{X}}_{\rm s} )$ 和$ P_{\rm t} ( {\boldsymbol{X}}_{\rm t} )$ 表示边缘分布，$ Q_{\rm s} ( {\boldsymbol{Y}}_{\rm s} | {\boldsymbol{X}}_{\rm s} ) $ 和$ Q_{\rm s} ( { {\boldsymbol{Y}}_{\rm t} |{\boldsymbol{X}}}_{\rm t} )$ 表示条件分布。此外，两域之间有不同的边缘分布和条件分布，即$ P_{\rm s} ( {\boldsymbol{X}}_{\rm s} ) \ne P_{\rm t} ( {\boldsymbol{X}}_{\rm t} )$ ，$ Q_{\rm s} ( {\boldsymbol{Y}}_{\rm s} | {\boldsymbol{X}}_{\rm s} ) \ne Q_{\rm s} ( { {\boldsymbol{Y}}_{\rm t} |{\boldsymbol{X}}}_{\rm t} ) $ 。本研究寻求一个源域和目标域的共享子空间，在新的特征分布中可以明显减少边缘分布差异和条件分布差异，使得满足$ P_{\rm s} ( {\boldsymbol{Z}}_{\rm s} ) \approx P_{\rm t} ( {\boldsymbol{Z}}_{\rm t} )$ ，$ Q_{\rm s} ( {\boldsymbol{Y}}_{\rm s} | {\boldsymbol{Z}}_{\rm s} ) \approx Q_{\rm s} ( { {\boldsymbol{Y}}_{\rm t} |{\boldsymbol{Z}}}_{\rm t} ) $ 。表1总结了本研究使用的主要符号。表 1 主要符号定义Table 1 Main notion definitions符号 定义 $d$ 原始特征的特征维度 $\lambda $ 正则化参数 ${n_{\rm s}}$/$ {n_{\rm t}} $ 源域或目标域的样本数目 $ {\boldsymbol{X}}_{\rm s} $/$ {\boldsymbol{X}}_{\rm t} $ 原始空间的源域或目标域的样本特征 $ {\boldsymbol{C}}_{\rm s} $/$ {\boldsymbol{C}}_{\rm t} $ 源域或目标域的TSK模糊规则的中心参数 $ {\boldsymbol{B}}_{\rm s} $/$ {\boldsymbol{B}}_{\rm t} $ 源域或目标域的TSK模糊规则的核宽度参数 ${{\boldsymbol{G}}_{\rm s}}$/${{\boldsymbol{G}}_{\rm t}}$ 经过前件部分映射的源域或目标域的样本特征 ${\boldsymbol{P}}$ TSK模糊规则的后件参数 ${\boldsymbol{W}}$ 最近邻图的路径权重矩阵 ${\boldsymbol{A}}$ 亲和矩阵 ${\boldsymbol{M}}$ MMD矩阵 $ {\boldsymbol{F}}_{\rm t} $ 目标域的软伪标签 $ {\boldsymbol{Z}}_{\rm s} $/$ {\boldsymbol{Z}}_{\rm t} $ 共享模糊特征空间的源域或目标域的样本特征 2.2 共享模糊特征空间构建
基于TSK模糊规则构建共享模糊特征空间的过程主要分为映射和线性降维两部分。前件部分进行非线性变换，后件部分实现降维，如图1所示。
本文采用经典的FCM聚类方法来确定TSK模糊规则的前件参数，即模糊隶属度函数中的中心参数和宽度参数。因此，基于式(5)，可以分别获得源域和目标域的中心参数
$ {\boldsymbol{C}}_{\rm s} $ 和$ {\boldsymbol{C}}_{\rm t} $ 。随后，基于式(6)分别计算源域和目标域的核宽度矩阵$ {\boldsymbol{B}}_{\rm s} $ 和$ {\boldsymbol{B}}_{\rm t} $ 。基于式(8)，源域中的单个实例
${x_{{\rm s}_i}}$ 和目标域中的单个实例${x_{{\rm t}_i}}$ 在经过前件部分映射后，分别变换为${{\boldsymbol{g}}_{{\rm s}_i} }$ 和${{\boldsymbol{g}}_{{\rm t}_i}}$ ：$$ {{\boldsymbol{g}}_{{\rm s}_i}} = {\left[ {{{\left( {{\tilde{\boldsymbol x}}_{{\rm s}_i}^1} \right)}^{\text{T}}} \quad {{\left( {{\tilde{\boldsymbol x}}_{{\rm s}_i}^2} \right)}^{\text{T}}} \quad \cdots \quad {{\left( {{\tilde{\boldsymbol x}}_{{\rm s}_i}^{{K}}} \right)}^{\text{T}}}} \right]^{\text{T}}} $$ $$ {{\boldsymbol{g}}_{{\rm t}_i}} = {\left[ {{{\left( {{\tilde{\boldsymbol x}}_{_{{\rm t}_i}}^1} \right)}^{\text{T}}} \quad {{\left( {{\tilde{\boldsymbol x}}_{_{{\rm t}_i}}^2} \right)}^{\text{T}}} \quad \cdots \quad {{\left( {{\tilde{\boldsymbol x}}_{_{{\rm t}_i}}^{{K}}} \right)}^{\text{T}}}} \right]^{\text{T}}} $$ 式中：
${{\boldsymbol{g}}_{{\rm s}_i} } \in {{\bf{R}}^{K\left( {d + 1} \right) \times 1}}$ ,${{\boldsymbol{g}}_{{\rm t}_i}} \in {{\bf{R}}^{K\left( {d + 1} \right) \times 1}}$ 。$ {\boldsymbol{g}}_{{\rm s}_i} $ 的所有实例集合${{\boldsymbol{G}}_{\rm s}}$ 以及${{\boldsymbol{g}}_{{\rm t}_i}}$ 的所有实例集合${{\boldsymbol{G}}_{\rm t}}$ 表示为$$ {{\boldsymbol{G}}_{\rm s}} = \left[ {{{\boldsymbol{g}}_{{{\mathrm{s}}_1}}} \quad {{\boldsymbol{g}}_{{{\mathrm{s}}_2}}} \quad \cdots \quad {{\boldsymbol{g}}_{{{\mathrm{s}}_{{n_{\rm s}}}}}}} \right] \in {{\bf{R}}^{K\left( {d + 1} \right) \times {n_{\rm s}}}} $$ $$ {{\boldsymbol{G}}_{\rm t}} = \left[ {{{\boldsymbol{g}}_{{{\mathrm{t}}_1}}} \quad {{\boldsymbol{g}}_{{{\mathrm{t}}_2}}} \quad \cdots \quad {{\boldsymbol{g}}_{{{\mathrm{t}}_{{n_{\rm t}}}}}}} \right] \in {{\bf{R}}^{K\left( {d + 1} \right) \times {n_{\rm t}}}} $$ 基于式(8)，将源域和目标域数据转换到模糊特征空间：
$$ {{\boldsymbol{Z}}_{\text{s}}} = {{\boldsymbol{P}}^{\rm T} }{{\boldsymbol{G}}_{\rm s}} $$ (9) $$ {{\boldsymbol{Z}}_{\rm t}} = {{\boldsymbol{P}}^{\rm T} }{{\boldsymbol{G}}_{\rm t}} $$ (10) 应当注意，源域和目标域不共享原始特征空间，因而前件参数不同。经过TSK模糊规则进行一系列的特征变换，假定两个域的后件参数共享相同模糊特征空间。
${{\boldsymbol{P}}^{\rm T} }$ 的求解见2.5节中的广义特征值求解。2.3 伪标签细化
伪标签细化包括伪标签预测和伪标签优化两个模块。DA-TSK-PLR-FC使用基于图随机游走方法预测伪标签，然后通过标签过滤提高伪标签质量。
DA-TSK-PLR-FC采用基于图随机游走算法[18]来预测伪标签，该方法使得目标域数据点能够在邻域相似度图的指导下从源域数据点中获取标签信息。将两域数据点视为图的节点，节点间的距离通过欧氏距离来衡量。点
$ x_i $ 和点$ x_j $ 之间的非负相似度计算为$ e^{ { - \left\| { x_i - x_j } \right\|}^2 / \sigma ^2 } $ ，其中$ \sigma ^2 $ 表示为方差。点$ x_j $ 的$ p $ 个最近邻构成集合$ N_p ( x_j ) $ 。基于此，图亲和矩阵${\boldsymbol{A}}$ 可以定义为$$ {\boldsymbol{A}}_{ij} = \left\{ {\begin{array}{*{20}{l}} { e^{ { - \left\| { x_i - x_j } \right\|}^2 / \sigma ^2 }, \quad i \ne j \wedge x_i \in N_p ( x_j )} \\ {0, \quad {\text{ 其他 }}} \end{array}} \right. $$ 在邻域相似度图中，路径权重
${\boldsymbol{W}}$ 可以被计算为$ {\boldsymbol{W = }} {\boldsymbol{D}}^{ - 1} {\boldsymbol{A}} $ 。其中，${\boldsymbol{D}}$ 是对角矩阵，它的每一项$ {\boldsymbol{D}}_{ii} = \displaystyle\sum\limits_{j = 1}^n { {\boldsymbol{W}}_{ij} } $ 。为了控制数据点的游走行为，引入方向系数${\alpha _i}$ 和${\beta _i}$ ，并分别构建对角矩阵${{\boldsymbol{I}}_{\alpha }}$ 和${{\boldsymbol{I}}_{\beta }}$ 。具体来说，如果第$i$ 点是目标域数据点，并且需要该点能够自由游走，则设置${\alpha _i} = 1$ ，${\beta _i} = 0$ 。如果第$i$ 点为源域数据点，则需要限制点的停留，此时令${\alpha _i} = 0$ ，${\beta _i} = 1$ 。一次随机游走可以被描述为（如图2）
图 2 基于图随机游走Fig. 2 Graph-based random walking下载:
全尺寸图片
$$ {{\tilde {\boldsymbol{W}}}} = {\boldsymbol{I}}_\beta + {\boldsymbol{I}}_\alpha {\boldsymbol{W}} $$ 令
$ {\hat{\boldsymbol W}} = {\boldsymbol{I}}_\alpha {\boldsymbol{W}} $ ，且$ {( {{\hat{\boldsymbol W}}}^h {\boldsymbol{I}}_\beta )}_{ij} $ 表示当前第$ i $ 点经过$ h $ 步随机游走后停在第$ j $ 点的概率。那么，随机游走的整个过程可以描述为$$ {\boldsymbol{Q}} = {\boldsymbol{I}}_\beta + {\hat{\boldsymbol W}} {\boldsymbol{I}}_\beta + {{\hat{\boldsymbol W}}}^2 {\boldsymbol{I}}_\beta + \cdot \cdot \cdot + {{\hat{\boldsymbol W}}}^h {\boldsymbol{I}}_\beta + \cdots $$ 因此，软标签矩阵
$ {\boldsymbol{F}} $ 可以表示为$$ {\boldsymbol{F}} = {\boldsymbol{QY}} $$ (11) 初次输入的
$ {\boldsymbol{Y}} $ 是源域数据的one-hot标签矩阵，在后续迭代中$ {\boldsymbol{Y}} $ 由上一轮迭代得到的软标签矩阵$ {\boldsymbol{F}} $ 进行更新。为了过滤掉目标域中可能标记错误的伪标签，本算法对随机行走预测的目标域标签进行标签过滤优化。
${\left( {{{\boldsymbol{F}}_{\rm t}}} \right)_{ic}}$ 表示目标域的第$ i $ 个样本经过随机游走后得到的伪标签向量属于第$ c $ 类的概率。${\hat y_i}$ 表示为使用最近质心分类器预测得到的标签，该分类器通过计算目标域样本与源域各类别质心之间的欧氏距离，并据此将样本分配给最近的质心所代表的类别。那么${\left( {{{\boldsymbol{F}}_{\rm t}}} \right)_{i{{\hat y}_i}}}$ 表示目标域的第$ i $ 个样本属于标签${\hat y_i}$ 的概率。因此，可以对$ {\left( {{{\boldsymbol{F}}_{\rm t}}} \right)_{ic}} $ 进行更新：$$ \left( {{{\boldsymbol{F}}_{\rm t}}} \right)_{ic}^* = \frac{{{{\left( {{{\boldsymbol{F}}_{\rm t}}} \right)}_{ic}}\varepsilon \left( {{{\left( {{{\boldsymbol{F}}_{\rm t}}} \right)}_{ic}} - {{\left( {{{\boldsymbol{F}}_{\rm t}}} \right)}_{i{{\hat y}_i}}}} \right)}}{{\displaystyle\sum_{j = 1}^C {{\left( {{{\boldsymbol{F}}_{\rm t}}} \right)}_{ij}}\varepsilon \left( {{{\left( {{{\boldsymbol{F}}_{\rm t}}} \right)}_{ij}} - {{\left( {{{\boldsymbol{F}}_{\rm t}}} \right)}_{i{{\hat y}_i}}}} \right)}} $$ 其中，单位阶跃函数
$\varepsilon (x)$ 定义为$$ \varepsilon (x) = \left\{ {\begin{array}{*{20}{c}} {1, \quad x \geqslant 0} \\ {0, \quad x < 0} \end{array}} \right. $$ 该更新规则仅保留
${\left( {{{\boldsymbol{F}}_{\rm t}}} \right)_{ic}} \geqslant {\left( {{{\boldsymbol{F}}_{\rm t}}} \right)_{i{{\hat y}_i}}}$ 的情况，以提高随机游走后得到的伪标签的质量，这是改善伪标签质量的第1步。第2步是使用软硬标签组合编码的方式来进一步提高伪标签质量。如图3给出了伪标签过滤的示意图。图中一个圆点指代一个经过随机游走后获得的伪标签，样本属于某一类的概率由对应颜色占据的面积来表示。定义
${{\mathrm{num}}} ({\boldsymbol{x}})$ 函数用于统计向量${\boldsymbol{x}}$ 中大于等于零值的个数。具体而言，当${{\mathrm{num}}} \left( {{{\left( {{{\boldsymbol{F}}_{\rm t}}} \right)}_{ic}} - {{\left( {{{\boldsymbol{F}}_{\rm t}}} \right)}_{i{{\hat y}_i}}}} \right) = 1$ (其中${{c}} = \displaystyle\sum\limits_{n = 1}^C n $ )时，表示仅有一个类别的伪标签的概率大于或等于使用最近质心分类器重新分配的标签的概率，此时该伪标签被认为是确定的，并被编码为硬标签。相反，如果该值大于等于3时(对于二分类，该值应设为2)，表示有多个类别的伪标签概率高于或等于最近质心分类器重新分配的标签概率，此时无法确定哪个类别的伪标签最可靠，应编码为软标签，即保留排名前三的类别对应的概率，舍弃其他类别。通过这种方法，可以有效地过滤掉不确定的标签，从而提高伪标签的质量。
图 3 伪标签过滤Fig. 3 Label filtering for pseudo labels下载:
全尺寸图片
2.4 分布对齐
为了最小化模糊特征空间中源域
$ {\boldsymbol{Z}}_{\rm s} $ 和目标域$ {\boldsymbol{Z}}_{\rm t} $ 之间边缘分布的距离，本文使用MMD衡量源域和目标域之间的距离，以对齐两个域的边缘分布：$$ \begin{gathered} {{\text{MMD}}}_{\boldsymbol{P}}^2 ( {\boldsymbol{Z}}_{\rm s} , {\boldsymbol{Z}}_{\rm t} ) = {\left\| {\frac{1}{{ n_{\rm s} }}\sum\limits_{i = 1}^{ n_{\rm s} } { {\boldsymbol{P}}^{\rm T} {\boldsymbol{g}}_{{\rm s}_i} } - \frac{1}{{ n_{\rm t} }}\sum\limits_{j = 1}^{ n_{\rm t} } { {\boldsymbol{P}}^{\rm T} {\boldsymbol{g}}_{ {\mathrm{t}}_j } } } \right\|}_K^2= \\ {\text{tr}}( {\boldsymbol{P}}^{\rm T} { {\boldsymbol{G}}_{\boldsymbol{X}} {\boldsymbol{M}}}_0 {\boldsymbol{G}}_{\boldsymbol{X}}^{\rm T} {\boldsymbol{P}}) \end{gathered} $$ (12) 式中：
$ {\boldsymbol{G}}_{\boldsymbol{X}} = [ {\boldsymbol{G}}_{\rm s} \quad {\boldsymbol{G}}_{\rm t} ] $ ，$ {\boldsymbol{G}}_{\rm s} \in {\bf{R}}^{K(d + 1) \times n_{\rm s} } $ ，$ {\boldsymbol{G}}_{\rm t} \in {\bf{R}}^{K(d + 1) \times n_{\rm t} } $ ，$ {\boldsymbol{P}} $ 表示TSK模糊规则的后件参数。MMD矩阵$ {\boldsymbol{M}}_0 \in {\bf{R}}^{( n_{\rm s} + n_{\rm t} ) \times ( n_{\rm s} + n_{\rm t} )} $ 的具体形式为$$ {( {\boldsymbol{M}}_0 )}_{ij} = \left\{ \begin{gathered} {\dfrac{1}{{ n_{\rm s} n_{\rm s} }},\quad i, j \leqslant n_{\rm s} } \\ {\dfrac{1}{{ n_{\rm t} n_{\rm t} }},\quad i, j > n_{\rm s} } \\ {\dfrac{{ - 1}}{{ n_{\rm s} n_{\rm t} }},\quad 其他} \\ \end{gathered} \right. $$ (13) 本研究希望最小化共享模糊特征空间中源域和目标域之间的条件分布距离。然而，目标域数据中缺乏标签信息，无法计算每个类的样本矩，本研究使用随机游走预测的目标域伪标签。因此，结合细化标签后，跨域条件分布距离可以重新定义为
$$ \begin{gathered} {{\text{MMD}}}_{\boldsymbol{Q}}^2 ( {\boldsymbol{Z}}_{\rm s} , {\boldsymbol{Z}}_{\rm t} )= \\ {\sum\limits_{{{c}} = 1}^C {\left\| {\frac{1}{{ {\tilde n}_{\rm s}^c }}\sum\limits_{i = 1}^{ n_{\rm s} } { {( {\boldsymbol{F}}_{\rm s} )}_{ic} {\boldsymbol{P}}^{\text{T}} {\boldsymbol{g}}_{{\rm s}_i} } } \right. - \left. {\frac{1}{{ {\tilde n}_{\rm t}^c }}\sum\limits_{j = 1}^{ n_{\rm t} } { {( {\boldsymbol{F}}_{\rm t} )}_{jc} {\boldsymbol{P}}^{\text{T}} {\boldsymbol{g}}_{ {\mathrm{t}}_j } } } \right\|} }_K^2 = \\ {\text{tr}}( {\boldsymbol{P}}^{\rm T} {\boldsymbol{G}}_{\boldsymbol{X}} {\boldsymbol{M}}_C {\boldsymbol{G}}_{\boldsymbol{X}}^{\rm T} {\boldsymbol{P}}) \\ \end{gathered} $$ (14) 式中：
$c = 1,2,\cdots,C$ ，$C$ 表示类的数目，$ {\boldsymbol{F}}_{\rm s} $ 和$ {\boldsymbol{F}}_{\rm t} $ 分别表示随机游走后得到的源域标签和目标域标签，$ {\tilde n}_{\rm s}^c = \displaystyle\sum\limits_{i = 1}^{ n_{\rm s} } { {( {\boldsymbol{F}}_{\rm s} )}_{ic} } $ ，$ {\tilde n}_{\rm t}^c = \displaystyle\sum\limits_{j = 1}^{ n_{\rm t} } { {( {\boldsymbol{F}}_{\rm t} )}_{jc} } $ ，$ {\boldsymbol{M}}_c \in {\bf{R}}^{( n_{\rm s} + n_{\rm t} ) \times ( n_{\rm s} + n_{\rm t} )} $ ，$ {\boldsymbol{M}}_c $ 具体表达为$$ {{({{{\boldsymbol{M}}}}_{c})}}_{ij}=\left\{\begin{gathered}\sum_{c=1}^{C}\frac{{{({{{\boldsymbol{F}}}}_{\rm{s}})}}_{ic}{{({{{\boldsymbol{F}}}}_{\rm{s}})}}_{jc}}{{{\tilde{n}}}_{\rm{s}}^{c}{{\tilde{n}}}_{\rm{s}}^{c}} \text{，} i,j \leqslant {{n}}_{\rm{s}} \\ {\sum_{c=1}^{C}\frac{{{({{{\boldsymbol{F}}}}_{{\rm{t}}})}}_{ic}{{({{{\boldsymbol{F}}}}_{{\rm{t}}})}}_{jc}}{{{\tilde{n}}}_{{\rm{t}}}^{c}{{\tilde{n}}}_{{\rm{t}}}^{c}}} \text{，} i,j > {{n}}_{\rm{s}} \\ \sum_{c=1}^{C}-\frac{{{({{{\boldsymbol{F}}}}_{\rm{s}})}}_{ic}{{({{{\boldsymbol{F}}}}_{{\rm{t}}})}}_{jc}}{{{\tilde{n}}}_{\rm{s}}^{c}{{\tilde{n}}}_{{\rm{t}}}^{c}} \text{，} \left\{\begin{gathered} i \leqslant {{n}}_{\rm{s}},j > {{n}}_{\rm{s}}\\ i > {{n}}_{\rm{s}},j \leqslant {{n}}_{\rm{s}}\end{gathered} \right. \\ 0 , \;\; \text{其他} \\ \end{gathered}\right. $$ (15) 仅关注同一类别的分布匹配是不足够的，还需要保证不同类别之间的可区分性。通过最大化模糊特征空间中源域和目标域中类别之间的距离，从而增加两域类别间的判别度。类间区分度可以定义为
$$ \begin{gathered} {{\text{MMD}}}_D^2 ( D^{{c}} , D^{{{ - {{c}}}}} ) = \\ {\sum\limits_{{{c}} = 1}^C {\left\| {\frac{1}{{ n^{{c}} }}\sum\limits_{ x_i \in D^c } { {\boldsymbol{F}}_{ic} } } \right. {\boldsymbol{P}}^{\rm T} {\boldsymbol{g}}_{{\rm s}_i} - \left. {\frac{1}{{ n^{{{ - {{c}}}}} }}\sum\limits_{ x_j \in D^{ - c} } { {\boldsymbol{F}}_{jc} } {\boldsymbol{P}}^{\rm T} {\boldsymbol{g}}_{ {\mathrm{t}}_j } } \right\|} }_K^2 = \\ {\mathrm{tr}}( {\boldsymbol{P}}^{\rm T} { {\boldsymbol{G}}_{\boldsymbol{X}} {\boldsymbol{{\rm M}}}}_d {\boldsymbol{G}}_{\boldsymbol{X}}^{\rm T} {\boldsymbol{P}}) \\ \end{gathered} $$ (16) 式中：
$ D^c $ 表示为由源域和目标域组成的联合域$ D $ 中第$ c $ 类子域，而$ D^{ - c} $ 表示为除第$ c $ 类外所有类别的子域，判别损失矩阵$ {\boldsymbol{M}}_d $ 的具体表达形式为$$ \begin{gathered}{( {\boldsymbol{M}}_d )}_{ij} = \sum_{c = 1}^C \left[ \frac{{ {({\boldsymbol{F}})}_{ic} {({\boldsymbol{F}})}_{jc} }}{{ {\widetilde n}^c {\widetilde n}^c }} + \frac{{ {({\boldsymbol{F}})}_{i( - c)} {({\boldsymbol{F}})}_{j( - c)} }}{{ {\widetilde n}^{ - c} {\widetilde n}^{ - c} }} - \right. \\ \left. \frac{{ {({\boldsymbol{F}})}_{ic} {({\boldsymbol{F}})}_{j( - c)} }}{{ {\widetilde n}^c {\widetilde n}^{ - c} }} - \frac{{ {({\boldsymbol{F}})}_{i( - c)} {({\boldsymbol{F}})}_{jc} }}{{ {\widetilde n}^c {\widetilde n}^{ - c} }}\right] \end{gathered} $$ (17) 2.5 总体目标函数及优化
在DA_TSK_PLR_FC方法中，总体目标函数可以通过合并式(12)、(14)、(16)获得：
$$ \begin{gathered}\min\limits_{\boldsymbol{P}^{\rm{T}}\boldsymbol{G}_{\boldsymbol{X}}\boldsymbol{H}\boldsymbol{G}_{\boldsymbol{X}}^{\rm{T}}\boldsymbol{P}=\boldsymbol{I}}\text{tr(}\boldsymbol{P}^{\rm{T}}\boldsymbol{G}_{\boldsymbol{X}}(\boldsymbol{M}_0+\boldsymbol{M}_c-\boldsymbol{M}_d\text{)}\boldsymbol{G}_{\boldsymbol{X}}^{\rm{T}}\boldsymbol{P}\text{)}+\lambda \left\| \boldsymbol{P} \right\| _{\mathrm{F}}^2\end{gathered} $$ (18) 式中：MMD矩阵
$ {\boldsymbol{M}}_d $ 、$ {\boldsymbol{M}}_c $ 和$ {\boldsymbol{M}}_d $ 使用细化的伪标签矩阵进行计算，$ \left\| \; \right\| _{\mathrm{F}}^2 $ 是保证模型得以良好优化的Frobenius范数，$ \lambda $ 表示为正则化参数。在优化问题中，可以通过最小化重建误差来优化特征表示。本文选择主成分分析作为重构数据的方法，$ {\boldsymbol{G}}_{\boldsymbol{X}} {\boldsymbol{H}} {\boldsymbol{G}}_{\boldsymbol{X}}^{\rm T} $ 为协方差矩阵，中心矩阵$ {\boldsymbol{H}} = {\boldsymbol{I}} - \left( {\dfrac{1}{n}} \right){{\boldsymbol{11}}}^{\rm T} $ ，其中$ n = n_{\rm s} + n_{\rm t} $ 且$ {\boldsymbol{I}} \in {\bf{R}}^{K(d + 1) \times K(d + 1)} $ 为单位矩阵，而$ {{\boldsymbol{1}}} $ 为全1的列向量。后件参数$ {\boldsymbol{P}} $ 可通过求解式(18)得到。为了进一步优化目标函数，需要对式(11)中描述的随机游走预测伪标签这一过程进行优化。假设在第h次随机游走后，所有数据点都停止移动过程，根据收敛准则，式(11)可以被重新表述为
$$ {\boldsymbol{F}} = \lim \limits_{h \to \infty } {\boldsymbol{Q}}(h){\boldsymbol{Y}} = {\left( {{\boldsymbol{I - }}{{\boldsymbol{I}}_\alpha }{\boldsymbol{W}}} \right)^{ - 1}}{{\boldsymbol{I}}_\beta }{\boldsymbol{Y}} $$ (19) 此外，由于缩放后件参数
$ {\boldsymbol{P}} $ 并不影响式(18)的结果，因此可以使用拉格朗日函数对式(18)进行优化，优化后改写为$$ \begin{gathered} \min \limits_{\boldsymbol{P}} {\text{tr(}} {\boldsymbol{P}}^{\rm T} ( {\boldsymbol{G}}_{\boldsymbol{X}} {\text{(}} {\boldsymbol{M}}_0 + {\boldsymbol{M}}_C - {\boldsymbol{M}}_d {\text{)}} {\boldsymbol{G}}_{\boldsymbol{X}}^{\rm T} + \lambda {\boldsymbol{I}}){\boldsymbol{P}}{\text{)}} + \\ {\text{tr((}}{\boldsymbol{I}} - {\boldsymbol{P}}^{\rm T} {\boldsymbol{G}}_{\boldsymbol{X}} {\boldsymbol{H}} {\boldsymbol{G}}_{\boldsymbol{X}}^{\rm T} {\boldsymbol{P}}{\text{)}}{\boldsymbol{\varPhi }}{\text{)}} \end{gathered} $$ (20) 式中
$ {\boldsymbol{\varPhi }} = {\text{diag}}( \varPhi _1 , \varPhi _2 \cdots , \varPhi _m ) \in {\bf{R}}^{m \times m} $ 为拉格朗日乘子。求取关于
$ {\boldsymbol{P}} $ 的偏导数，广义特征分解实现方式为$$ \begin{gathered} {\text{(}} {\boldsymbol{P}}^{\rm T} ( {\boldsymbol{G}}_{\boldsymbol{X}} {\text{(}} {\boldsymbol{M}}_0 {\text{ + }} {\boldsymbol{M}}_C - {\boldsymbol{M}}_d {\text{)}} {\boldsymbol{G}}_{\boldsymbol{X}}^{\rm T} + \lambda {\boldsymbol{I}}){\boldsymbol{P}}{\text{)}} = {\boldsymbol{G}}_{\boldsymbol{X}} {\boldsymbol{H}} {\boldsymbol{G}}_{\boldsymbol{X}}^{\rm T} {\boldsymbol{P\varPhi }} \end{gathered} $$ (21) 获得后件参数
$ {\boldsymbol{P}} $ 后，基于式(9)～(10)可以获得模糊特征空间中的源域$ {\boldsymbol{Z}}_{\rm s} $ 和目标域$ {\boldsymbol{Z}}_{\rm t} $ 。2.6 算法流程
DA-TSK-PLR-FC算法的伪代码如算法1所示。
算法1 DA-TSK-PLR-FC
输入 源域
$ \{ {\boldsymbol{X}}_{\rm s} , {\boldsymbol{F}}_{\rm s} \} $ ，目标域$ \{ {\boldsymbol{X}}_{\rm t} \} $ ，正则化参数$ \lambda $ ，最大迭代次数$ T $ ，模糊规则数$ K $ ，模糊特征空间的维度$ m $ ，高斯隶属函数的核宽度的可数$ h $ 。输出 目标域标签
${\boldsymbol{F}}_{\rm t}^*$ 。1) 使用FCM聚类方法，即式(5)～(6)，针对
$ {\boldsymbol{X}}_{\rm s} $ 和$ {\boldsymbol{X}}_{\rm t} $ 分别计算前件参数的中心参数$ {\boldsymbol{C}}_{\rm s} $ 和$ {\boldsymbol{C}}_{\rm t} $ ，前件参数的宽度参数$ {\boldsymbol{B}}_{\rm s} $ 和$ {\boldsymbol{B}}_{\rm t} $ ；2) 计算经过前件参数变换的源域和目标域的特征矩阵
${{\boldsymbol{G}}_{\rm s}}$ 、$ {{\boldsymbol{G}}_{\rm t}} $ ；3) 由
${\boldsymbol{X}}$ (后续更新为${\boldsymbol{Z}}$ )计算路径权重矩阵${\boldsymbol{W}}$ ；4) 基于式(19)进行基于图的随机游走计算伪标签
${{\boldsymbol{F}}_{\rm t}}$ ；5) 基于2.3节中描述的标签过滤原则，细化伪标签
${{\boldsymbol{F}}_{\rm t}}$ ；6) 基于式(13)、(15)、(17)分别计算MMD矩阵
${{\boldsymbol{M}}_0}$ 、${{\boldsymbol{M}}_c}$ 和判别损失矩阵${{\boldsymbol{M}}_d}$ ；7) 基于式(21)计算后件参数
${\boldsymbol{P}}$ ；8) 基于式(9)～(10)更新源域特征
${{\boldsymbol{Z}}_{\rm s}}$ 和目标域特征${{\boldsymbol{Z}}_{\rm t}}$ ；9) 重复3)～8)，直到迭代次数大于T；
10) 返回目标域标签
${\boldsymbol{F}}_{\rm t}^*$ 。2.7 复杂度分析
根据算法1给出DA-TSK-PLR-FC的时间复杂度。步骤1) 中关于
$ {\boldsymbol{C}}_{\rm s} $ 、$ {\boldsymbol{C}}_{\rm t} $ 、$ {\boldsymbol{B}}_{\rm s} $ 、$ {\boldsymbol{B}}_{\rm t} $ 的时间复杂度为$ O(2dnK) $ 。步骤2) 中关于${{\boldsymbol{G}}_{\rm s}}$ 、$ {{\boldsymbol{G}}_{\rm t}} $ 的时间复杂度为$ O(2dnK + 2nK) $ 。在一次迭代中，步骤3) 中关于${\boldsymbol{W}}$ 的时间复杂度为$ O( n^3 ) $ 。步骤4) 中关于伪标签${{\boldsymbol{F}}_{\rm t}}$ 的时间复杂度为$ O( {Cn}^2 ) $ 。步骤5) 中关于过滤优化伪标签${{\boldsymbol{F}}_{\rm t}}$ 的时间复杂度为$ O(n) $ 。步骤6) 中关于矩阵${{\boldsymbol{M}}_0}$ 、${{\boldsymbol{M}}_c}$ 、${{\boldsymbol{M}}_d}$ 的时间复杂度为$ O(C n^2 ) $ 。步骤7) 中使用广义特征值分解求解矩阵${\boldsymbol{P}}$ 的时间复杂度为$ O(m K^2 d^2 ) $ 。步骤8) 中关于构造特征矩阵${{\boldsymbol{Z}}_{\rm s}}$ 和${{\boldsymbol{Z}}_{\rm t}}$ 的时间复杂度为$ O(nmd) $ 。基于上述分析，经过$ T $ 次迭代，DA-TSK-PLR-FC的总时间复杂度为$ O(4dnK + 2nK + T( n^3 + 2Cn + n + m K^2 d^2 + nmd)) $ 。DA-TSK-PLR-FC的空间复杂度主要包含以下几个部分：第1部分是输入源域和目标域数据时需要占用的存储空间，空间复杂度为
$ O(nd) $ 。第2部分是存储路径权重矩阵、伪标签矩阵、MMD矩阵、经过前件参数变换的源域和目标域的特征矩阵、每次迭代更新的源域和目标域的特征矩阵等中间结果需要占用的空间，空间复杂度为$ O( n^2 + nC + K(d + 1)n + K^2 {(d + 1)}^2 + nm) $ 。第3部分是存储参数需要占用的空间，空间复杂度为$ O(1) $ 。因此，总的空间复杂度是$ O(nd + n^2 + d^2 ) $ 。2.8 泛化误差分析
定理1[19] 设
$ {{{H}}} $ 是VC维为d的假设空间，$ {\boldsymbol{U}}_{\rm s} $ 和$ {\boldsymbol{U}}_{\rm t} $ 分别是从$ {\boldsymbol{D}}_{\rm s} $ 和$ {\boldsymbol{D}}_{\rm s} $ 中抽取的大小为m的无标签样本。则对于任意$ h \in { H} $ ，在目标领域$ {\boldsymbol{D}}_{\rm t} $ 的期望风险至少以概率$ 1 - \delta $ 满足上界：$$ \begin{gathered} {{\epsilon }}_{{\rm{t}}}(h)\leqslant {{\epsilon}}_{\rm{s}}(h)+\frac{1}{2}{\widehat{d}}_{{ H}\Delta { H}}({{{\boldsymbol{U}}}}_{\rm{s}},{{{\boldsymbol{U}}}}_{{\rm{t}}})+\varOmega + \\ 4\sqrt{\frac{2 d \cdot \mathrm{log}(2m)+\mathrm{log}(4/\delta )}{m}} \end{gathered} $$ (22) 式中：
$ {{\epsilon}}_{{\rm{t}}}(h) $ 为目标域的泛化误差，$ {{\epsilon}}_{\rm{s}}(h) $ 为源域的泛化误差，$ {\widehat d}_{{ H}\Delta { H}} ( {\boldsymbol{U}}_{\rm s} , {\boldsymbol{U}}_{\rm t} ) $ 表示两域的经验距离，$ \varOmega ={{\epsilon}}_{\rm{s}}(h)+ {{\epsilon}}_{{\rm{t}}}(h) $ 表示两域的最优联合误差。上述定理表明，$ {{\epsilon}}_{\rm{s}}(h) $ 、$ {\widehat d}_{{ H}\Delta { H}} ( {\boldsymbol{U}}_{\rm s} , {\boldsymbol{U}}_{\rm t} ) $ 和$ \varOmega $ 三者均能决定目标域泛化误差的上界。在DA-TSK-PLR-FC算法公式(18)中，为了寻找最优投影（即后件参数P），通过引入正则化项控制模型复杂度来最小化
$ {{\epsilon}}_{\rm{s}}(h) $ ；通过使用MMD最小化模糊特征空间中源分布和目标分布的差异，即式(12)和(14)来最小化$ {\widehat d}_{{ H}\Delta { H}} ( {\boldsymbol{U}}_{\rm s} , {\boldsymbol{U}}_{\rm t} ) $ ；通过使用标签过滤和最大化类间区分度，即2.3节中描述的标签过滤原则和式(16)来最小化联合风险$ \varOmega $ 。3. 实验分析
3.1 数据集介绍
表2总结了本研究所采用的数据集。
表 2 用于评估域适应方法性能的3个基准数据集Table 2 Three benchmark datasets for evaluating the performance of domain adaptation methods数据集 类型 样本量 特征维度 类别数 子集 Office+Caltech 物体识别 2533 SURF:800
DeCAF6:4096 10 Amzaon、Webcam、DSLR、Caltech CMU-PIE 人脸识别 11554 1024 68 C05、C07、C09、C27、C29 Amazon_review 情绪分析 7996 400 2 Books、DVD、Electronics、Kitchen Office+Caltech Office+Caltech数据集由Office-31[20]和Caltech-256[21]两个数据集组成。Office-31数据集包含
1410 个样本，Caltech-256数据集则包含1123 个样本。Office + Caltech数据有浅层特征和深层特征两种特征表示，因此可以分别构造12个UDA任务，如“C→A”。CMU-PIE[22] 包含来自68人的面部图像样本，分辨率为32像素×32像素。从CMU-PIE中选择5个子集：C05、C07、C09、C27、C29，分别对应左侧、向上、向下、正面和右侧5种姿势。同样地，可以构造20个不同的UDA任务，如“C05→C07”。
Amazon_review Amazon_review[23]是情感分析文本数据集，包含亚马逊不同产品的评论。它分为4个子集：Books、DVD、Electronics和Kitchen，评论按星级（1～5星）分为正面（4～5星）和负面（1～3星）[24]。一共构造了12个UDA任务，如“B→D”。
3.2 实验设置
1）对比算法及参数设置：本实验共采用10种方法作为对比算法，包括1种非域适应方法和9种域适应方法。非域适应方法为单输出一阶TSK模糊分类器[13](TSK-FC (one-order))，9种域适应方法分别是测地线流式核方法(geodesic flow kernel, GFK)[6]、迁移成分分析(transfer component analysis, TCA)[8]、联合分布适配(joint distribution adaptation, JDA)[9]、迁移联合匹配(transfer joint matching, TJM)[25]、协方差对齐(correlation alignment, CORAL)[26]、联合几何和统计对齐(joint geometrical and statistical alignment, JGSA)[27]、联合概率适配(joint probability distribution adaptation, JPDA)[28]、自适应标签过滤学习(self-adaptive label filtering learning, SALFL)[18]和基于目标域类内相似度改善伪标签(target domain intra-class similarity to remedy the pseudo labels, TSRP)[29]。其中，TSK-FC (one-order)用于验证将TSK模糊规则与域适应方法结合的有效性。与经典TSK模糊线性模型不同，TSK-FC (one-order)利用前件部分进行特征映射，后件部分进行降维，并使用岭回归计算后件参数。由于目标域中的数据没有标签，因此不适合使用交叉验证来找到所有比较算法的最佳参数。除SALFL外，其他域适应方法的基分类器均为1最近邻分类器。TSRP作为一个附加项，与JDA结合使用。对于模型超参数，如果原文章中有推荐的默认值，本研究直接使用其默认值。否则，本研究参考原文章的推荐参数范围，采用网格搜索法对参数进行寻优。对于涉及联合分布自适应的算法，最大迭代次数统一设置为T = 8。
2）DA-TSK-PLR-FC算法的参数设置：联合分布自适应的最大迭代次数T的设置与对比算法的设置一致，唯一的正则化参数通过网格搜索λ={1, 3, 5, 7, 10, 50, 100, 200, 300, 400, 500, 600, 700, 800, 900,
1000 }进行优化设置。模糊规则的网格搜索范围k={2, 4, 6, 8, …, 20}。3.3 对比实验
表3～6给出了在不同数据集上本算法与各个算法的对比结果(最优分类结果已加粗)。其中“本文算法”表示为DA-TSK-PLR-FC算法。
表 3 基于Office+Caltech数据集的浅层特征的域适应准确率Table 3 Accuracy on Office+Caltech datasets using SURF features% 任务 TCA JDA TJM GFK CORAL JGSA JPDA SALFL TSRP TSK-FC
(one-order)本文算法 C→A 45.62 46.66 45.20 41.02 54.28 49.90 47.60 55.43 47.39 52.50 54.28 C→W 39.32 39.32 39.32 40.34 38.64 39.32 45.76 60.00 47.80 47.12 59.32 C→D 45.86 47.13 46.50 41.40 36.31 34.39 46.50 54.14 53.50 43.95 56.69 A→C 42.03 40.61 41.50 40.25 45.06 37.58 40.78 45.77 41.76 43.99 44.88 A→W 40.00 38.31 41.69 40.00 44.41 43.73 40.68 47.12 45.42 38.98 50.17 A→D 35.67 36.94 45.22 36.31 39.49 39.49 36.94 41.40 43.95 42.67 49.68 W→C 31.52 32.41 31.17 30.81 33.75 38.47 34.55 38.56 33.30 33.13 38.74 W→A 30.48 32.98 31.73 31.73 35.91 58.25 33.82 40.61 37.89 36.74 41.75 W→D 91.08 92.35 89.81 88.54 86.62 93.63 88.54 83.44 92.99 84.07 92.36 D→C 32.95 32.06 32.15 30.10 33.84 36.24 34.73 34.91 33.57 30.81 37.04 D→A 32.78 33.82 37.06 31.84 37.68 60.33 34.66 35.70 33.82 33.82 38.83 D→W 87.46 89.83 89.83 84.41 84.75 97.63 91.19 82.71 91.53 81.36 89.83 平均值 46.23 46.87 47.60 44.73 47.56 52.41 47.98 51.65 50.24 47.43 54.45 注：最优分类结果已加粗，下同。 表 4 基于Office+Caltech数据集的深层特征的域适应准确率Table 4 Accuracy on Office+Caltech datasets using DeCAF6 features% 任务 TCA JDA TJM GFK CORAL JGSA JPDA SALFL TSRP TSK-FC
(one-order)本文算法 C→A 89.46 90.29 89.04 88.83 91.54 90.08 91.23 92.17 92.38 90.81 92.59 C→W 82.03 85.76 75.93 82.37 74.58 87.46 88.81 93.56 88.47 76.94 92.54 C→D 85.99 89.80 80.25 88.54 84.08 86.62 89.81 88.54 89.17 84.71 89.17 A→C 83.79 82.37 80.41 77.56 82.10 78.18 85.04 85.57 85.40 84.32 86.20 A→W 74.92 84.59 72.88 73.90 72.88 89.49 78.31 81.02 86.44 78.30 87.80 A→D 84.71 84.42 77.71 82.80 80.89 91.72 84.08 87.26 87.26 86.62 87.90 W→C 76.49 83.25 76.31 69.55 71.15 79.25 84.24 81.83 84.33 70.70 80.77 W→A 80.58 88.10 87.37 74.43 79.02 86.95 90.08 85.80 89.98 78.81 88.20 W→D 100.00 100.00 100.00 100.00 100.00 100.00 100.00 96.82 100.00 100.00 100.00 D→C 81.30 85.04 80.32 67.68 70.88 81.12 84.51 74.00 86.46 75.24 80.50 D→A 88.83 91.85 89.56 82.05 79.54 90.08 91.02 88.73 92.80 83.19 90.19 D→W 99.32 99.32 97.29 95.25 98.98 98.98 99.66 93.90 98.31 99.66 99.32 平均值 85.62 88.73 83.92 81.91 82.14 88.33 88.90 87.43 90.08 84.11 89.60 表 5 基于CMU-PIE数据集的域适应准确率Table 5 Accuracy on CMU-PIE dataset% 任务 TCA JDA TJM GFK CORAL JGSA JPDA SALFL TSRP TSK-FC
(one-order)本文算法 C05→C07 40.88 58.63 51.93 39.59 34.32 73.97 59.36 61.69 62.49 34.56 71.21 C05→C09 41.79 52.53 51.23 38.91 35.29 72.06 66.67 75.61 58.46 45.65 70.47 C05→C27 59.57 83.59 75.22 58.10 43.98 83.87 83.99 95.31 86.12 61.40 91.74 C05→C29 29.11 47.61 35.78 32.17 24.94 63.48 49.51 67.10 48.16 26.96 61.03 C07→C05 41.63 55.97 47.57 26.92 28.99 66.42 63.00 74.49 59.78 31.90 74.79 C07→C09 51.35 62.82 67.28 60.36 39.71 71.20 60.85 86.27 70.04 35.60 80.39 C07→C27 64.82 77.92 70.44 43.62 53.71 80.05 77.05 89.52 76.54 57.34 89.73 C07→C29 33.58 42.58 37.62 40.63 26.72 73.41 47.67 67.65 44.42 39.03 53.74 C09→C05 34.96 50.12 42.71 28.09 33.25 66.42 59.78 72.72 55.97 37.84 74.52 C09→C07 47.58 57.33 64.27 59.55 44.50 80.85 63.35 81.83 72.44 55.56 77.47 C09→C27 56.77 72.00 69.99 43.29 54.25 81.23 74.47 88.19 76.45 48.09 92.70 C09→C29 33.82 41.97 43.26 44.79 27.45 76.04 52.7 75.43 54.96 31.31 64.95 C27→C05 55.85 79.08 79.44 58.22 46.67 74.67 84.87 93.22 85.23 55.64 94.30 C27→C07 67.71 83.97 78.14 56.29 60.10 84.47 83.24 94.66 83.30 36.03 91.71 C27→C09 75.80 87.43 80.69 61.76 64.40 84.93 87.44 90.62 84.68 76.10 92.89 C27→C29 40.38 56.18 51.84 43.75 41.73 75.25 65.38 80.22 70.96 58.02 77.27 C29→C05 27.19 46.33 40.40 18.58 26.98 64.17 53.63 56.15 45.02 26.50 66.45 C29→C07 30.14 47.88 49.29 37.08 32.72 78.76 51.32 73.30 53.96 44.51 66.11 C29→C09 30.02 49.75 44.36 38.36 31.18 74.88 55.76 79.78 56.80 49.82 74.82 C29→C27 33.49 57.31 53.89 29.53 41.96 77.71 58.49 90.24 62.75 43.74 81.59 平均值 44.82 60.55 56.77 42.98 39.64 75.19 64.93 79.70 65.43 44.78 77.47 表 6 基于Amazon_review数据集的域适应准确率Table 6 Accuracy on Amazon_review dataset% 任务 TCA JDA TJM GFK CORAL JGSA JPDA SALFL TSRP TSK-FC
(one-order)本文算法 B→D 64.93 61.23 69.03 67.03 78.09 68.23 61.03 78.94 66.18 78.24 80.19 B→E 65.02 62.86 66.02 64.76 76.67 68.47 61.86 79.53 68.02 76.37 79.88 B→K 66.88 60.68 68.08 65.53 78.38 67.08 62.53 79.24 70.04 78.68 80.99 D→B 65.70 59.10 70.60 66.90 78.80 65.45 61.25 78.90 69.05 78.30 79.35 D→E 63.01 60.26 69.27 65.67 76.38 70.52 60.46 79.73 70.92 73.72 81.13 D→K 63.28 60.48 67.68 67.78 78.28 72.04 60.68 80.79 70.99 77.43 84.79 E→B 62.65 56.55 68.35 64.7 74.75 64.25 59.70 74.95 67.50 73.65 76.45 E→D 61.98 57.53 69.43 67.13 73.94 66.23 59.28 77.19 67.83 72.64 78.29 E→K 69.33 64.53 74.74 70.64 83.59 75.24 65.93 84.64 73.94 82.79 85.19 K→B 62.60 58.80 66.10 65.65 74.75 66.95 59.25 74.95 64.95 74.20 76.60 K→D 60.33 62.48 67.48 66.18 74.43 62.98 62.78 75.19 66.38 74.08 77.04 K→E 70.22 65.41 76.13 72.72 82.88 73.12 67.17 81.73 75.78 82.78 82.43 平均值 64.66 60.83 69.41 67.06 77.58 68.38 61.83 78.82 69.30 76.91 80.19 Office+Caltech数据集的浅层特征和深层特征的分类准确率分别列于表3和表4。从表3中可以看出，所提出的DA-TSK-PLR-FC方法整体上优于其他对比方法。在浅层特征上，GFK方法准确率最低，而SALFL最高。相比GFK和SALFL，本方法的平均准确率分别提高了9.72百分点和2.80百分点。与浅层特征相比，所有方法在深层特征上均取得了显著提升，证明了深度学习在计算机视觉处理的优越性。在深层特征分类中，TSRP算法略微优于本算法，可能是因为TSRP算法消除了含有错误伪标签的样本，有效减少模型训练的干扰因素。此外，JGSA在浅层和深层特征的分类结果中均表现良好，说明综合考虑几何信息和统计信息是必要的。
在Office+Caltech数据集中，深层特征是稀疏的，因此DA-TSK-PLR-FC通过TSK模糊规则将原始特征进行高维映射可以更好地捕捉非线性特征间的关系。然而，这种维度补充的方法似乎不适用于CMU-PIE数据集。表5给出了所有算法在人脸数据集CMU-PIE上的准确率。与SALFL算法相比，DA-TSK-PLR-FC可能引入了冗余特征，反而削弱了模型能力。尽管如此，DA-TSK-PLR-FC的性能仍优于SALFL外的其他算法，与当前较优的域适应算法JGSA相比平均提升约2.28百分点。
在Amazon_review数据集上进行了一系列比较，结果如表6所示。整体来看，DA-TSK-PLR-FC具有最佳的平均准确率，相对于最佳基线SALFL取得了1.37百分点的提升。可以观察到，TSK-FC(one-order)在文本数据集上的平均准确率明显超越了多数域适应方法，表明其在处理二分类文本数据集时能够捕捉到更多有效特征信息。对比TSK-FC(one-order)方法，本方法的平均准确率提高了3.28百分点，验证了结合TSK模糊规则和域适应方法的有效性。此外，与JDA相比，TSRP的平均准确率显著提升，因为TSRP在JDA的基础上提高了伪标签的准确性。可见，错误的伪标签在迭代过程中会不断累积误差，从而对模型性能产生负面影响。这也是本研究希望通过标签过滤来提高伪标签质量的根本原因。
3.4 参数分析
3.4.1 模糊规则数
为了探究DA-TSK-PLR-FC算法的效果，本研究采用不同模糊规则数量进行实验。图4给出了Office+Caltech浅层特征数据集和CMU-PIE数据集中任意两个UDA任务的准确率。由于这两个数据集均为高维数据，随着规则数的增加，复杂度显著增加。然而，在高维CMU-PIE数据集中，更明显地观察到当规则数超过2时准确率下降，表明对于高维数据，增加规则数量可能增加算法过拟合的风险。因此，针对高维数据集，建议优先采用较少的模糊规则数量。同时，降低模糊规则的复杂性有助于提高分类器的可解释性[30]。
图 4 随着模糊规则数量变化而变化的准确率Fig. 4 Accuracy changes with the number of rules下载:
全尺寸图片
3.4.2 正则化参数
为了探究DA-TSK-PLR-FC中唯一的正则化参数λ，选取Office+Caltech浅层特征数据集中3个任务进行参数敏感度分析。3个任务分别是“A→C”、“A→W”和“A→D”。λ的取值设置为{0.01,0.1,1,10,100,
1000 }。如图5(a)所示，DA-TSK-PLR-FC方法的性能对正则化参数λ表现出敏感性，最佳分类结果集中出现在λ=100或 λ=1000 因此，为了进一步探究正则化参数λ对Accuracy的影响，在“A→C”、“A→W”和“A→D”这3个UDA任务中进一步进行参数敏感度分析。将λ的取值设置为{100, 200, 300, 400, 500, 600, 700, 800, 900,1000} ，分析结果如图5(b)所示。
图 5 正则化参数λ的分析Fig. 5 Analysis of regularization parameter λ下载:
全尺寸图片
3.5 消融分析
为了确定DA-TSK-PLR-FC算法中各模块的有效性，将DA-TSK-PLR-FC算法进行消融。具体而言，设计两个比较模型，分别去除基于图的随机游走和标签过滤两个模块。然后将DA-TSK-PLR-FC算法与两个比较模型进行对比。图6给出了基于Office+Caltech数据集的浅层特征的对比结果。可以看出，基于图的随机游走和标签过滤两个模块对算法性均有显著贡献，尤其是前者。
图 6 消融分析Fig. 6 Ablation analysis下载:
全尺寸图片
3.6 可解释性分析
区别于其他域适应算法，DA-TSK-PLR-FC方法基于多输出TSK模糊规则进行特征映射，其显著特点是可解释性，能够通过一组规则解释特征映射过程。DA-TSK-PLR-FC中关于模糊规则的构建如下：
IF:
$x_1 $ is$ \zeta _1^k\left( {c_1^k,\delta _1^k} \right) \wedge {x_2} $ is$\zeta _2^k\left( {c_2^k,\delta _2^k} \right) \wedge \cdots \wedge {x_d} $ is$ \zeta _d^k\left( {c_d^k,\delta _d^k} \right) $ ,$$ {\mathrm{Then}}:\; {{l}}_{k}\left({\boldsymbol{x}}\right)=\left[\begin{array}{l}{\left({p}_{0}^{k}\right)}^{1}+{\left({p}_{1}^{k}\right)}^{1}{x}_{1}+\cdots +{\left({p}_{d}^{k}\right)}^{1}{x}_{d} \\ {\left({p}_{0}^{k}\right)}^{2}+{\left({p}_{1}^{k}\right)}^{2}{x}_{1}+\cdots +{\left({p}_{d}^{k}\right)}^{2}{x}_{d} \\ \qquad\qquad\qquad \vdots \\ {\left({p}_{0}^{k}\right)}^{m}+{\left({p}_{1}^{k}\right)}^{m}{x}_{1}+\cdots +{\left({p}_{d}^{k}\right)}^{m}{x}_{d} \end{array}\right] $$ 针对任务“C→A”中的源域，DA-TSK-PLR-FC可以构建两条模糊规则和m个特征输出，其中m设置为50，为了便于观察和后续绘图，前件参数的数值统一放大
10000 倍。图7给出了所有模糊规则获得的模糊集对应的高斯隶属函数。图中仅给出该UDA任务的4个维度，包括第1、第2、第799和第800维度。每个模糊隶属度函数都被赋予一个语言描述。以第1个维度的特征为例，根据模糊集$\zeta _i^k $ (中心$c_i^k$ ，方差$\delta _i^k $ )，第1个模糊规则是(9.9015 ,46.0151 )，第2个模糊规则是(9.9023 ,46.0151 )。按照中心值降序排序，两个模糊规则的隶属函数可以描述为“高”和“低”，其他维度的特征同样按此规则分为两类。根据不同的实际应用，例如医学应用[31]，可以结合专业知识采用不同的语言方式进行描述。
图 7 不同模糊集相关的隶属度函数及其自然语言解释Fig. 7 Membership functions of different fuzzy sets and their natural linguistic interpretations下载:
全尺寸图片
最终，根据模糊规则IF部分的语言释义和THEN部分对应的线性函数，可以给出DA-TSK-PLR-FC模型的2个模糊规则。
第1条模糊规则 如果特征1的值为“低”，特征2的值为“高”，……，特征799的值为“低”，特征800的值为“高”。那么，此规则的50个输出如下：
第1个输出为
$$ \begin{gathered} {\text{0}}{\text{.122 1}} - {\text{0}}{\text{.176 9}}{x_1} + {\text{0}}{\text{.351 3}}{x_2} + \cdots - \\ {\text{0}}{\text{.206 5}}{x_{799}} - {\text{0}}{\text{.012 7}}{x_{800}} \end{gathered} $$ （中间输出省略）
第50个输出为
$$ \begin{gathered} 0.237\;4 + 0.142\;6{x_1} + 0.059\;2{x_2} + \cdots + \\ 0.213\;3{x_{799}} - 0.000\;1{x_{800}} \end{gathered} $$ 第2条模糊规则 如果特征1的值为“高”，特征2的值为“低”，…，特征799的值为“高”，特征800的值为“低”。那么，此规则的50个输出如下：
第1个输出为
$$ \begin{gathered}{\text{0}}{\text{.122 0}} - {\text{0}}{\text{.177 0}}{x_1} + {\text{0}}{\text{.351 6}}{x_2} + \cdots - \\ {\text{0}}{\text{.206 6}}{x_{799}} + {\text{0}}{\text{.012 7}}{x_{800}} \end{gathered} $$ （中间输出省略）
第50个输出为
$$ \begin{gathered}{\text{0}}{\text{.237 3}} + {\text{0}}{\text{.142 5}}{x_1} - {\text{0}}{\text{.059 1}}{x_2} + \cdots - \\ {\text{0}}{\text{.213 1}}{x_{799}}{\text{ + 0}}{\text{.000 1}}{x_{800}} \end{gathered} $$ 3.7 非参数统计分析
为了验证11种算法在3个数据集所有任务上的显著性差异，使用Friedman等级检验和Holm事后检验，显著性水平α设为0.05。首先，通过Friedman等级检验计算每种算法的平均排名。图8给出了各算法的排序结果，DA-TSK-PLR-FC具有明显的优越性。p值为0，表明这些算法之间存在显著的总体差异。随后，进行Holm事后检验，以观察DA-TSK-PLR-FC与其他算法的性能差异。在Holm检验中，通过比较p值与校正因子Holm，判断两种算法之间是否存在显著性差异。
图 8 对比算法的等级检验Fig. 8 Rank test for the comparison algorithm下载:
全尺寸图片
所有对比算法均按照检验过程中获得的z值从大到小排序。检验结果见表7。虽然未拒绝SALFL的假设，但较低的p值仍然表明DA-TSK-PLR-FC算法具有竞争力。
表 7 当α=0.05时，对比算法的Holm检验Table 7 Holm’s test for comparison algorithm when α=0.05$i$ 对比算法 ${\textit{z}} = {{( R_0 - R_i )} \mathord{\left/ {\vphantom {{( R_0 - R_i )} {SE}}} \right. } {{\mathrm{SE}}}}$ $p$ $H_{\mathrm{olm}} = {\alpha \mathord{\left/ {\vphantom {\alpha i}} \right. } i}$ 是否接受假设 10 GFK 10.968705 0 0.005000 拒绝 9 TCA 10.000041 0 0.005556 拒绝 8 CORAL 8.518553 0 0.006250 拒绝 7 JDA 7.863280 0 0.007143 拒绝 6 TSK-FC(one-order) 7.792054 0 0.008333 拒绝 5 TJM 7.777809 0 0.010000 拒绝 4 JPDA 6.039911 0 0.012500 拒绝 3 JGSA 3.945885 0.00008 0.016667 拒绝 2 TSRP 3.903150 0.000095 0.025000 拒绝 1 SALFL 1.666673 0.095579 0.050000 不拒绝 4. 结束语
本研究利用TSK模糊规则的非线性和线性映射能力在源域和目标域数据上学习共享模糊特征空间，基于此提出一种基于伪标签细化的域适应TSK模糊分类器。该分类器在模糊特征空间使用基于图的随机游走策略进行伪标签预测，并采用软标签和硬标签组合编码的方法自适应地优化伪标签质量。大量实验表明，本文提出的方法相较于其他经典的UDA方法具有更优越的性能，并且在统计学上显示出更强的竞争力。此外，本研究从敏感性和可解释性的角度评估了DA-TSK-PLR-FC的性能。
DA-TSK-PLR-FC的分类性能和可解释性虽然得到了验证，但是由于其训练需要目标域特征参与，这在一定程度上限制了DA-TSK-PLR-FC在真实世界数据上的应用。后续研究将探讨如何降低分类器训练时对目标域数据特征的需求。
-
图 1 DA-TSK-PLR-FC框架
Fig. 1 Framework of DA-TSK-PLR-FC
下载:
全尺寸图片
图 2 基于图随机游走
Fig. 2 Graph-based random walking
下载:
全尺寸图片
图 3 伪标签过滤
Fig. 3 Label filtering for pseudo labels
下载:
全尺寸图片
图 4 随着模糊规则数量变化而变化的准确率
Fig. 4 Accuracy changes with the number of rules
下载:
全尺寸图片
图 5 正则化参数λ的分析
Fig. 5 Analysis of regularization parameter λ
下载:
全尺寸图片
图 6 消融分析
Fig. 6 Ablation analysis
下载:
全尺寸图片
图 7 不同模糊集相关的隶属度函数及其自然语言解释
Fig. 7 Membership functions of different fuzzy sets and their natural linguistic interpretations
下载:
全尺寸图片
图 8 对比算法的等级检验
Fig. 8 Rank test for the comparison algorithm
下载:
全尺寸图片
表 1 主要符号定义
Table 1 Main notion definitions
符号 定义 $d$ 原始特征的特征维度 $\lambda $ 正则化参数 ${n_{\rm s}}$/$ {n_{\rm t}} $ 源域或目标域的样本数目 $ {\boldsymbol{X}}_{\rm s} $/$ {\boldsymbol{X}}_{\rm t} $ 原始空间的源域或目标域的样本特征 $ {\boldsymbol{C}}_{\rm s} $/$ {\boldsymbol{C}}_{\rm t} $ 源域或目标域的TSK模糊规则的中心参数 $ {\boldsymbol{B}}_{\rm s} $/$ {\boldsymbol{B}}_{\rm t} $ 源域或目标域的TSK模糊规则的核宽度参数 ${{\boldsymbol{G}}_{\rm s}}$/${{\boldsymbol{G}}_{\rm t}}$ 经过前件部分映射的源域或目标域的样本特征 ${\boldsymbol{P}}$ TSK模糊规则的后件参数 ${\boldsymbol{W}}$ 最近邻图的路径权重矩阵 ${\boldsymbol{A}}$ 亲和矩阵 ${\boldsymbol{M}}$ MMD矩阵 $ {\boldsymbol{F}}_{\rm t} $ 目标域的软伪标签 $ {\boldsymbol{Z}}_{\rm s} $/$ {\boldsymbol{Z}}_{\rm t} $ 共享模糊特征空间的源域或目标域的样本特征 表 2 用于评估域适应方法性能的3个基准数据集
Table 2 Three benchmark datasets for evaluating the performance of domain adaptation methods
数据集 类型 样本量 特征维度 类别数 子集 Office+Caltech 物体识别 2533 SURF:800
DeCAF6:4096 10 Amzaon、Webcam、DSLR、Caltech CMU-PIE 人脸识别 11554 1024 68 C05、C07、C09、C27、C29 Amazon_review 情绪分析 7996 400 2 Books、DVD、Electronics、Kitchen 表 3 基于Office+Caltech数据集的浅层特征的域适应准确率
Table 3 Accuracy on Office+Caltech datasets using SURF features
% 任务 TCA JDA TJM GFK CORAL JGSA JPDA SALFL TSRP TSK-FC
(one-order)本文算法 C→A 45.62 46.66 45.20 41.02 54.28 49.90 47.60 55.43 47.39 52.50 54.28 C→W 39.32 39.32 39.32 40.34 38.64 39.32 45.76 60.00 47.80 47.12 59.32 C→D 45.86 47.13 46.50 41.40 36.31 34.39 46.50 54.14 53.50 43.95 56.69 A→C 42.03 40.61 41.50 40.25 45.06 37.58 40.78 45.77 41.76 43.99 44.88 A→W 40.00 38.31 41.69 40.00 44.41 43.73 40.68 47.12 45.42 38.98 50.17 A→D 35.67 36.94 45.22 36.31 39.49 39.49 36.94 41.40 43.95 42.67 49.68 W→C 31.52 32.41 31.17 30.81 33.75 38.47 34.55 38.56 33.30 33.13 38.74 W→A 30.48 32.98 31.73 31.73 35.91 58.25 33.82 40.61 37.89 36.74 41.75 W→D 91.08 92.35 89.81 88.54 86.62 93.63 88.54 83.44 92.99 84.07 92.36 D→C 32.95 32.06 32.15 30.10 33.84 36.24 34.73 34.91 33.57 30.81 37.04 D→A 32.78 33.82 37.06 31.84 37.68 60.33 34.66 35.70 33.82 33.82 38.83 D→W 87.46 89.83 89.83 84.41 84.75 97.63 91.19 82.71 91.53 81.36 89.83 平均值 46.23 46.87 47.60 44.73 47.56 52.41 47.98 51.65 50.24 47.43 54.45 注：最优分类结果已加粗，下同。 表 4 基于Office+Caltech数据集的深层特征的域适应准确率
Table 4 Accuracy on Office+Caltech datasets using DeCAF6 features
% 任务 TCA JDA TJM GFK CORAL JGSA JPDA SALFL TSRP TSK-FC
(one-order)本文算法 C→A 89.46 90.29 89.04 88.83 91.54 90.08 91.23 92.17 92.38 90.81 92.59 C→W 82.03 85.76 75.93 82.37 74.58 87.46 88.81 93.56 88.47 76.94 92.54 C→D 85.99 89.80 80.25 88.54 84.08 86.62 89.81 88.54 89.17 84.71 89.17 A→C 83.79 82.37 80.41 77.56 82.10 78.18 85.04 85.57 85.40 84.32 86.20 A→W 74.92 84.59 72.88 73.90 72.88 89.49 78.31 81.02 86.44 78.30 87.80 A→D 84.71 84.42 77.71 82.80 80.89 91.72 84.08 87.26 87.26 86.62 87.90 W→C 76.49 83.25 76.31 69.55 71.15 79.25 84.24 81.83 84.33 70.70 80.77 W→A 80.58 88.10 87.37 74.43 79.02 86.95 90.08 85.80 89.98 78.81 88.20 W→D 100.00 100.00 100.00 100.00 100.00 100.00 100.00 96.82 100.00 100.00 100.00 D→C 81.30 85.04 80.32 67.68 70.88 81.12 84.51 74.00 86.46 75.24 80.50 D→A 88.83 91.85 89.56 82.05 79.54 90.08 91.02 88.73 92.80 83.19 90.19 D→W 99.32 99.32 97.29 95.25 98.98 98.98 99.66 93.90 98.31 99.66 99.32 平均值 85.62 88.73 83.92 81.91 82.14 88.33 88.90 87.43 90.08 84.11 89.60 表 5 基于CMU-PIE数据集的域适应准确率
Table 5 Accuracy on CMU-PIE dataset
% 任务 TCA JDA TJM GFK CORAL JGSA JPDA SALFL TSRP TSK-FC
(one-order)本文算法 C05→C07 40.88 58.63 51.93 39.59 34.32 73.97 59.36 61.69 62.49 34.56 71.21 C05→C09 41.79 52.53 51.23 38.91 35.29 72.06 66.67 75.61 58.46 45.65 70.47 C05→C27 59.57 83.59 75.22 58.10 43.98 83.87 83.99 95.31 86.12 61.40 91.74 C05→C29 29.11 47.61 35.78 32.17 24.94 63.48 49.51 67.10 48.16 26.96 61.03 C07→C05 41.63 55.97 47.57 26.92 28.99 66.42 63.00 74.49 59.78 31.90 74.79 C07→C09 51.35 62.82 67.28 60.36 39.71 71.20 60.85 86.27 70.04 35.60 80.39 C07→C27 64.82 77.92 70.44 43.62 53.71 80.05 77.05 89.52 76.54 57.34 89.73 C07→C29 33.58 42.58 37.62 40.63 26.72 73.41 47.67 67.65 44.42 39.03 53.74 C09→C05 34.96 50.12 42.71 28.09 33.25 66.42 59.78 72.72 55.97 37.84 74.52 C09→C07 47.58 57.33 64.27 59.55 44.50 80.85 63.35 81.83 72.44 55.56 77.47 C09→C27 56.77 72.00 69.99 43.29 54.25 81.23 74.47 88.19 76.45 48.09 92.70 C09→C29 33.82 41.97 43.26 44.79 27.45 76.04 52.7 75.43 54.96 31.31 64.95 C27→C05 55.85 79.08 79.44 58.22 46.67 74.67 84.87 93.22 85.23 55.64 94.30 C27→C07 67.71 83.97 78.14 56.29 60.10 84.47 83.24 94.66 83.30 36.03 91.71 C27→C09 75.80 87.43 80.69 61.76 64.40 84.93 87.44 90.62 84.68 76.10 92.89 C27→C29 40.38 56.18 51.84 43.75 41.73 75.25 65.38 80.22 70.96 58.02 77.27 C29→C05 27.19 46.33 40.40 18.58 26.98 64.17 53.63 56.15 45.02 26.50 66.45 C29→C07 30.14 47.88 49.29 37.08 32.72 78.76 51.32 73.30 53.96 44.51 66.11 C29→C09 30.02 49.75 44.36 38.36 31.18 74.88 55.76 79.78 56.80 49.82 74.82 C29→C27 33.49 57.31 53.89 29.53 41.96 77.71 58.49 90.24 62.75 43.74 81.59 平均值 44.82 60.55 56.77 42.98 39.64 75.19 64.93 79.70 65.43 44.78 77.47 表 6 基于Amazon_review数据集的域适应准确率
Table 6 Accuracy on Amazon_review dataset
% 任务 TCA JDA TJM GFK CORAL JGSA JPDA SALFL TSRP TSK-FC
(one-order)本文算法 B→D 64.93 61.23 69.03 67.03 78.09 68.23 61.03 78.94 66.18 78.24 80.19 B→E 65.02 62.86 66.02 64.76 76.67 68.47 61.86 79.53 68.02 76.37 79.88 B→K 66.88 60.68 68.08 65.53 78.38 67.08 62.53 79.24 70.04 78.68 80.99 D→B 65.70 59.10 70.60 66.90 78.80 65.45 61.25 78.90 69.05 78.30 79.35 D→E 63.01 60.26 69.27 65.67 76.38 70.52 60.46 79.73 70.92 73.72 81.13 D→K 63.28 60.48 67.68 67.78 78.28 72.04 60.68 80.79 70.99 77.43 84.79 E→B 62.65 56.55 68.35 64.7 74.75 64.25 59.70 74.95 67.50 73.65 76.45 E→D 61.98 57.53 69.43 67.13 73.94 66.23 59.28 77.19 67.83 72.64 78.29 E→K 69.33 64.53 74.74 70.64 83.59 75.24 65.93 84.64 73.94 82.79 85.19 K→B 62.60 58.80 66.10 65.65 74.75 66.95 59.25 74.95 64.95 74.20 76.60 K→D 60.33 62.48 67.48 66.18 74.43 62.98 62.78 75.19 66.38 74.08 77.04 K→E 70.22 65.41 76.13 72.72 82.88 73.12 67.17 81.73 75.78 82.78 82.43 平均值 64.66 60.83 69.41 67.06 77.58 68.38 61.83 78.82 69.30 76.91 80.19 表 7 当α=0.05时，对比算法的Holm检验
Table 7 Holm’s test for comparison algorithm when α=0.05
$i$ 对比算法 ${\textit{z}} = {{( R_0 - R_i )} \mathord{\left/ {\vphantom {{( R_0 - R_i )} {SE}}} \right. } {{\mathrm{SE}}}}$ $p$ $H_{\mathrm{olm}} = {\alpha \mathord{\left/ {\vphantom {\alpha i}} \right. } i}$ 是否接受假设 10 GFK 10.968705 0 0.005000 拒绝 9 TCA 10.000041 0 0.005556 拒绝 8 CORAL 8.518553 0 0.006250 拒绝 7 JDA 7.863280 0 0.007143 拒绝 6 TSK-FC(one-order) 7.792054 0 0.008333 拒绝 5 TJM 7.777809 0 0.010000 拒绝 4 JPDA 6.039911 0 0.012500 拒绝 3 JGSA 3.945885 0.00008 0.016667 拒绝 2 TSRP 3.903150 0.000095 0.025000 拒绝 1 SALFL 1.666673 0.095579 0.050000 不拒绝 -
[1] PAN S J, YANG Qiang. A survey on transfer learning[J]. IEEE transactions on knowledge and data engineering, 2009, 22(10): 1345−1359. [2] AJITH A, GOPAKUMAR G. Domain adaptation: a survey[M]//Computer Vision and Machine Intelligence. Singapore: Springer Nature Singapore, 2023: 591−602. [3] 李晶晶, 孟利超, 张可, 等. 领域自适应研究综述[J]. 计算机工程, 2021, 47(6): 1−13. LI Jingjing, MENG Lichao, ZHANG Ke, et al. Review of studies on domain adaptation[J]. Computer engineering, 2021, 47(6): 1−13. [4] KOUW W M, LOOG M. A review of domain adaptation without target labels[J]. IEEE transactions on pattern analysis and machine intelligence, 2021, 43(3): 766−785. doi: 10.1109/TPAMI.2019.2945942 [5] GOPALAN R, LI Ruonan, CHELLAPPA R. Domain adaptation for object recognition: an unsupervised approach[C]//2011 International Conference on Computer Vision. Barcelona: IEEE, 2011: 999−1006. [6] GONG Boqing, SHI Yuan, SHA Fei, et al. Geodesic flow kernel for unsupervised domain adaptation[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition. Providence: USA. IEEE, 2012: 2066−2073. [7] FERNANDO B, HABRARD A, SEBBAN M, et al. Unsupervised visual domain adaptation using subspace alignment[C]//2013 IEEE International Conference on Computer Vision. Sydney: IEEE, 2013: 2960−2967. [8] PAN S J, TSANG I W, KWOK J T, et al. Domain adaptation via transfer component analysis[J]. IEEE transactions on neural networks, 2011, 22(2): 199−210. doi: 10.1109/TNN.2010.2091281 [9] LONG Mingsheng, WANG Jianming, DING Guiguang, et al. Transfer feature learning with joint distribution adaptation[C]//2013 IEEE International Conference on Computer Vision. Sydney: IEEE, 2013: 2200−2207. [10] TAKAGI T, SUGENO M. Fuzzy identification of systems and its applications to modeling and control[J]. IEEE transactions on systems, man, and cybernetics: systems, 1985, SMC-15(1): 116−132. doi: 10.1109/TSMC.1985.6313399 [11] YANG Changjian, DENG Zhaohong, CHOI K S, et al. Takagi–Sugeno–Kang transfer learning fuzzy logic system for the adaptive recognition of epileptic electroencephalogram signals[J]. IEEE transactions on fuzzy systems, 2015, 24(5): 1079−1094. [12] FENG Hao, PENG Yaxin, ZHANG Guixu, et al. Joint distribution adaptation based TSK fuzzy logic system for epileptic EEG signal identification[C]//2016 IEEE International Conference on Bioinformatics and Biomedicine (BIBM). Shenzhen: IEEE, 2016: 340−345. [13] XU Peng, DENG Zhaohong, WANG Jun, et al. Transfer representation learning with TSK fuzzy system[J]. IEEE transactions on fuzzy systems, 2019, 29(3): 649−663. [14] WANG Wei, LI Baopu, WANG Mengzhu, et al. Confidence regularized label propagation based domain adaptation[J]. IEEE transactions on circuits and systems for video technology, 2021, 32(6): 3319−3333. [15] ZHANG Yuanpeng, WANG Guanjin, ZHOU Ta, et al. Takagi-Sugeno-Kang fuzzy system fusion: a survey at hierarchical, wide and stacked levels[J]. Information fusion, 2024, 101: 101977. doi: 10.1016/j.inffus.2023.101977 [16] CHUANG C C, HSIAO C C, JENG J T. Adaptive fuzzy regression clustering algorithm for TSK fuzzy modeling[C]//Proceedings 2003 IEEE International Symposium on Computational Intelligence in Robotics and Automation. Computational Intelligence in Robotics and Automation for the New Millennium. Kobe: IEEE, 2003: 201−206. [17] ZHU Lin, CHUNG F L, WANG Shitong. Generalized fuzzy C-means clustering algorithm with improved fuzzy partitions[J]. IEEE transactions on systems, man, and cybernetics, part B (cybernetics), 2009, 39(3): 578−591. doi: 10.1109/TSMCB.2008.2004818 [18] TIAN Qing, SUN Heyang, PENG Shun, et al. Self-adaptive label filtering learning for unsupervised domain adaptation[J]. Frontiers of computer science, 2022, 17(1): 171308. [19] BLITZER J, CRAMMER K, KULESZA A, et al. Learning bounds for domain adaptation[C]//Proceedings of the 21st International Conference on Neural Information Processing Systems. Vancouver: ACM, 2007: 129−136. [20] SAENKO K, KULIS B, FRITZ M, et al. Adapting visual category models to new domains[M]//Computer Vision – ECCV 2010. Berlin: Springer Berlin Heidelberg, 2010: 213−226. [21] GRIFFIN G, HOLUB A, PERONA P. Caltech-256 object category dataset[R]. California Institute of Technology, 2007. [22] SIM T, BAKER S, BSAT M. The CMU pose, illumination, and expression (PIE) database[C]//Proceedings of Fifth IEEE International Conference on Automatic Face Gesture Recognition. Washington, DC: IEEE, 2002: 53−58. [23] BLITZER J, DREDZE M, PEREIRA F. Biographies bollywood boom-boxes and blenders: Domain adaptation for sentiment classification[C]//Proceedings of the 45th Annual Meeting of the Association of Computational Linguistics. Prague: Association for Computational Linguistics, 2007, 7: 440−447. [24] NOZZA D, FERSINI E, MESSINA E. Deep learning and ensemble methods for domain adaptation[C]//2016 IEEE 28th International Conference on Tools with Artificial Intelligence (ICTAI). San Jose: IEEE, 2016: 184−189. [25] LONG Mingsheng, WANG Jianmin, DING Guiguang, et al. Transfer joint matching for unsupervised domain adaptation[C]//2014 IEEE Conference on Computer Vision and Pattern Recognition. Columbus: IEEE, 2014: 1410−1417. [26] SUN Baochen, FENG Jiashi, SAENKO K. Return of frustratingly easy domain adaptation[J]. Proceedings of the AAAI conference on artificial intelligence, 2016, 30(1): 2058−2065. [27] ZHANG Jing, LI Wanqing, OGUNBONA P. Joint geometrical and statistical alignment for visual domain adaptation[C]//2017 IEEE Conference on Computer Vision and Pattern Recognition. Honolulu: IEEE, 2017: 5150−5158. [28] ZHANG Wen, WU Dongrui. Discriminative joint probability maximum mean discrepancy (DJP-MMD) for domain adaptation[C]//2020 International Joint Conference on Neural Networks. Glasgow: IEEE, 2020: 1−8. [29] WANG Jie, ZHANG Xiaolei. Improving pseudo labels with intra-class similarity for unsupervised domain adaptation[J]. Pattern recognition, 2023, 138: 109379. doi: 10.1016/j.patcog.2023.109379 [30] QIN Bin, NOJIMA Y, ISHIBUCHI H, et al. Realizing deep high-order TSK fuzzy classifier by ensembling interpretable zero-order TSK fuzzy subclassifiers[J]. IEEE transactions on fuzzy systems, 2021, 29(11): 3441−3455. doi: 10.1109/TFUZZ.2020.3022574 [31] 丁卫平, 顾卫江, 董建成, 等. 模糊逻辑推理在电子病历智能辅助诊断系统中的应用研究[J]. 南通大学学报(自然科学版), 2006, 5(4): 77−81. DING Weiping, GU Weijiang, DONG Jiancheng, et al. Application of fuzzy logic reasoning in intelligent assistant diagnosis system of electronic patient record[J]. Journal of Nantong University (natural science), 2006, 5(4): 77−81.
