Multi-UAV within-visual-range air combat based on hierarchical multiagent reinforcement learning
-
摘要: 为提高无人机在视距内空战中的自主机动决策能力，本文提出一种基于自博弈理论(self-play，SP)和多智能体分层强化学习(mutil agent hierarchical reinforcement learning，MAHRL)的层次决策网络框架。该框架通过结合自身博弈和多智能体强化学习算法，研究了多无人机空战缠斗场景。复杂的空战任务被分解为上层导弹打击任务和下层飞行跟踪任务，有效地减少了战术行动的模糊性，并提高了多无人机空战场景中的自主机动决策能力。此外，通过设计新颖的奖励函数和采用自博弈方法，减少了大型战场环境导致的无意义探索。仿真结果表明，该算法不仅有助于智能体学习基本的飞行战术和高级的作战战术，而且在防御和进攻能力上优于其他多智能体空战算法。Abstract: To improve the autonomous maneuvering decision-making capabilities of unmanned aerial vehicles (UAVs) in within-visual-range air combat, a hierarchical decision network framework based on self-play theory (SP) and multiagent reinforcement learning (MARL) is proposed in this paper. A multi-UAV dogfight scenario is studied by combining SP and an MARL algorithm. The complex air combat task is divided into upper-level missile strike tasks and lower-level flight tracking tasks, which effectively reduces the fuzziness of tactical action and improves the autonomous maneuvering decision-making ability in a multi-UAV dogfight scenario. In addition, through an innovative reward function design and by adopting the SP method, the algorithm reduces the meaningless exploration of an agent due to the large battlefield environment. Simulation results show that this algorithm can help agents learn basic flight tactics and advanced combat tactics and has better defensive and offensive capabilities compared with other multiagent air combat algorithms.
-
近年来，人工智能技术在军事领域得到了广泛应用，如无人水面飞行器、无人飞行器等[1-2]。特别是采用传统的专家系统、优化、控制和规划进行空战研究[3]。最近，深度强化学习(deep reinforcement learning)的发展已经在空战中取得了各种成果。随着第五代战斗机的发展，空对空作战强调人−无人协同作战。为了保证无人战斗机的机动性，具有良好的视距内空战(within-visual-range air combat，WVR air combat)能力被认为是一项基本任务[4-5]。此外，在未来空战中使用无人机的研究项目正在进行中，包括多无人机超视距空战[6]。本文关注视距内空战的交战模型，即缠斗模型。
尽管现代空战在过去几十年中发生了巨大的变化[7]，但作为视距内空战的代表形式，缠斗仍然是一种不可避免的空对空战斗类型，具有动态变化最快、死亡风险最高、飞行员决策工作量最大的特点[8-10]。为无人机系统提供足够的自主决策能力以替代飞行员进行视距空战，是降低飞行员风险、提高作战效能的潜在途径，这一直是航空领域的研究热点。在智能战斗机援助中，有人驾驶飞机可对多架无人机执行基于任务的制导，从而提高任务性能并降低潜在风险[11]。然而，由于自主空战的高度动态性和复杂性，查阅文献未见针对这一目的的完整解决方案[12]。
缠斗训练的关键是要覆盖一个大的连续状态和行动空间，并在所有的机动中对敌军做出合适的机动。在空战中使用强化学习的挑战之一是缺乏明确定义的奖励函数，这需要专家花费大量时间和精力来设计。为训练创建复杂的奖励也存在问题，因为它们反映了人类的偏见和先入为主的观念，这可能导致智能体的行为被锁定，进而失去学习各种操作和策略的机会[13]。因此，如果在调整奖励反馈频率以鼓励智能体探索的环境中训练智能体，它的表现会更好，效率也会更高[14]。设计良好的对手对于一对一交战是必不可少的，如果智能体只面对策略有限的对手，它就有可能收敛到局部最小值，并且容易受到具有创造性策略的新对手的攻击。早期创造对手以鼓励玩家在不同关卡遇到对手的工作是基于启发式飞行规则或自我博弈[15]。本文提出了一种基于自博弈理论的分层MAPPO(multi-agent proximal policy optimization)算法，用于提升多无人机在空战中的自主决策能力。本文主要贡献如下：
1) 提出了一种分层决策网络，将空战分为上层导弹打击和下层飞行跟踪，使无人机能够更高效地执行机动，从而提升决策速度和准确性。
2) 通过结合自博弈和MAPPO，使得无人机在训练过程中能够对抗先前版本的策略，从而提高学习效率和战术灵活性。
3) 本文针对多无人机空战提出了一种新颖的奖励函数，它帮助智能体在防御和进攻之间取得平衡，同时减少了无目标探索，提高了训练的效率。
1. 相关工作
1.1 视距内空战
视距内空战作为一种不可避免的空战形式，一直是受到广泛关注的热点研究方向。人们一直在研究如何建立能够自主进行空战的算法。目前，典型的空战决策方法包括专家系统、优化理论、博弈论、强化学习算法等。专家系统是最早应用于空战的决策方法，它符合经验丰富的飞行员的分析判断，模拟空战决策过程[16]。在专家系统的基础上，将决策过程划分为态势感知评估[17]、机动意图预测[18]和作战战术决策[19]3个连续环节，并对空战模型进行细化。考虑特定空战场景的要求和约束，引入优化理论以确定某一对抗的最优机动[20]。博弈论作为研究多边决策的一种重要方法，适用于具有约束条件的特定对抗情景下智能体或群体的多方策略优化问题。Li等[21]提出了一种严格约束条件下多无人机空战协同决策的约束策略博弈方法。Ha等[22]建立了各种超视距空战场景的随机博弈模型，包括一系列常规博弈。Liu等[23]将博弈模型与直觉模糊集相结合，提出了弱连通对抗环境下的协同机动决策算法。上述研究均是基于特定场景建立的博弈模型，而对手的机动策略被认为是完全信息，这在实际空战中是未知的。因此，建立不完全信息动态博弈模型是进行协同机动决策的必要条件。
近年来，随着人工智能技术的发展，涌现出许多利用人工智能技术研究无人机空战的方法，这些方法在不同方面取得了突破性进展。当深度强化学习应用于该问题时，Yang等[24]使用深度q网络来训练智能体，该智能体在自定义的三维环境中从一组离散动作中进行选择。Zhang等[25]评估了AFSIM(advanced framework for simulation, integration, and modeling)中用于空中任务建模的各种强化学习算法，发现了能够学习合作策略的智能体。Yoo等[26]使用神经网络来有效地预测对手的运动轨迹。Sun等[27]开发了一种多智能体强化学习算法，该算法使用分层决策网络允许对基本动作(如爬升、转弯、下降等)和连续动作进行离散选择，从而约束这些动作。
1.2 多智能体强化学习
在强化学习(reinforcement learning, RL)中，智能体关注的是学习在给定环境的当前状态下采取什么行动来最大化数值奖励信号[28]。奖励信号由环境提供，智能体通过不断尝试和错误进行学习。因此，强化学习不同于监督学习和无监督学习：监督学习是在由外部提供的标记示例的训练集上执行的；无监督学习不处理标签，而是寻找数据中的一些隐藏结构[29]。强化学习的主要挑战之一是管理探索和利用之间的权衡。当RL智能体通过行动与环境相互作用时，它就开始学习最终产生更高回报的选项。自然地，为了获得最大的奖励，智能体应该通过选择能够带来高奖励的行为来使用它所学到的东西。然而，为了发现最优行为，智能体必须承担风险，探索可能比当前最优行为带来更高回报的新行为。
马尔可夫决策过程(Markov decision processes, MDP)为序列决策问题的建模提供了数学形式。MDP由状态集S、动作集a、传递函数T、奖励函数R组成元组<S, a, T, R>，在马尔可夫博弈中，多智能体环境由一个元组(N, S, a, R, P)表示，其中N为智能体数量，S = S1×S2×…× SN为所有智能体的状态集合，A = A1×A2×…×AN为所有智能体的动作集合，R = r1×r2×…×rN为所有智能体的奖励函数集合，P为环境的状态转移概率。多智能体强化学习的总体目标是为每个智能体学习一种策略，使其自身的累积奖励最大化[30]。
2. 视距内空战博弈对抗方法
人工智能空战的关键是无人机的战术机动规划。无人机的目标是根据双方的当前状态创建一套控制命令，以增强各自的优势。它是一个多输入到多输出的非线性映射问题。本文主要研究2v2缠斗场景，即双方分别为红色和蓝色，在一定空域内进行对抗行动。本节首先建立无人机模型，明确决策模型的状态空间、动作空间和奖励函数。然后介绍了多智能体强化学习算法MAPPO，并将自博弈与MAPPO相结合构建分层决策网络。
2.1 空战环境建模
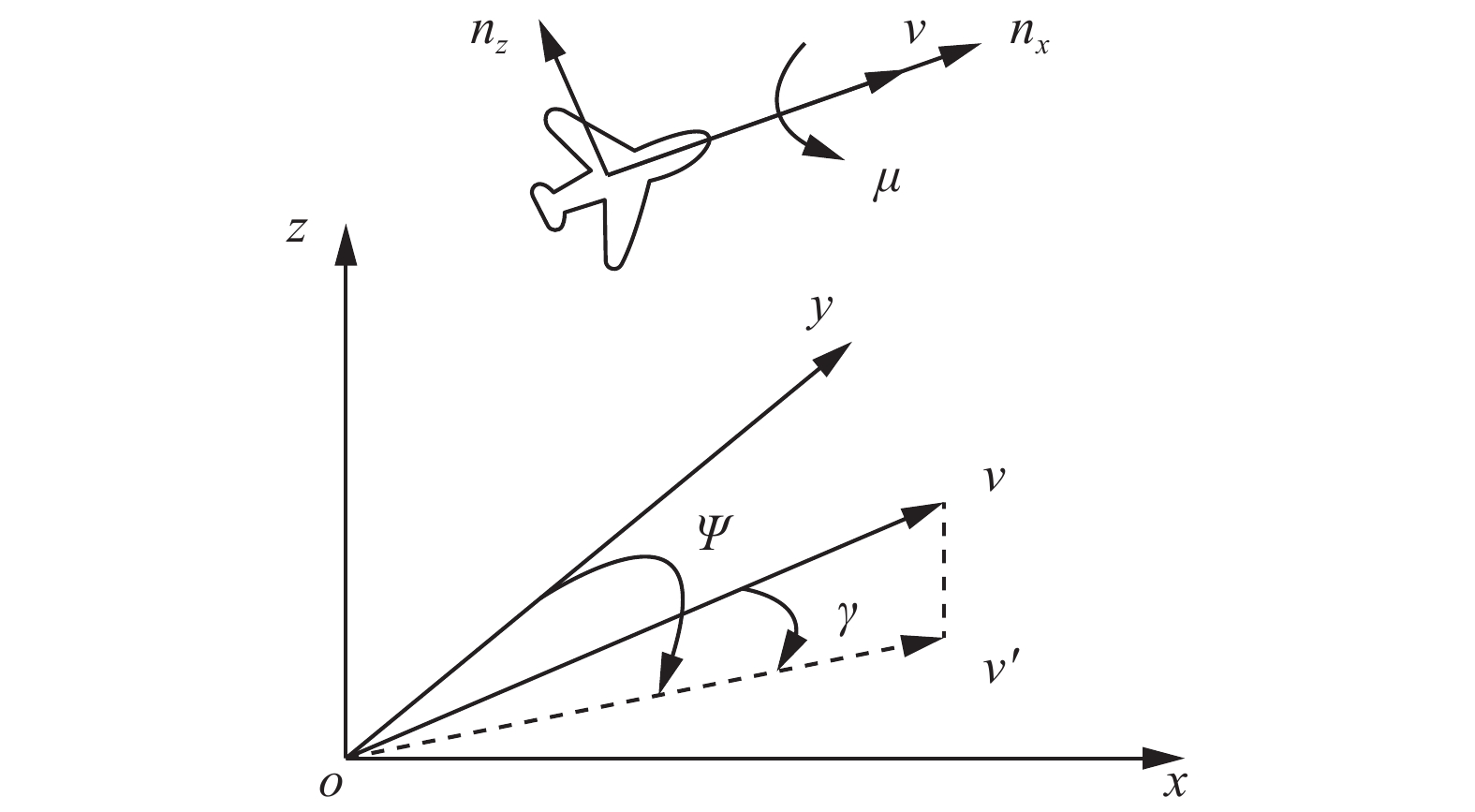
飞机动力学模型是空战模型的基础。由运动模型执行机动决策的控制命令，改变飞机的位置和速度，从而改变空战态势。机动决策主要考虑双方在三维空间中的位置关系和速度矢量，而身体姿态对机动决策的影响较小。因此，采用三自由度粒子模型作为飞机运动模型，在地面坐标系中，x轴为东方向，y轴为北方向，z轴为垂直方向。无人机在坐标系中的运动模型为
$$ \begin{array}{c}\dot{x}=v \cos \, \gamma \sin \, \varPsi \\ \dot{y}=v \cos \, \gamma \cos \, \varPsi \\ \dot{{\textit{z}}}=v \sin \, \gamma \end{array} $$ (1) 式中：(x, y, z)表示飞行器在坐标系中的位置，v表示速度，(
$ \dot{{x}} $ ,$ \dot{{y}} $ ,$ \dot{{\textit{z}}} $ )表示飞行器在3个坐标轴上的速度值，轨迹角γ表示速度矢量与o-x-y水平面的夹角，航向角Ψ表示速度矢量在o-x-y平面上的投影与y轴的夹角。$\gamma $ 和$\varPsi $ 都是飞行时间的函数。飞机的动力学模型为$$ \begin{gathered}\dot{v}= g({n}_{x}- \sin \, \gamma )\\ \dot{\gamma }=\frac{{g}}{v}({n}_{{\textit{z}}} \cos \, \mu - \cos \, \gamma )\\ {\varPsi =\frac{\dot{{g}}{n}_{\textit{z}} \sin \, \mu }{v \cos \, \gamma }}\end{gathered} $$ (2) 式中g表示重力加速度。(nx, nz, µ)是控制飞机机动的一组控制变量，其中nx为速度方向上的过载，表示飞机的推力和减速度；nz表示俯仰方向过载，为正常过载；µ为地面坐标系与人体坐标系的转角。nx控制飞行器的速度，nz和µ控制速度矢量的方向，从而控制飞行器的机动。这3个基本的控制命令可以完成所有的缠斗战术机动。飞机粒子参数模型如图1所示。
图 1 无人机粒子参数模型Fig. 1 Aircraft particle parameter model
下载:
全尺寸图片
完成无人机的模型构建之后，继续构建导弹模型。在惯性坐标系下，导弹运动学方程为
$$ \left\{\begin{array}{l}\dot{x}\left(t\right) =v\left(t\right) \cos \, \theta \left(t\right) \cos \, \phi \left(t\right)\\ \dot{y}\left(t\right) =v\left(t\right) \cos \, \theta \left(t\right) \sin \, \phi \left(t\right)\\ \dot{{\textit{z}}}\left(t\right) =v\left(t\right) \sin \, \theta \left(t\right)\end{array}\right. $$ (3) 式中：(
$ \dot{{x}} $ ,$ \dot{{y}} $ ,$ \dot{{\textit{z}}} $ )为导弹在惯性坐标系中的速度，(v,$ {\theta } $ ,$ {\phi } $ )为导弹的速度、航迹俯仰角和航迹偏航角，它们都是飞行时间t的函数。根据导弹的飞行情况分为主动段和被动段。在惯性系中，作用在导弹主动相上的力主要有推力T(t)、重力G=m(t)g和气动阻力D(t)。因此，在弹道坐标系中，导弹的质点动力学方程为$$ \left\{\begin{array}{c}\dot{v}\left(t\right)= g\left({n}_{x}\right(t) - \sin \, \theta \left(t\right))\\ {\dot \phi \left(t\right) =\dfrac{{g}}{v\left(t\right)}{n}_{y}}\left(t\right) \cos \, \theta \left(t\right)\\ \dot{\theta }\left(t\right) =\dfrac{g}{v\left(t\right)}\left({n}_{\textit{z}}\right(t) - \cos \, \theta \left(t\right))\end{array}\right. $$ (4) 式中：
$ {n}_{x}\left(t\right)=\dfrac{T\left(t\right)-D\left(t\right)}{m\left(t\right)g} $ 为速度方向上的过载，ny、nz为导弹横摆方向和俯仰方向上通过的侧向控制过载，采用过比例制导法计算。M(t)为导弹当前质量，g为重力加速度常数，g=9.81 m/s2。导弹制导模型 导弹制导采用比例制导律。假设两个垂直控制面的制导系数均为
$ {K}_{v} $ =3，则在横摆和俯仰方向上的两个侧向控制过载定义为$$ \left\{\begin{array}{c}{n}_{y}=\dfrac{{{K}}_{v}}{{g}} \dot{\beta } \cos \, \theta \\ {n}_{\textit{z}}=\dfrac{{{K}}_{v}}{{g}}\dot{\varepsilon }+ \cos \, \theta \end{array}\right. $$ (5) 式中：
$ \beta 、\varepsilon $ 为瞄准线角度和瞄准线倾角，$ \dot{\beta }、\dot{\varepsilon } $ 为瞄准线角度导数和瞄准线倾角导数。2.2 问题描述
在2v2无人机缠斗场景中，智能体需要控制两架无人机按目标编队进行战斗，因此所研究的缠斗场景可以看作是两个智能体之间的竞争。本文将该问题表述为一个多智能体马尔可夫决策过程，其中每个智能体由一组状态和一组联合动作组成。每个智能体i观察一个私有状态集
$ {\left\{{{s}}^{{i}}\right\}}_{2}^{{i}=0} $ 和一个与伙伴智能体共享的状态集$ {\left\{{{a}}^{{i}}\right\}}_{2}^{{i}=0} $ ，并通过策略 πi:Si×Ai→{0，1}从动作空间中选择相应的动作。根据状态转移矩阵P：S×$ {{A}}^{1} $ ×$ {{A}}^{2} $ ×S→{0，1}到达下一个状态。每个智能体的目标是最大化其期望的总收益：$$ {{R}}_{{t}}^{{i}}={{\mathrm{E}}}\left[\sum_{{t}=0}^{{T}}{{r}}_{{t}}^{{i}}{{\gamma }}^{{i}}\right] $$ (6) 式中：
$ {r}_{t}^{i} $ 为智能体i在时刻t的奖励值，$ {\mathrm{\gamma }}^{{i}} $ 为折现因子。为了选择最优策略，将优势函数、状态价值函数和行动价值函数定义为$$ \left\{\begin{array}{l}{A}_{{\pi }_{i}}({s}_{t},{a}_{t}^{i}) =Q({s}_{t},{a}_{t}^{i}) -{V}_{{\pi}_{i}}\left({s}_{t}\right)\\ {V}_{{\pi}_{i}}\left({S}_{t}\right) ={\mathrm{E}}\left[{R}_{t}^{i}{|s}_{t}\right]\\ Q({s}_{t},{a}_{t}^{i}) ={\mathrm{E}}\left[{R}_{t}^{i}{|s}_{t},{a}_{t}^{i}\right]\end{array}\right. $$ (7) 式中：
$ {V}_{{\pi }_{i}}({S}_{t}) $ 为状态值函数，Q($ {S}_{t},{a}_{t}^{i} $ )为动作值函数。支配函数反映了智能体i在时刻t采取行动的倾向。本文将2v2缠斗问题视为一个多智能体马尔可夫决策过程，其中每个智能体在每个时刻的行动不仅取决于当前状态，还取决于其历史信息和伙伴智能体的策略。2.3 状态空间和动作空间
多智能体空战决策过程中的状态空间应包括无人机的状态、友机和敌机的观测状态。无人机自身的状态空间为16维，包括无人机的位置信息(经度、纬度、高度)、无人机在地面坐标系和机体坐标系中的速度、无人机的机体角度信息(滚转角、俯仰角、偏航角)、无人机的状态信息(生存、坠毁、击落敌机)、无人机的航向角，以及无人机的加速度信息及其所携带导弹的位置和速度信息。为了完成空战任务，无人机需要计算与敌人的距离，以及无人机的攻角和分离角。
将无人机的动作空间设置为7维空间，包括加速、减速、爬升、俯冲、滚转、偏航和射击，主要由节流阀、副翼、升降舵、方向舵和射击旗控制。节流阀负责控制无人机的动力，完成无人机的加速和减速，副翼用于控制无人机的滚动运动，升降舵用于控制无人机的爬升和俯冲，方向舵控制无人机的偏航，射击旗用于控制导弹的发射。
2.4 奖励函数设计
在强化学习训练中，设计合理的奖励函数可以加速智能体的学习过程，提高智能体的性能，使其能够成功解决复杂环境下的各种任务。在多无人机视距内空战场景中，如果只有一方获胜或失败，则奖励函数过于稀疏。为了使智能体达到预期的效果，本文采用了奖励重塑的方法，根据无人机空战的各个方面，通过重塑奖励函数来加速和引导智能体的训练。
2.4.1 高度奖励
在空战环境中，无人机高度过高则不利于飞行性能，高度过低则会导致无人机坠毁。高度奖励旨在鼓励无人机保持在合适的飞行高度。因此，本文设计了高度奖励函数，对无人机的高度进行惩罚和奖励，确保其在安全范围内飞行。设置海拔奖励功能为
$$ \left\{\begin{array}{l}{R}_{{\mathrm{high}}}={P}_{{\mathrm{vertical}}}+{P}_{{\mathrm{horizontal}}}\\ {P}_{{\mathrm{vertical}}}= -{\mathrm{clip}}\left(\dfrac{{V}_{\textit{z}}}{{K}_{{\mathrm{V}}}}\times \dfrac{{H}_{{\mathrm{s}}}-H}{{H}_{{\mathrm{s}}}},\mathrm{0,1}\right), \quad H \leqslant {H}_{{\mathrm{s}}}\\ {P}_{{\mathrm{high}}}={\mathrm{clip}}\left(\dfrac{H}{{H}_{{\mathrm{d}}}},\mathrm{0,1}\right)-1 , \quad H \geqslant {H}_{{\mathrm{d}}}\end{array}\right. $$ (8) 式中：
$ {V}_{\textit{z}} $ 表示飞行器的垂直速度，H表示飞行器的当前高度，$ {H}_{{\mathrm{s}}} $ 为安全高度的设定值，$ {{H}}_{\mathrm{d}} $ 为危险高度值，KV为增益系数。clip(·,·,·)是截断函数，将取值限制在0～1。2.4.2 事件奖励
在无人机空战场景中有很多事件，如击落敌人、被敌人击落、坠毁等。事件奖励旨在鼓励无人机在战斗中取得胜利。当无人机击落敌人时给予正奖励，当无人机被击落或坠毁时给予负奖励。这样可以激励智能体在战斗中积极进攻，同时注意自身的安全。事件奖励设计为
$$ {R}_{{\mathrm{event}}}=\left\{\begin{array}{l}-200, \qquad 坠毁或被击毁\\ +200, \qquad 击毁敌方无人机\end{array}\right. $$ (9) 当无人机坠毁或被击毁时给予负奖励，当敌方无人机被击毁时给予正奖励。
2.4.3 无人机姿态奖励
姿态奖励旨在鼓励无人机向敌机移动并保持适当的距离。通过计算敌机的方位角和相对方位角，以及无人机与敌机的距离，我们设计了姿态奖励函数，使智能体能够更好地接近敌人并进行攻击。无人机姿态奖励设计为
$$ \left\{\begin{array}{l}{R}_{{\mathrm{p}}}={R}_{{\mathrm{o}}} \cdot {R}_{{\mathrm{r}}}\\ {R}_{{\mathrm{o}}}=\dfrac{1}{2+50 \cdot \dfrac{A_{\mathrm{o}}}{\text{π} }}+ \\ \qquad \min\left(\begin{split}\dfrac{{\tan h}^{-1}\left(1-\max\left(2 \cdot \dfrac{T_{\mathrm{A}}}{\text{π} },{10}^{-4}\right)\right)}{2 \cdot \text{π} }\end{split}\right)+1\\ {R}_{{\mathrm{r}}}={\mathrm{clip}}\left(\dfrac{1.2 \cdot \mathrm{m}\mathrm{i}\mathrm{n}({{\mathrm{e}}}^{-0.021(r-{r}_{t})},1)}{1+{{\mathrm{e}}}^{-0.8(r-{r}_{t}+1)}},\mathrm{0.3,1}\right)\end{array}\right. $$ (10) 式中：AO为敌机的方位角；TA为敌机与自身的相对方位角；r为无人机与敌机的距离，km。Rr表示飞机与敌人之间的期望距离。
2.4.4 导弹姿态奖励
导弹姿态奖励旨在评估导弹对飞机的威胁，从而指导智能体在遇到导弹时采取适当的行动。通过计算导弹与无人机的夹角和速度减少量，本文设计了导弹姿态奖励函数，使智能体能够有效躲避导弹攻击。导弹姿态奖励函数设计为
$$ {R}_{{\mathrm{mp}}}=\left\{\begin{array}{c}\dfrac{\theta }{\mathrm{m}\mathrm{a}\mathrm{x}(v_{\mathrm{d}},0)+1}, \qquad \theta < 0\\ \theta \cdot {\mathrm{max}}(v_{\mathrm{d}},0), \qquad \theta \geqslant 0\end{array}\right. $$ (11) 式中：
$ \theta $ 为导弹与无人机夹角，vd为速度减少量。2.4.5 相对高度奖励
相对高度奖励旨在控制当前战斗机和敌方战斗机的相对高度。通过计算当前战机和敌方战机的相对高度，本文设计了相对高度奖励函数，使智能体能够在战斗中占据有利位置。相对高度奖励函数设计为
$$ {R}_{{\mathrm{rh}}}=\mathrm{m}\mathrm{i}\mathrm{n}({K}_{{\mathrm{H}}}-|{H}_{{\mathrm{s}}}-{H}_{{\mathrm{e}}}|, 0) $$ (12) 式中：
$ {H}_{{\mathrm{s}}} $ 为当前战机的相对高度；He为敌方战机的相对高度；KH是高度差惩罚阈值参数，控制战斗机与敌机的最大允许高度偏差。2.4.6 射击惩罚奖励
射击惩罚奖励旨在避免一次性发射所有导弹。通过在每次发射导弹时给予固定的惩罚，鼓励智能体更谨慎地使用导弹，确保在战斗中有足够的弹药储备。奖励函数设计为
$$ {R}_{{\mathrm{sp}}}=\left\{\begin{array}{l}0, \qquad 无操作\\ -10, \qquad 发射导弹\end{array}\right. $$ (13) 2.5 分层决策网络
MAPPO[31]是一种用于多智能体最近策略优化的深度强化学习算法。在视距内空战缠斗场景下，为平衡飞行任务和导弹打击任务，本文引入了层次强化学习的概念来增强MAPPO，构建了基于自我博弈原则的层次自治决策网络。这种新结构集成了离散和连续的决策元素，使其适应复杂的多智能体环境。
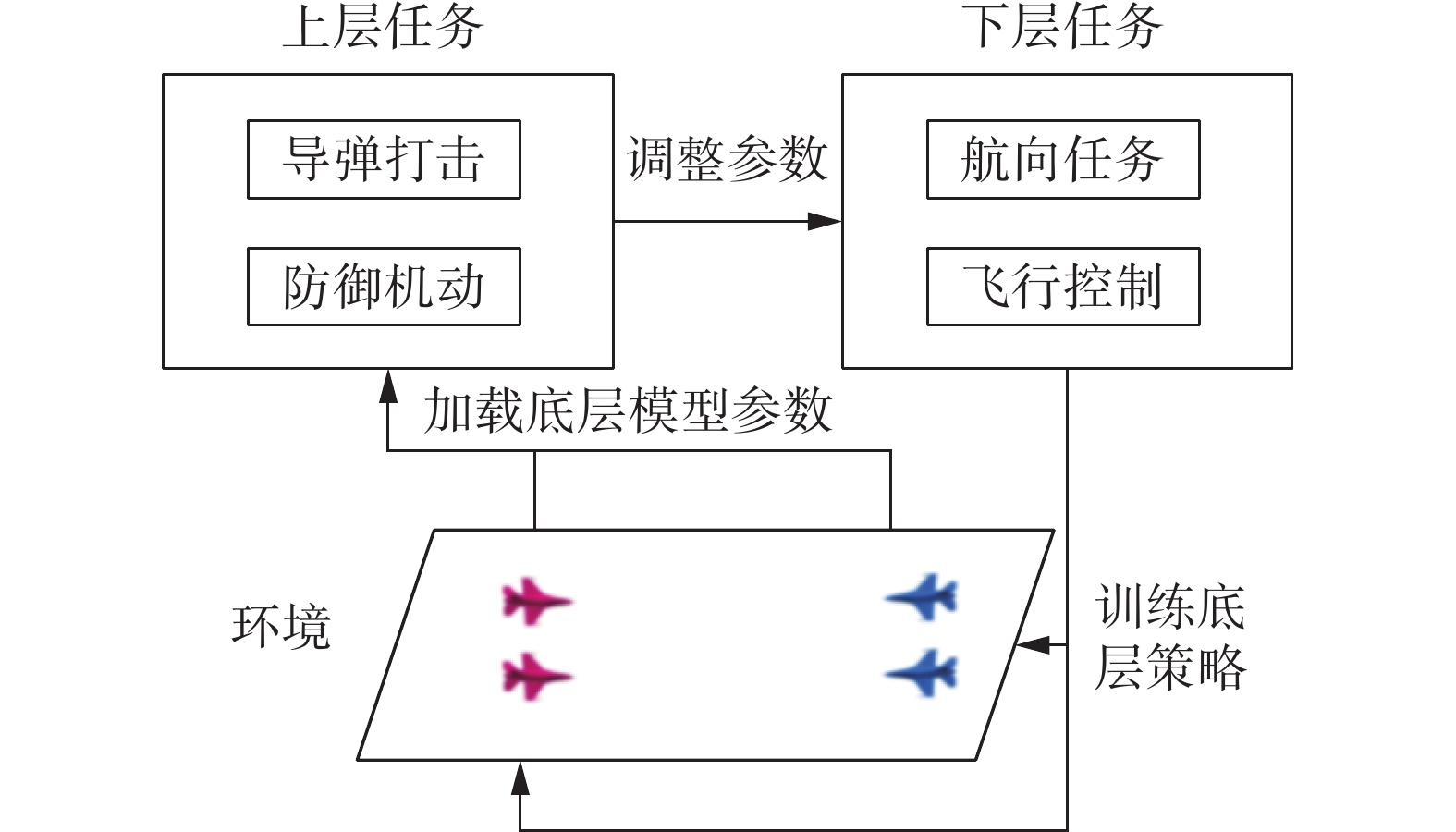
分层MAPPO的决策网络分为上层导弹任务和下层航向任务。上层导弹任务控制无人机学习如何发射导弹和躲避导弹。下层航向任务控制无人机学习飞行控制，以及机动到目标位置。视距内空战分层决策网络如图2所示。
图 2 视距内空战分层决策网络框架Fig. 2 Hierarchical decision network for WVR air combat下载:
全尺寸图片
为了提高算法的训练效率和战术灵活性，本文引入了自博弈技术。在训练过程中，智能体不仅与当前版本的对手策略进行对抗，还会与之前版本的策略进行对抗。通过这种方式，智能体可以不断优化自身的策略，提高在复杂动态环境中的适应能力。
算法训练过程：首先对下层飞行航线任务进行预训练，将预训练得到的模型参数直接输入基础策略网络；随后执行循环训练过程，通过基础策略网络的训练结果训练上层导弹任务，随后在下层网络对航向、飞行姿态的训练进行优化。具体优化过程为：上层网络通过处理观测数据(如无人机速度、位置、加速度、敌机位置等)生成特征表示，作为下层网络的输入；下层网络通过循环神经网络更新特征表示，然后输出具体的动作和概率。通过分层的方式达到降低导弹任务的学习难度的目的。
导弹任务要求无人机学会击落敌人和躲避导弹。在强化学习中，参数化射击策略的方法是训练一个以状态为输入、采样动作为输出的伯努利分布策略网络。然而，使用这种方法可能会导致无意义的探索或取值超出范围。为了解决这个问题，本文采用了一种自我博弈的方法，通过让智能体与不同版本的自己战斗或互动来学习和优化策略。算法1为自博弈算法。
算法1 自博弈算法
1) 初始化策略池和缓冲区。
2) 对于每个episode n：
3) 重置环境和缓冲区
4) for step < buffer_size:
5) 从策略池中获取智能体的动作
6) 从对手策略池中获取对手的动作
7) 获取奖励和当前观察
8) 收集数据并插入缓冲区
9) 计算回报并更新网络
10) 更新episode计数
11) episode = episode +1
12) End
通过在MAPPO算法中结合分层决策和自我博弈，该方法有效地解决了多智能体环境中大型搜索空间的挑战。它允许对战略进行更大的可伸缩和灵活的调整，其中上层战略决策有助于约束和指导下层战术行动的搜索空间。智能体可以在对抗中获得更多的训练数据，学习到更好的策略。特别是在没有真实对手或环境的情况下，这种方法有助于提高强化学习算法的学习效率和性能。
3. 实验结果
本章介绍了空战实验的仿真环境，并从不同的角度对上一章提到的算法进行了实验测试。并与常用多无人机视距空战缠斗自主决策算法进行比较，对实验结果进行了理论分析。
3.1 仿真参数设定
仿真环境基于JSBSim框架[32]，该框架是一种用C++编写的通用面向对象飞行动力学模型(flight dynamics model)。在此基础上，构建多无人机视距内空战缠斗场景，实现基于自演的分层MAPPO算法，对红蓝双方飞机进行对抗训练。
红色和蓝色无人机均使用F16战斗机并携带AIM-9L导弹。在学习过程中，采样时间步长为0.2 s，最大采样步数为
1000 。具体仿真环境参数如表1所示。当其中一架无人机被完全摧毁或两架无人机都处于极端状态或采样步数达到最大采样步数时，仿真结束。表 1 仿真参数Table 1 Simulation parameters仿真实体 变量 取值 飞机 最大速度/(m/s) 670 导弹容量/Pcs 2~5 初始高度/m 6096 俯仰角变化速率/(rad/s) −2×$ \text{π} $~2×$ \text{π} $ 导弹 时间限制/s 180 速度/(m/s) 150~750 重量/kg 84 重量减少速度/(kg/s) 6 最大攻击距离/km 14 环境 采样时间步长/s 0.2 最大采样步数/s
安全高度范围/m200 1000 ～15000 3.2 训练和测试
本节展示了多智能体在视距空战缠斗情况下自主决策算法的训练效果。本文对空战决策过程进行了分层训练。低空航向任务训练无人机按照预定的方向学习飞向目标位置。高级别导弹任务训练无人机执行高级别导弹打击和导弹规避任务。
3.2.1 下层航向任务
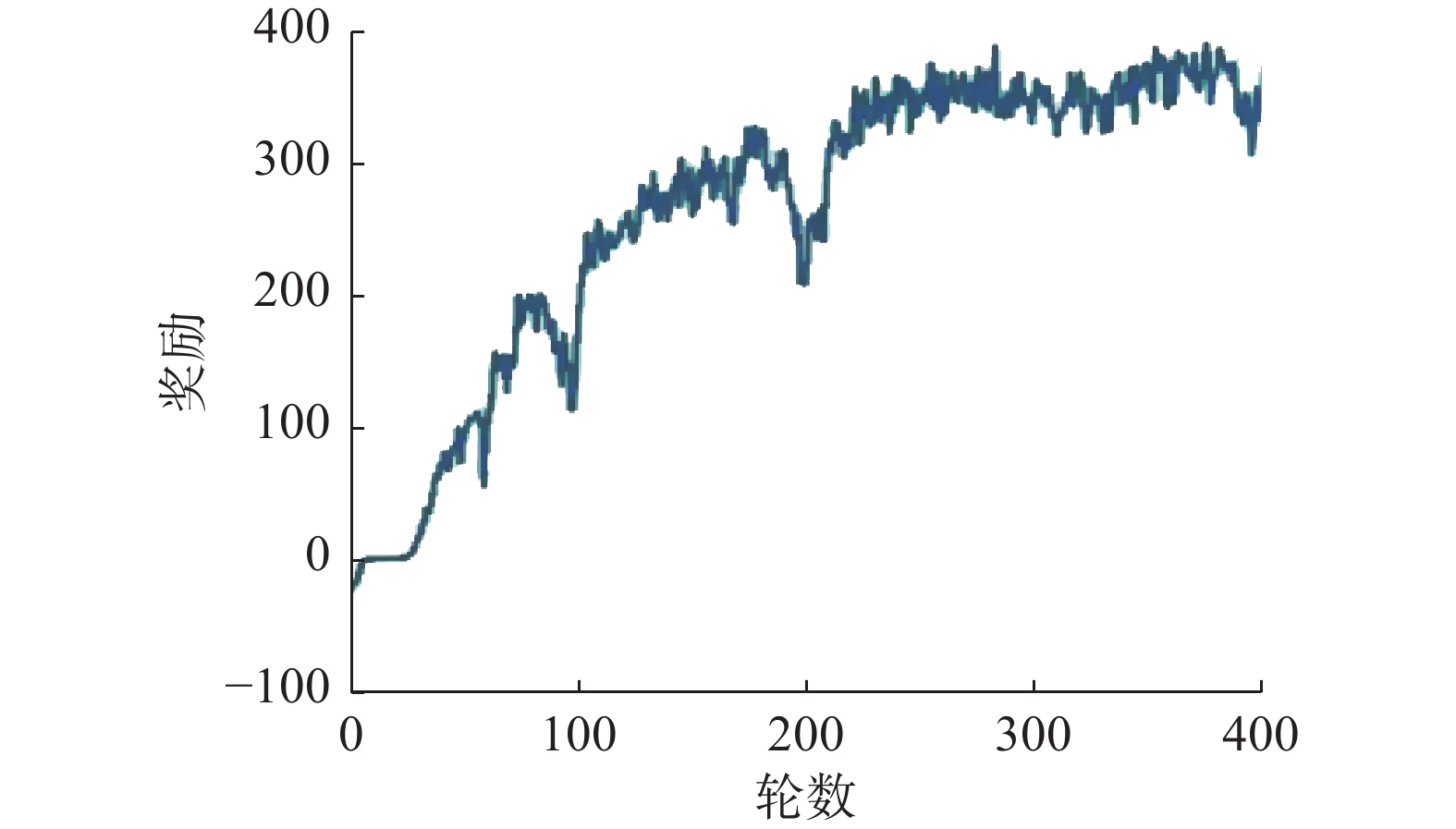
低空无人机智能体飞行学习是一种针对单智能体应用的强化学习方法，使用传统的PPO(proximal policy eptimization)算法进行训练。在训练过程中，蓝色无人机被预先编程，按照特定的轨迹飞行，然后训练红色无人机跟随蓝色无人机。具体的训练结果如图3和图4所示。图3给出了低标题任务的奖励曲线可以看出，经过250轮训练后，智能体的策略奖励逐渐收敛。
图 3 下层航向任务奖励曲线Fig. 3 Low level heading task reward curve下载:
全尺寸图片
图4为红色无人机在蓝色无人机不同预设轨迹下的跟随效果。从图4(a)可以看出，在初始状态下，红蓝无人机方向相反。当蓝色无人机按照预设的轨迹进行机动时，红色无人机可以立即根据蓝色无人机轨迹的变化进行机动，然后完成蓝色无人机的后续操作。图4(b)～(d)分别为蓝色无人机预设了不同的复杂轨迹，其中包含三角形、矩形、六边形轨迹。可以看出，红色无人机仍然能够及时根据蓝色的弹道进行相应的机动，说明在下层任务训练中获得的无人机能够在复杂的轨迹下完成后续任务，从而用于上层导弹打击任务的训练。
图 4 下层航向任务仿真场景Fig. 4 Low level heading task simulation scenario下载:
全尺寸图片
3.2.2 上层导弹任务
在上层导弹任务训练过程中，战场上的无人机首先预加载下层航向任务训练的模型参数，并基于此学习导弹任务。在初始训练状态下，双方无人机相互飞向对方，在随后的连续训练中学习何时发射导弹，并通过自身的机动学习躲避敌方导弹。具体的训练结果如图5和图6所示。
图 5 1v1视距内空战奖励曲线Fig. 5 1v1 WVR combat reward curve下载:
全尺寸图片
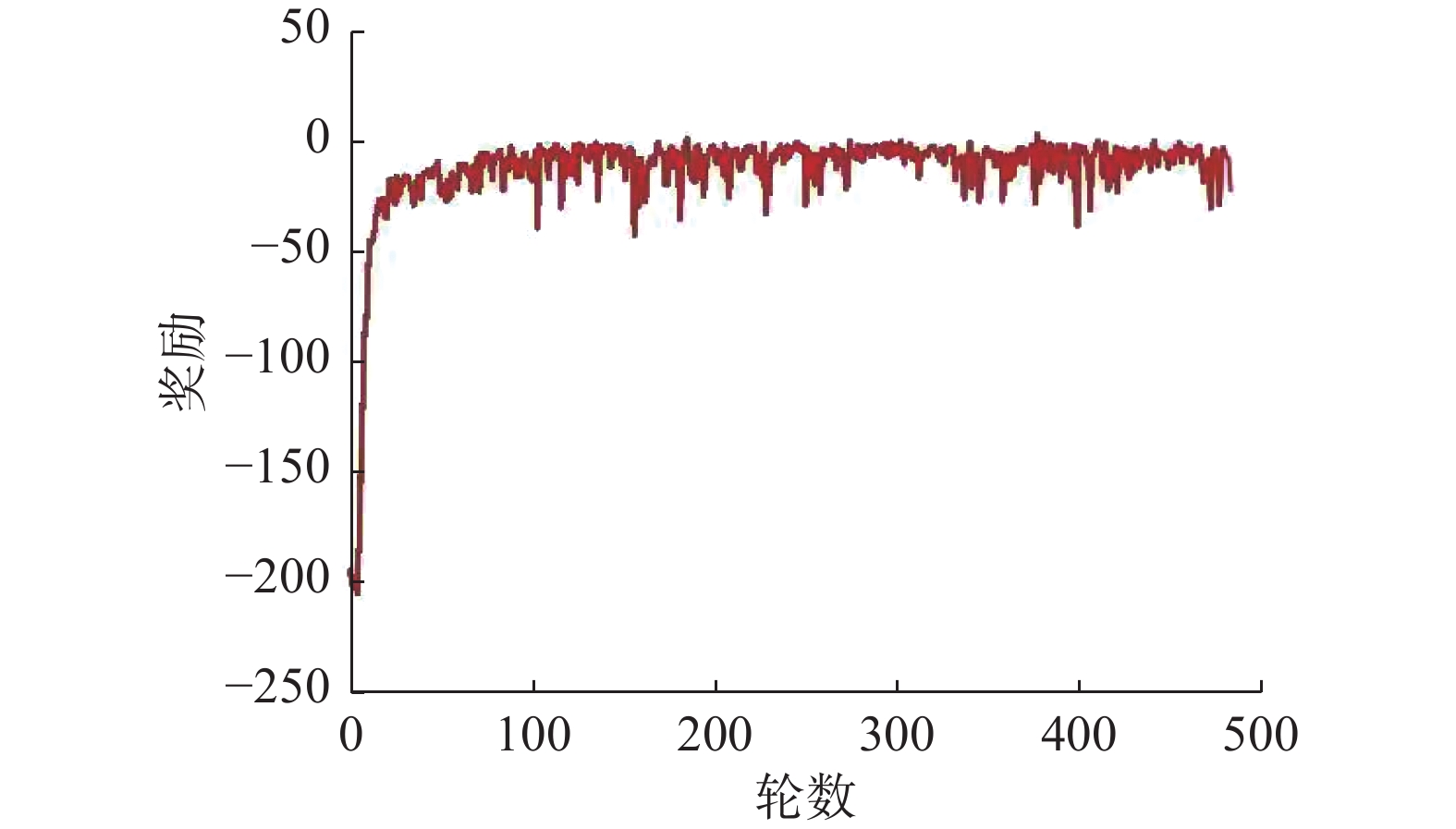
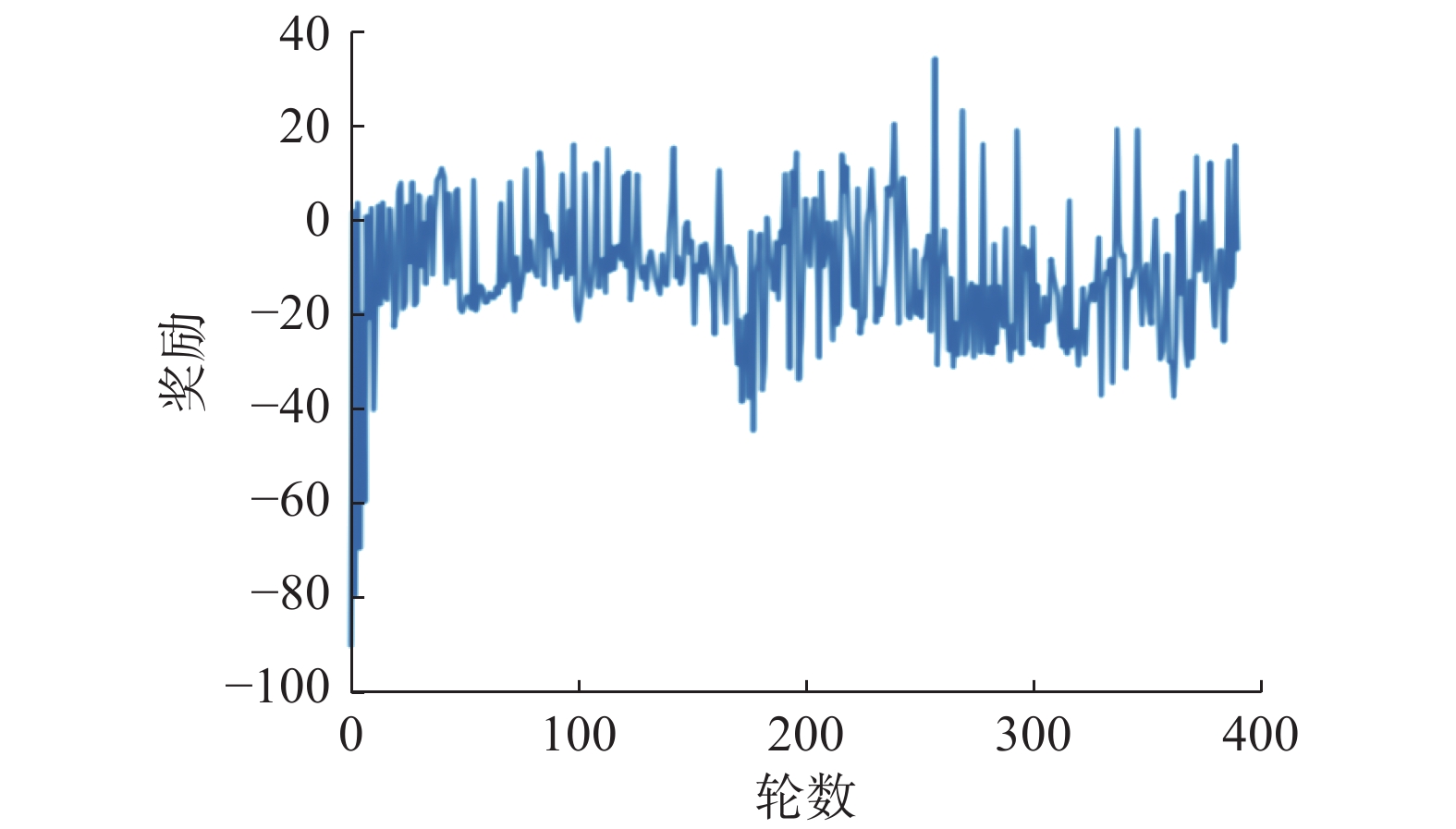
图5为1v1导弹打击任务中红蓝无人机的平均奖励函数。该算法收敛速度快，无人机能很好地学习导弹打击和躲避。图6给出了2v2导弹打击任务中红色和蓝色智能体的平均奖励曲线。从图中可以看出，平均奖励从负积分开始逐渐增加，这意味着本文算法可以帮助智能体在视距内空战中实现自主决策。同时，观察到平均奖励最终收敛于−20.0～20.0。这是因为在训练的初始阶段，两架无人机的起始方向是相对的，相互击中的概率非常高。平均奖励在正负范围内波动，这意味着红色和蓝色智能体力在对抗性训练中具有相似的战斗能力。
图 6 2v2视距内空战奖励曲线Fig. 6 2v2 WVR combat reward curve下载:
全尺寸图片
算法仿真测试结果如图7和图8所示。红色和蓝色无人机都是本文算法训练的智能体。不同之处在于红方智能体加载的模型参数训练效果较好，而蓝方智能体加载的模型参数效果一般。
图 7 防御转向战术Fig. 7 Defence turning after shoot下载:
全尺寸图片
图 8 击中敌方并逃脱Fig. 8 Shoot down enemy and escape下载:
全尺寸图片
图7和图8分别为红蓝无人机在作战过程中的自主决策情况。从图7中可以看出，当红蓝双方的无人机检测到对方的无人机进入打击区域后，会发射导弹进行打击。由于双方在战场上的初始路线是相互飞向对方的，为避免被对方的导弹击中，特工们立即采取防御转向战术。
图8给出了两架战斗机随后躲避导弹的战术决策。可以看出，红色无人机为躲避蓝色导弹的攻击，选择了转向和俯冲等机动动作。最终躲过了一架蓝色无人机的导弹。虽然蓝色战斗机也采取俯冲战术来躲避导弹，但由于其装载模型不够精良，最终被红方无人机的导弹击中。
3.3 对比实验
为了证明算法的学习性能，将本文提出的基于自博弈的分层MAPPO算法与传统的多智能体强化学习控制算法MAPPO和MADDPG的性能进行了比较[33]。MAPPO和MADDPG均是基于策略梯度的多智能体强化学习算法，基于分布式参与者和集中式评论家训练。两者的区别在于MAPPO是一种同策略算法，而MADDPG是一种策略外算法。
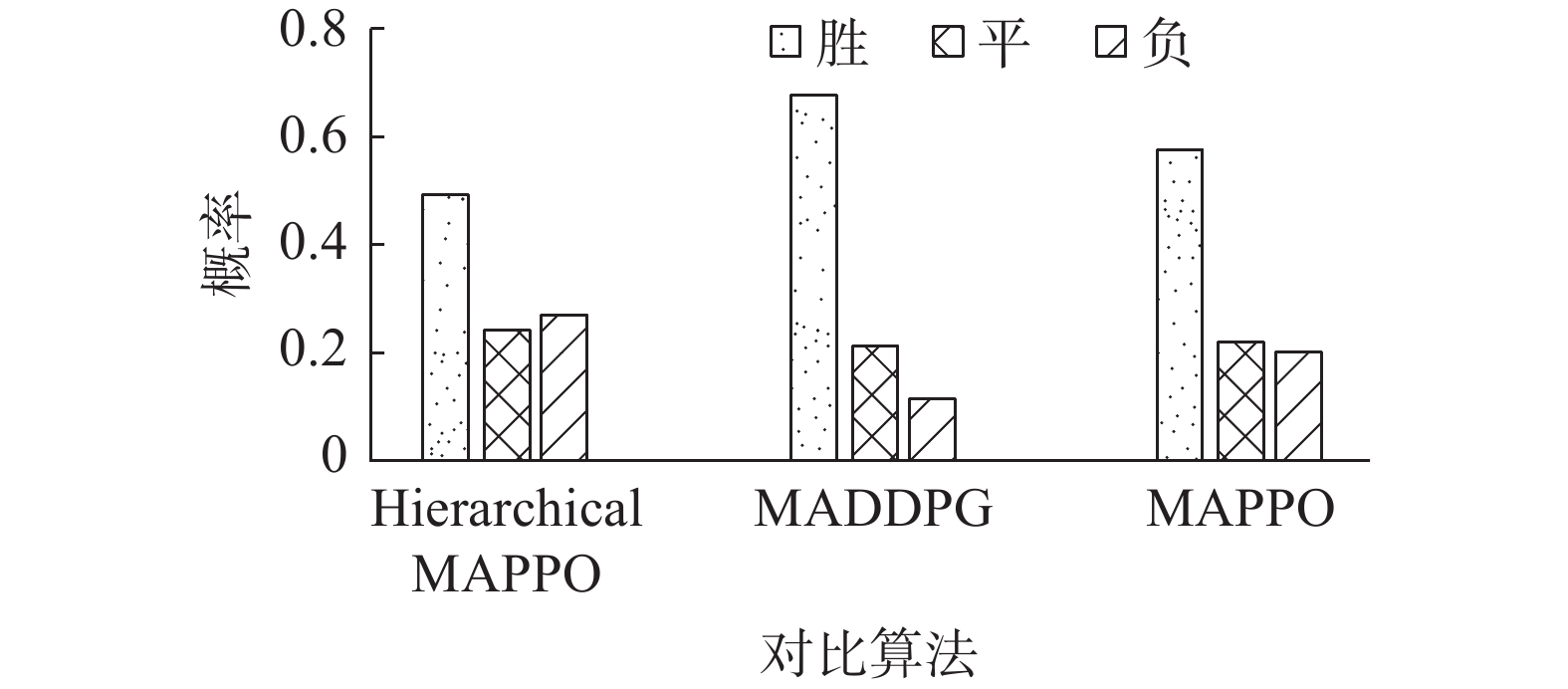
本文设计了30种不同初始条件的2v2视距空战场景，包括红蓝两方的初始相对角度和初始速度方向。在这些场景下，对该算法与传统的多智能体算法进行了仿真测试。仿真结束时，以双方剩余无人机数量作为胜负判定标准。结果如图9所示。
图 9 不同算法对应的空战仿真结果Fig. 9 Simulation results of air combat corresponding to different algorithms下载:
全尺寸图片
从图中可以看出，本文算法在复杂动态环境下的视距内空战任务中取得了显著的性能优势。与传统多智能体强化学习算法MAPPO和MADDPG相比，本文算法取得了更高的胜率，证明了分层强化学习算法在这种具有挑战性的任务环境下具有优异的性能。分析图中数据可以看出，加入了自博弈的分层MAPPO算法效果优于常规的分层MAPPO算法。并且可以明显看出，在对算法进行分层之后效果要比经典的多智能体强化学习算法性能更好。
分析表明，分层MAPPO算法的性能优势在于它能够在自我博弈的框架下有效地整合智能体决策。与传统算法相比，该方法通过自对抗机制使智能体具有更强的自适应能力，使其在复杂的动态环境中能够更好地理解和适应对手的策略。因此，本研究结果不仅对提升多智能体系统在空战任务中的性能具有重要意义，同时地为自演引导的分层强化学习方法的未来发展提供了强有力的支持。
4. 结束语
本文针对视距内空战中的多智能体自主决策问题，提出了一种基于自博弈的分层决策网络。建立了空战仿真环境和无人机、导弹的物理模型，并设计了充分的实验来证明该算法的有效性。实验结果表明，基于本文算法训练的无人机智能体不仅可以学习基本的机动动作，还可以通过不断的探索学习攻防战术，为视距内空战的自主决策场景提供了强有力的支持。后续工作将把研究扩展到涉及各种复杂任务和更多无人机的场景。
-
图 1 无人机粒子参数模型
Fig. 1 Aircraft particle parameter model
下载:
全尺寸图片
图 2 视距内空战分层决策网络框架
Fig. 2 Hierarchical decision network for WVR air combat
下载:
全尺寸图片
图 3 下层航向任务奖励曲线
Fig. 3 Low level heading task reward curve
下载:
全尺寸图片
图 4 下层航向任务仿真场景
Fig. 4 Low level heading task simulation scenario
下载:
全尺寸图片
图 5 1v1视距内空战奖励曲线
Fig. 5 1v1 WVR combat reward curve
下载:
全尺寸图片
图 6 2v2视距内空战奖励曲线
Fig. 6 2v2 WVR combat reward curve
下载:
全尺寸图片
图 7 防御转向战术
Fig. 7 Defence turning after shoot
下载:
全尺寸图片
图 8 击中敌方并逃脱
Fig. 8 Shoot down enemy and escape
下载:
全尺寸图片
图 9 不同算法对应的空战仿真结果
Fig. 9 Simulation results of air combat corresponding to different algorithms
下载:
全尺寸图片
表 1 仿真参数
Table 1 Simulation parameters
仿真实体 变量 取值 飞机 最大速度/(m/s) 670 导弹容量/Pcs 2~5 初始高度/m 6096 俯仰角变化速率/(rad/s) −2×$ \text{π} $~2×$ \text{π} $ 导弹 时间限制/s 180 速度/(m/s) 150~750 重量/kg 84 重量减少速度/(kg/s) 6 最大攻击距离/km 14 环境 采样时间步长/s 0.2 最大采样步数/s
安全高度范围/m200 1000 ～15000 -
[1] ZHAO Yujiao, QI Xin, MA Yong, et al. Path following optimization for an underactuated USV using smoothly-convergent deep reinforcement learning[J]. IEEE transactions on intelligent transportation systems, 2021, 22(10): 6208−6220. doi: 10.1109/TITS.2020.2989352 [2] WANG Yuan, ZHANG Xiwen, ZHOU Rong, et al. Research on UCAV maneuvering decision method based on heuristic reinforcement learning[J]. Computational intelligence and neuroscience, 2022, 2022(1): 1477078. [3] ERNEST N, COHEN K, KIVELEVITCH E, et al. Genetic fuzzy trees and their application towards autonomous training and control of a squadron of unmanned combat aerial vehicles[J]. Unmanned systems, 2015, 3(3): 185−204. doi: 10.1142/S2301385015500120 [4] CHAI Jiajun, CHEN Wenzhang, ZHU Yuanheng, et al. A hierarchical deep reinforcement learning framework for 6-DOF UCAV air-to-air combat[J]. IEEE transactions on systems, man, and cybernetics: systems, 2023, 53(9): 5417−5429. doi: 10.1109/TSMC.2023.3270444 [5] POPE A P, IDE J S, MIĆOVIĆ D, et al. Hierarchical reinforcement learning for air combat at DARPA’s AlphaDogfight trials[J]. IEEE transactions on artificial intelligence, 2023, 4(6): 1371−1385. doi: 10.1109/TAI.2022.3222143 [6] HU Dongyuan, YANG Rennong, ZUO Jialiang, et al. Application of deep reinforcement learning in maneuver planning of beyond-visual-range air combat[J]. IEEE access, 2021, 9: 32282−32297. doi: 10.1109/ACCESS.2021.3060426 [7] CRUMPACKER J B, ROBBINS M J, JENKINS P R. An approximate dynamic programming approach for solving an air combat maneuvering problem[J]. Expert systems with applications, 2022, 203: 117448. doi: 10.1016/j.eswa.2022.117448 [8] RUAN Wanying, DUAN Haibin, DENG Yimin. Autonomous maneuver decisions via transfer learning pigeon-inspired optimization for UCAVs in dogfight engagements[J]. IEEE/CAA journal of automatica sinica, 2022, 9(9): 1639−1657. doi: 10.1109/JAS.2022.105803 [9] WANG Maolin, WANG Lixin, YUE Ting, et al. Influence of unmanned combat aerial vehicle agility on short-range aerial combat effectiveness[J]. Aerospace science and technology, 2020, 96: 105534. doi: 10.1016/j.ast.2019.105534 [10] DOURADO A O, MARTIN C A. New concept of dynamic flight simulator, Part I[J]. Aerospace science and technology, 2013, 30(1): 79−82. doi: 10.1016/j.ast.2013.07.005 [11] PATIL V, POTPHODE V, POTDUKHE U, et al. Smart UAV framework for multi-assistance[C]//ICT with Intelligent Applications. Singapore: Springer Singapore, 2022: 241−249. [12] DONG Yiqun, AI Jianliang, LIU Jiquan. Guidance and control for own aircraft in the autonomous air combat: a historical review and future prospects[J]. Proceedings of the institution of mechanical engineers, Part G: journal of aerospace engineering, 2019, 233(16): 5943−5991. doi: 10.1177/0954410019889447 [13] NG A Y, HARADA D, RUSSEL S. Policy invariance under reward transformations: theory and application to reward shaping[C]//Proceedings of the International Conference on Machine Learning. Bled: ICML, 1999: 278−287. [14] HARTIKAINEN K, GENG Xinyang, HAARNOJA T, et al. Dynamical distance learning for semi-supervised and unsupervised skill discovery[EB/OL]. (2019−11−16)[2024−01−01]. https://arxiv.org/abs/1907.08225v4. [15] KONG Weiren, ZHOU Deyun, ZHOU Ying, et al. Hierarchical reinforcement learning from competitive self-play for dual-aircraft formation air combat[J]. Journal of computational design and engineering, 2023, 10(2): 830−859. doi: 10.1093/jcde/qwad020 [16] HUANG Changqiang, WEI Zhenglei, YANG Yuanzhi, et al. Knowledge acquisition for the air combat based on GWO[J]. Journal of physics: conference series, 2019, 1325(1): 012078. doi: 10.1088/1742-6596/1325/1/012078 [17] 陈虎. 多机协同多目标空战智能优化决策研究[D]. 南京: 南京航空航天大学, 2021. CHEN Hu. Research on intelligent optimization decision of multi-aircraft cooperative multi-target air combat[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2021. [18] 张鹏程. 基于博弈的空中目标航迹预测及攻防对抗研究[D]. 杭州: 浙江大学, 2023. ZHANG Pengcheng. Research on air target track prediction and attack-defense confrontation based on game theory[D]. Hangzhou: Zhejiang University, 2023. [19] 张立鹏, 魏瑞轩, 李霞. 无人作战飞机空战自主战术决策方法研究[J]. 电光与控制, 2012, 19(2): 92. doi: 10.3969/j.issn.1671-637X.2012.02.022 ZHANG Lipeng, WEI Ruixuan, LI Xia. Autonomous tactical decision-making of UCAVs in air combat[J]. Electronics optics & control, 2012, 19(2): 92. doi: 10.3969/j.issn.1671-637X.2012.02.022 [20] LI Weihua, SHI Jingping, WU Yunyan, et al. A Multi-UCAV cooperative occupation method based on weapon engagement zones for beyond-visual-range air combat[J]. Defence technology, 2022, 18(6): 1006−1022. doi: 10.1016/j.dt.2021.04.009 [21] LI Shouyi, CHEN Mou, WANG Yuhui, et al. Air combat decision-making of multiple UCAVs based on constraint strategy games[J]. Defence technology, 2022, 18(3): 368−383. doi: 10.1016/j.dt.2021.01.005 [22] HA J S, CHAE H J, CHOI H L. A stochastic game-theoretic approach for analysis of multiple cooperative air combat[C]//2015 American Control Conference. Chicago: IEEE, 2015: 3728−3733. [23] LIU Lu, ZHANG Lichuan, ZHANG Shuo, et al. Multi-UUV cooperative dynamic maneuver decision-making algorithm using intuitionistic fuzzy game theory[J]. Complexity, 2020, 2020(1): 2815258. [24] YANG Qiming, ZHANG Jiandong, SHI Guoqing, et al. Maneuver decision of UAV in short-range air combat based on deep reinforcement learning[J]. IEEE access, 2019, 8: 363−378. [25] ZHANG Liang , XU Jia , GOLD D, et al. Air dominance through machine learning: a preliminary exploration of artificial intelligence-assisted mission planning[M]. Santa Monica: RAND Corporation, 2020. [26] YOO J, KIM D, SHIM D H. Deep reinforcement learning based autonomous air-to-air combat using target trajectory prediction[C]//2021 21st International Conference on Control, Automation and Systems. Jeju: IEEE, 2021: 2172−2176. [27] SUN Zhixiao, PIAO Haiyin, YANG Zhen, et al. Multi-agent hierarchical policy gradient for air combat tactics emergence via self-play[J]. Engineering applications of artificial intelligence, 2021, 98: 104112. doi: 10.1016/j.engappai.2020.104112 [28] SUTTON R S, BARTO A G. Reinforcement learning: an introduction[M]. 2nd ed. Cambridge: Bradford Book, 2018. [29] MITCHELL T M. Machine learning[M]. New York: McGraw-Hill, 1997. [30] ZHANG Kaiqing, YANG Zhuoran, BAŞAR T. Multi-agent reinforcement learning: a selective overview of theories and algorithms[M]//Handbook of Reinforcement Learning and Control. Cham: Springer International Publishing, 2021: 321−384. [31] YU Chao, VELU A, VINITSKY E, et al. The surprising effectiveness of PPO in cooperative multi-agent games[C]//Proceedings of the 36th International Conference on Neural Information Processing Systems. New Orleans: ACM, 2022: 24611−24624. [32] BERNDT J. JSBSim: an open source flight dynamics model[J]. AIAA modeling and simulation technologies conference proceedings, 2004, 2004(4923): 1−12. [33] LOWE R, WU Y, TAMAR A, et al. Multi-agent actor-critic for mixed cooperative-competitive environments[J]. Advances in neural information processing systems, 2017, 30: 6380−6391.
