目前，一些配备了传感、计算和通信功能的智能设备，如可穿戴设备和车内传感装备等非常流行，用户在使用这些设备时，会产生大量的数据^[1]。设备利用这些数据来分析用户的行为和偏好，可以为用户提供智能和个性化的服务。在传统的集成式学习方法中，需要将不同设备上的数据传到一个统一中心来进行学习训练，这违反了数据隐私保护要求^[2]。现如今，数据的隐私问题受到越来越多的关注。欧盟在2018年5月实施了通用数据保护条例（general data protection regulation, GDPR）^[3]，该条例要求只能在有合法目的并在严格限制条件下才能够收集个人数据，并且数据的完全控制权属于数据所有者。随着对数据隐私保护要求的提升，限制了不同物联网设备之间的数据共享，为物联网的快速发展带来了挑战。

为解决此问题，2016年谷歌AI团队提出联邦学习（federated learning, FL）算法框架，应用于移动互联网手机终端的隐私保护。FL是一种分布式的机器学习技术，其思想是多个拥有本地数据用户在本地进行训练，仅通过交换训练得到的模型参数或中间结果进行联合训练，实现“数据不动模型动”的新范式。虽然FL避免了用户的数据直接暴露，但有研究表明，传输的模型梯度或参数信息仍会泄露用户的一些个人信息。例如，Phong等 ^[4]展示了如何利用一小部分梯度数据泄露有用的数据信息。Fredrikson等 ^[5]研发了一类新的模型反演攻击，可以通过多次访问机器学习模型来学习个人的敏感信息。此外，Nasr 等^[6]提出的白盒隶属度推理攻击，可以利用随机梯度下降（stochastic gradient descent, SGD）算法的隐私漏洞，在仅知道模型参数的情况下跟踪训练数据记录。为解决在数据传输过程中造成的隐私泄露，相关研究^[7-12]中将FL框架与差分隐私（differential privacy, DP）机制相结合，为数据提供安全保障。

DP是由Dwork等^[13]在2006年首次提出，用户评估一个隐私保护机制（算法）所能提供的隐私保护程度，其核心思想是给用户数据集或模型更新添加噪声，由于其严格的理论保证和较小的计算开销，在FL中得到了广泛的应用。尽管现有的方案已经能够很好地保证数据安全，但这些方案在联邦学习中的运用往往是简单的，即在联邦学习的每一轮都添加相同的噪声尺度，然而这种方法是存在一定弊端的。首先，模型的准确率依赖于预先设置的迭代轮数（T），若T设置得太小，则模型还未收敛就结束训练；若T设置得太大，则会造成每轮分配的隐私预算过小，噪声过大，影响模型精度。其次，在模型训练刚开始的时候，模型的准确率未趋于收敛，此时即使添加较大噪声，也不会对模型准确率造成较大影响；但当训练结果趋于收敛时，则应添加较小噪声。所以以往方案在每轮迭代中添加相同噪声的方案是不够合理的。同时，已有方案通常无法顾及数据拥有者的个人隐私偏好。为此，本研究提出了一种自适应加噪和计算学习率的联邦学习算法（differential privacy-federated learning adaptive gradient descent，DP-FLAGD），在模型刚开始训练时分配较小的隐私预算，即添加较大的噪声，而在模型训练后期分配较大的隐私预算，即添加较小的噪声，同时自适应地计算相应的学习率，使损失降到最小，并为具有不同隐私偏好的用户提供不同的隐私预算。

本研究主要贡献如下：

1）提出了一种自适应分配隐私预算的联邦学习算法，即在每一轮迭代中，通过更精细地分配隐私预算来改进原有的DP与FL相结合的算法。

2）提出自适应修改学习率的方案，在每一步更新中寻找更合适的学习率进行更新，以提供更高的准确度。

3）为每个用户提供了不同的隐私预算值，由于每个用户的隐私偏好不同，为每个用户添加相同程度的噪声方法是不合理的，因此，本研究为具有不同隐私偏好的用户提供了不同的隐私预算。

4）本研究在真实数据集上进行了相关实验，证明本方案在模型准确性和损失等方面优于现有的算法。

1.   相关工作

虽然FL允许用户将原始数据保存在本地，但已有研究表明^[14]，攻击者能够从交换的梯度等参数中推测出用户隐私信息。基于DP的联邦学习是一种为解决FL中所存在的安全问题而广泛使用的联邦学习框架，该框架通过在用户上传的梯度中添加噪声来保护本地数据的隐私。

Shokri等^[15]提出了一种分布式的训练方法，将噪声注入到参数的梯度中，以保护神经网络的隐私。然而，这种方法注入的噪声大小和隐私预算都会与训练的周期数和共享参数的数量成比例地累积，因此，该方案可能会消耗不必要的大部分隐私预算，因为训练的轮数和多方之间共享参数的数量往往是较大的^[16]。

为了改进这一点，基于Abadi等^[17]的组成定理，提出了一种时刻统计方法，该方法跟踪隐私预算支出并执行适用的隐私政策。然而，这仍然依赖于训练轮数，因为该方法在每个训练步骤中都会在参数的梯度中加入噪声。在隐私预算较小的情况下，只能使用少量的训练周期来训练模型。在实践中，当训练周期的数量需要很大时，这可能会影响模型的效用。

Phan等 ^[18]探索了一种针对差分隐私深度神经网络的方法。这项工作提出了深度私有自动编码器（dPAs），其中通过扰动自动编码器^[19]中的交叉熵误差来实现DP。但其算法是专门为自动编码器设计的，应用了特定的目标函数。

以上方法对所有参数注入的噪声量都是相同的，Phan等 ^[20]提出一种应用于神经网络的自适应拉普拉斯机制（adaptive laplace mechanism, AdLM），能够根据每个噪声对模型输出的贡献，自适应地将噪声注入到特征中的方案，在与模型输出不那么相关的特性中添加较多的噪声，而在那些与模型输出更为相关的特性上添加较少的噪声。

随机梯度下降（stochastic gradient descent，SGD）算法是一种常用的优化方法，是解决各种问题的常用工具，如模型拟合^[21]。出于安全考虑，人们推出了DP版本的SGD算法，然而，在这些方案中，通常是将总的隐私预算均分到每轮迭代中，这种方法所得到的准确率往往不会太高，现有的FL与DP结合的方案^[10]中多采用的也是这种SGD算法进行迭代优化。基于此，Lee等^[21]提出通过更加合理地分配隐私预算的方案来提高模型的准确度。在训练刚开始的时候，梯度值预计会比较大，此时不需要精确地测量，可以添加较少的隐私预算；然而，随着一轮又一轮的迭代，参数逐渐接近最优值时，梯度减小，此时需要更加精准地测量，因此需要更多的隐私预算添加到其中。

上述这些优化算法都是将自适应加噪运用到神经网络之中，而本研究所关注的是如何在联邦学习中将其进行应用，因此，这里创造性地提出了将Lee等^[21]的方案运用到联邦学习中，以提高训练模型的准确度。

2.   预备知识

2.1   联邦学习

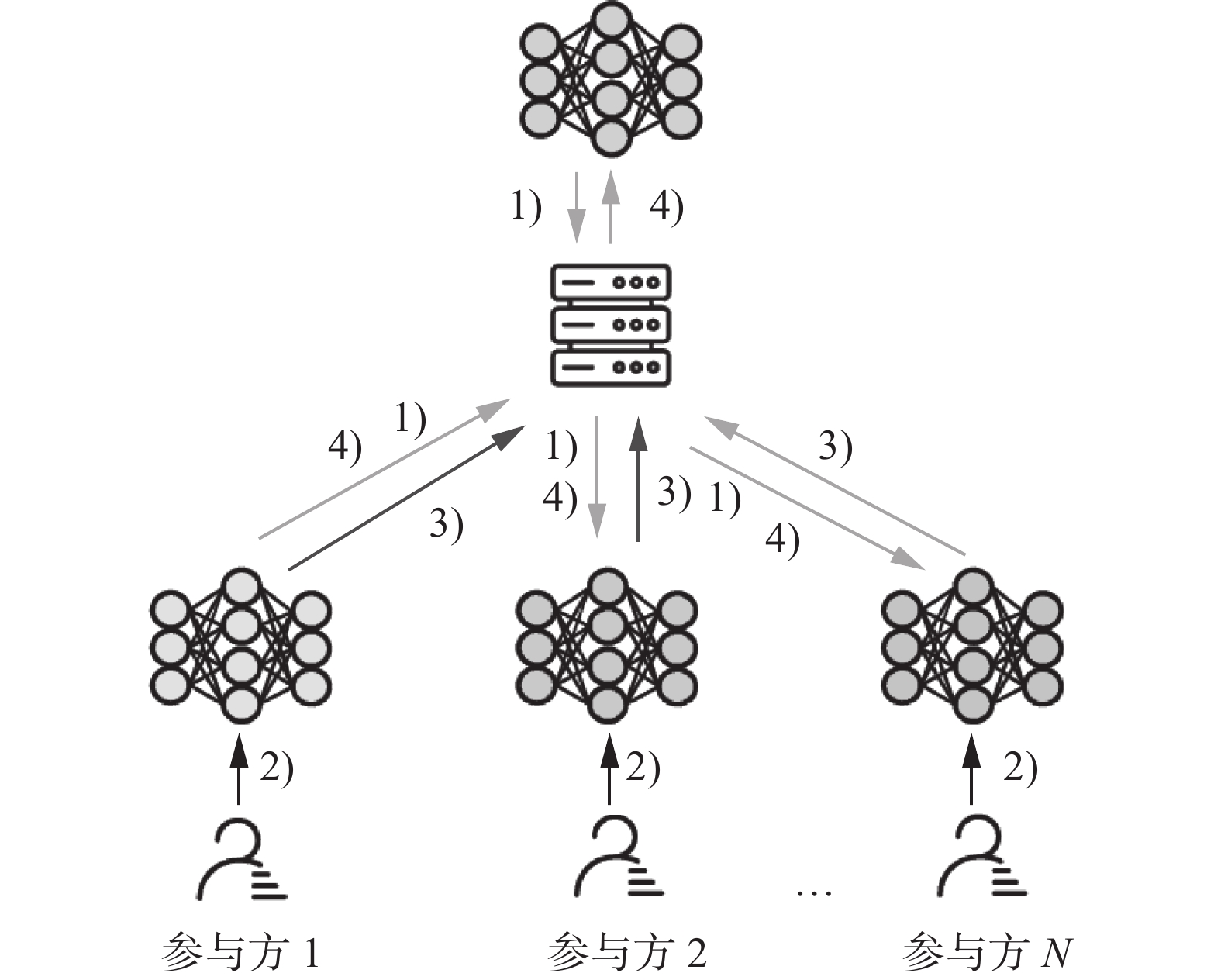
联邦学习是为解决数据孤岛问题而提出的方法，将训练数据分布在移动设备上，通过聚合本地计算的更新来学习共享模型，这种分散的方法就叫作联邦学习。用户集体由一个中央服务器进行协调，每次用户只需将模型更新上传到服务器，而无需上传数据本身，从而为数据的隐私安全提供一定的保障^[22]。

其具体算法如算法1所示，具体来说可以分为4个步骤^[14]。

1)初始化：服务器初始化全局模型参数，并选择客户端，将初始化的参数分发给客户端。

2)本地训练：客户端使用自己的本地数据集以及接收到的全局模型参数进行训练并更新参数。

3)本地上传：客户端将参数更新上传至服务器。

4)全局聚合及更新：服务器将各个客户端的参数更新进行聚合，并将更新的全局参数分发给客户端。

重复步骤2）~4）直至满足要求为止。

算法1　联邦平均算法（FedAvg）

输入　K个客户端（用k进行索引），局部小批量大小B，本地训练迭代轮数E，学习率α。

输出　全局模型参数w。

服务器端：

1) 服务器初始化模型参数$ \mathop w\nolimits_0 $

2) for each round t = 1, 2, … do

3) $ m $$ \leftarrow $$ (\mathrm{C}\mathrm{K},1) $

4) $ \mathop S\nolimits_t $$ \leftarrow $随机选择的m个用户

5) for each client $ k $$ \in \mathop S\nolimits_t $ in parallel do

6) $ \mathop w\nolimits_{t + 1}^k $$ \leftarrow $ClientUpdate(k, $ \mathop w\nolimits_t $)

7) $ \mathop w\nolimits_{t + 1} $$ \leftarrow \displaystyle\sum\limits_{k = 1}^K {\dfrac{{\mathop n\nolimits_k }}{n}\mathop w\nolimits_{t + 1}^k } $

客户端：

8) B$ \leftarrow $将客户按数量大小为B，分成小批量

9) for each local epoch i from 1 to E do

10) for batch $ b \in B $ do

11) $ w = w - $$ \alpha \nabla $$ l(w;b) $

12) return $ w $ to server

典型的横向联邦学习系统的架构示例如图1所示。

图  1  横向联邦学习系统示例

Fig.  1  Diagram of horizontal federated learning system

下载: 全尺寸图片

2.2   差分隐私

差分隐私解决了在了解到一个群体的有用信息后，但不能获得该群体中某一人信息的悖论^[13]，被广泛应用于解决联邦学习中的隐私问题。

定义1（$ \varepsilon -\mathrm{D}\mathrm{P} $）^[23]　一个算法A满足$ \varepsilon -\mathrm{D}\mathrm{P} $，其中$ \varepsilon \geqslant 0 $，当且仅当对于任意2个只在1个元素上不同的数据集$ D $和$ D' $，有

式中：$ \mathrm{R}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\left(A\right) $表示算法$ A $所有可能输出的集合，ɛ为(0, 1)的任意一个数，Pr[]表示概率。

定义2（$ (\varepsilon ,\delta )-\mathrm{D}\mathrm{P} $）　一个算法$ A $满足$ (\varepsilon ,\delta )- \mathrm{D}\mathrm{P} $，其中$ \varepsilon \geqslant 0 $，$ \delta \geqslant 0 $，当且仅当对于任意2个只在1个元素上不同的数据集$ D $和$ D' $，有

定义3（高斯机制）　$ \varepsilon $是(0, 1)的任意一个数；$ {\varDelta }_{2} $$ (A) $是算法$ A $的$ \mathop L\nolimits_2 $灵敏度；N表示正态分布；σ为尺度参数，决定了分布的幅度；高斯机制返回的结果为$ A(D) + N(0, $$ \mathop \sigma \nolimits^2 $$ ) $，其中

满足$ (\varepsilon ,\delta ) - {\text{DP}} $。

定义4（$ \rho - {\textit{z}}{\text{CDP}} $）　对于一个输出$ o\in \mathrm{R}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e}\left(A\right) $，算法$ A $的隐私损失随机变量$ Z $定义为

$ \rho -{\textit{z}}\mathrm{C}\mathrm{D}\mathrm{P} $ 对$ Z $的矩生成函数施加一个约束，并要求其集中在零附近。在形式上，需要满足

式中：$ \exp ( $$ \mathop D\nolimits_\alpha $$ (M(D)||M(D')) $为$ \alpha $-瑞丽散度，D_a为$ \alpha $散度，M为某种算法，$ \alpha \in (-\infty ,+\infty ) $。

引理1　假设2种机制分别满足$ \mathop \rho \nolimits_1 $$ - {\textit{z}}{\text{CDP}} $和$ \mathop \rho \nolimits_2 $$ - {\textit{z}}{\text{CDP}} $，则其组合满足($ \mathop \rho \nolimits_1 $+$ \mathop \rho \nolimits_2 $)$ - {\textit{z}}{\text{CDP}} $，其中，$ {\rho }_{1} $和$ {\rho }_{2} $代表隐私参数。

引理2　返回结果为$ A(D) + N(0, $$ \mathop \sigma \nolimits^2 $$ ) $的高斯机制满足$ {\Delta }_{2}\left({A}^{\tfrac{2}{2{\sigma }^{2}}}\right)-{\textit{z}}\mathrm{C}\mathrm{D}\mathrm{P} $。

引理3　算法$ A $满足$ \rho - {\textit{z}}{\text{CDP}} $，则$ A $满足$ (\mathit{\varepsilon },\mathit{\delta })- \mathrm{D}\mathrm{P} $对于任意的$ \delta > 0 $，并且$ \varepsilon = \rho + \sqrt {4\rho \log \left(\dfrac{1}{\delta }\right)} $。

3.   自适应加噪联邦学习方法

3.1   算法描述

DP-FLAGD算法的主要思想是保持预设总的隐私预算大小不变，在模型迭代的每一轮中，通过自适应计算隐私预算的方式，为梯度加入大小不同的噪声。

1）自适应加噪

在已有的方案中^[24-25]，隐私预算$ \varepsilon $被平均分配到每一轮本地迭代中，即$ \mathop \varepsilon \nolimits_1 = \mathop \varepsilon \nolimits_2 = \cdots = \mathop \varepsilon \nolimits_T = \dfrac{\varepsilon }{T} $，但这样的分配方式是存在一定问题的。首先，模型的准确率依赖于预先设定的迭代轮数T，如果T设置得太小，则还没有达到模型最优效果，迭代就已停止；而若T太大，则分配给每一轮的隐私预算$ \mathop \varepsilon \nolimits_t $的值就会太小，即添加的噪声太大，噪声太大也会影响到模型的准确度。因此，预算设定迭代轮数T的方案是不合理的。其次，在训练过程中为每一轮迭代平均分配隐私预算的方案也是不够合理的。在训练刚开始的时候，梯度参数往往不够精确，而当迭代进行几轮之后，参数趋于收敛，梯度下降的方向变得精确。因此，若每轮迭代都提供较小的隐私预算，则可能会影响到最后梯度参数的准确性；若每轮都提供较大的隐私预算，则可能会造成精度还未收敛，就因隐私预算耗尽而终止训练。无论是哪种情况，都会导致模型准确率较低。因此，本研究提出一种自适应分配隐私预算的方式，通过更合理地分配隐私预算来提高模型准确度。

在没有考虑隐私的设置中，随机优化方法使用从一小组随机选择的数据中计算近似梯度，而非精确梯度。因此，每个更新的梯度方向$ -\tilde g $可能并不是一个下降方向，而是一个期望的下降方向，但在使用了DP的算法中，不能依赖于期望中的保证。当本研究提出的算法认定$ -\tilde g_t $可能并不代表一个下降方向时，本方案将当前的隐私预算份额从$ \mathop \rho \nolimits_t $增加到更大的一个值$ \mathop \rho \nolimits_{t + 1} $，即$ \mathop \rho \nolimits_{t + 1} \leftarrow (1 + \eta )\mathop \rho \nolimits_t $，利用$ \mathop \rho \nolimits_{t + 1} - \mathop \rho \nolimits_t $再次计算噪声梯度，得到$ -\tilde g_2 $，利用GRADAVG算法将2次计算的噪声梯度合并，得到$\tilde S $。具体细节如算法2所示。重复此过程，直到找到一个下降方向。

式中$ {\Delta }_{2}(\nabla {f}^{2}) $是$ f $的梯度的$ \mathop L\nolimits_2 $灵敏度。

通过计算可以得到：

算法2　梯度平均算法（GRADAVG）

输入　 $ {\rho }_{\mathrm{o}\mathrm{l}\mathrm{d}} $,$ {\rho }_{\mathrm{n}\mathrm{g}} $,g,$\tilde g$,$ {C}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}} $。

输出　全局模型参数$\tilde S$。

1) $ {\tilde{g}}_{2}\leftarrow g+N\left(0,\left(\dfrac{{C}_{\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{d}}^{2}}{2\left({\rho }_{\mathrm{n}\mathrm{g}}-{\rho }_{\mathrm{o}\mathrm{l}\mathrm{d}}\right)}\right)I\right) $

2) $ \tilde{S}\leftarrow \dfrac{{\rho }_{\mathrm{o}\mathrm{l}\mathrm{d}}\tilde{g}+\left({\rho }_{\mathrm{n}\mathrm{g}}-{\rho }_{\mathrm{o}\mathrm{l}\mathrm{d}}\right){\tilde{g}}_{2}}{{\rho }_{\mathrm{n}\mathrm{g}}} $

3) return $\tilde S$

4) end

2）自适应计算学习率

为了获得最小的损失，本方案构建了一个集合$\varOmega = \left\{ {f\left( {{w_t} - \alpha {{\tilde g}_t}} \right):\alpha \in \phi } \right\}$，其中$\phi $是预定义的学习率集。然后将集合$\phi $带入到Noisy_Min^[21]算法中来选择使得函数$f\left( {{w_t} - \alpha {{\tilde g}_t}} \right)$值最小即损失值最小的$\alpha $。在本研究的设置中，$\phi $的第一个元素为0，即此时的学习率设置为0。设$ i $是由算法Noisy_Min返回的索引值，当$i > 0$时，说明已找到使损失最小的学习率，此时算法使用所选择的学习率${\alpha _i}$更新${w_t}$；而当$i = 0$时，说明−${\tilde g_t}$可能并不代表一个下降方向，因此将$\alpha $设置为0，即不更新。此时需要重新分配较大的隐私预算，并计算得到${\tilde g_2}$，再调用算法2得到$\tilde S$，重复此过程，至$i > 0$，即可以进行更新为止。自适应计算学习率的具体细节如算法3的第9)~20)所示。

3）为隐私需求不同的用户提供相应的隐私预算

由于每个用户的隐私偏好有所不同，所以本研究采取了给隐私要求较高的用户提供了较小的隐私预算，而给隐私保护要求较低的用户提供了较大的隐私预算的方式，以满足不同用户的要求，从而提高用户参与FL的积极性^[26]。

DP-FLAGD算法的具体细节如算法4所示。首先，为不同隐私偏好的用户设置不同的隐私预算集合$\left\{ \varepsilon \right\}_{k = 0}^K$，同时初始化模型参数${w_0}$和学习率集$\phi $，并将其广播给选中的m个参与者。其次，参与者本地使用具有差分隐私保护的自适应梯度下降算法（DP-AGD）进行更新。用户根据${\varepsilon _i}$计算相应的$\rho $，当$\rho > 0$时，即隐私预算没有耗尽时，将索引$i$初始化为0，计算并裁剪梯度获得${g_t}$，并为梯度参数添加噪声$ {\tilde{g}}_{t}\leftarrow {g}_{t}+N\left(0,({C}^{2}/2{\rho }_{\mathrm{n}\mathrm{g}}\right)I) $ ，得到${\tilde g_t}$，然后减掉相应的隐私预算。通过Noisy_Min算法获取使得损失最小的索引$i$的值，若计算出的索引$i$的值为0，则说明$ - {\tilde g_t}$可能并不代表一个下降方向，此时重新分配隐私预算并得到新的${\tilde g_t}$，其具体细节如算法4的第15)~18)所示。如算法4的第12)~13)所示，若计算得到的$i > 0$，则说明此时的$ - {\tilde g_t}$代表下降方向，此时进行更新，即${w_{t + 1}} \leftarrow {w_t} - {\alpha _i}{\tilde g_t}$，并将更新结果上传至服务器。最后，服务器聚合来自不同客户端的参数更新，并对其进行聚合，将最终的更新结果发送给客户，重复此过程，直至隐私预算耗尽。

算法3　具有差分隐私保护的自适应梯度下降算法（differential privacy-g adaptive gradient descent , DP-AGD）

输入　隐私预算$ {\rho }_{\mathrm{n}\mathrm{g}} $、ε、$ {\delta }_{\mathrm{t}\mathrm{o}\mathrm{t}} $，模型参数$w$，步长集合$\phi $，隐私预算增长率η，裁剪阈值C，用户数据{${d_1}$,${d_2}$,…,${d_n}\} $,目标函数$f\left( w \right) = \displaystyle\sum _{i = 1}^nl\left( {w;{d_i}} \right)$。

输出　模型参数w。

1) $t \leftarrow 0$

2) $\rho \leftarrow $根据$ \varepsilon $计算

3) while $\rho > 0$ do

4) $i \leftarrow 0$

5) ${g_t} \leftarrow \displaystyle\sum _{i = 1}^n\left( {\nabla l\left( {{w_t};{d_i}} \right)/{\text{max}}\left( {1,\dfrac{{\left| {\left| {\nabla l\left( {{w_t}} \right)} \right|} \right|}}{C}} \right)} \right)$

6) ${\tilde g_t} \leftarrow {g_t} + N\left( {0,({C^2}/2{\rho _{ng}}} \right)I)$

7) $\rho \leftarrow \rho - {\rho _{ng}}$

8) ${\tilde g_t} \leftarrow {\tilde g_t}/{\left| {\left| {{{\tilde g}_t}} \right|} \right|_2}$

9) while $i = 0$ do

10) $ \varOmega =\left\{f\left({w}_{t}-\alpha {\tilde{g}}_{t}\right):\alpha \in \phi \right\} $

11) $ i\leftarrow \mathrm{N}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{y}\_\mathrm{M}\mathrm{i}\mathrm{n}\left(\phi \right) $

12) if $i > 0$ then

13) if $\rho > 0$ then ${w_{t + 1}} \leftarrow {w_t} - {\alpha _i}{\tilde g_t}$

14) else

15) $ {\rho }_{\mathrm{o}\mathrm{l}\mathrm{d}}\leftarrow {\rho }_{\mathrm{n}\mathrm{g}} $

16) $ {\rho }_{\mathrm{n}\mathrm{g}}\leftarrow \left(1+\eta \right){\rho }_{\mathrm{n}\mathrm{g}} $

17) $ {\tilde{g}}_{t}\leftarrow \mathrm{G}\mathrm{R}\mathrm{A}\mathrm{D}\mathrm{A}\mathrm{V}\mathrm{G}\left({\rho }_{\mathrm{o}\mathrm{l}\mathrm{d}},{\rho }_{\mathrm{n}\mathrm{g}},{g}_{t},{\tilde{g}}_{t},C\right) $

18) $ \rho \leftarrow \rho -\left({\rho }_{\mathrm{n}\mathrm{g}}-{\rho }_{\mathrm{o}\mathrm{l}\mathrm{d}}\right) $

19) end

20) end

21) $t \leftarrow t + 1$

22) end

23) return ${w_t}$

算法4　自适应加噪联邦学习算法（DP-FLAGD）

输入　隐私预算集合$\left\{ \varepsilon \right\}_{k = 0}^K$、δ，全局通信轮数T，联邦学习的参与者人数K（k为索引），每轮的参与者数m。

输出　模型参数w。

服务器端：

1) 服务器初始化模型参数$ \mathop w\nolimits_0 $和$\phi $，并广播给所有参与者

2) for $ 1 \leqslant {\text{t}} \leqslant T $ do

3) $ m $$ \leftarrow $$ (\mathrm{C}\mathrm{K},1) $

4) $ \mathop S\nolimits_t $$ \leftarrow $随机选择的m个用户

5) for $ i \in m $ do

6) $ \mathop w\nolimits_{t + 1}^k $$ \leftarrow $ClientUpdate($ \mathop \varepsilon \nolimits_i $$ /T $,$ \mathop w\nolimits_t $)

7) $w_{t + 1}^i \leftarrow {w_t} + \displaystyle\sum _{i = 1}^N\dfrac{{{n_k}}}{n}w_{t + 1}^k$

客户端：

8) $ \mathrm{C}\mathrm{l}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{U}\mathrm{p}\mathrm{d}\mathrm{a}\mathrm{t}\mathrm{e}\left(\varepsilon ,{w}_{t}\right) $:

9) $\hat w \leftarrow {w_t}$

10) $ w=\mathrm{D}\mathrm{P}-\mathrm{A}\mathrm{G}\mathrm{D}\left(\rho ,{w}_{t}\right) $

11) ${w_{t + 1}} = w - \hat w$

12) return ${w_{t + 1}}$

3.2   隐私性分析

本方案使用DP对在FL中传输的数据进行隐私保护，通过为梯度参数添加噪声的方式来避免攻击者通过模型还原出原始训练数据。

本方案分别在DP-AGD算法的第6)步和GRADAVG算法的第1)步添加了高斯噪声，下面证明添加的噪声满足$ \mathit{\rho }-{\textit{z}}\mathrm{C}\mathrm{D}\mathrm{P} $ ，以在DP-AGD算法中添加的噪声为例。

定义$f\left( y \right) = \log\left( {{\rm{P}}\left[ {M\left( x \right) = y\left] {/{\rm{P}}} \right[M\left( {x' = y} \right)} \right]} \right)$，其中假设$ x $、$ x' $相邻，设$ \mathit{Y}\sim \mathit{M}\left(\mathit{x}\right) $，$Z = f\left( Y \right)$，${\text{α }} \in \left( {1,\infty } \right)$。根据定义4有

所以

由马尔可夫不等式

当$\alpha = \left( {\varepsilon + \rho } \right)/2\rho > 1$时，有

对于任何可测量的$S \subset \gamma $，

即${\rm{P}}\left[ {M\left( x \right) \in S} \right] = $$\exp (\varepsilon ){\rm{P}}\left[ {M\left( {x'} \right) \in S} \right] + \delta $， $ M $满足$ (\mathit{\varepsilon },\mathit{\delta })-\mathrm{D}\mathrm{P} $。由于$ (\mathit{\varepsilon },\mathit{\delta })-\mathrm{D}\mathrm{P} $在$ \delta > 0 $的情况下等效于${\textit{z}}-\mathrm{C}\mathrm{D}\mathrm{P} $ ^[27]，所以该算法满足$\rho - \textit{z}{\mathrm{CDP}}$。

与在GRADAVG算法中添加的噪声同理，由上述证明和引理2可以证明每次添加的噪声都是满足$ \rho -{\textit{z}}\mathrm{C}\mathrm{D}\mathrm{P} $ 的。

隐私损失会在每次的迭代中累积，根据引理1可得到添加的噪声在迭代后满足$( {\rho _1} + {\rho _2} + \cdots + {\rho _n} ) - \textit{z}{\text{CDP}}$仍满足$ \rho -{\textit{z}}\mathrm{C}\mathrm{D}\mathrm{P} $。同时，本方案在DP-AGD算法的第3)~13)步中检查更新是否会导致隐私预算小于0，若小于0即表示隐私预算已耗尽，则不再继续迭代。因此证明了本方案是严格满足$ \rho -{\textit{z}}\mathrm{C}\mathrm{D}\mathrm{P} $的。

4.   结果与分析

实验平台是6核Inter GPU(2.90 GHz)、16 GB内存、Win11系统，代码采用Python实现。实验采用MNIST（modiffe national institute of standard and technology）和CIFAR-10数据集。

MNIST数据集由7万张手写体数字灰度图像组成，包括6万张训练图像和1万张测试图像。每张图像的大小是28×28。标签是从0~9的数字，如图2所示。

图  2  MNIST数据集示例

Fig.  2  Example figure of MNIST dataset

下载: 全尺寸图片

CIFAR-10数据集由10类RGB彩色图像组成。图像大小为32×32。这10个类别包括飞机、汽车、鸟、猫、鹿、狗、青蛙、马、船和卡车。数据集共有5万个训练示例和1万个测试示例，如图3所示。

图  3  CIFAR-10数据集示例

Fig.  3  Example figure of CIFAR-10 dataset

下载: 全尺寸图片

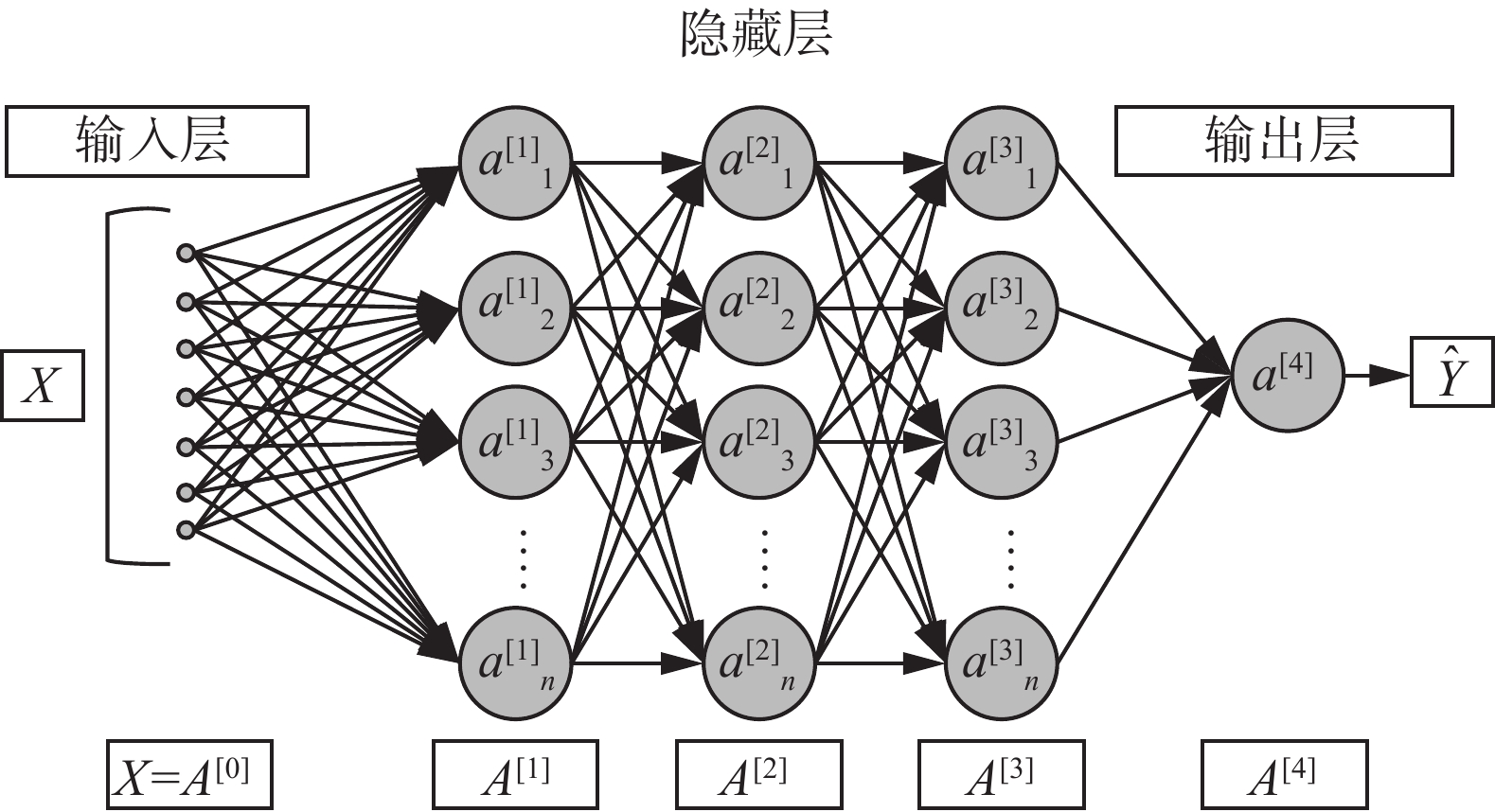
由于卷积神经网络（convolutional neural network, CNN）具有较好的特征提取能力，所以使用CNN作为神经网络体系结构。CNN网络示意如图4所示。

图  4  CNN网络示意

Fig.  4  CNN network diagram

下载: 全尺寸图片

将本方案DP-FLAGD与FedAvg、LDP-FL^[27]和AdLM^[28]进行对比实验，并记录结果。其中，AdLM是自适应的Laplace机制模型，对模型输出影响较大的特征加入更少的噪声，而对模型输出影响较小的特征加入更多的噪声，同时具有使噪声添加独立于训练过程的特性。

4.1   通信轮数对实验结果的影响

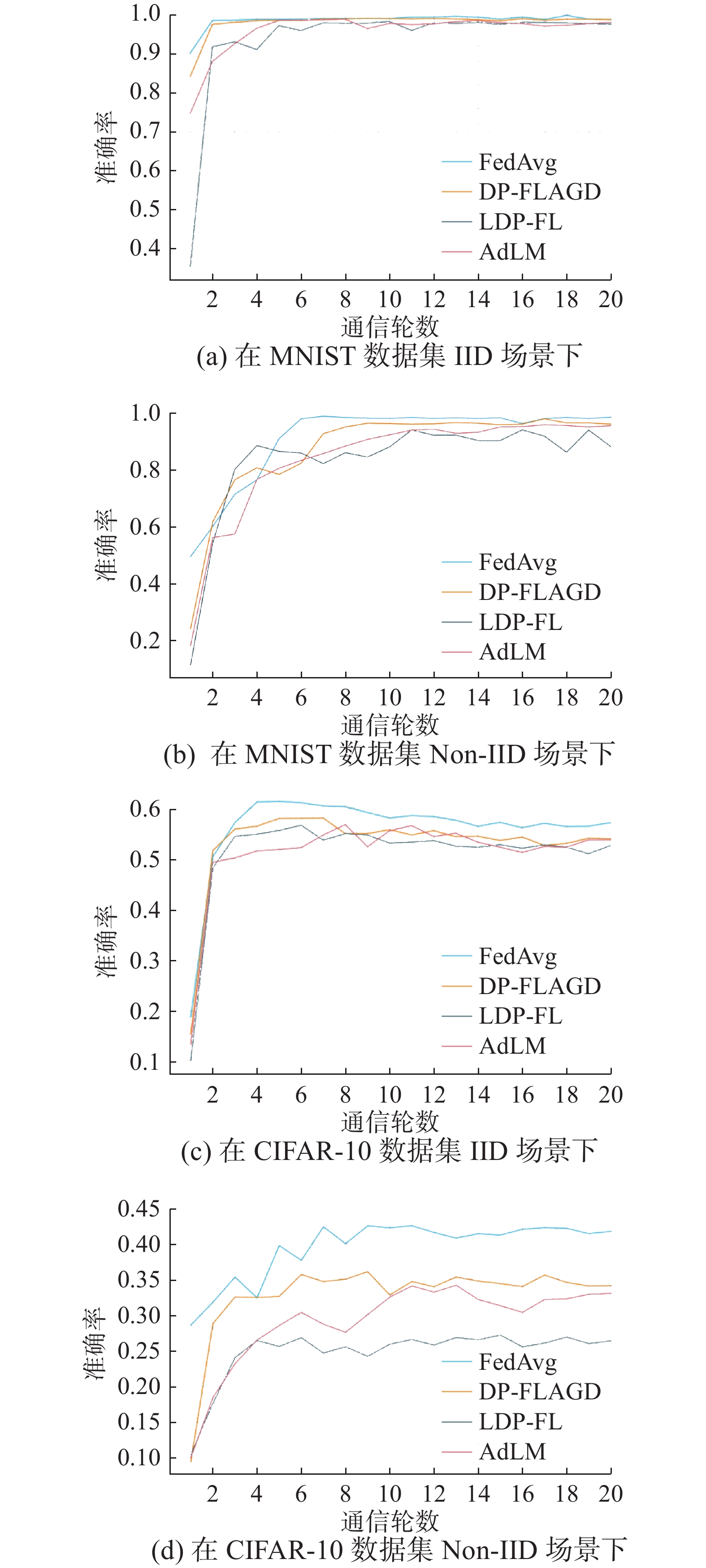
本组实验固定2个客户端，本地训练两轮。分别记录了在独立同分布（IID）和非独立同分布（Non-IID）2种情况下，DP-FLAGD、FedAvg、LDP-FL和AdLM 4种算法在MNIST和CIFAR-10数据集上准确率随通信轮数变化的变化，见表1和表2。

图5(a)给出了4种算法在MINIST数据集IID场景下准确率随通信轮数变化的趋势，图5(b)给出了4种算法在MNIST数据集Non-IID场景下准确率随通信轮数变化的趋势。图5(c)给出了4种算法在CIFAR-10数据集IID场景下准确率随通信轮数变化的趋势，图5(d)给出了4种算法在CIFAR-10数据集Non-IID场景下准确率随通信轮数变化的趋势。其中，FedAvg算法前期随着通信轮数的增大，准确率上升，之后准确率几乎没有波动，这是因为在该算法中，没有噪声扰动梯度，模型训练至后期逐渐趋于稳定。而DP-FLAGD算法、LDP-FL算法以及AdLM算法因为有噪声的扰动，从而准确率有所波动。最终DP-FLAGD的准确率接近FedAvg，证明了本研究提出的算法在保护隐私的同时，也保证了训练的准确率。

图  5  4种算法在2个数据集上准确率随通信轮数的变化

Fig.  5  Diagram of the accuracy variation of four algorithms with the number of communication rounds on two datasets

下载: 全尺寸图片

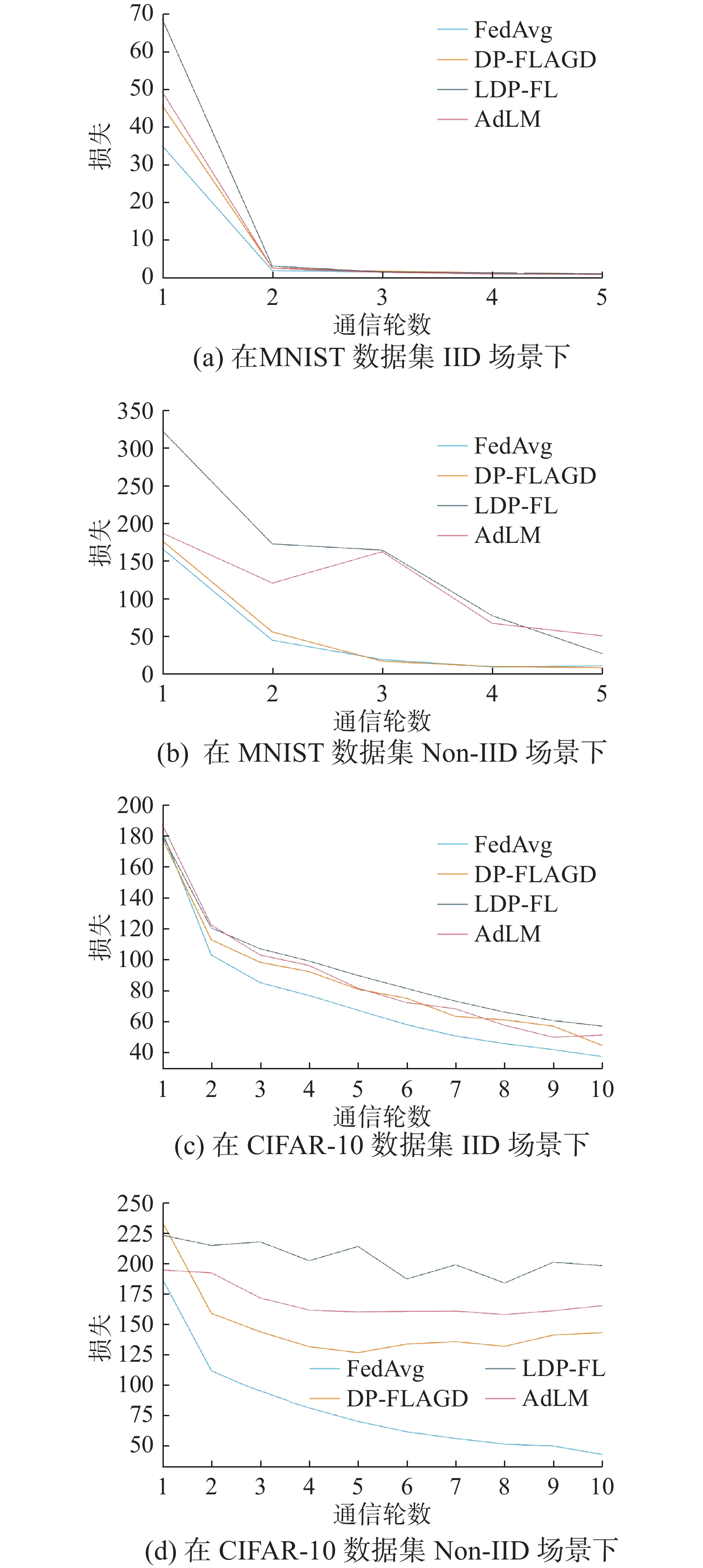
图6(a)给出了4种算法在MINIST数据集IID场景下损失随通信轮数变化的趋势，图6(b)给出了4种算法在MNIST数据集Non-IID场景下损失随通信轮数变化的趋势。图6(c)给出了4种算法在CIFAR-10数据集IID场景下损失随通信轮数变化的趋势，图6(d)给出了4种算法在CIFAR-10数据集Non-IID场景下损失随通信轮数变化的趋势。由此看出，在2个数据集和2种场景下，DP-FLAGD算法的表现都要优于LDP-FL算法和AdLM算法，同时损失与FedAvg算法较为接近，从而可证明本方案的有效性。

图  6  4种算法在2个数据集上损失随通信轮数的变化

Fig.  6  Diagram of the loss variation of four algorithms with the number of communication rounds on two datasets

下载: 全尺寸图片

4.2   隐私预算对实验结果的影响

本组实验固定MNIST数据集全局训练5轮，CIFAR-10数据集全局训练10轮。

图7(a)给出了在不同隐私预算下，DP-FLAGD算法和LDP-FL算法以及AdLM算法在MNIST数据集上的准确率，而图7(b)则给出了Non-IID的场景下的准确率，图7(c)和图7(d)分别是2种算法在CIFAR-10数据集上对应IID和Non-IID情境下的准确率。

图  7  3种算法在2个数据集上准确率随隐私预算的变化

Fig.  7  Diagram of the accuracy variation of three algorithms with privacy budget on two datasets

下载: 全尺寸图片

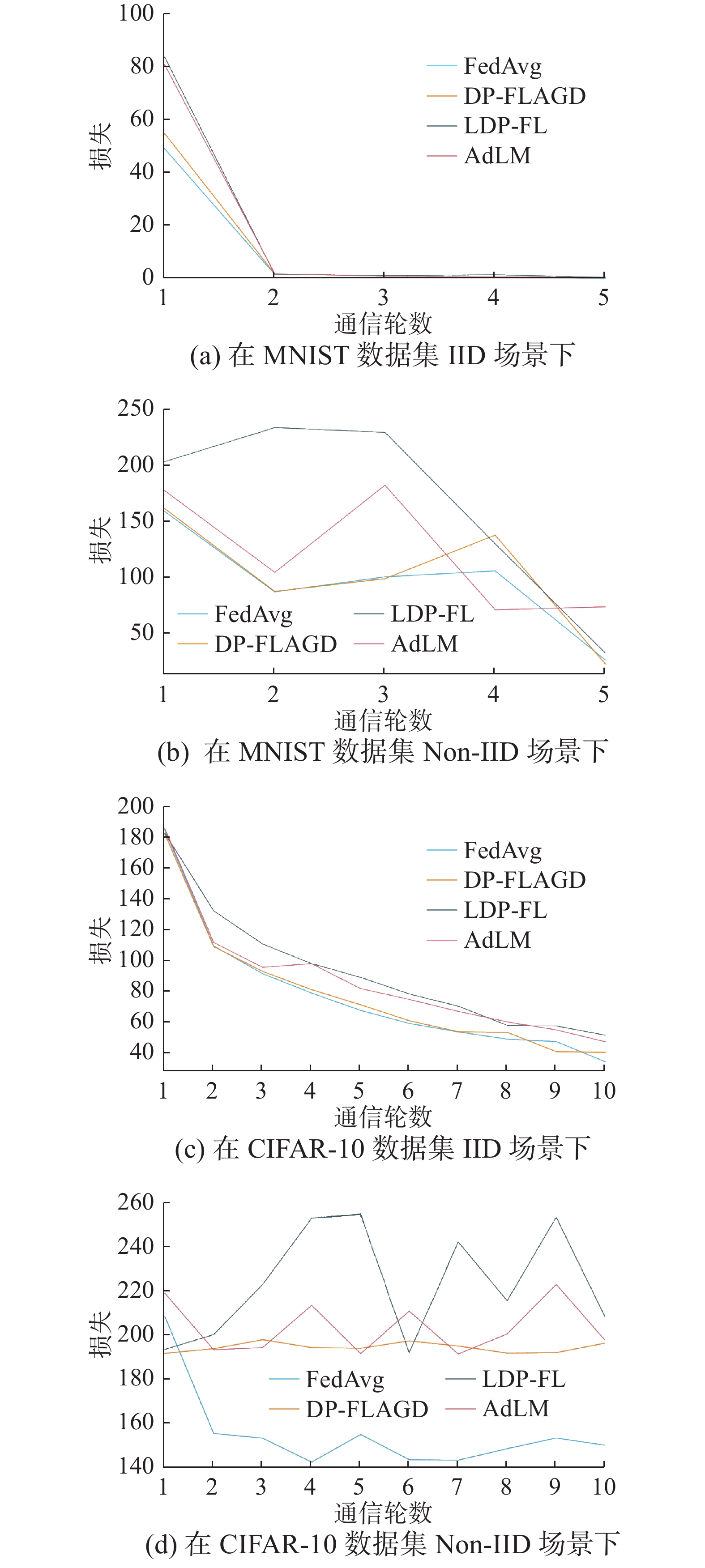
由图7可以看出，随着$ \varepsilon $的增大，准确率在增大，这是因为$ \varepsilon $越大，添加的噪声就越小，这符合DP机制。由于本研究提出的DP-FLAGD算法能够更加精细地分配隐私预算，而LDP-FL和AdLM由于给模型加入的噪声过大，造成准确率偏低，所以可以看出此算法在2个数据集的2种场景下几乎都要优于现有的算法，由此可证明本方案要优于现有的方案，具有更高的准确性。

图8~10分别给出了在$ \varepsilon $=10、5、1的3种情况下，4种算法在MNIST和CIFAR-10数据集上对于IID和Non-IID情况下的损失值变化。

图  8  4种算法在2个数据集上损失变化 ($ \varepsilon $=10)

Fig.  8  Diagram of the loss variation of four algorithms on two datasets ($ \varepsilon $=10)

下载: 全尺寸图片

图  9  4种算法在2 个数据集上损失变化 ($ \varepsilon $=5)

Fig.  9  Diagram of the loss variation of four algorithms on two datasets ($ \varepsilon $=5)

下载: 全尺寸图片

可以看出，随着$ \varepsilon $的增大，损失也有所减小，并且本方案的损失几乎始终小于LDP-FL算法和AdLM算法。

图  10  4种算法在2个数据集上损失变化 ($ \varepsilon $=1)

Fig.  10  Diagram of the loss variation of four algorithms on two datasets ($ \varepsilon $=1)

下载: 全尺寸图片

4.3   参与用户的个数对实验结果的影响

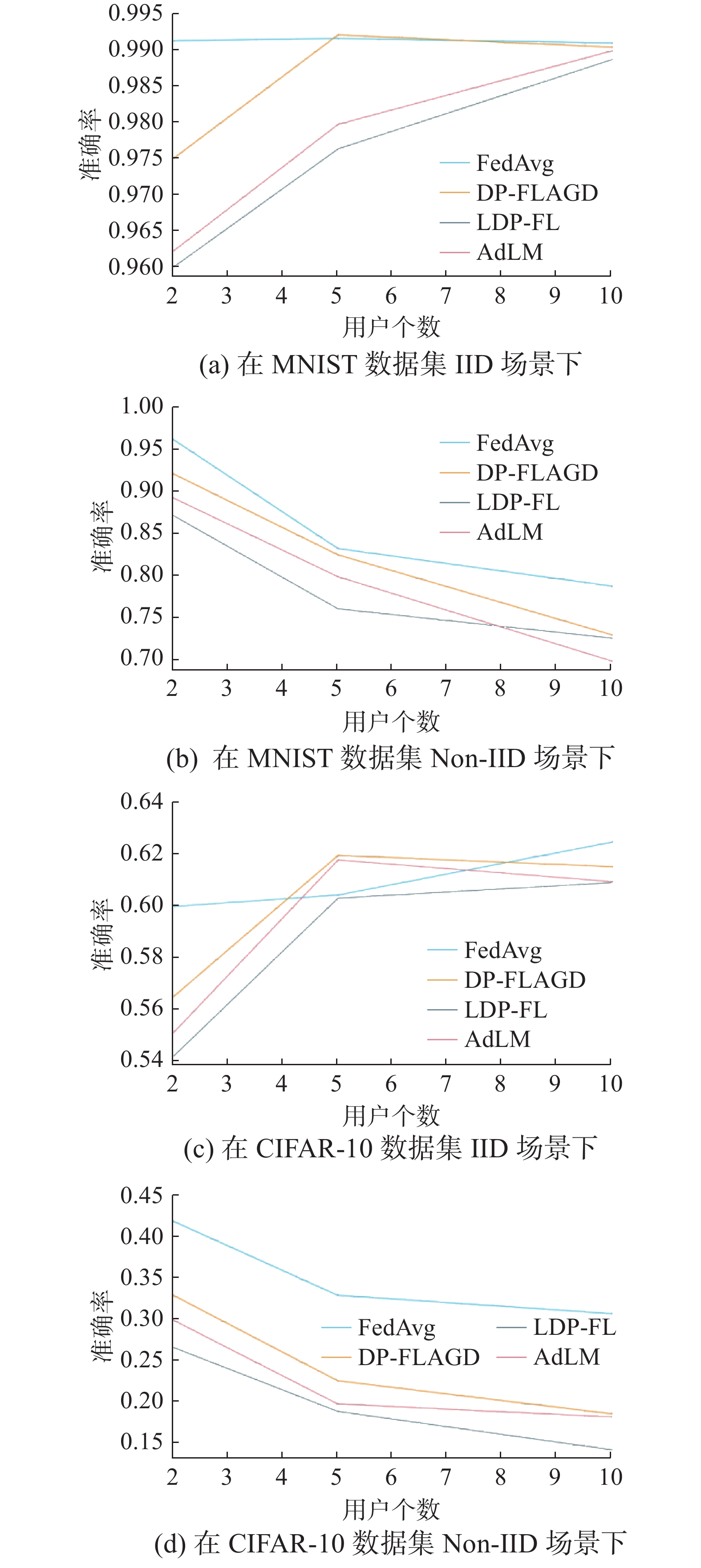
本组实验固定MNIST数据集全局训练5轮，CIFAR-10数据集全局训练10轮。4种算法在2个数据集上准确率随用户个数的变化如图11所示。由图11可以看出，在IID的场景下，准确率几乎是随着用户数量的增多而增加的，而在Non-IID场景下，随用户数量的增加，准确率却在下降，这是由于不同用户之间的数据是来自不同的数据分布模型所导致的。

图  11  4种算法在2个数据集上准确率随用户个数的变化

Fig.  11  Diagram of the accuracy variation of four algorithms with the number of clients on two datasets

下载: 全尺寸图片

总体来说，本研究提出的方法虽在Non-IID场景下准确率较FedAvg算法有一定的降低，但仍优于LDP-FL算法和AdLM算法。

5.   结束语

在本研究中，为解决以往方案固定通信轮数和在每轮训练中平均分配隐私预算的不合理性，提出了一种自适应分配隐私预算和自适应计算学习率的DP-FLAGD方法。在训练刚开始的几轮添加较大噪声，而在梯度参数趋于精确时添加较小的噪声，当隐私预算耗尽时则停止训练。本研究所提出的方案有效解决了固定迭代轮数和均分隐私预算带来的一系列问题，并通过相应的实验证明了本方案的有效性。今后的工作将考虑如何提高算法在Non-IID场景下的准确性以及如何激励更多用户参与到FL之中。