A facial semantic extraction method based on axiomatic fuzzy sets and granular computing
-
摘要: 在人脸检索和验证领域，人类更倾向于通过描述对象特征的“语义”或“概念”来对人脸进行相似性判别，而传统的图像检索已无法满足这一需求。因此，本文提出了一种基于公理模糊集(axiomatic fuzzy sets, AFS)与信息粒的人脸语义提取方法(IAFSGD)。首先，对人脸图像进行校正并检测人脸关键点，进而基于关键点提取人脸特征；然后，对人脸面部特征样本进行聚类，构建类中心，在AFS框架下求取每类的信息粒，并通过得到的信息粒对人脸图像再次进行分类，从而得到最终的聚类结果和具有可解释性的面部语义描述；最后，将本文提出的算法在Multi-PIE、AR、FEI人脸数据库进行实验验证。实验结果表明，与FCM(fuzzy c-means)、CAN(clustering with adaptive neighbors)、FCMGD、AFSGD、KTM(K-means tree)算法相比，本文提出的语义提取方法可以获得与人类感知更为接近的聚类结果，且结果具备很好的可解释性。Abstract: People prefer to distinguish the similarity of faces in the field of face retrieval and verification by describing the “semantics” or “concept” of object features, which cannot be satisfied by traditional image retrieval technology. Therefore, this paper presents a facial semantic extraction algorithm (IAFSGD) that is based on axiomatic fuzzy sets (AFS) and information granules. First, the face images are corrected to detect the critical points where facial features are extracted; then, the samples of facial features are clustered to construct the class center; the information granules of each class are obtained under the AFS framework; and then the facial images are reclassified through the information granules, to obtain the final clustering results and interpretable facial semantic description; finally, the efficacy of this algorithm is demonstrated on such facial datasets as Multi-PIE, AR, and FEI. Experimental results show that compared with FCM, CAN, FCMGD, AFSGD, and KTM, the semantic extraction method proposed in this paper can obtain clustering results closer to human perception and that the results are of good interpretability.
-
近年来随着数码相机的广泛使用和数码相册的出现，以人脸为对象的索引和检索已经引起了人们的浓厚兴趣。传统的人脸检索以人脸图像底层视觉特征的相似程度来判断人脸是否相似。然而，从人类认知角度，人类更倾向于通过描述对象特征的“语义”或“概念”来对人脸进行相似性判别。以一条语义查询条件“一个留着络腮胡子的戴着眼镜的阿拉伯裔中年男性”为例，基于图像底层视觉特征的人脸检索无法完成这样的任务，然而这样的检索在日常生活中需求量很大。由于人与计算机对图像相似性判别依据之间的不同，造成了人所理解的“语义相似”与计算机理解的“视觉相似”之间的“语义鸿沟”。这是目前人脸检索系统面临的一个挑战。
当前，大多数人脸检索系统仍受查询条件的限制，源于人类更倾向于用“语义”或是“概念”检索图像，而传统的图像检索已无法满足这一需求。在大多数情况下，用户无法提供被检索人的照片，只能够提供目击者关于被检索人特征的语言描述，因此，人脸图像的语义提取方法对于人脸检索、人脸验证有着至关重要的作用。
目前人脸图像语义的提取方式主要有基于知识的语义提取、人工交互语义提取、利用外部信息源的语义提取。这3种方法在应用上有各自的优势，但通过这3种方法将图像低层特征映射到高层语义，即缩小“语义鸿沟”还存在费时、费力且精度得不到保障等局限性。
针对上述问题，Ren等[1]学者基于AFS理论设计了人脸语义描述，用来刻画人脸的眼睛、鼻子、嘴等主要区域的大小特征，实验结果表明该方法提取的面部语义更接近人类感知。Palacios等学者提出FARLAT-LQD方法[2]从数据中来获取合适的隶属度函数和模糊关联规则，但该方法中隶属函数是事先给定的三角隶属函数，这类隶属函数的定义是独立于原始数据和客观事实的。这对现实大规模智能系统是不适用的。Karczmarek等[3]对未来人脸语义刻画的前景进行了展望，提出未来的研究应该基于更复杂、客观的模糊集的人脸特征表示。当前文献中的这类表示都受限于隶属函数的形式，如三角形或梯形。因此，建立更自然的方式来表示人脸特征的语义必将成为该研究的潜在目标。
综上，本文将公理模糊集框架下的隶属函数与信息粒深度结合提出了一种新的人脸语义提取算法(IAFSGD)。该方法的关键思想是利用公理模糊集框架下的隶属函数来优化信息粒的边界。这是由于该隶属函数是基于被观测数据和整个空间上表示的模糊逻辑运算定义的。该隶属函数是由概率分布确定的，因此，基于由从一个概率空间抽取的观测数据确定的隶属函数和它们的逻辑运算发现的规律能够被应用到整个空间中去。这样的隶属函数定义要优于独立于原始数据和客观事实的三角形、梯形等隶属函数，适用于更复杂、更客观的系统。我们相信本文的研究结果将有助于推动人脸相关应用的发展。
1. AFS理论
刘晓东教授于1995年提出了公理模糊集(axiomatic fuzzy sets，AFS)理论[4]。公理模糊集AFS理论为处理模糊信息的语义提供了一个新的研究方向，其本质是研究如何把蕴含在训练数据或数据库中的内在规律或模式转化到模糊集及其逻辑运算中。目前AFS 理论已经被应用到诸多领域，例如商业智能[5]、图像处理[6]、金融数据分析[7-8]等。
下面给出AFS结构和隶属函数的定义。
定义1[9-10] X为论域，M为X上简单概念m的集合，
$ {2^M} $ 是M中所有子集构成的集合，如果$ (M,\tau ,X) $ 满足下面公理AX1和AX2，则$ (M,\tau ,X) $ 为一个AFS结构。$${\bf{AX1}}: \forall ({x_1},{x_2}) \in X,\tau ({x_1},{x_2}) \subseteq \tau ({x_1},{x_1})$$ $${\bf{AX2}} :\forall ({x_1},{x_2}),({x_2},{x_3}) \in X \times X,\tau ({x_1},{x_2}) \cap ({x_2},{x_3}) \subseteq \tau ({x_1},{x_3})$$ 在实际应用中，τ可以根据线性有序关系“
$ { \succcurlyeq _m} $ ”来构造，即$$ \tau (x,y) = \{ m\left| {m \in M,x} \right.{ \succcurlyeq _m}y\} \subset {2^M} $$ 令
${{\rm{EM}}^ * } = \left\{ {\displaystyle\sum\limits_{i \in I} {\left( {\prod\limits_{m \in {A_i}} m } \right)\left| {{A_i} \in M,i \in I} \right.} } \right\}$ 为简单概念集合$ M = \{ {m_{i,j}}{\text{\} }} $ 的EI代数形式。假设有两个概念集合$ {A_{\text{1}}}{\text{ = \{ }}{m_{2,3}}{\text{,}}{m_{3,1}}{\text{\} , }}{A_2}{\text{ = \{ }}{m_{4,1}}{\text{\} }} \subseteq M $ ，由它们组成的语义概念可以表示为$$ \begin{gathered} \displaystyle\sum\limits_{u = 1}^2 {\left( {\prod\limits_{m \in {A_u}} m } \right)} = \prod\limits_{m \in {A_1}} m + \prod\limits_{m \in {A_2}} m = {m_{2,3}}{m_{3,1}} + {m_{4,1}} \\ \end{gathered} $$ (1) 定义2[9] 设
$(\varOmega ,\mathcal{F},P)$ 是一个概率空间，M是$\varOmega$ 上的一个模糊集，X是来自概率空间$(\varOmega ,\mathcal{F},P)$ 的一组有限的样本，$ {\rho _\xi } $ 为模糊概念$ \xi $ 上的权函数。对任意$m \in M, x \in \varOmega ,\{ m\} \succcurlyeq \left( x \right) \in \mathcal{F}$ ，以下隶属度计算公式皆成立：如果隶属函数族
$T = \{ {\mu _\xi }(x)\left| \xi \right. \in {\rm EM}\}$ [11]与AFS模糊逻辑系统$({\rm EM}, \vee , \wedge )$ 以及AFS结构$ (M,\tau ,X) $ 和谐一致，则称其为一致隶属函数。样本x属于模糊概念$\xi = \displaystyle\sum\nolimits_{i \in I} \left(\prod\nolimits_{m \in {A_i}} m \right) \in {\rm EM}$ 的一致隶属函数[12]被定义为$$ {\mu }_{\xi }(x)=\underset{i\in I}{\mathrm{sup}}{\displaystyle \prod _{\xi \in {A}_{i}}\dfrac{{\displaystyle\sum _{u\in {A}_{i}^{\tau }(x)}{\rho }_{\xi }(u){N}_{u}}}{{\displaystyle\sum_{u\in X}{\rho }_{\xi }(u){N}_{u}}}}\text{，}\forall x\in X $$ (2) $$ {\mu _\xi }(x) = \mathop {\sup }\limits_{i \in I} \prod\limits_{\xi \in {A_i}} {\dfrac{{{\int_{A_{i}^{\tau}} (x)} {{\rho _\xi }(t){\rm{d}}P(t)} }}{{\int_\varOmega {{\rho _\xi }(t){\rm{d}}P(t)} }}} ,\forall x \in \varOmega $$ (3) 其中，
$ A_i^\tau (x) = \{ y \in X\left| {x{ \succcurlyeq _m}y,\forall m \in {A_i}} \right.\} $ 是论域X的一个子集，$ {N_u} $ 为$ u \in X $ 的次数。关于AFS基础理论及应用研究的详细介绍见参考文献[9]。
2. 人脸语义提取算法
本文提出了一种基于公理模糊集与信息粒理论的人脸语义提取算法（IAFSGD），算法流程如图1所示，算法流程为：
图 1 人脸语义提取算法流程Fig. 1 Flowchart of the proposed semantic extraction algorithm
下载:
全尺寸图片
1) 将人脸图像转化为人脸关键点。对全部人脸图像进行裁剪与矫正，并通过AR模型检测出人脸关键点。
2) 将人脸关键点转化为类簇。根据人脸关键点计算得到人脸特征值，并对特征值进行AFS聚类，得到聚类结果(类簇)。
3) 将类簇转化为信息粒。根据AFS聚类结果构建信息粒，并通过信息粒对人脸特征值再分类。然后，提取粒度描述，计算每个信息粒的覆盖率和特异性。最后，通过AFS语义刻画提取出具有可解释性的语义描述。
IAFSGD算法的优势在于利用AFS一致隶属函数来优化信息粒的上下边界，得到的信息粒对于人脸五官的刻画将更加客观、稳定，同时还能提取出具有可解释性的人脸语义描述。
2.1 人脸关键点检测与图像裁剪校正
本文利用AR人脸关键点检测模型[13]在人脸五官中提取130个关键点
${L_i} = \{ {l_i}\} ,i = 1,2, \cdots ,130$ ，$ {l_i} = ({x_i},{y_i}) $ ，其中$ {x_i} $ 、$ {y_i} $ 分别是第i个人脸关键点的横、纵坐标，如图2中人脸所示。
图 2 第k个人脸图像$ {I_k} $ 右眼成分的特征提取Fig. 2 Feature extraction of the right eye of the k-th face image$ {I_k} $ 下载:
全尺寸图片
由于人脸的大小在尺度空间上略有不同，因此为了提取准确的人脸特征，需要事先对人脸图像进行校正，将人脸关键部分裁剪出来，并对数据库中人脸图像进行缩放。
2.2 特征提取
本节将介绍如何提取出人脸特征。首先令
${I^{\rm Face}} = \{ {I_1},{I_2}, \cdots, {I_N}\}$ 为人脸图像的集合，其中$ {I_k} $ 是集合${I^{\rm Face}}$ 中第k个人脸图像，N是人脸图像的数量。令
$ f $ 为人脸主要区域，这里的f以右眼为例。${V^f} = \{ V_1^f,V_2^f, \cdots ,V_n^f\}$ 为右眼特征集合，每个右眼特征$ V_j^f $ 含义如表1所示，其中$ n = 4 $ ，对应右眼的特征值为$ x_{kj}^f,j = 1,2,3,4 $ 。表 1 右眼的每个特征$ V_j^f $ 及其语义概念$ m_{j,s}^f $ Table 1 Each feature of the right eye$ V_j^f $ and its semantic concept$ m_{j,s}^f $ 右眼特征 $ V_j^f $ 对应特征的含义 简单概念 $ m_{j,s}^f $ $ V_1^f $ 右眼的周长 大、小、中 $ V_2^f $ 右眼的高 $ V_3^f $ 右眼边界到质心距离之和 $ V_4^f $ 外眼角 在每个特征
$ V_j^f $ 上定义3个简单概念，概念集合为$ {M^f} = \{ m_{j,s}^f\left| {1 \leqslant j \leqslant 4,1 \leqslant s \leqslant 3} \right.\} $ ，$m_{j,{\text{1}}}^f、m_{j,{\text{2}}}^f、m_{j,{\text{3}}}^f$ 分别表示特征$ V_j^f $ 的3个语义概念“大”“小”“中”，对应的具体含义详见表1。2.3 基于AFS理论与信息粒的语义提取
在提取人脸特征后，对人脸主要区域f进行语义特征的提取。首先，对人脸主要区域f的特征值进行聚类；然后，对每类样本构建信息粒；利用得到的信息粒对人脸主要区域f进行再分类；最后，得到具有解释性强的类描述。
2.3.1 AFS语义描述
1) 计算样本
$I^f_k$ 属于每个简单概念$m_{j,s}^f$ 的隶属度${\mu_m}(I^f_k)$ ，通过隶属度${\mu_m}(I^f_k)$ 找到该样本最显著的简单概念$B_{I^f_k}$ ，并将显著概念结合起来得到该样本的描述$ {\zeta _{I_k^f}} $ 。$$ {B_{I_k^f}} = \left. {\left\{ {m \in {M^f}\left| {\mathop {\max }\limits_{m \in {M^f}} } \right.} \right.\left({\mu _m}\left(I_k^f\right)\right)} \right\} $$ (4) $$ {\zeta _{I_k^f}} = { \wedge _{\beta \in {B_{I_k^f}}}}\beta $$ (5) 式中˄是AFS代数中定义的模糊逻辑运算。
2) 计算两张人脸
$ {I_i} $ 和$ {I_j} $ 的等价关系$ {r_{ij}} $ ，进而建立所有样本的模糊等价关系矩阵R。$ {r_{ij}} $ 的计算公式为$$ {r_{ij}} = \min \{ {\mu _{{\zeta _{{I_i}}} \wedge {\zeta _{{I_j}}}}}({I_i}),\;{\mu _{{\zeta _{{I_i}}} \wedge {\zeta _{{I_j}}}}}({I_j})\} $$ (6) 3) 从模糊等价关系矩阵R中选择阈值，使聚类有效性指标
$ {I_\theta } $ 达到最小，从而确定最优阈值θ[14]。当$ {r_{ij}} \geqslant \theta $ 时，说明两张人脸$ {I_i} $ 和$ {I_j} $ 处于同一类，进而得到划分最清晰的聚类结果${C_i},i = 1,2, \cdots ,l$ 。4) 根据聚类结果，选择每类类内样本的描述
$ {\zeta _{I_k^f}} $ 来构建每类的语义描述：$$ {\varGamma _i} = \left\{ {{\zeta _{I_k^f}}\left| {\frac{{\left| {\left\{ {y\left| {y \in {C_i},{\mu _{{\zeta _{I_k^f}}}}(y) \geqslant \lambda } \right.} \right\}} \right|}}{{\left| {{C_i}} \right|}} \geqslant \omega ,I_k^f \in {C_i}} \right.} \right\} $$ (7) 对于模糊描述
$ {\zeta _{I_k^f}} $ ，如果类$ {C_i} $ 中隶属于$ {\zeta _{I_k^f}} $ 的程度大于λ的样本个数与$ {C_i} $ 中的样本总数的比值大于ω的话，那么$ {\zeta _{I_k^f}} $ 被认为是能够表现出类样本共性的描述。因此参数ω、λ控制着类$ {C_i} $ 语义描述的普遍性和特殊性。在实验过程中，设置ω、λ为相同的参数值，实验结果表明当$ \lambda \in [0.5,0.9] $ 和$ \omega \in [0.5,0.9] $ 时，聚类效果是稳定的，当参数在合理的范围内取值时，聚类算法对于参数的设置并不敏感，所以本文令参数$ \omega {\text{ = 0}}{\text{.6,}}\lambda {\text{ = 0}}{\text{.6}} $ 。${\varGamma _i}$ 是类$ {C_i} $ 中有代表性的样本语义描述集合，接着将${\varGamma _i}$ 中最显著的模糊描述结合起来得到类$ {C_i} $ 的描述$ {\zeta _{{C_i}}} $ ：$$ {\zeta }_{{C}_{i}}={\wedge }_{\zeta \in {\varGamma }_{i}}\zeta \text{，}{\varGamma }_{i}\ne \varnothing $$ (8) 2.3.2 信息粒及其解释
首先，通过上述聚类结果，构建每一类样本的类中心
$ {v_{ij}} $ ：$$ {v_{ij}} = \dfrac{{\displaystyle\sum_{k \in {v_i}} {x_{kj}^f} }}{{{N_i}}},j = 1,2, \cdots ,n $$ (9) 式中
$ {N_i} $ 是类$ {C_i} $ 的样本个数。然后，在类中心周围根据合理粒度的原则[15]构造信息粒[16]，信息粒的范围为
$ [a{\text{ }}b] $ 。信息粒的参数形式由隶属函数来描述，并且满足$ {\mu _{m_{j,3}^f}}({v_{ij}}) = 1 $ 。隶属函数为$$ {\mu _{m_{j,3}^f}}(x_{kj}^f) = \mathop {\sup }\limits_{i \in I} \left\{ \prod\limits_{m_{j,3}^f \in {A_i}} {\left(\dfrac{{\displaystyle\sum_{u \in {A_{i}^\tau} (x)} {{\rho _{m_{j,3}^f}}(u)} }}{{\displaystyle\sum_{u \in X} {{\rho _{m_{j,3}^f}}(u)} }}\right)} \right\} $$ (10) 由于在AFS框架下，数据被处理成数据间的线性有序关系，因此采用AFS一致隶属函数定义信息粒的参数形式，并用其来校准隶属度
$ {\mu _{{C_i}}}(x) $ ，校准机制为$$ \phi ({\mu _{{C_i}}}(x)) = \left\{ {\begin{array}{*{20}{c}} {{\mu _{{C_i}}}(x)，{\text{ }}{\mu _{{C_i}}}(x) < {\mu _{m_{j,3}^f}}(x_{kj}^f)} \\ {{\mu _{m_{j,3}^f}}(x_{kj}^f)，{\text{ }}{\mu _{{C_i}}}(x) \geqslant {\mu _{m_{j,3}^f}}(x_{kj}^f)} \end{array}} \right. $$ (11) 式中：
$ {\mu _{{C_i}}}(x) $ 为AFS聚类后样本对第i类$ {C_i} $ 的隶属度，因此式(14)可以理解为$$ \phi ({\mu _{{C_i}}}(x)) = \min \left({\mu _{{C_i}}}(x), {\mu _{m_{j,3}^f}}\left(x_{kj}^f\right)\right) $$ 信息粒由类中心
$ {v_{ij}} $ 及下边界a、上边界b构成，其对数据的覆盖范围[15]由$ f{}_1 $ 和$ {f_2} $ 两个量来确定：$$ {f_1}(a) = \max \left[ {0,\;\sum\limits_{x_{kj}^f \in {{\rm{concept}}_{[a,\;{v_{ij}}]}}} {\phi ({u_i}(x)) - \gamma \sum\limits_{x_{kj}^f \notin {{\rm{concept}}_{[a,\;{v_{ij}}]}}} {\phi ({u_i}(x))} } } \right] $$ (12) $$ {f_2}(a) = \exp ( - \alpha \left| {{v_{ij}} - a} \right|) $$ (13) 式中：
$x_{kj}^f \in {\rm{concep}}{{\rm{t}}_{[a,{v_{ij}}]}}$ 表示$ x_{kj}^f $ 是属于区间的样本；而$x_{kj}^f \notin {{\rm concept}_{[a,{v_{ij}}]}}$ 则表示不属于区间$ [a{\text{ }}{v_{ij}}] $ 的样本；$ \gamma $ 为非负折现因子，所以$ f{}_1 $ 描述了属于区间的样本与不属于区间的样本之间的差异。接下来，本文将
$ {f_{\text{1}}}(a) $ 和$ {f_{\text{2}}}(a) $ 的乘积作为优化最优下边界${a_{\rm opt}}$ 的指标，即$$ {a_{\rm opt}} =\arg\; \mathop { \max }\limits_{a \in A} \;{f_{\text{1}}}(a) \times {f_{\text{2}}}(a) $$ (14) 其中，
$A = \{ x_{kj}^f\left| {x_{kj}^f < {v_{ij}},k = 1,2, \cdots ,N} \right.\}$ ，即A中元素为下边界a的候选值，通过求取令$ {f_{\text{1}}} \times {f_{\text{2}}} $ 达到最大的a作为${a_{\rm opt}}$ 。同理，B中元素为上边界b的候选值
$b \in B, B = \{ x_{kj}^f\left| {x_{kj}^f > {v_{ij}},k = 1,2, \cdots ,N} \right.\}$ ，根据式(13)~(17)，可得到最优上边界${b_{\rm opt}}$ 。由此一维数据的信息粒$ G $ 构建完成，依次构建n维信息粒，将n维信息粒的最小值作为人脸图像$ {I_k} $ 的信息粒，即：$$ G({X_{\text{1}}},\;{X_2}, \cdots ,\;{X_n}) = \min ({G_1}({X_1}),\;{G_2}({X_2}),\; \cdots ,\;{G_n}({X_n})) $$ (15) 最后，通过信息粒对人脸图像进行再分类，获得了新的类别
${C_q},q = 1,2, \cdots ,l$ 及每类的语义描述$ {\zeta _{{C_q}}} $ 。下面给出粒度描述的覆盖率[15]和特异性的求取方法。
1) 覆盖率
首先，计算
$ x_{kj}^f $ 属于一维信息粒$ {G_{ij}} $ 的隶属度$ {G_{ij}}(x_{kj}^f) $ ：$$ {G_{ij}}(x_{kj}^f) = {\mu _{m_{j,3}^f}}(x_{kj}^f) = \mathop {\sup }\limits_{i \in I} \left\{ \prod\limits_{m_{j,3}^f \in {A_i}} {\left(\dfrac{{\displaystyle \sum\nolimits_{u \in {A_{i}^\tau} (x)} {{\rho _{m_{j,3}^f}}(u)} }}{{\displaystyle \sum\nolimits_{u \in X} {{\rho _{m_{j,3}^f}}(u)} }}\right)} \right\} $$ (16) 其中
$ {G_{ij}} $ 为第i类在第j个特征上的信息粒。进而，由一维隶属度值
$ {G_{ij}}(x_{kj}^f) $ 得到$ x_k^f $ 属于第i类信息粒的隶属度$ {G_i}(x_k^f) $ ，其计算公式为$$ {G_i}(x_k^f) = \mathop {\min }\limits_{j = 1,2, \cdots ,n} {G_{ij}}(x_{kj}^f) $$ (17) 最终，信息粒对样本的覆盖率为
$$ {\rm{Coverage}}({G_i}) = \dfrac{{\displaystyle \sum_{k = 1}^N {{G_i}(x_k^f)} }}{N} $$ (18) 2) 特异性
特异性旨在描述信息粒刻画样本的细致程度。本文如下定义带有良好语义的信息粒
$ {G_i} $ 的特异性：$$ {\rm{Specificity}}({G_i}) = \dfrac{1}{n}\displaystyle \sum\limits_{j = 1}^n {\left(1 - \dfrac{{{ Z}({G_{ij}})}}{{{N_i}}}\right)} $$ (19) 式中：
${Z}({G_{ij}})$ 为信息粒$ {G_{ij}} $ 内第i类样本的个数；Ni为第i类样本的总数；2.4 算法时间复杂度
通过每张图像的人脸关键点来构造特征值矩阵
${{\boldsymbol{x}}^f}$ ，其时间复杂度为$ O(N) $ ；AFS聚类结果$ {C_i} $ 的时间复杂度为$ O({l^2}) $ ；构建信息粒$ G $ 的时间复杂度为$ O(nl) $ ；通过信息粒对人脸特征值再分类的时间复杂度为$ O(nl{N^2}) $ ；AFS语义提取的时间复杂度为$ O({l^2}) $ ，其中N是人脸图像${I^{\rm Face}}$ 的总数，l为聚类数目，n为特征值${{\boldsymbol{x}}^f}$ 的维度。因此，IAFSGD算法的整体时间复杂度为$ O(nl{N^2}) $ 。3. 实验结果与分析
本章在Multi-PIE数据库[17]、AR数据库[18]和FEI数据库[19]上对算法进行了验证。
3.1 Multi-PIE数据库
Multi-PIE数据库包含337个主题的755370张人脸图像。本文选择249张人脸的正面图像作为实验数据，来验证IAFSGD算法的可行性。
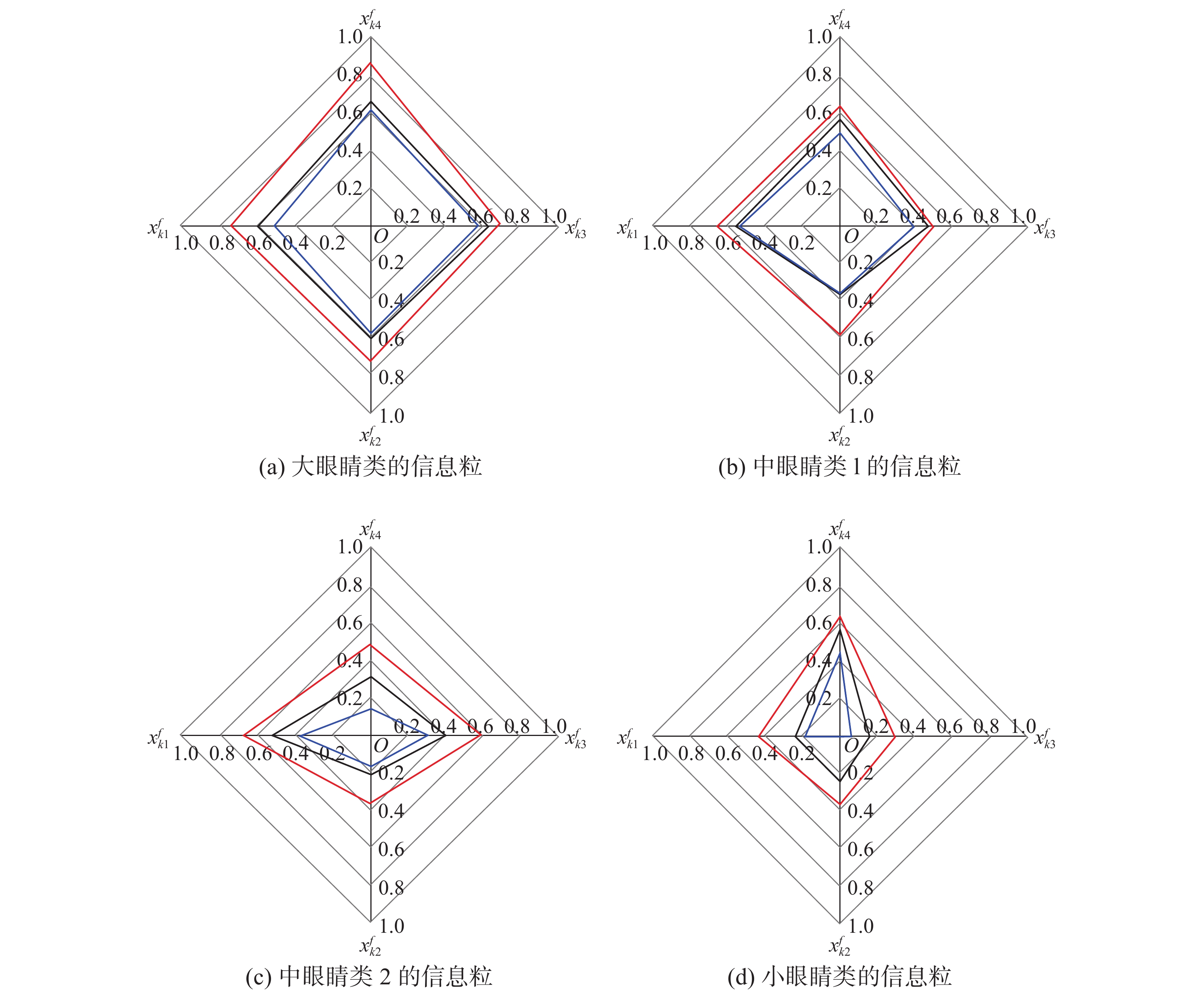
当聚类有效性指标
$ {I_\theta } $ 达到最小，阈值θ=0.9558时，聚类结果最清晰，数据被聚成4类。在上述聚类结果的基础上，进一步求得每类的信息粒。表2举例给出了当参数$ \alpha =2.0，\gamma =0 $ 时大眼睛类、中眼睛类1、中眼睛类2、小眼睛类具有信息粒特征的语义描述，每类的信息粒如图3 所示。表 2 Multi-PIE数据库中4类右眼的语义描述Table 2 Semantic descriptions of the four clusters for the right eyes on Multi-PIE database类 模糊概念及信息粒类中心 语义描述 大眼睛 $ {\zeta _{{C_1}}} = m_{2,1}^fm_{3,1}^fm_{4,1}^f $
${v_1} = [0.{\text{472\;1} },0.{\text{800\;0} },0.{\text{784\;4} },0.{\text{750\;6} }]$具有大眼高、大中心距、大外眼角的眼睛
覆盖率：0.0062，特异性：0.7500中眼睛1 $ {\zeta _{{C_2}}} = m_{4,3}^f $
${v_2} = [0.469\;3,0.762\;6,0.724\;9,0.688\;4]$具有中等外眼角的眼睛
覆盖率：0.2343，特异性：0.7443中眼睛2 $ {\zeta _{{C_3}}} = m_{1,3}^f $
${v_3} = [0.277\;2,0.655\;1,0.575\;4,0.556\;3]$具有中等周长的眼睛
覆盖率：0.0821，特异性：0.4891小眼睛 $ {\zeta _{{C_4}}} = m_{2,2}^fm_{3,2}^fm_{4,2}^f $
${v_4} = [0.530\;2,0.425\;7,0.482\;4,0.292\;2]$具有小眼高、小中心距、小外眼角的眼睛
覆盖率：0.0011，特异性：0.5658
图 3 Multi-PIE数据库的信息粒可视化，其中参数$ \alpha = 2.0,\gamma = 0 $ Fig. 3 Granular prototypes visualization on Multi-PIE database, and the selected values of parameters$ \alpha = 2.0,\gamma = 0 $ 下载:
全尺寸图片
图4给出了Multi-PIE数据库“大眼睛”类的4个人脸图像样本和“小眼睛”类的4个人脸图像样本。比较结果表明，“大眼睛”类的人的眼睛明显大于“小眼睛”类的人的眼睛。
图 4 “大眼睛”和“小眼睛”的结果对比(Multi-PIE数据库)Fig. 4 Comparison of “large eyes” and “small eyes” (Multi-PIE database)下载:
全尺寸图片
3.2 AR数据库
AR人脸数据库包含896张正面人脸图像，包括58名男性和54名女性的面部图像。数据库还提供了这112人的4种面部表情（自然、微笑、愤怒、尖叫）的图像，这896张图像是这112名参与者分两次采集的。本文选择两次采集的112个人的自然面部表情图像作为实验数据。
当阈值
$\theta = 0.901\;8$ 时，聚类有效性指标$ {I_\theta } $ 达到最小，此时类别数为4。在AFS聚类结果上构建信息粒，对AR人脸数据进行再分类。表3举例给出了当参数$ \alpha =2.0，\gamma =0 $ 时4类具有信息粒特征的语义描述，4类的信息粒如图5所示。表 3 AR数据库中4类右眼的语义描述Table 3 Semantic descriptions of four clusters for the right eyes on AR database类 模糊概念及信息粒类中心 语义描述 大眼睛 $ {\zeta _{{C_1}}} = m_{2,1}^fm_{3,1}^fm_{4,1}^f $
${v_1} = [0.600\;1,0.606\;2,0.628\;3,0.654\;1]$具有大眼高、大中心距、大外眼角的眼睛。
覆盖率：0.0449，特异性：0.3364中眼睛1 $ {\zeta _{{C_{}}}} = m_{2,3}^fm_{4,3}^f $
${v_2} = [0.563\;8,0.364\;7,0.472\;7,0.564\;2]$具有中等眼高、中等外眼角的眼睛。
覆盖率：0.1409，特异性：0.4262中眼睛2 $ {\zeta _{{C_3}}} = m_{3,3}^fm_{4,2}^f $
${v_3} = [0.538\;1,0.209\;8,0.413\;4,0.313\;2]$具有中等中心距、小外眼角的眼睛。
覆盖率：0.0224，特异性：0.2868小眼睛 $ {\zeta _{{C_4}}} = m_{2,2}^fm_{3,2}^f $
${v_4} = [0.242\;9,0.246\;4,0.155\;6,0.573\;0]$具有小眼高、小中心距的眼睛。
覆盖率：0.0478，特异性：0.5574
图 5 AR数据库的信息粒可视化，其中参数$ \alpha = 2.0,\gamma = 0 $ Fig. 5 Granular prototypes visualization on AR database, and the selected values of parameters$ \alpha = 2.0,\gamma = 0 $ 下载:
全尺寸图片
图6给出了AR数据库“大眼睛”类的4个人脸图像样本和“小眼睛”类的4个人脸图像样本。“大眼睛”类的人的眼睛明显大于“小眼睛”类的人的眼睛，证明了本文提出方法的有效性。
图 6 “大眼睛”和“小眼睛”的语义描述提取结果对比(AR数据库)Fig. 6 Comparison of “large eyes” and “small eyes” (AR database)下载:
全尺寸图片
3.3 FEI数据库实验及分析
FEI数据库是由FEI人工智能实验室拍摄的一组人脸图像，其中男性女性各100人，由每人角度各不相同的14张图像组成共2800张图像。本文选择这200人的正面图像作为实验图像。
表4举例给出了当参数
$ \alpha =2.0，\gamma =0 $ 时，从FEI数据库中提取的具有信息粒特征的语义描述。图7显示了FEI数据库中“大眼睛”类的4个人脸图像样本和“小眼睛”类的4个人脸图像样本。表 4 FEI数据库中4类右眼的语义描述Table 4 The semantic descriptions of four clusters for the right eyes on FEI database类 模糊概念及信息粒类中心 语义描述 大眼睛 $ {\zeta _{{C_1}}} = m_{2,1}^fm_{3,1}^f $
${v_1} = [0.625\;3,0.852\;8,0.739\;3,0.627\;2]$具有大眼高、大外眼角的眼睛。
覆盖率：0.0896，特异性：0.7036中眼睛1 $ {\zeta _{{C_{}}}} = m_{1,3}^fm_{2,2}^fm_{3,3}^f $
${v_2} = [0.498\;9,0.656\;8,0.643\;1,0.614\;6]$具有中等眼高、中等外眼角的眼睛。
覆盖率：0.0520，特异性：0.6336中眼睛2 $ {\zeta _{{C_3}}} = m_{2,2}^fm_{4,2}^f $
${v_3} = [0.603\;2,0.652\;0,0.667\;4,0.352\;7]$具有中等中心距、小外眼角的眼睛。
覆盖率：0.0603，特异性：0.7839小眼睛 $ {\zeta _{{C_4}}} = m_{1,2}^fm_{3,2}^f $
${v_4} = [0.304\;8,0.727\;9,0.474\;3,0.517\;3]$具有小眼高、小中心距的眼睛。
覆盖率：0.1099，特异性：0.8316
图 7 “大眼睛”和“小眼睛”的语义描述提取结果对比 (FEI数据库)Fig. 7 Comparison of “large eyes” and “small eyes” (FEI database)下载:
全尺寸图片
3.4 实验结果与其他文献的对比
本节将FCM[20]、CAN[21]、FCMGD[22]、AFSGD[23]、KMT[24]与本文提出的IAFSGD算法进行比较分析。
3.4.1 参数设置与评价指标
AFS聚类算法的参数取值为
$ \omega {\text{ = 0}}{\text{.6,}}\lambda {\text{ = 0}}{\text{.6}} $ ；由式(15)、(16)可知，信息粒的上、下边界受参数α、γ的影响，所以接下来的对比实验选取了不同的α、γ值，并对结果进行了分析。同时，由于FCM算法随机选取初值，其聚类结果受初值影响，因此本文对FCM和FCMGD算法进行100次实验，并给出了聚类结果的平均值。为验证IAFSGD聚类结果的清晰程度，通过每类右眼面积的平均值(Area)和兰德系数[25](Rand Index，RI)对聚类性能进行评价。其中，Area的计算公式如下：
$$ \begin{gathered} {\rm{Area}} = [({x_{34}} + {x_{35}})({y_{34}} - {y_{35}}) + ({x_{35}} + {x_{36}})({y_{35}} - {y_{36}}) +\\ ({x_{36}} + {x_{37}})({y_{36}} - {y_{37}}) + ({x_{37}} + {x_{38}})({y_{38}} - {y_{39}})+\\ ({x_{39}} + {x_{45}})({y_{39}} - {y_{45}}) + ({x_{45}} + {x_{44}})({y_{45}} - {y_{44}}) +\\ ({x_{44}} + {x_{43}})({y_{44}} - {y_{43}}) + ({x_{43}} + {x_{42}})({y_{43}} - {y_{42}}) + \\ ({x_{42}} + {x_{41}})({y_{42}} - {y_{41}}) + ({x_{41}} + {x_{40}})({y_{41}} - {y_{40}}) + \\ ({x_{40}} + {x_{34}})({y_{40}} - {y_{34}}) + ]/2 \\ \end{gathered} $$ (23) 聚类结果中“大眼睛”类的Area应越大越好，“小眼睛”类的Area应越小越好，这能够说明算法获得了较好的聚类效果。
RI[25]是一种用排列组合原理来对聚类进行评价的方法，其中
$$\rm RI = \frac{{TP + TN}}{{TP + FP + FN + TN}} $$ (24) 式中：TP为同一类的人脸被分到同一个类簇；TN为不同类的人脸被分到不同类簇；FP为不同类的人脸被分到同一个类簇；FN为同一类人脸被分到不同类簇。
本实验共征集了10位实验人员，分别对3个人脸数据库右眼标记类别。由于每个人对于人脸右眼类别的判断不同，因此在计算兰德系数时，先分别统计10个人的类标结果与聚类结果的兰德系数值，再将其平均值作为最终该聚类算法的兰德系数。RI的值应在[0,1]之间，且越大越好。
3.4.2 对比试验及分析
表5、表6分别给出FCM、CAN、FCMGD、AFSGD、KMT、IAFSGD算法在Multi-PIE、AR人脸数据库右眼面积Area的对比实验结果，可以发现IAFSGD算法得到的“大眼睛”类右眼面积的平均值明显大于其他5种算法得到的“大眼睛”类右眼面积的平均值；该算法得到的“小眼睛”类右眼面积的平均值小于其他5种算法得到的“小眼睛”类右眼面积的平均值。
表 5 FCM、CAN、FCMGD、AFSGD、KMT、IAFSGD 在 Multi-PIE 数据库实验结果的比较Table 5 Comparison of FCM, CAN, FCMGD, AFSGD, KMT and IAFSGD on Multi-PIE database类 α γ FCM CAN FCMGD AFSGD KMT IAFSGD 大眼睛 0.5 0 452.8451 448.5333 447.6485 440.5714 427.7107 476.0000 1 0 452.8451 448.5333 447.7716 456.0000 427.7107 476.0000 2 0 452.8451 448.5333 453.9911 453.7043 427.7107 476.0000 3 0 452.8451 448.5333 451.6857 452.7568 427.7107 476.0000 2 1 452.8451 448.5333 454.5421 454.8966 427.7107 476.0000 2 2 452.8451 448.5333 454.5204 452.8440 427.7107 476.0000 2 3 452.8451 448.5333 454.4159 454.3423 427.7107 476.0000 小眼睛 0.5 0 331.7778 369.3299 342.5714 264.0000 356.5333 275.5121 1 0 331.7778 369.3299 334.8077 284.4453 356.5333 275.5121 2 0 331.7778 369.3299 338.7070 336.9756 356.5333 284.4453 3 0 331.7778 369.3299 331.6078 336.9164 356.5333 284.4453 2 1 331.7778 369.3299 336.3265 333.6951 356.5333 272.7496 2 2 331.7778 369.3299 336.3265 336.9164 356.5333 272.7496 2 3 331.7778 369.3299 336.3265 342.1115 356.5333 272.7496 表 6 FCM、CAN、FCMGD、AFSGD、KMT、IAFSGD算法对AR数据库的对比Table 6 Comparisons of FCM, CAN, FCMGD, AFSGD, KMT and IAFSGD algorithm on AR database类 α γ FCM CAN FCMGD AFSGD KMT IAFSGD 大眼睛 0.5 0 596.2934 567.0905 584.3200 599.8560 567.0905 607.9871 1 0 596.2934 567.0905 588.9309 607.8544 567.0905 607.9871 2 0 596.2934 567.0905 594.5129 607.6849 567.0905 607.9871 3 0 596.2934 567.0905 593.7129 608.602 567.0905 607.9871 2 1 596.2934 567.0905 593.6778 607.6849 567.0905 607.9871 2 2 596.2934 567.0905 592.0102 607.2003 567.0905 607.9871 2 3 596.2934 567.0905 594.8776 607.9152 567.0905 607.9871 小眼睛 0.5 0 459.5044 463.5722 458.6418 456.8767 463.5722 458.4211 1 0 459.5044 463.5722 455.0292 456.8767 463.5722 458.4211 2 0 459.5044 463.5722 454.8871 459.1579 463.5722 456.973 3 0 459.5044 463.5722 464.8395 461.7465 463.5722 456.973 2 1 459.5044 463.5722 463.1164 459.1579 463.5722 456.973 2 2 459.5044 463.5722 471.3855 459.1579 463.5722 456.973 2 3 459.5044 463.5722 470.4846 459.1579 463.5722 456.973 在表5中，当
$ \alpha = {\text{0}}{\text{.5}},\gamma = 0 $ 时IAFSGD算法在处理Multi-PIE数据库时，“小眼睛”类的平均面积值稍大于AFSGD算法，但低于其他算法。由于两种算法优化信息粒的参数形式不同，所以出现了表5中的结果。在表6中，当$ \alpha = 1.0,\gamma = 0 $ 时，$ \alpha = 2.0,\gamma = 0 $ 时，IAFSGD算法在AR数据库上得到的结果中，“小眼睛”类的面积平均值稍大于FCMGD算法，但低于其他算法。这是由于FCMGD算法得到的“小眼睛”类样本数量少，所以小眼睛类的面积平均值相对小一点。基于兰德系数在Multi-PIE、AR、FEI人脸数据库上验证聚类算法的结果如表7、8、9所示。IAFSGD算法的RI值全部大于FCM、CAN、FCMGD、AFSGD、KMT算法的RI值，更符合人类感知。
表 7 FCM、CAN、FCMGD、AFSGD、KMT、IAFSGD算法对Multi-PIE数据库的聚类有效性对比Table 7 Comparisons of clustering effectiveness via FCM, CAN, FCMGD, AFSGD, KMT and IAFSGD algorithms on Multi-PIE databaseα γ FCM CAN FCMGD AFSGD KMT IAFSGD 0.5 0 0.5265 0.5247 0.5242 0.5289 0.5247 0.5296 1 0 0.5265 0.5247 0.5288 0.5254 0.5247 0.5296 2 0 0.5265 0.5247 0.5295 0.5283 0.5247 0.5304 3 0 0.5265 0.5247 0.5237 0.5283 0.5247 0.5304 2 1 0.5265 0.5247 0.5231 0.5283 0.5247 0.5304 2 2 0.5265 0.5247 0.5206 0.5276 0.5247 0.5304 2 3 0.5265 0.5247 0.5213 0.5275 0.5247 0.5304 表 8 FCM、CAN、FCMGD、AFSGD、KMT、IAFSGD算法对AR数据库的聚类有效性对比Table 8 Comparisons of clustering effectiveness via FCM, CAN, FCMGD, AFSGD, KMT and IAFSGD algorithms on AR databaseα γ FCM CAN FCMGD AFSGD KMT IAFSGD 0.5 0 0.5047 0.5043 0.5086 0.5413 0.5237 0.5509 1 0 0.5047 0.5043 0.5048 0.521 0.5237 0.5509 2 0 0.5047 0.5043 0.5015 0.5246 0.5237 0.5503 3 0 0.5047 0.5043 0.4974 0.5239 0.5237 0.5503 2 1 0.5047 0.5043 0.5015 0.5275 0.5237 0.5457 2 2 0.5047 0.5043 0.5015 0.5244 0.5237 0.5457 2 3 0.5047 0.5043 0.5019 0.5191 0.5237 0.5457 表 9 FCM、CAN、FCMGD、AFSGD、KMT、IAFSGD算法对FEI数据库的聚类有效性对比Table 9 Comparisons of clustering effectiveness via FCM, CAN, FCMGD, AFSGD, KMT and IAFSGD algorithms on FEI databaseα γ FCM CAN FCMGD AFSGD KMT IAFSGD 0.5 0 0.5262 0.5357 0.5279 0.5392 0.5399 0.5427 1 0 0.5262 0.5357 0.5268 0.5389 0.5399 0.5427 2 0 0.5262 0.5357 0.5255 0.5377 0.5399 0.5434 3 0 0.5262 0.5357 0.5255 0.5367 0.5399 0.5430 2 1 0.5262 0.5357 0.5249 0.5369 0.5399 0.5431 2 2 0.5262 0.5357 0.5249 0.536 0.5399 0.5428 2 3 0.5262 0.5357 0.5249 0.5359 0.5399 0.5435 综上所述，本研究提出的IAFSGD算法可以将人脸图像聚类得到清晰的聚类结果，并提取出可解释的人脸语义描述，实验结果说明本研究提出的人脸语义提取方法是合理且有效的。而且其他方法获得的聚类结果只是样本的类别信息，IAFSGD算法可通过简单概念构建类的语义描述，这些语义描述能够被计算机理解并处理。
4. 结束语
本文基于公理模糊集与信息粒理论提出了一种人脸语义提取算法，利用AFS一致隶属函数优化信息粒的边界，构建出更符合人类感知的信息粒，对面部五官重新聚类并提取语义，使得人脸具有精确、简洁，可解释性的特点。本文还将IAFSGD算法与其他聚类算法进行比较，实验结果表明，本文提出的IAFSGD算法在Multi-PIE、AR、FEI数据库中均取得良好的结果，使每一类人脸图像具有可解释的语义描述。下一步，本文研究的算法将应用在基于语义的人脸图像检索上。
-
图 1 人脸语义提取算法流程
Fig. 1 Flowchart of the proposed semantic extraction algorithm
下载:
全尺寸图片
图 2 第k个人脸图像
$ {I_k} $ 右眼成分的特征提取Fig. 2 Feature extraction of the right eye of the k-th face image
$ {I_k} $ 下载:
全尺寸图片
图 3 Multi-PIE数据库的信息粒可视化，其中参数
$ \alpha = 2.0,\gamma = 0 $ Fig. 3 Granular prototypes visualization on Multi-PIE database, and the selected values of parameters
$ \alpha = 2.0,\gamma = 0 $ 下载:
全尺寸图片
图 4 “大眼睛”和“小眼睛”的结果对比(Multi-PIE数据库)
Fig. 4 Comparison of “large eyes” and “small eyes” (Multi-PIE database)
下载:
全尺寸图片
图 5 AR数据库的信息粒可视化，其中参数
$ \alpha = 2.0,\gamma = 0 $ Fig. 5 Granular prototypes visualization on AR database, and the selected values of parameters
$ \alpha = 2.0,\gamma = 0 $ 下载:
全尺寸图片
图 6 “大眼睛”和“小眼睛”的语义描述提取结果对比(AR数据库)
Fig. 6 Comparison of “large eyes” and “small eyes” (AR database)
下载:
全尺寸图片
图 7 “大眼睛”和“小眼睛”的语义描述提取结果对比 (FEI数据库)
Fig. 7 Comparison of “large eyes” and “small eyes” (FEI database)
下载:
全尺寸图片
表 1 右眼的每个特征
$ V_j^f $ 及其语义概念$ m_{j,s}^f $ Table 1 Each feature of the right eye
$ V_j^f $ and its semantic concept$ m_{j,s}^f $ 右眼特征 $ V_j^f $ 对应特征的含义 简单概念 $ m_{j,s}^f $ $ V_1^f $ 右眼的周长 大、小、中 $ V_2^f $ 右眼的高 $ V_3^f $ 右眼边界到质心距离之和 $ V_4^f $ 外眼角 表 2 Multi-PIE数据库中4类右眼的语义描述
Table 2 Semantic descriptions of the four clusters for the right eyes on Multi-PIE database
类 模糊概念及信息粒类中心 语义描述 大眼睛 $ {\zeta _{{C_1}}} = m_{2,1}^fm_{3,1}^fm_{4,1}^f $
${v_1} = [0.{\text{472\;1} },0.{\text{800\;0} },0.{\text{784\;4} },0.{\text{750\;6} }]$具有大眼高、大中心距、大外眼角的眼睛
覆盖率：0.0062，特异性：0.7500中眼睛1 $ {\zeta _{{C_2}}} = m_{4,3}^f $
${v_2} = [0.469\;3,0.762\;6,0.724\;9,0.688\;4]$具有中等外眼角的眼睛
覆盖率：0.2343，特异性：0.7443中眼睛2 $ {\zeta _{{C_3}}} = m_{1,3}^f $
${v_3} = [0.277\;2,0.655\;1,0.575\;4,0.556\;3]$具有中等周长的眼睛
覆盖率：0.0821，特异性：0.4891小眼睛 $ {\zeta _{{C_4}}} = m_{2,2}^fm_{3,2}^fm_{4,2}^f $
${v_4} = [0.530\;2,0.425\;7,0.482\;4,0.292\;2]$具有小眼高、小中心距、小外眼角的眼睛
覆盖率：0.0011，特异性：0.5658表 3 AR数据库中4类右眼的语义描述
Table 3 Semantic descriptions of four clusters for the right eyes on AR database
类 模糊概念及信息粒类中心 语义描述 大眼睛 $ {\zeta _{{C_1}}} = m_{2,1}^fm_{3,1}^fm_{4,1}^f $
${v_1} = [0.600\;1,0.606\;2,0.628\;3,0.654\;1]$具有大眼高、大中心距、大外眼角的眼睛。
覆盖率：0.0449，特异性：0.3364中眼睛1 $ {\zeta _{{C_{}}}} = m_{2,3}^fm_{4,3}^f $
${v_2} = [0.563\;8,0.364\;7,0.472\;7,0.564\;2]$具有中等眼高、中等外眼角的眼睛。
覆盖率：0.1409，特异性：0.4262中眼睛2 $ {\zeta _{{C_3}}} = m_{3,3}^fm_{4,2}^f $
${v_3} = [0.538\;1,0.209\;8,0.413\;4,0.313\;2]$具有中等中心距、小外眼角的眼睛。
覆盖率：0.0224，特异性：0.2868小眼睛 $ {\zeta _{{C_4}}} = m_{2,2}^fm_{3,2}^f $
${v_4} = [0.242\;9,0.246\;4,0.155\;6,0.573\;0]$具有小眼高、小中心距的眼睛。
覆盖率：0.0478，特异性：0.5574表 4 FEI数据库中4类右眼的语义描述
Table 4 The semantic descriptions of four clusters for the right eyes on FEI database
类 模糊概念及信息粒类中心 语义描述 大眼睛 $ {\zeta _{{C_1}}} = m_{2,1}^fm_{3,1}^f $
${v_1} = [0.625\;3,0.852\;8,0.739\;3,0.627\;2]$具有大眼高、大外眼角的眼睛。
覆盖率：0.0896，特异性：0.7036中眼睛1 $ {\zeta _{{C_{}}}} = m_{1,3}^fm_{2,2}^fm_{3,3}^f $
${v_2} = [0.498\;9,0.656\;8,0.643\;1,0.614\;6]$具有中等眼高、中等外眼角的眼睛。
覆盖率：0.0520，特异性：0.6336中眼睛2 $ {\zeta _{{C_3}}} = m_{2,2}^fm_{4,2}^f $
${v_3} = [0.603\;2,0.652\;0,0.667\;4,0.352\;7]$具有中等中心距、小外眼角的眼睛。
覆盖率：0.0603，特异性：0.7839小眼睛 $ {\zeta _{{C_4}}} = m_{1,2}^fm_{3,2}^f $
${v_4} = [0.304\;8,0.727\;9,0.474\;3,0.517\;3]$具有小眼高、小中心距的眼睛。
覆盖率：0.1099，特异性：0.8316表 5 FCM、CAN、FCMGD、AFSGD、KMT、IAFSGD 在 Multi-PIE 数据库实验结果的比较
Table 5 Comparison of FCM, CAN, FCMGD, AFSGD, KMT and IAFSGD on Multi-PIE database
类 α γ FCM CAN FCMGD AFSGD KMT IAFSGD 大眼睛 0.5 0 452.8451 448.5333 447.6485 440.5714 427.7107 476.0000 1 0 452.8451 448.5333 447.7716 456.0000 427.7107 476.0000 2 0 452.8451 448.5333 453.9911 453.7043 427.7107 476.0000 3 0 452.8451 448.5333 451.6857 452.7568 427.7107 476.0000 2 1 452.8451 448.5333 454.5421 454.8966 427.7107 476.0000 2 2 452.8451 448.5333 454.5204 452.8440 427.7107 476.0000 2 3 452.8451 448.5333 454.4159 454.3423 427.7107 476.0000 小眼睛 0.5 0 331.7778 369.3299 342.5714 264.0000 356.5333 275.5121 1 0 331.7778 369.3299 334.8077 284.4453 356.5333 275.5121 2 0 331.7778 369.3299 338.7070 336.9756 356.5333 284.4453 3 0 331.7778 369.3299 331.6078 336.9164 356.5333 284.4453 2 1 331.7778 369.3299 336.3265 333.6951 356.5333 272.7496 2 2 331.7778 369.3299 336.3265 336.9164 356.5333 272.7496 2 3 331.7778 369.3299 336.3265 342.1115 356.5333 272.7496 表 6 FCM、CAN、FCMGD、AFSGD、KMT、IAFSGD算法对AR数据库的对比
Table 6 Comparisons of FCM, CAN, FCMGD, AFSGD, KMT and IAFSGD algorithm on AR database
类 α γ FCM CAN FCMGD AFSGD KMT IAFSGD 大眼睛 0.5 0 596.2934 567.0905 584.3200 599.8560 567.0905 607.9871 1 0 596.2934 567.0905 588.9309 607.8544 567.0905 607.9871 2 0 596.2934 567.0905 594.5129 607.6849 567.0905 607.9871 3 0 596.2934 567.0905 593.7129 608.602 567.0905 607.9871 2 1 596.2934 567.0905 593.6778 607.6849 567.0905 607.9871 2 2 596.2934 567.0905 592.0102 607.2003 567.0905 607.9871 2 3 596.2934 567.0905 594.8776 607.9152 567.0905 607.9871 小眼睛 0.5 0 459.5044 463.5722 458.6418 456.8767 463.5722 458.4211 1 0 459.5044 463.5722 455.0292 456.8767 463.5722 458.4211 2 0 459.5044 463.5722 454.8871 459.1579 463.5722 456.973 3 0 459.5044 463.5722 464.8395 461.7465 463.5722 456.973 2 1 459.5044 463.5722 463.1164 459.1579 463.5722 456.973 2 2 459.5044 463.5722 471.3855 459.1579 463.5722 456.973 2 3 459.5044 463.5722 470.4846 459.1579 463.5722 456.973 表 7 FCM、CAN、FCMGD、AFSGD、KMT、IAFSGD算法对Multi-PIE数据库的聚类有效性对比
Table 7 Comparisons of clustering effectiveness via FCM, CAN, FCMGD, AFSGD, KMT and IAFSGD algorithms on Multi-PIE database
α γ FCM CAN FCMGD AFSGD KMT IAFSGD 0.5 0 0.5265 0.5247 0.5242 0.5289 0.5247 0.5296 1 0 0.5265 0.5247 0.5288 0.5254 0.5247 0.5296 2 0 0.5265 0.5247 0.5295 0.5283 0.5247 0.5304 3 0 0.5265 0.5247 0.5237 0.5283 0.5247 0.5304 2 1 0.5265 0.5247 0.5231 0.5283 0.5247 0.5304 2 2 0.5265 0.5247 0.5206 0.5276 0.5247 0.5304 2 3 0.5265 0.5247 0.5213 0.5275 0.5247 0.5304 表 8 FCM、CAN、FCMGD、AFSGD、KMT、IAFSGD算法对AR数据库的聚类有效性对比
Table 8 Comparisons of clustering effectiveness via FCM, CAN, FCMGD, AFSGD, KMT and IAFSGD algorithms on AR database
α γ FCM CAN FCMGD AFSGD KMT IAFSGD 0.5 0 0.5047 0.5043 0.5086 0.5413 0.5237 0.5509 1 0 0.5047 0.5043 0.5048 0.521 0.5237 0.5509 2 0 0.5047 0.5043 0.5015 0.5246 0.5237 0.5503 3 0 0.5047 0.5043 0.4974 0.5239 0.5237 0.5503 2 1 0.5047 0.5043 0.5015 0.5275 0.5237 0.5457 2 2 0.5047 0.5043 0.5015 0.5244 0.5237 0.5457 2 3 0.5047 0.5043 0.5019 0.5191 0.5237 0.5457 表 9 FCM、CAN、FCMGD、AFSGD、KMT、IAFSGD算法对FEI数据库的聚类有效性对比
Table 9 Comparisons of clustering effectiveness via FCM, CAN, FCMGD, AFSGD, KMT and IAFSGD algorithms on FEI database
α γ FCM CAN FCMGD AFSGD KMT IAFSGD 0.5 0 0.5262 0.5357 0.5279 0.5392 0.5399 0.5427 1 0 0.5262 0.5357 0.5268 0.5389 0.5399 0.5427 2 0 0.5262 0.5357 0.5255 0.5377 0.5399 0.5434 3 0 0.5262 0.5357 0.5255 0.5367 0.5399 0.5430 2 1 0.5262 0.5357 0.5249 0.5369 0.5399 0.5431 2 2 0.5262 0.5357 0.5249 0.536 0.5399 0.5428 2 3 0.5262 0.5357 0.5249 0.5359 0.5399 0.5435 -
[1] REN Y, LI Q, LIU W, et al. Semantic facial descriptor extraction via Axiomatic Fuzzy Set[J]. Neurocomputing, 2016, 171: 1462–1474. doi: 10.1016/j.neucom.2015.07.096 [2] PALACIOS A, PALACIOS J, SANCHEZ L, et al. Genetic learning of the membership functions for mining fuzzy association rules from low quality data[J]. Information sciences, 2015, 295: 358–378. doi: 10.1016/j.ins.2014.10.027 [3] KARCZMAREK P, KIERSZTYN A, RUTKA P, et al. Linguistic descriptors in face recognition: a literature survey and the perspectives of future development[C]// 2015 Signal Processing: Algorithms, Architectures, Arrangements, and Applications (SPA). [S.l.]. IEEE, 2015: 98−103. [4] LIU Xiaodong. A new mathematical axiomatic system of fuzzy sets and systems[J]. Journal of Dalian Maritime University, 1995, 3: 559–560. [5] CAI Y, ZHANG H, SUN S, et al. Axiomatic fuzzy set theory-based fuzzy oblique decision tree with dynamic mining fuzzy rules[J]. Neural computing and applications, 2020, 32(15): 11621–11636. doi: 10.1007/s00521-019-04649-0 [6] LI Zedong, DUAN Xiaodong, ZHANG Qingling, et al. Multi-ethnic facial features extraction based on axiomatic fuzzy set theory[J]. Neurocomputing, 2017, 242: 161–177. doi: 10.1016/j.neucom.2017.02.070 [7] WANG Weina, LIU Xiaodong. Fuzzy forecasting based on automatic clustering and axiomatic fuzzy set classification[J]. Information sciences, 2015, 294: 78–94. doi: 10.1016/j.ins.2014.09.027 [8] LIU Mengmeng, LIU Xiaodong, JIA Wenjuan, et al. The trading strategy of inflection point futures analysis based on AFS theory[C]//2020 39th Chinese Control Conference (CCC). Shenyang, China. IEEE, 2020: 2170−2175. [9] 储德润, 周治平. 公理化模糊共享近邻自适应谱聚类算法[J]. 智能系统学报, 2019, 14(5): 897–904. doi: 10.11992/tis.201810002 CHU Derun, ZHOU Zhiping. Shared nearest neighbor adaptive spectral clustering algorithm based on axiomatic fuzzy set theory[J]. CAAI transactions on intelligent systems, 2019, 14(5): 897–904. doi: 10.11992/tis.201810002 [10] LIU X, PEDRYCZ W. Axiomatic fuzzy set theory and its applications[M]. Berlin, Heidelberg: Springer, 2009. [11] DUAN Xiaodong, WANG Yuangang, PEDRYCZ W, et al. AFSNN: a classification algorithm using axiomatic fuzzy sets and neural networks[J]. IEEE transactions on fuzzy systems, 2018, 26(5): 3151–3163. doi: 10.1109/TFUZZ.2017.2788875 [12] JIA W, LIU X, WANG Y, et al. Semisupervised learning via axiomatic fuzzy set theory and SVM[J]. IEEE transactions on cybernetics, 2020(99): 1–14. [13] LIANG A, LIU W, LI L, et al. Accurate facial landmarks detection for frontal faces with extended tree-structured models[J]. IEEE, 2014: 538–543. [14] LIU Xiaodong, REN Yan. Novel artificial intelligent techniques via AFS theory: feature selection, concept categorization and characteristic description[J]. Applied soft computing, 2010, 10(3): 793–805. doi: 10.1016/j.asoc.2009.09.009 [15] PEDRYCZ W, SUCCI G, SILLITTI A, et al. Data description: a general framework of information granules[J]. Knowledge-based Systems, 2015, 80: 98–108. doi: 10.1016/j.knosys.2014.12.030 [16] 刘翠君, 赵才荣, 苗夺谦, 等. 粒化的Mean Shift行人跟踪算法[J]. 智能系统学报, 2016, 11(4): 433–441. doi: 10.11992/tis.201605033 LIU Cuijun, ZHAO Cairong, MIAO Duoqian, et al. Granular mean shift pedestrian tracking algorithm[J]. CAAI transactions on intelligent systems, 2016, 11(4): 433–441. doi: 10.11992/tis.201605033 [17] GROSS R, MATTHEWS I, COHN J, et al. Multi-PIE[J]. Image and vision computing, 2010, 28(5): 807–813. doi: 10.1016/j.imavis.2009.08.002 [18] MARTINEZ A, BENAVENTE R. The AR face database[R]. Computer Vision Center Technical Report, 1998, 24. [19] LIN S, CHEN W, LIN C, et al. Building a Chinese facial expression database for automatically detecting academic emotions to support instruction in blended and digital learning environments[J]. Innovative technologies and learning, 2019, 11937: 155–162. [20] PAL N R, PAL K, KELLER J M, et al. A possibilistic fuzzy c-Means clustering algorithm[J]. IEEE transactions on fuzzy systems, 2005, 13(4): 517–530. doi: 10.1109/TFUZZ.2004.840099 [21] NIE F, WANG X, HUANG H. Clustering and projected clustering with adaptive neighbors[M]. New York: ACM, 2014. [22] REN Y, GUAN W, LIU W, et al. Facial semantic descriptors based on information granules[J]. Information sciences, 2019, 479: 335–354. doi: 10.1016/j.ins.2018.11.056 [23] REN Y, ZHANG S, LIU W, et al. An advisable facial semantic characterization based on Axiomatic Fuzzy Set theory and information granules[J]. Information sciences, 2020, 523: 133–151. doi: 10.1016/j.ins.2020.02.068 [24] TAVALLALI P, TAVALLALI P, SINGHAL M. K-means tree: an optimal clustering tree for unsupervised learning[J]. The journal of supercomputing, 2021, 77(5): 5239–5266. doi: 10.1007/s11227-020-03436-2 [25] HUBERT L, ARABIE P. Comparing partitions[J]. Journal of classification, 1985, 2(1): 193–218. doi: 10.1007/BF01908075
