2. 华南理工大学计算机与工程学院, 广东广州 510006;
3. 中山大学数据科学与计算机学院, 广东广州 510006
2. School of Computer Science and Engineering, South China University of Technology, Guangzhou 510006, China;
3. School of Data and Computer Science, Sun Yat-Sen University, Guangzhou 510006, China
随机启发式搜索(randomized search heuristics,RSHs)算法是近年来发展较快的研究领域,在许多应用中取得了丰富的成果。这类启发式算法主要包括随机局部搜索(randomized local search,RLS)、禁忌搜索(tabu search)、模拟退火(simulated annealing,SA) 、演化算法(evolutionary algorithms,EAs) 以及粒子群优化算法(particle swarm optimization,PSO)等。这些算法经常用来作为一些难解优化问题的近似求解方法。由于这类智能算法的智能性、普适性以及全局搜索能力,使得其为求解NP难解优化问题开辟了一条新的途径。蚁群优化算法(ant colony optimization,ACO)是这类算法的杰出代表 之一。
蚁群算法是受蚂蚁群体觅食行为的启发,由意大利学者Dorigo等[1]提出的一种基于种群的模拟进化算法。蚂蚁觅食过程中借助于信息素(pheromone)这种化学物质进行信息的交流和传递,能够根据所走路径长度自主选择下一个将要行走的地方,并表现出正反馈现象。这种正反馈机制能帮助蚂蚁很快找到最优觅食路径。蚁群算法以信息素更新和概率转移为基本操作,并以此指导搜索方向。蚁群算法作为一种新型的智能仿生类进化算法,已在许多领域获得了广泛的应用。例如在TSP(traveling salesman problem)问题、二次规划问题、 函数优化、网络路由优化、机器人路径规划、数据挖掘、作业流程规划、图形着色等领域获得了广泛的应用,并取得了较好的效果,具体可以参考张军等的译著[2]。此外,国内学者段海滨等[4]对蚁群算法的应用领域的研究成果做了较全面的综述。
自从蚁群算法提出后,许多研究者在蚁群算法的设计及应用方面取得了丰富的研究成果。大量的实验也表明其针对一些优化问题的求解非常有效。然而,从理论上来看,蚁群算法缺乏比较完备的理论基础。目前更迫切地希望为该算法建立坚实的理论基础[10, 13],以帮助更好地理解算法的运行机制,了解算法对于求解什么类型的问题有效。为算法的设计,参数选取以及算法的运用指明改进的方向。当前蚁群算法理论研究远远落后于算法的数值实验和真实应用,主要原因在于随机启发式算法理论分析的艰难性[15]。蚁群算法具有随机性、群体性、普适性等特性,这些特征使得算法表现出复杂的动态行为,由此引出的复杂多变的随机过程增加了算法理论分析的难度,经典算法设计与分析的方法和工具也难以直接应用于这类新型随机仿生算法。
在2006年之前,研究人员主要关注于ACO收敛性分析[19, 20, 21, 26]以及ACO算法与其他优化算法的关系[25],从理论上探索算法为什么有效。 Gutjahr[19]提出了一个基于图的蚂蚁系统(graph-based ant system,GBAS),Gutjahr首次证明了该模型蚁群算法在一定条件下以概率1-ε收敛到最优解,其中ε为任意小的常数且ε>0。Stützle and Dorigo[20]等给出了普通蚁群算法(ant colony system,ACS)和MMAS(max-min ant system)的收敛性证明。 Gutjahr[21]进一步提出使用常微分方程逼近ACO随机过程,并基于此来对ACO算法的收敛速度进行粗糙的理论预测。国内学者黄翰、郝志峰等[22]根据蚁群算法的特性,基于吸收态Markov 过程的数学模型,提出了蚁群算法的收敛速度分析理论,并给出了ACO-难和ACO-易两类问题的界定方法。蚁群算法理论研究的另一个方向是将蚁群算法和其他学习算法进行比较,如Birattari[23]、Meuleau[24]等分别建立了ACO与最优控制加强学习算法、随机梯度下降算法的联系。
近年来,以遗传算法为基础的演化算法时间复杂性研究取得了一些重要进展。以Droste[11]、Wegener[12]等为代表的德国学派分析了群体规模为1的简单爬山演化算法(1+1)EA求解一些拟布尔函数(OneMax,LeadingOnes,Trap Function)的平均计算时间,取得了一系列研究成果。He Jun和Yao Xin使用吸收马尔可夫链[16]、漂移分析[17]等工具建立演化算法时间复杂性分析模型和方法以及分析群体在演化算法时间复杂性分析中的作用[18]等。这些研究极大地激发和推动了蚁群算法的理论研究工作。
蚁群算法最初用于旅行商问题的求解,进而推广到各种组合优化问题(甚至连续函数优化问题)。Dorigo和Blum[3]总结了截至2005年蚁群算法理论研究及应用中取得的阶段性研究成果,并特别指出蚁群算法时间复杂性将是今后一个重要的、有意义的研究方向,将其列为蚁群算法理论研究的公开性问题。
时间复杂度研究是指算法找到优化问题最优解或近似最优解的计算时间,是衡量算法性能最基本、最重要的指标。W.J.Gutjahr[10]总结了截止2007年的蚁群算法时间复杂性研究成果和方法,并指出了一些发展方向。目前,蚁群算法时间复杂性研究正处于启动阶段,研究内容、深度都非常有限,很多基本问题尚未涉及。当前仅仅研究了蚂蚁规模为1的1-ANT的情形,而与真实的蚁群算法相关的问题,如多蚂蚁蚁群系统求解真实的组合优化问题等,都有待深入研究。可以预计,这些研究将会有重要意义,同时又将是富有挑战性的、艰难的工作。目前ACO算法理论研究主要是关于一些人工拟布尔函数以及一些经典的组合优化问题的时间复杂性分析。最具代表性的如国内学者Zhou Yuren [45]研究了ACO求解经典TSP问题的时间复杂度,这也是ACO算法在NP难解问题理论分析上的首项工作。
一般情况下,对于典型的难问题—NP-完全(难)(non-deterministic polynomial-complete hard)优化问题,人们找不到多项式时间的确定性算法。由于NP难解组合优化问题本身结构的复杂性,确定性算法(穷举法、分支界定、动态规划等)无法保证在多项式内获得精确解,转而寻求一些近似算法[6]。蚁群优化作为随机启发式方法,不能期待其在多项式时间内找到NP-完全(难)优化问题所有实例的精确解。实际上,蚁群算法在很多优化问题上扮演着近似算法的角色,一般用于获得满意解或者近似解。因此蚁群优化算法的近似性能分析就变得尤为重要。希望在平均多项式时间内获得近似最优或者可接受的解,对于理解蚁群算法在NP难优化问题上的工作原理以及寻求其能获得的近似性能非常关键,并将进一步推进蚁群算法的理论研究及应用进展。对于丰富和发展近似算法和组合优化理论,切实有效地解决一些实际问题具有重要现实意义。
1 蚁群优化算法:模型、描述、变体 1.1 优化问题及算法描述蚁群算法是一种随机启发式搜索方法,它具有较强的鲁棒性,优良的分布式计算机制并易于与其他方法相结合等优点。目前人们对蚁群算法的研究已经由当初单一的旅行商问题(TSP)领域渗透到了多个其他应用领域[2],由解决一维、静态优化问题发展到解决多维、动态优化问题,由离散求解空间逐渐拓展到连续求解空间,使得该群智能算法在科学研究及实际问题求解中表现出了巨大的潜力和优势。
优化问题可以分为两类:连续的优化问题和离散的优化问题。连续的优化问题是指其具有连续的变量、经常需要计算导数、使用牛顿方法或者线性规划技术等。本文关注的是离散的优化问题。离散优化问题也称为组合优化问题,是指在有限的或者可数无限的潜在解集中搜索满足给定约束条件的最优解。然而,组合优化问题通常包含大量的局部极值点,而且许多组合优化问题为NP完全(难)问题。
一个组合优化问题P通常可描述为一个三元组(S,f,Ω),其中S为给定的由所有状态构成的搜索空间,f:S→ R+为目标函数,一般为最大化或者最小化;Ω为可行解满足的约束条件集合。一个可行解s*∈S,如果对于最小化问题有∀s∈S,f(s*)≤f(s),对于最大化问题有∀s∈S,f(s*)≥f(s),则称s*为一个全局最优解。定义最优解集合为S*⊆S,算法的目标是从优化问题的可行解集中找到最优解s*∈S*。
给定算法A和优化问题P,对于一个给定的P的实例I,其最优解为fopt(I)。如果算法A能在多项式时间内获得最优解A(I),则算法A在问题P上的近似比r为:若为最大化问题,r=$\mathop {\max }\limits_{I \in P} {{{f_{opt}}\left( I \right)} \over {A\left( I \right)}}$;若为最小化问题,r=$\mathop {\max }\limits_{I \in P} {{A\left( I \right)} \over {{f_{opt}}\left( I \right)}}$。也就是说,算法A能获得r-近似比。若r=1,表明算法找到最优解。
蚁群算法的启发来自于一个蚂蚁群体对食物源的搜索,是一种杰出而具有代表性的群智能算法,对于其算法描述可以参考相关文献[1, 2, 3, 4, 5]。ACO算法有一些不同的变体,为了分析的方便,在当前理论分析方面,还是主要考虑一只蚂蚁的情况。下面给出蚁群优化算法理论研究中用到的一个简单的ACO算法(1+1)蚂蚁算法((1+1)Ant Algorithm,(1+1)AA),其类似于演化算法理论分析中的(1+1)EA。不失一般性,考虑最小化问题。(1+1)AA算法描述如下
Algorithm 1: (1+1)AA
Begin
初始化:参数设置,信息素值,选择一个初始解s, While(不满足终止条件)
使用构造过程构建一个新的解s′;
选择:如果f(s′)<f(s),则s=s′;更新信息素值。
End while
End
(1+1)AA算法使用简单的爬山选择策略,如果当前蚂蚁解的函数值大于新的蚂蚁解的函数值,则当前蚂蚁解被新蚂蚁解替代。以下两节分别介绍理论分析中蚁群算法解的构建以及信息素更新机制。
1.2 解的构建对于一个给定的优化问题,其解通过蚂蚁在一个具有信息素值的构造图(construction graph)的边上随机游走获得。另外,蚁群算法也使用启发式信息来指导随机游走的方向。蚂蚁从构造图的任意一个初始状态出发,随机游走到下一个邻域结点。这个移动是基于概率规则,依赖于信息素和启发式信息。
令G=(V,E)为一给定问题的构造图。τ(u,v)为边e=(u,v)∈E上的信息素值,η(u,v)为启发式信息。假设蚂蚁当前所在位置为顶点u,其允许访问的后续结点为Nu。蚂蚁在下一步访问结点v∈Nu的概率由以下公式给出:
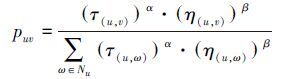
当算法完成一次迭代之后,路径上的信息素将会更新。信息素更新的目的是使得较优路径上的信息素增加,同时模拟一种挥发的方式削弱较差路径上的信息素。通常根据挥发因子ρ(0≤ρ≤1)的不同,信息素值会减少不同的数量。假设更新之前的边(u,v)∈E上的信息素值为τ(u,v),在第一步,其值减少到(1-ρ)τ(u,v)。这意味着,在算法的运行过程中,路径上的信息素将会有一定程度的挥发,避免信息素的无限积累,这样也有利于算法逃脱局部最优。各路径上的信息素根据以下方式进行更新:

根据信息素更新方式的不同,也就产生具有不同信息素更新机制的蚁群算法[8]。为了防止算法的早熟,Stützle 和 Hoos[9]提出了最大最小蚂蚁系统。在信息素的更新过程中,将其限制在一个最大最小信息素范围内[τmin,τmax]。根据边 e=(u,v)∈E是否包含在至今最好的解x中,其信息素更新规则如下:
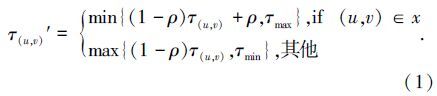
称使用上述信息素更新规则的(1+1)AA算法为(1+1)MMAA。 类似的(1+1)MMAA在文献[28, 34]中分别叫做MMAS*和MMASbs。
2 理论分析方法及数学工具对于一个确定的优化问题,蚁群算法找到一个最优解的迭代次数用随机变量t表示。在蚁群算法的理论分析中 通常需要估计最好情况、平均情况、最坏情况下,以什么样的概率Pr(t≤T)在什么样的期望运行时间E(t)内,找到什么样的解(近似解)。本节介绍一些蚁群算法的理论分析方法和基本的数学工具。不失一般性,考虑最小化问题。
2.1 适应值划分对于给定的优化问题,感兴趣的是算法找到最优解的平均迭代次数。这里介绍适应值划分技术,该技术在演化算法的理论分析中得到了成功运用。其原理是种群中最好的个体适应值一直都确保不会变差。因此通过估计最好的个体适应值变好的期望时间界来获得优化时间。这种方法称为基于适应度划分的方法(fitness-based partitions)或者适应度等级方法[14]。
定义1 (适应值划分)给定一个有限的搜索空间S,不失一般性,假设函数 f:S→R最小化,考虑函数f的所有可能的不同的函数值A0,A1,…,Am,对于∀a∈Ai和∀b∈Aj,如果f(a)<f(b),则记为Ai<fAj。若有A0<fA1<fA2<f … <fAm,定义 Ai={x∈S|f(x)=fi},i=0,1,2,…,m。则称{A0,A1,…,Am}为基于适应值的划分。
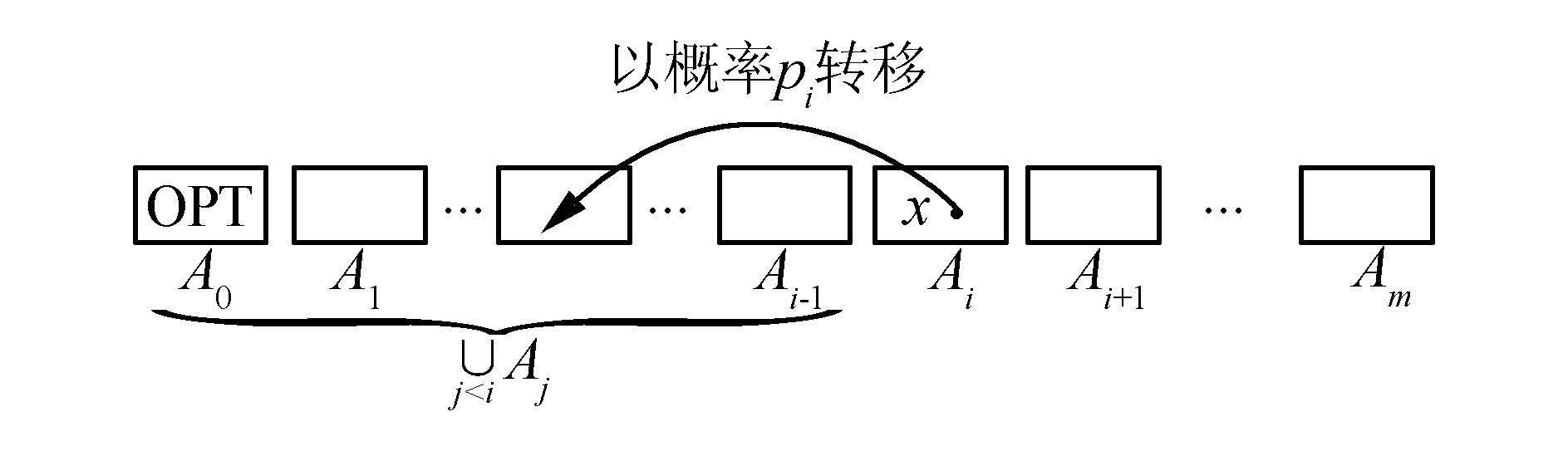
对于ACO,算法每次接受优于当前最好的解,算法每次运行都朝着最优解的方向前进,如图 1所示。下面给出一个简单ACO算法的期望运行时间估计的定理,其由Gutjahr和Sebastiani[34]提出。
|
| 图 1 适应值划分 Fig. 1 Fitness values partition |
定理2 给定一个适应值划分 {A0,A1,…,Am}。令Xt(t=1,2,...)为 ACO算法的解序列,pi(i=1,2,…,m)为算法运行所得适应值所在集合从Ai跳转到Ai-1∪…∪A0的概率下界,并且集合A0包含最优解。则ACO算法求解函数f的期望时间上界为:$\sum\limits_{i = 1}^m {\left( {t_i^* + {1 \over {{p_i}}}} \right)} $,其中ti* 为算法每次迭代时信息素达到饱和的时间,也就是信息素值达到τmax或τmin。
根据文献[34]知道ti*≤${{\ln n} \over \rho }$。因此,对于ACO理论分析,最关键的是计算一步转移概率pi。一般来说,由该方法获得的时间上界不是紧界。
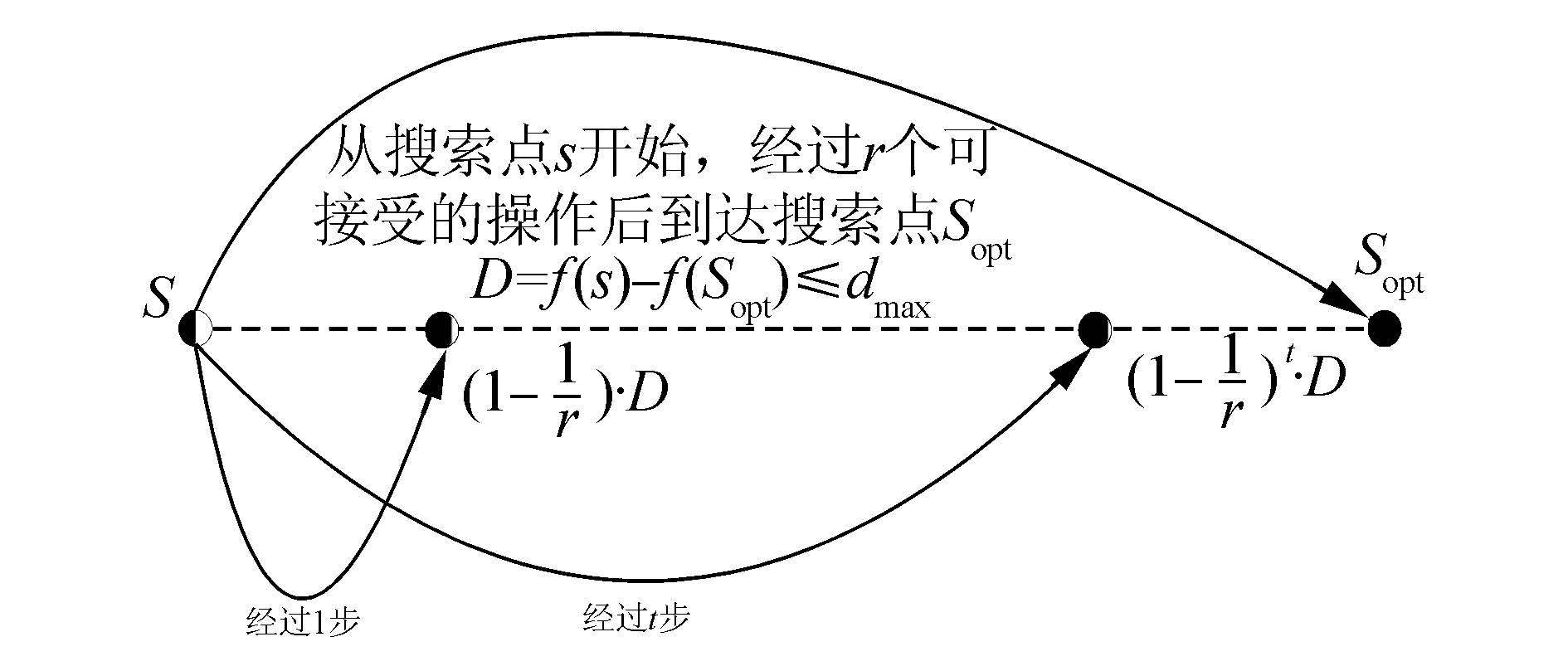
2.2 期望倍增距离减少函数适应值个数非常大(指数级)的情况,适应值划分技术已经不再适用。期望倍增减少距离(expected multiplicative distance decrease)的方法正好能够应对函数适应值数量非常大的情况,该方法如图 2所示。
|
| 图 2 期望倍增距离减少 Fig. 2 Expected multiplicative distance decrease |
给定一个具有操作序列Op={op0,op1,op2, …,opt,…},每一操作发生的概率相同,假设为 P(opt)=pm≥α(t=1,2,….)。给定任意初始解s,算法通过执行操作opt∈Op,一步一步逐渐到达最优解sopt。不失一般性,考虑最小化问题。定义优化问题的适应值函数f(st)(t=1,2,...),d(st)=f(st)-f(sopt)为第t代时的解st与目标最优解sopt相差的适应值距离。根据随机启发式算法的特点,给定不同的初始解,其求解问题的迭代次数也不一样,因此考虑的是期望迭代次数。算法找到可接受的操作,使得st+1优于st。假定算法通过执行给定的操作使得减少的期望距离至少为
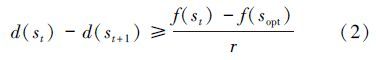
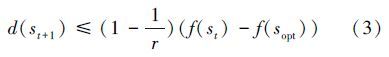
当前解离目标最优解距离减少由两部分产生:可接受的操作和不接受的操作,而不接受的操作距离减少的贡献为0。
因此,如果d(st)>0,有
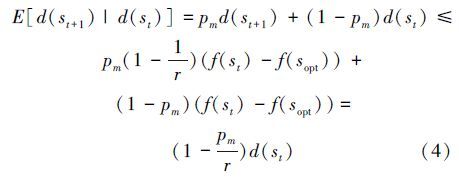
令Yt=d(st),有
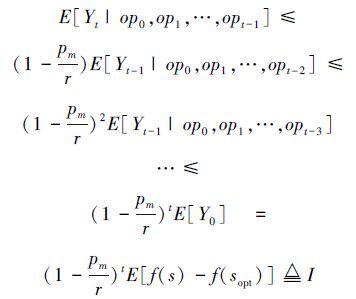
考虑搜索空间中离最优搜索点sopt距离最远的情况。如图 2所示,令该最远距离D=f(s)-f(sopt)≤dmax,则有I≤(1-${\alpha \over r}$)tD, α为常数,且0<α<1。
令T=O(r·logD),当t≥T,有E[Yt|op0,op1,…,opt-1]≤(1-${\alpha \over r}$)tD≤${1 \over 2}$。根据Markov不等式,算法执行T步之后,离最优解距离至少为1的概率P(Yt≥1)≤${1 \over 2}$因此P(Yt<1)≥${1 \over 2}$。也就是说T步之后与目标最优解距离小于1的概率至少为1/2。 假设函数适应值均为正整数,则算法获得最优解(离目标最优解距离为0)的概率至少为1/2。因此,算法最终到达目标找到最优解的期望时间上界为2T=O(r·logD)。
2.3 尾概率不等式偏差不等式广泛应用于随机算法的分析中。在许多启发式搜索算法的例子中,对于分析启发式的典型行为是非常有用的。其通常用于估计随机变量偏离期望值的概率。
2.3.1 Markov不等式
马尔可夫不等式(Markov’s inequality)适用于非负随机变量。对一非负的随机变量X:Ω→R +,对于t∈R+,有P(X>t)≤${{E\left( X \right)} \over t}$。
2.3.2 Chebyshev不等式切比雪夫不等式 (Chebyshev's inequality)适用于任何的(可正可负)随机变量,有两种形式:
1)令X为一随机变量,其中E(X)=μ, Va(X)=σ2。对于k>0,
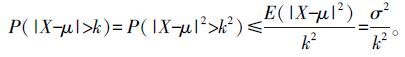
2)令Xi~iid(independent and identically distributed),独立同分布,期望E(Xi)=μ 且Va(Xi)=σ2,${\bar X}$为μ的估计,则
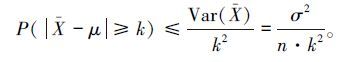
切尔诺夫界(Chernoff bounds):Xi∈{0,1}(1≤i≤n)为独立泊松分布事件,令X=$\sum\limits_{i = 1}^n {{X_i}} $,P(Xi=1)=pi, μ=E(X)=$\sum\limits_{i = 1}^n {{P_i}} $,0<pi<1。
则对于δ>0,P[X≥(1+δ)μ]≤${\left( {{{{e^\delta }} \over {{{\left( {1 + \delta } \right)}^{\left( {1 + \delta } \right)}}}}} \right)^\mu }$;对于0<δ<1,P[X≤(1-δ)μ]≤${\left( {{{{e^{ - \delta }}} \over {{{\left( {1 - \delta } \right)}^{\left( {1 - \delta } \right)}}}}} \right)^\mu }$; 对于0<δ<1,P[X≥(1+δ)μ]≤e${{\mu {\delta ^2}} \over 3}$; 对于0<δ<1,P[X≤(1-δ)μ]≤e${{\mu {\delta ^2}} \over 2}$; 对于0<δ<1,P(X-μ)≥δμ]≤2e-${{u{\delta ^2}} \over 3}$。
3 一些理论研究结果及问题讨论 3.1 参数ρ、α、β对算法性能影响到目前为止,蚁群算法中挥发因子、信息素值控制参数、启发式信息(能见度)控制参数的设置,对于界定蚁群算法的难问题和易问题并没有从理论上真正得以解释说明。从蚁群算法求解一些实际问题的实验效果来看,信息素挥发因子是一个比较关键的参数。挥发因子越大,表现出的正反馈作用越强,以往走过的路径被再次选择的可能性就越大,搜索随机性变弱;相反,挥发因子越小,算法的随机性就越大,其全局搜索能力也就变强。信息素挥发因子设置对于算法性能影响至关重要。
Neumann[27, 29]等研究了信息素挥发因子 ρ对蚁群算法性能的影响,指出如果ρ≥${{n - 2} \over {3n - 2}}$,即当n→∞,ρ≥1/3时,算法 1-ANT的行为类似于(1+1)ANT,就是说,1-ANT在每个函数上的期望运行时间和(1+1)ANT相同。同时指出,如果取 ρ=O(n-1-ε),ε>0为常数,则算法 1-ANT以1-2-Ω(nε/3)的概率求解 OneMax函数的时间为2Ω(nε/3);如果取ρ=Ω(n-1+ε),ε>0为常数,则算法1-ANT以1-2-Ω(nε/2)的概率求解 OneMax函数的时间为O(n2),给出了 1-ANT算法求解OneMax函数的时间复杂度从指数时间到多项式时间的相变现象。Doerr等[31]使用一个信息素模型简化了文献[29]的分析,进一步研究了挥发因子ρ∈[1/n1+ε,1/n1-ε]的优化时间。并指出,存在常数c∈(0,1)和N∈N,使得当n≥N和ρ≤c,对于n个变元的OneMax函数,算法1-ANT以小于1/e${c \over \rho }$的概率优化时间最多为e${c \over \rho }$。Doerr等[32, 33]研究了挥发因子ρ对于1-ANT算法的性能影响,指出对于LeadingOnes和BinVal两个函数,存在一个相变现象,且阈值为ρ~1/(nlogn),其期望时间为指数级到多项式。
蚁群算法中信息素控制参数α反映蚂蚁在行走过程中所积累的信息素对指导蚂蚁搜索方向的相对重要性,能见度控制参数β反映启发式信息对指导蚂蚁搜索方向的相对重要性。 Zhou[45]通过构造TSP实例,研究了参数 α和β对算法计算时间的影响,指出对于完全图实例,参数设置α=1,β=0到α=1,β=1,其期望运行时间上界也由O(n6)变为O(n5)。Kötzing等[46]通过构建一个TSP实例分析了启发式信息对于蚁群算法的性能影响,指出对于该实例取α=1,如果β=1,算法需要指数级运行时间找到最优解;如果β=n,则算法以趋近于1的概率在一次迭代就能找到最优解。
蚁群算法参数较多,设置也较复杂。目前理论分析主要通过一些构造实例来分析不同参数设置对于算法性能的影响。针对一般性的问题,参数如何设置对于蚁群算法来说是有效的,还有待于进一步深入探究。
3.2 从1-ANT到n-ANT当前对于蚁群优化算法的理论研究,研究人员主要还是考虑一只蚂蚁的情况。不同的文献采用的算法框架名称不同,主要有1-ANT[29, 31, 32]、(1+1)MMAA [45]、MMAS*[28]、MMASbs[34]以及MMASOrd*和MMASArb * [46]等。 这些算法在每次迭代之后只构造一个解,是一种比较简单的情况。
Neumann等人[36]研究了λ-MMASIB算法求解拟布尔函数的性能。他们指出,当 λ=2,也即构造2个蚂蚁解时,该算法在挥发因子足够小的情况下,能够在多项式时间内求解OneMax函数。
Attiratanasunthron和Fakcharoenphol[41]研究了ACO算法求解有向无环图单源最短路径问题的多项式时间界。特别地,对于顶点数为n,边数为m的有向无环图,具有n只蚂蚁的n-ANT算法能够在期望时间O(n2mlogn/ρ)内求解单源最短路径问题。
蚂蚁的数量决定了每次迭代构造的解的个数。在不同参数情况下,真实的多蚂蚁蚁群系统如何影响算法性能,如何设置蚂蚁个数,以及n-ANT算法求解组合优化问题的性能,能够在什么样的时间内获得什么样的解,是值得进一步研究的问题。
3.3 从拟布尔函数到NP难问题 3.3.1 拟布尔函数以下7个函数为分析演化和蚁群算法时间复杂性的典型人工拟布尔函数:
1)OneMax(x)=$\sum\limits_{i = 1}^n {{x_i}} $;
2)LeadingOnes(x)=$\sum\limits_{i = 1}^n {\prod\limits_{j = 1}^i {{x_i}} } $;
3)Trap(x)=$\sum\limits_{i = 1}^n {{x_i}} $+(n+1)·$\prod\limits_{i = 1}^n {} $(1-xi);
4)BinVal(x)=$\sum\limits_{i = 1}^n {{2^{n - i}}} {x_i}$;
5)Needle(x)=$\prod\limits_{i = 1}^n {{x_i}} $;
6)NH-OneMax(x)=($\prod\limits_{i = 1}^k {{x_i}} $)=($\sum\limits_{i = k + 1}^n {{x_i}} $);
7) F(x)= $\sum\limits_{i = 1}^n {{w_i}} {x_i}$。
从2006年开始,蚁群算法关于时间复杂性分析的理论研究也相继出现,Neumann[27, 29]等通过模拟(1+1)EA建立了一个简单的ACO算法1-ANT分析模型,给出了1-ANT求解简单拟布尔函数OneMax平均时间复杂度为O(nlogn),并且指出挥发因子对时间复杂度起着关键性的影响。与此同时,Gutjahr[30]采用近似的常微分方程组估计算法时间复杂度,研究了GBAS和AS两个ACO算法的同一分析。 Doerr等[31]以1-ANT求解关于OneMax为例,分析了随着挥发系数的变化,1-ANT算法时间复杂度从指数时间到多项式时间的相位转移。Doerr等[32, 33]研究了1-ANT算法信息素更新机制对时间复杂度的影响,指出如果挥发因子设置过小,算法很容易陷入停滞状态。对于拟布尔函数LeadingOnes和BinVal,找到最优解的期望时间也是指数级的。相反,如果参数设置合理,期望时间也从指数级降低到多项式时间。
学者们也研究了最大最小蚂蚁系统(max-min ant system ,MMAS)[9] 算法的性能。该算法是蚁群优化的一个变体,其使用Best-So-Far更新机制。对于一些优化问题,最大最小蚂蚁系统能够有效地避免停滞,并能获得一个更有效的运行时间界。Gutjahr 和 Sebastiani[34]分析了MMAS在求解Needle-in-a-Haystack和LeadingOnes两个拟布尔函数的时间复杂度,并基于演化算法中适应值划分技术的基础上提出了一种ACO的时间复杂度理论分析框架,将作为一般分析的一个非常有用的工具。 2007年,Neumann等[35]将ACO算法扩展到单峰函数和高原函数的期望运行时分析上,并使用非齐次过程估计了信息素边界的首达时间,进一步研究了1-ANT算法关于LeadingOnes、Needle等其他拟布尔函数的时间复杂度;Kötzing等[37]也进一步研究了两种MMAS算法求解线性拟布尔函数的时间复杂度,并给出了求解所有线性函数的一般时间上界 O(n3logn/ρ)。Neumann、Sudholt和Witt[38]研究了ACO与局部搜索混合算法的影响,他指出对于一些人工构造的函数,ACO算法结合局部搜索能够以较高的概率将指数时间转为多项式时间。对于另外一些函数,情况则相反。
以上所有研究分析使用的方法和工具为组合优化问题的更深层次的分析奠定了坚实的基础。
3.3.2 P问题一些确定性的算法能够在多项式时间内求解P类的组合优化问题,实验表明ACO算法进行求解也显示出了其优越性。 ACO算法在一些简单函数上的分析所使用的方法和工具,也进一步推广到实际的组合优化问题上的分析中。目前ACO算法针对多项式可求解问题的理论分析也获得了一些结果。我们并不期望蚁群优化算法在这些优化问题上能够优于那些最好的算法,而关键是对于其理论分析能够更深入地了解蚁群算法工作机制,更好指导算法的设计及应用。
最小生成树(minimum spanning trees)问题是数据结构与算法设计中一个经典的图论问题。两个著名的确定性算法Kruskal和Prim分别有最坏情况下的时间复杂度 O((m+n)logn)和O(nlogn+m) (n为顶点数,m为边数)。 Neumann 和 Witt[39]分析了ACO算法求解最小生成树问题的时间复杂度,其蚂蚁解的构建是基于两种不同的构造图,Broder-based和Kruskal-based,并证明了最大最小蚂蚁系统求解最小生成树问题的期望时间上界为 O(mnlogn)。
最小割 (minimum cut) 问题是图论中经典的组合优化问题,其存在一些多项式求解算法。跟最小割相关的问题如最小k-割和multiway割等问题都是NP难问题[6]。Kötzing 等[40]分析了ACO算法在求解经典的最小割问题的时间复杂度,并研究了参数设置对于不同实例的运行时行为的影响。若参数α=0,β=1,对于任意给定的带权图,算法MMAS*找到一个最小割的期望时间上界为O(n2);若参数α=1,β=1,则算法的优化时间为$O\left( {{{\left( {n - 2 + 2{c_n}} \right)!} \over {\left( {n - 2} \right)!\left( {2{c_n}} \right)!}}} \right)$,其中cn=h/l,h和l为最大、最小蚂蚁算法的信息素边界值;若cn=k为常数,则期望时间变为O(n2k)。
最短路径问题的目标是搜索图中两结点之间的最短路径。Dijkstra算法是求解该问题的典型路由算法,用于计算一个节点到其他所有节点的最短路径。文献[41, 42, 43]研究了最短路径问题,并分别分析了ACO算法求解无环、有环、带有噪声情况下最短路径问题的计算时间。 Attiratanasunthron和Fakcharoenphol[41] 研究了ACO算法求解有向无环图单目标最短路径问题(single destination shortest path,SDSP)的多项式时间界。对于顶点数为n边数为m的有向无环图,具有n只蚂蚁的n-ANT算法能够在期望时间O(n2mlogn/ρ)内求解单源最短路径问题。
在此基础上,Horoba和Sudholt[42]将结果扩充到最大最小蚂蚁系统(MMAS),得到MMASSDSP关于单目标最短路径(SDSP)问题和 MMASAPSP关于全部顶点对的最短路径问题(all-pairs shortest path,APSP)的计算时间上界分别为O(lm+n/ρ)和 O(nlog n+logllog(Δl)/ρ),后者为目前元启发式算法 (meta-heuristic)关于APSP问题最好的界。进一步,Sudholt和Thyssen[43]讨论了边权数带噪声随机最短路径问题,给出了噪声强度、近似保证以及平均时间复杂度之间的权衡关系。
最近,Lissovoi和Witt[44]研究了λ只蚂蚁的最大最小蚂蚁系统λ-MMAS算法在动态SDSP问题上的时间复杂度。他们指出每个顶点上放一定数量的蚂蚁甚至是常数只蚂蚁就能有效地求解动态SDSP问题,给出了蚂蚁数量、挥发因子及计算时间之间的关系。此外,他们还研究了MMAS算法在动态MAZE函数上的性能[47]。
3.3.3 NP难问题
旅行商问题(traveling salesman problem,TSP)是组合优化中著名的NP难问题,也是蚁群算法的首个成功的测试问题。Zhou[45]首次分析了蚁群算法求解两个TSP实例的计算时间,从理论上首次证实了蚁群算法求解NP难问题的有效性,是蚁群算法关于NP难问题时间复杂性分析的首项工作。作者首次提出ACO求解TSP的严格计算时间分析,构造了完全图和非完全图的两个TSP实例,分析和估计了(1+1)MAX-MIN Ant Algorithm求解TSP实例的平均计算时间上界;同时讨论了算法中关于能见度和信息素值等控制参数的变化对算法计算时间的影响。 Kötzing等人[46]在文献[45]的基础上进行了有效的扩展,使用了一种新的蚂蚁解的构造图的方式,表明其具有更强的局部属性,并证明了能够得到一个更好的计算时间界。对于一些实例,算法容易陷入局部最优,计算时间为指数级。然而,当启发式因子足够大时,很快就能够找到最优解。
实际上,许多经典的组合优化问题都为NP难解问题[7]。由复杂性理论可知对于这类问题,不存在多项式时间的确定性算法除非P=NP。蚁群优化算法求解更多的NP难问题的性能目前还未知,这方面的工作才刚开始,对于更深入的了解蚁群算法的运行机理,求解NP难问题的性能,以及指导算法设计及应用有重要的现实意义。
表 1列举了近十年来蚁群优化算法理论研究的一些典型研究成果,包括从简单的拟布尔函数到NP难问题,不同的信息素更新机制,以及参数设置对算法性能影响等方面的理论研究成果。
| 问题 | 说明 | 算法模型 | 时间复杂度 | 相关文献 |
| OneMax | OneMax(x)=$\sum\limits_{i = 1}^n {{x_i}} $ | 1-ANT | O(nlogn) | Neumann [27, 29] |
| LeadingOnes | LeadingOnes(x)=$\sum\limits_{i = 1}^n {\prod\limits_{j = 1}^i {{x_i}} } $ | MMAS* | O(n2+(nlogn)/ρ) | Neumann等[35] |
| Linear function | F(x)= $\sum\limits_{i = 1}^n {{w_i}} {x_i}$i | MMAS/ MMAS* | O((n3logn)/ρ) | Kötzing等[37] |
| Minimum spanning tree | 最小生成树问题 | 1-ANT | O(mn(logn+logwmax)) | Neumann 和 Witt [39] |
| Minimum cut problem | 最小割问题(带权图);信息素的界为[l,h],cn=${h \over l}$, | MMAS* | O(n2)(α=0,β=1); | Kötzing 等[40] |
| $O\left( {{{\left( {n - 2 + 2{c_n}} \right)!} \over {\left( {n - 2} \right)!\left( {2{c_n}} \right)!}}} \right)$ | ||||
| 若cn=k为常数, | ||||
| O(n2k)(α=1,β=1); | ||||
| Single Destination Shortest Path, SDSP | 其中m为给定图的边数,Δ为最大出度,l为所有最短路径(如果不止一条)的最大边数,ρ为ACO算法的挥发因子 | n-ANT | O(${{m\Delta l\log \left( {\Delta l} \right)} \over \rho }$) | Attiratanasunthron等[41] |
| All-pairs Shortest Path(APSP) | MMASAPSP | O(Δll*+l/ρ) | Horoba和Sudholt [42] | |
| Dynamic SDSP | λ-MMAS | O(l+lln(τmax/τmin)/ρ)(λ= 2e/τmin) | Lissovoi和Witt[44] | |
| TSP | 完全图实例 | (1+1)MMAA | O(n6+(1/ρ)nlnn)(α=1,β= 0);O(n5+(1/ρ)nlnn)(α=1,β=1) | Zhou[45] |
| TSP | G1 | MMASArb* | O(n3logn+nlogn/ρ)(α=1,β=1) | Kötzing等[46] |
本文从蚁群算法框架、理论分析方法以及理论研究结果等方面出发,对蚁群优化算法的理论研究进展进行了归纳和介绍。此外,还对蚁群优化算法理论研究中的若干问题进行了分析讨论。当前蚁群算法的理论研究成果仍然有限,其理论分析方法和数学工具有待进一步完善和探索。蚁群算法理论研究中还有许多亟待解决的问题。
1)蚁群算法理论分析工具还非常有限,这也是阻碍其向前发展的一个主要因素。现有的理论分析方法主要是马尔可夫链理论、适应值划分技术及漂移分析等方法。这些工具或者本身比较复杂,或者只是适应一些特殊情形的分析,甚至还需要满足一些严格的条件才能使用。因此寻求新的方法和工具也是未来的一个方向。
2)当前蚁群优化算法理论研究局限于一些简化的算法模型,基于种群的、更加复杂的构造过程还有待于进一步深入研究。对于n-ANT算法的有效性如何,是否蚂蚁的数量与算法的时间复杂度存在某种关系还未知。通过研究群体规模、构造过程、算法参数等对算法性能的影响,深入挖掘蚁群优化算法的潜能,更好地指导算法设计及应用。对于一个NP难解组合优化问题,蚁群算法能否获得比已有算法更好的近似比?如何获得更紧的时间界等,这些问题都有待于深入研究。
3)将现有蚁群优化算法的理论分析结果扩展到更多的智能算法中。目前在差分进化算法、分布评估算法、粒子群算法以及Memetic算法等随机启发式搜索的理论研究还非常有限,可以尝试将现有的理论分析结论进行有效扩展。此外,当前蚁群算法主要关注离散空间优化,可以向连续优化做进一步扩充。通过对更多算法、更多问题的研究,从中找出一些共性的东西,进一步丰富和增强群智能搜索算法的理论基础。
蚁群优化算法理论研究中涉及到的问题很多,本文不可能做到面面俱到,希望能够起到一个抛砖引玉的作用,对于今后更加深入的研究能够有所帮助和启发。
| [1] | DORIGO M, MANIEZZO V, COLORNI A. Theantsystem:An autocatalytic optimizing process Technical Report 91-016[R]. Milan, Italy:Dipartimento di Elettronica, Politecnico di Milano, 1991. |
| [2] | DORIGO M, STUTZLE T. 蚁群优化[M]. 张军, 胡晓敏, 罗旭耀, 译. 北京:清华大学出版社, 2007:110-246. |
| [3] | DORIGO M, BLUM C. Ant colony optimization theory:a survey[J]. Theoretical computer science, 2005, 344(2-3):243-278. |
| [4] | 段海滨, 王道波, 于秀芬. 蚁群算法的研究现状及其展望[J]. 中国工程科学, 2007, 9(2):98-102.DUAN Haibin, WANG Daobo, YU Xiufen. Ant colony algorithm:survey and prospect[J]. Engineering science, 2007, 9(2):98-102. |
| [5] | NOCEDAL J, WRIGHT S J. Numerical optimization[M]. New York:Springer, 2000. |
| [6] | VAZIRANI V V. Approximation algorithms[M]. Berlin Heidelberg:Springer, 2003. |
| [7] | GAREY M R, JOHNSON D S. Computers and Intractability-A Guide to the Theory of NP-Completeness[M]. New York:Freeman W H and Company, 1979. |
| [8] | COLORNI A, DORIGO M, MANIEZZO V. An investigation of some properties of an "Ant algorithm"[C]//Proceedings of Parallel Problem Solving from Nature II (PPSN 92). Brussels, Belgium, 1992:515-526. |
| [9] | STVTZLE T, HOOS H H. MAX-MIN ant system[J]. Future generation computer systems, 2000, 16(8):889-914. |
| [10] | GUTJAHR W J. Mathematical runtime analysis of ACO algorithms:survey on an emerging issue[J]. Swarm intelligence, 2007, 1(1):59-79. |
| [11] | DROSTE S, JANSEN T, WEGENER I. On the analysis of the (1+1) evolutionary algorithm[J]. Theoretical computer science, 2002, 276(1-2):51-81. |
| [12] | WEGENER I, WITT C. On the analysis of a simple evolutionary algorithm on quadratic pseudo-boolean functions[J]. Journal of discrete algorithms, 2005, 3(1):61-78. |
| [13] | WEGENER I. Towards a theory of randomized search heuristics[M]//ROVAN B, VOJTÁŠ P. Mathematical Foundations of computer science 2003. Berlin Heidelberg:Springer, 2003:125-141. |
| [14] | WEGENER I. Methods for the analysis of evolutionary algorithms on pseudo-boolean functions[M]//Evolutionary Optimization. Dordrecht:Kluwer Academic Publishers, 2002, 48:349-369. |
| [15] | BEYER H G, SCHWEFEL H P, WEGENER I. How to analyse evolutionary algorithms[J]. Theoretical computer science, 2002, 287(1):101-130. |
| [16] | HE J, YAO X. Towards an analytic framework for analysing the computation time of evolutionary algorithms[J]. Artificial intelligence, 2003, 145(1-2):59-97. |
| [17] | HE J, YAO X. Drift analysis and average time complexity of evolutionary algorithms[J]. Artificial intelligence, 2001, 127(1):57-85. |
| [18] | HE J, YAO X. From an individual to a population:an analysis of the first hitting time of population-based evolutionary algorithms[J]. IEEE transactions on evolutionary computation, 2002, 6(5):495-511. |
| [19] | GUTJAHR W J. A graph-based ant system and its convergence[J]. Future generation computer systems, 2000, 16(8):873-888. |
| [20] | STVTZLE T, DORIGO M. A short convergence proof for a class of ACO algorithms[J]. IEEE transactions on evolutionary computation, 2002, 6(4):358-365. |
| [21] | GUTJAHR W J. On the finite-time dynamics of ant colony optimization[J]. Methodology and computing in applied probability, 2006, 8(1):105-133. |
| [22] | 黄翰, 郝志峰, 吴春国,等. 蚁群算法的收敛速度分析[J]. 计算机学报, 2007, 30(8):1344-1353. HUANG Han, HAO Zhifeng, WU Chunguo, et al. The convergence speed of ant colony optimization[J]. Chinese journal of computers, 2007, 30(8):1344-1353. |
| [23] | BIRATTARI M, Dicaro G, DORIGO M. Toward the formal foundation of ant programming[M]//DORIGO M, DI CARO G, SAMPELS M. Ant Algorithms. Berlin Heidelberg:Springer-Verlag, 2002, 2463:188-201. |
| [24] | MEULEAU N, DORIGO M. Ant colony optimization and stochastic gradient descent[J]. Artificial life, 2002, 8(2):103-121. |
| [25] | ZLOCHIN M, BIRATTARI M, MEULEAU N, et al. Model-based search for combinatorial optimization:a critical survey[J]. Annals of operations research, 2004, 131(1-4):373-395. |
| [26] | GUTJAHR W J. A generalized convergence result for the graph-based ant system metaheuristic[J]. Probability in the engineering and informational sciences, 2003, 17(4):545-569. |
| [27] | NEUMANN F, WITT C. Runtime analysis of a simple ant colony optimization algorithm[C]//Proceedings of the 17th International Symposium on Algorithms, ISAAC 2006. Kolkata, India, 2006, 4288:618-627. |
| [28] | NEUMANN F, SUDHOLT D, Wit C. Comparing variants of MMAS ACO algorithms on pseudo-Boolean functions[C]//Proceedings of International Workshop, SLS 2007. Brussels, Belgium, 2007:61-75. |
| [29] | NEUMANN F, WITT C. Runtime analysis of a simple ant colony optimization algorithm[J]. Algorithmica, 2009, 54(2):243-255. |
| [30] | GUTJAHR W J. First steps to the runtime complexity analysis of ant colony optimization[J]. Computers & operations research, 2008, 35(9):2711-2727. |
| [31] | DOERR B, JOHANNSEN D. Refined runtime analysis of a basic ant colony optimization algorithm[C]//Proceedings of the IEEE Congress on Evolutionary Computation (CEC 2007). Singapore, 2007:501-507. |
| [32] | DOERR B, NEUMANN F, SUDHOLT D, et al. On the runtime analysis of the 1-ANT ACO algorithm[C]//Proceedings of Genetic and Evolutionary Computation Conference (GECCO'2007). London, England, 2007:33-40. |
| [33] | DOERR B, NEUMANN F, SUDHOL D, et al. Runtime analysis of the 1-ANT ant colony optimizer[J]. Theoretical computer science, 2011, 412(17):1629-1644. |
| [34] | GUTJAHR W J, SEBASTIANI G. Runtime analysis of ant colony optimization with best-so-far reinforcement[J]. Methodology and computing in applied probability, 2008, 10(3):409-433. |
| [35] | NEUMANN F, SUDHOLT D, WITT C. Analysis of different MMAS ACO algorithms on unimodal functions and plateaus[J]. Swarm intelligence, 2009, 3(1):35-68. |
| [36] | NEUMANN F, SUDHOLT D, WITT C. A few ants are enough:ACO with Iteration-best update[C]//Proceedings of Genetic and Evolutionary Computation Conference (GECCO'2010). Portland, USA, 2010:63-70. |
| [37] | KÖTZING T, NEUMANN F, SUDHOLT D, et al. Simple Max-Min ant systems and the optimization of linear pseudo-Boolean functions[C]//Proceedings of the 11th Work-shop on Foundations of Genetic Algorithms (FOGA 2011). New York, NY, USA, 2011:209-218. |
| [38] | NEUMANN F, SUDHOLT D, WITT C. Rigorous analyses for the combination of ant colony optimization and local search[C]//Proceedings of the 6th International Conference on Ant Colony Optimization and Swarm Intelligence (ANTS08). Brussels, Belgium, 2008:132-143. |
| [39] | NEUMANN F, WITT C. Ant colony optimization and the minimum spanning tree problem[J]. Theoretical computer science, 2010, 411(25):2406-2413. |
| [40] | KÖTZING T, LEHRE P K, OLIVETO P S, et al. Ant colony optimization and the minimum cut problem[C]//Proceedings of the 12th Annual Conference on Genetic and Evolutionary Computation Conference (GECCO'10). New York, NY, USA, 2010:1393-1400. |
| [41] | ATTIRATANASUNTHRON N, FAKCHAROENPHOL J. A running time analysis of an ant colony optimization algorithm for shortest paths in directed acyclic graphs[J]. Information processing letters, 2008, 105(3):88-92. |
| [42] | SUDHOLT D, THYSSEN C. Running time analysis of Ant Colony Optimization for shortest path problems[J]. Journal of discrete algorithms, 2012, 10:165-180. |
| [43] | SUDHOLT D, THYSSEN C. A simple ant colony optimizer for stochastic shortest path problems[J]. Algorithmica, 2012, 64(4):643-672. |
| [44] | LISSOVOI A, WITT C. Runtime analysis of ant colony optimization on dynamic shortest path problems[J]. Theoretical computer science, 2015, 561:73-85. |
| [45] | ZHOU Y R. Runtime analysis of an ant colony optimization algorithm for TSP instances[J]. IEEE transactions on evolutionary computation, 2009, 13(5):1083-1092. |
| [46] | KÖTZING T, NEUMANN F, RÖGLIN H, et al. Theoretical analysis of two ACO approaches for the traveling sales man problem[J]. Swarm intelligence, 2012, 6(1):1-21. |
| [47] | LISSOVOI A, WITT C. MMAS versus population-based EA on a family of dynamic fitness functions[J]. Algorithmica, 2015, doi:10.1007/s00453-015-9975-z. |



