2. 西安交通大学航天航空学院;
3. 中国船舶重工集团公司第七一九研究所;
4. 陕西省先进飞行器服役环境与控制重点实验室
2. School of Aerospace Engineering, Xi'an Jiaotong University;
3. The 719 th Research Institute of China Shipbuilding Industry Corporation;
4. Shaanxi Key Laboratory of Advanced Aircraft Service Environment and Control
0 引言
压力管道在石油化工、电厂和核反应堆等工业生产中起着非常重要的作用,由压力管道失效而引起的事故逐年增多并且损失严重。因此如何正确评价含缺陷管道结构的危害性,是一个与整个生产系统的安全性和经济性直接相关的问题。
表面裂纹引起的疲劳断裂破坏是工程实际中最为常见的破坏形式之一,表面裂纹形状一般用半椭圆进行描述[1]。线弹性断裂力学是预测疲劳裂纹扩展寿命的一种有效方法,该方法考虑了在循环应力作用下,应力强度因子幅值与裂纹扩展速率之间的关系,从而确定增长的裂纹长度。因此,求解管道所含裂纹的应力强度因子是预测裂纹扩展寿命的关键所在。对于含表面裂纹的管道,很多学者采用有限元方法求解管道中不同形状裂纹的应力强度因子并以此来进行管道疲劳裂纹扩展分析[2-7]。A.ZAREEI等[8]采用有限元方法计算了不同裂纹形状的管道内表面裂纹的应力强度因子。H.J.HOH等[9]基于有限元方法计算了焊接管中不同几何形状的半椭圆周向表面裂纹的应力强度因子。张攀峰等[10]根据断裂力学的基本理论和有限元分析方法计算了油井管横向和纵向表面裂纹的应力强度因子。程友祥等[11]利用节点位移法、单元应力法及有限元法计算了T形管节点处撑杆周向上单个穿透裂纹的应力强度因子,对撑杆和弦杆上的两条异面周向穿透裂纹的应力强度因子进行了有限元计算。但是,国内对于管道外表面周向裂纹应力强度因子的相关研究较少,尚无适用于管道外表面裂纹应力强度因子的工程计算解析模型,在工程应用中无法简捷地进行管路结构的初期设计,也很难对含缺陷管道进行准确的安全评估。
本文的主要工作是基于扩展有限元方法(Extended Finite Element Method,XFEM)求解了不同管道半径厚度比、裂纹形状参数、裂纹相对深度下的管道外表面裂纹的应力强度因子,进而构建含外表面裂纹管道疲劳寿命的预测模型,同时进行0Cr18Ni10Ti材料管道的三点弯曲疲劳试验,以对所建计算模型的有效性进行验证。
1 应力强度因子及其解析模型建立裂纹扩展寿命模型的核心工作是确定管道裂纹的应力强度因子,并以此来进行裂纹扩展寿命的预测。本节内容主要基于扩展有限元法[12],通过有限元软件ABAQUS对轴向应力和弯曲应力作用下的管道外表面裂纹的Ⅰ型应力强度因子进行求解,进而建立管道外表面裂纹最深处的Ⅰ型应力强度因子的工程计算模型。
断裂力学研究表明,对于有限尺寸的构件,应力强因子KⅠ可以表示为[1]:

|
(1) |
式中:σ为作用应力;a为裂纹长度;F(a, W, ……)为形状因子,反映构件和裂纹几何尺寸对裂纹尖端应力场的影响。
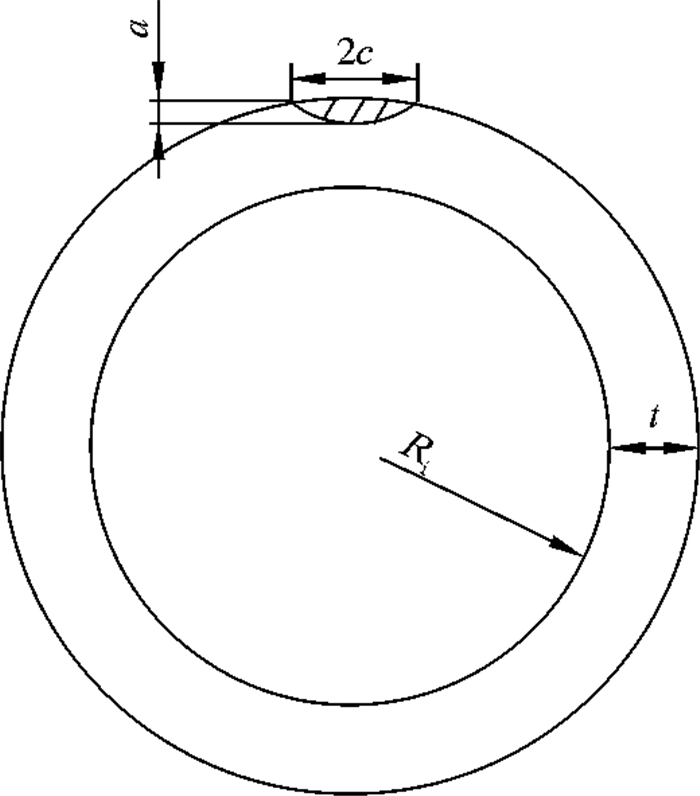
1.1 有限元建模含外表面裂纹管道的几何模型(其中Ri为管道内半径,t为管道壁厚,a为裂纹深度,c为裂纹半长)如图 1所示。由于管道的对称性,文中选取管道的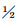
|
| 图 1 管道几何模型 Fig.1 Pipe geometry model |
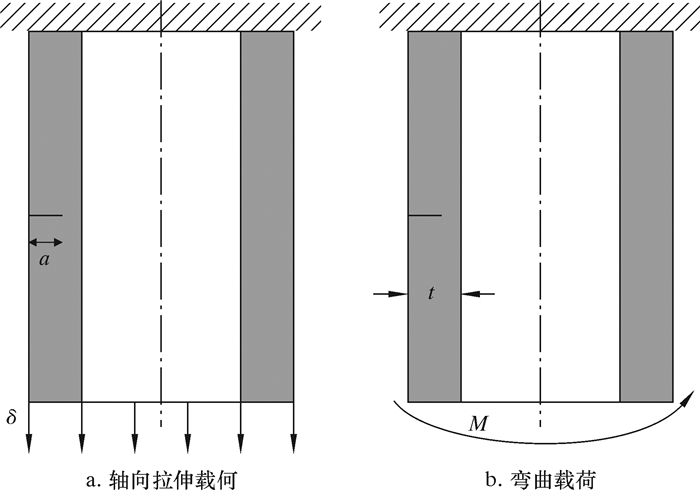
模型材料参数如下:弹性模量E=195 GPa,泊松比υ=0.30。在ABAQUS的part模块中选择3D,shell(planar)建立半椭圆表面裂纹模型,在interaction模块中定义XFEM型裂纹及其属性。管道一端施加全约束,另一端施加轴向载荷或弯曲载荷(见图 2),管道轴向截面施加对称约束[9]。
|
| 图 2 载荷和边界条件 Fig.2 Loads and boundary conditions |
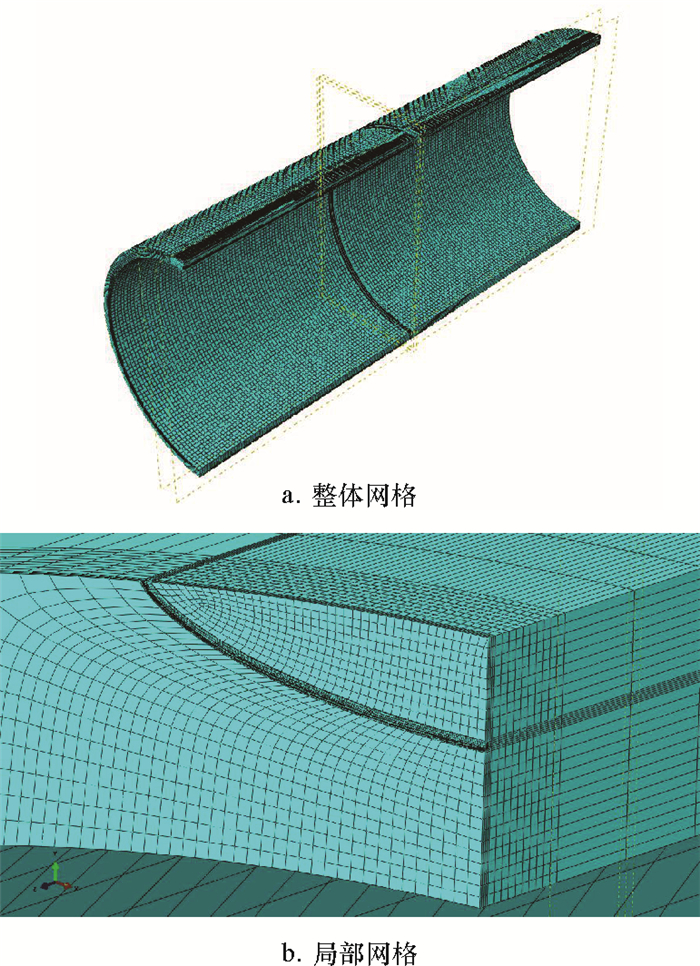
对含裂纹的区域进行精细网格划分,以减小裂纹尖端的奇异性,提高应力强度因子的计算精度。整体网格尺寸为2 mm,局部网格尺寸为0.01~0.20 mm。有限元网格划分如图 3所示。
|
| 图 3 有限元网格划分 Fig.3 Finite element meshing |
1.2 计算结果
基于上述建立的有限元模型,经计算得到的Ri/t=10, 2c/a=4, a/t=0.20管道的外表面裂纹如图 4所示。有限元计算中共有5层积分路径,取2~5层计算结果的平均值作为Ⅰ型应力强度因子值[13],计算结果见表 1。裂纹的形状因子可以通过式(1)计算得到。

|
| 图 4 Ri/t=10, 2c/a=4, a/t=0.20下的外表面裂纹 Fig.4 External surface cracks under Ri/t=10, 2c/a=4, a/t=0.20 |
| 积分层号 | 1 | 2 | 3 | 4 | 5 |

|
5.81 | 5.15 | 5.17 | 5.11 | 4.94 |
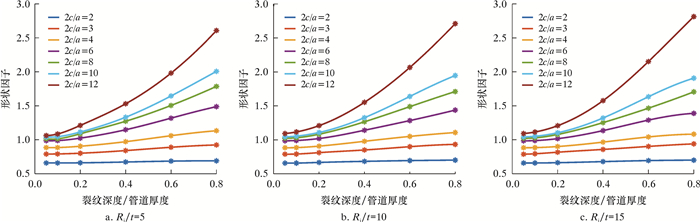
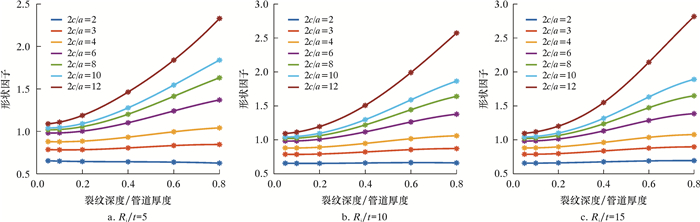
针对工程常用的管道尺寸,在有限元分析获得的轴向拉伸载荷和弯曲载荷作用下,管道半径厚度比Ri/t=5、10和15时,不同裂纹相对深度、裂纹形状参数对应的裂纹形状因子分别如图 5和图 6所示。研究表明:管道外表面裂纹形状因子随裂纹相对深度的增加而增大,且随着裂纹形状参数的增大,增加趋势更加显著;裂纹相对深度相同时,裂纹形状参数越大,形状因子越大;管道半径厚度比对管道外表面半椭圆裂纹形状因子的影响较小。
|
| 图 5 轴向拉伸载荷作用下管道外表面裂纹的形状因子 Fig.5 Shape factor of the crack on the external surface of the pipe under axial tension |
|
| 图 6 弯曲应力作用下管道外表面裂纹的形状因子 Fig.6 Shape factor of the crack on the outer surface of the pipe under bending stress |
1.3 应力强度因子的计算模型
根据式(1)对有限元结果进行拟合,得到轴向拉伸载荷作用下的管道外表面裂纹最深处的Ⅰ型应力强度因子KⅠ1计算方法如下:
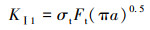
|
(2) |
其中
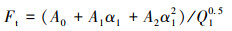
|
(3) |
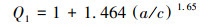
|
(4) |
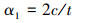
|
(5) |
式中:σt为轴向拉伸应力,A0=1.023 4,A1和A2取值如表 2所示。
| 裂纹形状 | 参数取值 |
| 2≤2c/a < 4 |
A1=0.008 31+0.121 8Q1-0.037 89Q12 A2=0.057 58-0.046 25Q1+0.006 057Q12 |
| 4≤2c/a < 8 |
A1=-0.630 6+1.024Q1-0.356 2Q12 A2=-0.033 25+0.084 89Q1-0.041 12Q12 |
| 8≤2c/a≤20 |
A1=-3.94+6.857Q1-2.926Q12 A2=-0.618 9+1.108Q1-0.488 2Q12 |
同理,弯曲载荷作用下的管道外表面裂纹最深处的Ⅰ型应力强度因子KⅠ2计算方法如下:
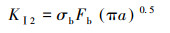
|
(6) |
其中
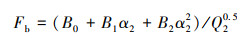
|
(7) |

|
(8) |

|
(9) |
式中:σb为最大弯曲应力,B0=1.007,B1和B2取值如表 3所示。
| 裂纹形状 | 参数取值 |
| 2≤2c/a < 4 |
B1=0.051 19+0.070 86Q2-0.033 86Q22 B2=0.060 73-0.053 73Q2+0.008 166Q22 |
| 4≤2c/a < 8 |
B1=-0.449 6+0.778Q2-0.283 2Q22 B2=-0.025 03+0.069 82Q2-0.036 2Q22 |
| 8≤2c/a≤20 |
B1=-3.464+6.107Q2-2.639Q22 B2=-0.513 7+0.920 3Q2-0.406 3Q22 |
拉弯条件下管道外表面裂纹最深处的Ⅰ型应力强度因子可由轴向拉伸载荷和弯曲载荷作用下的应力强度因子解的叠加得出:
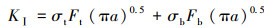
|
(10) |
式(2)、式(6)和式(10)适用范围为:5≤Ri/t≤15,0.1≤a/c < 1.0,0.05≤a/t≤0.80。
2 管道裂纹扩展寿命预测模型疲劳裂纹扩展寿命预测模型有很多种,本文选取了考虑应力比影响的Forman公式[14]:
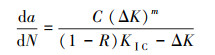
|
(11) |
式中:da/dN为裂纹扩展速率;C、m为材料参数;KⅠC为断裂韧度;R为循环应力比;ΔK为应力强度因子幅度。
孙伟明等[15]对0Cr18Ni10Ti管道钢进行了疲劳裂纹扩展试验和断裂韧性测定试验。文中JⅠC的测定值为277.06 kJ/m2。对于平面应变条件及线弹性范围,KⅠC的计算式为:
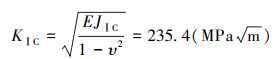
|
(12) |
Forman公式中的材料参数C、m通过以下方法获得[16],对式(11)两边取对数得:

|
(13) |
令式(13)中
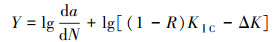
|
(14) |
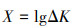
|
(15) |
可得到如下线性方程:

|
(16) |
根据试验(da/dN)i-ΔKi数据,由式(8)和式(15)可得到(Xi,Yi)数据,应用最小二乘法可得到A和B值。通过得到的数据进行数值拟合,得到了0Cr18Ni10Ti材料不同可靠度下Forman公式的各个参数[16](见表 4)。根据得到的0Cr18Ni10Ti材料疲劳裂纹扩展参数,由式(10)和式(11)即可进行含外表面裂纹管道疲劳寿命的预测及可靠性分析。
| 材料参数 | 50%可靠度 | 99%可靠度 |
| C | 9.332 5×10-9 | 1.056 0×10-7 |
| m | 4.607 | 4.035 |

|
235.4 | 225.3 |
3 含外表面裂纹管道疲劳试验及分析
本文开展了管道三点弯曲疲劳试验,用以验证所建立的含外表面裂纹管道疲劳寿命预测模型的有效性。采用的试验件是直径为114 mm,厚度为5 mm,长1 300 mm的直管,其材料为0Cr18Ni10Ti。试验件外表面均预制了一个深度约为1 mm,半长约为10 mm的裂纹。
3.1 试验过程为保证管道三点弯曲疲劳寿命试验的正常开展,设计了专用加载工装。试验采用等幅应力谱进行,波形为正弦波形,最大载荷值为66 kN,最小载荷值为7 kN,试验加载频率为3 Hz。试验在MTS电液伺服疲劳试验机上进行。试验装置如图 7所示。

|
| 图 7 试验装置图 Fig.7 Diagram of test device |
3.2 试验结果
三点弯曲疲劳试验结果如表 5所示。试件断口及裂纹扩展示意图如图 8所示。管道断口面光滑平整,呈现明显的疲劳裂纹扩展过程。
| 试样号 | 疲劳寿命/次 | 对数寿命 |
| 1 | 32 566 | 4.512 8 |
| 2 | 27 572 | 4.440 5 |
| 3 | 25 888 | 4.413 1 |
| 4 | 30 936 | 4.490 5 |
| 5 | 22 234 | 4.347 0 |
| 6 | 22 566 | 4.347 4 |
| 7 | 19 786 | 4.296 4 |
| 8 | 23 752 | 4.375 7 |
| 9 | 25 632 | 4.408 8 |
| 10 | 17 498 | 4.243 0 |
| 11 | 16 278 | 4.211 6 |
| 12 | 18 112 | 4.258 0 |
| 13 | 15 396 | 4.187 4 |
| 平均值 | 22 940 | 4.349 1 |

|
| 图 8 试验件裂纹扩展过程 Fig.8 Fatigue life distribution |
三点弯曲疲劳试验一共获得13组有效数据,将表 5中的数据在正态概率纸上进行描点,结果如图 9所示。由图 9可见,试验得到的对数疲劳寿命X~Ps(存活率)数据在正态概率纸上呈直线分布,表明X=lgN服从正态分布。

|
| 图 9 疲劳寿命分布 Fig.9 Fatigue life distribution |
3.3 试验结果分析
基于前文建立的含外表面裂纹管道疲劳寿命预测模型,利用MATLAB软件进行数值计算。图 10给出了疲劳寿命试验值和计算值与可靠度的关系曲线。不同可靠度下对应的寿命试验值和计算值如表 6所示。
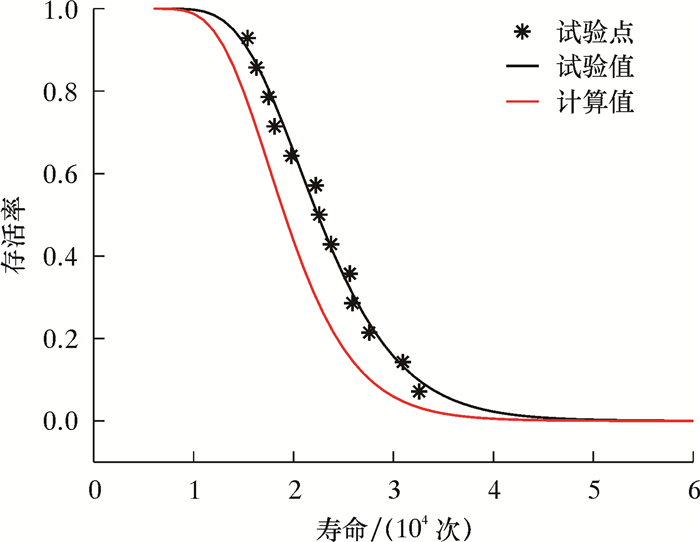
|
| 图 10 疲劳寿命与可靠度的关系曲线 Fig.10 The relationship between fatigue life and reliability |
| 可靠度 | 疲劳寿命/次 | |
| 试验值 | 计算值 | |
| 0.50 | 22 940 | 19 107 |
| 0.90 | 15 726 | 13 293 |
| 0.95 | 14 132 | 11 996 |
| 0.99 | 11 564 | 9 892 |
由图 10和表 6可知,寿命预测模型计算所得的寿命分布规律与试验结果很接近,表明了本文所建含外表面裂纹管道疲劳寿命预测模型的有效性。同时,寿命预测模型的计算结果与试验结果存在一定的误差,这主要是由于本文采用线弹性断裂力学理论来求解裂纹的应力强度因子,并不能完全准确地描述裂纹的实际扩展过程,所以会造成一定的误差。但是,在相同可靠度下的寿命计算值均小于试验值,说明含外表面裂纹管道疲劳寿命预测模型得到的寿命预测值相对偏保守。因此,该寿命预测模型可以为管路结构的工程设计提供偏保守的安全估计。
4 结论(1) 基于扩展有限元法计算了不同管道半径厚度比(Ri/t)、裂纹形状参数(2c/a)、裂纹相对深度(a/t)下的管道外表面裂纹的应力强度因子,结果表明管道外表面裂纹形状因子随裂纹相对深度的增加而增大,且随着裂纹形状参数的增大,其增加趋势更加显著;裂纹相对深度相同时,裂纹形状参数越大,裂纹形状因子越大;管道半径厚度比对管道外表面半椭圆裂纹形状因子的影响较小。
(2) 建立了管道外表面裂纹应力强度因子的工程计算解析模型及基于Forman方程的含外表面裂纹管道的疲劳寿命预测模型。
(3) 含外表面缺陷管道的三点弯曲疲劳试验结果表明,管道疲劳裂纹扩展对数寿命X=lgN服从正态分布,验证了本文所建含外表面裂纹管道疲劳寿命预测模型的有效性。该疲劳寿命预测模型可为管道结构工程设计提供参考。
| [1] |
陈传尧. 疲劳与断裂[M]. 武汉: 华中科技大学出版社, 2002. CHEN C Y. Fatigue and fracture[M]. Wuhan: Huazhong University of Science and Technology Press, 2002. |
| [2] |
SHAHANI A R, HABIBI S E. Stress intensity factors in a hollow cylinder containing a circumferential semi-elliptical crack subjected to combined loading[J]. International Journal of Fatigue, 2007, 29(1): 128-140. DOI:10.1016/j.ijfatigue.2006.01.017 |
| [3] |
CARPINTERI A, BRIGHENTI R, VANTADORI S. Circumferentially notched pipe with an external surface crack under complex loading[J]. International Journal of Mechanical Sciences, 2003, 45(12): 1929-1947. DOI:10.1016/j.ijmecsci.2004.02.007 |
| [4] |
BERGMAN M. Stress intensity factors for circumferential surface cracks in pipes[J]. Fatigue & Fracture of Engineering Materials & Structures, 1995, 18(10): 1155-1172. |
| [5] |
POETTE C, ALBALADEJO S. Stress intensity factors and influence functions for circumferential cracks in pipes[J]. Engineering Fracture Mechanics, 1991, 39(4): 641-650. DOI:10.1016/0013-7944(91)90214-L |
| [6] |
李宁, 廖建敏, 周思柱, 等. 含裂纹自增强厚壁圆筒残余应力研究[J]. 石油机械, 2015, 43(7): 75-79. LI N, LIAO J M, ZHOU S Z, et al. A study on residual stress in self-reinforced crack-containing thick-wall cylinder[J]. China Petroleum Machinery, 2015, 43(7): 75-79. |
| [7] |
许爱荣, 邹云, 杨向同, 等. 内压作用下含裂纹射孔套管临界开裂应力分析[J]. 石油机械, 2012, 40(4): 22-25. XU A R, ZOU Y, YANG X T, et al. An analysis of the critical cracking stress of perforated casing with cracks under the effect of internal pressure[J]. China Petroleum Machinery, 2012, 40(4): 22-25. |
| [8] |
ZAREEI A, NABAVI S M. Calculation of stress intensity factors for circumferential semi-elliptical cracks with high aspect ratio in pipes[J]. International Journal of Pressure Vessels and Piping, 2016, 146: 32-38. DOI:10.1016/j.ijpvp.2016.05.008 |
| [9] |
HOH H J, PANG J H L, TSANG K S. Stress intensity factors for fatigue analysis of weld toe cracks in a girth-welded pipe[J]. International Journal of Fatigue, 2016, 87: 279-287. DOI:10.1016/j.ijfatigue.2016.02.002 |
| [10] |
张攀峰, 林元华, 李天雷, 等. 含裂纹油井管三维应力强度因子的有限元分析[J]. 石油机械, 2009, 37(1): 45-47. ZHANG P F, LIN Y H, LI T L, et al. Finite element analysis of three-dimensional stress intensity factors of cracked oil well pipe[J]. China Petroleum Machinery, 2009, 37(1): 45-47. |
| [11] |
程友祥, 赵毅, 蒋科, 等. T形管节点处双裂纹干涉分析研究[J]. 石油机械, 2017, 45(6): 56-62. CHENG Y X, ZHAO Y, JIANG K, et al. Analysis on dual-crack interference on T-tubular joints[J]. China Petroleum Machinery, 2017, 45(6): 56-62. |
| [12] |
汪必升, 李毅波, 廖雅诗, 等. 基于扩展有限元模型的动态应力强度因子计算[J]. 中国机械工程, 2019, 30(11): 1294-1301. WANG B S, LI Y B, LIAO Y S, et al. Calculation of dynamic stress intensity factors based on XFEM model[J]. China Mechanical Engineering, 2019, 30(11): 1294-1301. DOI:10.3969/j.issn.1004-132X.2019.11.005 |
| [13] |
卢岳川, 臧峰刚. 含轴向贯穿裂纹三通断裂有限元计算方法[J]. 核动力工程, 2008(3): 32-34, 40. LU Y C, ZANG F G. Analysis method by fracture finite element for tee with longitudinal through-wall crack[J]. Nuclear Power Engineering, 2008(3): 32-34, 40. |
| [14] |
董聪, 夏人伟. 疲劳裂纹扩展寿命预测概率模型[J]. 强度与环境, 1994(4): 13-18. DONG C, XIA R W. A probabilistic model for predicting propagation life of fatigue cracks[J]. Structure & Environment Engineering, 1994(4): 13-18. |
| [15] |
孙伟明, 任欣, 金伟娅, 等. 321奥氏体不锈钢断裂疲劳性能的试验研究[C]//第十三届全国反应堆结构力学会议论文集.成都: 核动力工程杂志社, 2004: 183-186. SUN W M, REN X, JIN W Y, et al. Experimental study on fracture fatigue properties of 321 austenitic stainless steel[C]//Proceedings of the 13th National Conference on Structural Mechanics of Reactors. Chengdu: Nuclear Power Engineering, 2004: 183-186. |
| [16] |
杨冰, 赵永翔, 张卫华. 基于Forman方程的随机疲劳长裂纹扩展概率模型[J]. 交通运输工程学报, 2006(1): 25-28. YANG B, ZHAO Y X, ZHANG W H. Probabilistic models of random fatigue crack propagation based on Forman equation[J]. Journal of Traffic and Transportation Engineering, 2006(1): 25-28. DOI:10.3321/j.issn:1671-1637.2006.01.005 |



