0 引言
水下采油树是水下生产系统的关键生产设施,可以实现水下井口和管汇等设施的连接[1],位于水下井口的顶端。水下采油树的主要功能是控制井外油气的流动,也可以用于控制向非生产井注入气体或水[2]。随着我国海洋石油开发技术的不断发展,水下采油树的安装技术已经成为深水油气开发建设中的关键技术之一。
水下采油树的安装方法很多,在我国目前应用较多的为钢丝绳下放安装和钻杆下放安装,许多学者对水下采油树的安装进行了研究。龚铭煊等[3]建立了水下采油树下放安装过程中钻杆的力学分析模型,确定了不同安装阶段的载荷情况与边界条件。脱浩虎等[4]采用OrcaFlex建立了1 500 m水深时采油树下放安装过程的数值模型,研究了不同环境因素对安装钻杆的偏移和受力的影响。周美珍等[5]基于水下采油树月池导向安装流程,在考虑不同特征的情况下,建立了水下采油树月池导向安装不同阶段的力学分析模型。WANG Y.Y.等[6]基于小变形理论通过OrcaFlex软件,建立了1 500 m水深时采油树下放安装过程的数值模型,研究了不同环境因素和水下安装阶段对安装钻杆偏移和受力的影响。HU Y.L.等[7]以钻杆下放水下采油树为研究对象,基于Keller-box方法求解出不同长度钻杆的差分控制方程,得到采油树的运动响应规律。梁海青[8]基于莫里森方程对钢丝绳安装法和纤维绳安装法进行对比,研究了海流作用引起的水下采油树横向偏移和缆绳拉伸长度。
调研发现,国内外学者[9-11]大多研究的安装方法为钻杆安装法和钢丝绳安装法,且多集中在其受力、横向位移和变形情况,鲜见水下采油树两种下放方式的对比情况。本文基于OrcaFlex有限元仿真模型,研究了水深500 m、质量70 t的水下采油树在日常风、浪、流等环境载荷下的下放安装情况。研究结果对我国水下采油树的安装具有一定的参考价值。
1 水下采油树模型建立与基本参数 1.1 水下采油树模型建立水下采油树是任何水下生产系统中不可缺少的组成部分,它由采油树下放工具、本体、阀组和油管悬挂器等部件组成。笔者对采油树下放工具和采油树本体采用6Dbuoy模型建模,而采油树阀组和框架等则采用Shape模型中的Elastic solid种类进行模拟。因Elastic solid可以模拟障碍物,从而模拟挡水面积,由于挡水面积影响水动力参数,故而简化满足等面积原则,确保水下采油树简化的正确性。将建好的模型连接到相应的采油树树体或下放工具上,其中采油树本体质量约68 t,下放工具质量约2 t,作业水深500 m。
采油树下放工具和采油树树体连接后的3D模型如图 1所示。
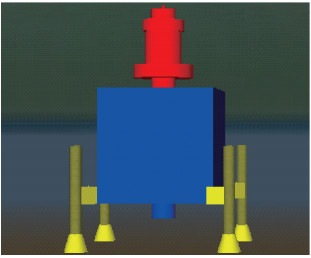
|
| 图 1 采油树树体和下放工具3D模型图 Fig.1 The 3D model of the subsea Christmas tree and running tool |
1.2 基本参数
对于水下采油树所受载荷,风载荷的比例高达15%。在黏性阻力系数和迎风面积一定的情况下,风速是影响风载荷的关键因素。风参数如表 1所示。表 1中T表示重现期。
| 时间/s | 风速/(m·s-1) | |||
| T=1 a | T=10 a | T=50 a | T=100 a | |
| 3 | 33.1 | 46.0 | 55.8 | 59.6 |
| 60 | 27.9 | 38.8 | 47.0 | 50.2 |
| 600 | 24.4 | 34.0 | 41.2 | 44.0 |
| 3 600 | 22.1 | 30.7 | 37.2 | 39.7 |
我国海域浪高普遍较高,100 a重现期内的浪高已达11.7 m。由于浪高对船舶的运动影响较大,对于未安装有效补偿系统的船舶来讲,浪高超过4.9 m(T=1 a)不会进行下放安装作业,波浪参数如表 2所示。针对我国海域的海况特点,选择Jonswap谱作为计算分析的波浪谱。
| 重现期/a | 日常 | 1 | 10 | 50 | 100 |
| 有效波高/m | 3.0 | 4.9 | 7.6 | 10.4 | 11.7 |
| 最大浪高/m | 5.2 | 8.4 | 13.0 | 18.0 | 20.1 |
| 跨零周期/s | 5.0 | 6.6 | 8.1 | 9.6 | 10.2 |
| 最大波周期/s | 5.3 | 8.3 | 10.2 | 12.0 | 12.9 |
| 谱峰周期/s | 6.3 | 9.3 | 11.3 | 13.4 | 14.3 |
由于海洋环境复杂多变,受天气等的影响,海水的流速会产生一定的变化,特别是一些极端天气时,流速变化则会很大,海流参数如表 3所示。需要注意的是:根据实际工程经验,为了实现工程船的定位要求,来流方向要保持与船艏方向一致。
| 水深/m | 流速/(m·s-1) | |||
| T=1 a | T=10 a | T=50 a | T=100 a | |
| 0 | 0.85 | 1.21 | 1.64 | 2.04 |
| 100 | 0.74 | 1.02 | 1.26 | 1.79 |
| 200 | 0.57 | 0.63 | 0.67 | 1.37 |
| 300 | 0.46 | 0.52 | 0.56 | 0.69 |
| 400 | 0.40 | 0.48 | 0.51 | 0.58 |
| 500 | 0.38 | 0.41 | 0.46 | 0.51 |
2 基于OrcaFlex的水下采油树钻杆下放安装过程模拟仿真 2.1 钻杆下放安装过程分析
钻杆下放安装采油树一般分为两个阶段:①下放过程,即水下采油树钻杆下放穿越飞溅区接近井口的过程。此过程受半潜式平台运动以及风、波浪力和海流力共同作用的影响,将会直接决定整个下放安装作业的安全性。②安装过程,即水下采油树与水下井口进行对接安装,其钻杆下放水下采油树的模型示意图如图 2所示。
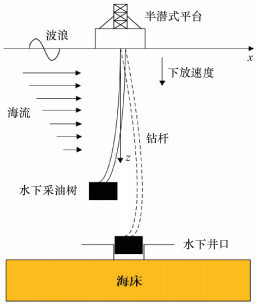
|
| 图 2 钻杆下放水下采油树模型示意图 Fig.2 Schematic diagram of the model of the subsea Christmas tree running by drill pipe |
在水下采油树下放安装过程中,钻杆上部与半潜式平台相连,下部通过下放工具与水下采油树连接。在钻杆下放安装过程中,钻杆通常是以硬悬挂的方式与半潜式平台连接,即钻杆直接与卡盘刚性连接,所以建立模型时钻杆与半潜式平台也是刚性接触,同时钻杆选用的是线单元,全长500 m。在OrcaFlex软件中绘制了半潜式平台模型,其模型参照了半潜式平台的特征轮廓,并进行了适当简化。整个半潜式平台被模拟成一个刚体,由输入的RAO参数赋予其运动特性。在OrcaFlex软件中总的钻杆下放系统分析模型如图 3所示,水下采油树与井口对接安装3D模型图如图 4所示。

|
| 图 3 钻杆下放系统3D模型图 Fig.3 3D model of the drill pipe running system |

|
| 图 4 水下采油树与井口对接安装3D模型图 Fig.4 3D model of docking installation of subsea Christmas tree and wellhead |
2.2 应力和弯矩对钻杆受力的影响
水下采油树本体与钻杆下放工具总质量约为70 t,安装水深500 m。通过OrcaFlex软件,在日常浪高3.0 m、流速0.85 m/s的海况下对水下采油树钻杆下放进行了模拟仿真分析,其Von Mises应力分布情况和弯矩分别如图 5和图 6所示。
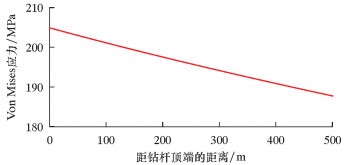
|
| 图 5 Von Mises应力变化曲线 Fig.5 Von Mises stress curve |
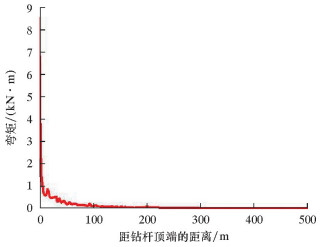
|
| 图 6 弯矩变化曲线 Fig.6 Bending moment variation curve |
由图 5和图 6可知:钻杆受到的最大Von Mises应力和弯矩均位于钻杆顶端处,分别为204.75 MPa和8.53 kN·m;Von Mises应力随深度的增加而呈线性减小,最小值在钻杆底端,为187.76 MPa;水深变化所引起的弯矩变化主要集中在钻杆上部靠近钻杆顶端处,其他部位的变化很小,其弯矩值几乎为0。
2.3 钻杆偏移量对水下采油树安装过程的影响在水下采油树下放安装过程中,钻杆的偏移量对水下采油树的安装有着很大的影响,直接决定水下采油树与井口的对接作业风险。通过OrcaFlex软件,在浪高3.0 m、流速0.85 m/s的海况下对水下采油树钻杆下放进行了模拟仿真分析,钻杆在X、Y方向的偏移量、水下采油树下放深度以及安装姿态(用倾斜角表示)变化情况如图 7~图 10所示。
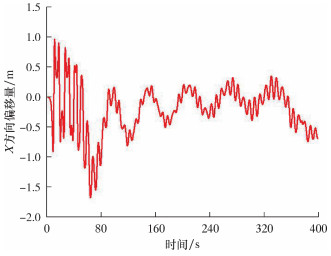
|
| 图 7 钻杆在X方向偏移量随时间的变化曲线 Fig.7 The offset of the drill pipe in the X direction with time |
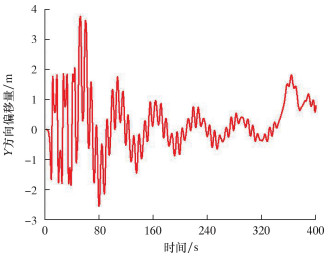
|
| 图 8 钻杆在Y方向偏移量随时间的变化曲线 Fig.8 The offset of the drill pipe in the Y direction with time |
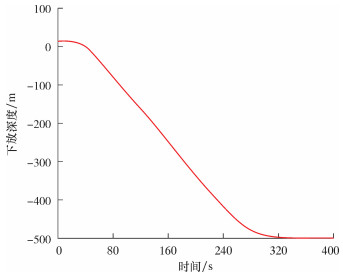
|
| 图 9 采油树下放深度随时间的变化曲线 Fig.9 The running depth of the Christmas tree with time |
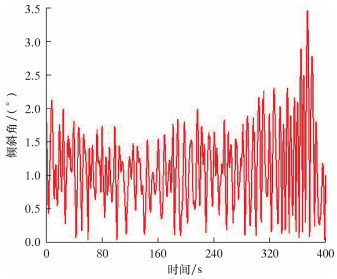
|
| 图 10 采油树安装姿态随时间的变化曲线 Fig.10 The installation posture of Christmas tree with time |
由图 7~图 10可以看出:水下采油树在入水过程中钻杆在X和Y方向的偏移量变化范围波动较大,分别为2.639和6.307 m;钻杆底端在X、Y方向最大偏移量(绝对值)分别为1.548和3.749 m,其下放接近井口时在X、Y方向的偏移量分别为0.689和0.769 m;水下采油树从月池中央上方距海平面15 m处下放,下放深度为500 m;当水下采油树下放到493 m时,倾斜角达到最大值3.467°。
2.4 浪高对钻杆应力和弯矩的影响我国海域浪高普遍较大,100 a重现期内的浪高已达11.7 m,但是由于浪高对半潜式平台的运动响应影响较大,所以只选取3.0~11.7 m范围内的浪高来讨论浪高对钻杆所受Von Mises应力和偏移量的影响。本文选择3.0 m(日常)、4.9 m(T=1 a)、7.6 m(T=10 a)、10.4 m(T=50 a)和11.7 m(T=100 a)5种浪高进行了模拟仿真分析,仿真结果如图 11和图 12所示。
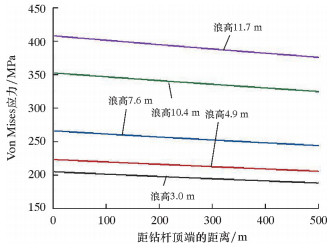
|
| 图 11 不同浪高钻杆的Von Mises应力 Fig.11 Von Mises stress of drill pipe under different wave heights |
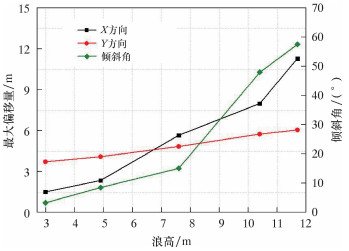
|
| 图 12 不同浪高钻杆最大偏移量和安装姿态 Fig.12 The maximum offset and installation posture of drill pipe under different wave heights |
由图 11和图 12可知:随着波浪高度的增大,钻杆的Von Mises应力、X和Y方向最大偏移量以及水下采油树倾斜角都增大,说明不同浪高对钻杆Von Mises应力、X和Y方向最大偏移量以及水下采油树倾斜角影响较大,同时也能看出钻杆受到的最大Von Mises应力均位于钻杆顶端处;当浪高为11.7 m时,钻杆顶端Von Mises应力为409 MPa,小于钻杆(S135)的屈服强度930 MPa,满足屈服准则;钻杆在X、Y方向最大偏移量分别为11.311和6.078 m,水下采油树的最大倾斜角为57.6°。
3 基于OrcaFlex的水下采油树钢丝绳下放安装过程模拟仿真 3.1 钢丝绳下放安装过程分析钢丝绳下放安装采油树与钻杆下放安装划分的阶段大致相同:①飞溅区,此过程极易受到风、浪、流载荷的影响,使水下采油树产生缆绳松弛以及大幅旋转运动现象,对水下采油树下放安装造成不利影响;②安装阶段,即通过ROV对水下采油树定向对中下放与井口锁紧安装。在OrcaFlex软件中建立的安装船钢丝绳下放采油树系统3D模型如图 13所示。

|
| 图 13 钢丝绳下放采油树系统3D模型图 Fig.13 3D model of wire rope running system |
3.2 钢丝绳受力分析
水下采油树本体与钢丝绳下放工具总质量约为70 t,安装水深500 m,通过OrcaFlex软件,在浪高3.0 m、流速0.85 m/s的海况下对水下采油树钢丝绳下放进行了模拟仿真分析,其钢丝绳受到的有效张力变化情况如图 14所示。
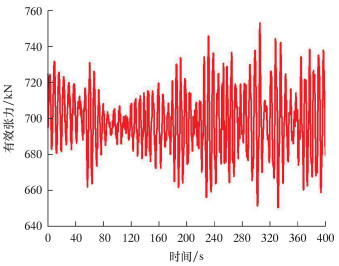
|
| 图 14 钢丝绳受到的有效张力变化时历图 Fig.14 Time-history diagram of the effective tension on the wire rope |
由图 14可知:当水下采油树下放深度达到370 m时,钢丝绳受到的有效张力最大,为753.11 kN;当水下采油树下放深度达到410 m时,钢丝绳受到的有效张力最小,为650.60 kN。
3.3 钢丝绳偏移量对水下采油树安装过程的影响水下采油树采用舷侧方式进行下放安装,此时钢丝绳在Y方向的偏移量不宜过大,否则会造成钢丝绳与安装船发生碰撞的风险,在工程安装作业中应保持既定的安全距离,确保水下采油树能够顺利、平稳、安全下放安装。通过OrcaFlex软件,在浪高3.0 m、流速0.85 m/s的海况下对水下采油树钢丝绳下放进行了模拟仿真分析,水下采油树在X和Y方向的偏移量、下放深度以及安装姿态变化情况如图 15~图 18所示。
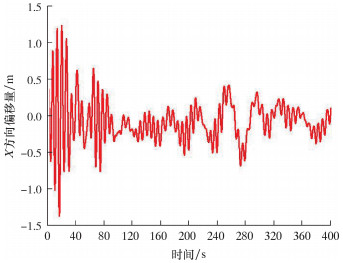
|
| 图 15 钢丝绳在X方向的偏移量变化时历图 Fig.15 Time-history diagram of the wire rope offset in the X direction |
|
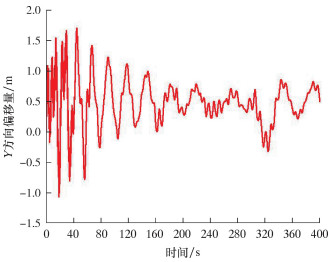
| 图 16 钢丝绳在Y方向的偏移量变化时历图 Fig.16 Time-history diagram of the wire rope offset in the Y direction |
|
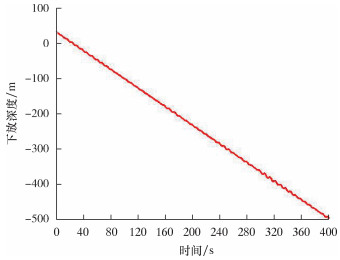
| 图 17 水下采油树下放深度变化时历图 Fig.17 Time-history diagram of the running depth of the subsea Christmas tree |
|
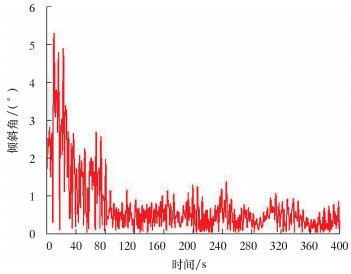
| 图 18 水下采油树安装姿态变化时历图 Fig.18 Time-history of the installation posture of the subsea Christmas tree |
由图 15~图 18可以看出:水下采油树下放过程中钢丝绳在X、Y方向最大偏移量分别为1.370和1.691 m,其下放接近井口时在X、Y方向的偏移量分别为0.107和0.489 m;水下采油树从舷侧距海平面32 m处下放,下放深度为500 m,下放深度变化曲线出现波动状态,这是由于受到环境载荷和安装船运动的影响;当水下采油树下放到19.5 m时,倾斜角达到最大值5.288°。
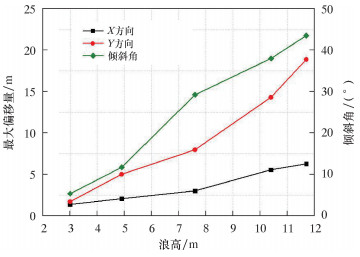
3.4 浪高对钢丝绳偏移量和水下采油树安装姿态的影响该部分以浪高为变化参数,其他条件保持不变。在浪高为3.0 m(日常)、4.9 m(T=1 a)、7.6 m(T=10 a)、10.4 m(T=50 a)和11.7 m(T=100 a)5种浪高情况下,钢丝绳在X、Y方向最大偏移量和水下采油树最大倾斜角仿真结果如图 19所示。由图 19可以看出:随着波浪高度的增大,钢丝绳在X和Y方向最大偏移量以及水下采油树最大倾斜角都增大,说明不同浪高对钢丝绳在X和Y方向最大偏移量以及水下采油树最大倾斜角影响较大;当浪高为11.7 m时,钢丝绳在X和Y方向最大偏移量分别为6.28和18.91 m,水下采油树的最大倾斜角为43.6°。
|
| 图 19 不同浪高下钢丝绳最大偏移量和安装姿态 Fig.19 The maximum offset and installation posture of wire rope under different wave heights |
3.5 对比分析
通过考虑钢丝绳安装法和钻杆安装法工艺特点,结合水下采油树钢丝绳下放和钻杆下放的模拟结果对比分析可以发现:钢丝绳安装法日费率低;安装水下采油树时钢丝绳的横向偏移量较小,以至于ROV操作时间较短,安装风险降低;钢丝绳两端所受载荷相差不大,受力比较均匀,而钻杆的Von Mises应力和弯矩都集中在钻杆上部靠近钻杆顶端处,受力不均匀;浪高对钻杆顶端的Von Mises应力、偏移量以及安装姿态敏感性影响很大。因此认为,水深500 m、质量70 t的水下采油树下放安装采用钢丝绳安装法更合理。
4 结论通过分别对钻杆下放和钢丝绳下放这两种安装方法进行模拟仿真分析,研究了日常天气下钻杆和钢丝绳受力、偏移量以及采油树安装姿态变化,同时研究了不同浪高下对其产生的影响情况,可以得到如下结论:
(1) 在日常天气下,钻杆受到的最大Von Mises应力和弯矩均位于钻杆顶端处,且分别为204.75 MPa和8.53 kN·m,钢丝绳受到的最大有效张力和最小有效张力分别为753.11和650.60 kN。
(2) 在日常天气下,钻杆底端在X和Y方向最大偏移量分别为1.548和3.749 m,水下采油树的最大倾斜角为3.467°,而钢丝绳在X和Y方向最大偏移量分别为1.370和1.691 m,水下采油树的最大倾斜角为5.288°。
(3) 浪高因素对钻杆下放和钢丝绳下放影响很大且为正相关关系。
(4) 综合考虑经济性、安全性和可操作性等方面,对水下采油树钻杆下放和钢丝绳下放模拟结果进行了对比分析,推荐工程上采用钢丝绳安装法。
| [1] |
蒋东雷, 李中, 秦桦, 等. 陵水17-2气田水下采油树选型与功能设计[J]. 石油机械, 2018, 46(7): 31-38. JIANG D L, LI Z, QIN H, et al. Type selection and function design of subsea christmas tree in Lingshui 17-2 gas filed[J]. China Petroleum Machinery, 2018, 46(7): 31-38. |
| [2] |
李志刚, 贾鹏, 王洪海, 等. 水下生产系统发展现状和研究热点[J]. 哈尔滨工程大学学报, 2019, 40(5): 944-952. LI Z G, JIA P, WANG H H, et al. Developments and hotspots of subsea production system[J]. Journal of Harbin Engineering University, 2019, 40(5): 944-952. |
| [3] |
龚铭煊, 刘再生, 段梦兰, 等. 深海水下采油树下放安装过程分析与研究[J]. 石油机械, 2013, 41(4): 50-54. GONG M X, LIU Z S, DUAN M L, et al. Research on the running installment process of deep sea underwater Christmas tree[J]. China Petroleum Machinery, 2013, 41(4): 50-54. |
| [4] |
脱浩虎, 李华, 张赢今, 等. 基于OrcaFlex的深水采油树下放安装过程仿真研究[J]. 石油机械, 2017, 45(3): 58-62. TUO H H, LI H, ZHANG Y J, et al. Simulation of running and installation of deep water X-tree based on OrcaFlex[J]. China Petroleum Machinery, 2017, 45(3): 58-62. |
| [5] |
周美珍, 尚照辉, 阮伟东, 等. 水下采油树月池导向安装过程力学分析方法[J]. 中国海上油气, 2015, 27(3): 96-100. ZHOU M Z, SHANG Z H, RUAN W D, et al. Mechanical analysis for subsea tree installation through moon pool guidance[J]. China Offshore Oil and Gas, 2015, 27(3): 96-100. |
| [6] |
WANG Y Y, TUO H H, LI L W, et al. Dynamic simulation of installation of the subsea cluster manifold by drilling pipe in deep water based on OrcaFlex[J]. Journal of Petroleum Science and Engineering, 2018, 163: 67-78. |
| [7] |
HU Y L, CAO J J, YAO B H, et al. Dynamic behaviors of a marine riser with variable length during the installation of a subsea production tree[J]. Journal of Marine Science and Technology, 2018, 23(2): 378-388. |
| [8] |
梁海青.水下采油树下水安装过程动力学分析[D].青岛: 中国石油大学(华东), 2016. LIANG H Q. Dynamic analysis of installation of the subsea tree[D]. Qingdao: China University of Petroleum(Huadong), 2016. |
| [9] |
付剑波, 邢传胜, 苏峰, 等. 深水吊放缆绳受力分析方法研究及有限元模拟[J]. 石油机械, 2015, 43(2): 55-59. FU J B, XING C S, SU F, et al. Analysis method of force on suspended cable in deep sea[J]. China Petroleum Machinery, 2015, 43(2): 55-59. |
| [10] |
ZHAO Y, WANG Y Y, LI L W, et al. Numerical simulation of subsea cluster manifold installation by the sheave method[C]. ASME 201837th International Conference on Ocean, Offshore and Arctic Engineering, Madrid, Spain, June 17-22, 2018: 1-11.
|
| [11] |
王莹莹, 杨超, 梁卫平, 等. 基于滑轮法的水下管汇安装静力学分析[J]. 石油机械, 2019, 47(4): 54-60. WANG Y Y, YANG C, LIANG W P, et al. Static analysis of subsea manifold installation by the sheave method[J]. China Petroleum Machinery, 2019, 47(4): 54-60. |


