2. 中国石油大学(北京)机械与储运工程学院
2. College of Mechanical and Transportation Engineering, China University of Petroleum(Beijing)
0 引言
附壁脉冲射流喷嘴利用附壁效应原理,以流体为工作介质,在不需要外界作用力和运动部件条件下产生周期性振荡效果。当前对于附壁脉冲射流喷嘴的研究主要集中于流量测量[1-3]与井下脉冲射流等领域,在井下脉冲射流的应用主要集中于清洗和破岩方向。其原理主要是利用流体的脉冲振荡性能,在井筒和地层流体中产生压力波,用于从近井筒区域、射孔和筛网中清除沉积物。自激脉冲喷嘴专为高压、水下作业和最大压力脉动幅值而设计,可以产生交替爆发的流体,减小对近井眼处的损害,提高射孔效率,提升近井筒区的渗透率。
目前对附壁脉冲射流喷嘴的研究通常为常压试验和二维常压数值模拟,忽略了三维结构尺寸对振荡效果的整体优化。XU C.等[4]试验研究了附壁振荡器入口宽度、反馈通道宽度和振荡腔形状等几何因素对附壁脉冲射流喷嘴性能的影响。LI Y.等[5]对小型脉冲射流喷嘴的流动特性进行数值模拟与试验研究,研究了低雷诺数下小型喷嘴的流动特性,得出流动振荡由附壁效应和周期性振荡射流引起,并给出了该结构喷嘴的振荡特性与流量和斯特劳哈尔数之间的关系。MENG X.等[6]设计并加工了小型脉冲射流喷嘴,以水为工质试验研究了喷嘴入口宽度对振荡频率的影响,并且分析了雷诺数对喷嘴振荡特性的影响。XIE T.等[7]采用二维非定常模拟和试验相结合的方法,研究了低雷诺数对振荡频率和压降的影响,分析了基于附壁效应的流体振荡的切换机理。
响应面法(RSM)是综合了数学方法和统计方法的优化设计方法,通过对局部点进行试验,从而拟合全局得到回归方程,进而得到各因素的最优水平值。近年来,该方法广泛用于机械结构的优化设计[8-10]。通过响应面分析,可以全面分析各关键结构参数对振荡效果的影响,进而进行整体优化,同时节约计算成本。本文以某油田深井下附壁脉冲射流喷嘴为研究对象,对不同结构尺寸的喷嘴在井下高围压环境下的流场进行三维数值模拟,通过响应面法探究反馈通道直径、附壁夹角和出口直径等结构尺寸对喷嘴出口压力脉动幅值的影响,并对喷嘴的整体结构参数进行了优化。
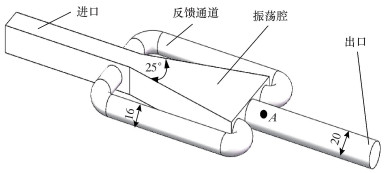
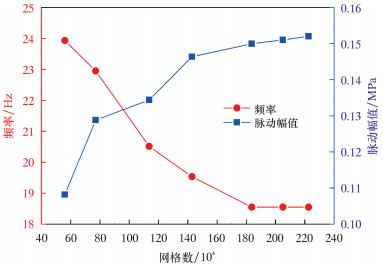
1 数值模拟模型 1.1 几何模型数值模拟的模型为某油田高围压超深井下的附壁脉冲射流喷嘴,如图 1所示。模拟模型由进口、出口、振荡腔和两个反馈通道组成,整个模型初始尺寸如下:出口直径20 mm,附壁夹角25°,反馈通道直径16 mm。点A为出口中心点,用来监测喷嘴出口的压力变化。由于模型较为复杂,采用四面体网格对模型进行网格划分,通过网格无关性验证(见图 2),综合考虑准确性与计算量,最终选定的数值模拟网格总数为184万个。
|
| 图 1 附壁脉冲射流喷嘴模型图 Fig.1 Model diagram of the Coanda effect jet-nozzle |
|
| 图 2 网格无关性验证 Fig.2 Grid independence verification |
1.2 数学模型及边界条件
柳鹤[11]对射流冲击系统湍流模型调研得出,RNG k-ε模型具有较高的精确度。同时,由于RNG k-ε模型能模拟射流撞击、二次流、分离流和旋流等复杂流动,所以本文选择的湍流模型为RNG k-ε模型。
模拟时,采用15 m/s的速度入口,出口压力设置为井底围压30 MPa,用来模拟高围压环境。采用标准壁面函数,同时壁面无滑移。采用SIMPLE算法对压力和速度进行耦合,使用PRESTO!格式对压力项进行空间离散。为了模拟流场的脉冲效果,采用非定常方式进行计算,时间步长设定为0.5 ms。
1.3 压力脉动计算采用统计学中的脉动幅值来描述压力脉动特性。采集同一时间段的压力信号样本,总样本按照脉动周期划分若干子区间,用每个区间的最大压力平均值pmax减去最小压力平均值pmin,定义为压力脉动幅值Δp[12]:
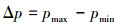
|
(1) |
高速流体从进口流入振荡腔内,振荡腔壁面使得流场卷吸受限制,产生压力差,导致射流产生偏转,有一部分流体进入反馈通道,冲击主流,造成主流偏转到另一个壁面,如此产生周期性振荡。通过监测图 1中A点的压力变化值,即可计算喷嘴出口产生的压力脉动幅值。本文以A点压力脉动幅值为优化目标,采用响应面法开展优化设计,利用中心复合设计法设计试验样本,采用数值模拟方法对试验样本的压力脉动幅值进行预测。
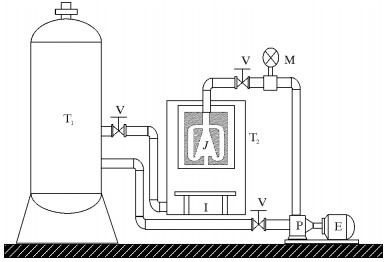
1.4 试验验证为保证模拟结果的可靠性,进行了附壁脉冲射流喷嘴冲击性能试验。试验平台如图 3所示,由进水系统、离心泵系统、喷嘴可视化系统和储水罐系统组成。本文通过对冲击台上冲击压力的测量来验证自激脉冲喷嘴的脉冲特性。
|
| M—电磁流量计;T1—储水罐;T2—冲击水箱;V—阀门;P—离心泵;E—电机;J—喷嘴;I—冲击台。 图 3 附壁脉冲射流喷嘴冲击试验台示意图 Fig.3 Schematic diagram of the impulse test bench of the Coanda effect jet-nozzle |
试验中采用的压力测量装置为粘贴在冲击台上型号为KFW-5-120-C1-11L1M2R的应变片,该应变片常被应用于水下应力应变测量。数据采集装置为NI-9235的应变仪模块,其内部主时基频率为12.8 MHz。
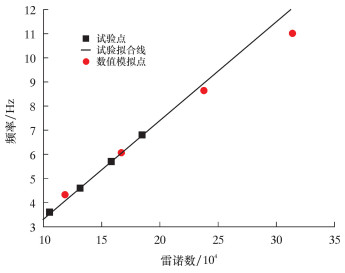
对不同流量下喷嘴射流冲击性能进行试验并与模拟结果对比。图 4为喷嘴入口雷诺数与振荡频率的关系图。从图 4可以看出,数值模拟结果与试验值匹配良好。当流量增加到23.76 m3/h(即雷诺数为31.37×104)时,数值模拟值与试验值之间的相对误差最大,为8.34%,该误差在试验允许范围内。这说明模拟计算结果可靠,计算方法可行。
|
| 图 4 雷诺数与频率的关系图 Fig.4 The relationship between Reynolds number and frequency |
2 响应面法 2.1 响应面法理论
响应面法对指定取值范围内的因素进行有限次数的试验,构造不同阶次的多项式拟合响应值和各个因素之间的函数关系,从而得到最优解[13-14]。一般地,响应面值Y与各因素X1、X2、X3……之间的函数关系为:
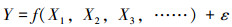
|
(2) |
式中:f为响应面近似函数;ε为总误差,包括随机误差和观测误差等。
引入二阶多项式函数对式(2)进行拟合,则响应面法最终的函数式为:
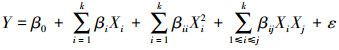
|
(3) |
式中:k为因素个数,右边函数式各项依次为常数项、一次项、平方项、二次交互项和误差项。
2.2 中心复合设计中心复合设计(Central Composite Design, CCD)是响应面法常用的设计试验方法之一。以本文的三因素CCD设计为例,整个设计包括:①中心点,位于立方体中心;②部分析因设计或者完全析因设计,位于立方体顶点,称为立方点;③附加设计(星点设计),位于立方体中心轴线上[15]。
2.3 试验设计及模拟结果在入口尺寸不变的前提下,为考察反馈通道直径、附壁夹角和出口直径的组合对脉动幅值的影响,对以上3个因素进行编码,编码的因素和水平见表 1。
| 因素 | 水平 | ||||
| -2 | -1 | 0 | 1 | 2 | |
| 反馈通道直径/mm | 12 | 13 | 14 | 15 | 16 |
| 附壁夹角/(°) | 22.5 | 25.0 | 26.0 | 27.5 | 30.0 |
| 出口直径/mm | 14 | 15 | 16 | 17 | 18 |
根据CCD设计原理,设计了三因素五水平响应面分析试验。其中,在17组试验中,零点试验重复3次,用以估计试验误差[16]。表 2是响应面法设计表和数值模拟得到的脉动幅值结果。
| 试验次数 | 反馈通道直径水平 | 附壁夹角水平 | 出口直径水平 | 脉动幅值/MPa |
| 1 | -1 | -1 | -1 | 0.226 244 |
| 2 | 0 | 0 | 2 | 0.179 134 |
| 3 | 1 | 1 | -1 | 0.257 258 |
| 4 | 0 | 2 | 0 | 0.234 269 |
| 5 | 1 | -1 | -1 | 0.256 491 |
| 6 | 0 | 0 | 0 | 0.228 322 |
| 7 | -1 | 1 | -1 | 0.250 990 |
| 8 | -2 | 0 | 0 | 0.204 608 |
| 9 | 0 | 0 | -2 | 0.279 482 |
| 10 | 1 | 1 | 1 | 0.214 763 |
| 11 | -1 | -1 | 1 | 0.150 220 |
| 12 | 1 | -1 | 1 | 0.167 202 |
| 13 | 0 | -2 | 0 | 0.168 675 |
| 14 | -1 | 1 | 1 | 0.171 670 |
| 15 | 0 | 0 | 0 | 0.228 322 |
| 16 | 0 | 0 | 0 | 0.228 322 |
| 17 | 2 | 0 | 0 | 0.243 612 |
3 结果与讨论 3.1 回归方程分析
对表 2中的所有数据进行回归拟合,最终得到以脉动幅值为响应值的回归方程。基于水平因子的拟合回归方程为:
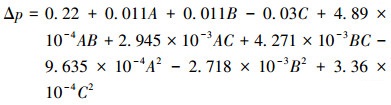
|
(4) |
式中:A代表反馈通道直径,B代表附壁夹角,C代表出口直径。
基于实际值的拟合回归方程为:
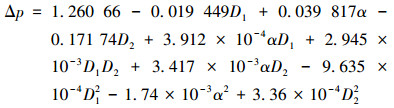
|
(5) |
式中:D1为反馈通道直径,mm;α为附壁夹角,(°);D2为出口直径,mm。
对拟合的回归方程的方差进行分析,结果如表 3所示。其中,P为权重指标,当P值小于0.05时,认为该项是显著项;当P值小于0.01时,认为该项是极显著项。
| 类型 | 平方和 | 自由度 | 均方 | F值 | P |
| 模型 | 0.021 | 9 | 2.317e-3 | 9.11 | 0.004 1 |
| A | 1.885e-3 | 1 | 1.885e-3 | 7.41 | 0.029 7 |
| B | 3.043e-3 | 1 | 3.043e-3 | 11.96 | 0.010 6 |
| C | 0.014 | 1 | 0.014 | 55.72 | 0.000 1 |
| AB | 1.951e-6 | 1 | 1.951e-6 | 7.67e-3 | 0.937 2 |
| AC | 6.938e-5 | 1 | 6.938e-5 | 0.27 | 0.617 7 |
| BC | 1.489e-4 | 1 | 1.489e-4 | 0.58 | 0.469 4 |
| A2 | 1.783e-5 | 1 | 1.783e-5 | 0.07 | 0.798 9 |
| B2 | 7.327e-4 | 1 | 7.327e-6 | 2.88 | 0.133 6 |
| C2 | 1.782e-6 | 1 | 2.168e-6 | 8.52e-3 | 0.929 1 |
| 残差 | 1.782e-3 | 7 | 2.545e-4 |
从表 3可以看出:反馈通道直径和附壁夹角的P值都小于0.05,这两个因素为显著项;出口直径P值为0.000 1,这个因素为极显著项;而其他二次项和平方项的P值都大于0.05,为不显著项。之后会通过等高线图对各个参数的交互作用进行更加直观的分析。从结果上看,3个因素对脉动幅值的影响由大到小排列为:出口直径>附壁夹角>反馈通道直径。
从表 3可以看出,模型的整体P值为0.004 1,小于0.01,可以认为是极显著模型,说明该响应面近似模型的拟合精度较高。
采用回归方程误差统计分析方法,在Design Expert软件中对拟合方程相关误差进行分析。最终,模型拟合系数R2=0.921 3,说明模型中有92.13%的数据与实际模拟结果拟合程度良好,可以用来较为准确地预测脉动幅值的大小。本次模拟试验的CV值为7.35%,当CV < 10%时说明模拟结果的精确度和可信度较高。有效信号与噪声的比值为精密度,当精密度大于4视为模型合理,本文结果的精密度为10.107。
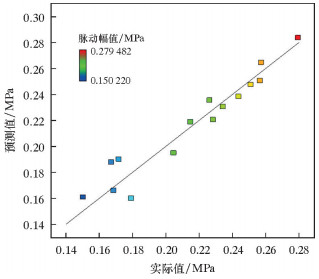
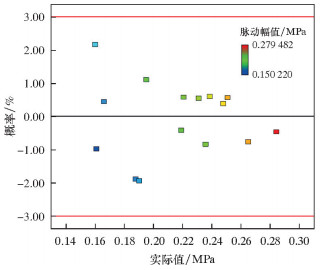
图 5、图 6和图 7分别为残差的正态概率分布图、预测值与实际值分布图以及残差与预测值分布图。当模型的适应性较好时,图 5中概率和残差应该在一条直线上,图 6中模型的预测值和实际值应该尽量在一条直线上,图 7中模型的概率和预测值分布应该随机没有规律。综合以上判断条件,分析图 5~图 7可以发现,本文利用CCD响应面法得到的喷嘴脉动幅值模型适应性较好,拟合得到的回归方程符合标准,符合以上各项检验原则。

|
| 图 5 残差的正态概率分布图 Fig.5 Normal probability distribution of residuals |
|
| 图 6 预测值与实际值分布图 Fig.6 Distribution of predicted and actual values |
|
| 图 7 概率与预测值分布图 Fig.7 Distribution of probability and predicted value |
3.2 各影响因素分析
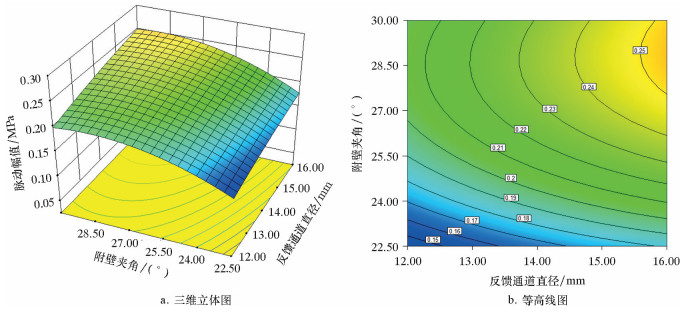
图 8~图 10是在某一个因素取0水平时,其余两个因素交互作用下对压力脉动幅值的影响图。
|
| 图 8 附壁夹角和反馈通道直径对脉动幅值的交互影响 Fig.8 The interactive effect of wall angle and feedback channel diameter on fluctuation amplitude |
|
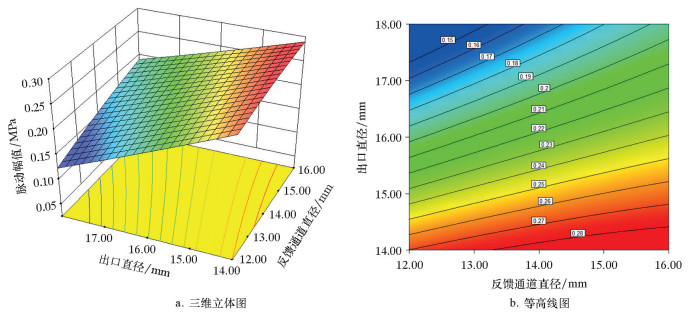
| 图 9 出口直径和反馈通道直径对脉动幅值的交互影响 Fig.9 The interactive effect of outlet diameter and feedback channel diameter on fluctuation amplitude |
|
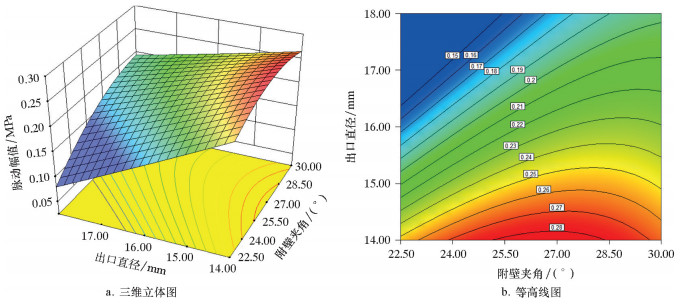
| 图 10 出口直径和附壁夹角对脉动幅值的交互影响 Fig.10 The interactive effect of outlet diameter and wall angle on fluctuation amplitude |
从图 8三维立体图可以看出,出口直径不变时,附壁夹角和反馈通道直径的交互作用不显著。这是由于附壁夹角主要影响主流摆动周期的长短,对脉动幅值影响不够明显。从等高线中可以看出,在图 8各个因素的取值范围内,增大附壁夹角和增大反馈通道直径都能获得较大的脉动幅值,其中当反馈通道直径取15.5~16.0 mm,附壁夹角取27°~30°时,有着较大的脉动幅值。
从图 9三维立体图可以看出,附壁夹角不变时,出口直径和反馈通道直径的三维立体图类似平面形状,这两个因素之间的交互作用不够显著。脉动幅值沿着出口直径方向梯度变化明显,反馈通道直径对脉动幅值的影响可忽略不计,说明出口直径对脉动幅值的影响占主要地位。从等高线中可以看出,在图 9各个因素的取值范围内,减小出口直径和增大反馈通道直径都能获得较大的脉动幅值,其中当反馈通道直径取14~16 mm,出口直径取14.0~14.5 mm时,有着较大的脉动幅值。
从图 10三维立体图可以看出,附壁夹角不变时,出口直径和反馈通道直径之间有着一定的交互作用。脉动幅值沿着出口直径方向梯度变化明显,说明出口直径对脉动幅值的影响占主要地位。这是由于出口直径与反馈通道直径的比值反应了反馈回流与主体流量的比值。这会较为明显地影响流动压降,进而影响脉动幅值。而出口直径的改变对主流流速也能产生大幅影响,因此出口直径对脉动幅值的影响占主要地位。从等高线中可以看出,在图 10各个因素的取值范围内,减小出口直径能获得较大的脉动幅值,其中出口直径取14.0~14.5 mm,附壁夹角取25.5°~28.5°时,有着较大的脉动幅值。
3.3 优化结构验证通过对三维立体响应曲面图和等高线图的分析,可以直观地得到模型最佳结构尺寸的范围,并能看出模型存在极值点。通常,可以对拟合出来的三元二次回归方程的三个影响因素单独求导,联立求导方程,求解出最优解。本文直接使用Design Expert软件自带的Numerical功能,设定3个因素的取值范围后,以脉动幅值的最大值为目标函数,最终优化得到了附壁脉冲射流喷嘴的最优结构尺寸:反馈通道直径16 mm,附壁夹角27°,出口直径14 mm。该条件下得到脉动幅值的预测值为0.291 MPa。
为了检验响应面法的可靠性,需要对优化所得到的理论最优结构进行验证。对最优结构尺寸的附壁脉冲射流喷嘴进行建模和数值模拟,最终得到振荡频率为11 Hz,实际脉动幅值为0.308 MPa,结构优化后的喷嘴流场脉动幅值明显提高。同时,该实际脉动幅值与采用CCD响应面法得到的预测值0.291 MPa相差不大,认为CCD响应面法所得的结果可靠、模型有效,可为今后的设计提供指导。
4 结论(1) 运用CCD响应面法设计并分析附壁脉冲射流喷嘴结构参数对脉动幅值的影响,最终回归方程中有92.13%数据与实际模拟结果拟合程度良好,可较为准确地预测脉动幅值的大小。
(2) 以脉动幅值为响应值,得到反馈通道直径、附壁夹角和出口直径这3个因素对响应值的影响程度,依次为出口直径>附壁夹角>反馈通道直径。
(3) 基于响应面法得到的15 m/s入口速度、30 MPa围压下附壁脉冲射流喷嘴的优化结构尺寸为:反馈通道直径16 mm,附壁夹角27°,出口直径14 mm。采用优化结构得到的脉动幅值为0.308 MPa,显著提高了脉动幅值,且该模拟结构和优化预测值非常接近。
| [1] |
白亚磊, 明晓. 附壁射流元件的仿真研究[J]. 南京航空航天大学学报, 2008, 40(1): 32-36. BAI Y L, MING X. Numerical simulation of wall-attached jet device[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2008, 40(1): 32-36. |
| [2] |
邹久朋, 刘学武, 程蛟, 等. 射流附壁振荡器能效分析与提升[J]. 大连理工大学学报, 2017, 57(3): 233-240. ZOU J P, LIU X W, CHENG J, et al. Analysis and improvement of energy efficiency of jet wall-attached oscillator[J]. Journal of Dalian University of Technology, 2017, 57(3): 233-240. |
| [3] |
王莹, 黄学章, 张承丽. 小流量射流流量计的数值模拟与设计[J]. 仪表技术与传感器, 2017(6): 29-31. WANG Y, HUANG X Z, ZHANG C L. Numerical simulation and design of fluidic flowmeter for small flow[J]. Instrument Technique and Sensor, 2017. |
| [4] |
XU C, MENG X. Performance characteristic curve insensitive to feedback fluidic oscillator configurations[J]. Sensors & Actuators A-Physical, 2013, 189(2): 55-60. |
| [5] |
LI Y, SOMEYA S, KOSO T, et al. Characterization of periodic flow structure in a small-scale feedback fluidic oscillator under low-Reynolds-number water flow[J]. Flow Measurement & Instrumentation, 2013, 33(33): 179-187. |
| [6] |
MENG X, XU C, YU H. Feedback fluidic flowmeters with curved attachment walls[J]. Flow Measurement & Instrumentation, 2013, 30(6): 154-159. |
| [7] |
XIE T, XU C. Numerical and experimental investigations of chaotic mixing behavior in an oscillating feedback micromixer[J]. Chemical Engineering Science, 2017(171): 303-317. |
| [8] |
杨晓丽, 赵弘, 王维斌, 等. 基于响应面法的油气管道磁化特征研究与退磁[J]. 石油机械, 2019, 47(3): 111-117. YANG X L, ZHAO H, WANG W B, et al. Magnetization characteristics of oil and gas pipeline and demagnetization[J]. China Petroleum Machinery, 2019, 47(3): 111-117. |
| [9] |
吴鹏, 师涛, 赵世刚, 等. 基于ANSYS和响应面法的排管机立柱优化设计[J]. 石油机械, 2019, 47(2): 40-48. WU P, SHI T, ZHAO S G, et al. Optimal design of pipe racking column with ansys and response surface method[J]. China Petroleum Machinery, 2019, 47(2): 40-48. |
| [10] |
赵弘, 张岩, 张毅然. 岩心3D打印装置的喷嘴优化设计[J]. 石油机械, 2017, 45(7): 11-15. ZHAO H, ZHANG Y, ZHANG Y R. Optimal design of nozzle for 3D core printing device[J]. China Petroleum Machinery, 2017, 45(7): 11-15. |
| [11] |
柳鹤.射流式水力振荡器理论分析与试验研究[D].长春: 吉林大学, 2014. LIU H. Theoretical analysis and experimental research on liquid jet oscillation tool[D]. Changchun: Jilin University, 2014. |
| [12] |
高传昌, 胡一伟, 李欢, 等. 结构参数对自激脉冲射流特性影响的统计分析[J]. 排灌机械工程学报, 2018, 36(4): 327-333. GAO C C, HU Y W, LI H, et al. Statistical analysis of effects of structural parameters on characteristics of underwater self-excited pulse jet[J]. Journal of Drainage and Irrigation Machinery Engineering, 2018, 36(4): 327-333. |
| [13] |
王同, 丛培武, 李勇, 等. 响应面法在气淬风道结构优化中的应用[J]. 金属热处理, 2018, 43(5): 203-206. WANG T, CONG P W, LI Y, et al. Application of response surface methodology in structural optimization of gas quenching[J]. Metal Heat Treatment, 2018, 43(5): 203-206. |
| [14] |
龙江启, 张轶波, 周建锡, 等. 基于响应面法的全地形车排气系统结构优化研究[J]. 内燃机工程, 2018, 39(4): 9-14. LONG J Q, ZHANG Y B, ZHOU J X, et al. The research on structural optimization of ATV exhaust system based on response surface method[J]. Chinese Internal Combustion Engine Engineering, 2018, 39(4): 9-14. |
| [15] |
张永学, 于丹丹, 胡承云, 等. 基于响应面法的油田蓄热式加热炉燃烧器优化设计[J]. 中国石油大学学报(自然科学版), 2017, 41(2): 156-162. ZHANG Y X, YU D D, HU C Y, et al. Optimization design of oilfield regenerative heating furnace burner based on response surface method[J]. Journal of China University of Petroleum (Natural Science Edition), 2017, 41(2): 156-162. |
| [16] |
OBENG D P, MORREL S, NAPIER-MUNT T J. Application of central composter rotatable design to modeling the effect of some operating variables on the performance of the three-product cyclone[J]. International Journal of Mineral Processing, 2005, 76(3): 181-192. |



