2. 中国石油化工股份有限公司石油工程技术研究院;
3. 页岩油气富集机理与有效开发国家重点实验室;
4. 中国石化河南油田分公司采油二厂
2. Sinopec Research Institute of Petroleum Engineering;
3. State Key Laboratory of Shale Oil and Gas Enrichment Mechanisms and Effective Development;
4. No. 2 Oil Production Plant, Sinopec Henan Oilfield Company
0 引言
重复压裂技术[1-3]是油田开发后期增产稳产、有效开发难采储量的重要措施,以重张旧缝为原则进行的重复压裂,只能使裂缝沿着老裂缝延伸,这在老裂缝采出程度较高情况下,达不到理想的增产效果。常规压裂优先沟通高渗透层,而对增产改造极其重要的低渗透层却很难产生作用。针对这种现状,转向压裂技术应运而生,通过向流体中加入转向剂,暂时封堵这些高渗透通道,迫使流体流向低渗透层,从而实现转向压裂。
蒋廷学等[4]研究了单个暂堵球在垂直井筒中的受力,提出了一种新的前置投球选择性分压方法,该方法在现场应用中效果较好。李昊[5]通过研发可视化多层射孔投球分压试验装置,在实验室模拟了封堵球对炮眼的封堵效率,但是试验只研究了垂直套管中上、中、下3个孔眼的封堵状态;他还将数值模拟分析的结果与试验结果对比,验证了数值模拟的可靠性。C.CARPENTER[6]研究了适用于水平井重复压裂的暂堵剂特性,现场应用中地层的改造压力提升近27.6 MPa。国外压裂服务商Drill2frac[7-8]和Thru Tubing Solutions公司的SlicFrac技术[9]通过优化完井压裂方案,分析地层的非均匀性,准确指导在何处、何时加入转向剂,使转向压裂的效果大大提高。
虽然国内在转向压裂技术方面取得很多研究成果,但大多集中在暂堵剂制备及其性能的提升,应用方面始终与国外技术存在一定差距,主要的因素就是对暂堵球的施工工艺及具体的参数匹配没有很好的理论支撑,有关封堵射孔孔眼的暂堵球在水平井中的运移和封堵状态的研究报导较少。鉴于此,本文结合页岩气的压裂施工工况,采用数值模拟的方法,利用统计学规律,在考虑暂堵球密度、液体黏度及泵送排量等参数条件下,得到暂堵球在水平段内的运移轨迹,以及对不同位置孔眼的封堵效率。研究结论可为优化暂堵球转向压裂施工参数提供参考。
1 球体受力分析暂堵球在水平井筒中的运动状态分为如下4种:①在垂直井段运移;②在水平井段内非射孔段运移;③在水平井段内射孔段运移;④在水平井射孔段封堵孔眼。由于射孔孔眼在水平段内,所以在垂直井段中的运移状态本文暂不予讨论。图 1为暂堵球在水平井井筒中不同位置运动状态下的受力分析,其中,暂堵球所受的重力Fg可表示为:
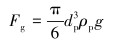
|
(1) |
|
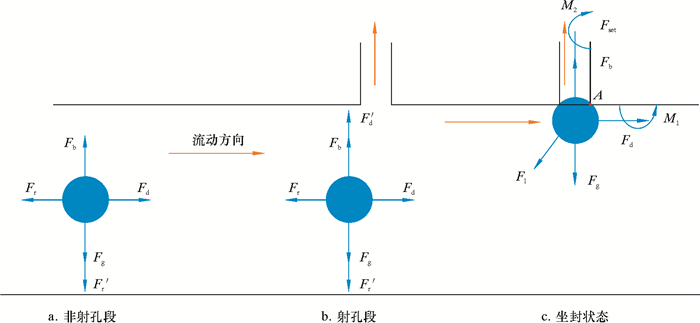
| 图 1 暂堵球在水平井井筒中运移的受力分析 Fig.1 Analysis on the force of temporary plugging ball during its migration in the horizontal casing |
式中:dp为暂堵球直径,ρp为暂堵球密度,g为重力加速度。
暂堵球所受的浮力为:
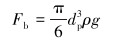
|
(2) |
式中:ρ为流体密度。
暂堵球在流体的携带下运动,所受的携带力[10-11]计算式为:
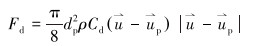
|
(3) |
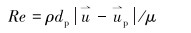
|
(4) |
式中: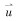
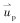
暂堵球在套管中随流体水平运移时(见图 1a),垂直方向上受到重力和浮力的作用,当暂堵球密度与流体密度不同时,暂堵球在垂直方向上还受到黏滞阻力Fr′的作用,水平方向上受到流体的携带力和黏滞阻力Fr。当暂堵球运移到射孔孔眼周围时(见图 1b),由于部分液体从射孔孔眼中流出,会在垂直方向上对暂堵球产生携带力Fd′。当暂堵球坐封在射孔孔眼上时(见图 1c),垂直方向上除受到重力和浮力外,套管内和地层之间的压力差也作用在暂堵球上,形成的坐封力使暂堵球密封孔眼,其中坐封力为:
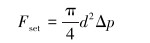
|
(5) |
式中:d为射孔孔眼直径,Δp为套管内与被封堵的孔眼外的压力差。
暂堵球在水平方向上仍然受到流体的携带力,只是此时暂堵球坐封在孔眼上且无速度,即式(3)中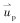
根据页岩气水平井压裂工况,选取公称直径139.7 mm(5½ in)套管为完井尾管,其三维模型如图 2所示。套管长5 m,内径115.0 mm,取射孔段长度1 m,射孔孔眼位于管道中间段,采用螺旋布孔,孔密20孔/m,孔径9.5 mm,相位角60°。左端为速度入口,20个射孔孔眼为压力出口(假定出口压力一致),底部封堵。

|
| 图 2 计算模型 Fig.2 Calculation model |
入口端的网格模型如图 3所示。模型全部为六面体网格,网格数量4 402 332,投球点均匀分布在入口处,共25个投球点。为了便于统计暂堵球封堵规律,将射孔孔眼分为上、中、下3部分,具体分布见图 3。
|
| 图 3 入口处网格及投球分布状态 Fig.3 Inlet grid and ball distribution |
该计算模型采用双精度求解器,标准k-ε湍流模型,增强壁面函数,SIMPLE算法,二阶迎风格式[12]。对于颗粒追踪采用DPM模型,激活流体与颗粒耦合模型,投入的暂堵球直径为15.0 mm,且其初始速度与流体入口速度一致。为了较好地追踪湍流流动下暂堵球的运移特性,激活离散随机游动模型[13],投入的颗粒可以从各个射孔孔眼流出。
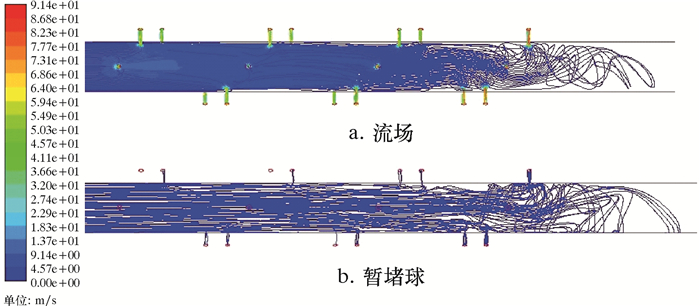
2.2 暂堵球运移轨迹为了观察流体的流动状态及其对暂堵球运移的影响,图 4列出了流体排量6 m3/min、密度1 100 kg/m3、黏度72 mPa·s时,流体和暂堵球在套管中的流动迹线。
|
| 图 4 流体及暂堵球运移状态 Fig.4 Migration process of fluid and temporary plugging ball |
在图 4a中流体未达到射孔区域时,其流线基本沿水平方向;在射孔区域范围内,流体向各个孔眼区域流动;当流体流过射孔孔眼段时,会对孔眼段后部的液体产生一定的扰动,从迹线的走向来看,大部分液体又重新流入到射孔段尾部的孔眼中。图 4b显示了暂堵球随流体的运移状态,在暂堵球经过射孔段时,靠近孔眼的暂堵球在孔眼流体携带力的作用下从孔眼流出,在射孔段尾部能明显观察到颗粒的轨迹与流体流线吻合,大量颗粒被回流的流体带回到尾部的孔眼中,使射孔段尾端的封堵效率大大提高,其余部分颗粒沉降到孔眼后的套管下部,无法封堵射孔段。
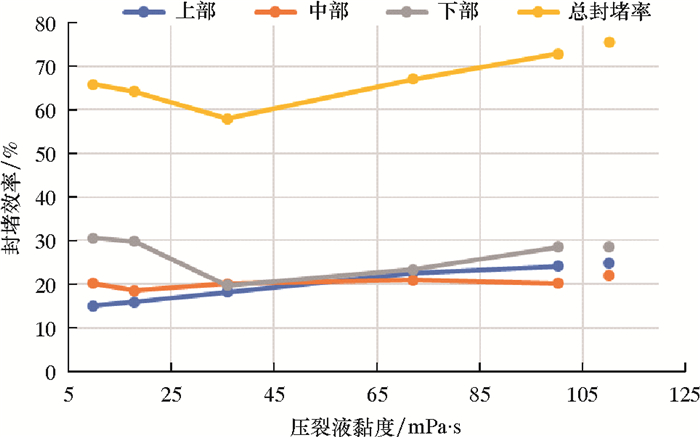
2.3 运移规律为了得到较好的暂堵球泵送工况,对暂堵球泵送过程中关键参数的影响进行了模拟。图 5为排量6 m3/min、暂堵球密度1 100 kg/m3时,在不同流体黏度下暂堵球对套管各部位的封堵效率。在此工况下,暂堵球的重力大于浮力,在水平段内运移过程中,球体会逐渐下沉,而流体的黏滞阻力将减小其下沉速度,套管下部的封堵效率将会提高。由图 5可知,当流体黏度为10和18 mPa·s时,暂堵球对下部孔眼的封堵效率为30%左右。当流体的黏度逐渐增大时,暂堵球在套管截面的分布将逐渐趋于均匀,套管下部孔眼的封堵规律会逐渐与其他部位的孔眼一致。由于暂堵球的重力大于浮力,球体在水平段内还会有一定的下沉,暂堵球进入下部孔眼所需的携带力小于进入其他孔眼,所以下部孔眼的封堵效率会高于其他部位。对于中部孔眼的封堵效率,在流体模拟参数范围内其变化较小,说明在此计算区域内,暂堵球的沉降对其影响不大。而对于上部孔眼的封堵效率,随着流体黏度的增大而逐渐增大,这是因为较大的黏度会对暂堵球产生较大的黏滞阻力和携带力,减小因暂堵球密度过大而引起的上部孔眼封堵效率降低的问题。
|
| 图 5 排量6 m3/min、暂堵球密度1 100 kg/m3时各区封堵效率随流体黏度的变化 Fig.5 Variation of the plugging efficiency with the fluid viscosity in different zones at the flow rate of 6 m3/min and the ball density of 1 100 kg/m3 |
由于压裂液属于非牛顿流体,计算中还对比了非牛顿流体特性对暂堵球封堵效率的影响。油田现场压裂液常用幂律性流体来模拟其非牛顿特性,其黏度计算式为:
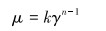
|
(6) |
式中:k、n分别为稠度系数和流性指数,根据参考文献[14-15]中关于常用压裂液的流变参数值,取k=3,n=0.6;γ为剪切速率。
为了便于对比,将非牛顿流体的黏度值限定在10~100 mPa·s,其他计算条件不变,结果见图 5中孤立数据点,其封堵效率高于流体黏度100 mPa·s时的封堵效率,说明按照牛顿流体计算的结果具有一定的保守性,此处采用牛顿流体来模拟便于对比压裂液黏度的影响效果。
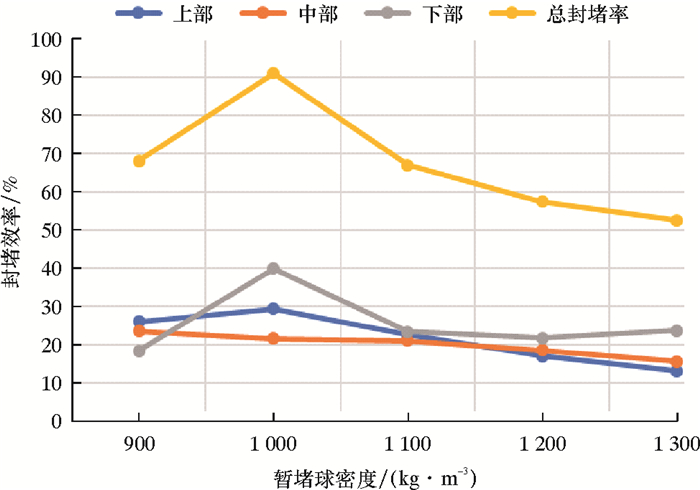
图 6为排量6 m3/min、流体黏度72 mPa·s时,暂堵球密度变化对封堵效率的影响。当暂堵球密度小于流体密度时,暂堵球受到的浮力大于重力,暂堵球在水平段运移过程中会逐渐上浮,因此其上部孔眼的封堵效率最高。而当暂堵球密度大于流体密度时,暂堵球受到的浮力小于重力,暂堵球在水平段运移过程中会逐渐下降。从图 6可以看出,暂堵球对中部和下部孔眼的封堵效率随着其密度的增加而下降,而对下部孔眼的封堵效率有所提高。
|
| 图 6 排量6 m3/min、流体黏度72 mPa·s时各区封堵效率随暂堵球密度的变化 Fig.6 Variation of the plugging efficiency with the ball density in different zones at the flow rate of 6 m3/min and the fluid viscosity of 72 mPa·s |
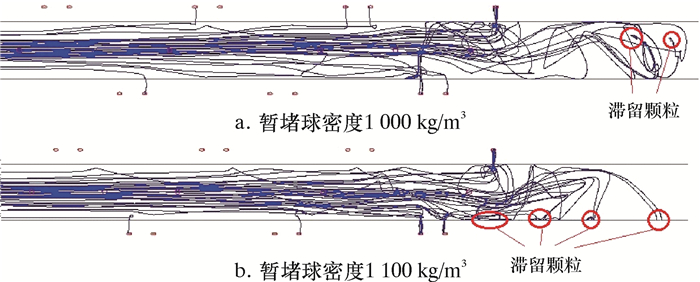
当暂堵球密度与流体密度相同时,暂堵球在运移过程中,垂直方向上的重力和浮力保持平衡,图 6显示了此工况下暂堵球对孔眼的封堵效率达到91%。为了分析此工况下暂堵球封堵效率高的原因,图 7显示了暂堵球密度为1 000与1 100 kg/m3工况下的运移轨迹,当暂堵球经过射孔孔眼时,有明显向孔眼运动的趋势,但密度较大的暂堵球几乎不会在运移过程中封堵上部孔眼,而靠近尾部的孔眼主要是旋流被带入。当暂堵球密度与流体密度相同时,经过射孔段时暂堵球会封堵上部孔眼,而运移到射孔段之后的暂堵球大部分在流体的作用下被重新带到了射孔段尾部,从而使射孔段尾部的封堵效率大大提高。为此,在暂堵球的投放过程中,之所以应控制好投放的速度,是因为处于最尾端的孔眼其封堵效率最高。当尾端的孔眼被封堵后,靠近尾端前面的孔眼就成为新的尾端孔眼,其封堵效率将提高,延长暂堵球的投放间隔,有助于从射孔段尾部逐渐向前封堵。在图 7b中,暂堵球运移到射孔段之后,由于暂堵球密度较大,相当部分的暂堵球无法被流体重新带回到孔眼处,而是留在了套管里面。
|
| 图 7 不同密度下暂堵球颗粒运移轨迹 Fig.7 Migration track of the particles of temporary plugging balls with different densities |
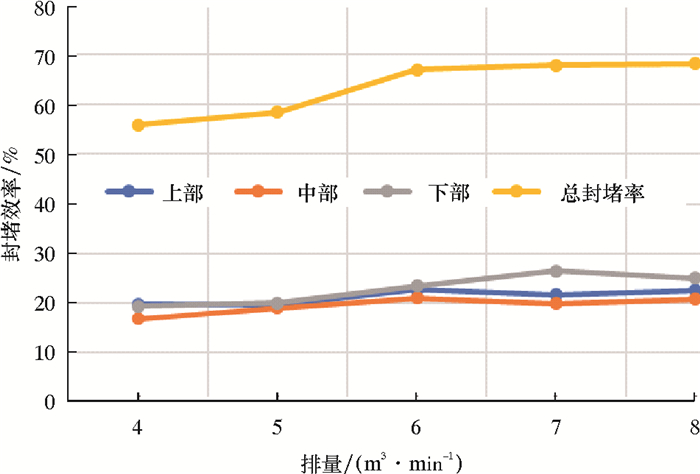
图 8为暂堵球密度1 100 kg/m3、流体黏度72 mPa·s时,不同排量下暂堵球的封堵效率。总的封堵效率随着排量的增加而逐渐增大,因为排量增大后,从射孔簇流出的液体的流速会增大,对经过孔眼的暂堵球的携带作用也会增强,更利于暂堵球向孔眼运动,从而提高导流性能好的孔眼的封堵效率。但是当排量大于6 m3/min时,封堵效率随排量变化上升趋势不明显。
|
| 图 8 暂堵球密度1 100 kg/m3、流体黏度72 mPa·s时各区封堵效率随排量的变化 Fig.8 Variation of the plugging efficiency with the flow rate in different zones at the ball density of 1 100 kg/m3 and the fluid viscosity of 72 mPa·s |
3 结论及建议
(1) 在对水平段射孔孔眼的封堵过程中,暂堵球密度变化对其运移规律影响最为明显,当暂堵球密度与流体密度相同时,其封堵效率达到90%,因此,暂堵球制备及应用时应尽量使其密度接近泵送流体的密度。
(2) 由于运移到射孔段尾部的暂堵球在旋流的作用下被重新带到了射孔段尾部,从而使射孔段尾部的封堵效率大大提高,建议延长暂堵球的投放时间间隔,这将有助于暂堵球从射孔段尾部逐渐向前封堵。
(3) 随着流体黏度的增大,暂堵球对孔眼的封堵效率先降低后增加,原因是黏度对暂堵球沉降过程有较大影响,建议将泵送液体的黏度控制在施工要求范围内尽量高;增大排量有利于提高暂堵球的封堵效率,但当泵送排量高于6 m3/min时,封堵效率提升不明显,因此在实际施工过程中,无需追求高排量泵送。
| [1] |
王彦玲, 原琳, 任金恒. 转向压裂暂堵剂的研究及应用进展[J]. 科学技术与工程, 2017, 17(32): 196-204. WANG Y L, YUAN L, REN J H. The progress in research and application of temporary plugging agent for diverting fracturing[J]. Science Technology and Engineering, 2017, 17(32): 196-204. |
| [2] |
杨国丰, 周庆凡, 李颖. 美国页岩油气井重复压裂提高采收率技术进展及启示[J]. 石油科技论坛, 2016, 35(2): 46-51, 65. YANG G F, ZHOU Q F, LI Y. Technological progress in re-fracturing of US shale oil and gas wells for higher production factor[J]. Oil Forum, 2016, 35(2): 46-51, 65. |
| [3] |
RASSENFOSS S. Getting more from fracturing with diversion[J]. Journal of Petroleum Technology, 2017, 69(6): 42-47. |
| [4] |
蒋廷学, 胥云, 李治平, 等. 新型前置投球选择性分压方法及其应用[J]. 天然气工业, 2009, 29(9): 88-90. JIANG T X, XU Y, LI Z P, et al. A new method of selective separate layer fracturing by delivering seal balls in pad stage and its application[J]. Natural Gas Industry, 2009, 29(9): 88-90. |
| [5] |
李昊.可降解球井筒中运移规律及炮眼内封堵工艺研究[D].北京: 中国石油大学(北京), 2017. LI H. Study on the degradable ball sealer movement rule in the wellbore and plugging process in the perforation[D]. Beijing: China University of Petroleum (Beijing), 2017. http://cdmd.cnki.com.cn/Article/CDMD-11414-1019808150.htm |
| [6] |
CARPENTER C. Use of biodegradable materials during refracturing of a horizontal well[J]. Journal of Petroleum Technology, 2015, 67(5): 137-139. |
| [7] |
WUTHERICH K, SRINIVASAN S, RAMSEY L, et al. Engineered diversion: using well heterogeneity as an advantage to designing stage specific diverter strategies[C]//SPE Canada Unconventional Resources Conference. Alberta: Society of Petroleum Engineers, 2018.
|
| [8] |
HARPEL J, RAMSEY L, WUTHERICH K. Improving the effectiveness of diverters in hydraulic fracturing of the wolfcamp shale[C]//SPE Annual Technical Conference and Exhibition. Dallas: Society of Petroleum Engineers, 2018.
|
| [9] |
SENTERS C W, JOHNSON M D, LEONARD R S, et al. Diversion optimization in new well completions[C]//SPE Hydraulic Fracturing Technology Conference and Exhibition. The Woodlands: Society of Petroleum Engineers, 2018.
|
| [10] |
GOSMAN A D, LOANNIDES E. Aspects of computer simulation of liquid-fueled combustors[J]. Journal of energy, 1983, 7(6): 482-490. |
| [11] |
AN ON. ANSYS fluent user's guide[M]. Canonburg: ANSYS Inc., 2017.
|
| [12] |
李鹏飞, 徐敏义, 王飞飞. 精通CFD工程仿真与案例实战[M]. 2版. 北京: 人民邮电出版社, 2017. LI P F, XU M Y, WANG F F. Proficient in CFD engineering simulation and case study[M]. 2nd ed. Beijing: Post & Telecom Press, 2017. |
| [13] |
GORENFLO R, MAINARDI F, MORETTI D, et al. Time fractional diffusion:a discrete random walk approach[J]. Nonlinear Dynamics, 2002, 29(1/2/3/4): 129-143. |
| [14] |
MONTGOMERY C.Fracturing fluids[C]//ISRM International Conference for Effective and Sustainable Hydraulic Fracturing. Brisbane: International Society for Rock Mechanics and Rock Engineering, 2013.
|
| [15] |
ESKIN D, MILLER M J. A model of non-Newtonian slurry flow in a fracture[J]. Powder Technology, 2007, 182(2): 313-322. |



