2. 西南油气田重庆气矿
2. Chongqing Gas Mine, PetroChina Southwest Oil and Gas Field Company
0 引言
伴随“一带一路”和“油气管网”等政策的逐步实施,作为能源输送主要方式的管道将迎来蓬勃发展期。由于路由限制的影响,双管或者多管并行敷设方式不可避免。然而,管道不可避免地会受到腐蚀、第三方破坏[1-3]及自然灾害[4-6]等导致的多种损伤,容易引发泄漏,从而导致气云爆炸,与之相邻的并行管道极有可能受到威胁从而造成冲击破坏,引发二次事故。因此,开展爆炸载荷作用下埋地并行输气管道的动力响应研究就显得尤为重要。
当前,国外对爆炸载荷作用于并行邻管的研究相对较少,多以弹坑模型[7-8]界定并行管道的安全间距。国内则开展了大量研究,笔者所在团队[9-12]前期针对并行管道泄漏及物理爆炸对邻管的冲击破坏开展了一系列研究。此外,部分国内学者[13-18]也开展了相关的研究工作。以上研究对于模型精度的验证大都基于经验描述,缺乏基于试验的精确验证,即使部分涉及试验验证,数值模拟的精度也有待进一步提高,其次在ALE数值分析中不能很好地描述土体变形与管道瞬态响应的内在联系。
为此,笔者首先基于土中爆炸试验提高ALE算法的精度;其次选用TNT当量模型估算气云爆炸能量,建立了管土-炸药耦合三维模型,分析了泄漏量和管间距对管道动力响应规律的影响;最后基于应力和应变失效准则评估了管道的安全状况。所得结论可为并行输气管道的安全评估提供参考。
1 小孔泄漏模型与TNT当量法 1.1 小孔泄漏模型天然气管道的泄漏通常为小孔泄漏。图 1中管输流量为Q1,1点为管段起始点,距起点L处的点3处发生泄漏,泄漏点与点2垂直于管道轴线。假设理想气体在管内做一维稳态绝热流动,且气体在孔口处做等熵流动。
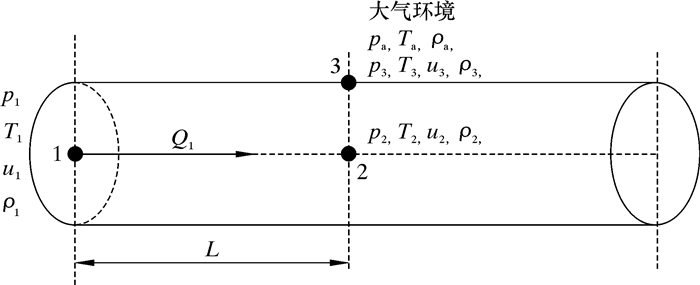
|
| 图 1 天然气泄漏示意图 Fig.1 Schematic diagram of natural gas leakage |
依据理想气体状态方程和欧拉运动微分方程及临界压力比,得到临界流的小孔泄漏模型计算公式,即有:
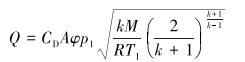
|
(1) |
式中:Q为气体泄漏率,kg/s; CD为泄漏系数,取值范围0.61~1.00,圆形孔口取1.00;A为泄漏孔口面积,m2;φ为流速系数,表示实际流速与理论流速之比,由于实际流速小于理论流速,一般取0.97~0.98;p1为泄漏起点的压力,Pa;k为气体绝热系数,燃气取1.3;M为气体摩尔质量,燃气取0.016 kg/mol;R为摩尔气体常数,取8.314 J/(mol·K);T1为泄漏点温度,K。
1.2 TNT当量法定量计算蒸汽云爆炸能量的方法主要有TNT当量法、数值模拟、球形数值模型及自相似等方法。TNT当量法依据能量相当法则,将气云爆炸产生的威力等效为凝聚相TNT爆炸产生的威力,可直接通过数学转换方式进行转换。TNT当量计算公式为:
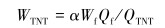
|
(2) |
式中:WTNT为TNT当量,kg;α为蒸汽云爆炸当量系数,取值范围0.01~0.10,燃气通常取0.04;Wf为参与爆炸的蒸汽云质量,kg;Qf为可燃物燃烧值,取54×106 J/kg;QTNT为TNT爆炸热,取4.52×106 J/kg。
2 材料本构与管体失效准则 2.1 材料本构土体选用MAT_SOIL_AND_FOAM模型,本构方程为:
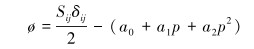
|
(3) |
式中:Sij为Cauchy偏应力张量;δij为Kronecker符号;a0为与土体摩擦角相关的参数,取3.4×109 Pa2;a1为与土体黏聚力相关的参数,取7.033×104 Pa;a2为与土体动载效应相关的参数,取0.3;p为土体剪压力,GPa。
此外,建模中土体密度为1.8 g/cm3,剪切模量为63.8 MPa,体积模量为30 GPa。
埋地管线为西二线常用的X80管线钢,输送压力12 MPa,规格为ø1 219 mm×26.4 mm。本构方程采用随动硬化双线性弹塑模型,该模型遵从Von Mises屈服准则,表达式如下:
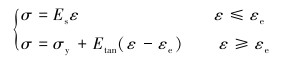
|
(4) |
式中:σ为管材应力,MPa;Es为弹性模量,取210 GPa;Etan为切线模量,取1 500 GPa;σy为屈服应力,取590 MPa;ε、εe分别为应变和弹性极限应变。
建模时管材密度为7 900 kg/m3,泊松比为0.3。
建模时炸药选用MAT_HIGH_EXPLOSIVE_BURN本构模型与JWL状态方程,方程表达式为:
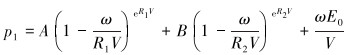
|
(5) |
式中:p1为爆轰压力,MPa;E0为单位体积爆轰产物的内能,取0.06 J/m3;V为爆轰产物的相对体积;A、B、R1、R2和ω为常数,分别取值373.77 GPa、3.747 1 GPa、4.15、0.9和0.35。
建模中炸药密度为1.63 g/cm3,爆速为6 930 m/s,爆压为21 GPa。
2.2 管体失效准则《输气管道工程设计规范》(GB 50251—2015)规定:工作载荷条件下,管道可能出现的最大应力应小于其屈服应力。第四强度理论综合考虑了管道的环向应力、轴向应力和径向应力的作用,表达式为:
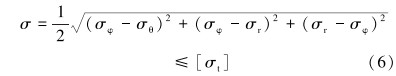
|
(6) |
式中:σφ为管道的环向应力,σr为径向薄膜应力,σθ为轴向薄膜应力,[σt]为管体许用应力,单位均为MPa。
管道变形包含椭圆化(度)变形、拉伸变形和压缩变形。评判管体因变形引发的失效常用椭圆化失效准则,表达式为[19]:
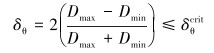
|
(7) |
式中:δθ为椭圆度,无量纲常数;δθcrit为临界椭圆度,通常取3%[20];Dmax为管道外径最大值,mm;Dmin为管道外径最小值,mm。
3 计算模型 3.1 模型精度验证加拿大防务研究所对100 g炸药在土中进行了一系列爆炸试验[21],试验装置及装置简图分别如图 2a和图 2b所示。试验主要包含一个装满土体的铁桶、土中不同埋深下的3个压力传感器以及大气中设置的5个压力传感器(见图 2b黑色方块)。研究仅针对地下部分,因此建立如图 2c所示的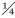
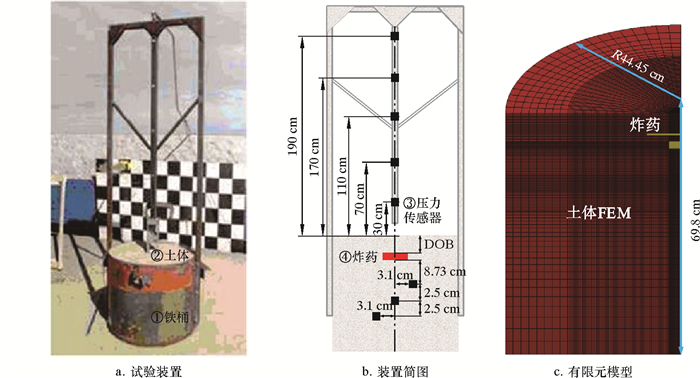
|
| 图 2 试验装置及有限元模型 Fig.2 Test device and finite element model |
图 3为土中3个压力传感器的实测值与模拟结果对比图。
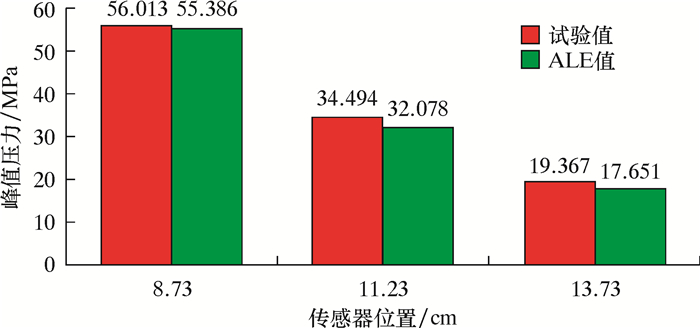
|
| 图 3 试验值与模拟峰值压力对比图 Fig.3 Comparison between test results and simulated peak pressure |
由图 3可知,模拟所得结果与试验值存在一定偏差,但整体接近,偏差分别为1.12%、7.00%和8.86%,处于工程可接受范围,因此该试验定量验证了数值模拟的可行性。
3.2 有限元模型若处于同一高度上的3条输气管道等间距同沟并行敷设,中间管道发生小孔泄漏,高速气流与孔壁间产生摩擦生热,存在爆炸安全隐患。选取TNT当量法作为气云泄漏爆炸的估算模型,利用对称性建立
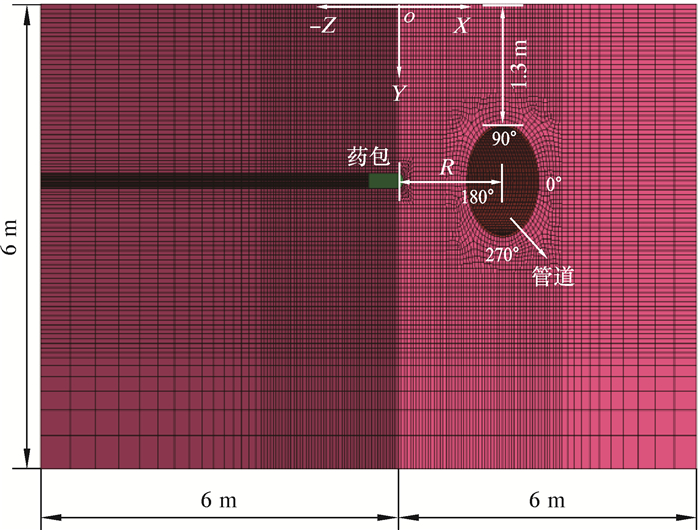
|
图 4
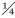 |
|
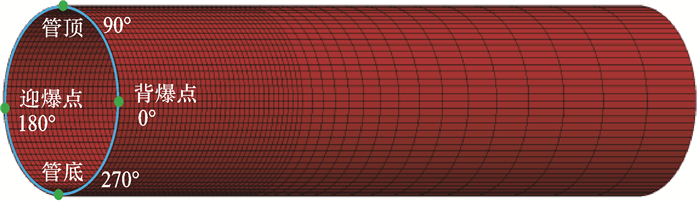
| 图 5 管体有限元模型及网格划分 Fig.5 Finite element model of the pipe body and meshing |
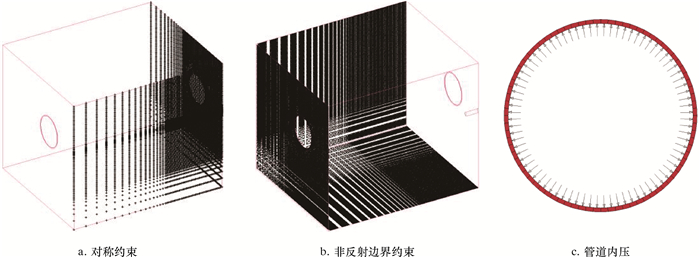
整体有限元模型顶面为自由表面,在XOY及YOZ平面内施加如图 6a所示的对称约束。为了模拟无限域环境,在其余面上施加如图 6b所示的非反射边界条件,管道内壁施加如图 6c所示的内压载荷,载荷大小为12 MPa。
|
| 图 6 边界条件及载荷 Fig.6 Boundary conditions and loads |
4 结果分析 4.1 压力波在土中的传播规律
假定燃气泄漏一定时间后,气云爆炸的等效TNT当量为15 kg,炸药为直径16 cm、高46 cm的
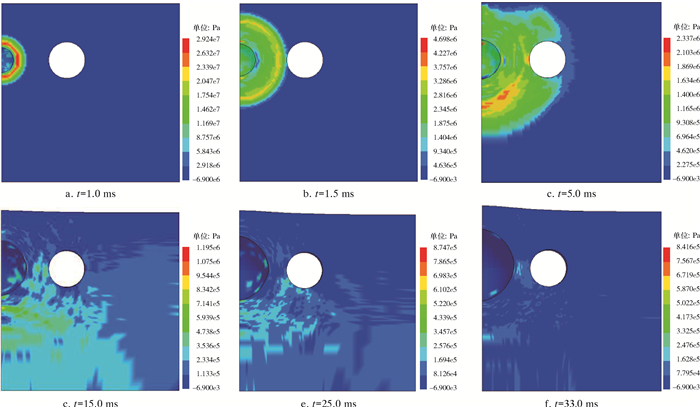
|
| 图 7 压力波在土中的传播规律 Fig.7 Propagation law of pressure wave in soil |
4.2 动力响应分析
考虑到气云泄漏爆炸的复杂性,基于能量相当法则得到不同泄漏时长下装药量G为36、52、68及84 kg,简化药包为半径12 cm,高度为49、70、92和114 cm的
由于爆炸载荷下管道的迎爆面为受力最敏感的部位,这里提取了不同炸药量下管体迎爆点的应力时程曲线(见图 8)。由图 8可知,药包起爆后,4种炸药量下管体迎爆点的应力时程曲线趋势基本一致,均呈现先减小后陡然增大,然后再急剧减小后小幅度增长,最后缓慢减小并逐渐趋于稳定的趋势。
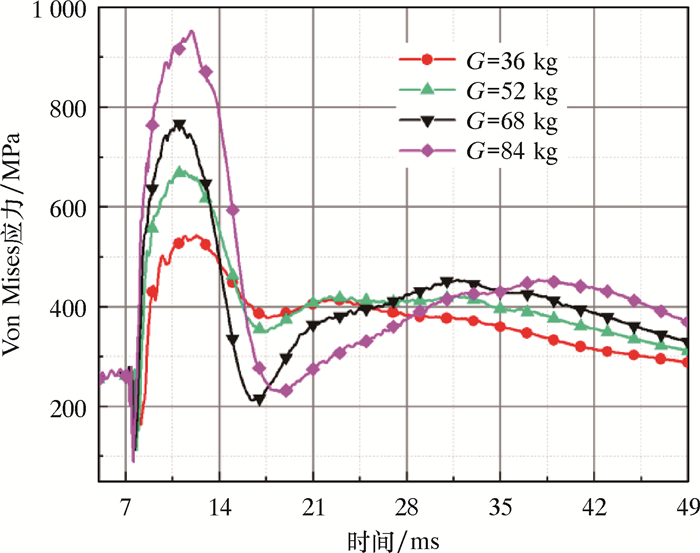
|
| 图 8 迎爆点应力时程曲线 Fig.8 Stress time-history curve of the bursting point |
这是因为管道起始时刻在纯内压的作用下处于应力拉伸状态,4种工况下的初始应力为256.5 MPa,药包起爆后,冲击波率先抵达管道,抵消了部分由于内压产生的拉应力,4种工况下的应力瞬间降至极小值。此后,冲击波得到源源不断的补充,管道受力又开始反向急剧增大,达到极大值后由于冲击波得不到补充,且管道变形部分恢复,应力又开始急剧减小达到第二处极小值,各工况下的应力极值如表 1所示。此刻之后由于爆腔继续扩大,对管道的作用力增大,管道应力又开始缓慢增大,最终随着能量的耗尽与爆腔扩张速率的减慢管道应力又开始减小。
| G=36 kg | G=52 kg | G=68 kg | G=84 kg | |||||||
| 时间/ ms |
应力/ MPa |
时间/ ms |
应力/ MPa |
时间/ ms |
应力/ MPa |
时间/ ms |
应力/ MPa |
|||
| 8.2 | 163.2 | 7.8 | 112.7 | 7.7 | 112.5 | 7.6 | 89.1 | |||
| 11.3 | 540.5 | 11.2 | 671.1 | 11.1 | 765.1 | 11.9 | 952.7 | |||
| 17.6 | 376.8 | 17.4 | 349.1 | 16.5 | 211.4 | 18.6 | 229.4 | |||
将表 1中不同药量下管体迎爆点的最大应力进行函数拟合,拟合曲线近似呈线性关系。拟合公式如下:
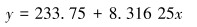
|
(8) |
式中:y为不同药量下管体迎爆点的最大应力,MPa;x为药包的质量,kg。
为了确保管道安全平稳运行,需满足应力校核准则,即管道的最大应力应小于其抗拉强度719 MPa。由公式(8)得到管道的极限抗爆能力(TNT当量)为58.4 kg。
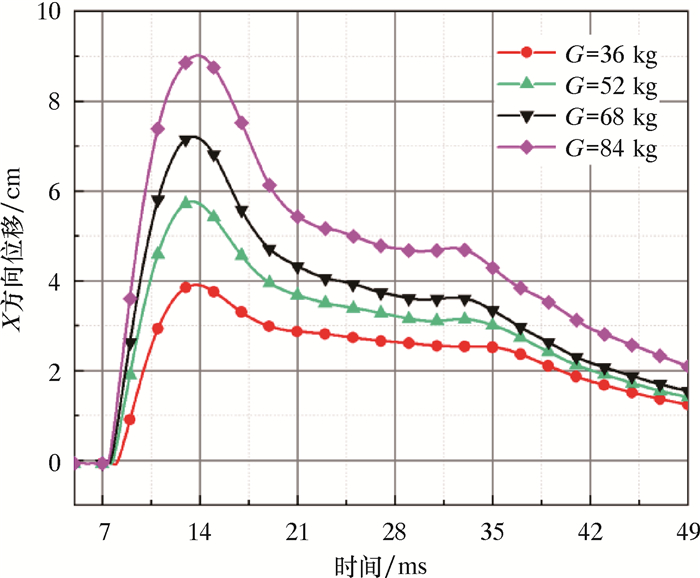
4.2.2 位移响应分析(1) X向位移响应分析。迎爆点X方向位移时程曲线如图 9所示。正对爆心管道截面上迎爆点、背爆点、管顶及管底4个观测点X向位移随时间的推移均呈现先增大后减小的趋势。以图 9为例,测点位移存在一极大值点,该点之前位移随着时间的变化而增大,之后随着时间的变化而减小。不同药量下各测点不同时刻对应的位移极值如表 2所示。由表 2可以看出:药量越大管体位移响应越明显;管底和管顶的位移响应基本一致,而迎爆点、管顶(管底)和背爆点的位移响应依次滞后。
|
| 图 9 迎爆点X方向位移时程曲线 Fig.9 Time-history curve of displacement in X direction at the bursting point |
| 观测点 | G=36 kg | G=52 kg | G=68 kg | G=84 kg | |||||||
| 时间/ ms |
位移/ cm |
时间/ ms |
位移/ cm |
时间/ ms |
位移/ cm |
时间/ ms |
位移/ cm |
||||
| 迎爆点 | 13.7 | 3.9 | 13.6 | 5.8 | 13.7 | 7.2 | 13.8 | 9.1 | |||
| 背爆点 | 25.5 | 3.2 | 24.9 | 4.1 | 24.4 | 4.6 | 24.2 | 5.8 | |||
| 管顶 | 21.4 | 3.0 | 20.7 | 3.9 | 20.3 | 4.6 | 20.1 | 5.6 | |||
| 管底 | 21.4 | 2.9 | 20.3 | 3.8 | 19.7 | 4.5 | 19.4 | 5.5 | |||
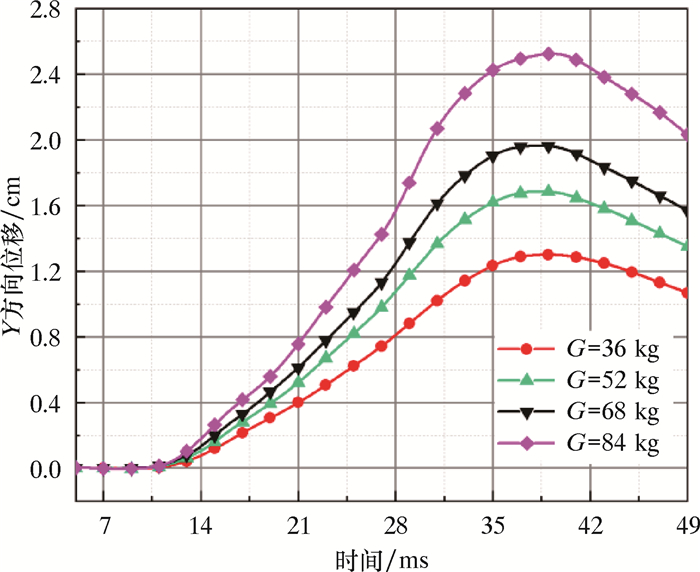
(2) Y向位移响应分析。Y方向的位移时程曲线与测点位置相关,其中迎爆点与背爆点的位移随时间的变化呈现先增大后减小的趋势,仅是响应时刻及响应值存在微小差别。因此,笔者只给出了迎爆点的时程曲线,如图 10所示。
|
| 图 10 迎爆点Y方向位移时程曲线 Fig.10 Time-history curve of displacement in Y direction at the bursting point |
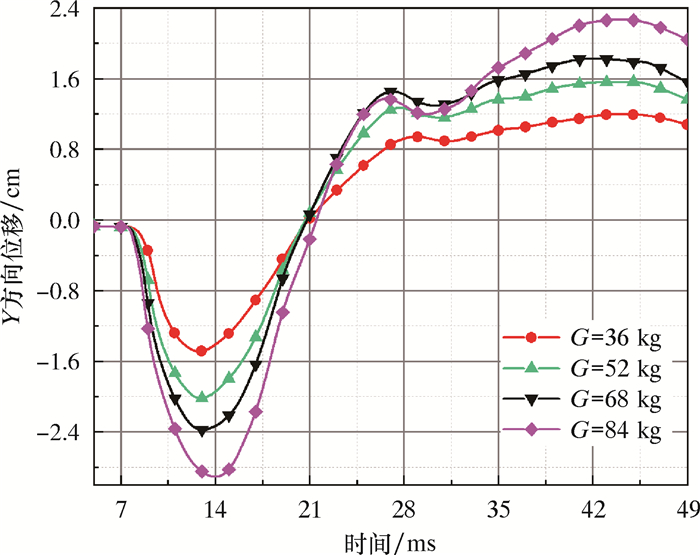
图 11为管底Y方向位移时程曲线。
|
| 图 11 管底Y方向位移时程曲线 Fig.11 Time-history curve of displacement in Y direction at the pipe bottom |
由图 11可知,管底位移呈现由负向位移(先增大后减小)向正向位移(先增大后减小到再增大后减小)过渡的现象。这是因为球形冲击波及爆炸空腔的挤压作用,管道一开始产生负向位移,之后爆腔向上发展速度较其他方向快,爆腔失去球形对称性,迫使管道被抬升,产生向上的位移。图 12为管顶Y方向位移时程曲线。由图 12可以看出,管顶位移呈现先增大后减小的二次脉动现象。这是因为管道首先受到爆炸波的冲击应力急剧增大,之后冲击波得不到持续补充,管道受力开始急剧衰减,爆炸空腔继续扩张,对管道挤压作用增强,管道受力又开始增大,最终随着能量耗散,管道变形部分恢复,因而受力减小。各测点不同时刻Y向位移极值如表 3所示。
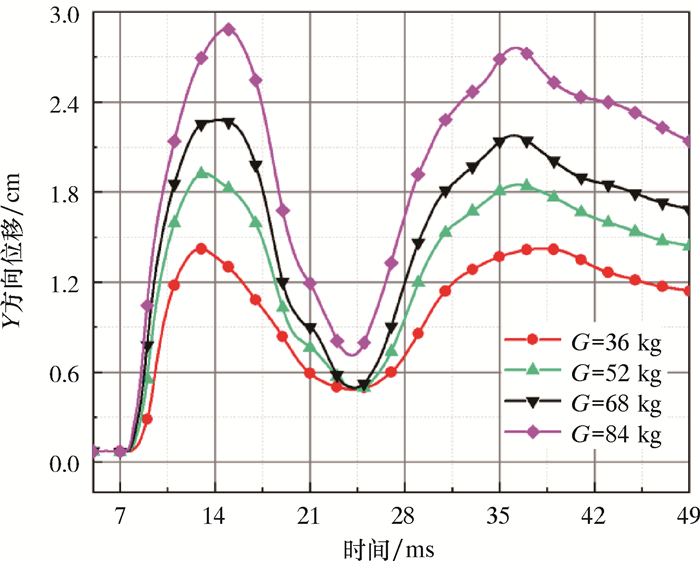
|
| 图 12 管顶Y方向位移时程曲线 Fig.12 Time-history curve of displacement in Y direction at the pipe top |
| 观测点 | G=36 kg | G=52 kg | G=68 kg | G=84 kg | |||||||
| 时间/ ms |
位移/ cm |
时间/ ms |
位移/ cm |
时间/ ms |
位移/ cm |
时间/ ms |
位移/ cm |
||||
| 迎爆点 | 39.1 | 1.3 | 38.5 | 1.7 | 38.5 | 2.0 | 39.4 | 2.5 | |||
| 背爆点 | 40.1 | 1.2 | 39.5 | 1.6 | 38.9 | 1.9 | 39.7 | 2.4 | |||
| 12.9 | 1.4 | 13.2 | 1.9 | 14.4 | 2.3 | 14.8 | 2.9 | ||||
| 管顶 | 24.2 | 0.47 | 24.6 | 0.48 | 24.3 | 0.49 | 24.1 | 0.71 | |||
| 38.1 | 1.41 | 36.3 | 1.85 | 36.1 | 2.18 | 36.2 | 2.72 | ||||
| 管底 | 12.8 | -1.49 | 12.9 | -2.02 | 13.1 | -2.38 | 14.1 | -2.91 | |||
| 44.2 | 1.19 | 45.1 | 1.57 | 43.9 | 1.83 | 44.4 | 2.27 | ||||
4.3 定量失效风险评估
管道作为国家能源输送的命脉,确保其安全运行具有重要意义,这里分别基于应变和应力失效判据评估不同装药量及不同爆心距下管体的运行状态,评估结果分别如表 4和表 5所示。
| G/kg |
Dmax/ mm |
Dmin/ mm |
椭圆度/% | 应变判据 | 应力/ MPa |
应力判据 |
| 36 | 124.81 | 121.2 | 2.93 | 安全 | 540.5 | 安全 |
| 52 | 125.83 | 120.2 | 4.58 | 失效 | 671.1 | 安全 |
| 68 | 126.59 | 119.3 | 5.93 | 失效 | 765.1 | 失效 |
| 84 | 127.72 | 118.6 | 7.41 | 失效 | 952.7 | 失效 |
| R/cm |
Dmax/ mm |
Dmin/ mm |
椭圆度/% | 应变判据 | 应力/ MPa |
应力判据 |
| 175 | 127.74 | 116.37 | 9.32 | 失效 | 1 207.7 | 失效 |
| 205 | 125.83 | 120.2 | 4.58 | 失效 | 671.1 | 安全 |
| 240 | 124.32 | 121.56 | 2.24 | 安全 | 479.6 | 安全 |
| 280 | 123.55 | 121.73 | 1.48 | 安全 | 398.9 | 安全 |
由表 4可以看出,同一爆心距下,管道的失效风险均随着装药量的增大而增加,基于应力的失效判据较应变失效判据相对偏保守。考虑到工程实际中管体本身的缺陷,研究工况下建议采用椭圆度失效准则。
不同爆心距下,管体各测点的参数时间历程与不同装药量下的规律大体相同,在此不做赘述,仅评估其安全状态。由表 5可知,管道的失效风险随着爆心距的增大而减小。这是因为爆心距越大,管道间的覆土越多,冲击波及土壤的塑性挤压作用越弱。为确保管道留有一定的安全余量,研究工况下建议管道的并行安全间距不小于240 cm。
5 结论(1) 基于加拿大土中爆炸试验验证了ALE法的精度,ALE法可以较好地描述爆炸波在土中的传播规律,以及爆炸空腔及地表土丘的宏观演化过程。
(2) 同一爆心距下,应力和位移均随着装药量的增大而增大;应力随着时间的变化先增大后减小;X向位移随着时间的变化先增大后减小;Y向位移与时间的关系取决于测点的位置,迎爆点与背爆点的位移随着时间的变化先增大后减小,管顶位移随着时间的变化呈现先增大后减小的二次脉冲现象,管底位移随着时间的变化由负向位移向正向位移过渡。
(3) 基于应力的管道安全评定较应变失效准则偏保守,评定准则的选取应视具体工况而定。
| [1] |
姚安林, 赵璐, 陈谦, 等. 埋地管道强夯动力响应对土体参数的敏感性分析[J]. 天然气工业, 2017, 37(7): 94-100. YAO A L, ZHAO L, CHEN Q, et al. Sensitivity of dynamic response of buried line pipes under dynamic compaction to soil parameters[J]. Natural Gas Industry, 2017, 37(7): 94-100. |
| [2] |
徐涛龙, 姚安林, 曾祥国, 等. 埋地钢质输气管道动态挖掘响应的试验研究及模拟分析[J]. 振动与冲击, 2017, 36(1): 230-239. XU T L, YAO A L, ZENG X G, et al. Tests and simulation for dynamic digging response of buried steel gas pipelines under excavator loading[J]. Journal of Vibration and Shock, 2017, 36(1): 230-239. |
| [3] |
王威翔, 姚安林, 徐涛龙, 等.车辆载荷下PE燃气管道的虚拟仿真技术及其动力响应分析[C]//第28届全国结构工程学术会议论文集(第Ⅰ册).[出版地不详]: 中国力学学会, 2019. WANG W X, YAO A L, XU T L, et al. Virtual simulation tethnology and dynamic response analysis of PE gas pipeline under vehicle load[C]//Proceedings of the 28th National Academic Conference on Structural Engineering (Volume I).[S.l.]: Chinese Society of Theoretical and Applied Mechanics, 2019. |
| [4] |
赵新威, 曾祥国, 姚安林, 等. 地震载荷作用下埋地输气管道的数值模拟[J]. 石油机械, 2014, 42(3): 104-109. ZHAO X W, ZENG X G, YAO A L, et al. Numerical simulation of the dynamic response of buried gas pipeline under seismic load[J]. China Petroleum Machinery, 2014, 42(3): 104-109. |
| [5] |
黄文, 谢锐, 陈小华. 落石冲击载荷下埋地油气管道力学分析[J]. 石油机械, 2019, 47(9): 138-144. HUANG W, XIE R, CHEN X H. Mechanical analysis of buried oil and gas pipeline under rockfall impact load[J]. China Petroleum Machinery, 2019, 47(9): 138-144. |
| [6] |
田江平, 张东山, 雷震, 等. 斜滑断层作用下埋地管道的力学性能试验研究[J]. 石油机械, 2019, 47(9): 123-131. TIAN J P, ZHANG D S, LEI Z, et al. Experimental study on mechanical properties of buried pipeline under the action of oblique slip fault[J]. China Petroleum Machinery, 2019, 47(9): 123-131. |
| [7] |
Pipeline Research Council International (PRCI). Line rupture and the spacing of parallel lines[R]. Huston:Pipeline Research Council International (PRCI), 2002:13-16.
|
| [8] |
SILVA E P, NELE M, MELO P F F, et al. Underground parallel pipelines domino effect:an analysis based on pipeline crater models and historical accidents[J]. Journal of Loss Prevention in the Process Industries, 2016, 43: 315-331. |
| [9] |
文霞, 姚安林, 陈谦, 等. 隧道并行输气管道爆炸对邻管的冲击效应分析[J]. 中国安全生产科学技术, 2017, 13(1): 156-162. WEN X, YAO A L, CHEN Q, et al. Analysis on impact effect of gas pipeline explosion to adjacent pipeline for parallel pipeline in tunnel[J]. Journal of Safety Science and Technology, 2017, 13(1): 156-162. |
| [10] |
梁博, 蒋宏业, 徐涛龙, 等. 基于SPH-FEM耦合算法的埋地输气管道近场爆炸冲击动力响应[J]. 石油学报, 2017, 38(11): 1326-1334. LIANG B, JIANG H Y, XU T L, et al. Impact dynamic response of near-field explosion in buried gas pipeline based on SPH-FEM coupling algorithm[J]. Acta Petrolei Sinica, 2017, 38(11): 1326-1334. |
| [11] |
田晓建, 姚安林, 徐涛龙, 等. 基于SPH-FEM耦合法的含缺陷输气管道爆炸冲击响应研究[J]. 中国安全生产科学技术, 2018, 14(9): 55-62. TIAN X J, YAO A L, XU T L, et al. Research on explosion impact response of defective gas pipeline based on SPH-FEM coupling method[J]. Journal of Safety Science and Technology, 2018, 14(9): 55-62. |
| [12] |
徐涛龙, 梁博, 文霞, 等. 天然气泄漏爆炸冲击同沟并行邻管的模拟方法[J]. 工程力学, 2019, 36(增刊1): 329-338. XU T L, LIANG B, WEN X, et al. Explosion impact simulation methods for parallel pipeline laying in the same ditch after gas leakage[J]. Engineering Mechanics, 2019, 36(S1): 329-338. |
| [13] |
王德国. 基于管道爆炸数值模拟的架空天然气管道并行间距研究[J]. 中国石油大学学报(自然科学版), 2013, 37(5): 175-180. WANG D G. Safe distance of overhead parallel pipeline calculated by numerical simulation of gas pipeline explosion[J]. Journal of China University of Petroleum(Edition of Natural Science), 2013, 37(5): 175-180. |
| [14] |
朱渊, 师吉浩, 陈国明, 等. 长输天然气埋地并行管道泄漏爆炸的安全间距[J]. 油气储运, 2016, 35(6): 591-595. ZHU Y, SHI J H, CHEN G M, et al. Safety distance for leakage-induced explosion of long-distance parallel buried gas pipelines[J]. Oil & Gas Storage and Transportation, 2016, 35(6): 591-595. |
| [15] |
刘向峰, 安宇, 董绍华, 等. 埋地输气管道安全并行距离分析[J]. 辽宁工程技术大学学报, 2017, 36(4): 396-401. LIU X F, AN Y, DONG S H, et al. Parallel safe distance analysis of buried gas pipeline[J]. Journal of Liaoning Technical University(Natural Science), 2017, 36(4): 396-401. |
| [16] |
刘阳阳.地下管道爆炸对埋地管网的毁伤数值模拟[D].南京: 南京理工大学, 2016. LIU Y Y. Numerical simulation of the damage of underground pipeline explosion to buried pipe network[D]. Nanjing: Nanjing University of Science and Technology, 2016. |
| [17] |
杨明. 同沟敷设条件下埋地高压长输管道爆炸危害的试验研究[J]. 安全与环境学报, 2018, 18(4): 1334-1338. YANG M. Experimental study on explosion hazard of buried high-pressure long-distance pipeline under the same ditch[J]. Journal of Safety and Environment, 2018, 18(4): 1334-1338. |
| [18] |
谢萍, 杨明, 尚臣, 等. 天然气管道爆破对同沟敷设管道的影响试验[J]. 油气储运, 2019, 38(2): 179-184. XIE P, YANG M, SANG C, et al. The influence of gas pipeline blasting on the pipelines laid in the same ditch[J]. Oil & Gas Storage and Transportation, 2019, 38(2): 179-184. |
| [19] |
刘冰, 刘学杰, 张宏. 基于应变的管道设计准则[J]. 天然气工业, 2008, 28(2): 129-131. LIU B, LIU X J, ZHANG H. Pipeline design code based on morphotropy strain[J]. Natural gas industry, 2008, 28(2): 129-131. |
| [20] |
ANON. Submarine pipeline systems: DNV-0S-F101[S]. Norway: Det Norske Veritas, 2010.
|
| [21] |
BERGERON D, WALKER R, COFFEY C. Detonation of 100-gram anti-personnel mine surrogate charges in sand:test case for computer code validation[J]. Defence Research Establishment Suffield, 1998(3): 2-20. |

