2. 重庆页岩气勘探开发有限责任公司;
3. 中国石油工程建设有限公司西南分公司
2. Chongqing Shale Gas Exploration and Development Co., Ltd.;
3. Southwest Branch of CNPC Petroleum Engineering and Construction Co., Ltd
0 引言
油气管道是一个不断退化的系统,不同类型的缺陷(如腐蚀、裂纹和机械损伤等)都会造成管道强度的降低,威胁管道安全[1-3]。管道内检测是量化和定位各种缺陷的有效方式[4-5],但由于其费用较高、作业风险较大,合理安排管道内检测周期成为学者关注的课题。目前工程上多采用固定的内检测周期,这极有可能造成管道的过检或缺检。过检会造成资源的浪费,缺检则易导致管道面临较大的安全风险,因此,准确地预测管道内检测周期具有重要意义[6]。
腐蚀是油气管道完整性的主要威胁之一。针对腐蚀管道,国内外学者主要通过比较可靠性评价结果与失效概率(POF)阈值来确定内检测周期,相关研究包括管道剩余寿命计算[7]、可靠性评价和风险矩阵比对等[8-12]。这类方法的实施需要考虑随机变量的不确定性以及建立管道可靠性评价方法。大量文献[13-16]基于概率方法定量评价了腐蚀管道的可靠性,然而其中多是关于可靠性和风险评价方法的研究,未有文献基于失效概率阈值建立模型对内检测周期进行优化。本文基于腐蚀管道提出了一种考虑成本的以失效概率阈值为决策变量的内检测周期优化方法。当管道系统的失效概率到达既定阈值时,管道需再次进行内检测和可靠性评价。依据评价结果和相应的维修准则,实施不同的维修方案,以保证整个管道系统的安全。
在基于成本的内检测周期优化方法中,由于涉及管道可靠性评价、随机变量的不确定性和相关性、维修准则和成本计算,且变量众多,优化过程变得相对复杂,本文基于蒙特卡罗仿真的方法执行了优化过程,以总成本率最低确定最优失效概率阈值和最优内检测周期,以期在保证管道安全运行的基础上提高管道运营的经济效益。
1 腐蚀管道可靠性评价模型腐蚀管道的失效模式可分为两类:小孔泄漏和爆裂,分别对应两个极限状态方程[17]。小孔泄漏的极限状态方程通过比较缺陷深度与管道壁厚来定义,其一般形式为:
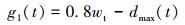
|
(1) |
式中:wt为管道壁厚,mm;t是最近一次内检测后经过的时间,a;dmax(t)表示时间t时腐蚀缺陷的最大深度,mm。
爆裂的极限状态方程通过比较缺陷处的管道爆破压力与运行压力来定义,其数学表达式为[18]:
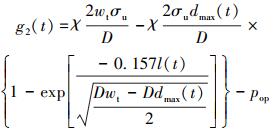
|
(2) |
式中:pop是管道运行压力,MPa;χ是模型的误差;σu是管道材料的极限抗拉强度,MPa;D是管道直径,mm;l(t)是时间t时腐蚀缺陷的轴向长度,mm。
由式(1)和式(2)可知,两个极限状态函数均与时间有关。
g1(t)≤0和g2(t)≤0分别代表发生小孔泄漏失效和爆裂失效。因此,单个腐蚀缺陷的失效概率为:
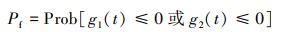
|
(3) |
为了计算腐蚀缺陷的失效概率,采用线性随机变量模型来描述腐蚀缺陷增长,将多个腐蚀缺陷的增量量化为具有相关性且服从特定分布的多维随机变量。
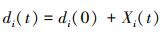
|
(4) |
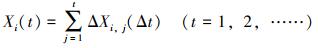
|
(5) |
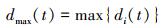
|
(6) |
式中:di(t)是腐蚀缺陷i在t时的深度,mm;di(0)是腐蚀缺陷i的初始深度,mm;Xi(t)是缺陷i的深度增量,mm;ΔXi, j(Δt)是缺陷i在第j年的深度增量(即生长速率),mm/a;Δt是模拟时间步长,取为1 a。
假设缺陷长度不随时间增长,等于初始缺陷长度。由于设计、制造和运行工况,管道的结构参数、缺陷的尺寸参数之间相互关联,多个腐蚀缺陷的增长相互依赖,在统计意义上表现出一定程度的相关性,本文采用Copula函数产生具有相关性的随机变量样本。考虑到文章的篇幅和侧重点,关于Copula函数的应用可以参照文献[19],在此不再做赘述。
采用管道上腐蚀缺陷的失效概率的最大值表征该管道的失效概率[16],将式(1)、式(2)、式(4)、式(5)和式(6)带入式(3),可以预测任意时刻腐蚀管道的失效概率Ppipe(t)。
2 内检测周期优化方法 2.1 维修准则与维修方案根据管道内检测获得的缺陷信息,建立腐蚀增长模型,可以预测腐蚀缺陷的生长、评估管道系统的失效概率,并对管道系统进行维修决策。针对腐蚀管道的预防性维修方法包括添加涂层和加装套管两类。如果腐蚀缺陷被成功检测到,可以依据相应的维修准则来确定维修方案[19]。
准则1:
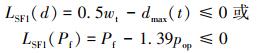
|
(7) |
准则2:
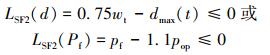
|
(8) |
若腐蚀缺陷不满足准则1,则不需要进行开挖和维修;若腐蚀缺陷满足准则1,则进行开挖并检查是否满足准则2。若满足准则2,则采用加装套管的维修方案,否则采取添加涂层的维修方案。
2.2 基于成本的优化模型基于成本的内检测周期优化方法是以最优POF阈值作为决策变量,预测管道POF达到最优POF阈值的时间。最优POF阈值对应于最低总成本,总成本包含内检测成本、维修成本和失效成本。该优化问题可描述为:
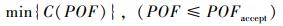
|
(9) |
式中:C(POF)为给定POF阈值下的总成本;POFaccept表示可接受的最大失效概率阈值,对于不同的安全等级,该值通常在10-5~10-3之间[15],本文选取为10-3。
根据最近一次内检测获得的缺陷信息,结合管道几何和材料信息,在考虑不确定性的前提下,生成管道极限状态方程所涉及的所有随机变量的样本。假设检测到k个腐蚀缺陷,在每次迭代中,使用式(4)~式(6)描述腐蚀缺陷的增长(考虑相关性和不确定性)。利用第2节描述的极限状态方程模拟计算不同时间管道系统的失效概率Ppipe(t)。当Ppipe(t)达到POF阈值时,记录时间t*并计算总成本现值Ct*。总成本现值Ct*计算式为:
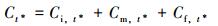
|
(10) |
式中:Ci,t*、Cm,t*,Cf,t*分别表示内检测成本、维修成本和失效成本的现值。
各成本现值的计算公式如下。
内检测成本现值:
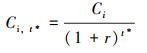
|
(11) |
式中:Ci为内检测成本,r为折现率。
失效成本为:
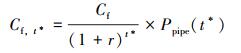
|
(12) |
式中:Cf是将生命财产损失和环境破坏转化为经济损失后的成本。
维修成本:
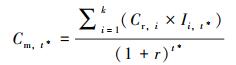
|
(13) |

|
(14) |
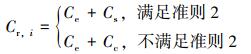
|
(15) |
式中:Cr,i为单个缺陷的维修成本;k为腐蚀缺陷的个数;Ce为开挖成本;Cs和Cc分别代表加装套管的成本和添加涂层的成本。
假设进行N次蒙特卡罗迭代模拟,每次迭代j均可以得到内检测成本现值Ci,t*,j,维修成本现值Cm,t*,j,失效成本现值Cf,t*, j,总成本现值Ct*,j和内检测周期Tj。对任一给定的POF阈值,总成本率CR为:
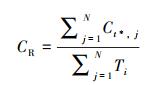
|
(16) |
内检测成本率、维修成本率和失效成本率的计算只需将Ct*,j更换为Ci,t*,j、Cm,t*,j和Cf,t*,j即可。给定POF阈值对应的内检测周期为T,则:
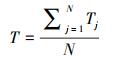
|
(17) |
以POF阈值为自变量,计算不同POF阈值对应的总成本率CR,拟合得到相应的函数曲线。通过寻优,结合可靠性预测结果,可以得出最优POF阈值和最优内检测周期。
3 案例分析 3.1 敏感性分析优化采用所提出的方法,选取我国某长输天然气管道的一个管段进行分析,得出其最优POF阈值和内检测周期。该管道于2006年进行了在线检测,所选管段长5 km,包含10个腐蚀缺陷。依据内检测数据并结合文献推荐的参数分布做统计分析[8, 17],确定了描述管道和缺陷参数概率特征的分布类型与参数取值,如表 1所示。案例考虑了随机变量之间的相关性,其中管道壁厚与管径的相关系数为0.8,腐蚀缺陷的初始深度和初始长度之间的相关系数是0.5,管段上不同腐蚀缺陷的深度生长速率之间的相关系数为0.5。同时在2016年该管道由于腐蚀发生了一起泄漏失效事故。为便于分析,在算例中采取了相对成本[16],检测成本Ci=2.5,管道开挖成本Ce=3.5,添加涂层的成本为1,加装套管成本Cs=1.75,失效成本Cf=200,折现率取为2%。
| 参数 | 均值 | 变异系数/% | 分布类型 |
| pop/MPa | 10 | 2.0 | 甘贝尔分布 |
| D/mm | 1 016 | 3.0 | 正态分布 |
| wt/mm | 17.5 | 3.3 | 正态分布 |
| σu/MPa | 570 | 3.5 | 正态分布 |
| χ | 0.97 | 10.5 | 对数正态分布 |
| d(0)/mm | 0.582 | 72 | 威布尔分布 |
| l(0)/mm | 35.68 | 80 | 对数正态分布 |
| ΔX(Δt)/(mm·a-1) | 0.5 | 70.3 | 威布尔分布 |
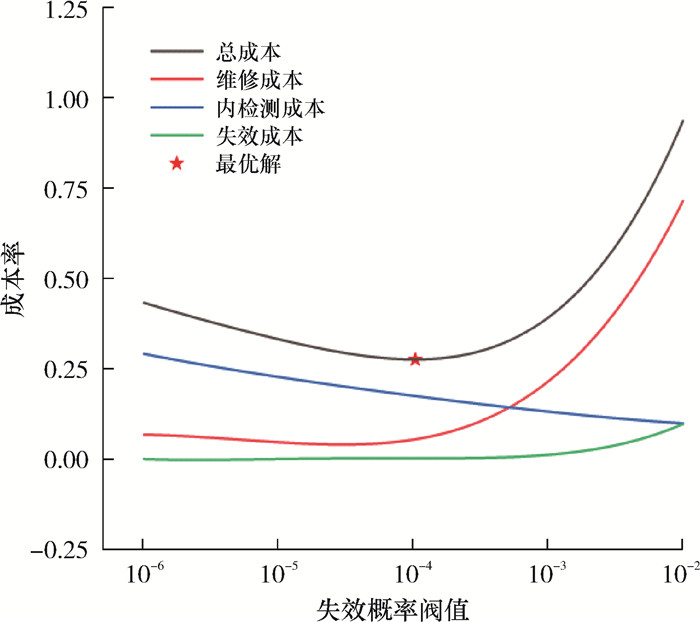
采用本文提出的优化方法对上述管道进行研究,得出其最优POF阈值为1.033×10-4,对应的总成本率为0.276,最优内检测周期为9.6 a。成本率随POF阈值的变化如图 1所示。由图 1可知,总成本率被分解为内检测成本率、维修成本率和失效成本率,随着POF阈值的增大,检测成本率呈下降趋势,而维修成本率和失效成本率均呈上升趋势。这是因为研究认为内检测成本是固定的,POF阈值越大,内检测周期越长,现值越低。而随着POF阈值的增大,维修和失效的可能性均增大,相应的成本率也增大。此外优化结果显示该管道的最优内检测周期为9.6 a,这与该管道于第10年发生腐蚀泄漏的历史数据十分接近,反映了所提出优化方法的合理性和有效性。
|
| 图 1 成本率随POF阈值变化图 Fig.1 Cost rate vs. POF threshold |
为了研究各参数对内检测周期优化结果的影响,本文进行了敏感性分析。表 2列出了敏感性分析涉及的所有参数的取值和相应的优化结果。假设参数在表 1中的取值为对照组,对照组的优化结果即为图 1所示。表 2中的d(0)表示缺陷初始深度均值,CV[d(0)]表示初始深度的变异系数。
| 参数 | d(0)/mm | CV[d(0)] | ΔX(Δt)/(mm·a-1) | Cf | |||||||||||
| 0.582 | 0.873 | 1.164 | 0.520 | 0.720 | 0.920 | 0.3 | 0.5 | 0.7 | 100 | 200 | 2 000 | ||||
| 最优POF阈值 | 1.033×10-4 | 3.488×10-4 | 7.360×10-4 | 7.960×10-6 | 1.033×10-4 | 6.650×10-4 | 1.664×10-5 | 1.033×10-4 | 1.699×10-4 | 5.995×10-5 | 1.033×10-4 | 3.262×10-5 | |||
| 总成本率 | 0.276 | 0.299 | 0.256 | 0.266 | 0.276 | 0.291 | 0.120 | 0.276 | 0.437 | 0.287 | 0.276 | 0.281 | |||
| 最优内检测周期/a | 9.6 | 9.1 | 8.5 | 9.7 | 9.6 | 9.6 | 16.8 | 9.6 | 6.7 | 9.6 | 9.6 | 9.5 | |||
图 2~图 5描绘和比较了其他情况下成本率随POF阈值的变化情况。针对不同情况得到的最优POF阈值最小为7.960×10-6,最大为7.360×10-4,均满足POFaccept的约束。
|
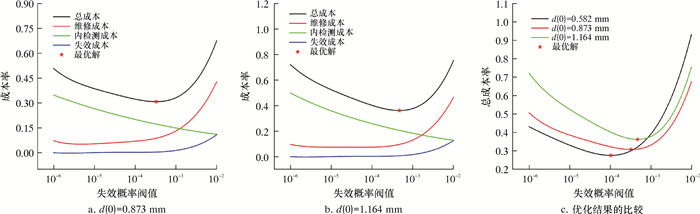
| 图 2 不同缺陷初始深度下成本率随POF阈值变化图 Fig.2 Cost rate vs. POF threshold at different initial defect depths |
|
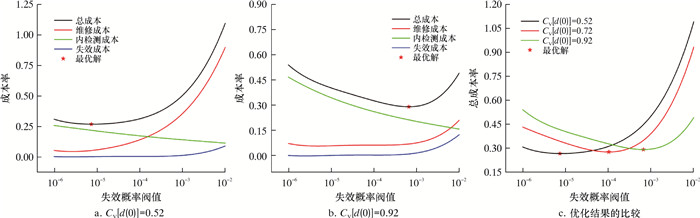
| 图 3 不同初始深度变异系数下成本率随POF阈值变化图 Fig.3 Cost rate vs. POF threshold at different variation coefficients of initial defect depth |
|
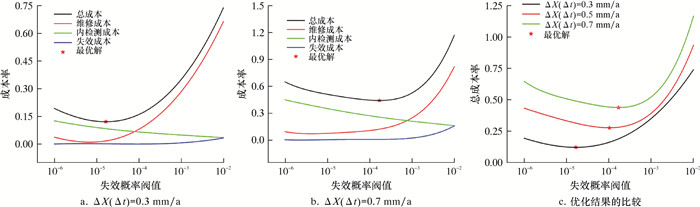
| 图 4 不同缺陷深度生长速率下成本率随POF阈值变化图 Fig.4 Cost rate vs. POF threshold at different growth rates of defect depth |
|
| 图 5 不同失效成本下成本率随POF阈值变化图 Fig.5 Cost rate vs. POF threshold at different failure costs |
3.2 缺陷初始深度
对缺陷初始深度均值分别为0.582、0.873和1.164 mm情况下进行分析。图 2a和图 2b分别描绘了缺陷初始深度均值为0.873和1.164 mm的情况的优化结果。图 2c基于总成本率对3种缺陷初始深度的优化结果进行了比较。
由图 2可知,缺陷初始深度对总成本率的影响较大,缺陷的初始深度越大,管道失效和进行维修的可能性越大,维修成本率、失效成本率和总成本率越高。此外,最优POF阈值随着缺陷初始深度的增大而增大,但最优内检测周期却随着初始缺陷深度的增大而减小。这是因为初始深度较大的缺陷达到既定POF阈值所需的时间更短。
3.3 初始深度变异系数初始深度变异系数是内检测数据误差的反映。对初始深度变异系数分别为0.52、0.72和0.92的情况进行分析。图 3a和图 3b分别展示了初始深度变异系数为0.52和0.92情况下的优化结果。图 3c基于总成本率对3种初始深度变异系数对应的优化结果进行了比较。
由图 3可以看出,随着初始深度变异系数的增加,最优POF阈值增大,但最优内检测周期非常接近。这主要是因为缺陷初始深度变异系数越大,预测周期内管道失效概率也越大。
3.4 缺陷深度生长速率对缺陷生长速率均值为0.3、0.5和0.7 mm/a 3种情况进行分析。图 4a和图 4b分别展示了缺陷深度生长速率均值为0.3和0.7 mm/a情况下的优化结果。图 4c基于总成本率对3种缺陷深度生长速率对应的优化结果进行了比较。
由图 4可以看出,随着缺陷深度生长速率的不断增加,总成本率呈现增加的趋势,最优POF阈值增大,但最优内检测周期减小。这是因为深度生长速率较高的缺陷达到一定POF所需的时间更短。
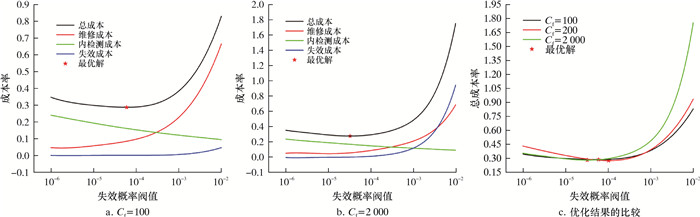
3.5 失效成本由于人员伤亡和环境破坏很难转化为经济损失,所以有必要研究失效成本对优化结果的影响。选取3个不同的相对失效成本值100、200和2 000进行分析,结果如图 5所示。
图 5a和图 5b分别展示了失效成本为100和2 000情况下的优化结果。图 5c对3种失效成本对应的优化结果进行了比较。
由图 5可以看出:对于Cf=2 000的情况,当管道POF阈值大于8×10-3时,失效成本率对总成本率的贡献最大,而当Cf取值为其他两种情况时,维修成本率对总成本率的贡献最大;当管道POF阈值较小时,总成本率接近,当管道POF阈值较大时,Cf =2 000对应的总成本率显著高于其他两种情况。
此外,失效成本对最优管道POF阈值和最优内检测周期影响较小。
4 结论及认识(1) 为了在保证管道安全运行的基础上提高管道运营的经济效益,针对腐蚀管道提出了一种基于成本的以失效概率阈值为决策变量的内检测周期优化方法,该方法包含腐蚀管道的可靠性评价和基于成本的内检测周期优化,在此过程中考虑了随机变量的不确定性和相关性,引入了内检测成本、维修成本和失效成本,经过仿真计算得出管道的最优内检测周期。
(2) 研究结果表明,腐蚀缺陷深度生长速率对管道最优内检测周期影响最大,其次是缺陷初始深度。最优内检测周期随着缺陷初始深度和缺陷深度生长速率的增大而减小,缺陷初始深度变异系数和失效成本对最优内检测周期无显著影响。
(3) 由于内检测周期的优化涉及管道的可靠性评价,而目前国内的相关管道数据积累还不够充分,所以需要管道运营者注重收集整理管道相关数据,确保数据的完整可靠,助力管道的安全经济管理。
| [1] |
姚伟. 油气管道安全管理的思考与探索[J]. 油气储运, 2014, 33(11): 1145-1151. YAO W. Thinking and exploration on the safety management of oil/gas pipeline[J]. Oil & Gas Storage and Transportation, 2014, 33(11): 1145-1151. |
| [2] |
杨辉, 王富祥, 王婷, 等. 基于漏磁内检测的管道补口失效识别与判定方法[J]. 油气储运, 2019, 38(5): 516-521. YANG H, WANG F X, WANG T, et al. Identification and determination method of pipeline joint coating failure based on MFL ILI[J]. Oil & Gas Storage and Transportation, 2019, 38(5): 516-521. |
| [3] |
帅健, 单克. 基于失效数据的油气管道定量风险评价方法[J]. 天然气工业, 2018, 38(9): 129-138. SHUAI J, SHAN K. A quantitative risk assessment method for oil and gas pipelines based on failure data[J]. Natural Gas Industry, 2018, 38(9): 129-138. |
| [4] |
王金龙, 何仁洋, 张海彬, 等. 海底管道检测最新技术及发展方向[J]. 石油机械, 2016, 44(10): 112-118. WANG J L, HE R Y, ZHANG H B, et al. State-of-the-art advancement and development direction of submarine pipeline inspection technology[J]. China Petroleum Machinery, 2016, 44(10): 112-118. |
| [5] |
孙吉业, 樊建春, 张来斌, 等. 基于磁记忆效应的新型管道机器人[J]. 石油机械, 2011, 39(1): 51-53. SUN J Y, FAN J C, ZHANG L B, et al. The magnetic memory effect-based pipeline robot[J]. China Petroleum Machinery, 2011, 39(1): 51-53. |
| [6] |
林现喜, 杨勇, 裴存锋, 等. 油气长输管道内检测周期预测方法[J]. 油气田地面工程, 2018, 37(5): 65-69. LIN X X, YANG Y, PEI C F, et al. Prediction methods for the long distance oil and gas pipeline internal inspection period[J]. Oil-Gasfield Surface Engineering, 2018, 37(5): 65-69. DOI:10.3969/j.issn.1006-6896.2018.05.016 |
| [7] |
郭章林, 王勇华, 李富梅. 城市燃气管道检测周期研究[J]. 油气储运, 2009, 28(3): 25-28. GUO Z L, WANG Y H, LI F M. Study on inspection cycles of city gas pipeline[J]. Oil & Gas Storage and Transportation, 2009, 28(3): 25-28. |
| [8] |
张欣, 余建星, 梁静. 基于风险的检测(RBI)在海底管道定量风险评估中的应用[J]. 石油矿场机械, 2015, 44(1): 9-12. ZHANG X, YU J X, LIANG J. Application of risk based inspection (RBI) in the quantitative risk assessment of subsea pipeline[J]. Oil Field Equipment, 2015, 44(1): 9-12. DOI:10.3969/j.issn.1001-3482.2015.01.003 |
| [9] |
张汝义, 刘海俊, 杜莎. 埋地钢质原油集输管道检测技术探讨[J]. 油气田地面工程, 2017, 36(6): 81-83. ZHANG R Y, LIU H J, DU S. Research on inspection technologies of buried crude oil gathering and transportation steel pipelines[J]. Oil-Gasfield Surface Engineering, 2017, 36(6): 81-83. DOI:10.3969/j.issn.1006-6896.2017.06.023 |
| [10] |
GOMES W J S, BECK A T, HAUKAAS T. Optimal inspection planning for onshore pipelines subject to external corrosion[J]. Reliability Engineering & System Safety, 2013, 118: 18-27. |
| [11] |
XIE M J, TIAN Z G. Risk-based pipeline reassessment optimization considering corrosion defects[J]. Sustainable Cities and Society, 2018, 38: 746-757. DOI:10.1016/j.scs.2018.01.021 |
| [12] |
ZHANG S W, ZHOU W X. Cost-based optimal maintenance decisions for corroding natural gas pipelines based on stochastic degradation models[J]. Engineering Structures, 2014, 74: 74-85. DOI:10.1016/j.engstruct.2014.05.018 |
| [13] |
张鹏, 彭杨. 考虑随机变量相关性的腐蚀管道失效概率[J]. 石油学报, 2016, 37(10): 1293-1301. ZHANG P, PENG Y. Failure probability of corroded pipeline considering random variables correlation[J]. Acta Petrolei Sinica, 2016, 37(10): 1293-1301. DOI:10.7623/syxb201610010 |
| [14] |
YU W C, ZHANG J, WEN K, et al. A novel methodology to update the reliability of the corroding natural gas pipeline by introducing the effects of failure data and corrective maintenance[J]. International Journal of Pressure Vessels and Piping, 2019, 169: 48-56. DOI:10.1016/j.ijpvp.2018.11.001 |
| [15] |
曾海龙, 王振林, 马继升, 等. 考虑参数相关的腐蚀管道可靠性评价[J]. 化工机械, 2011, 38(1): 14-18. ZENG H L, WANG Z L, MA J S, et al. Reliability assessment of corroded pipelines based on correlation between variables[J]. Chemical Engineering & Machinery, 2011, 38(1): 14-18. DOI:10.3969/j.issn.0254-6094.2011.01.004 |
| [16] |
ZHOU W X. System reliability of corroding pipelines[J]. International Journal of Pressure Vessels and Piping, 2010, 87(10): 587-595. DOI:10.1016/j.ijpvp.2010.07.011 |
| [17] |
ZHANG S, ZHOU W X. System reliability of corroding pipelines considering stochastic process-based models for defect growth and internal pressure[J]. International Journal of Pressure Vessels and Piping, 2013, 111/112: 120-130. DOI:10.1016/j.ijpvp.2013.06.002 |
| [18] |
NELSEN R B. Dependence and order in families of archimedean copulas[J]. Journal of Multivariate Analysis, 1997, 60: 111-122. DOI:10.1006/jmva.1996.1646 |
| [19] |
ZHOU W X, NESSIM M A. Optimal design of onshore natural gas pipelines[J]. Journal of Pressure Vessel Technology, 2011, 133(3): 031702. DOI:10.1115/1.4002496 |



