0 引言
螺纹接头是油套管的重要组成部分,对油套管的性能具有直接影响,也是油套管容易发生失效的部位[1-2]。螺纹参数的精确测量对油套管接头的设计开发和加工制造有重要作用。井筒中的油套管接头发生力学损坏后,在失效分析时需对接头进行计算机几何建模,此时需要对失效接头进行精确测量,并按照实测数据建立接头三维模型。在螺纹的众多参数中,中径与螺距是主要参数,是判定接头是否合格的重要指标,也是测量难度大的参数。另外,在油套管特殊螺纹接头优化设计中,有时需借助逆向工程技术对现有产品进行测量分析,这也需要对螺纹中径和螺距等关键参数进行高精度测量。
业内一直都在探索油套管螺纹中径和螺距的测量手段,以往采用的测量方法主要有三针法、垂直投影法和影像法等。三针法[3-5]是一种间接测量方法,这种方法先要根据被测螺纹的理论螺距和牙型角计算最佳量针直径,然后将3个量针放入螺纹沟槽中,再通过千分尺测量三针外表面之间的尺寸,最后利用公式计算螺纹中径和螺距。该方法在测量过程中要保持最佳测针和螺纹牙侧面的稳定接触,人为因素影响大,且不适用于未知理论螺距和牙型角的螺纹。垂直投影法和影像法[6-8]将光线射入待测螺纹,得到螺纹影像,然后使用精密仪器测量螺纹影像,得到螺纹中径和螺距。这两种方法获得的螺纹牙影像质量由仪器和螺纹表面精度决定,易产生误差,且操作过程繁琐。
三坐标测量机是一种高精密测量仪器,可以在一个三维空间范围内获取被测物体上各测点的坐标,再通过数学计算得到所需的几何尺寸,被广泛应用于机械、航空、国防及交通等行业[9-11]。2002年,王庆广等[12]在三坐标测量机的测杆上安装了辅助装置,当辅助装置上的高精度圆柱与螺纹牙槽两侧接触后,再用三坐标测量机测头测量圆柱上的点,最后根据辅助测头在不同位置时的圆心坐标测量数据计算螺纹中径和螺距。2013年,刘浩等[13]研究了用三坐标测量机测量螺纹量规的方法,利用细小的探针将整个牙侧面全部测量出来,得到螺纹牙侧面直线,根据两条牙侧面直线计算理论最佳测球的球心位置,进而计算各个沟槽的球心位置,通过数据处理计算螺纹中径和螺距。2017年,张欣等[14]研究了利用三坐标测量机测量大尺寸圆柱螺纹量规中径的方法,根据最佳测球直径选择测量机探针,利用三坐标测量机的自定心功能采集4个方向上母线的自定心点数据,再对采集数据处理,得到圆柱螺纹中径和螺距。2017年,张波等[15]研制了一套基于三坐标测量机和激光干涉仪的大尺寸圆锥螺纹量规基面中径测量系统。该系统中的T形测头直径为最佳测球直径,移动T形测头分别与3个螺纹沟槽两侧面相切,采集测点数据,再根据数学公式计算螺纹中径和螺距。
上述方法对利用三坐标测量机测量螺纹的方法进行了有益尝试,促进了螺纹测量方法的发展。但这些方法大多是针对螺纹量规的测量开展的研究,测量目的与油套管螺纹测量目的不同,所以在测量方法上与油套管螺纹测量的考虑不尽相同。比如,文献[13-15]的方法都需要事先知道螺纹的理论螺距和牙型角,这不适用于未知参数螺纹的测量与建模;文献[12]和[15]的方法还需要借助辅助装置进行测量;文献[14]的方法不适用于油套管上锥螺纹的测量;文献[15]的方法测得的仅仅是螺纹基面的中径值等。本文在前人研究的基础上,研发了油套管螺纹中径和螺距的测量方法。该方法不需要事先知道螺纹的理论螺距和牙型角,也不需要借助辅助装置。该测量方法的提出,为未知理论螺矩和牙型角的螺纹测量提供了新方法。
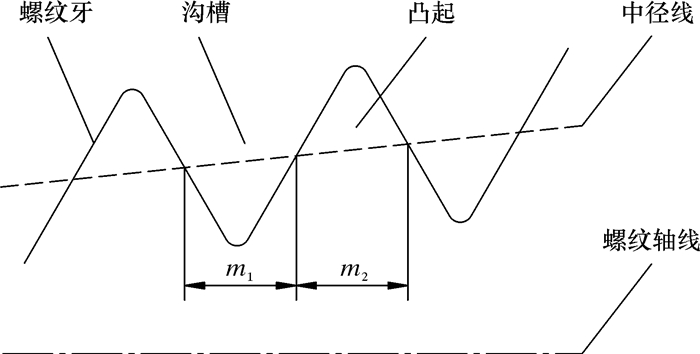
1 测量方案采用锥螺纹结构的油套管螺纹,其中径线构成一个圆锥面,中径线的位置处于该圆锥的母线通过螺纹牙形上沟槽和凸起宽度相等的地方[16]。中径线与螺纹轴线之间存在夹角,沟槽宽度为构成沟槽的两螺纹面与中径线交点间的轴向距离,记作m1。凸起宽度为构成凸起的两螺纹面与中径线交点间的轴向距离,记作m2。中径线与螺纹牙相交,如图 1所示。
|
| 图 1 中径线与螺纹牙相交示意图 Fig.1 Schematic diagram of the intersection of the middle diameter line and the thread teeth |
在三坐标测量机测量空间内,根据螺纹接头结构建立空间坐标系,沿着轴线方向对螺纹牙侧面进行采点测量,每一个侧面上的点构成一条直线,所有直线相互连接形成完整的螺纹牙,相邻直线间互不平行。根据螺纹中径线上凸起宽度等于沟槽宽度的原则,通过计算相邻直线间的轴向距离,确定每一个螺纹牙与中径线的交点,利用最小二乘法对所有交点进行直线拟合,得到螺纹中径线方程。计算相邻交点间的轴向距离得到螺纹螺距,通过中径线方程确定每个螺纹牙处的螺纹中径。
2 测量过程及数据处理 2.1 建立空间坐标系三坐标测量机将零件安装在工作台上进行测量,本身带有初始坐标系。在测量零件时,为了提高测量精度,需要根据零件结构建立空间坐标系,该空间坐标系为零件各部位提供方向和角度参考,相对于初始坐标系提高了零件各部位的定位精度。建立空间坐标系需要确定X、Y、Z 3个坐标轴和坐标原点。本文依据三轴两两垂直原则,只要两轴确定,第三轴自然确定,具体方法是:首先找正空间坐标第一轴,将基准平面绕第一轴进行空间旋转,使坐标系第一轴方向为所选基准平面的法向矢量方向;然后确定第二轴,测量一条直线在基准平面上进行投影,该投影直线绕第一轴旋转到第二轴的位置,投影直线的矢量方向为第二轴方向;最后用特征坐标值确定坐标系的零位,在基准平面上确定一点作为原点[17-18]。
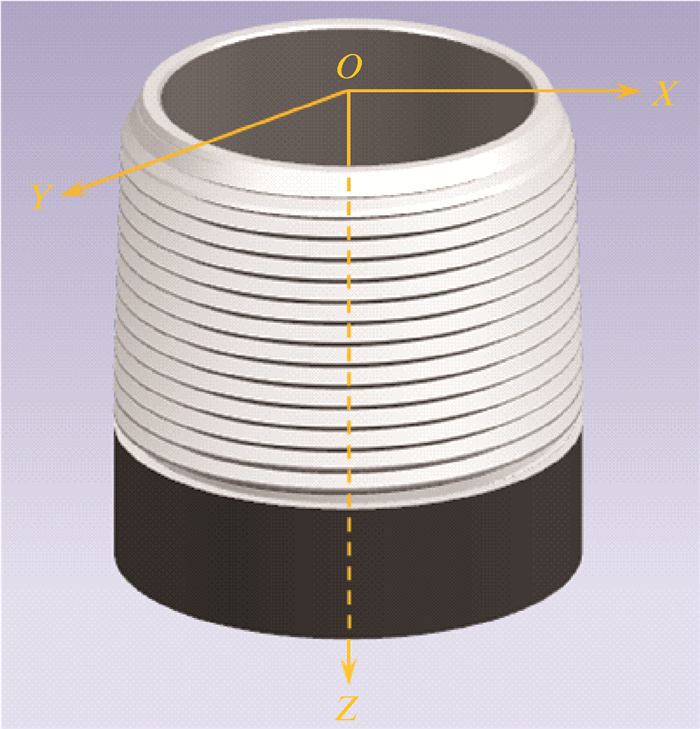
本文以油套管螺纹接头端面作为基准平面,首先测量基准平面,将测量得到的基准平面绕Z轴做空间旋转,使基准平面的法向矢量方向为Z轴方向;然后在基准平面上测量一条直线(该直线在基准平面上的投影是它本身),将该直线绕Z轴旋转到X轴,直线的矢量方向为X轴方向,Y轴方向自动确定;最后测量中心孔,中心孔的轴线方向与基准平面的交点即为原点,从而建立空间坐标系,如图 2所示。
|
| 图 2 螺纹接头空间坐标系 Fig.2 Spatial coordinate system of thread joint |
2.2 规划测量路线和测点数
沿着螺纹接头轴线方向(Z轴方向)对螺纹牙侧面进行测点,为了便于计算,在X-Z平面内确定测量路线,且取X轴正向。由于油套管螺纹牙型较小,螺纹牙之间测量空间较小,可测量点数少,所以在各个螺纹牙上每个侧面测点两处。
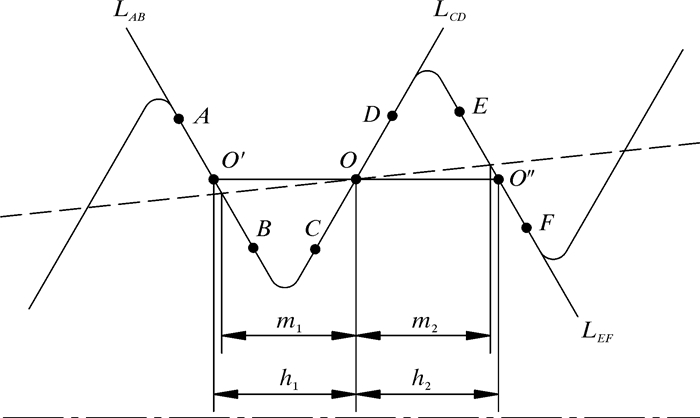
2.3 中径线与螺纹牙侧线交点的确定中径线与螺纹牙的交点如图 3所示。在X-Z平面内,Y轴坐标值为0,则测点坐标为(X, 0, Z),对两个相邻螺纹牙上的3个侧面测点6处,分别记为点A、B、C、D、E、F,则6个测点的坐标分别可以表示为(XA, 0, ZA)、(XB, 0, ZB)、(XC, 0, ZC)、(XD, 0, ZD)、(XE, 0, ZE)、(XF, 0, ZF)。用测点A和B构造直线LAB,测点C和D构造直线LCD,测点E和F构造直线LEF。
|
| 图 3 中径线与螺纹牙的交点 Fig.3 The intersection of the middle diameter line and the thread teeth |
绘制一条与螺纹接头轴线平行的直线,该直线与LAB的交点为O′,与LCD的交点为O,与LEF的交点为O″。则在LCD上必然存在一点O,使得线段O′O的长度h1等于线段OO″的长度h2。根据几何知识,点O同时满足m1=m2,根据螺纹中径线的定义,O点的位置即为螺纹中径线与直线LCD的交点。
直线LAB的数学表达式为:
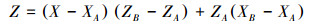
|
(1) |
直线LCD的数学表达式为:
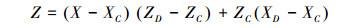
|
(2) |
直线LEF的数学表达式为:
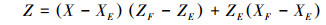
|
(3) |
设交点O的坐标为(X, 0, Z),过点O处相邻两直线间轴向距离为h,即有h1=h2=h,则O′点坐标是(X, 0, Z+h)、O″点坐标是(X, 0, Z-h),如图 3所示。
现将坐标O(X, 0, Z)、O′(X, 0, Z+h)、O″(X, 0, Z-h)分别带入式(1)、式(2)和式(3)中,则有:
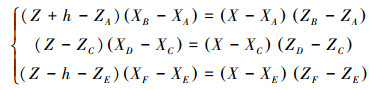
|
(4) |
引入直线斜率计算公式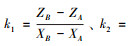
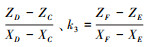
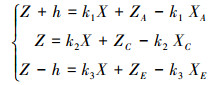
|
(5) |
由式(5)得:
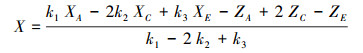
|
(6) |
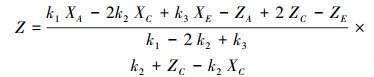
|
(7) |
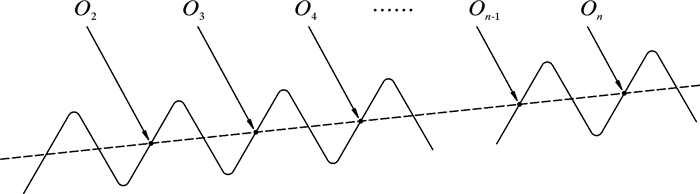
利用上述计算方法得到了中径线和一个螺纹牙的交点O(X, 0, Z),根据该方法可以得到中径线与各个螺纹牙的交点。由于该方法会少计算一个螺纹牙与中径线的交点,所以不能得到参与测量的第一个螺纹牙与中径线的交点,但这不影响螺纹中径线结果的获取。设中径线与各螺纹牙的交点为Oi,对应的交点坐标为Oi(Xi, 0, Zi),Xi和Zi分别由式(6)和式(7)计算得到。其中,i=2,3,4,……,n(n为参与测量的螺纹牙个数)。图 4为中径线与各螺纹牙的交点示意图。
|
| 图 4 中径线与各螺纹牙的交点示意图 Fig.4 Schematic diagram of the intersection of the middle diameter line and each thread tooth |
2.4 中径线拟合计算
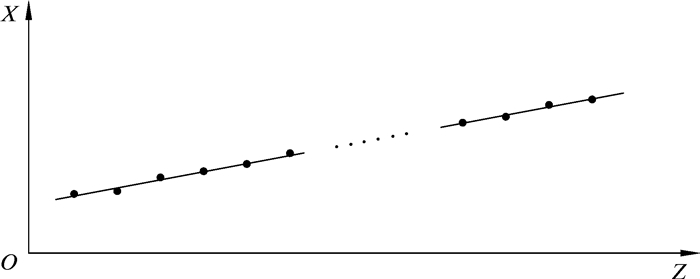
利用最小二乘法对各个交点进行直线拟合[19],得到螺纹中径线,如图 5所示。图 5中Z轴表示中径线和各螺纹牙的交点与螺纹接头端面的轴向距离,X轴表示各螺纹牙处中径值的1/2。
|
| 图 5 各交点的直线拟合 Fig.5 Straight line fitting of each intersection |
设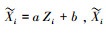
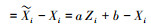
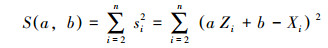
|
(8) |
式(8)取得极值的必要条件是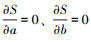
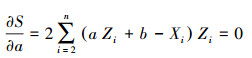
|
(9) |
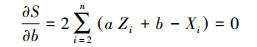
|
(10) |
通过计算可得:
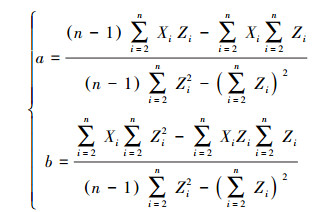
|
(11) |
中径线方程为:
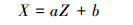
|
(12) |
由于计算方法较为复杂,计算量相对较大,可利用计算机编程进行计算。
2.5 螺纹中径计算根据中径线方程计算每个螺纹牙交点处中径,由式(12)得:
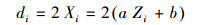
|
(13) |
式中:Zi为第i个螺纹牙交点Z轴坐标值,mm;Xi为第i个螺纹牙交点X轴坐标值,mm;di为第i个螺纹牙交点处的中径值,mm。
2.6 螺纹螺距计算根据所有交点计算螺距,计算式为:
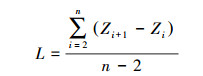
|
(14) |
式中:L为螺纹螺距,mm。
3 油管螺纹中径与螺距三坐标测量试验与应用为了验证本文的测量方法,采用西安爱德华测量设备股份有限公司生产的Daisy564型三坐标测量机对特殊螺纹油管接头进行测量。该测量机采用英国RENISHAW光栅尺,德国MORA控制系统,测头分辨率为0.5 μm,探测误差为2.0 μm。
3.1 测量结果在油管螺纹接头上对11个螺纹牙进行测量,螺纹牙编号为1~11号,1号螺纹牙只在一个侧面各测点两处,2到11号螺纹牙两个侧面测点两处,每个侧面两处空间点坐标分别记作测点一坐标和测点二坐标,测量结果见表 1。三坐标测量机测量时,3个轴的直线度误差、回转角误差和测量力造成的力变形误差使得测头不能按照理想路线运动,从而出现测量误差,表现在Y轴坐标值达不到理想精度(理想精度数值为0)。由表 1可知,Y轴坐标最大偏差值为0.007 3 mm,该偏差值小于0.01 mm,测量误差小,为了便于计算,取Y轴坐标值为0。
| 螺纹牙编号 | 测点一坐标 | 测点二坐标 | |||||
| X | Y | Z | X | Y | Z | ||
| 1 | 31.357 6 | -0.004 6 | 7.184 6 | 30.655 1 | -0.004 7 | 7.614 6 | |
| 2 | 30.836 5 | -0.004 1 | 8.030 9 | 31.605 5 | -0.003 3 | 8.435 4 | |
| 2 | 31.800 3 | -0.001 7 | 10.141 2 | 30.914 6 | -0.004 1 | 10.697 5 | |
| 3 | 31.095 3 | 0.003 0 | 11.282 3 | 31.715 9 | 0.001 0 | 11.613 3 | |
| 3 | 31.636 5 | 0.002 9 | 13.463 5 | 30.990 5 | 0.003 9 | 13.862 7 | |
| 4 | 31.147 8 | 0.001 7 | 14.426 4 | 31.847 3 | -0.002 3 | 14.799 7 | |
| 4 | 31.862 6 | 0.001 9 | 16.563 3 | 31.161 0 | 0.004 2 | 16.998 9 | |
| 5 | 31.246 2 | 0.000 1 | 17.617 5 | 31.852 3 | 0.001 9 | 17.936 8 | |
| 5 | 31.830 9 | 0.006 0 | 19.811 3 | 31.161 4 | 0.001 9 | 20.225 9 | |
| 6 | 31.365 6 | -0.001 9 | 20.800 6 | 32.011 7 | 0.002 7 | 21.140 5 | |
| 6 | 31.966 4 | -0.001 4 | 22.966 9 | 31.212 8 | -0.000 8 | 23.434 4 | |
| 7 | 31.425 6 | -0.003 8 | 23.956 2 | 32.042 7 | 0.004 9 | 24.280 5 | |
| 7 | 31.852 6 | 0.005 7 | 26.290 3 | 31.182 6 | 0.006 6 | 26.703 9 | |
| 8 | 31.439 1 | 0.006 9 | 27.088 3 | 32.335 5 | -0.005 6 | 27.561 3 | |
| 8 | 32.416 4 | 0.003 1 | 29.161 5 | 31.435 1 | 0.002 2 | 29.783 2 | |
| 9 | 31.652 4 | 0.004 7 | 30.316 6 | 32.583 3 | 0.004 9 | 30.829 2 | |
| 9 | 32.177 1 | 0.001 8 | 32.551 2 | 31.360 9 | 0.000 7 | 33.048 6 | |
| 10 | 31.669 9 | -0.000 5 | 33.440 5 | 32.529 8 | 0.002 5 | 33.893 1 | |
| 10 | 32.159 9 | -0.001 0 | 35.774 1 | 31.570 5 | -0.003 8 | 36.138 9 | |
| 11 | 31.704 9 | -0.007 3 | 36.585 0 | 32.478 9 | -0.000 5 | 36.993 5 | |
| 11 | 32.282 4 | 0.001 0 | 38.949 3 | 31.651 4 | 0.000 1 | 39.341 0 | |
3.2 交点计算
根据式(1)~式(7)编写MATLAB程序,对中径线与2~11号螺纹牙的交点进行计算,计算结果见表 2。
| 交点 | X | Y | Z |
| O2 | 31.792 1 | 0 | 8.533 1 |
| O3 | 31.881 1 | 0 | 11.701 0 |
| O4 | 31.980 3 | 0 | 14.871 0 |
| O5 | 32.067 7 | 0 | 18.050 0 |
| O6 | 32.167 5 | 0 | 21.222 0 |
| O7 | 32.273 8 | 0 | 24.403 0 |
| O8 | 32.370 7 | 0 | 27.580 0 |
| O9 | 32.455 3 | 0 | 30.759 0 |
| O10 | 32.571 5 | 0 | 33.915 0 |
| O11 | 32.660 6 | 0 | 37.089 0 |
3.3 中径线计算
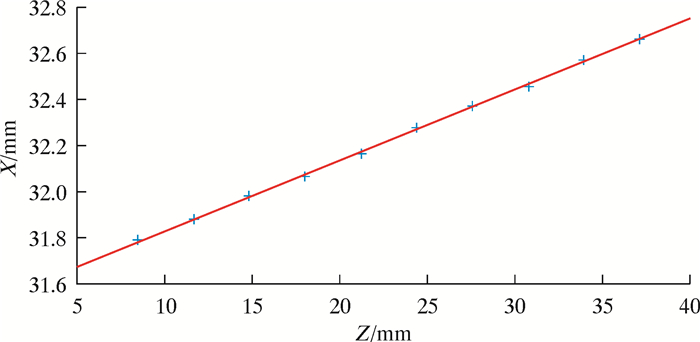
根据最小二乘法直线拟合原理编写了MATLAB程序,对表 2中各交点进行直线拟合,得到中径线如图 6所示。图 6中,横坐标为Z轴方向,即螺纹轴线方向;纵坐标为X轴方向,即垂直于螺纹轴线方向。
该中径线方程的数学表达式为:
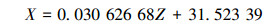
|
(15) |
|
| 图 6 中径线拟合图 Fig.6 Fitting diagram of middle diameter line |
分析图 6,对中径线进行误差评定,由式(8)得误差平方和:
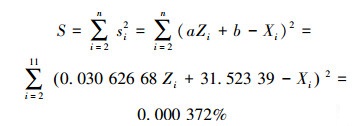
|
(16) |
最大偏差为:
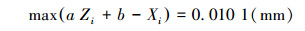
|
(17) |
由计算结果可知:各个交点的误差平方和为0.037 2%,小于0.1%;交点的最大偏差为0.010 1 mm,小于0.1 mm。两者误差小,各交点与中径线在整体上符合性好,说明中径线拟合精度高。
3.4 螺纹中径和螺距计算 3.4.1 螺纹中径由式(13)得:
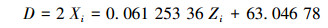
|
(18) |
利用得到的中径线方程对2~11号螺纹牙的交点处中径值进行计算,然后将计算得到的螺纹中径值与实际值进行比较,得到计算值相对于实际值的误差,如表 3所示。
| 螺纹牙编号 | Z轴取值/mm | 计算中径值/mm | 实际中径值/mm | 误差/% |
| 2 | 8.530 0 | 63.569 3 | 63.583 6 | 0.022 5 |
| 3 | 11.700 4 | 63.763 5 | 63.783 8 | 0.031 8 |
| 4 | 14.870 8 | 63.957 7 | 63.978 2 | 0.032 0 |
| 5 | 18.041 2 | 64.151 9 | 64.167 0 | 0.023 5 |
| 6 | 21.211 6 | 64.346 1 | 64.367 2 | 0.032 8 |
| 7 | 24.382 0 | 64.540 3 | 64.561 7 | 0.033 1 |
| 8 | 27.552 4 | 64.734 5 | 64.758 1 | 0.036 4 |
| 9 | 30.722 8 | 64.928 7 | 64.950 7 | 0.033 9 |
| 10 | 33.893 2 | 65.122 9 | 65.145 2 | 0.034 2 |
| 11 | 37.063 6 | 65.317 1 | 65.339 6 | 0.034 4 |
3.4.2 螺纹螺距
由式(14)得:
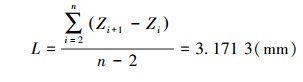
|
(19) |
利用本文方法计算得到的螺距是3.171 3 mm,实际螺距是3.170 4 mm,螺距计算值相对于实际值的误差是0.028 4%。
对比螺纹中径以及螺距的计算值和实际值可以得出,各螺纹牙中径和螺距测量精度高,误差不超过1%。
4 结论及认识(1) 给出了利用三坐标测量机测量油套管螺纹中径和螺距的方法,该方法适用于锥管螺纹,测量时不需要辅助测量装置。同时,该方法不但适用于已知理论中径和螺距的螺纹测量,而且适用于未知理论中径和螺距的螺纹测量。经过试验证明,该方法测量精度高、误差小,测量过程方便快捷。
(2) 在本文方法的基础上,可以通过三坐标测量机编程自动测量螺纹牙侧数据,再利用计算机编程并结合最小二乘法拟合得到油套管锥螺纹中径线方程。
(3) 在本文方法测得油套管螺纹接头关键参数的基础上,可以快速在计算机中建立测量接头的三维几何模型,依托几何模型可以开展有限元力学分析,或者在逆向工程中进行产品的优化设计。
| [1] |
朱加强, 史交齐. API圆螺纹接头连接强度的影响因素研究[J]. 石油机械, 2014, 42(5): 91-95. ZHU J Q, SHI J Q. Research on the factors influencing the connection strength of API knuckle thread joint[J]. China Petroleum Machinery, 2014, 42(5): 91-95. DOI:10.3969/j.issn.1001-4578.2014.05.021 |
| [2] |
崔继强, 徐和林, 刘学强, 等. 连接螺纹在塑性变形下的受力特性及参数优化[J]. 石油机械, 2014, 42(8): 49-52. CUI J Q, XU H L, LIU X Q, et al. Stress characteristics and parameters optimization of coupling thread with plastic deformation[J]. China Petroleum Machinery, 2014, 42(8): 49-52. DOI:10.3969/j.issn.1001-4578.2014.08.012 |
| [3] |
邵莉. 外螺纹中径三针法测量技术研究[J]. 计量与测试技术, 2016, 43(12): 37-38, 40. SHAO L. The external thread diameter three measured by technology research[J]. Metrology & Measurement Technique, 2016, 43(12): 37-38, 40. |
| [4] |
沈志平. 关于三针法测量螺纹中径计算公式的探讨[J]. 机械制造与自动化, 2010, 40(3): 59-62. SHEN Z P. Discussion on formulas of measuring pitch diameter of thread by measuring 3-pin[J]. Machine Building & Automation, 2010, 40(3): 59-62. DOI:10.3969/j.issn.1671-5276.2010.03.019 |
| [5] |
张小梅, 魏华, 王韵龙, 等. 圆锥螺纹三针法检测技术浅析[J]. 计测技术, 2013, 33(增刊2): 12-14, 23. ZHANG X M, WEI H, WANG Y L, et al. Analysis on the detection technology of conical thread three-needle method[J]. Metrology & Measurement Technology, 2013, 33(S2): 12-14, 23. |
| [6] |
何燕侠, 刘振宁. 浅析螺纹的几种测量方法[J]. 汽车实用技术, 2016(4): 127-128. HE Y X, LIU Z N. The comparison among several measuring methods of thread[J]. Automobile Applied Technology, 2016(4): 127-128. |
| [7] |
王朋, 马铁华, 崔春生. 对螺纹中径直接测量仪的设计研究[J]. 电子器件, 2017, 40(4): 1049-1052. WANG P, MA T H, CUI C S. The design and research of the measuring instrument for the diameter of thread[J]. Chinese Journal of Electron Devices, 2017, 40(4): 1049-1052. DOI:10.3969/j.issn.1005-9490.2017.04.050 |
| [8] |
GADELMAWLA E S. Computer vision algorithms for measurement and inspection of external screw threads[J]. Measurement, 2017, 100(1): 36-49. |
| [9] |
张现东, 卜昆, 董一巍. 航空发动机叶片三坐标测量优化采样方法[J]. 航空动力学报, 2019, 34(1): 168-176. ZHANG X D, BU K, DONG Y W. Optimal sampling strategy for aero-engine blade inspection with coordinate measuring machine[J]. Journal of Aerospace Power, 2019, 34(1): 168-176. |
| [10] |
YOUNES E, ABDERRAZAK E O, AHMED C. Experimental investigation of dynamic errors in coordinate measuring machines for high speed measurement[J]. International Journal of Precision Engineering and Manufacturing, 2018, 19(8): 1115-1124. DOI:10.1007/s12541-018-0132-x |
| [11] |
陈大伟, 陈岳坪, 杨翊, 等. 复杂曲面的三坐标测量机采样参数选取[J]. 机械设计与制造, 2018(1): 209-211. CHEN D W, CHEN Y P, YANG Y, et al. Sampling parameter selection of CMM for complex surface[J]. Machinery Design & Manufacture, 2018(1): 209-211. DOI:10.3969/j.issn.1001-3997.2018.01.059 |
| [12] |
王庆广, 马树元, 吴平东, 等. 三坐标测量机测量外螺纹螺距和中径的方法[J]. 计量技术, 2002(4): 11-13. WANG Q G, MA S Y, WU P D, et al. Method for measuring external thread pitch and medium diameter by coordinate measuring machine[J]. Measurement Technique, 2002(4): 11-13. DOI:10.3969/j.issn.1000-0771.2002.04.004 |
| [13] |
刘浩, 党养正, 程锡铜, 等. 三坐标测量机测量螺纹量规的一种方法[J]. 计测技术, 2013, 33(1): 29-31. LIU H, DANG Y Z, CHENG X T, et al. Thread gauge measurement with CMM[J]. Metrology & Measurement Technology, 2013, 33(1): 29-31. DOI:10.3969/j.issn.1674-5795.2013.01.008 |
| [14] |
张欣, 李凌梅, 马艺清, 等. 大尺寸圆柱螺纹量规中径测量方法[J]. 中国标准化, 2017(14): 47-48. ZHANG X, LI L M, MA Y Q, et al. Large-size cylindrical thread gauge medium diameter measuring method[J]. China Standardization, 2017(14): 47-48. DOI:10.3969/j.issn.1002-5944.2017.14.039 |
| [15] |
张波, 曾燕华, 张文建, 等. 大尺寸圆锥螺纹量规基面中径测量方法[J]. 上海计量测试, 2017, 44(1): 10-14. ZHANG B, ZENG Y H, ZHANG W J, et al. Measuring method for base level middiameters of large size conical thread gauges[J]. Shanghai Measurement and Testing, 2017, 44(1): 10-14. DOI:10.3969/j.issn.1673-2235.2017.01.006 |
| [16] |
刘兴富. 非最佳量针测量螺纹的定义中径[J]. 汽车零部件, 2013(10): 103-106. LIU X F. Analysis of non optimal amount of needle measure out defined pitch diameter of thread[J]. Automobile Parts, 2013(10): 103-106. |
| [17] |
冯娜.基于三坐标测量技术在石油用螺纹量规校准中的应用[D].西安: 西安石油大学, 2010. FENG N. The application of coordinate measuring technology in the oil screw gauge calibration[D]. Xi'an: Xi'an Shiyou University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10705-1012296332.htm |
| [18] |
赵卿.石油螺纹标准量具的三坐标测量机检测方法[D].天津: 天津大学, 2016. ZHAO Q. Standard measuring tool of petroleum thread gauge using coordinate measuring machine[D]. Tianjin: Tianjin University, 2016. |
| [19] |
陈欣, 曲绍波, 刘芳, 等. 数值分析[M]. 北京: 电子工业出版社, 2018. CHEN X, QU S B, LIU F, et al. Numerical analysis[M]. Beijing: Publishing House of Electronics Industry, 2018. |


