2. 江苏省油气储运重点实验室
2. Jiangsu Key Laboratory of Oil-Gas Storage and Transportation Technology
0 引言
管道螺旋流动是一种剪切力大、悬浮能力强、能够提高颗粒物料输送浓度的流动。国内外学者通过多方面研究发现螺旋流输送可以有效解决颗粒团聚沉积、管道堵塞和管壁磨损等问题,在涡管排砂、气力输煤和旋风分离等方面有着广泛应用。孙西欢[1]和路明[2]论述了导叶安放角对螺旋流周向运动和阻力的重要影响,认为局部起旋器的导流条安放角控制在0°~20°可以使水流不脱流,从而获得较充分的周向流动且避免较大的阻力。王树立等[3-5]研究了在管道螺旋流动体系下扭带诱导的气液两相的特点,发现在弥散流时,其生成的效果最为显著。F.T.KANIZAWA等[6]对以扭带起旋的气液两相流进行了试验研究,得到5种流型,并提出一种新方法来预测气液两相螺旋流的压降。刘雯等[7]研究了短螺旋扭带引发的单相及气液两相螺旋流动的特点,发现在单相流动中随着雷诺数增大螺旋涡的螺距减小,在气液两相环雾状流中气相轴向速度出现两个峰值,液相沿周向分布不均匀。YIN J.L.等[8-9]设计了一种螺旋流起旋装置,采用高速可视化和图像处理技术对不同气泡尺寸和雷诺数下气泡的分离轨迹进行了试验研究。窦梅等[10]分析认为螺旋流动不仅强化了传热,而且可以清洗污垢。A.E.ZOHIR等[11]研究发现螺旋桨位置和螺旋弹簧螺距对换热增强有影响,使螺旋桨的压力增加。吴金星等[12]研究发现内置双螺旋线管能够强化传热,雷诺数在5 000~25 000范围内,努塞尔数提高了30%~100%。K.NANAN等[13]研究发现打孔扭带能够有效地减小压力,但是在传热方面却不如传统扭带,这是因为扭带打孔减小了流体阻力从而减小了湍流度。
管道输送作为五大运输方式之一,是天然气输送的最主要方式,但在输送过程中会生成水合物而堵塞管道。J.S.GUDMUNDSSON[14]基于动态控制理论,提出了天然气水合物浆液管道输送技术,使生成的水合物以微小晶粒的形式均匀稳定地分散在流体相中随流体向前流动,从而避免天然气输送管道因水合物聚集而堵塞, 保证输气管道的安全流动。由于平直流动会使水合物颗粒沉积,所以用螺旋流动来保证水合物浆液管输技术的安全将会成为一个研究热点。
目前直管内起旋器以扭带叶轮等为主并且都是在入口端局部起旋,而对于全管段起旋的研究较少。为此,本文采用导流条全管段起旋研究不同导流条安放角对旋流数、湍流动能、水合物颗粒的沉积规律、速度场和温度场的影响。模拟方案中颗粒相采用DPM(Discrete phase model)模型,流体流场采用RNG k-ε模型进行耦合计算。研究结果可为螺旋管流安全输送天然气水合物提供理论依据和技术指导。
1 数值模拟理论模型 1.1 控制方程连续性方程为:
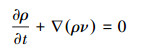
|
(1) |
动量方程为:
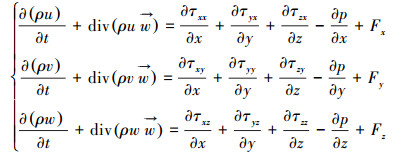
|
(2) |
能量方程为:
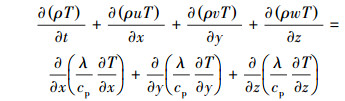
|
(3) |
本文采用RNG k-ε湍流模型, 因为它适合强旋流的复杂剪切流动[15]。湍流动能k和耗散率ε的传输方程模型为:
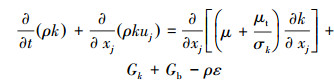
|
(4) |
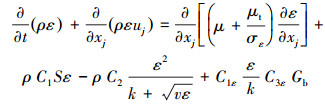
|
(5) |
其中:
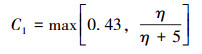
|
(6) |
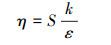
|
(7) |
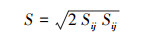
|
(8) |
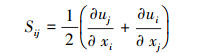
|
(9) |
式中:Gk和Gb分别表示由平均速度梯度和浮力而产生的湍流动能,C2、C1ε和C3ε为常数,σk和σε分别是k和ε的湍流普朗特数,ρ、cp、T、λ分别为气体密度、定压比热容、温度和热导率,u、v、w均为速度,t为时间。
其中包含密度和黏度在内的整体性质由两种流体的体积分数加权平均值确定。湍流黏度μt由下式确定:
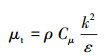
|
(10) |
DPM模型通过计算颗粒受到的作用力得到颗粒运动方程,将DPM模型的颗粒运动方程对时间积分可以得到颗粒运动轨迹。在z方向固体颗粒轨迹的运动方程为[16]:
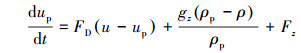
|
(11) |
式中:u为流体相速度,m/s;up为颗粒速度,m/s;gz为重力加速度在z方向上的分量,m/s2; ρ为流体密度,kg/m3;ρp为颗粒密度,kg/m3。
颗粒受到的其他作用力Fz主要包括颗粒周围流体加速而引起的附加质量力、布朗力和Staffman升力等。附加质量力主要作用于流体相密度大于颗粒密度的情况,管道内水合物颗粒密度大于气流密度,故不需要考虑附加质量力。
FD的计算式为:
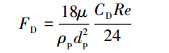
|
(12) |
Re为相对雷诺数,计算式如下:
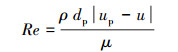
|
(13) |
式中:dp为颗粒直径,m。
曳力系数CD可采用如下表达式:
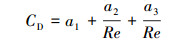
|
(14) |
式中:当5 000 < Re < 1 0000时,a1=0.46,a2=-490.546,a3=578 700;当Re>10 000时,a1=0.519 1,a2=-16 625.5,a3=5 416 700。
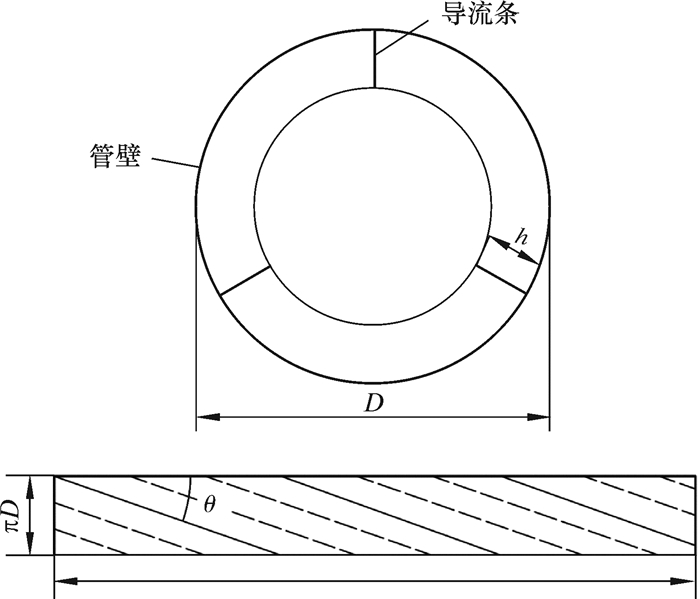
1.2 几何模型导流条断面结构如图 1所示。在起旋器管段内壁固定导流条,导流条是由长方形板条扭转而成的曲面,其长边与管壁固定相连,短边垂直于管壁切线。短边长度为导流条的高度h,导流条个数为n,导流条在管壁一侧的交线与轴向方向的夹角为导流条的安放角θ。
|
| D—管壁内径;h—导流条高度;θ—导流条安放角;πD—管道周长;L—管道总长。 图 1 导流条断面结构示意图 Fig.1 Schematic diagram of the cross-section structure of the guide strip |
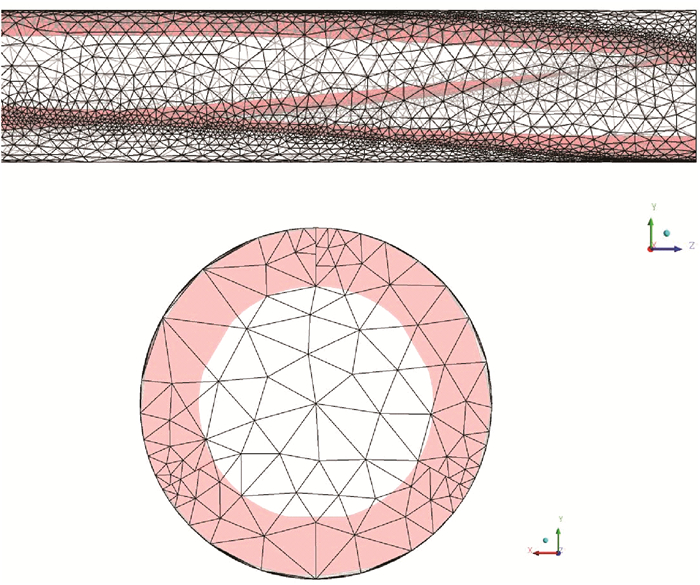
采用SolidWorks软件建立了不同规格导流条与管道组合的几何模型,如图 2所示。水平管道直径D=0.03 m,长L=2 m,从入口处开始加装导流条。采用ICEM-CFD软件对三维几何模型进行网格划分,全管采用非结构性网格,网格划分如图 3所示。

|
| 图 2 导流条几何模型 Fig.2 Guide strip geometry model |
|
| 图 3 网格划分 Fig.3 Mesh generation |
1.3 初始条件
气相为甲烷,连续流体,其密度为0.77 kg/m3,动力黏度为1.103 5×10-5 Pa·s,定压比热容为2.182 kJ/(kg·K),热导率为0.033 2 W/(m·K)。固相为天然气水合物颗粒,其密度为915 kg/m3。计算时采用直角坐标系,Z轴是流动方向,重力沿Y轴负方向,重力加速度为-9.81 m/s2。在管道入口端设置速度入口为边界条件,出口边界条件采用outflow条件。入口温度为280 K,壁面温度为277 K。选取DPM模型和RNG k-ε湍流模型进行气固两相三维瞬态模拟,采用压力基和分离求解器。壁面条件采用无滑移边界条件和标准壁面函数法。天然气管道中流体以及水合物颗粒温度相同,不存在温差,而且模拟中设定水合物颗粒为同一粒径的均质球体。由于本次模拟的是全管段加装导流条,安放角增大不会引起水流产生脱流现象,故在模拟方案中导流条的安放角适当增大到25°。根据研究内容来选定参数:颗粒体积分数8%,颗粒粒径10 μm,Re=20 000;导流条高度为D/6,数量为3,安放角θ=10°、15°、20°、25°。
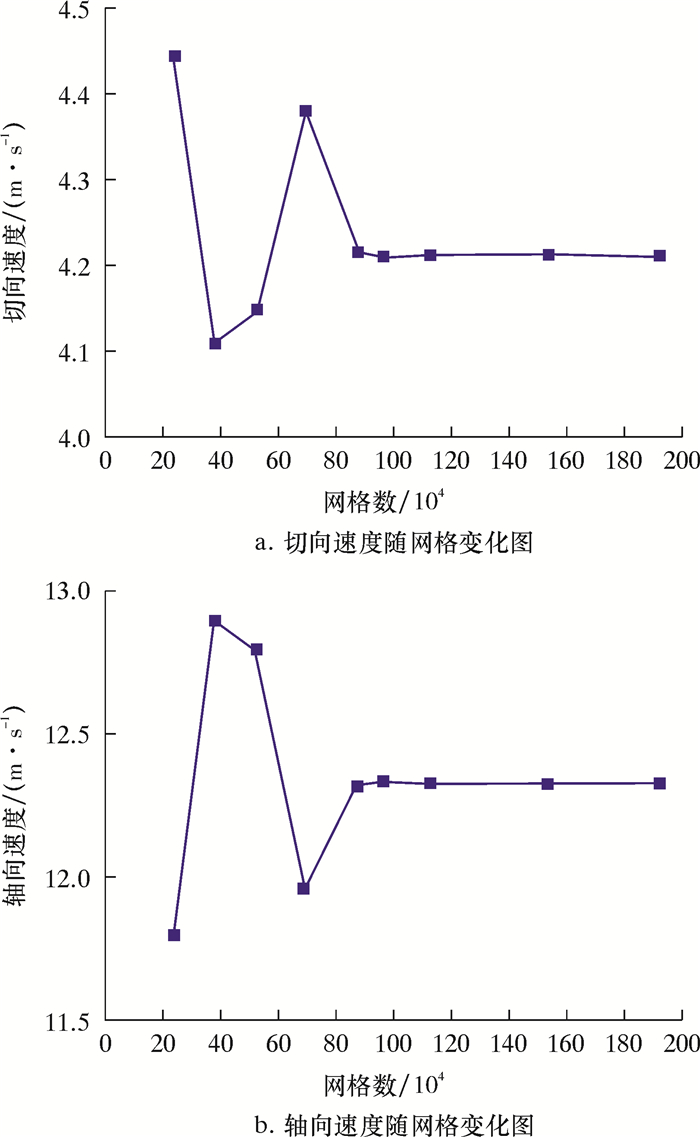
1.4 网格无关性验证网格无关性验证结果如图 4所示。
|
| 图 4 网格无关性验证 Fig.4 Grid independence verification |
为了减小网格数量对计算结果的影响、提高模拟效率,采用网格无关性验证对网格数量进行筛选。在相同试验工况下取(2~20)×105的网格进行模拟,并取管道同一截面位置的平均轴向流速和切向流速进行对比。由图 4可见,当网格数大于8×105时,网格数的变化对切向速度和轴向速度的影响非常小,故在考虑了计算效率和结果的精确性后,最终选取1×106左右的网格作为模拟试验用网格。
2 模拟结果与分析 2.1 旋流数变化规律旋流数S是表征螺旋流流动特性的重要物理量,气固两相管道螺旋流动的旋流数S定义如下:
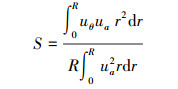
|
(15) |
式中:ua为轴向速度, m/s; uθ为切向速度, m/s; R为管道直径, m; r为螺旋管道的径向坐标。
湍流扰动(脉动)可以忽略不计,因此可认为式(15)中的速度是时均速度。
式(15)化简得:
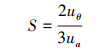
|
(16) |
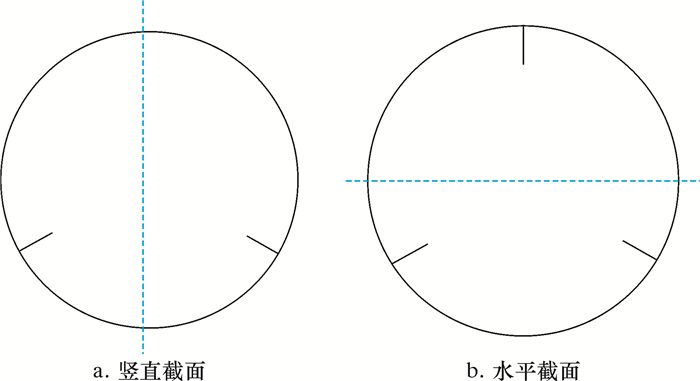
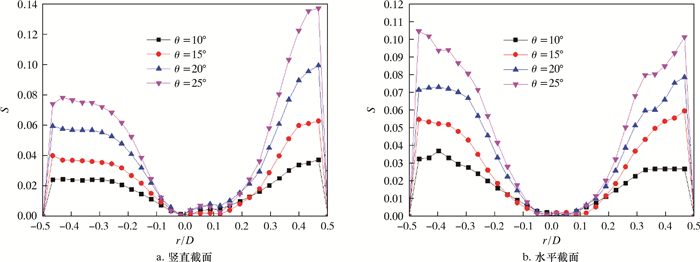
图 5是两种径向旋流数获取的方法。图 5a是导流条在第一个导程结束位置竖直截面的数据,图 5b是导流条在第一个导程结束位置水平截面的数据。两种旋流数获取方法所得到的结果有明显区别,如图 6所示。
|
| 图 5 两种径向旋流数获取方法 Fig.5 Two obtaining methods of radial swirl number |
|
| 图 6 导流条安放角对管道内旋流数径向变化的影响 Fig.6 he influence of the guide strip angle on the radial change of the swirl number in the pipe |
从图 6可以看出,用图 5a所得的径向旋流数过导流条一侧明显高于不过导流条的一侧,而用图 5b水平切线所得的径向旋流数两侧保持平衡。除此区别外,两种方法还有相同之处:径向旋流数整体数值随着安放角增大而增大,其极大值出现在靠近管壁处,管道轴心处旋流数趋向于0。
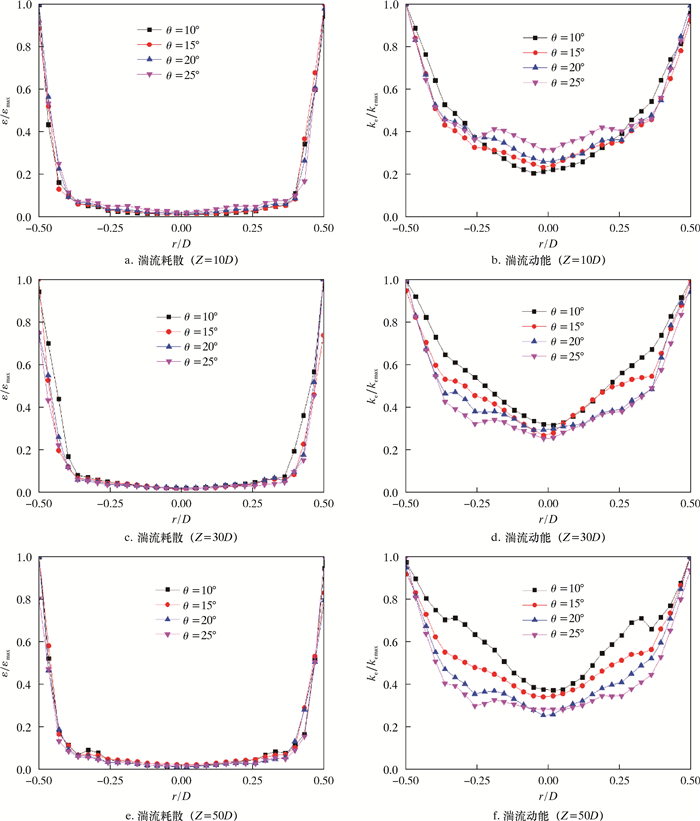
2.2 湍流涡流耗散和湍流动能变化规律湍流动能ke是对湍流强度的度量,决定了流动维持湍流或发展成湍流的能力,因而是流动稳定性的标志。导流条安放角不同,其整管段的导程周期也不同,在相同位置截面处导流条所处的位置也不同。因此,为了获得更好的对比效果,不按相同距离选取截面,而是先选取相同距离的基准截面,再分别选取距离基准面最近的半周期位置(导流条旋转未满一个周期,在旋转120°和240°时3片导流条位置与入口“人”字状初始位置相同,即为半周期位置)或全周期位置(导流条从入口端开始旋转了360°,此处即为全周期位置)。图 7所示为不同安放角导流条在不同基准面附近半周期位置的归一化湍流耗散和湍流动能变化图。图 7中的横坐标r/D为检测点所在位置距管轴心距离和管径的比值,纵坐标为归一化后的湍流耗散和湍流动能。从图 7可以看出,湍流涡流耗散ε和湍流动能ke在管壁附近较高并且左右两侧不相等,越靠近轴心区域越小。随着流动距离的增加,流体在不间断地做螺旋运动,湍流涡流耗散ε和湍流动能ke的极大值位置不断地左右变化。这是由于湍流不守恒,所以在湍流产生最多的地方会出现湍流动能的最大值,因此也会出现最大的耗散率。湍动能变化越剧烈,该处的脉动越强,二次涡的形成效率增加,而涡耗散越大形成的二次涡或者尾流的小涡也越多,二者相辅相成所形成的螺旋流强度越强。ε/εmax和ke/kemax在管壁非极大值侧的数值随安放角θ增大而减小,并且随着输送距离的增加越来越小。这说明安放角θ越大,螺旋流强度越大,整管段流体与导流条的碰撞越剧烈。
|
| 图 7 不同基准面附近半周期位置导流条安放角与归一化后湍流耗散和湍流动能的关系 Fig.7 The relationship between the guide strip angle at the half-period position near different reference planes and the normalized turbulent dissipation and turbulent flow energy |
2.3 颗粒体积分数变化规律
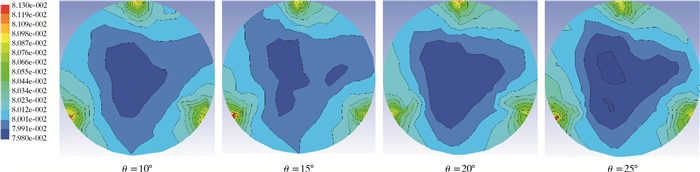
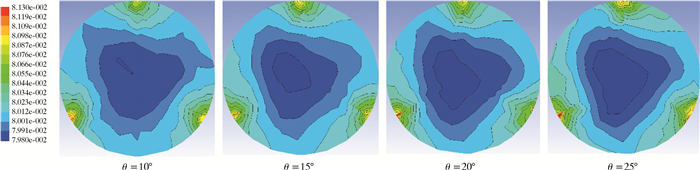
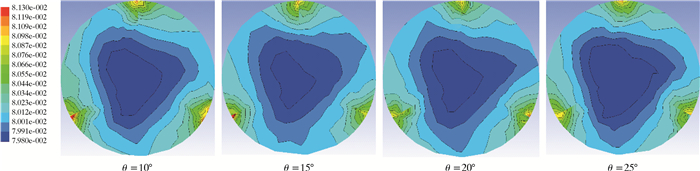
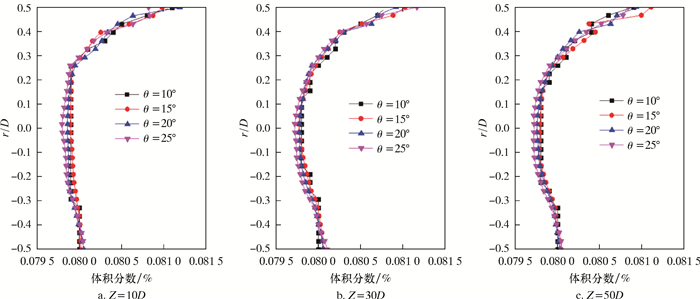
图 8~图 10是Z=10D、30D和50D基准面附近半周期或全周期截面位置导流条安放角对管内水合物颗粒体积分数分布的影响。从图 8~图 10可以看出,颗粒高体积分数区域集中在3块导流条附近,并且导流条迎风面颗粒体积分数明显高于背风面,轴心位置体积分数极小值区域随流动距离的增加逐渐变大。这说明螺旋有良好的颗粒携带效果,颗粒不会因重力影响沉积在管底中央。其中在安放角θ=25°的导流条管道中,导流条迎风面颗粒体积分数大于位于其他3个不同安放角的管道。这说明此时螺旋流较大,颗粒所受到的螺旋流离心力太大使颗粒向导流条附近集中,但由于强旋流提供的剪切应力使水合物颗粒不会沉积下来,而是紧贴着导流条向前做螺旋流动。图 11是不同基准面附近半周期或全周期位置竖直切线导流条安放角对水合物颗粒体积分数径向分布的影响。图 11中横坐标为体积分数,纵坐标为检测点所在位置距管轴心距离和管径的比值。从图 11可以看出,管底位置体积分数基本没变化,没有出现沉积现象,管上端导流条附近颗粒体积分数最大,安放角对导流条附近颗粒体积分数极大值无明显影响。这说明颗粒在导流条附近只是聚集在一起流动,并非聚集沉积或者贴附在导流条上不动。
|
| 图 8 Z=10D基准面附近半周期或全周期截面位置导流条安放角对管内水合物颗粒体积分数分布的影响 Fig.8 The effect of the guide strip angle on the half-period or full-period cross-section near the Z=10D reference plane on the volume distribution of hydrate particles in the pipe |
|
| 图 9 Z=30D基准面附近半周期或全周期截面位置导流条安放角对管内水合物颗粒体积分数分布的影响 Fig.9 The effect of the guide strip angle on the half-period or full-period cross-section near the Z=30D reference plane on the volume distribution of hydrate particles in the pipe |
|
| 图 10 Z=50D基准面附近半周期或全周期截面位置导流条安放角对管内水合物颗粒体积分数分布的影响 Fig.10 The effect of the guide strip angle on the half-period or full-period cross-section near the Z=50D reference plane on the volume distribution of hydrate particles in the pipe |
|
| 图 11 不同基准面附近半周期或全周期位置竖直切线导流条安放角对水合物颗粒体积分数径向分布的影响 Fig.11 The effect of the vertical tangent guide strip angle on the radial distribution of hydrate particle volume fraction at the half-period or full-period positions near different reference planes |
2.4 速度变化规律
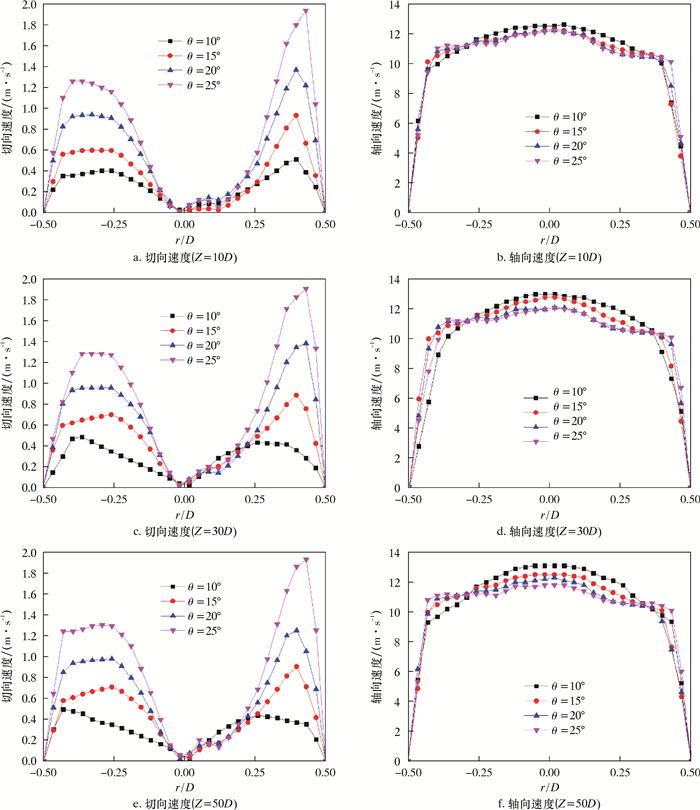
图 12是不同截面位置导流条安放角对切向速度和轴向速度分布的影响。从图 12可以看出,导流条安放角越大,切向速度越大,轴向速度越小。切向速度的极大值出现在靠近管壁处,轴心区域切向速度趋于0,而且右侧明显大于左侧。这是因为此处切线为b类水平切线(不过导流条),螺旋流是顺时针旋转,左侧切向速度方向向上,右侧切向速度方向向下,重力对右侧下降的颗粒起加速作用,对左侧上升的颗粒起减速作用。轴向速度极大值出现在管道轴心处,越靠近管壁轴向速度越小,并且左侧轴向速度略大于右侧轴向速度。除此以外,随着流动距离的增加,轴向速度极大值的差距逐渐变大,导流条安放角越大,轴向速度极大值区域的值越小。在过Z=10D基准面位置后,导流条安放角θ=10°和θ=15°的管道轴向速度极大值显著升高,并且极大值区域开始向轴心收缩,曲线开始呈尖头状。导流条安放角θ=20°和θ=25°的管道轴向速度极大值略减小。这是因为管内流体撞击导流条进行螺旋运动时存在动能损失,导流条安放角θ越大,流体撞击导流条越猛烈,动能损失得越多,当起旋距离很长时,这些动能的损耗会体现在轴向速度的衰减上。
|
| 图 12 不同截面位置导流条安放角对切向速度和轴向速度分布的影响 Fig.12 The effect of guide strip installation angle at different cross-sectional positions on tangential velocity and axial velocity |
2.5 温度变化规律
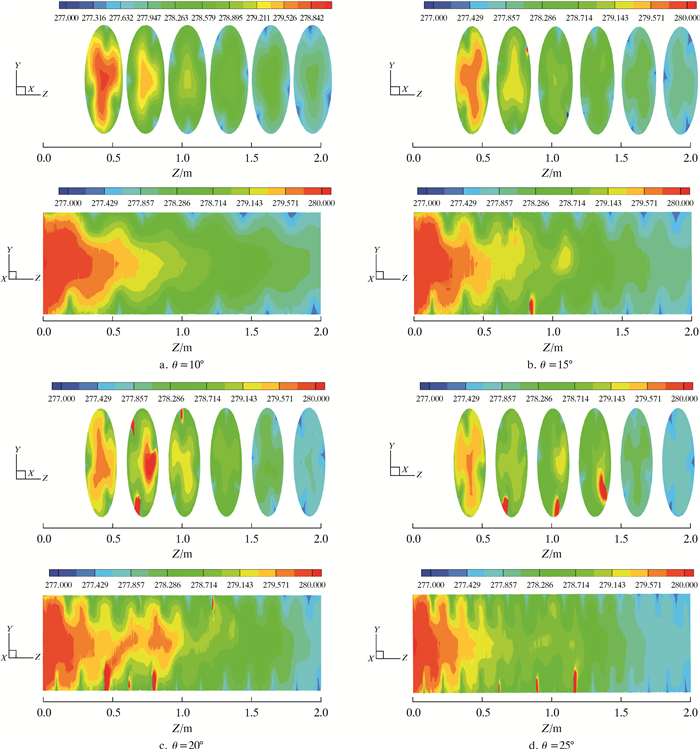
图 13是导流条安放角对管道内温度分布的影响。从图 13可以看出,导流条安放角越大,管道出口段温度越低,说明导流条有提高传热效率的作用。在导流条安放角θ=10°的管道内,温度分布呈均匀衰减状,而在导流条安放角θ=15°、20°和25°的管道内,0.5~1.2 m范围内出现局部温度升高的现象,除入口处的温度极大值外,其余的温度极大值区域出现在导流条附近及其至后方轴心范围。由上文湍流耗散率规律可知,由于湍流耗散率增加了二次涡的形成,从而增加了流体温度间的掺混,使温度的传递加快。在导流条安放角θ=20°时管道内这一现象尤其明显,温度梯度变化较快,传热效率最高。
|
| 图 13 导流条安放角对管内温度分布的影响 Fig.13 The effect of guide strip installation angle on the temperature distribution in the pipe |
2.6 压降变化规律
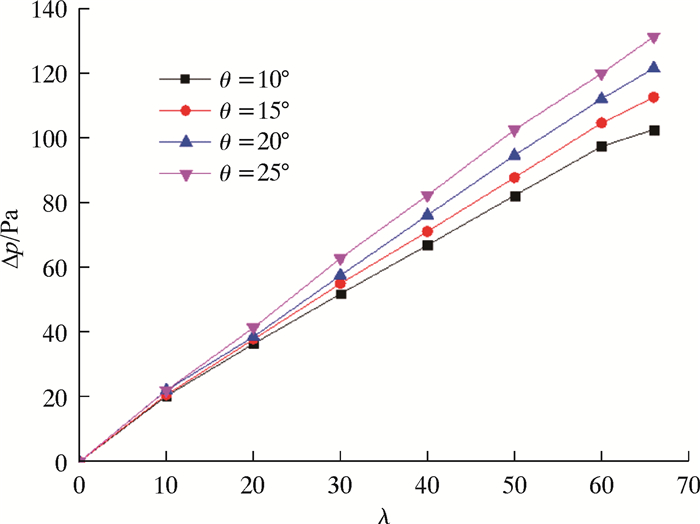
图 14是导流条安放角对压降的影响,图中横坐标λ为轴向方向流动距离与管道总长的比值,纵坐标(Δp)为压降。从图 14可以看出,随着输送距离的增加,安放角对管道压降的影响逐渐变大,安放角越大,压降越大,在管道出口端由于出口效应的存在,压力增长幅度变缓。
|
| 图 14 导流条安放角对压降的影响 Fig.14 The effect of guide strip installation angle on the pressure drop |
为了更好地判定导流条安放角的优良,引入管道旋流效能评价参数ξ,其物理意义为单位长度的压降所产生的旋流数,定义式为:
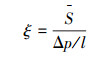
|
(17) |
式中: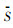
计算结果如表 1所示。从表 1可知:安放角越大,ξ越大,安放角在10°~25°范围内每增加5°,ξ增加0.12,在安放角为25°时达到极值;而安放角大于25°时,ξ开始缓慢减小,说明此时安放角过大导致导流条对流体的阻力过大。因此,从经济效益角度考虑,25°为导流条最佳安放角。
| θ/(°) | 10 | 15 | 20 | 25 | 30 | 35 |
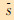
|
0.016 | 0.025 | 0.037 | 0.046 | 0.052 | 0.060 |
| ΔP/l | 0.051 | 0.056 | 0.061 | 0.066 | 0.073 | 0.085 |
| ξ | 0.321 | 0.442 | 0.610 | 0.727 | 0.716 | 0.705 |
3 结论
(1) 竖直截面所得的径向旋流数靠近导流条一侧的数值明显高于另一侧,而水平截面所得的径向旋流数两侧数值基本相等。径向旋流数整体数值随着安放角增大而增大,其极大值出现在靠近管壁处,管道轴心处旋流数趋向于0。
(2) 湍流耗散和湍流动能在管壁附近最高并且左右两侧不相等,越靠近轴心区域越小。切向速度与湍动能强度有关,切向速度越大,湍动能越强,增加了流体间的掺混,强化传热传质。安放角越大,螺旋流强度越大,整管段流体与导流条的碰撞越剧烈。
(3) 在计算工况范围内整管段颗粒不会沉积在管底中央,颗粒高体积分数区域集中在三块导流条附近,并且导流条迎风面颗粒体积分数明显高于背风面,轴心位置体积分数极小值区域随流动距离的增加逐渐变大。在安放角25°的导流条管道中,导流条迎风面颗粒体积分数高于位于其他三个不同安放角的管道。
(4) 导流条安放角越大,切向速度越大,轴向速度越小。切向速度的极大值出现在靠近管壁处,向下一侧的切向速度明显高于另一侧。轴向速度极大值出现在管道轴心处,越靠近管壁轴向速度越小。导流条安放角10°和15°的管道轴向速度随流动距离增加其极大值显著升高,并且极大值区域开始向轴心收缩,曲线开始呈尖头状。
(5) 导流条安放角越大,管道出口段的温度越低,传热效果越好。在导流条安放角15°、20°和25°的管道内,0.5~1.2 m范围内出现局部温度升高的现象,安放角20°的管道内这一现象尤其明显,温度梯度变化较快,传热效率最高。
(6) 随着输送距离的增加,安放角对管道压降的影响逐渐变大。安放角越大,压降越大,效能评价参数ξ越大,安放角在10°~25°范围内每增加5°,ξ增加0.12;而安放角大于25°时,ξ开始减小,因此25°为最佳安放角。
| [1] |
孙西欢.水平轴圆管螺旋流水力特性及固粒悬浮机理试验研究[D].西安: 西安理工大学, 2000. SUN X H. Experimental research on the hydraulic charateristics and particle suspended mechanics in spiral pipe flow with horizontal axis[D]. Xi'an: Xi'an University of Technology, 2000. |
| [2] |
路明.导流条安放角对筒装料管道水力输送特性影响的试验研究[D].太原: 太原理工大学, 2007. LU M.Experimental study of the effect of guide vanes installing angle on characteristics of tube-contained raw material transportation[D]. Taiyuan: Taiyuan University of Technology, 2007. |
| [3] |
王树立, 饶永超, 周诗岽, 等. 水合物法天然气管道输送的实验研究[J]. 天然气工业, 2014, 34(11): 101-107. WANG S L, RAO Y C, ZHOU S D, et al. An experimental study on deepwater natural gas transmission based on the hydrate slurry flow technology[J]. Natural Gas Industry, 2014, 34(11): 101-107. DOI:10.3787/j.issn.1000-0976.2014.11.014 |
| [4] |
王树立, 饶永超, 武玉宪, 等. 以纽带起旋的气液螺旋流实验研究[J]. 水动力学研究与进展A辑, 2013, 28(1): 105-110. WANG S L, RAO Y C, WU Y X, et al. Experimental study on gas-liquid spiral flow generated by twist tape[J]. Chinese Journal of Hydrodynamics, 2013, 28(1): 105-110. |
| [5] |
李建敏, 王树立, 饶永超, 等. 咪唑离子液体抑制甲烷水合物生成实验研究[J]. 科学技术与工程, 2014, 14(21): 230-233. LI J M, WANG S L, RAO Y C, et al. Experimental study of methane hydrate inhibition by imidazole ionic liquid[J]. Science Technology and Engineering, 2014, 14(21): 230-233. DOI:10.3969/j.issn.1671-1815.2014.21.042 |
| [6] |
KANIZAWA F T, RIBATSKI G. Two-phase flow patterns and pressure drop inside horizontal tubes containing twisted-tape inserts[J]. International Journal of Multiphase Flow, 2012, 47: 50-65. DOI:10.1016/j.ijmultiphaseflow.2012.07.003 |
| [7] |
刘雯, 骆政园, 白博峰. 管内含螺旋纽带诱导的螺旋涡特性[J]. 化工学报, 2011, 62(11): 3115-3122. LIU W, LUO Z Y, BAI B F. Helical vortices in circular pipe with twisted tape[J]. CIESC Journal, 2011, 62(11): 3115-3122. DOI:10.3969/j.issn.0438-1157.2011.11.020 |
| [8] |
YIN J L, QIAN Y L, MA Y F, et al. Experimental study on the bubble trajectory in an axial gas-liquid separator applied for tritium removal for molten salt reactors[J]. Nuclear Engineering and Design, 2017, 320: 133-140. DOI:10.1016/j.nucengdes.2017.05.015 |
| [9] |
YIN J L, QIAN Y L, ZHANG T T, et al. Numerical investigation on the bubble separation in a gas-liquid separator applied in TMSR[J]. Annals of Nuclear Energy, 2018, 114: 122-128. DOI:10.1016/j.anucene.2017.12.009 |
| [10] |
窦梅, 南碎飞, 段培清. 换热器内置弹簧脉冲流动防垢除垢实验研究[J]. 高校化学工程学报, 2010, 24(5): 893-896. DOU M, NAN S F, DUAN P Q. Experimental research on anti-fouling of heat exchanger by inserted spring and pulse flow[J]. Journal of Chemical Engineering of Chinese Universities, 2010, 24(5): 893-896. DOI:10.3969/j.issn.1003-9015.2010.05.028 |
| [11] |
ZOHIR A E, ABDEL-AZIZ A A, HABIB M A. Heat transfer characteristics in a sudden expansion pipe equipped with swirl generators[J]. International Journal of Heat & Fluid Flow, 2011, 32: 352-361. |
| [12] |
吴金星, 张灿灿, 郭桂宏, 等. 内置双旋线换热管内流动与传热数值模拟[J]. 工程热物理学报, 2014, 35(8): 1603-1605. WU J X, ZHANG C C, GUO G H, et al. Numerical simulation on flow and heat transfer for the tube inserted with double-spiral-line[J]. Journal of Engineering Thermophysics, 2014, 35(8): 1603-1605. |
| [13] |
NANAN K, THIANPONG C, PROMVONGE P, et al. Investigation of heat transfer enhancement by perforated helical twisted-tapes[J]. International Communications in Heat and Mass Transfer, 2014, 52: 106-112. DOI:10.1016/j.icheatmasstransfer.2014.01.018 |
| [14] |
GUDMUNDSSON J S. Cold flow hydrate technology[C]//Proceedings of the Fourth International Conference on Gas Hydrate. Yokohama: Tapir Academic Press, 2002: 912-916.
|
| [15] |
SHIH T H, LIOU W W, SHABBIR A, et al. A new k-ε eddy viscosity model for high Reynolds number turbulent flows[J]. Computers & Fluid, 1995, 24(3): 227-238. |
| [16] |
温正, 石良辰, 任毅如. FLUENT流体计算应用教程[M]. 北京: 清华大学出版社, 2009. WEN Z, SHI L C, REN Y R. FLUENT fluid computing application tutorial[M]. Beijing: Tsinghua Univeristy Press, 2009. |



