2. 中石油江汉机械研究所有限公司
2. Jianghan Machinery Research Institute Limited Company of CNPC
0 引言
连续管钻完井方式与传统钻完井方式相比,极大缩短了作业周期,减轻了劳动强度,降低了开采成本。连续管作业机因应用范围广,使用方便,被誉为“万能作业装备”[1-4]。连续管失效的4个主要原因是腐蚀、机械损伤、制造缺陷和人为误伤,这些因素导致的连续管失效占连续管失效的80%~92%。然而,无论是腐蚀还是其他原因,都会表现为连续管截面处产生缺陷,并在缺陷处产生应力集中现象,最终会在缺陷处引起裂纹萌生,使连续管过早疲劳失效[5-6]。
为了揭示连续管疲劳失效机理,并对其疲劳寿命进行准确和有效预测,国内外学者进行了大量试验和理论研究。YANG S.Y.[7]提出了塑性弯曲应变能方程,通过材料强度试验建立了连续管的直径增长预测模型。P.A.BROWN等[8]提出并改进了直径增长预测模型。K.P.NEWMAN[9]和S.M.TIPTON等[10-11]根据疲劳损伤的Miner线性累积理论,建立了完整连续管寿命评估模型。J.A.COLLINS[12]提出了连续管等效应力和等效总应变幅的概念。N.A.AVAKOV等[13]提出了以等效应变作为主应变的失效准则。WU J.[14]采用经验系数方法对连续管的工作寿命进行了预测。学者们针对完整连续管疲劳寿命开展了大量研究,但是有关含凹坑缺陷连续管疲劳失效机理的研究鲜见报道。
本文采用有限元方法研究含凹坑缺陷的连续管疲劳失效机理,建立了含凹坑缺陷连续管的有限元模型,在缺陷形状参数不同时对连续管缺陷处应力和应变进行了分析,所得结论为后续准确预测连续管疲劳寿命理论模型的建立提供了参考。
1 失效机理与模型建立 1.1 连续管低周疲劳失效机理连续管因其特殊性,需要缠绕在滚筒架上,在起下作业过程中需经过导向器。连续管1个工作行程发生6次弯直,即弯→直→弯→直→弯→直→弯。连续管在不断地弯直变形过程中将产生应力集中和塑性变形,应力集中和塑性变形加剧了连续管疲劳裂纹的萌生,从而使连续管疲劳失效。在运输和作业过程中连续管会产生凹坑缺陷,凹坑缺陷造成的应力集中大大降低了其疲劳性能[15-17]。
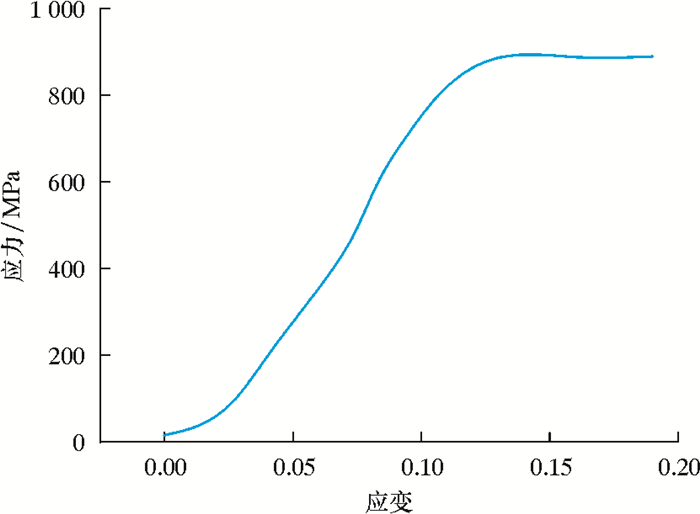
1.2 有限元模型建立与验证 1.2.1 CT110连续管材料性能随着油气勘探开发技术的不断发展,超高强度CT110连续管在页岩气开发中得到广泛应用[18-19]。笔者选用CT110连续管为研究对象,该连续管外径50.8 mm、壁厚4.4 mm。为满足CAE软件数值计算的需要,笔者参考文献[20],给出了CT110连续管材料试验的应力-应变曲线,如图 1所示。
|
| 图 1 CT110连续管材料试样应力-应变曲线 Fig.1 Stress-strain curve of CT110 coiled tubing material sample |
1.2.2 有限元模型
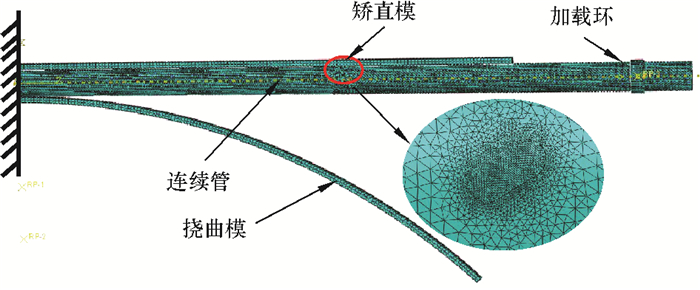
连续管的工作形式主要是带压作用下的弯-直交替变形,根据连续管工作特性,在CAE软件中建立如图 2所示的连续管低周疲劳寿命有限元模型。该模型由矫直模、挠曲模、加载环和连续管4部分组成。
|
| 图 2 连续管低周疲劳寿命有限元模型 Fig.2 Finite element model of low cycle fatigue life of coiled tubing |
该模型一端固定,另一端通过加载环施加位移载荷,实现连续管在挠曲模和矫直模之间的弯-直循环。挠曲模和矫直模材料为普通结构钢,并给两个模施加固定约束。连续管与2个模板的接触选择实体的面面接触,接触类型为无摩擦接触,求解方程选择惩罚函数法。缺陷处采用四面体单元网格进行细化,网格数目为304 531。
CT110连续管材料的弹性模量为191 GPa, 泊松比为0.3,屈服应力为758 MPa, 循环应变硬化系数为898。通过CAE软件计算连续管在挠曲模和矫直模之间的1次弯直循环,得到循环过程中的应力应变结果,然后提取1个完整循环过程的应力应变数据。通过数据分析,得到影响连续管疲劳性能的主要因素和疲劳失效机理。
1.2.3 有限元模型验证为了验证有限元模型的可靠性,根据文献[21]中的试验建立如图 2所示模型。该模型中连续管钢级为CT110,直径为60.3 mm,壁厚为5 mm。文中分别将完整连续管和含缺陷连续管的有限元应变值与试验应变值进行对比,结果如表 1所示。由表 1可知,试验值和有限元值的最大误差为9.8%。这个误差在工程可接受范围内,说明所建立的有限元模型准确。
| 试样 | 试验值 | 有限元值 | 误差 |
| 完整管 | 2.53 | 2.30 | 9.0 |
| 缺陷管1 | 5.00 | 4.51 | 9.8 |
| 缺陷管2 | 4.80 | 4.51 | 6.0 |
2 缺陷参数对连续管疲劳失效的影响
对含凹坑缺陷的连续管带压循环弯曲过程进行有限元分析,研究凹坑轴向角度、长度、深度、宽度和缺陷环向分布个数5个因素对连续管疲劳失效的影响,从而得出影响疲劳寿命的敏感参数。
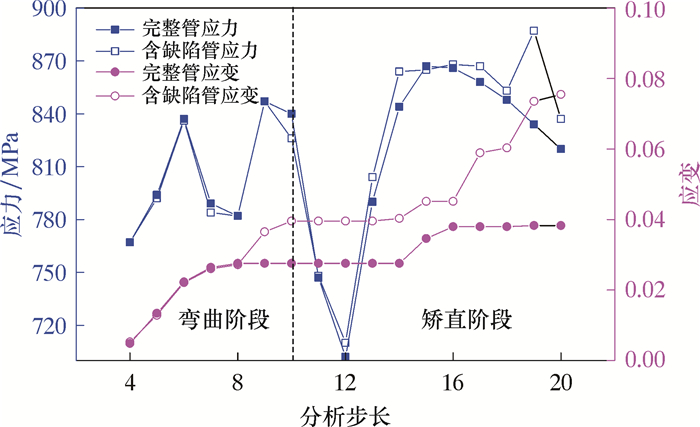
2.1 缺陷连续管与完整连续管对比分析对完整连续管和含凹坑缺陷的连续管在1个循环弯曲过程中的应力-应变变化过程进行了对比分析,所选钢级为CT110,管径为50.8 mm,壁厚为4.4 mm。分析时设凹坑缺陷深度为1 mm,长度为11 mm,轴向角度为30°,宽度为5 mm。图 3是完整连续管与含缺陷连续管应力及应变对比曲线。
|
| 图 3 完整连续管与含缺陷连续管应力及应变对比曲线 Fig.3 Comparison curves of stress-strain between intact coiled tubing and coiled tubing with defects |
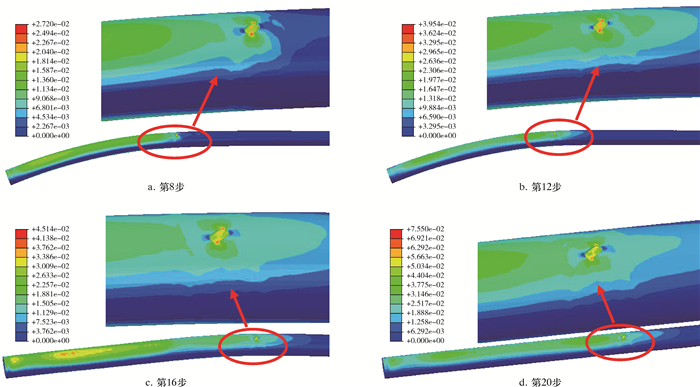
1个循环过程包括弯曲和矫直2个阶段,在弯曲阶段后期,缺陷管的应力已经大于完整管的应力,等效塑性应变明显大于完整管等效塑性应变。矫直阶段完成后,完整管和缺陷管的应变分别达到0.038 31和0.075 50。图 4为含缺陷连续管1个完整循环过程的等效塑性应变云图。
|
| 图 4 含缺陷连续管等效塑性应变云图 Fig.4 Equivalent plastic distribution of coiled tubing with defect |
2.2 凹坑轴向角度对连续管疲劳失效的影响
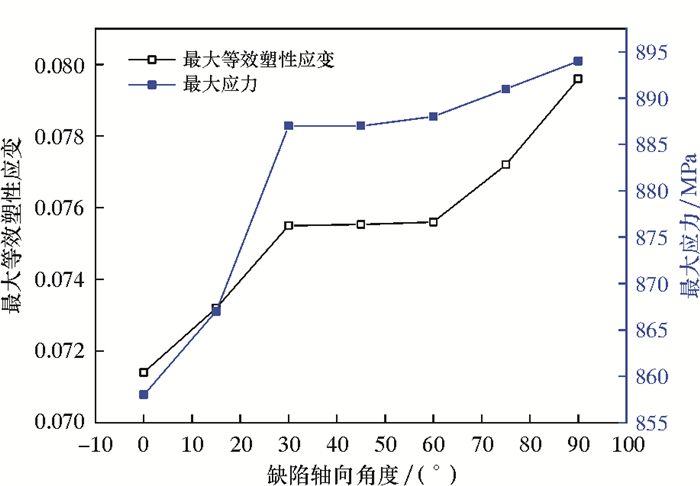
凹坑缺陷沿轴向角度范围为0°~90°,缺陷沿轴向角度的变化对连续管疲劳失效的影响如图 5所示。由图 5可知:当缺陷轴向角度为0°和90°时,连续管的等效塑性应变分别是0.071 4和0.079 6,增大幅度达11.48%;当缺陷轴向角度在0°~30°范围内时,应力和应变随着缺陷角度的增加近似呈线性增加;当缺陷轴向角度在30°~60°范围内时,应力应变值没有明显的波动;当缺陷轴向角度在60°~90°范围内时,应变仍然有大幅增大。在同种工况下,与完整连续管疲劳失效情况对比,含缺陷连续管应变上升幅度达107.78%。图 6为连续管在缺陷轴向角度为30°时的断裂图。由图 6可知,连续管的断裂路径与有限元分析结果一致,都沿着凹坑的对角线断裂,进一步证实了有限元计算结果的准确性。
|
| 图 5 缺陷轴向角度对连续管失效的影响曲线 Fig.5 The effect of the defect axial angle on the failure of the coiled tubing |

|
| 图 6 连续管在缺陷轴向角度为30°时的断裂图 Fig.6 Fracture diagram of the coiled tubing when the axial angle of the defect is 30° |
由以上分析可知:在工程应用中,当缺陷轴向角度为0°~30°和60°~90°时,连续管的性能随着角度的增加下降幅度很大;当缺陷轴向角度在30°~60°范围内时,缺陷轴向角度的变化对连续管的疲劳性能没有明显影响。
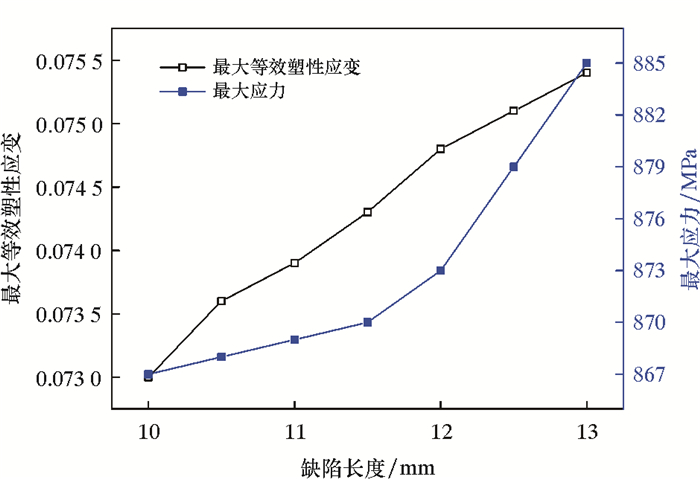
2.3 凹坑长度对连续管疲劳失效的影响保持内压35 MPa、缺陷深度1 mm、缺陷宽度5 mm、缺陷轴向角度30°不变,改变缺陷长度,分析缺陷长度对连续管疲劳失效的影响,结果如图 7所示。由图 7可知,在缺陷长度从10 mm增大到13 mm的过程中,连续管的应变由0.073 0增大到0.075 4,上升幅度约为3.29%。在同种工况下,与完整连续管疲劳性能进行对比,含缺陷连续管应变上升幅度达96.80%。
|
| 图 7 缺陷长度对连续管疲劳失效的影响曲线 Fig.7 The effect of defect length on fatigue failure of coiled tubing |
2.4 凹坑深度对连续管疲劳失效的影响
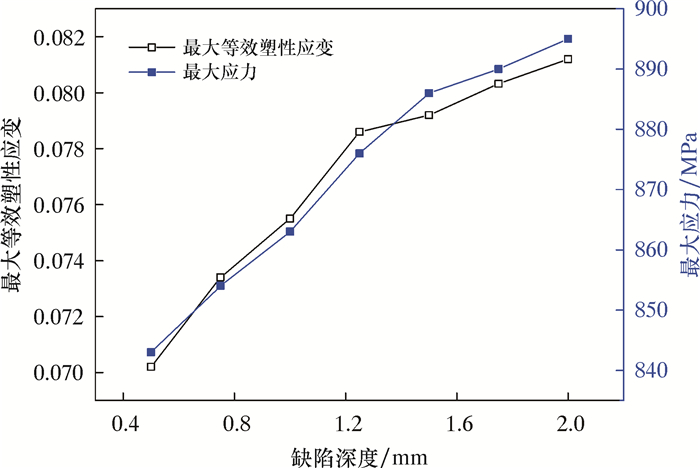
保持内压35 MPa、缺陷宽度5 mm、缺陷长度11 mm、缺陷轴向角度30°不变,改变缺陷深度,分析缺陷深度对连续管疲劳失效的影响,结果如图 8所示。由图 8可知,连续管应变由0.070 2上升到0.081 2,上升幅度为15.67%。在同种工况下,与完整连续管进行对比,含缺陷连续管应变上升幅度达111.96%。
|
| 图 8 缺陷深度对连续管疲劳失效的影响曲线 Fig.8 The effect of defect depth on fatigue failure of coiled tubing |
2.5 凹坑宽度对连续管疲劳失效的影响
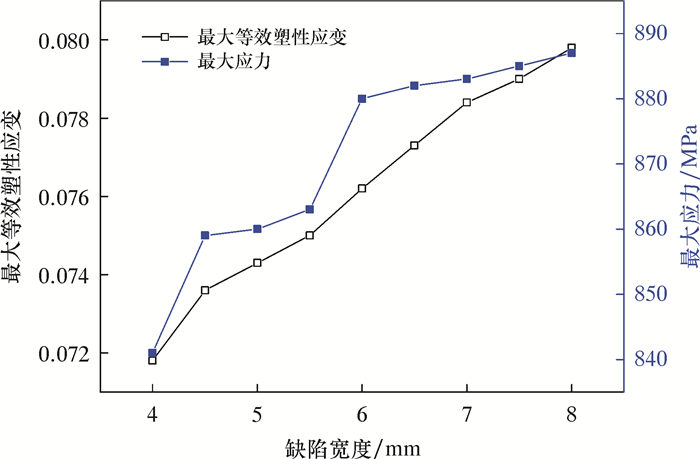
保持2.4节中所选其他参数不变,仅改变缺陷宽度,分析缺陷宽度对连续管疲劳失效的影响,结果如图 9所示。由图 9可知,当缺陷宽度由4 mm增大到8 mm时,连续管的应变由0.071 8上升到0.079 8,上升幅度达11.42%。在同种工况下,与完整连续管进行对比,含缺陷连续管应变上升幅度达108.30%。
|
| 图 9 缺陷宽度对连续管疲劳失效的影响曲线 Fig.9 The effect of defect width on fatigue failure of coiled tubing |
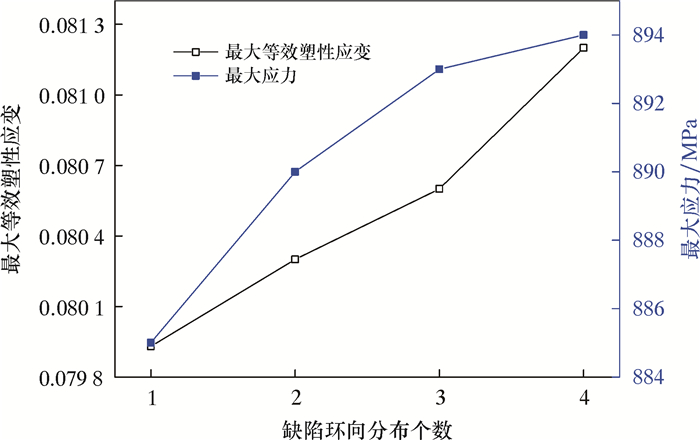
2.6 凹坑环向分布数量对连续管疲劳失效的影响
以上分析中缺陷(凹坑)的数量为1,现将缺陷的数量改变,分别取1、2、3和4,分析内压35 MPa、缺陷轴向角度30°、缺陷长度11 mm、缺陷宽度5 mm、缺陷深度1 mm时连续管的疲劳性能,分析结果如图 10所示。由图 10可以看出,当缺陷数量由1变到4时,连续管的应变由0.079 93上升到0.081 20,上升幅度达1.59%。在同种工况下,与完整连续管应变进行对比,含缺陷连续管应变上升幅度达111.96%。
|
| 图 10 缺陷环向分布数量对连续管疲劳失效的影响曲线 Fig.10 The effect of the circumferential distribution of defects on the fatigue failure of coiled tubing |
2.7 参数敏感性
从以上对比结果来看,缺陷的轴向角度、长度、深度、宽度和环向分布数量对连续管疲劳失效的影响程度不同。表 2是各参数对连续管疲劳失效影响的对比表。由表 2可知,缺陷深度和缺陷宽度对连续管疲劳失效的影响较大,应变增幅均超过11%。因此,在后期含缺陷连续管疲劳寿命理论模型建立的过程中,应考虑这些因素的影响,同时在连续管现场使用中应加强对其检测和维护。
| 参数名称 | 应变增幅/% | 敏感参数 |
| 缺陷角度 | 5.78 | |
| 缺陷长度 | 3.29 | |
| 缺陷深度 | 15.67 | √ |
| 缺陷宽度 | 11.42 | √ |
| 缺陷数量 | 1.59 |
3 结论
(1) 连续管在带压弯直循环过程中,缺陷处会产生明显的应力集中现象,最后发生疲劳失效。在一定角度的凹坑缺陷处,径向的两个角落塑性应变最大,连续管会沿着这两个位置发生断裂。
(2) 缺陷的轴向角度、长度、深度、宽度和环向分布个数对连续管疲劳失效的影响程度不同,缺陷深度和缺陷宽度对连续管疲劳寿命的影响较大,缺陷深度的影响最为显著。缺陷深度在0.5~2.0 mm时,与同种工况下完整连续管相比,含缺陷连续管应变上升幅度达111.96%。在含缺陷连续管疲劳寿命理论模型建立的过程中,应把这两个参数作为主要考虑参数。
| [1] |
贺会群, 熊革, 刘寿军, 等. 我国连续管钻井技术的十年攻关与实践[J]. 石油机械, 2019, 47(7): 1-8. HE H Q, XIONG G, LIU S J, et al. Ten years of key problems tackling and practice of coiled tubing drilling technology in China[J]. China Petroleum Machinery, 2019, 47(7): 1-8. |
| [2] |
袁发勇, 马卫国. 连续管水平井工程技术[M]. 北京: 科学出版社, 2018: 1-19. YUAN F Y, MA W G. Coiled tubing engineering technology in horizontal wells[M]. Beijing: Science Press, 2018: 1-19. |
| [3] |
平恩顺, 张曙光, 胡永雄, 等. 水平井连续油管高效钻磨技术研究[J]. 钻采工艺, 2018, 41(5): 56-58. PING E S, ZHANG S G, HU Y X, et al. Research on efficient milling by coiled tubing in horizontal wells[J]. Drilling & Production Technology, 2018, 41(5): 56-58. |
| [4] |
侯学军, 金锐, 宋洪奇, 等. 基于赫-巴模型的微小井眼钻井连续油管内钻井液流阻计算分析[J]. 天然气工业, 2019, 39(2): 76-83. HOU X J, JIN R, SONG H Q, et al. Calculation and analysis of drilling fluid flow resistance in coiled tubing for slimhole drilling based on the Herschel-Buckley Model[J]. Natural Gas Industry, 2019, 39(2): 76-83. |
| [5] |
PADRON T, CRAIG S H. Past and present coiled tubing string failures-history and recent new failures mechanisms[R]. SPE 189914-MS, 2018.
|
| [6] |
刘寿军, 于东兵, 王刚庆, 等. 有缆连续管钻井系统在侧钻水平井中的应用现状[J]. 石油机械, 2018, 46(10): 1-5. LIU S J, YU D B, WANG G Q, et al. Application of e-line coiled tubing drilling system in sidetracking horizontal wells[J]. China Petroleum Machinery, 2018, 46(10): 1-5. |
| [7] |
YANG Y S. Bending torque and strain energy in reeling coiled tubing[R]. SPE 38459-PA, 1997.
|
| [8] |
BROWN P A, DICKERSON J L. Development and use of an analytical model to predict coiled tubing diameter growth[R]. SPE 38409-MS, 1997.
|
| [9] |
NEWMAN K P, NEWBURN D A. Coiled-tubing life modeling[R]. SPE 22820-MS, 1991.
|
| [10] |
TIPTON S M. Coiled-tubing surface characteristics and effects on fatigue behavior[R]. SPE 62096-PA, 2000.
|
| [11] |
TIPTON S M. Coiled tubing deformation mechanics: diametral growth and elongation[R]. SPE 36336-MS, 1996.
|
| [12] |
COLLINS J A. Fatigue of materials in mechanical design[M]. New York: Analysis Prediction Prevention, 1981: 629-633.
|
| [13] |
AVAKOV V A, FOSTER J C, SMITH E J.Coiled tubing life prediction[R]. OTC 7325-MS, 1993.
|
| [14] |
WU J. Coiled tubing working life prediction[R]. SPE 29461-MS, 1995.
|
| [15] |
赵章明. 连续油管工程技术手册[M]. 北京: 石油工业出版社, 2011: 39-49. ZHAO Z M. Coiled tubing engineering technical manual[M]. Beijing: Petroleum Industry Press, 2011: 39-49. |
| [16] |
LIU S H, XIAO H, GUAN F, et al. Coiled tubing failure analysis and ultimate bearing capacity undermulti-group load[J]. Engineering Failure Analysis, 2017, 79(9): 803-811. |
| [17] |
周浩, 刘少胡, 管锋. 内压、弯扭耦合载荷下连续管疲劳寿命评估[J]. 高压物理学报, 2019, 33(4): 92-98. ZHOU H, LIU S H, GUAN F. Fatigue life evaluation of coiled tube under coupled load of internal pressure, bending and torsion[J]. Chinese Journal of High Pressure Physics, 2019, 33(4): 92-98. |
| [18] |
秦桦, 安晨, 管锋, 等. 诱发扭矩下连续管螺旋屈曲研究[J]. 石油机械, 2018, 46(8): 107-112. QIN H, AN C, GUAN F, et al. Induced torque effect on helical buckling of coiled tubing[J]. China Petroleum Machinery, 2018, 46(8): 107-112. |
| [19] |
毕宗岳, 鲜林云, 汪海涛, 等. 国产超高强度CT110连续管组织与性能[J]. 焊管, 2017, 40(3): 24-27, 31. BI Z Y, XIAN L Y, WANG H T, et al. Microstructure and mechanical properties of domestic ultra-high strength CT110 grade coiled tubing[J]. Welded Pipe, 2017, 40(3): 24-27, 31. |
| [20] |
王振.基于扩展有限元法的连续管裂纹扩展研究[D].荆州: 长江大学, 2019. WANG Z. Crack propagation of coiled tubing based on extended finite element method[D]. Jingzhou: Yangtze University, 2019. |
| [21] |
ISHAK J. Numerical evaluation of cyclic strains in physically small defects in coiled tubing[D]. Tulsa: University of Tulsa, 2016.
|



