2. 广东海洋大学寸金学院
2. Guangdong Ocean University Cunjin College
0 引言
近年来,旋转尾管固井技术与套管钻井技术开始应用。旋转尾管技术可以使水泥浆在套管环空均匀分布,改善固井质量,且可以有效应对复杂井眼轨迹和井壁坍塌导致的套管下入困难等问题[1]。套管钻井技术通过套管取代传统钻杆进行钻进,完钻后无需起钻,将套管留在井内直接完井,可有效缩短作业时间,节约钻井成本[2]。旋转尾管固井与套管钻井技术均需要旋转套管,使套管承受扭矩。套管在加工、运输、存储以及使用工程中,受腐蚀及其他因素的影响,可能存在局部缺陷。钻井时套管可能会出现磨损等局部缺陷,局部缺陷导致的管壁减薄将降低套管的抗扭强度。
目前对套管强度相关研究已比较成熟[3],对含局部缺陷套管的剩余强度研究主要集中在套管抗内压、抗外挤强度等方面[4-12],另有文献对含缺陷管柱的抗弯强度进行了研究[13-14]。闫相祯等[15]在材料弹性范围内分析了套管外部月牙形、8字形缺陷对套管剩余抗扭强度的影响。但针对材料塑性失效下缺陷管柱的抗扭强度研究还很少。对含缺陷套管进行强度分析时,较少考虑缺陷宽度和管柱径厚比的影响,少见含缺陷管柱抗扭强度预测公式报道。鉴于此,本文基于材料的塑性失效准则,利用非线性有限元方法并结合正交试验设计,分析缺陷长度、宽度、深度、套管外径和套管径厚比等参数对内缺陷套管剩余抗扭强度的影响规律,并拟合了抗扭强度预测公式,以期为工程上含缺陷套管强度评价提供参考。
1 含局部缺陷套管非线性有限元分析 1.1 失效准则失效准则是分析套管强度的依据,材料的失效准则有弹性失效准则与塑性失效准则。弹性失效准则只分析套管的弹性应力状态,认为当缺陷处的最大等效应力达到屈服强度时管柱失效。海上套管材料(如N80钢材)有较好的韧性,其失效模式主要是局部塑性失效,因此选用塑性失效准则较为合理[5]。
本文基于材料塑性失效准则,认为缺陷处Von Mises等效应力全部达到屈服应力后套管失效。在三维主应力空间,Von Mises等效应力表达式为:
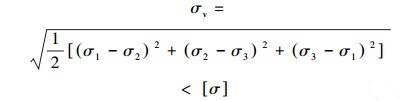
|
(1) |
式中:σv为Von Mises等效应力,MPa;[σ]为许用应力,MPa;σ1、σ2、σ3为第1、第2、第3主应力,MPa。
1.2 模型结构实际套管缺陷形状复杂,分析时需要对缺陷进行一定的简化。将局部缺陷形状简化处理为方形均匀壁厚缺陷,即缺陷处的壁厚为定值,同时为减小应力集中效应,在缺陷端部以光滑圆弧面过渡。
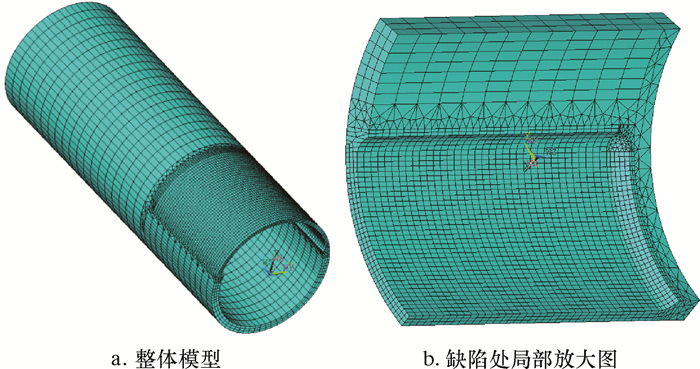
根据求解问题的对称性,为减少计算单元,取缺陷套管模型的1/2建立三维有限元模型。为消除边界效应,取计算套管长度为套管外径的3倍,当缺陷长度超过套管外径时,计算长度为缺陷长度的3倍。计算单元采用三维20节点六面体等参单元。在套管厚度方向划分三层网格。由于缺陷处应力变化梯度较大,所以对缺陷及附近区域划分较密的网格[14]。划分网格后的计算模型如图 1所示。
|
| 图 1 局部内缺陷套管几何模型 Fig.1 Geometry model of the casing with partial inner defects |
1.3 边界条件
只考虑扭矩对套管的影响,忽略其他载荷。扭矩为反对称载荷,需要在靠近缺陷的套管端面施加反对称约束,在远离缺陷的端面施加扭矩载荷。另外,为避免刚体位移造成计算不收敛,需要选取一个节点约束轴向位移。
1.4 材料模式材料的硬化效应对套管的强度影响很大,因此该分析模型中采用Ramberg-Osgood幂硬化应力-应变法则代替材料的真实应力-应变曲线[16],其表达式为:
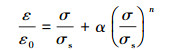
|
(2) |
式中:ε0为初始应变,ε0=σs/E;σs为屈服应力,MPa;E为弹性模量,MPa;α为材料硬化系数,无量纲;n为材料幂硬化指数,无量纲。
本文主要针对海上常用N80钢级的套管进行计算,其屈服强度为552 MPa,抗拉强度为689 MPa,弹性模量为206 GPa,泊松比为0.3。
2 剩余抗扭强度变化规律分析为研究方便,并使结果具有推广意义,定义无因次参数:局部缺陷相对深度(h/T)、缺陷环向相对宽度(θ/π)、缺陷轴向相对长度(L/D)、套管径厚比(D/T)、无因次抗扭强度TD。其中:L为缺陷长度,mm;h为缺陷深度,mm;θ为缺陷环形周角(缺陷宽度),rad;T为套管壁厚,mm;D为套管外径,mm;TD=TL/TO,TL为含缺陷套管剩余抗扭强度,kN·m,TO为原始套管抗扭强度,kN·m。
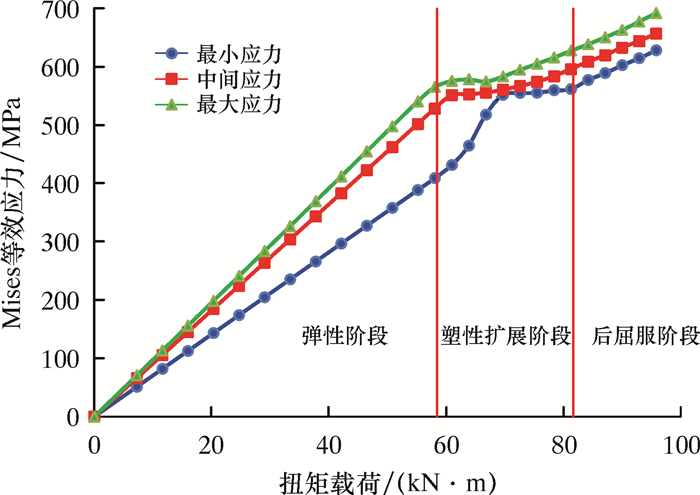
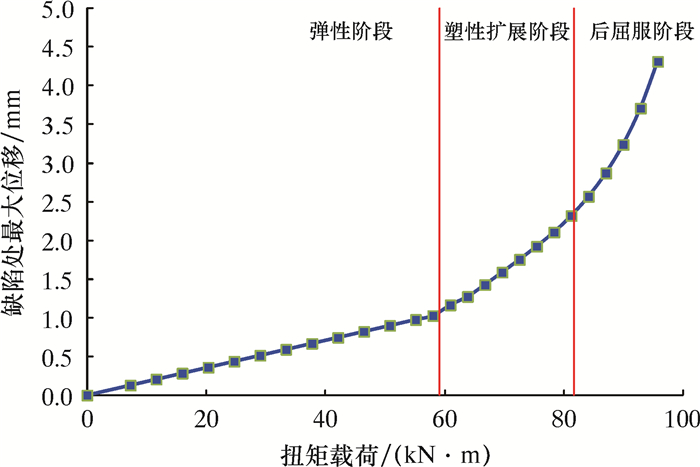
2.1 扭矩载荷下缺陷处应力及变形状态图 2、图 3分别为缺陷套管在扭矩加载过程中缺陷处应力和变形随载荷的关系曲线,其缺陷套管参数为:D=177.8 mm,T=10.36 mm,h/T=0.6,θ/π=2/3,L/D=1.2。在扭矩加载过程中,缺陷处的应力可分为三个阶段:弹性阶段、塑性扩展阶段和后屈服强化阶段。在弹性阶段,首先在缺陷中间出现最大应力,同时缺陷与管体过渡处由于应力集中效应也出现较大的应力,该阶段套管应力、变形均随载荷增加呈线性增加。当加载至58 kN·m时,缺陷中间最大应力超过550 MPa,出现屈服,开始进入塑性扩展阶段。此阶段虽然载荷增大,但最大等效应力变化不大;缺陷区变形速度比弹性加载阶段加快,但大致保持线性关系。当载荷超过82 kN·m后,塑性区扩展至整个缺陷处,进入后屈服阶段,应力开始大幅度增加,变形速率急剧增加,缺陷区发生较大的屈曲变形,模型失稳。
|
| 图 2 等效应力与载荷的关系曲线 Fig.2 Equivalent stress versus load |
|
| 图 3 缺陷处变形与载荷的关系曲线 Fig.3 Deformation versus load in the position with defects |
套管原始抗扭强度为145 kN·m,若按线弹性失效准则,则含缺陷套管抗扭强度为58 kN·m,仅为原始抗扭强度的40%;按腐蚀缺陷处最小应力达到屈服应力考虑,则强度为82 kN·m,为原始套管强度的56%。由此可见缺陷对套管强度影响较大,基于线弹性失效准则相对保守。
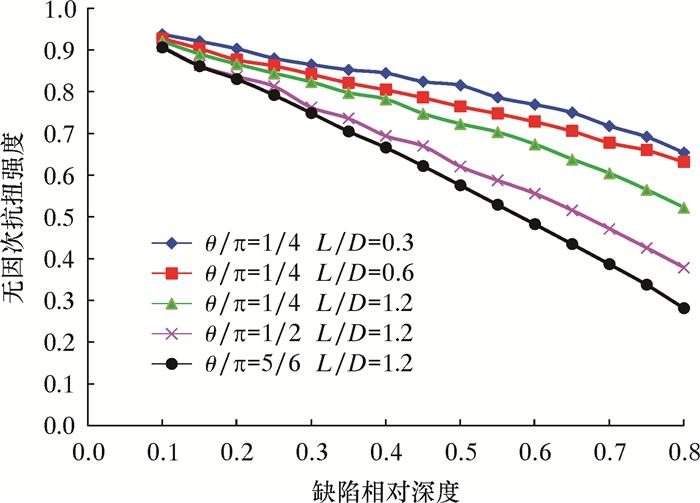
2.2 缺陷深度的影响缺陷套管抗扭强度随缺陷深度增加基本呈线性降低,如图 4所示。当缺陷长度和宽度较小时,抗扭强度随深度的增加降低幅度较小,当θ/π=1/4,L/D=0.3,缺陷深度增加10%时,抗扭强度下降3%左右;当缺陷长度和宽度较大时,抗扭强度降低的幅度较大,如θ/π=5/6,L/D=1.2时,缺陷深度(h/T)增加10%时,抗扭强度最大降低9%左右。当缺陷深度(h/T)增加到0.8时,剩余抗扭强度仅为原始强度的26%。
|
| 图 4 缺陷深度对无因次抗扭强度的影响(D=177.8 mm,T=10.36 mm) Fig.4 Effect of defect depth on dimensionless torsional strength (D=177.8 mm, T=10.36 mm) |
2.3 缺陷长度的影响
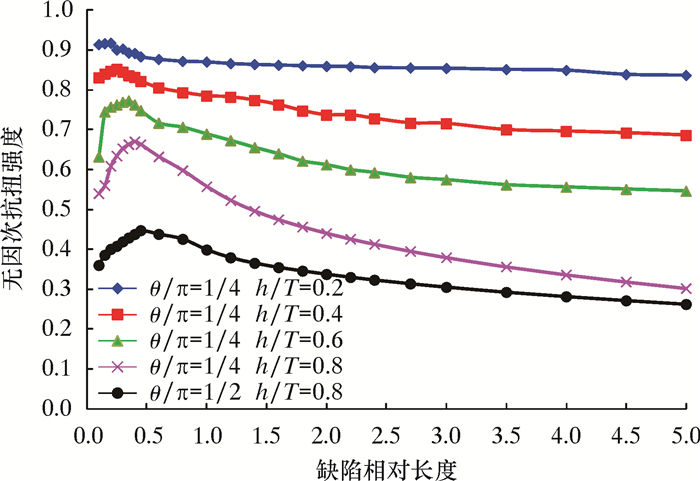
缺陷长度对抗扭强度影响曲线大致分为两阶段,如图 5所示。
|
| 图 5 缺陷长度对无因次抗扭强度的影响(D=177.8 mm,T=10.36 mm) Fig.5 Effect of defect length on dimensionless torsional strength (D=177.8 mm, T=10.36 mm) |
第一阶段:当缺陷长度L小于临界长度Le时,抗扭强度随长度增加而增加。其原因是长度小于临界长度时,长度越小,缺陷越接近环向沟槽,近似沟槽形缺陷导致的应力集中将显著降低套管的抗扭强度,特别是当缺陷相对深度(h/T)超过0.4时,这种影响更为明显。分析表明临界长度Le与缺陷深度和宽度均有关系,通过拟合确定临界长度Le计算式为:
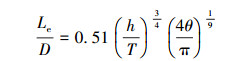
|
(3) |
式中:Le/D为无因次临界缺陷长度,无量纲。
第二阶段:当缺陷长度L超过临界长度Le后,抗扭强度随缺陷长度的增加而减小。当缺陷相对长度(L/D)大于3时,长度对抗扭强度的影响已经不明显,但下降趋势依然存在。出于安全考虑,相对长度大于3时仍应考虑缺陷长度对强度的影响。
2.4 缺陷宽度的影响缺陷宽度对抗扭强度影响曲线也大致分为两阶段,如图 6所示。总体而言,缺陷宽度对抗扭强度影响较大,而缺陷宽度对管道的抗内压与抗弯强度影响较小,二者差异较大[11, 14]。
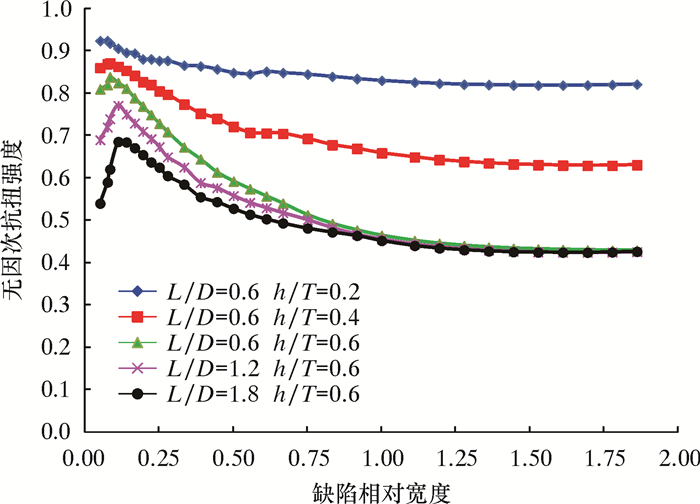
|
| 图 6 缺陷宽度对无因次抗扭强度的影响(D=177.8 mm,T=10.36 mm) Fig.6 Effect of defect width on dimensionless torsional strength (D=177.8 mm, T=10.36 mm) |
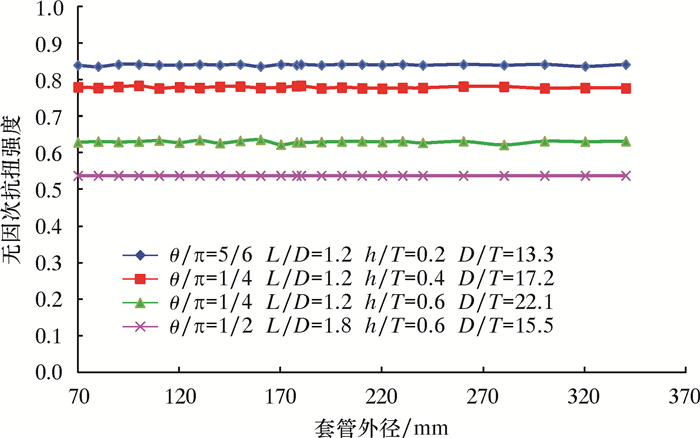
第一阶段:当缺陷宽度θ小于临界宽度θe时,抗扭强度随宽度增加而增大。此时缺陷接近轴向沟槽,应力集中明显。特别是当缺陷相对深度(h/T)超过0.6时,应力集中将显著降低套管的抗扭强度。相比轴向沟槽形缺陷,环向沟槽形缺陷对抗扭强度影响更大。分析表明,临界宽度θe主要与缺陷深度有关系,与缺陷长度关系不大。本文确定临界宽度θe计算式为:
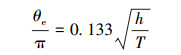
|
(4) |
式中:θe/π为无因次临界缺陷宽度,无量纲。
第二阶段:当缺陷宽度θ超过临界宽度θe后,抗扭强度随缺陷宽度增加而减小,但其减小幅度变小;当θ超过1.5π时,抗扭强度已基本接近套管整体减薄时的抗扭强度。
2.5 套管径厚比的影响套管径厚比对无因次抗扭强度的影响如图 7所示。从图 7可以看出,随着套管径厚比(D/T)的增加,缺陷套管无因次抗扭强度逐渐下降。当套管径厚比在12~32之间时,抗扭强度随径厚比增加近似呈线性减小。在分析不同尺寸缺陷套管的无因次抗扭强度时,应考虑径厚比对其强度的影响,否则会引起较大的误差。
|
| 图 7 套管径厚比对无因次抗扭强度的影响(D=177.8 mm) Fig.7 Effect of casing diameter-thickness ratio on dimensionless torsional strength (D=177.8 mm) |
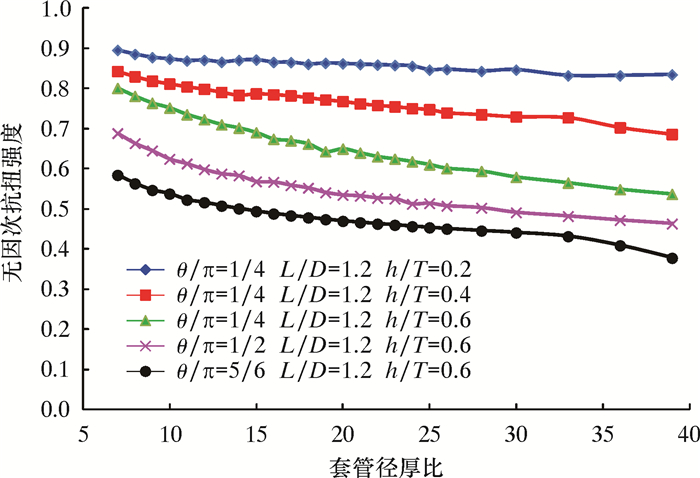
2.6 套管外径的影响
套管外径对无因次抗扭强度的影响如图 8所示。从图 8可以看出,当缺陷的相对深度、相对宽度、相对长度和套管径厚比一定时,套管外径对无因次抗强度基本无影响。如果两种缺陷套管几何尺寸相似,则可认为其无因次抗扭强度相同。
|
| 图 8 套管外径对无因次抗扭强度的影响 Fig.8 Effect of casing outer diameter on dimensionless torsional strength |
2.7 无因次抗扭强度主控因素分析
为定量分析多因素对抗扭强度的影响规律,采用正交试验设计方法,对缺陷长度、宽度、深度、套管外径和套管径厚比这5个影响因子各取4种不同水平,通过正交试验L16(45)设计了16个计算模型,对每个模型采用有限元分析计算无因次抗扭强度,通过极差分析确定各因素对抗扭强度的影响程度。
正交试验结果见表 1。从表 1可以看出,缺陷深度与宽度对无因次抗扭强度有显著影响,缺陷长度与套管径厚比有一定的影响。深度是影响无因次抗扭强度最显著的因素,影响幅度大约是缺陷宽度的3倍,是套管径厚比的6倍,是缺陷长度的8倍,而外径对无因次抗扭强度影响微弱。
| 序号 | L/D | h/T | θ/π | D/mm | D/T | TD |
| 1 | 0.3 | 0.15 | 1/6 | 80 | 10 | 0.955 1 |
| 2 | 0.3 | 0.30 | 2/3 | 160 | 15 | 0.803 3 |
| 3 | 0.3 | 0.45 | 7/6 | 240 | 20 | 0.640 0 |
| 4 | 0.3 | 0.60 | 5/3 | 320 | 25 | 0.476 9 |
| 5 | 1.2 | 0.15 | 2/3 | 240 | 25 | 0.827 5 |
| 6 | 1.2 | 0.30 | 1/6 | 320 | 20 | 0.838 4 |
| 7 | 1.2 | 0.45 | 5/3 | 80 | 15 | 0.622 2 |
| 8 | 1.2 | 0.60 | 7/6 | 160 | 10 | 0.475 6 |
| 9 | 2.1 | 0.15 | 7/6 | 320 | 15 | 0.846 5 |
| 10 | 2.1 | 0.30 | 5/3 | 240 | 10 | 0.702 7 |
| 11 | 2.1 | 0.45 | 1/6 | 160 | 25 | 0.690 3 |
| 12 | 2.1 | 0.60 | 2/3 | 80 | 20 | 0.477 8 |
| 13 | 3.0 | 0.15 | 5/3 | 160 | 20 | 0.837 6 |
| 14 | 3.0 | 0.30 | 7/6 | 80 | 25 | 0.698 7 |
| 15 | 3.0 | 0.45 | 2/3 | 320 | 10 | 0.633 1 |
| 16 | 3.0 | 0.60 | 1/6 | 240 | 15 | 0.634 9 |
| 极差 | 0.039 5 | 0.350 4 | 0.119 8 | 0.013 2 | 0.053 4 | |
| 因素主次 | 4 | 1 | 2 | 5 | 3 |
3 剩余抗扭强度工程计算
根据以上规律,考虑到缺陷长度、宽度、深度、套管外径和套管径厚比等参数对抗扭强度的影响,对550例缺陷套管抗扭强度有限元分析结果进行拟合,得到局部内缺陷套管无因次抗扭强度的预测公式:
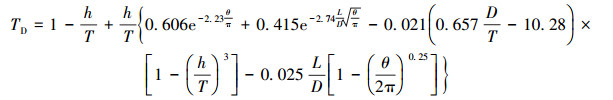
|
(5) |
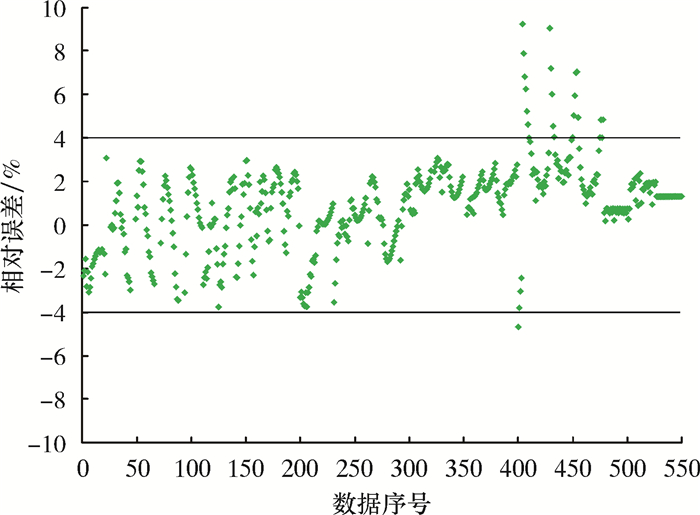
拟合公式相关系数为0.976 5,图 9为预测结果与有限元计算结果的相对误差。误差为正则表明公式预测值小于有限元计算结果,平均绝对误差1.82%,除22个点相对误差较大之外,其余点的计算误差均较小,均在4%以内,且相对保守,说明拟合结果较为理想。误差较大的点主要集中在套管径厚比小于10或径厚比大于32的情况,考虑到钻井工程所用套管的径厚比一般处于12~30之间,因此预测公式可基本满足工程需要。用无因次抗扭强度TD乘以原始套管的抗扭强度TO,即可得到含缺陷套管剩余抗扭强度TL。
|
| 图 9 公式预测值与有限元计算结果的相对误差 Fig.9 Relative error between formula prediction value and finite element calculation result |
需要说明的是,本公式不适用于环向和轴向沟槽形缺陷抗扭强度的计算,关于沟槽形缺陷后续将做进一步研究。
4 应用实例南海西部某油田生产井X1,三开ø215.9 mm井眼完钻斜深3 339 m,垂深2 173 m。该井在ø244.5 mm套管鞋1 780 m处以约60°井斜角稳斜至井底,裸眼井段长1 560 m,穿越易垮塌地层涠二段泥岩地层680 m,钻井期间掉块严重。因尾管下入难度较大,故采用旋转ø177.8 mm尾管下入技术。
作业过程中,部分ø177.8 mm套管存在局部内腐蚀缺陷,实测部分缺陷参数见表 2。计算无因次参数后,依据式(5)预测抗扭强度,结果见表 2。套管最小无因次抗扭强度TD=0.819,剩余抗扭强度为117 kN·m。模拟预测该井尾管下入过程中最大旋转扭矩为37 kN·m,即缺陷套管可满足抗扭强度要求,另外该缺陷套管也可满足抗拉、抗内压和抗外挤强度要求。
| 套管参数 | 实测缺陷尺寸 | 无因次参数 | 强度预测 | ||||||||||
| 外径/mm | 壁厚/mm | 长度/mm | 宽度/mm | 深度/mm | L/D | θ/π | h/T | D/T | 无因次强度 | 抗扭强度/(kN·m) | |||
| 177.8 | 10.36 | 135 | 149 | 2.4 | 0.76 | 0.61 | 0.24 | 17.2 | 0.819 | 117 | |||
| 177.8 | 10.36 | 69 | 62 | 1.9 | 0.39 | 0.25 | 0.19 | 17.2 | 0.926 | 134 | |||
| 177.8 | 10.36 | 96 | 129 | 2.1 | 0.54 | 0.52 | 0.21 | 17.2 | 0.864 | 125 | |||
| 177.8 | 10.36 | 94 | 81 | 1.8 | 0.53 | 0.33 | 0.18 | 17.2 | 0.909 | 132 | |||
该井ø177.8 mm尾管下入过程中,在多处遇阻,采用旋转方式下入通过遇阻点,最大旋转扭矩为41 kN·m,在缺陷套管的剩余抗扭强度范围之内。尾管下到位后实施旋转尾管固井作业,后期电测结果表明固井质量优。
5 结论(1) 局部内缺陷套管抗扭强度随缺陷深度增加呈线性大幅度降低;缺陷长度和宽度对抗扭强度影响均存在临界值;当缺陷长度小于临界长度时,抗扭强度随缺陷长度增加而增大,超过临界长度后,抗扭强度随缺陷长度增加而降低;当缺陷宽度小于临界宽度时,抗扭强度陷缺陷宽度增加而增大,超过临界宽度后,抗扭强度随缺陷宽度增加而降低;无因次抗扭强度随套管径厚比增加近似呈线性减小。
(2) 缺陷深度是影响无因次抗扭强度最重要的因素,缺陷宽度次之,缺陷长度与套管径厚比有一定的影响,而套管外径的影响可以忽略。
(3) 基于非线性有限元模拟结果,拟合了抗扭强度计算公式,公式预测值与有限元结果误差较小,可为工程上局部内缺陷套管强度评价提供参考。
| [1] |
郑友志, 刘伟, 余才焌, 等. 旋转套管固井工艺技术在LG-A井的应用[J]. 天然气工业, 2010, 30(4): 74-76. ZHENG Y Z, LIU W, YU C J, et al. Application of rotating-casing cementing technology in the Well LG-A of the LG Gas Field[J]. Natural Gas Industry, 2010, 30(4): 74-76. |
| [2] |
李春吉, 单正明, 孟祥奎. 套管钻井技术简介[J]. 石油钻探技术, 2002, 30(6): 74. LI C J, SHAN Z M, MENG X K. The introduction of casing drilling technology[J]. Petroleum Drilling Tech-niques, 2002, 30(6): 74. DOI:10.3969/j.issn.1001-0890.2002.06.028 |
| [3] |
覃成锦, 高德利. 套管强度计算的理论问题[J]. 石油学报, 2005, 26(5): 123-126. QIN C J, GAO D L. Theoretic problems about calculation of casing strength[J]. Acta Petrolei Sinica, 2005, 26(5): 123-126. DOI:10.3321/j.issn:0253-2697.2005.05.028 |
| [4] |
张健, 孙奇北, 王文燕, 等. 天然气管道缺陷模型的建立及有限元分析[J]. 石油机械, 2019, 47(4): 129-134. ZHANG J, SUN Q B, WANG W Y, et al. Modeling and finite element analysis of natural gas pipeline defect[J]. China Petroleum Machinery, 2019, 47(4): 129-134. |
| [5] |
张智, 孔维伟, 刘志伟, 等. 腐蚀缺陷套管的剩余强度研究[J]. 中国科技论文, 2016, 11(21): 2467-2472. ZHANG Z, KONG W W, LIU Z W, et al. Study on residual strength of corrosion defect casing[J]. China Sciencepaper, 2016, 11(21): 2467-2472. DOI:10.3969/j.issn.2095-2783.2016.21.013 |
| [6] |
徐颖强, 原园, 吕国志, 等. 含凹坑缺陷在役石油管道剩余极限强度分析[J]. 石油机械, 2004, 32(10): 11-13. XU Y Q, YUAN Y, LÜ G Z, et al. Analysis of retained limit strength of in service oil pipelines with drop pits[J]. China Petroleum Machinery, 2004, 32(10): 11-13. DOI:10.3969/j.issn.1001-4578.2004.10.004 |
| [7] |
王刚庆, 刘旭辉, 王小增, 等. 月牙形和偏心圆筒形内壁磨损套管应力分析[J]. 石油机械, 2013, 41(4): 35-39. WANG G Q, LIU X H, WANG X Z, et al. Stress analysis of the crescent and eccentric cylinder-shaped inner wall worn casing[J]. China Petroleum Machinery, 2013, 41(4): 35-39. DOI:10.3969/j.issn.1001-4578.2013.04.009 |
| [8] |
宋生印, 刘永刚, 王力, 等. 套管钻井用套管外表面磨损后剩余强度分析[J]. 石油机械, 2006, 34(2): 7-10. SONG S Y, LIU Y G, WANG L, et al. Analysis on residual strength after casing surface wear caused in casing drilling[J]. China Petroleum Machinery, 2006, 34(2): 7-10. DOI:10.3969/j.issn.1001-4578.2006.02.003 |
| [9] |
张继信, 汪彤, 樊建春, 等. 外表面体积型缺陷对高压管件剩余强度的影响[J]. 石油机械, 2013, 41(6): 72-76. ZHANG J X, WANG T, FAN J C, et al. Effects of external surface volumetric defect on the residual strength of high pressure pipe[J]. China Petroleum Machinery, 2013, 41(6): 72-76. DOI:10.3969/j.issn.1001-4578.2013.06.017 |
| [10] |
符方杰, 樊建春, 张继信. 腐蚀缺陷对高压管汇剩余强度的影响分析[J]. 石油机械, 2012, 40(6): 66-69. FU F J, FAN J C, ZHANG J X. Effects of corrosion defect on residual strength of high pressure manifold[J]. China Petroleum Machinery, 2012, 40(6): 66-69. |
| [11] |
马钢, 李俊飞, 白瑞, 等. 基于PCA-SVR模型的油气管道剩余强度预测[J]. 油气储运, 2019, 38(10): 1119-1124. MA G, LI J F, BAI R, et al. Prediction on the residual strength of oil and gas pipelines based on PCA-SVR model[J]. Oil & Gas Storage and Transportation, 2019, 38(10): 1119-1124. |
| [12] |
韩烨, 孙伟栋, 席少龙, 等. 含腐蚀缺陷占压管道的安全评估[J]. 油气储运, 2019, 38(2): 137-144. HAN Y, SUN W D, XI S L, et al. Safety assessment on buried pipeline subjected to ground load and corrosion defect[J]. Oil & Gas Storage and Transportation, 2019, 38(2): 137-144. |
| [13] |
沈士明, 郑逸翔. 含局部减薄缺陷管道的极限载荷与安全评定[J]. 石油机械, 2004, 32(6): 17-20. SHEN S M, ZHENG Y X. The limit loads and safety assessment of the pipe with LAT[J]. China Petroleum Machinery, 2004, 32(6): 17-20. DOI:10.3969/j.issn.1001-4578.2004.06.006 |
| [14] |
韩晓毅, 张平生, 刘玉标, 等. 钻杆管体体积型缺陷的有限元分析[J]. 石油机械, 2002, 30(4): 20-21. HAN X Y, ZHANG P S, LIU Y B, et al. Finite element analysis of defects in drill pipe body[J]. China Petroleum Machinery, 2002, 30(4): 20-21. DOI:10.3969/j.issn.1001-4578.2002.04.007 |
| [15] |
闫相祯, 邓卫东, 高进伟, 等. 套管钻井中套管柱疲劳可靠性及相关力学特性研究[J]. 石油学报, 2009, 30(5): 769-773. YAN X Z, DENG W D, GAO J W, et al. Analysis on mechanics and fatigue reliability of casing string during casing drilling[J]. Acta Petrolei Sinica, 2009, 30(5): 769-773. DOI:10.3321/j.issn:0253-2697.2009.05.025 |
| [16] |
崔铭伟, 曹学文. 腐蚀缺陷对中高强度油气管道失效压力的影响[J]. 石油学报, 2012, 33(6): 1086-1092. CUI M W, CAO X W. Impact of corrosion defects on failure pressure of medium-high strength oil-gas pipeline[J]. Acta Petrolei Sinica, 2012, 33(6): 1086-1092. |


