0 引言
连续管具有可连续起下以及可带压作业等优点[1],广泛应用于致密气藏和页岩气藏水平段的分层压裂等大规模改造[2]。但是连续管刚度小,在下入过程中极易发生屈曲,导致连续管与井壁之间的摩阻增大,甚至会造成锁死现象[3-5]。为解决连续管因入井摩阻较大导致下入困难的问题,可配制连续管减阻器,这样将增大其在水平段的延伸范围[6]。
按照减阻动力源将连续管减阻器分为机械式减阻器和水力式减阻器。机械式减阻器利用井内流体或其他动力驱动机械机构,输出周期性振动或冲击力。文献[7]介绍了Ander Gauge公司研制的AGT机械式轴向减阻器,其主要由轴向振动总成、流体动力总成和固定总成3部分组成。流体驱动转子转动,使阀组周期性开闭,产生压差驱动振动总成轴向振动。文献[8]介绍了Baker Hughes公司研发的一种机械式阀体减阻器,它主要由阀体总成和冲击短节组成。流体驱动阀体运动在极限位置开、闭流道,流体驱动活塞杆产生冲击,由碟形弹簧恢复力使活塞杆回位。文献[9]介绍了一种机械式滚轮减阻器,它主要通过减阻器上的滚轮将连续管与井壁的静摩擦转化为滑动摩擦,实现减阻功能,但滚轮易磨损,需定期更换。文献[10]介绍了一种新型机械式连续管减阻器,它主要由涡轮组、振动节和凸轮等组成。流体驱动涡轮旋转,通过联轴器将动力传递给凸轮,凸轮驱动振动节做周期性振动,以达到减阻目的。机械式减阻器的机械机构驱动比较复杂,且受井内流体性质限制较大,于是研究人员提出利用井内流体诱发结构振动的水力式减阻器。
水力式减阻器依据流体力学原理,设计可以产生流体压力变化的流道,激发流体与结构的振动。文献[11]介绍了National Oilwell Varco公司研发的E-line Agitator水力式减阻器,该减阻器主要由水力振荡短节、螺杆动力短节和阀组短节等组成。流体驱动螺杆动力短节运动,与阀组短节等结构激发脉动压力,驱动水力振荡短节工作,产生持续振荡。文献[12]介绍了Thru Tubing Solutions公司设计的XRV水力式减阻器,该减阻器主要由中心阀组组成。流体流经中心阀组,在阀组调节压力后输出轴向冲击力。研究和现场应用反馈表明:机械式连续管减阻器只有当流体压力达到阈值时才能驱动其机械部分工作,而水力式连续管减阻器依靠特制流道诱发流体与结构发生振动而达到减阻目的,具有结构简单和工作稳定的优点。
本文基于附壁效应和卡门涡街效应,创新性地设计了一种机械、水力混合动力,可以激发轴向和径向振动的双向耦合连续管减阻器,该减阻器能减小连续管下入过程中与井壁之间的摩阻,增大连续管在水平段的延伸范围。
1 双向耦合连续管减阻器方案设计在总结国内外现有减阻器设计资料和施工现场对减阻器的性能要求的基础上,笔者认为连续管减阻器应具备动力源稳定、减阻效果明显、结构简单可靠以及使用寿命长的性能特点。根据以上性能要求,参考现有设计资料,结合油田现场施工需求,基于附壁效应(Coanda Effect)[13-14]、卡门涡街效应(Karman Vortex Street)和耦合效应等流体振动原理,创新设计了一种新型双作用耦合连续管减阻器,设计思路如图 1所示。

|
| 图 1 双向耦合连续管减阻器设计思路示意图 Fig.1 Schematic diagram of the design idea of the bidirectional coupling coiled tubing drag reducer |
双向,即减阻器可产生轴向和径向两个方向的振动;耦合,即减阻器产生两个轴向振动源振动耦合、两个径向振动源振动耦合、轴向振动与径向振动耦合。
流体驱动多级涡轮叶片转动产生的轴向压力脉动与流体振动腔室诱发的轴向振动耦合;偏心质量旋转诱发的径向振动与流体振动腔室诱发的径向振动耦合;减阻器自身的轴向振动、径向振动也存在耦合效应。通过多级振动的耦合产生持续可靠的振动以克服连续管与井壁之间的摩阻,甚至可以避免连续管锁死现象。
2 双向耦合连续管减阻器流体振动腔室设计流体振动腔室是本减阻器的主要工作部件之一,主要依据附壁效应和卡门涡街效应进行设计,通过设计合理的物理结构以诱发结构在流体作用下的振动。
2.1 附壁效应结构设计附壁效应是指流体在流经弯曲表面时贴附于固体表面,偏离原有流动路径流动的现象。尤其在高速射流的喷射过程中,在贴附曲面流动时会对周围的气体产生卷吸作用,并与高速射流相混合一起向前流动。
流体振动腔室的设计模型如图 2a所示,将设计模型进行合理简化后得到理论计算模型,如图 2b所示。本文通过流体振动腔室计算模型得到合理的尺寸参数,以确保结构可以诱发附壁效应。

|
| 图 2 流体振动腔室设计计算模型 Fig.2 Design and calculation model of fluid vibration chamber |
在流体振动腔室计算模型中,做以下三点假设:流体为不可压缩流体;流体的黏性作用极小,可以忽略不计;流体为定常流动。
由流体力学中的伯努利定理可得:
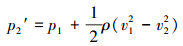
|
(1) |
式中:p1为截面1的流体压力,MPa;p2′为截面2的流体压力,MPa;v1为截面1的流体速度,m/s;v2为截面2的流体速度,m/s;ρ为流体密度,kg/m3。
取ABCDEF为控制面,由流体连续性方程得:

|
(2) |
式中:S1表示截面1的面积,m2;S2表示截面2的面积,m2。
流过控制面流体的动量流为:

|
(3) |
则作用于控制面的面力FΩ为:

|
(4) |
由动量定理可知,截面2瞬时压力p2为:

|
(5) |
联立公式(1)和公式(5)可得:

|
(6) |
联立公式(2)和公式(6)可得:

|
(7) |
公式(7)可以等价表述为:
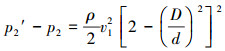
|
(8) |
式中:D为涡街球直径,m;d为附壁腔室内径,m。
由于涡街球的存在,使得附壁腔室的截面从S1变化到S2,即腔室内截面积从小逐渐变大。流体从小截面1以平均速度v1流入,在涡街球的边界产生了双列不规则的漩涡,使得射流流体与周围流体发生混合现象,然后混合流体以平均速度v2从截面2流出。在流体发生混合的同时,伴随着机械能的损失,用截面2的压力变化p2′-p2评估机械能的损失程度。由公式(8)可知,D/d的值越小,压力损失越大,附壁效应诱发的振动越显著。因此,在设计附壁腔室时,腔室内径确定后,选取合理的涡街球直径,使得D/d尽可能地小,以提高流体流过流体振动腔室的压力损失。
2.2 卡门涡街诱发结构设计一定条件下的定常来流绕过某些物体时,物体两侧会周期性地脱落出旋转方向相反、并排列成有规则的双列线涡。开始时,这两列线涡分别保持自身的运动前进,接着互相干扰,互相吸引,而且干扰越来越大,形成非线性涡街[15-18]。卡门涡街模型主要采用斯特劳哈尔数、升力系数和阻力系数进行描述,计算方法如式(9)~式(11)所示。
为了表征惯性力与位移惯性力之比,定义物理相似与模化时引入斯特劳哈尔数Sr。

|
(9) |
式中:fs为漩涡脱落频率,Hz,D0为模型喷口直径,m。
对升力L(t)进行无量纲处理,得到升力系数CL:

|
(10) |
式中:L(t)为升力,N;l为水力直径,m;ku为特征系数,kg/s2,
对阻力D(t)进行无量纲处理,得到阻力系数CD:

|
(11) |
式中:D(t)为阻力,N。
基于卡门涡街效应和附壁效应,设计了如图 3所示的利用流体诱发结构振动的流体振动腔室三维模型。流体振动腔室主要由附壁效应振动腔室和漩涡脱落球两部分组成。工作原理如图 4所示。

|
| 图 3 流体振动腔室三维模型图 Fig.3 Three-dimensional model diagram of fluid vibration chamber |

|
| 图 4 流体振动腔室原理示意图 Fig.4 Schematic diagram of fluid vibration chamber |
由图 4可知,流体流经上整流接口进入振动腔室,流经漩涡脱落球在其表面边界层堆积、形成漩涡,漩涡脱落,产生轴向及径向振动。漩涡脱落球与内壁曲面曲率变化的外壳体构成附壁效应振动腔室,流体流经附壁效应振动腔室,流速减缓,随着流体循环产生持续的轴向振动。
2.3 流体振动腔室工作过程仿真将图 3所建立的三维模型进行简化,导入Workbench DM中,提取出流体振动腔室的内部流道,作为前处理模型[19]。将处理好的简化模型导入XFlow软件,并从模型库中添加球体模型置入内部流道,作为流体振动腔室的漩涡脱落球。限制漩涡脱落球在径向、周向的自由度,轴向自由;为了接近真实模型,在两个脱落球之间添加弹簧约束;在模型入口、出口设置质量流边界条件,将模型中的流道、漩涡脱落球表面设置为壁面条件。为检验所设计模型的合理性和可靠性,监测流体振动腔室在工作过程中流体涡量变化。
用XFlow软件对处理好的模型进行计算,得到流体涡量分布云图,如图 5所示。图 5a~图 5c为上腔室流体涡量变化动态过程。图 5a中流体在漩涡脱落球和腔室壁面曲率变化处发生边界层的堆积,图 5b中流体在漩涡脱落球和腔室壁面曲率变化处形成漩涡,图 5c中流体形成的漩涡开始脱落。图 5d为流体振动腔室的涡量分布,可以明显地看到在漩涡脱落球和壁面曲率变化处涡量较大。因此,依据式(1)~式(11)附壁效应和卡门涡街计算模型设计的流体振动腔室结构合理,能够发生附壁效应和卡门涡街效应,诱发轴向和径向振动。

|
| 图 5 流体振动腔室附壁效应和卡门涡街效应激发过程涡量分布云图 Fig.5 Vorticity distribution during fluid wall attachment effect and Karman vortex effect excitation |
3 双向耦合连续管减阻器设计
双向耦合连续管减阻器结构如图 6所示,主要由上接头、涡轮动力源、径向振动组、流体振动腔室和下接头等5部分组成。涡轮动力源的主要部件为多级涡轮叶片,井内流体驱动涡轮叶片转动,为径向振动组的偏心质量凸轮的旋转提供持续动力。另外,当井内流体流过多级涡轮叶片时,经过多级涡轮叶片的压力调节,会输出低频的轴向脉动压力,与流体振动腔室的振动发生耦合效应。径向振动组由多组不平衡偏心质量凸轮组成,在涡轮动力源的驱动之下产生旋转运动。由于不平衡质量的存在,偏心质量凸轮在旋转过程中会产生径向振动。

|
| 1—上接头;2—卡簧;3—支承座;4—涡轮;5—上壳体;6—偏心质量凸轮;7—定位套;8—上心轴;9—连接接头;10—中心管;11—漩涡脱落球;12—弹簧;13—下接头。 图 6 双向耦合连续管减阻器结构图 Fig.6 Structure diagram of bidirectional coupling coiled tubing drag reducer |
流体流经上整流接口,进入流体振动腔室,一部分流体在漩涡脱落球的作用下,经过边界层堆积、形成漩涡、漩涡脱落的过程发生卡门涡街效应;另一部分流体沿腔室内壁流动,在曲率变化的腔室内壁处形成漩涡,发生附壁效应。流体在上、下两个腔室中循环,诱发持续不断的流体和结构振动,并与涡轮动力源和径向振动组不同方向的振动发生耦合效应,实现在振动冲击瞬时增大时进行连续管的减阻。
4 径向振动组结构安全性评价在减阻器工作过程中,由于径向振动组存在偏心质量,若减阻器固有频率接近工作频率,则减阻器会因共振而发生结构破坏。为确保减阻器不发生结构破坏,必须进行径向振动组的模态分析。
依据能量法原理[20],先将多级涡轮等效为一个实体圆柱,再用Space Claim模块对径向振动组进行建模。在ANSYS Workbench Model模块中对减阻器径向振动组进行模态分析,网格划分如图 7所示。

|
| 图 7 径向振动组网格划分 Fig.7 Meshing of radial vibration modular |
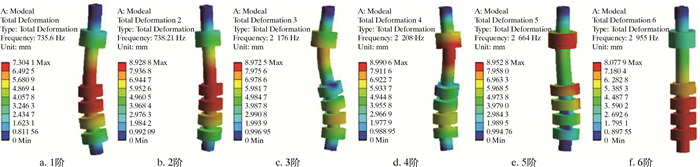
对模型两端施加轴承约束后进行求解,得到无预应力状态下径向振动组的前6阶模态对应的固有频率和振型。1~6阶模态对应的固有频率依次为735、738、2 176、2 208、2 664和2 955 Hz,各阶振型如图 8所示。从图 8可见,减阻器的最大工作振动频率远小于其1阶固有频率,有效地避开了结构共振区。
|
| 图 8 无预应力状态下前6阶振型 Fig.8 The first 6 modes of vibration without prestress |
5 减阻效率试验研究
为验证所设计的双向耦合连续管减阻器能否实现减阻功能并评估减阻器减阻性能,笔者于2019年3月对双向耦合连续管减阻器进行了减阻效率试验。
5.1 测试原理设计通过水泵供液驱动双向耦合连续管减阻器,改变水泵的排量模拟不同注液排量下减阻器的轴向冲击力; 将电阻式应变片粘贴于减阻器流体振动腔室外壳体上,并连接数据采集系统和信号处理系统。流体驱动减阻器工作时,轴向振动和冲击力使电阻式应变片电阻值发生改变,信号传输至采集系统,经信号处理软件处理后即可将电信号转化为力[21-22]
5.2 测试原理设计为验证减阻器的轴向冲击力能否达到预期的减阻效果,设计了如图 9所示的轴向冲击力测试系统。该测试系统主要由水泵、减阻器(无径向振动模块)、电阻式应变片、数据采集系统和信号处理系统[23-24]等组成。

|
| 图 9 轴向冲击力测试系统 Fig.9 Axial impact force test system |
5.3 数据处理与试验结果分析
水泵排量分别达到10、14和18 L/s时,测得时域波形分别如图 10~图 12所示。

|
| 图 10 排量10 L/s的注液工况传感器时域波形 Fig.10 Time domain waveform of the sensor under 10 L/s injection condition |

|
| 图 11 排量14 L/s的注液工况传感器时域波形 Fig.11 Time domain waveform of the sensor under 14 L/s injection condition |

|
| 图 12 排量18 L/s的注液工况传感器时域波形 Fig.12 Time domain waveform of the sensor under 18 L/s injection condition |
图 10~图 12中的大部分曲线幅值较低且具有周期性,这些曲线代表了各个模块在非耦合周期内的时域图形。曲线在某些点处幅值突然增大,由设计原理可知,这些幅值突变的点即为各个模块发生耦合的时刻点。
由测试系统转换特性可知,电压每15 mV折算为1 kN。由图 10可知,在轴向耦合点处最大幅值约为350 mV,即23.3 kN;由图 11可知,在排量14 L/s的注液工况下,轴向耦合点处最大幅值约为450 mV,即30.1 kN;由图 12可知,在排量18 L/s的注液工况下,轴向耦合点处最大幅值约为520 mV,即34.6 kN。随着水泵排量线性增加,减阻器输出的轴向冲击力呈现出非线性增长趋势,继续增大水泵排量,可进一步提高减阻器的轴向冲击力。
6 结论本文创新运用附壁效应、卡门涡街效应和耦合效应等流体振动原理,设计了一种新型连续管减阻器,利用有限元软件对减阻器进行了结构分析校核,采用试验手段评估了减阻器实际减阻效果,得到以下结论:
(1) 设计的新型连续管减阻器利用两个轴向振动源、两个径向振动源的耦合以及轴向、径向振动的耦合,增强了减阻效果,可增大连续管在水平段的延伸范围。
(2) 基于有限元软件对减阻器径向振动组进行了模态分析,结果表明减阻器的最大工作频率远小于其一阶固有频率,有效地避开了结构共振区。
(3) 随着水泵排量的线性增加,双向耦合连续管减阻器输出的轴向冲击力呈现出非线性增长趋势。在10、14和18 L/s的注液排量下可分别产生23.3、30.1和34.6 kN的耦合轴向冲击力,继续增大排量则可产生更大的轴向冲击力。
| [1] |
贺会群. 连续油管技术与装备发展综述[J]. 石油机械, 2006, 34(1): 1-6. HE H Q. Development of coiled tubing technique and equipment[J]. China Petroleum Machinery, 2006, 34(1): 1-6. |
| [2] |
王庆群. 同心连续管作业装备研究与应用分析[J]. 石油机械, 2018, 46(5): 105-109. WANG Q Q. Research and application of concentric coiled tubing unit[J]. China Petroleum Machinery, 2018, 46(5): 105-109. |
| [3] |
吕涨, 周志宏, 张琴, 等. 一种井下减摩振动器的设计[J]. 石油机械, 2017, 45(10): 16-21. LÜ Z, ZHOU Z H, ZHANG Q, et al. A design method of downhole friction reduction vibrator[J]. China Petroleum Machinery, 2017, 45(10): 16-21. |
| [4] |
王海涛, 李相方. 连续油管技术在井下作业中的应用现状及思考[J]. 石油钻采工艺, 2008, 30(6): 120-124. WANG H T, LI X F. Application situation and thinking about coiled tubing techniques in downhole operation[J]. Oil Drilling & Production Technology, 2008, 30(6): 120-124. |
| [5] |
马连山, 赵威, 谢梅, 等. 连续油管技术的应用与发展[J]. 石油机械, 2000, 28(9): 57-60. MA L S, ZHAO W, XIE M, et al. Application and development of coiled tubing technology[J]. China Petroleum Machinery, 2000, 28(9): 57-60. |
| [6] |
张云飞, 贺会群, 都亚男, 等. 连续管井下减阻器研究进展[J]. 石油机械, 2015, 43(7): 36-41. ZHANG Y F, HE H Q, DU Y N, et al. The development of downhole drag reduction device for coiled tubing[J]. China Petroleum Machinery, 2015, 43(7): 36-41. |
| [7] |
WICKS N, PABON J A, ZHENG A. Modeling and field trials of the effective tractoring force of axial vibration tools[R]. SPE 170327-MS, 2014.
|
| [8] |
Baker Hughes Inc(US). Downhole vibrator: 6474421[P]. 2002-11-05.
|
| [9] |
中国石油化工股份有限公司, 中国石油化工股份有限公司西南油气分公司.一种钻具减阻短节: CN201220718129.2[P]. 2013-06-19. China Petroleum & Chemical Corporation, China Petroleum & Chemical Corporation Southwest Oil & Gas Branch. A short section of drilling tools: CN201220718129.2[P]. 2013-06-19. |
| [10] |
覃光芬. 一种新型连续管减阻器的设计与研究[J]. 机电工程技术, 2018, 47(5): 63-65. QIN G F. Design and research of a new type of continuous tube drag reducer[J]. Mechanical & Electrical Engineering Technology, 2018, 47(5): 63-65. |
| [11] |
BARTON S, BAEZ F. Drilling performance improvements in gas shale plays using a novel drilling agitator device[R]. SPE 144416-MS, 2011.
|
| [12] |
WARNER M, HALL R A. Benefits of using downhole vibratory casing tools in the niobrar/codell formations[R]. SPE 178800-MS, 2016.
|
| [13] |
柴鹏, 何先君, 白海龙. 水平分支井射流驱动引导工具控制阀设计[J]. 石油机械, 2019, 47(3): 29-33. CHAI P, HE X J, BAI H L. Design of control valve on the jet-drive guide tool for horizontal multilateral wells[J]. China Petroleum Machinery, 2019, 47(3): 29-33. |
| [14] |
PAN F F, XU Z K, JIN L, et al. Designed simulation and experiment of a piezoelectric energy harvesting system based on vortex induced vibration[J]. IEEE Transactions on Industry Applications, 2017, 53(4): 3890-3897. |
| [15] |
PITTON G, QUAINI A, ROZZA G. Computational reduction strategies for the detection of steady bifurcations in incompressible fluid-dynamics:applications to Coanda effect in cardiology[J]. Journal of Computational Physics, 2017, 344: 534-557. |
| [16] |
CERRETELLI C, KIRTLEY K. Boundary layer separation control with fluidic oscillators[J]. Journal of Turbomachinery, 2009, 131(4): 041001-041009. |
| [17] |
闫炎, 管志川, 杨才, 等. 领眼与扩眼双级PDC钻头井底流场数值模拟[J]. 石油钻采工艺, 2019, 41(1): 31-37. YAN Y, GUAN Z C, YANG C, et al. Numerical simulation on the downhole flow field of the pilot and reaming two-stage PDC bit[J]. Oil Drilling & Production Technology, 2019, 41(1): 31-37. |
| [18] |
段新胜. 环形射流泵射流附壁效应与自吸性能的实验研究[J]. 西部探矿工程, 1999, 11(5): 67-69. DUAN X S. The experimental study on jet attaching effect and self-priming of the annular jet pump[J]. West-China Exploration Engineering, 1999, 11(5): 67-69. |
| [19] |
郑杰, 吴简, 窦益华, 等. 连续油管井下液压涡轮牵引器流场模拟及结构优化[J]. 中国科技论文, 2018, 13(10): 105-110. ZHENG J, WU J, DOU Y H, et al. Flow field simulation and structural optimization of hydraulic turbine tractor in continuous tubing[J]. China Sciencepaper, 2018, 13(10): 105-110. |
| [20] |
倪振华. 振动力学[M]. 西安: 西安交通大学出版社, 1988: 52-56. NI Z H. Vibration mechanics[M]. Xi'an: Xi'an Jiaotong University Press, 1988: 52-56. |
| [21] |
许艺青, 杨晓翔, 韦铁平, 等. 电阻应变式传感器应变传递影响因素分析[J]. 中国测试, 2018, 44(1): 136-142. XU Y Q, YANG X X, WEI T P, et al. Analysis of strain transfer influence factors of resistance strain sensor[J]. China Measurement & Test, 2018, 44(1): 136-142. |
| [22] |
李朋, 王来, 郭海燕, 等. 基于FBG传感技术的深海立管涡激振动测试研究[J]. 振动.测试与诊断, 2016, 36(4): 756-763. LI P, WANG L, GUO H Y, et al. Study on vortex-induced vibration testing of deep-sea riser based on FBG sensing technology[J]. Journal of Vibration, Measurement & Diagnosis, 2016, 36(4): 756-763. |
| [23] |
雪增红, 刘兴发, 白小榜, 等. 离心泵轴向力测试系统的设计[J]. 流体机械, 2018, 46(2): 46-49. XUE Z H, LIU X F, BAI X B, et al. The system design of axial force test for centrifugal pump[J]. Fluid Machinery, 2018, 46(2): 46-49. |
| [24] |
魏娟, 张志杰, 赵晨阳, 等. 冲击波测试系统中压力传感器的实时动态补偿实现[J]. 传感技术学报, 2018, 31(4): 545-550. WEI J, ZHANG Z J, ZHAO C Y, et al. Real-time dynamic compensation of pressure sensor in shock wave measurement system[J]. Chinese Journal of Sensors and Actuators, 2018, 31(4): 545-550. |


