0 引言
作为连接水下井口至浮式钻井平台(船)的通道,海洋钻井隔水管系统在深海油气开发的重要性毋庸置疑。浮式钻井平台(船)往往采用动力定位(DP)系统,可使船舶与水下井口保持在一个特定的范围之内。但是当动力定位系统失效或者遇到极端恶劣天气时,船舶往往无法保持正常钻井位置。此时,必须断开隔水管下部连接总成(LMRP)与水下防喷器(BOP)的连接,并关闭井口,该过程称作隔水管紧急脱离程序(EDS)[1]。如果不能及时的断开隔水管系统,可能导致船体倾覆或隔水管拉断等事故。
业界往往利用隔水管张紧器开展隔水管紧急脱离时的抗反冲控制研究。该技术在国外已经较为成熟,国外学者对紧急脱离作业操作规程和抗反冲控制规程等均有深入的研究[2-3]。国内对于抗反冲控制技术的研究还停留在理论分析和样机试验阶段。鞠少栋等[4-8]在抗反冲控制方法和隔水管-张紧器-平台耦合动力学分析等方面做了大量工作。李韩玮等[9-11]完成了隔水管张紧器样机的试制工作,但是由于抗反冲控制试验缺乏海试条件,无法对抗反冲控制算法进行进一步的验证。本文以250K钢丝绳式隔水管张紧器为原型,开展抗反冲控制算法的研究,分析两种抗反冲控制算法在不同初始条件下的适应性。针对前期研究成果[12],引入了钻井液模型,使仿真更接近实际情况。本文的研究内容可为后续产品设计及性能优化提供理论依据。
1 抗反冲控制理论当EDS执行时,隔水管张紧系统进入抗反冲控制模式,通过水下液压连接器直接控制LMRP与BOP脱开,隔水管在顶部张力作用下加速向上运动,LMRP将迅速脱离BOP,隔水管系统向上“反冲”。如果“反冲”超出控制范围,可能导致伸缩节与钻井船或钻井平台甲板碰撞、LMRP与BOP发生碰撞碰及张紧装置失效等严重事故。为降低隔水管系统“反冲”带来的风险,应该进行抗反冲控制,主要包括:①降低隔水管反冲加速度和速度,防止与平台碰撞;②紧急脱离后,LMRP需迅速上升到足够高度,防止由于船体升沉引起LMRP与BOP碰撞;③控制液缸的伸出速度,避免速度过快导致液缸“冲缸”和钢丝绳“跳槽”。
2 抗反冲控制仿真模型与算法 2.1 隔水管系统模型不考虑横向受力及隔水管的细长杆特性,在振动力学中通常采用瑞利法来近似模拟。隔水管系统总质量分布为上、下两个集中质量块M1和M2,忽略钻井液和隔水管之间的摩擦力,隔水管串简化模型如图 1所示。上部质量块M1的重力为水面附近不带浮力块的重力,下部质量块M2的重力为剩余隔水管串总重力的⅓,水下LMRP、钻井液(MUD)和下部质量块为一个集中载荷,放置在弹簧模型的末端。
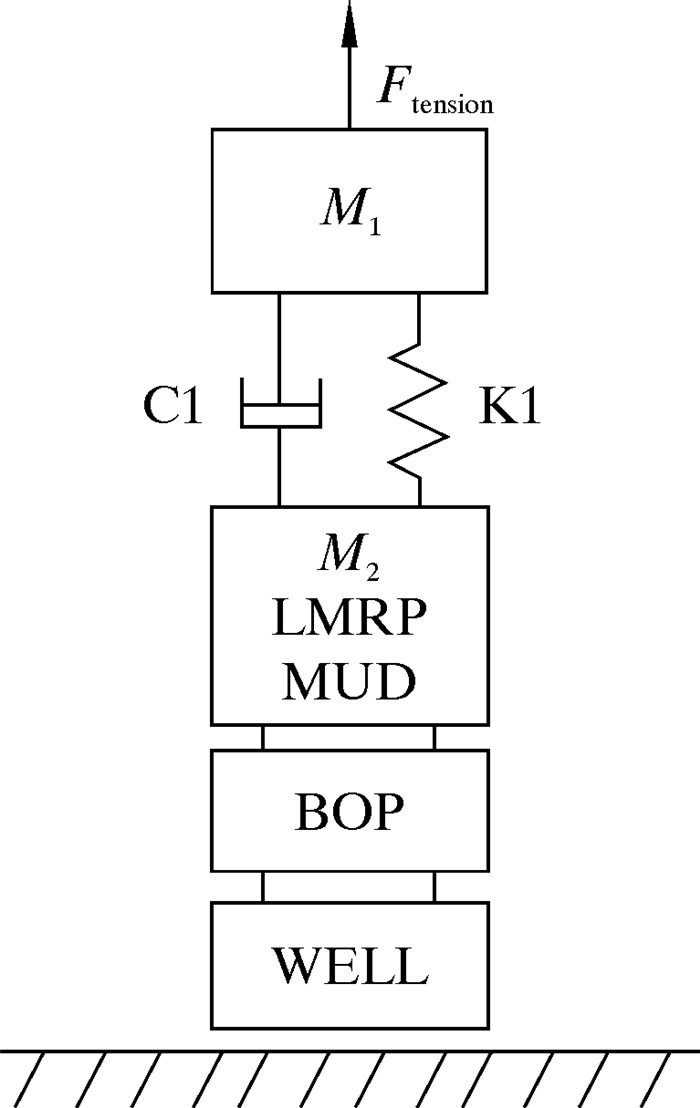
|
| 图 1 隔水管串简化模型 Fig.1 Simplified model of riser |
假设隔水管串在反冲过程中为弹簧模型,其刚度计算公式为:
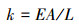
|
(1) |
式中:E为隔水管弹性模量,取210 GPa;A为隔水管等效截面积,m2;L为隔水管串长度,m。
海水对隔水管串的运动阻力可用幂律流体进行简化计算,计算公式为:
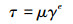
|
(2) |
式中:τ为剪切力,μ为稠度系数,γ为剪切速率,e为流变指数。
将海水设定为牛顿流体,流变指数e取1,可以得到海水的阻力计算公式为:
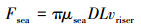
|
(3) |
式中:μsea为海水稠度系数,取1.5;D为隔水管串动力学外径,m;vriser为隔水管串上升速度,m/s。
2.2 钻井液模型紧急脱离前隔水管内充满钻井液,LMRP与BOP脱离时,钻井液开始排入海水中,经过一段时间流动后,隔水管底部内外压力差为0,钻井液液柱受力平衡,钻井液流动停止,如图 2所示。
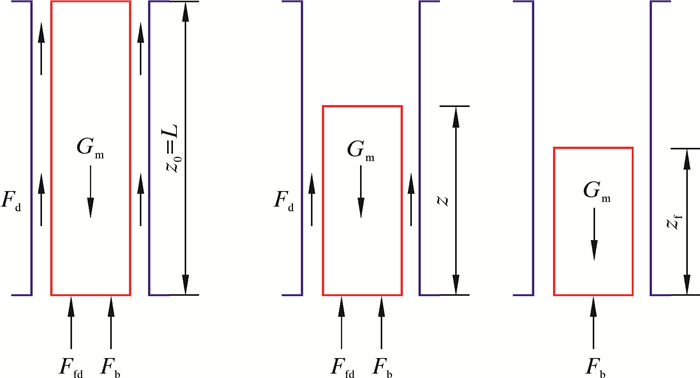
|
| 图 2 钻井液释放模型 Fig.2 Mud releasing model |
图 2中,Gm为钻井液液柱重力,Fd为液柱与隔水管之间摩擦力,Ffd为液柱底部受到的压差阻力,也称为形状阻力,Fb为液柱底部受到的海水压力。
钻井液在隔水管中释放时压力降公式为:
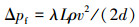
|
(4) |
式中:Δpf为钻井液释放产生的压力降,Pa;λ为达西摩擦因数;d为隔水管直径,m;v为隔水管内钻井液的平均流速,m/s;ρ为钻井液密度,kg/m3。
达西摩擦因数λ的计算与钻井液流动状态有关,假定钻井液为幂律流体且释放过程中为紊流,雷诺数Re的计算公式为:
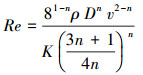
|
(5) |
相应的λ计算公式为:
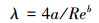
|
(6) |
式中:n为钻井液行为指数,取值为0.50;K为钻井液稠度系数,其值为0.13;a、b是与液体流动特性有关的系数,其值分别为0.071 2和0.307 0。
钻井液释放时受到的压差阻力与钻井液液柱横截面积及钻井液释放速度有关。钻井液在隔水管中释放时的摩擦力即为压力降与管柱内截面积的乘积。压差阻力计算公式为:
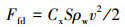
|
(7) |
式中:Cx为压差阻力系数;S为钻井液液柱横截面积,m2;ρw为海水密度,kg/m3。
根据建立的钻井液释放分析模型,得到钻井液液柱释放时的受力平衡方程:
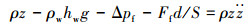
|
(8) |
式中:z为钻井液剩余长度,m;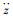
考虑到波浪的随机性,以正弦波进行模拟,浮式钻井船的升沉周期与波浪周期相同[13]。升沉波高遵循衰减系数K1,升沉运动简化计算公式为:
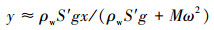
|
(9) |
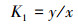
|
(10) |
式中:y为船体在相对坐标系中的高度,m;x为水面在相对坐标系中的高度,m;ρw=1 030 kg/m3;M为船体质量,取3×107 kg;g为重力加速度,取9.8 m/s2;S′为船体吃水线处与海水的接触面积,S′=5 000 m2;ω为波浪角频率,rad/s。
通过计算可得到不同海况下船体升沉运动参数,如表 1所示。表 1中的波高和波周期为南海实际海况数据。
| 海况/级 | 波高/m | 周期/s | 衰减系数 | 升沉波高/m |
| 5 | 4.0 | 12 | 0.676 | 2.704 |
| 6 | 6.0 | 14 | 0.763 | 4.578 |
| 7 | 9.0 | 17 | 0.869 | 7.821 |
| 8 | 14.0 | 20 | 0.902 | 12.623 |
2.4 抗反冲控制算法
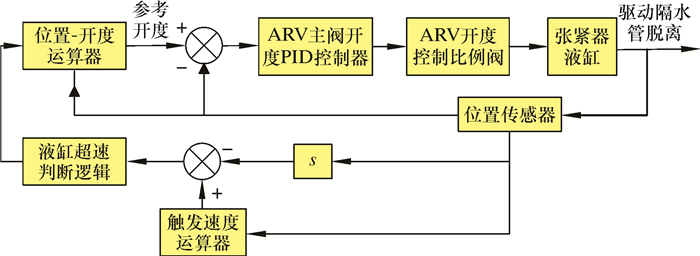
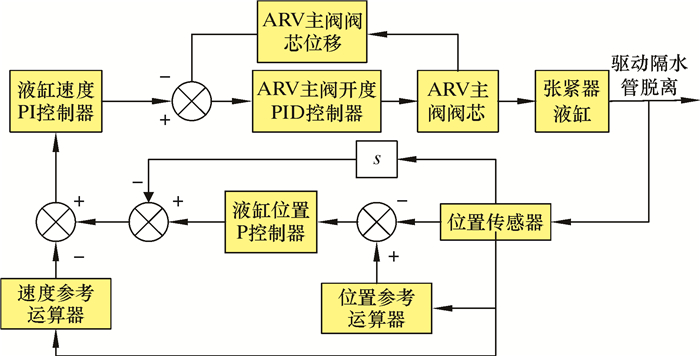
本文提出基于位置和速度控制两种类型的抗反冲控制算法。位置控制算法如图 3所示,速度控制算法如图 4所示。
|
| 图 3 位置控制算法示意图 Fig.3 Schematic diagram of position control algorithm |
|
| 图 4 速度控制算法示意图 Fig.4 Schematic diagram of speed control algorithm |
位置-开度运算器和触发速度运算器都是根据液缸活塞杆的实时位移运算触发速度和主阀参考开度。紧急脱离时,控制系统检测液缸活塞杆的实时速度,当速度超过触发速度时,调用ARV(抗反冲阀)主阀开度PID控制器,按照主阀参考开度进行闭环控制,实现对液缸活塞杆速度和位移的调节。速度控制算法采用双重闭环结构,该闭环分内环和外环,内环为液缸活塞杆速度控制,外环为位置控制,如图 4所示。位置参考运算器和速度参考运算器根据脱离时刻,按照时间运算出液缸活塞杆的参考位移和参考速度,速度控制环采用PI控制,位置环采用P控制,内环比外环有更快的动态响应。
3 抗反冲控制算法适应性本文采用AMESim平台对张紧器抗反冲控制系统进行模型搭建,进行两种抗反冲控制算法对比,采用不同海况、钻井液密度及脱离时间等模型输入参数,研究算法的适应性。
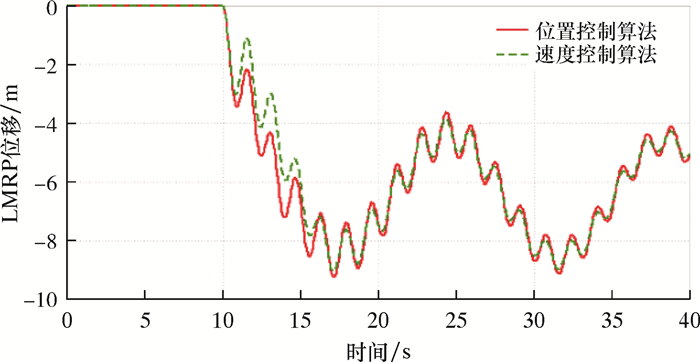
3.1 海况适应性设定作业水深2 355 m,钻井液密度1 916 kg/m3,取6、7和8级3种海况进行仿真,紧急脱离时间为第10 s。仿真结果如图 5~图 10所示。
|
| 图 5 6级海况下LMRP位移曲线 Fig.5 LMRP displacement curve under 6-level sea condition |
|
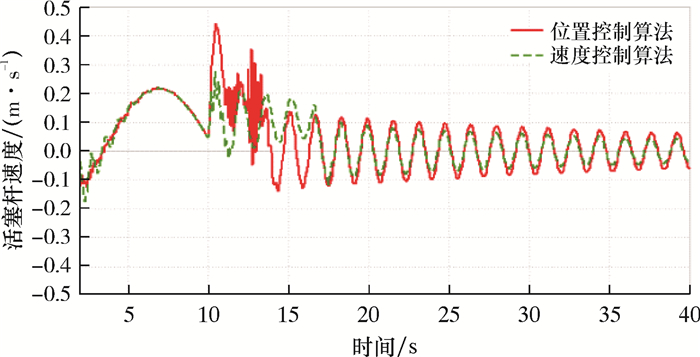
| 图 6 6级海况下活塞杆速度曲线 Fig.6 Speed curve of piston rod under 6-level sea condition |
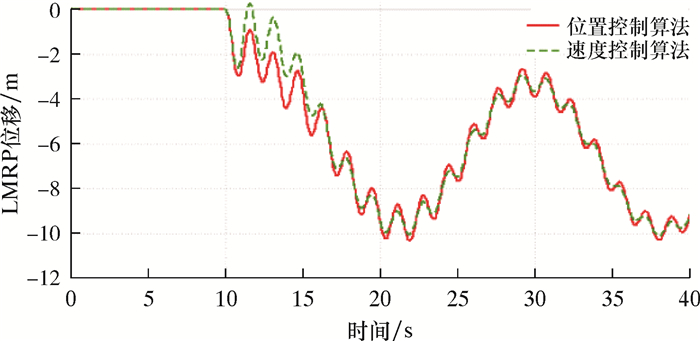
|
| 图 7 7级海况下LMRP位移曲线 Fig.7 LMRP displacement curve under 7-level sea condition |
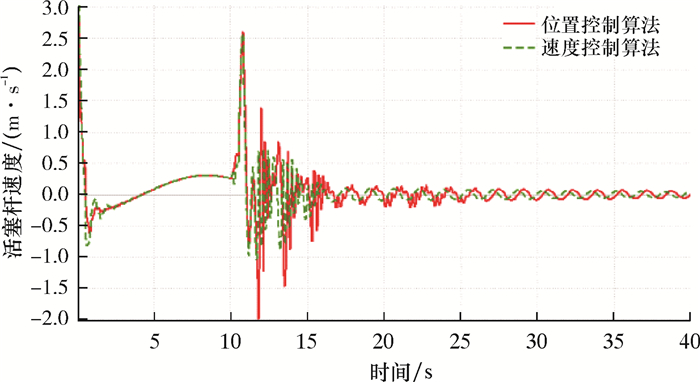
|
| 图 8 7级海况下活塞杆速度曲线 Fig.8 Speed curve of piston rod under 7-level sea condition |
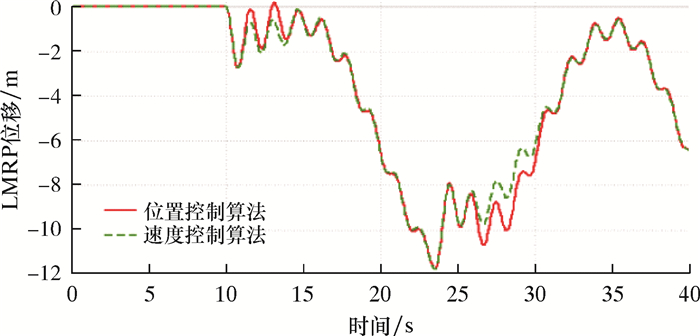
|
| 图 9 8级海况下LMRP位移曲线 Fig.9 LMRP displacement curve under 8-level sea condition |
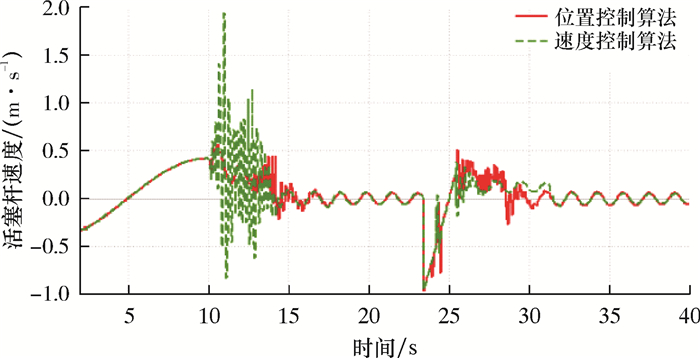
|
| 图 10 8级海况下活塞杆速度曲线 Fig.10 Speed curve of piston rod under 8-level sea condition |
由图 5和图 6可知,在6级海况下,两种控制算法均能满足要求,但是位置控制算法在紧急脱离时活塞杆速度突变较为严重。由图 7和图 8可知,在7级海况下,两种控制算法对于活塞杆速度的控制效果一致,但是速度控制算法在紧急脱离时LMRP有触底的风险。由图 9和图 10可知,在8级海况下,两种控制算法的LMRP均发生碰撞,位置控制算法在活塞杆速度控制方面表现更优。但是液缸完全缩回之后,在23 s左右,液缸出现LMRP下降现象,导致该情况主要是船体升沉加速度过大,ARV的开启程度无法提供足够的加速度,进而引起液缸回缩。
综上所述,随着海况的逐渐恶劣,抗反冲控制算法的控制效果将变差,7级海况下进行紧急脱离存在LMRP与BOP碰撞的风险。故隔水管紧急脱离的极限海况为7级,且该海况必须采用位置控制算法,超过7级海况再行脱离极易引发事故。
3.2 钻井液密度适应性设定作业水深2 355 m,7级海况下执行紧急脱离,取1 198、1 437及1 677 kg/m3 3种钻井液密度进行仿真。仿真结果如图 11~图 16所示。
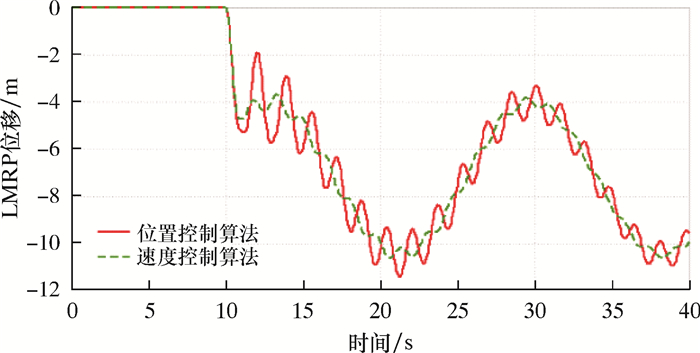
|
| 图 11 钻井液密度为1 198 kg/m3时LMRP位移曲线 Fig.11 LMRP displacement curve at mud density of 1 198 kg/m3 |
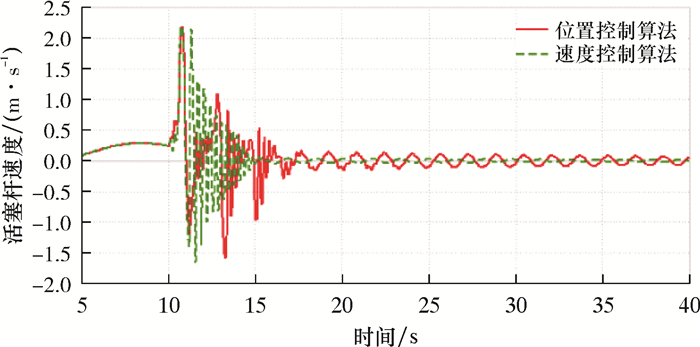
|
| 图 12 钻井液密度为1 198 kg/m3时活塞杆速度曲线 Fig.12 Speed curve of piston rod at mud density of 1 198 kg/m3 |
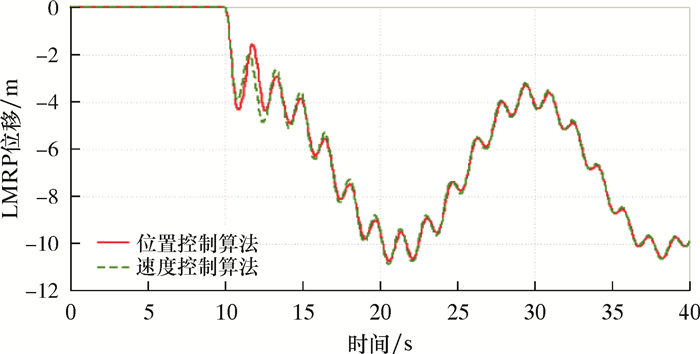
|
| 图 13 钻井液密度为1 437 kg/m3时LMRP位移曲线 Fig.13 LMRP displacement curve at mud density of 1 437 kg/m3 |
|
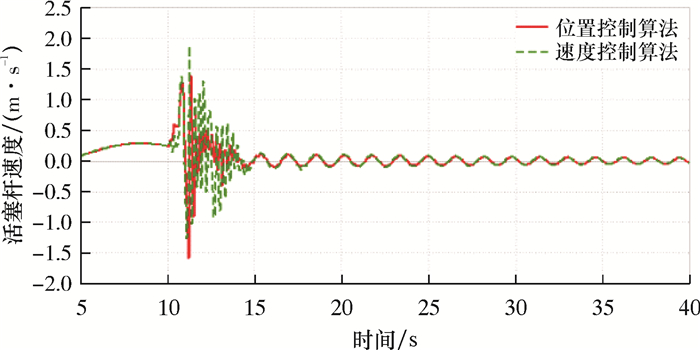
| 图 14 钻井液密度为1 437 kg/m3时活塞杆速度曲线 Fig.14 Speed curve of piston rod at mud density of 1 437 kg/m3 |
|
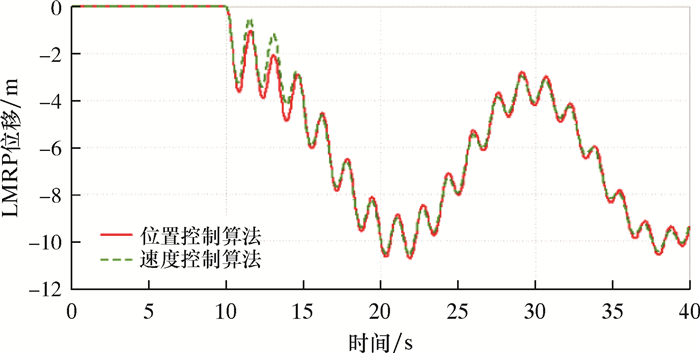
| 图 15 钻井液密度为1 677 kg/m3时LMRP位移曲线 Fig.15 LMRP displacement curve at a mud density of 1 677 kg/m3 |
|
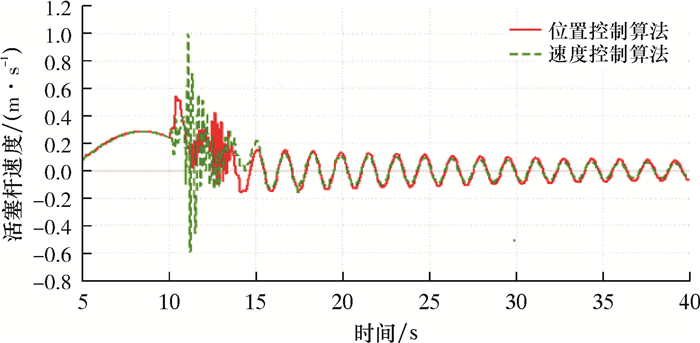
| 图 16 钻井液密度为1 677 kg/m3时活塞杆速度曲线 Fig.16 Speed curve of piston rod at mud density of 1 677 kg/m3 |
由图 11和图 12可知,在钻井液密度为1 198 kg/m3时,速度控制算法在紧急脱离时LMRP位移震荡较小,整个隔水管串受力情况更优。
由图 13和图 14可知,在钻井液密度为1 437 kg/m3时,两种控制算法控制效果基本一致。
由图 15和图 16可知,在钻井液密度较高时进行脱离,位置控制算法比速度控制算法更优。
综上所述,钻井液密度对张紧系统抗反冲性能影响较大。随着钻井液密度增大,紧急脱离时LMRP与BOP的距离越小。在低钻井液密度情况下,速度控制算法对应的LMRP运动更平缓;高钻井液密度时,位置控制算法对应的液缸速度控制效果更好。
3.3 脱离时间适应性设定作业水深2 355 m,钻井液密度1 916 kg/m3,7级海况,升沉周期17 s,取8.50、12.75、17.00及21.25 s等4个时间点作为脱离时间进行仿真,该4个时间点对应升沉周期中的0°、90°、180°和270°等4个相位点,仿真结果如图 17~图 24所示。
|
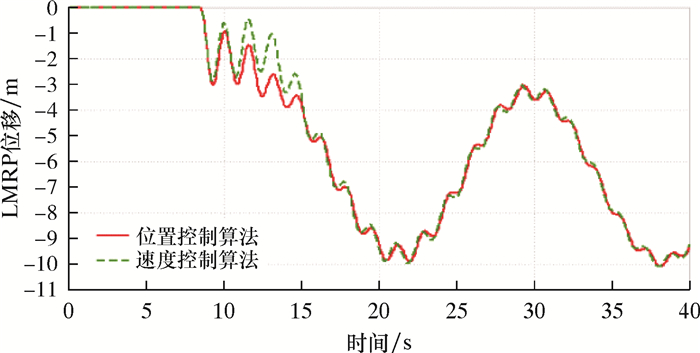
| 图 17 紧急脱离时间8.50 s时LMRP位移曲线 Fig.17 LMRP displacement curve for emergency disconnect sequence time at 8.50 s |
|
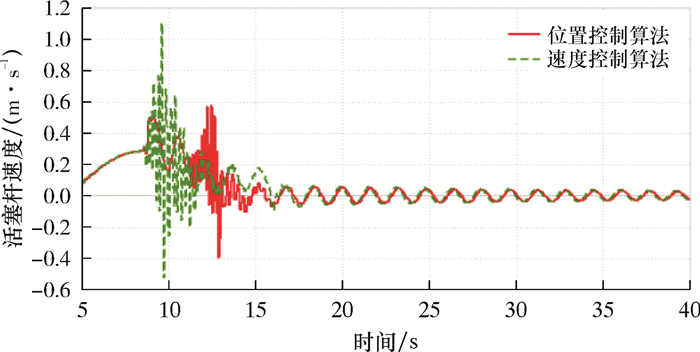
| 图 18 紧急脱离时间8.50 s时活塞杆速度曲线 Fig.18 Piston rod speed curve for emergency disconnect sequence time at 8.50 s |
|
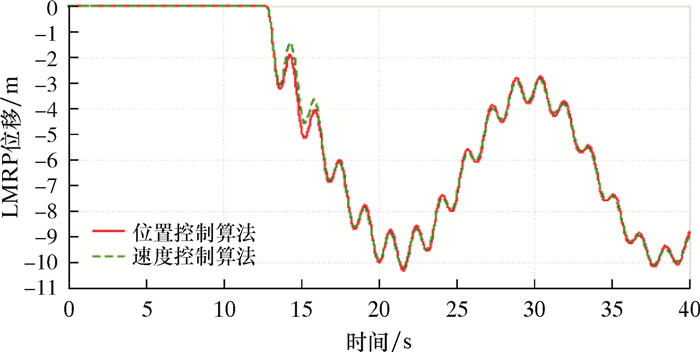
| 图 19 急脱离时间12.75 s时LMRP位移曲线 Fig.19 LMRP displacement curve for emergency disconnect sequence time at 12.75 s |

|
| 图 20 紧急脱离时间12.75 s时活塞杆速度曲线 Fig.20 Piston rod speed curve for emergency disconnect sequence time at 12.75 s |
|
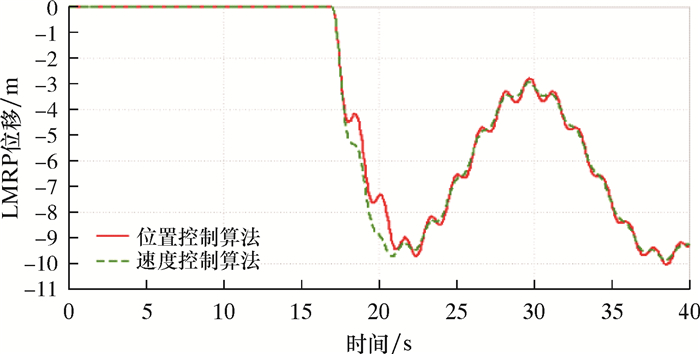
| 图 21 紧急脱离时间17.00 s时LMRP位移曲线 Fig.21 LMRP displacement curve for emergency disconnect sequence time at 17.00 s |
|
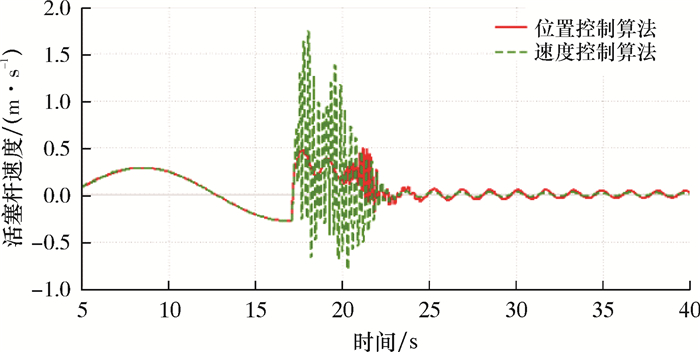
| 图 22 紧急脱离时间17.00 s时活塞杆速度曲线 Fig.22 Piston rod speed curve for emergency disconnect sequence time at 17.00 s |
|
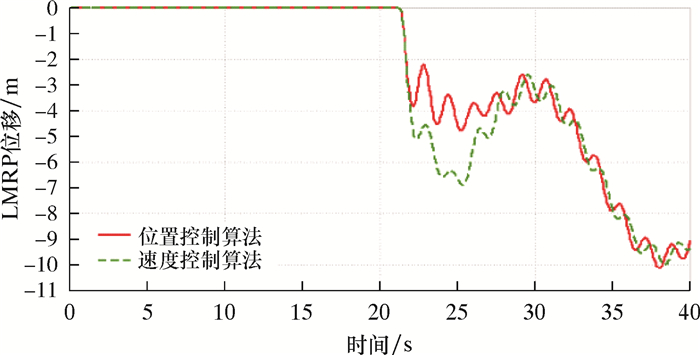
| 图 23 紧急脱离时间21.25 s时LMRP位移曲线 Fig.23 LMRP displacement curve for emergency disconnect sequence time at 21.25 s |
|
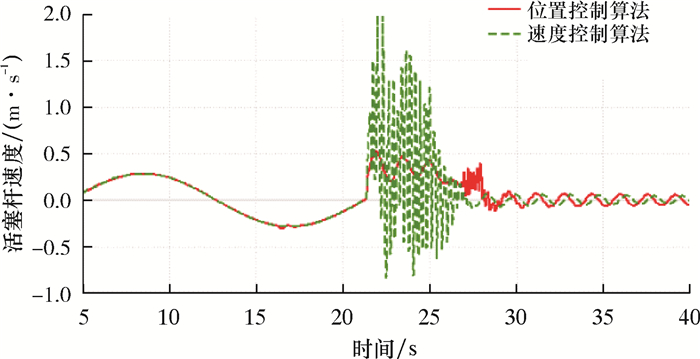
| 图 24 紧急脱离时间21.25 s时活塞杆速度曲线 Fig.24 Piston rod speed curve for emergency disconnect sequence time at 21.25 s |
分析图 17~图 24可以得到,在脱离时间为8.50 s时,LMRP与BOP距离最近(小于1 m),其余脱离时间距离均超过2 m。在脱离时间12.75 s时,对于活塞杆的速度控制,两种算法控制效果相似。在其余脱离时间,速度控制算法则在紧急脱离之后出现活塞杆速度大幅度的突变,最高可超过2 m/s,而位置控制算法对于活塞杆的速度控制效果更优(不超过0.6 m/s)。因此,在考虑钻井平台紧急脱离时机时,建议在12.75和17.00 s之间(即船舶处于升沉的最高点处到向中位下降的区间),并优先考虑位置控制抗反冲算法。
4 结论(1) 利用张紧装置进行隔水管紧急脱离的抗反冲控制是一种切实有效的途径,为防止油液堵塞导致抗反冲失效,抗反冲阀的比例控制功能须重点进行定期维护。
(2) 张紧装置适配船型的最大紧急脱离海况为7级,超过该海况级别将导致事故发生。
(3) 两种抗反冲控制算法适应性各不相同,速度控制算法适用于钻井液密度较低的情况,而位置控制算法适应性更广。
(4) 紧急脱离时间宜选在船体处于升沉最高点处到向中位下降的区间,且选用位置控制算法,可使紧急脱离时安全性能更高。
| [1] |
ANON. Design, selection, operation, and maintenance of marine drilling riser systems: API RP 16Q SECOND EDITION[S]. Washington DC: American Petroleum Institute, 2017.
|
| [2] |
ANON. Specification for marine drilling riser equipment: API SPEC 16F SECOND EDITION[S]. Washington D C: American Petroleum Institute, 2017.
|
| [3] |
DYGVOLD S H Ø. Development of simulation model for virtual testing and design of riser tensioner system[D]. Arendal: University of Agder, 2011.
|
| [4] |
鞠少栋, 畅元江, 陈国明, 等. 深水钻井隔水管连接作业窗口分析[J]. 石油勘探与开发, 2012, 39(1): 105-110. JU S D, CHANG Y J, CHEN G M, et al. Envelopes for connected operation of the deepwater drilling riser[J]. Petroleum Exploration and Development, 2012, 39(1): 105-110. |
| [5] |
畅元江.深水钻井隔水管设计方法及其应用研究[D].东营: 中国石油大学(华东), 2008. CHANG Y J. Design approach and its application for deepwater drilling risers[D]. Dongying: China University of Petroleum (Huadong), 2008. |
| [6] |
畅元江, 鞠少栋, 陈国明, 等. 深水钻井隔水管单根基本参数确定方法[J]. 中国石油大学学报, 2012, 36(1): 117-121. CHANG Y J, JU S D, CHEN G M, et al. Determining methods for basic parameters of deepwater drilling riser single[J]. Journal of China University of Petroleum, 2012, 36(1): 117-121. DOI:10.3969/j.issn.1673-5005.2012.01.020 |
| [7] |
刘秀全, 李家仪, 任克忍, 等. 基于反冲响应的深水钻井隔水管张紧力计算方法[J]. 石油钻探技术, 2016, 44(4): 47-51. LIU X Q, LI J Y, REN K R, et al. Acalculation method for the top ternsion of deepwater drilling risers based on recoil respone[J]. Petroleum Drilling Techniques, 2016, 44(4): 47-51. |
| [8] |
张磊, 畅元江, 刘秀全, 等. 基于AMESim的深水平台隔水管张紧器建模与仿真研究[J]. 石油机械, 2013, 41(12): 38-42. ZHANG L, CHANG Y J, LIU X Q, et al. AMESim-based modeling and simulation of platform riser tensioner[J]. China Petroleum Machinery, 2013, 41(12): 38-42. DOI:10.3969/j.issn.1001-4578.2013.12.010 |
| [9] |
李朝玮, 樊洪海, 汪志明, 等. 深水钻井隔水管紧急脱离后的反冲响应[J]. 海洋工程, 2015, 33(4): 121-127. LI C W, FAN H H, WANG Z M, et al. Recoil response of deepwater drilling riser during emergency disconnection[J]. The Ocean Engineering, 2015, 33(4): 121-127. |
| [10] |
任钢峰, 王定亚, 邓平, 等. 海洋钻井隔水管张紧器技术分析[J]. 石油机械, 2013, 41(10): 43-45. REN G F, WANG D Y, DENG P, et al. Technological analysis of the riser tensioner in offshore drilling[J]. China Petroleum Machinery, 2013, 41(10): 43-45. DOI:10.3969/j.issn.1001-4578.2013.10.012 |
| [11] |
周天明, 毋勇锋, 刘远波, 等. 200K钢丝绳式隔水管张紧器动载试验研究[J]. 石油机械, 2017, 45(10): 38-42. ZHOU T M, WU Y F, LIU Y B, et al. Testing on dynamic load of 200K wire rope type riser tensioner[J]. China Petroleum Machinery, 2017, 45(10): 38-42. |
| [12] |
李欢, 李鹏, 范松, 等. 基于AMESim的隔水管张紧器抗反冲控制研究[J]. 石油机械, 2019, 47(9): 84-89, 131. LI H, LI P, FAN S, et al. AMESim-based research on anti-recoil control of riser tensioner[J]. China Petroleum Machinery, 2019, 47(9): 84-89, 131. |
| [13] |
王维旭, 周天明, 于兴军, 等. 浮式钻井平台升沉运动分析[J]. 石油机械, 2011, 40(9): 36-38. WANG W X, ZHOU T M, YU X J, et al. Analysis of heave motion of floating drilling platform[J]. China Petroleum Machinery, 2011, 40(9): 36-38. |


