0 引言
涡轮叶片作为涡轮钻具的核心部件,其加工精度直接影响涡轮钻具的性能[1]。目前,涡轮钻具叶片的加工工艺主要为传统加工工艺,如铸造和铣削加工等。但是,对于叶片这类结构复杂的工件,使用传统加工方法均有其局限性,如加工过程不好控制、工件的成型精度低以及生产成本高等[2-5]。相对于传统加工工艺,电解加工作为新型特种加工工艺,具有刀具无损耗、工件表面质量高、试验周期短以及生产效率高等优点。正是因为电解加工存在上述优点,被广泛应用于航空航天领域[6]。近年来,随着精密电解加工和复合电解加工等技术的发展,电解加工技术已成为现代制造工艺的重要技术。因此,本文将电解加工技术应用于涡轮钻具叶片的加工中。
电解加工是利用电化学的原理对工件阳极进行腐蚀,随着阴极工具的进给,工件最终会变成与阴极相差无几的形状。因此阴极工具的设计将会直接影响工件最终的成型。即要使用电解加工工艺加工制造涡轮钻具叶片,则需要解决的首要问题便是阴极工具设计[7]。对于阴极工具设计,早期采用的方法大多停滞于二维阴极设计问题,这些方法主要应用于一些具有简单或规则形状的对象,设计误差较大,无法解决三维阴极的设计问题。近些年来,随着国内外高校对于电解加工不断深入的探索,电解加工阴极工具的设计有了很大的进步,目前常采用的方法有差分法、有限元分析法和边界元法,这些方法大多基于拉普拉斯方程,采用迭代调整的思路,通过调整阴极的截面边界曲线,直至满足所有条件[8]。
为方便计算,本文使用基于多项式拟合[9]的方法设计涡轮钻具叶片并将设计得到的叶片在FLUENT软件中进行实际工况的仿真模拟,以验证设计的合理性。最后,将设计得到的叶片作为涡轮钻具叶片电解加工工艺的阴极工具。
1 涡轮钻具叶片的基本参数笔者通过调查获取现场及文献中涡轮钻具的技术参数,根据国家设计生产标准,确定选用国产小直径涡轮钻具ø127 mm作为研究对象。
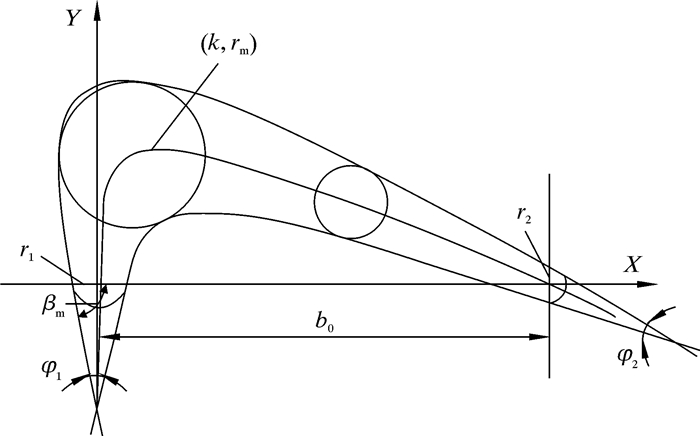
图 1为涡轮钻具叶片的几何描述图。图 1中:横纵坐标表示叶片的x、y取值,r1为前缘半径,r2为后缘半径,b0为叶型弦长,φ1为进口前缘楔角,φ2为出口后缘楔角,rm为叶型最大厚度,k为叶片最大厚度位置,t为叶栅距,θ为叶片转折角。
|
| 图 1 涡轮钻具叶片的几何描述图 Fig.1 The geometry of the blade of the turbodrill |
叶栅节距t是指相邻两翼型对应点之间沿弦长方向的距离,表示叶栅中叶片排列的稠密程度。本设计取t=9 mm。
前、后缘楔角φ1、φ2是前、后缘上、下切线之间的夹角。根据实践经验,进口边楔角φ1通常取10°~30°,出口边楔角φ2通常取7°~15°,本设计取φ1=20°、φ2=11°。
前、后缘半径r1、r2是指进、出口处圆弧半径的大小。根据现有经验和加工条件,前缘半径r1通常取0.6~1.0 mm,后缘半径r2通常取0.4~0.6 mm。前、后缘的半径越小,叶型损失就越小,流速变化的连续性就越强。但考虑到前后缘半径太小会增大叶片的加工成本,因此取r1=0.8 mm、r2=0.5 mm。弦长b0是叶型前缘到尾缘的距离,表示叶片尺寸的大小。其计算公式如下:
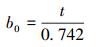
|
(1) |
代入t=9 mm,可得b0=12.13 mm。
叶片数目z影响涡轮钻具的压力变化和效率。叶片数目过多会加大制造难度,增加轴向力及水力输出功率[10]。综合考虑到本设计中涡轮的结构和选材强度等方面,本设计取z=22。
涡轮叶片的最大相对厚度rm关系着叶片的高速运转。且有:
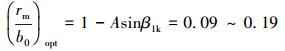
|
(2) |
由此得出叶栅的主要参数如下:b0=12.13 mm,t=9 mm,叶片高度S=10 mm,r1=0.8 mm,r2=0.5 mm,φ1=20°,φ2=11°,转子进口结构角β1k=129.79°,转子出口结构角β2k=18.27°,定子出口结构角α1k=18.27°,定子进口结构角α2k=129.79°,安装角βm=42.3°。
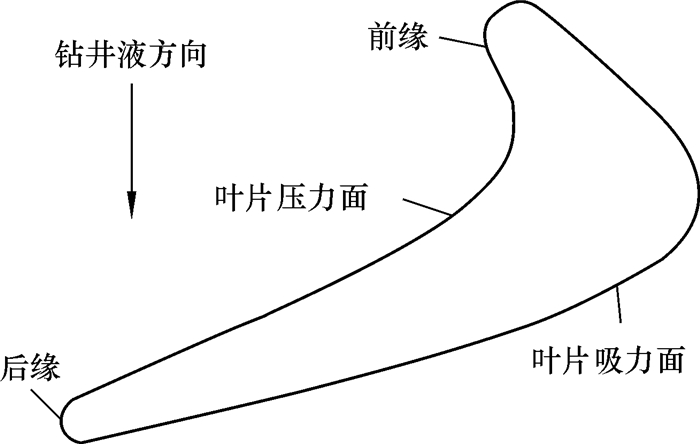
2 基于多项式曲线的叶片型线设计 2.1 涡轮叶片型线设计方法及过程涡轮叶片叶型示意图如图 2所示。叶片截面型线主要包括前缘、后缘、叶片吸力面以及叶片压力面。
|
| 图 2 涡轮叶片叶型示意图 Fig.2 Schematic diagram of turbine blade structure |
在进行涡轮叶片叶型的设计过程中,为了保证叶型表面速度和压力的均匀分布,设计时应注意:①保证叶片曲线光滑柔顺,降低水力损失;②保证各部分曲线连接处的曲率变化均匀,保证叶片截面型线光滑;③前、后缘应保证为圆弧,且分布的变化规律相同。
涡轮叶片曲线越光滑,流体在叶栅通道内的流动性能越好。同时,叶片压力面和吸力面型线的曲率半径R对流动情况的影响较大。因此在设计过程中,应保证叶片型线方程一、二阶导数连续。
设叶型曲线为y=f(x),则有:
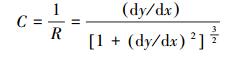
|
(3) |
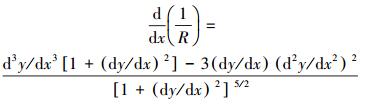
|
(4) |
本文借助于形为y=∑akxk的函数多项式对曲线进行了拟合。使用这种方法,可以通过改变高阶多项式中与形状相关的系数,进而快速获得需要的不同曲线,在保证设计质量的同时提高了叶片型线的优化设计效率。同时,高阶多项式的高次可微性,保证了拟合出的叶型截面曲线光滑连续[11],避免出现压力梯度突变点,改善了叶型表面的流动情况,均衡了压力,减小了摩擦。为了后续计算过程的简便,本文采用五次多项式对叶片型线进行拟合,前、后缘使用圆弧连接,且可保证连接处的点具有二阶连续导数[12],故所得的叶片曲线没有多余拐点,符合设计要求。
2.2 基于MATLAB的叶片型线设计本文选择使用MATLAB软件编程计算叶片型线,具体计算方法如下。
2.2.1 叶片型线方程的构建与求解建立矩阵方程并求解。设涡轮叶片的压力面和吸力面型线方程分别为Yp=f(x)和Ys=g(x),具体方程如下:
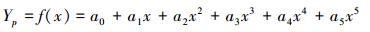
|
(5) |
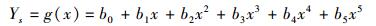
|
(6) |
分别对其取一阶导数有:
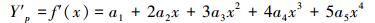
|
(7) |
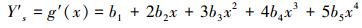
|
(8) |
再对其取二阶导数有:
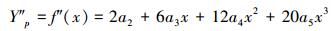
|
(9) |
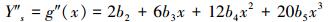
|
(10) |
假设压力面首点坐标为(xp1, yp1),压力面尾点坐标为(xpn, ypn),吸力面首点坐标为(xs1, ys1),吸力面尾点坐标为(xsn, ysn)。对于一阶导数,压力面首点为y′p1,尾点y′pn,吸力面首点为y′s1,尾点为y′sn;对于二阶导数,压力面首点为y″p1,尾点为y″pn;吸力面首点为y″s1,尾点为y″sn。
将叶片型线方程及其导数表示为矩阵形式,如式(11)和式(12)所示。从式(11)和式(12)可以看出,只要先计算出xp1、yp1、xs1、ys1、xpn、ypn、xsn、ysn、y′p1、y″p1、y′pn、y″pn、y′s1、y″s1、y′sn和y″sn,然后代入叶片型线方程,即可求出系数a和b。
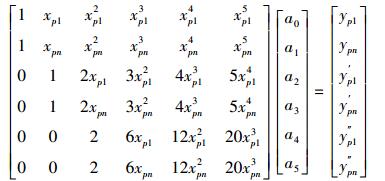
|
(11) |
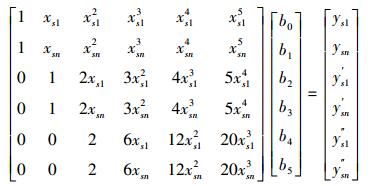
|
(12) |
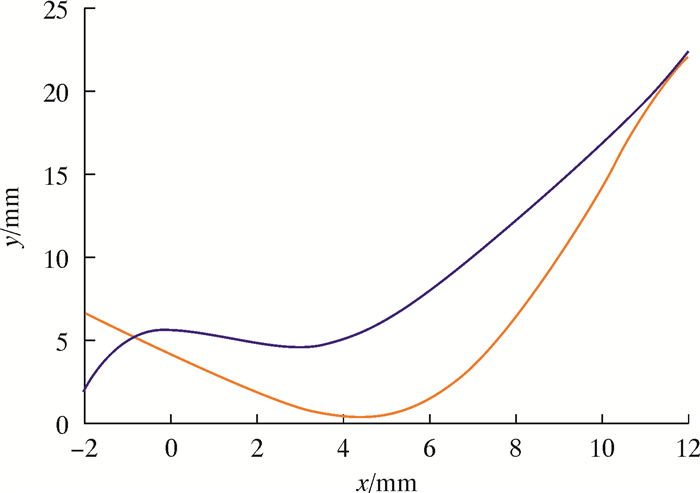
现在根据前述的涡轮叶片几何参数,求解上述未知数。建立如图 3所示的平面直角坐标系(横纵坐标表示叶片的x、y取值),取涡轮轴流方向为X轴正方向,取叶片前缘水平线方向为Y轴正方向,½叶片节距处设为坐标原点。现设定初始条件:AB和AC为前缘的两条切线,前缘楔角∠BAC=φ1,过前缘圆心O1,直线AO1与Y轴反向夹角为β1k。EF和EG为后缘的两条切线,后缘楔角∠FEG=φ2,过后缘圆心O2,直线EO2与Y轴正方向夹角为β2k。前后缘半径分别为r1和r2,安装角为βm。
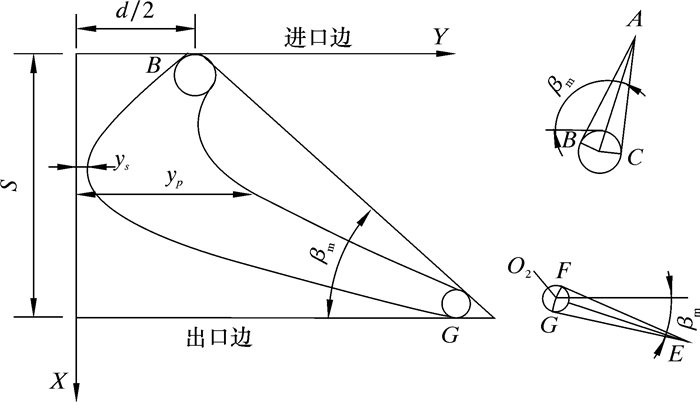
|
| 图 3 涡轮叶片截面型线关系坐标图 Fig.3 Coordinate diagram of shape and line of turbine blade cross-sectional profile |
设前缘圆心O1(xo1, yo1),其中xo1=r1, yo1= 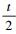
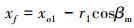
|
(13) |
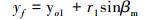
|
(14) |
同时后缘圆心O1(xo2, yo2)可通过下面的计算求出。
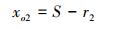
|
(15) |
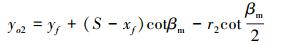
|
(16) |
推导出切点h(xh, yh),则有:
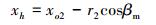
|
(17) |
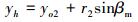
|
(18) |
吸力面首点B(xs1, ys1)计算:
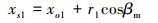
|
(19) |
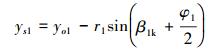
|
(20) |
其一阶导数为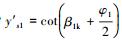
压力面首点C(xp1, yp1)计算公式为:
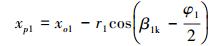
|
(21) |
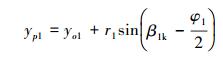
|
(22) |
其一阶导数为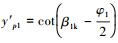
吸力面尾点G(xsn, ysn)计算公式为:
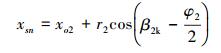
|
(23) |
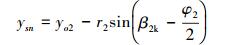
|
(24) |
其一阶导数为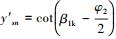
压力面尾点F(xpn, ypn)计算公式为:
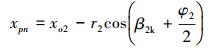
|
(25) |
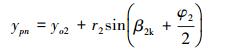
|
(26) |
其一阶导数为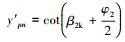
吸力面和压力面首点与尾点的二阶导数为:
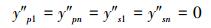
|
(27) |
将数据代入上述各式,通过计算可以得到xp1、yp1、xs1、ys1、xpn、ypn、xsn、ysn、y′p1、y″p1、y′pn、y″pn、y′s1、y″s1、y′sn和y″sn的数值,然后在MATLAB中编程求解方程组,得到叶片最终的型线方程为:
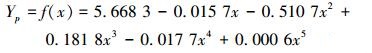
|
(28) |
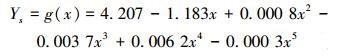
|
(29) |
在MATLAB中绘制叶片型线方程,得到压力面与吸力面的曲线如图 4所示。
|
| 图 4 MATLAB运行输出叶型曲线 Fig.4 Blade shape curve output by MATLAB |
2.2.2 导入AutoCAD绘制二维叶型
MATLAB中得到的叶片型线只是初步的压力面与吸力面曲线,前、后缘部分并没有达到设计要求。因此需要将MATLAB中得到的曲线导入AutoCAD,做进一步的绘制。由于AutoCAD不能读取MATLAB输出的DAT文件,所以为得到MATLAB生成的曲线并进行修补绘制,此处首先将MATLAB中的曲线输出为散点坐标[13],然后用AutoCAD中的绘制多点功能得到曲线的散点,最后使用样条曲线拟合的方式,将数量极多的多点连接形成一条光滑的曲线。根据前述得到的叶片几何参数,最终绘制得到的叶片型线如图 5所示。
|
| 图 5 涡轮叶片截面型线设计图 Fig.5 Turbine blade cross section profile design |
3 基于Fluent的涡轮叶片建模分析 3.1 流场数学模型
为了检验设计的涡轮叶片是否可以很好地应用在实际工况中,本文对涡轮叶片做了CFD仿真分析。因为涡轮的所有叶片具有相同的形状和尺寸,所以本文只画出两对单周期叶片实体进行流场分析,这样既可以研究出相邻两个叶片之间流体的走向变化,又可以得出同一对叶片之间的流体走向变化。同时这种方法占用计算机的资源较少,可以提高计算速度,缩短分析时间。图 6为涡轮叶片的仿真模型。为了减小计算过程中进口及出口位置对叶片内部流场的影响,使流场模拟计算得出稳定解,在定、转子出口与入口处加长了一段距离[14]。
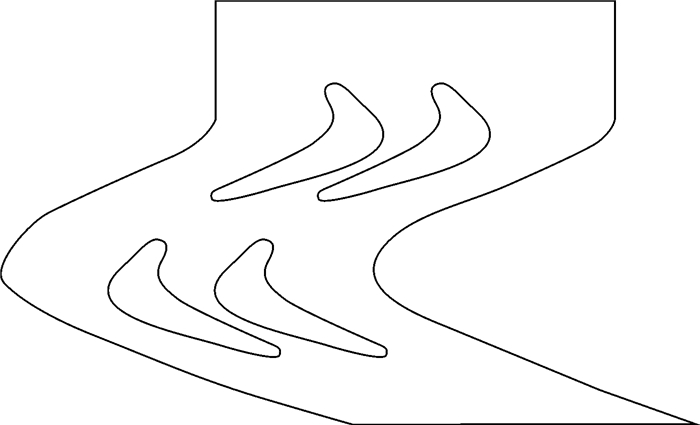
|
| 图 6 涡轮定、转子叶片流场模型设计图 Fig.6 Flow field model design for turbine stator and rotor blade |
涡轮叶片正常工作时的流场可以认为是连续的流场,并且所涉及的速度场和压力场可微。因此在求解时可将N-S方程作为控制方程。使用N-S方程分析内流场时需满足以下条件[15]:
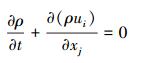
|
(30) |
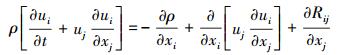
|
(31) |
式中:ρ为液体密度;ui为速度分量,i=x、y、z;Rij为雷诺应力张量。
其中:
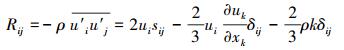
|
(32) |
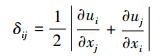
|
(33) |
式中:ui为湍流黏性系数;u′i、u′j为脉动速度;k为湍流动能;δij为克罗内克尔函数,表示变形率张量。
3.2 仿真结果分析利用有限元分析软件Fluent对图 7所示模型进行仿真计算。本文在CFD求解过程中,将定子进口的边界条件设定为速度进口,转子出口的边界条件设定为压力出口,定义定子和转子的周期边界为periodic类型,黏性模型选择为标准的湍流模型。
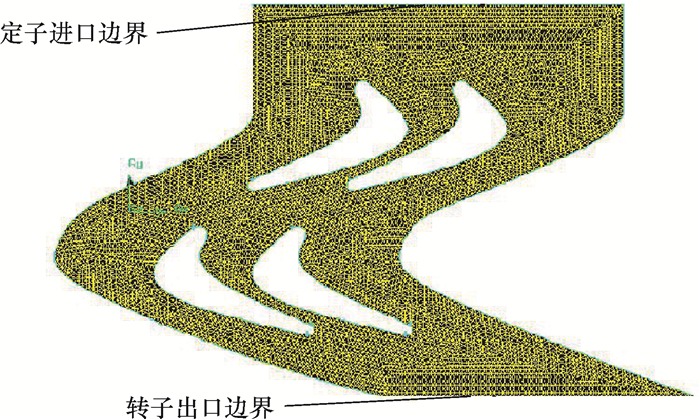
|
| 图 7 涡轮定、转子叶片流道CFD离散化模型图 Fig.7 CFD discretization model of turbine stator and rotor blade flow channel |
涡轮钻具常用于油田的超深钻探,为保证试验不具有偶然性,更具有说服力,本文对ø127 mm的轴流式涡轮钻具在不同工况下的不同输出性能进行了研究,分析不同状态下涡轮钻具的水力性能,并对涡轮叶片的水力性能进行预测。
在进行流量计算时,需要考虑容积效率损失,取容积率为0.8。当井深超过3 000 m,钻井液的黏度范围一般取5~35 mPa·s。模拟时分别对以下3种情况进行分析:①排量10 L/s,黏度5 mPa·s;②排量12 L/s,黏度5 mPa·s;③排量14 L/s,黏度5 mPa·s。借助Tecplot360软件绘制出流场仿真的压力、液流流向和速度图,如图 8所示。
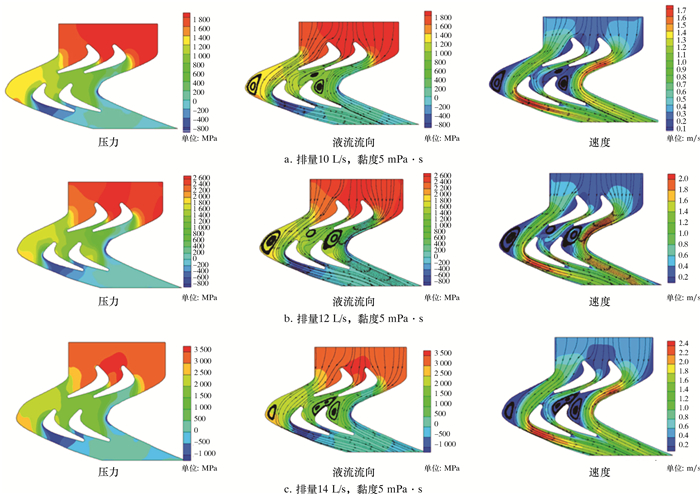
|
| 图 8 不同工况下叶片分析云图 Fig.8 Blade analysis under different working conditions |
观察图 8中的压力和速度变化趋势,可得到以下结论:
(1) 流体流经涡轮叶片前缘后,会分别沿着叶背曲线和叶盆曲线流动。
(2) 流体刚流进涡轮定子时,速度几乎不会发生变化,由于一开始叶型收缩,早收缩的叶栅中流体压力开始转化为增加的速度,因此会有一个增速的过程。直至经过叶片的最大厚度后,压力减小,流体的速度明显增加。
(3) 由于叶片尾缘处会有损失,在定子和转子的后缘处都会有一个速度明显降低的过程。叶片出口处的厚度导致沿叶片两侧流动的两部分流体在离开叶栅之后继续流动,不立刻汇合,形成尾迹区,尾迹区内的流体速度与其他部位的速度相差很大。
(4) 流体经过涡轮的定子叶片后流入转子叶片,液流再次被划分为两部分,叶片吸力面的流体速度要小于压力面的流体速度。
(5) 由流场的压力分布图可知,叶片压力面的压力要大于吸力面的压力,说明叶片的输出扭矩较好。
综上所述,叶片设计合理,满足实际工况的要求。
4 结束语阴极工具设计是涡轮钻具叶片电解加工的一个重要环节,合理的阴极工具设计可以保证零件加工精度高。本文针对涡轮钻具叶片的电解加工,进行了最基本的阴极工具设计,并基于Fluent进行了流场的数值模拟研究。研究结果表明,利用基于多项式的叶片曲面造型方法设计的叶片可以满足实际工况的要求。这为涡轮钻具叶片的电解加工研究奠定了良好基础。
| [1] |
翁炜, 张德龙, 赵志涛, 等. ø127 mm涡轮钻具在干热岩钻井取心钻进中的试验研究[J]. 探矿工程(岩土钻掘工程), 2017, 44(9): 68-72. WENG W, ZHANG D L, ZHAO Z T, et al. Experimental research on the application of ø127 mm turbodrill in hot dry rock core drilling[J]. Exploration Engineering (Rock & Soil Drilling and Tunneling), 2017, 44(9): 68-72. |
| [2] |
LEE J H, KANG S H, YANG D Y. Novel forging technology of a magnesium alloy impeller with twisted blades of micro-thickness[J]. CIRP Annals-Manufacturing Technology, 2008, 57(1): 261-264. |
| [3] |
KANG B S, KIM N S, KOBAYASHI S. Computer aided preform design in forging of an airfoil section blade[J]. Int. J. Mach. Tools Manufact., 1990, 30(1): 43-52. |
| [4] |
全荣, 陈尔昌, 陈日耀. 国外叶片锻造技术概况[J]. 航空工艺技术, 1994(4): 8-9. QUAN R, CHEN E C, CHEN R Y. Overview of foreign blade forging technology[J]. Aviation technology, 1994(4): 8-9. |
| [5] |
ZHAN H, ZHAO W, WANG G. Manufacturing turbine blisks[J]. Aircraft Engineering and Aerospace Technology, 2000, 72(3): 247-251. |
| [6] |
朱荻. 国外电解加工的研究进展[J]. 电加工与模具, 2000(1): 11-16. ZHU D. The latest advances and the principal issues in ECM[J]. Electromachining & Mould, 2000(1): 11-16. |
| [7] |
RAJURKAR K P, ZHU D, MEGEOUGH J A, et al. New developments in electro-chemical machining[J]. Annals of the CIRP, 1999, 48(2): 567-579. |
| [8] |
王蕾.发动机叶片高精度电解加工阴极设计系统及实验研究[D].南京: 南京航空航天大学, 2006. WANG L. The study on precisely cathode design system of turbine blades and experiment in electrochemical machining(ECM)[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10287-2007194055.htm |
| [9] |
何顺, 冯进, 陈斌, 等. 基于Bezier曲线的涡轮叶片造型方法[J]. 长江大学学报(自科版), 2017, 14(21): 45-50. HE S, FENG J, CHEN B, et al. Modeling method of turbine blades based on bezier curve[J]. Journal of Yangtze University(Natural Science Edition), 2017, 14(21): 45-50. |
| [10] |
荆宝德, 王智明, 曲海乐, 等. 随钻测井用井下发电机系统的涡轮设计[J]. 光学精密工程, 2012, 20(3): 616-624. JING B D, WANG Z M, QU H L, et al. Turbine design of turbine generator system for LWD[J]. Optics and Precision Engineering, 2012, 20(3): 616-624. |
| [11] |
赵洪波.涡轮钻具涡轮叶片设计及水力性能仿真优化研究[D].北京: 中国地质大学(北京), 2012. ZHAO H B. study on turbodrill blade design and hydraulic performance simulation and optimization[D]. Beijing: China University of Geosciences (Beijing), 2012. http://cdmd.cnki.com.cn/Article/CDMD-11415-1012364596.htm |
| [12] |
虞跨海, 李立州, 岳珠峰. 基于解析及特征造型的涡轮冷却叶片参数化设计[J]. 推进技术, 2007, 28(6): 637-640. YU K H, LI L Z, YUE Z F. Parametric design for cooling turbine blades based on analytic and feature modeling[J]. Journal of Propulsion Technology, 2007, 28(6): 637-640. |
| [13] |
SONG F F, NI Y H, TAN Z Q. Optimization design, modeling and dynamic analysis for composite wind turbine blade[J]. Procedia Engineering, 2011, 16: 15. |
| [14] |
刘孝光, 潘培道, 胡昌军. 涡轮钻具叶栅水力性能仿真优化技术研究[J]. 冶金设备, 2007(1): 21-24. LIU X G, PAI P D, HU C J. The study of numerical simulation and optimize for turbine drill hydrodynamic performance[J]. Metallurgical Equipment, 2007(1): 21-24. |
| [15] |
贾雷.涡轮钻具叶片设计及CFD分析[D].呼和浩特: 内蒙古工业大学, 2013. JIA L. The turbodrill blade design and CFD analysis[D]. Huhhot: Inner Mongolia Industrial University, 2013. http://d.wanfangdata.com.cn/Thesis/D369346 |



