0 引言
随着大位移井横向长度的不断延长,管柱上高摩阻、高扭矩以及作业极限问题日益突出[1-7],这对管柱组合设计提出了更高的要求。直井和常规定向井中的管柱可以采用解析法进行设计[8],但是该方法无法满足大位移井和水平井中管柱作业的需求。
相关学者开展了大量研究[9-12],主要设计原则是在大斜度和水平段采用普通钻杆或者加重钻杆以降低摩阻,在垂直段和小井斜段采用钻铤或者加重钻杆以提供足够的管柱重力,具体设计方法主要包括经验法和试算法。针对管柱接头位置设计,少部分可采用解析法,例如考虑套管居中要求的扶正器间距设计问题[13-14],大部分还是依赖于经验。但对于高难度大位移井中管柱和接头的设计,要同时考虑管柱屈曲、减摩减扭、管柱居中和管柱失效等因素的综合影响,常规的设计方法难以解决该问题。鉴于此,笔者构建了一种基于大位移井钻井延伸极限的管柱分段优化设计方法,对钻柱和套管组合以及接头位置进行精细的优化设计,以保障大位移井管柱安全高效作业。
1 管柱优化设计问题的简化大位移井钻柱优化设计时需要考虑各种工况下的约束条件,具体如下。
(1) 对于滑动导向钻进工况,垂直段和小井斜段钻柱质量尽量大,大斜度段钻柱摩阻应尽量小,以保证钻柱顺利下入而不发生屈曲锁死,钻头上有足够的钻压破碎岩石。
(2) 对于旋转导向钻进工况,钻柱上的扭矩应小于钻机额定扭矩和钻柱抗扭强度,以保证顺利的旋转钻进作业。
(3) 对于管柱上提工况,管柱抗拉强度要留有余量,以满足上提解卡需要。
(4) 对于管柱倒划眼工况,管柱抗扭强度要留有余量,以满足旋转憋扭矩需要。
关于大位移井套管下入,需要考虑以下约束条件。
(5) 对于滑动下入工况,套管要下入到井底。
(6) 对于旋转下入工况,套管扭矩要小于钻机额定扭矩和套管抗扭强度。
(7) 大斜度段套管居中度应尽量高,以满足固井质量要求。
目前主要采用试算法来考虑多工况、多约束条件的影响,即通过设置不同的管柱设计备选方案,代入管柱力学模型中计算管柱受力结果,分析是否满足上述条件。如果不满足,则改变相应的方案;如果满足,则从中选择最优的设计方案。这种方法的缺点是计算效率低、优化效果不充分。
笔者提出了基于大位移井延伸极限的管柱优化设计方法,设计问题可表示为:
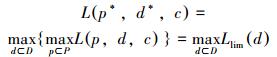
|
(1) |
式中:L为井眼延伸长度,m;Llim为井眼延伸极限,m;p、d和c分别为约束参数、设计参数和操作工况;p*和d*分别为井深达到最大值时的最优约束参数和最优设计参数。
在井眼延伸极限计算模型中(Llim)充分考虑了约束条件(1)~(6)的影响[1, 15];设计模型(1)将条件(7)作为附加约束条件。考虑到大位移作业中极限问题突出,因此将大位移井延伸极限作为目标函数合理。
设计问题(1)求解难度大,主要体现在:
(1) 求解过程中需要频繁计算延伸极限,而延伸极限的计算量较大,导致优化问题求解耗时过长。
(2) 优化设计问题中需要考虑套管居中度的约束,将增大优化设计问题的复杂性。
(3) 管柱设计参数包括管柱长度、尺寸、材料性能等以及管柱接头类型、尺寸、间距等,包括离散和连续两类参数,这增大了设计问题的求解难度。
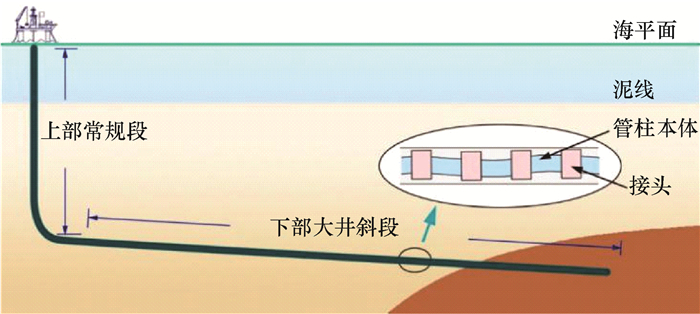
本文提出了一种大位移井管柱分段优化设计方法。该方法将大位移井分成下部大井斜段和上部常规段,如图 1所示。
|
| 图 1 大位移井的上部常规段和下部大井斜段 Fig.1 The upper conventional section and lower high inclination section of extended reach well |
下部大井斜段的井斜角大,横向延伸距离长,裸眼段长,在该井段上的管柱高摩阻和高扭矩问题突出,是限制大位移井延伸极限的主要原因。同时,对大井斜段的固井质量要求高,设计时需要考虑套管居中度的要求。因此对大井斜段采用加权目标函数的方法,目标函数中包括摩阻扭矩和套管居中度,并采取相应的算法进行快速求解。
受下部大井斜段的影响,上部常规段管柱受力非常复杂,常规定向井设计方法难以满足上部常规段管柱作业要求。如果采用加权目标函数设计方法,则无法兼顾多种工况下约束因素的影响。因此,采用延伸极限作为目标函数,不但解决了延伸极限求解低效问题,而且可以利用延伸极限的近似值作为目标函数进行快速求解。
为了解决离散和连续设计参数同时存在导致求解困难的问题,以单根或立柱作为设计单元,则所有的设计参数统一转换为离散形式。一个单根或立柱称之为局部管柱,多个局部管柱的组成可称之为整体管柱,例如大斜度段或者上部常规段的管柱为整体管柱。此时,整体管柱的优化设计问题可转换为一系列局部管柱的优化设计问题。
2 下部大井斜段的优化设计方法降低摩阻可有效提高大井斜段井眼延伸极限。为了提高固井质量,需要在套管上安装许多扶正器来提高套管在井眼中的居中度,如果扶正器太少则达不到居中要求,太多则失效概率增大,扶正器成本高,且套管上机械阻力也增大,不利于套管安全下入。因此,设计下部大井斜段管柱时要综合考虑摩阻、居中度和扶正器数量等因素的综合影响。
2.1 局部管柱设计模型局部管柱摩阻扭矩对应的目标函数为:
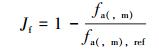
|
(2) |
式中:fa(, m)为单位长度管柱上的摩阻(扭矩),N/m(N);fa(, m), ref为fa(, m)的参考值,N/m(N)。
管柱居中度对应的目标函数为:
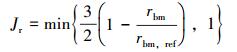
|
(3) |
式中:rbm为管柱横向偏移最大处与井壁的径向间隙,m;rbm, ref为rbm的参考值,m。
管柱接头个数对应的目标函数为:
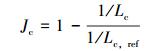
|
(4) |
式中:Lc为相邻接头之间管柱长度,m;Lc, ref为Lc的参考值。
综合考虑上述3个目标函数,可以得到综合目标函数:
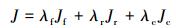
|
(5) |
式中:λf、λr和λc为相应的权重系数,三者之和等于1。
此时,局部管柱优化设计问题表示为:
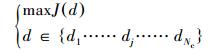
|
(6) |
式中:J(d)为方程(6)定义的目标函数;d为设计参数向量,包括管柱尺寸、接头尺寸和接头间距等参数组成的向量;dj表示设计参数可选择的第j项;Nc为设计参数可选择的项数。
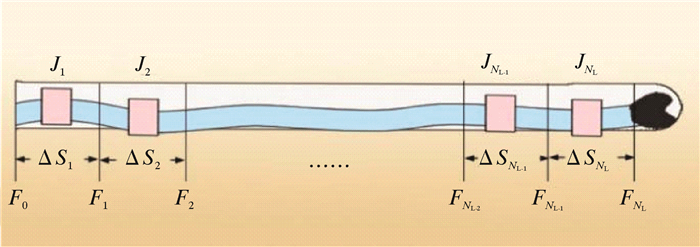
2.2 整体管柱的设计模型大斜度段上整体管柱可看成多个局部管柱的组合,因此整体管柱的设计目标等于局部管柱设计目标之和(见图 2)。整体管柱优化设计问题的数学模型为:
|
| 图 2 水平井眼中整体管柱分解为多个局部管柱 Fig.2 The whole drill string in horizontal wellbore is divided into multiple partial drill strings |
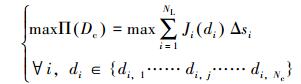
|
(7) |
式中:Π为整体管柱设计问题的目标函数,Δsi为第i段局部管柱的长度,m;Dc为整体管柱的设计参数矩阵,即Dc= [d1…dNL]T;di为第i个局部管柱的设计参数;di, j为第i个局部管柱设计参数可选择的第j项;NL为局部管柱的个数。
方程(7)潜在设计方案个数为NcNL,涉及局部管柱优化设计问题(6)的次数为NcNL·NL,当Nc和NL比较大时,直接求解该模型很耗时。
为解决该问题,相关研究[16]采用先局部后整体的求解方法,整体优化设计问题(7)可转换为从最后一段局部管柱优化设计依次到第一段局部管柱优化设计。然而由于该方法假定了优化顺序,所以优化效果存在不充分等问题。
在此处引入局部管柱组的概念,局部管柱组是指由多个相邻局部管柱组成的管柱段。通常,整体管柱可分成多个局部管柱组,每一局部管柱组又可分成多个子局部管柱组,直至局部管柱组分成几个局部管柱。因此,最大的局部管柱组为整体管柱,最小的局部管柱组为局部管柱。
将大井斜段整体管柱分解为多个局部管柱组,则优化设计问题可转换为:
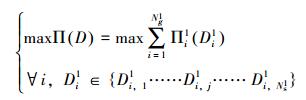
|
(8) |
式中:Πi1为第i个局部管柱组的优化设计目标函数;Di1为第i个局部管柱组的设计参数矩阵;Ns1为第i个局部管柱组设计参数的可选择项的个数;Di, j1为第i个局部管柱组的设计参数可选择的第j项;Ng1为整体管柱包含的局部管柱组个数;上述各参数中上标“1”表示第1层局部组管柱。
问题(8)中Πi1和Di, j1都未确定,因此无法直接求解,需要首先求解各个局部管柱组优化设计问题。第i个局部组管柱的优化问题为:
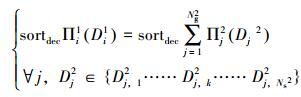
|
(9) |
式中:sortdec为对Πi1的结果进行排序后筛选出前Ns1名的设计结果,即问题(8)中的可选择项;Di1为当前局部管柱组(第1层中第i个)的设计参数,为下一层中各个子局部管柱组设计参数的组合,即Di1= [D12……D2Ng2]T;Πj2为下一层(第2层)第j个子局部管柱组的优化设计目标函数;Dj2为下一层第j个子局部管柱组的设计参数;Dj, k2为下一层第j个子局部管柱组的设计参数可选择的第k项;Ns2为子局部管柱组的设计参数可选择项数;上述各参数中上标“2”表示第2层局部组管柱。
同样,问题(9)中的Πj2和Dj2未确定,需要先求解更下一层的局部组管柱优化设计问题。对于第k层局部组管柱优化设计问题,其一般模式为:
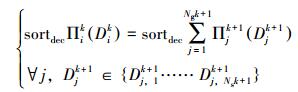
|
(10) |
式(10)中相关变量的含义与公式(9)中变量类似,上标“k+1”表示第k+1层局部组管柱。
方程(10)筛选出前Ngk个的设计结果,即上一层设计问题中设计参数的可选择项。将上述过程一直细分下去,直至最后一层局部组管柱为局部管柱,此时优化设计问题为:
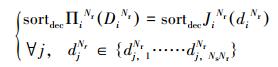
|
(11) |
式中:ΠiNr为最后一层局部管柱组的目标函数,对应局部管柱的目标函数(JiNr);DiNr为最后一层局部管柱组的设计参数,对应局部管柱的设计参数(diNr)。
设计问题(11)与(6)相同,只是sortdec相对于max而言要保留前几项最优解,因此设计问题(11)可直接求解。将设计问题(11)的设计结果代入上一层设计问题中,则上一层设计问题可求解。上述过程一直追溯到最高一层的设计问题,即问题(8),至此则得到整体管柱的设计结果。
通过估算,新设计方法的计算量约为NsNg·NL(Ns < Nc,Ng≈logNrNL),其数值一般远小于直接法的计算量NcNL·NL,因此保证了计算的高效性。同时,该方法考虑了尽可能多的设计情形,避免设计结果陷入局部最优。
3 上部常规井段的优化设计方法对于上部常规段管柱,为了充分考虑不同工况下的各种约束条件,采用井眼延伸极限作为目标函数进行优化设计。
3.1 延伸极限的近似求解由井眼延伸极限预测模型[16]可以知道,约束条件包括地面大钩载荷小于钻机额定提拉力、大钩载荷大于0、地面扭矩小于钻机额定扭矩以及管柱等效应力小于屈服强度等,相关的约束条件可以统一记为:
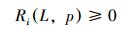
|
(12) |
式中:Ri为第i个约束条件。
第i个约束条件对应的延伸极限Llim, i在约束条件方程等于0时取得,即满足如下方程:
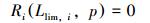
|
(13) |
给定某一参考井深L0,将L=L0+ΔL代入方程(13),对ΔL进行泰勒展开保留前二阶项,并进行简化处理,得到延伸极限的近似计算公式:
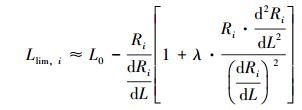
|
(14) |
式中:Llim, i为为第i个约束条件对应的近似延伸极限,m;λ为人为引入的无因次参数。
最终的延伸极限为各个约束条件对应结果的最小值,即:
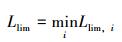
|
(15) |
关于管柱优化设计问题,可将整体管柱设计参数D看作一系列局部管柱设计参数的组合,即:
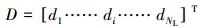
|
(16) |
为了简化计算,将整体优化设计问题转换为从最后一段局部管柱到第一段局部管柱的局部最优设计问题。其中第i个局部管柱设计问题为:
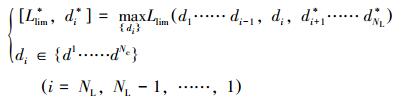
|
(17) |
式中:di*表示第i个局部管柱的最优设计参数。
上述过程重复多次执行,且在每一次循环过程中参考井深L0不断更新,直至两次设计结果偏差小于允许值为止。
4 计算结果与讨论 4.1 钻柱优化设计分析以一口大位移水平井为例进行设计分析,其中造斜点深度为1 000 m,造斜段曲率半径为300 m,水平段稳斜角为90°,井眼内径为215.9 mm。钻进过程中钻柱与井壁摩擦因数为0.25,钻头钻压为50 kN。以井深4 871 m为目标进行管柱优化设计,此时水平段设计长度为3 400 m。设计问题中采用多种类型的管柱。
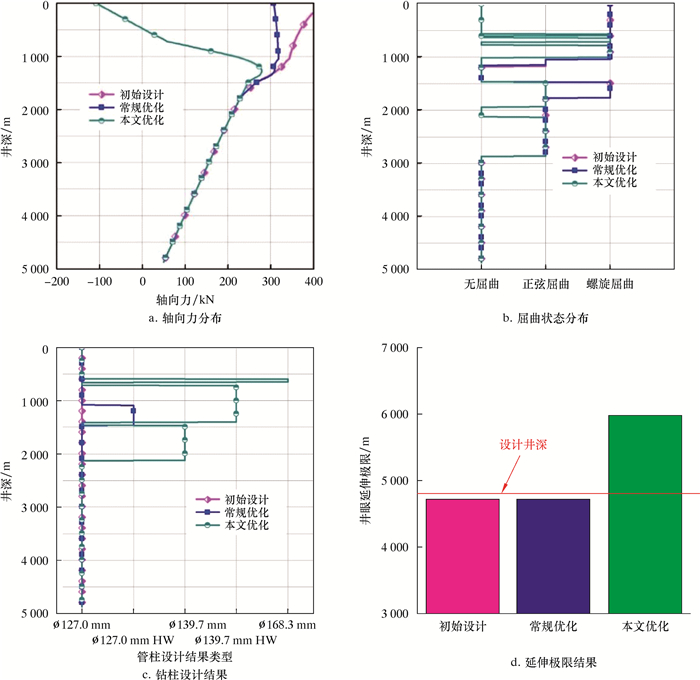
不同设计方法下的钻柱优化设计结果如图 3所示。初始设计全部采用ø127.0 mm钻杆,常规优化是指在垂直段下部采用ø127.0 mm加重钻杆。由图 3可见,采用加重钻杆后屈曲状态没有得到改善,垂直段和水平段上管柱屈曲问题突出(见图 3b),达到设计井深时地面大钩处轴向力为压力(见图 3a),代表无法安全钻达设计井深。初始设计和常规优化下的井眼延伸极限小于设计值(见图 3d),因此常规方法无法满足设计要求。
|
| 图 3 不同设计方法下的钻柱优化设计结果 Fig.3 Optimal design results of drill string under different design methods |
采用本文模型进行优化设计,在垂直段底部采用ø168.3 mm钻杆和ø127.0 mm加重钻杆,水平开始段采用ø127.0 mm钻杆(见图 3c)。替换后的管柱具有更高的屈曲临界载荷,因此在垂直段和水平段上管柱屈曲问题得到有效抑制(见图 3b),地面处管柱轴向力由压力转换为拉力(见图 3a),井眼延伸极限大幅度提高(见图 3d),达到了设计井深要求。
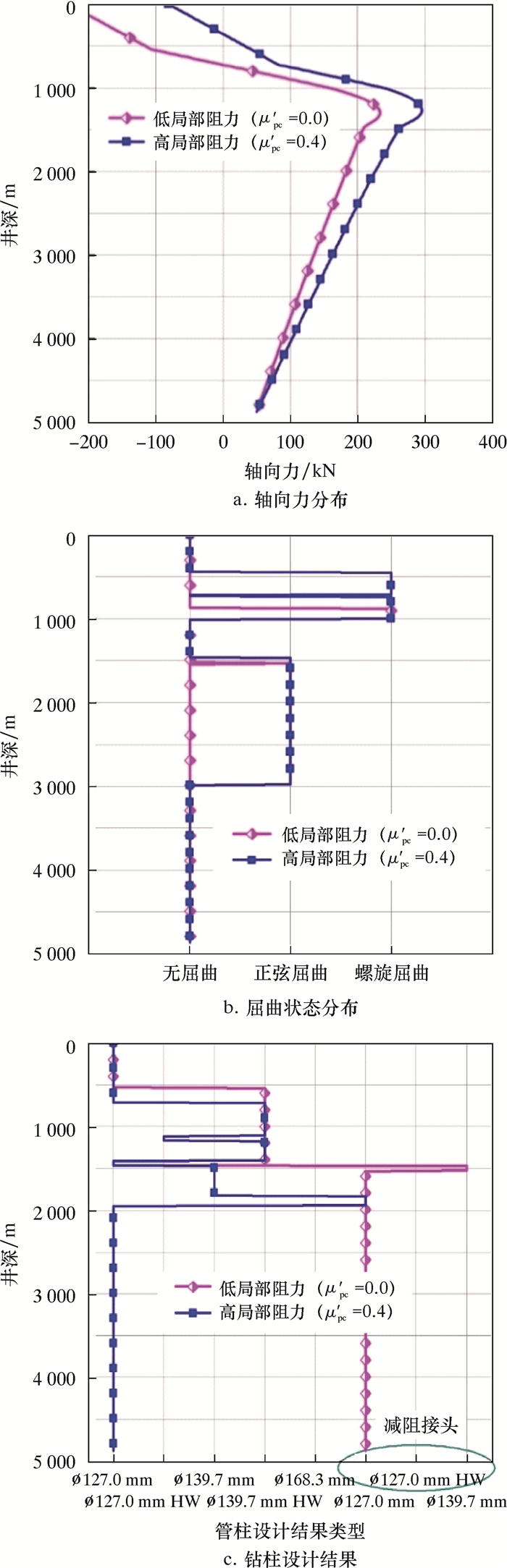
在裸眼段钻进过程中,井眼不规则性、岩屑床等因素会导致管柱接头产生附加局部机械阻力。文献[14]提出利用局部阻力系数(μpc)来描述井眼状况,该系数与局部机械阻力成正比。图 4给出了不同局部阻力系数下的优化设计结果。由图 4可知,对于套管段或者局部阻力系数小的裸眼段,建议安装减阻接头(见图 4c)。减阻接头既可以降低摩阻,提高屈曲临界载荷,又不会产生较大的局部阻力,从而可以抑制水平段上管柱屈曲问题(见图 4b),提高轴向力传递效率。对于局部阻力系数大的裸眼段,不建议采用减阻接头(见图 4c)。这是因为局部阻力的累计效应大于减阻接头的减阻效应。采用接头尺寸较小的常规钻杆可避免产生较大的局部机械阻力。因此,当井眼状况良好时,建议采用减阻接头;当井眼状况较差时,不建议采用减阻接头。即使通过管柱优化设计,井眼状况良好时地面大钩提拉载荷仍然高于井眼状况较差下的数值(见图 4a),井眼延伸极限也具有相同的规律。因此,为了提高井眼延伸极限,需要从提高井眼清洁程度和优化管柱组合两方面同时采取措施。
|
| 图 4 裸眼段上钻柱优化设计结果 Fig.4 Optimal design results of the drill string in the open hole section |
4.2 套管优化设计分析
假定在井深3 500~4 500 m时存在扩径问题,井眼内径为225.9 mm。套管优化设计中有3种壁厚的ø177.8 mm套管,分别为9.19、11.51和13.72 mm;采用两种类型扶正器:①弹簧扶正器,外径为216.8 mm,摩阻系数0.25;②刚性减阻扶正器,外径为165.9 mm,略小于井眼内径,摩阻系数为0.125。
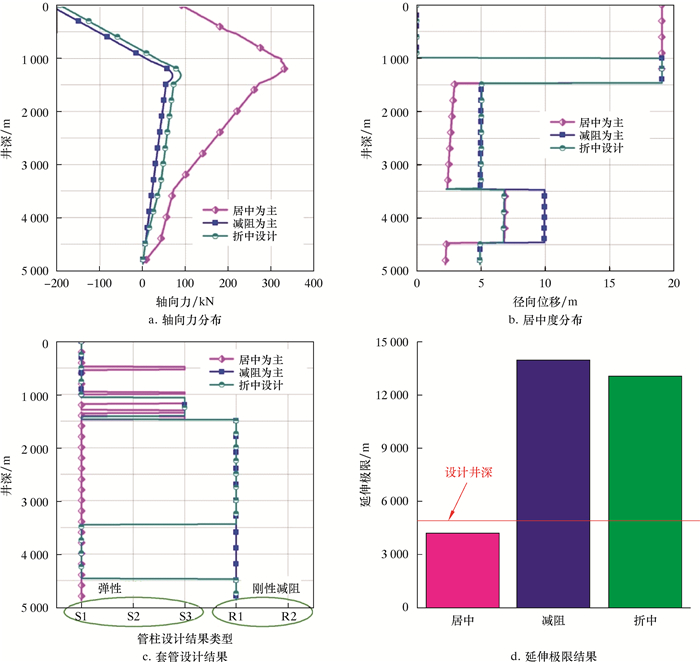
图 5为漂浮下套管作业工况下采取不同权重系数的设计结果。根据权重相对大小,分成3种方案:套管居中为主、降阻为主和折中方案。
|
| 图 5 不同优化设计方法下的套管优化设计结果 Fig.5 Optimal design results of casing under different optimization design methods |
当采取以套管居中为主方案时,水平段套管上全采用尺寸偏大的弹簧扶正器(见图 5c)。但是,弹簧扶正器的局部阻力高于刚性减阻扶正器,水平段上的摩阻较高,导致地面大钩提拉载荷为压力,套管下入极限小于设计井深(见图 5d)。当采用以降低摩阻为主方案时,水平段套管上全采用摩阻系数偏小的刚性减阻扶正器(见图 5c)。相对于以套管居中为主的设计结果,套管上的整体摩阻大幅度降低,套管下入到设计井深更容易(见图 5a)。但是,此时水平段上套管居中程度最差,尤其是井眼扩大段,将导致固井质量较差(见图 5b)。
当采用折中方案时,水平段上非井眼扩大段采用刚性减阻扶正器以降低摩阻,在井眼扩大段采用弹簧扶正器以提高居中度(见图 5c),保证了地面大钩载荷为拉力。因此,折中方案使得套管可下入到设计深度,且保证了较好的套管居中度。因此,相对于前面两个方案而言,折中方案的设计效果更优。
5 结论(1) 常规设计方法难以有效解决高难度大位移井中管柱设计时存在的问题,提出的管柱分段优化设计方法综合考虑了不同作业工况下各种约束因素的影响,可有效解决高难度大位移井管柱和接头优化设计问题。
(2) 大位移井钻柱的优化设计结果与井眼状况密切相关,对于套管段或者井眼状况良好的裸眼段,可安装减阻接头来降低摩阻;对于井眼状况较差的裸眼段,可采用小尺寸接头钻柱且不安装减阻接头来降低局部机械阻力。
(3) 大位移井套管优化设计需要同时兼顾套管居中和减阻等目标,同时采用弹簧扶正器和刚性减阻扶正器并进行位置合理优化,其设计结果要优于仅考虑套管居中或下入减阻的结果。
| [1] |
高德利, 黄文君, 李鑫. 大位移井钻井延伸极限研究与工程设计方法[J]. 石油钻探技术, 2019, 47(3): 1-8. GAO D L, HUANG W J, LI X. Research on extension limits and engineering design methods for extended reach drilling[J]. Petroleum Drilling Techniques, 2019, 47(3): 1-8. |
| [2] |
GAO D L, TAN C J, TANG H X. Limit analysis of extended reach drilling in South China Sea[J]. Petroleum Science, 2009, 6(2): 166-171. |
| [3] |
BLIKRA H, DREVDAL K E, AARRESTAD T V. Extended reach, horizontal and complex design wells: challenges, achievements and cost-benefits[R]. SPE 28005, 1994.
|
| [4] |
SONOWAL K, BENNETZEN B, WONG K M, et al. How continuous improvement lead to the longest horizontal well in the world[R]. SPE 119506, 2009.
|
| [5] |
闫铁, 张凤民, 刘维凯, 等. 大位移井钻井极限延伸能力的研究[J]. 钻采工艺, 2010, 33(1): 4-7. YAN T, ZHANG F M, LIU W K, et al. Mechanical analysis on the limit extended capacity for an extended reach well[J]. Drilling & Procuction Technology, 2010, 33(1): 4-7. |
| [6] |
相玉辉, 屈展, 陈军斌, 等. 大位移井钻井工程优化设计与应用[J]. 石油机械, 2006, 34(10): 60-61, 64. XIANG Y H, QU Z, CHEN J B, et al. Optimization design and application of drilling engineering for extended-reach well[J]. China Petroleum Machinery, 2006, 34(10): 60-61, 64. |
| [7] |
胡贵, 李令东, 刘新云, 等. 扎哈泉致密油水平井钻井技术对策[J]. 石油机械, 2016, 44(2): 23-28. HU G, LI L D, LIU X Y, et al. Horizontal well drilling technique for Zahaquan tight oil[J]. China Petroleum Machinery, 2016, 44(2): 23-28. |
| [8] |
钻井手册(甲方)编写组. 钻井手册(甲方)[M]. 北京: 石油工业出版社, 1990. Drilling Manual (Party A) Writing Group. Drilling manual (Party A)[M]. Beijing: Petroleum Industry Press, 1990. |
| [9] |
彭高华, 赵洪激. 水平井钻柱设计[J]. 石油机械, 1991, 19(12): 1-6, 43. PENG G H, ZHAO H J. Drillstem design for horizontal holes[J]. China Petroleum Machinery, 1991, 19(12): 1-6, 43. |
| [10] |
夏忠跃, 陈建兵, 徐荣强, 等. 大位移井钻柱优化设计方法及应用[J]. 石油钻采工艺, 2008, 30(6): 37-41. XIA Z Y, CHEN J B, XU R Q, et al. Optimization design methods of drilling strings in extended reach wells[J]. Oil Drilling & Production Technology, 2008, 30(6): 37-41. |
| [11] |
韩志勇. 水平井钻柱的优化设计问题[J]. 石油大学学报(自然科学版), 1997, 21(5): 24-26. HAN Z Y. Optimum design of drillstring in horizontal drilling[J]. Journal of the University of Petroleum(Natural Science Edition), China, 1997, 21(5): 24-26. |
| [12] |
李乾, 纪国栋, 张辉, 等. 滑动钻进中顶驱扭摆减阻控制技术研究[J]. 石油机械, 2018, 46(5): 1-6. LI Q, JI G D, ZHANG H, et al. Drag reduction control for torsion and oscillation in top drive system slide drilling[J]. China Petroleum Machinery, 2018, 46(5): 1-6. |
| [13] |
石油钻井工程专业标准化委员会.套管扶正器安装间距计算方法: SY/T 5334-1996[S].北京: 石油工业出版社, 1996. Oil Drilling Engineering Professional Standardization Committee. Calculation method of casing centralizer mounting distance: SY/T 5334-1996[S]. Beijing: Petroleum Industry Press, 1996. |
| [14] |
步玉环, 张大千, 郭权庆. 大位移井顶替效率最优的套管居中度设计方法[J]. 中国石油大学学报(自然科学版), 2015, 39(2): 53-57. BU Y H, ZHANG D Q, GUO Q Q. A method for casing-centralizing design in extended-reach wells with optimized cement displacement efficiency[J]. Journal of the University of Petroleum(Natural Science Edition), 2015, 39(2): 53-57. |
| [15] |
黄文君.旋转钻井机械延伸极限研究[D].北京: 中国石油大学(北京), 2016. HUANG W J. Research on mechanical extending limits in rotary drilling[D]. Beijing: China University of Petroleum(Beijing), 2016. |
| [16] |
HUANG W J, GAO D L, LIU Y H. Mechanical model and optimal design method of tubular strings with connectors constrained in extended-reach and horizontal wells[J]. Journal of Petroleum Science & Engineering, 2018, 166: 948-961. |



