0 引言
近年来,PDC钻头的结构和类型都发生了巨大变化,因此有必要对PDC钻头的布齿方法进行进一步研究,以提高布齿设计的效率[1-2]。应用计算机软件进行破岩仿真可以有效预测PDC钻头的破岩效率,判断布齿结构的合理性。
PDC钻头的切削结构是影响钻头破岩效果的重要因素之一,合理的布齿设计可以提高钻头的机械钻速,降低破岩能耗以及减少切削齿的磨损等,相关学者对此进行了大量的理论与试验研究[3-4]。目前PDC钻头的布齿设计一般遵循等切削量、等功率和等磨损3个原则[5]。但PDC钻头的破岩过程是一个复杂的过程,其破岩效率除了与本身的设计参数有关之外,往往还需要考虑到相互作用的岩石性质、钻头的振动和井下钻具等因素的影响。因此,在遵循一定设计原则的基础上,还需要进一步的试验或仿真,从而实现对布齿参数的优化调整。随着仿真技术的成熟与进步,计算机仿真逐渐成为研究PDC钻头工作效率的最佳选择[6]。
常规布齿设计通常采用三维CAD软件人工建立钻头的布齿结构模型。在建模过程中,由于切削齿数量多,涉及参数量大,所以工作效率较低且易产生人为的设计失误。
针对上述问题,本文介绍了一种既可高效进行PDC钻头的参数化布齿,又能快速建立破岩仿真模型并进行破岩性能分析的方法。采用该方法可以大幅度提高布齿设计和破岩分析的效率,缩短PDC钻头的研发时间。
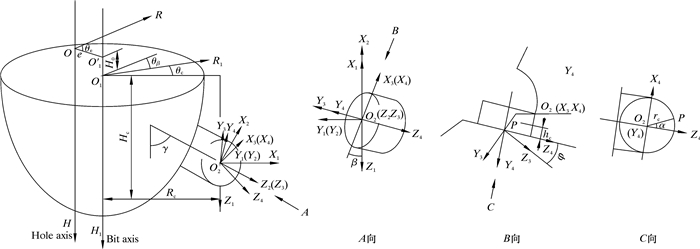
1 PDC切削齿几何参数PDC切削齿的空间位置由其在钻头上的3个空间位置参数和3个空间方向参数[7]决定。如图 1所示,空间位置参数包括:切削齿定位点到钻头轴线上的距离Rc,定位参考点到高度方向基准面之间的距离Hc,定位参考点在钻头圆周方向上的位置角θc。其中Rc和Hc取决于钻头冠部形状和径向布置,θc取决于切削齿的周向布置空间。方向参数包括:前倾角φ(切削齿工作面与钻头半径平面的夹角),侧向角β(切削齿工作平面与过切削齿中心点和钻头中心线的平面之间的夹角),法向角γ(切削齿轴线与钻头轴线的夹角)。
|
| 图 1 PDC钻头的基本几何参数 Fig.1 Basic geometric parameters of PDC bits |
2 实现方法
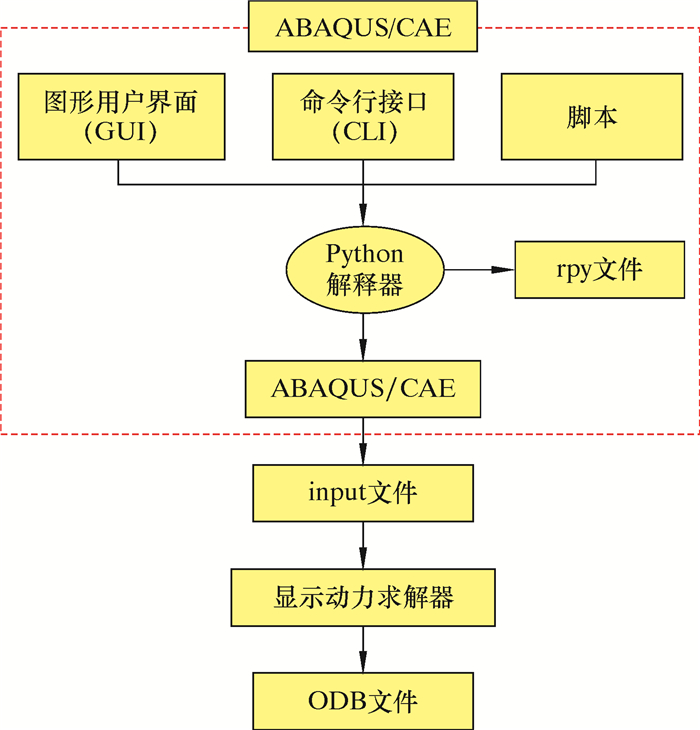
ABAQUS作为国际上公认的大型非线性有限元分析软件,被广泛应用于机械制造、岩土工程和汽车交通等广大领域[8]。为了满足不同用户的特定功能,ABAQUS软件提供了基于Python语言的脚本接口,方便用户开发前后处理工具、参数化建模和数据处理等工作。如图 2所示,ABAQUS脚本接口可以通过图形用户界面(GUI)、主窗口下部命令交互界面(CLI)和执行脚本(script)3种方式与ABAQUS/CAE内核程序交互。
|
| 图 2 命令脚本与ABAQUS/CAE的通信关系 Fig.2 Command script and ABAQUS/CAE communication relationship |
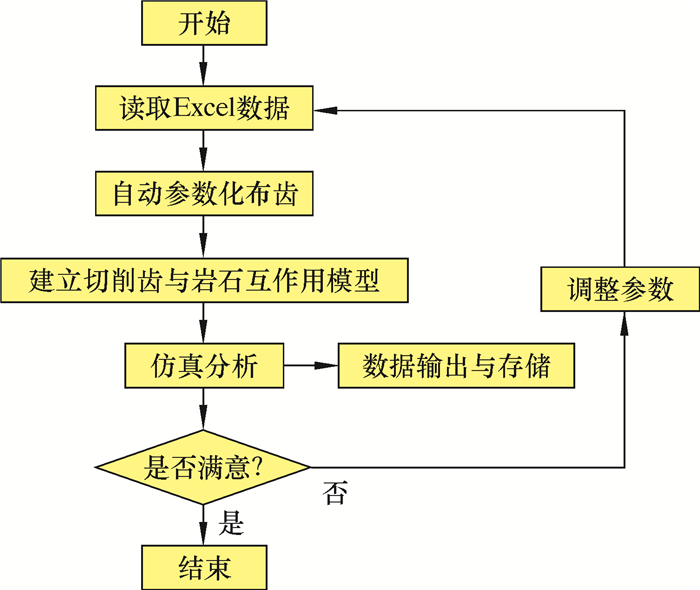
本文采用在ABAQUS软件内运行脚本实现Python语言对ABAQUS内核程序的控制,图 3为参数化布齿与破岩仿真方法流程图。其中,Python脚本可以实现PDC切削齿的参数化布齿、PDC切削齿与岩石的破岩仿真模型的快速建立、仿真结果的输出与保存,从而节省了大量的人工操作时间。
|
| 图 3 参数化布齿设计与破岩仿真流程图 Fig.3 Flow chart of parameterized cutter layout design and rock breaking simulation |
2.1 PDC钻头的参数化布齿 2.1.1 PDC切削齿几何参数的自动读取
Xlrd是Python语言中读取Excel的扩展工具,可以实现用户指定单元格的读取,在ABAQUS中使用时需要用户添加相关的工具包。PDC切削齿几何参数读取的实现代码如下:
import xlrd
workbook=xlrd.open_workbook(filename=r'C:\ \Users\ \lenovo\ \Desktop\ \data.xlsx')
Data_sheet = workbook.sheets()[0]
nrows =Data_sheet.nrows
for i in range(1, nrows):
B_rows = Data_sheet.row_values(i)[1]
…
2.1.2 PDC切削齿在ABAQUS中的定位方法定位参考点的位置坐标确定了切削齿在钻头中的位置, 而定位参考点与前中心点或后中心点的连线则完全将切削齿固定在钻头上。因此,根据定位参考点和前后中心点的值即可确定切削齿的基本几何参数。
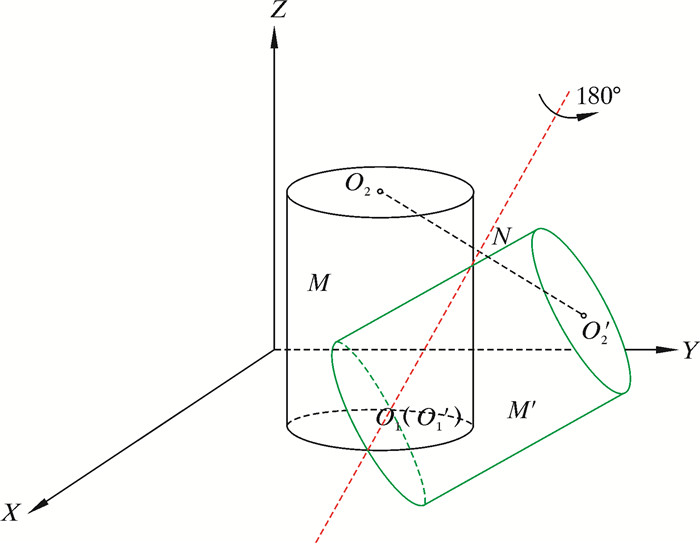
如图 4所示,首先确定前中心点O1柱坐标(R1、θ1、H1)和直角坐标(R1cosθ1,R1sinθ1,H1),以切削齿半径为半径画圆并沿Z轴拉伸h(齿厚),形成切削齿M,后中心点O2坐标即为(R1cosθ1,R1sinθ1,H1+h)。以前中心点O1为定位参考点,切削齿M经过旋转法向角、旋转前倾角和旋转侧转角后,记作切削齿M′。前中心点O′1坐标与O1相同,后中心点O′2的坐标可由式(1)~式(3)求出[9]。确定O1、O2和O′2坐标后,绘制过O1N的轴线,使切削齿M绕轴线旋转180°,得到切削齿M′。
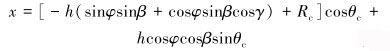
|
(1) |
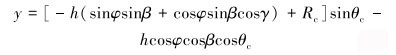
|
(2) |
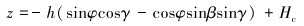
|
(3) |
|
| 图 4 PDC切削齿定位方法 Fig.4 PDC cutter placement method |
式中:Rc、θc、Hc分别为后中心点O2在切削齿柱坐标下的3个坐标值。
综上所述,在ABAQUS中计算得到过O1、N两点轴线的坐标,使PDC切削齿绕该轴旋转180°,即可得到该切削齿的空间位置。具体脚本实现代码如下:
#创建PDC切削齿
…
for i in range(1, nrows):
s.CircleByCenterPerimeter(center=(0.0, 0.0), point1=(E_rows, 0.0))
p = mdb.models['Model-1'].Part(name='chi'+str(i), dimensionality=THREE_D, type=DEFORMABLE_BODY)
…
#PDC切削齿定位
…
a1 = mdb.models['Model-1'].rootAssembly
a1.rotate(instanceList=('chi'+str(i), ), axisPoint=(x1, y1, z1), axisDirection=((x2-x1)/2, (y2-y1+h)/2, (z2-z1)/2), angle=180.0)
…
2.2 PDC切削齿与岩石的破岩仿真模型 2.2.1 建模说明(1) 条件假设。考虑到PDC切削齿的强度远大于岩石,因此将切削齿视为刚体,以加快破岩仿真速度。
(2) 材料定义。岩石破坏准则选用线性Drucker-Prager模型。其考虑了围压对屈服特性的影响,也可以反映岩石剪切时的膨胀性质,可以准确地模拟岩石性质[10]。
(3) 网格划分。PDC牙齿和岩石均采用六面体结构网格划分方法,单元类型采用六面体缩减积分(C3D8R),并且只对与切削齿相互作用的区域进行网格细分处理,从而可减少单元数量,缩短仿真时间。
(4) 接触定义。接触类型选择面-面接触方式,用该方式模拟PDC切削齿与岩石的接触破碎过程,以满足岩石单元删除过程中切削齿与岩石连续接触的条件。
(5) 边界条件。岩石底端进行全固定约束,岩石周围施加压力以模拟真实井底环境。施加角速度实现布齿模型的旋转,施加钻压实现布齿模型的钻进。
2.2.2 建立破岩仿真模型的代码实现方法使用Python语言编写脚本代码,可以快速完成PDC切削齿与岩石互作用模型的前处理定义,包括实现自动网格划分、材料定义、接触设置及边界条件定义等功能。部分脚本代码如下:
#材料定义
…
mdb.models['Model-1'].Material(name='rock')
mdb.models['Model1'].materials['rock'].Density(table=((p1, ), ))
mdb.models['Model-1'].materials['rock'].Elastic(table=p2)
…
#网格划分
…
for i in range(1, nrows):
p.seedPart(size=1.0, deviationFactor=0.1, minSizeFact-or=0.1)
p = mdb.models['Model-1'].parts['chi'+str(i)]
p.generateMesh()
…
#接触设置
mdb.models['Model-1'].SurfaceToSurfaceContactExp-(name ='Int-'+str(i), ……)
…
#载荷定义
…
mdb.models['Model-1'].ConcentratedForce(name='Load-1', createStepName='Step-1', region=region, cf2=20000.0, distributionType=UNIFORM, field='', localCsys=None)
…
2.3 仿真结果输出与保存仿真数据的输出与储存功能可以方便用户对仿真数据的处理分析。ABAQUS后处理中的历史变量记录着仿真过程中各数据与时间的变化关系,通过历史变量输出可以得到变量随时间的变化曲线。以切削力为例,通过以下脚本代码可以实现历史变量中PDC切削齿切削力的输出,并且将其储存到Excel:
#切削力输出
…
xy1=xyPlot.XYDataFromHistory(odb=odb, outputVariableName='Reaction force: RF2 PI: rootAssembly Node 1 in NSET SET-3', steps=('Step-1', ), )
…
#切削力储存
abq_ExcelUtilities.excelUtilities.XYtoExcel(xyDataNames='_temp_2', trueName='From Current XY Plot')
3 实例应用 3.1 参数优化布齿创建名为data.xlsx的Excel表格,将优化的PDC钻头布齿数据以一定的规则导入,表 1所示为本次示例所用PDC钻头的布齿数据。优化的目标是使PDC钻头侧向力最小,优化参数包括前倾角、侧转角和刀翼螺旋角等。使用PDC钻头与岩石互作用专用软件可以计算出PDC钻头的侧向力[11]。
| 齿编号 | 半径/mm | 齿厚/mm | Rc/mm | θc/(°) | Hc/mm | γ/(°) | φ/(°) | β/(°) |
| 1 | 9.525 | 8 | 10.00 | -2.50 | 125.49 | -14.25 | 20 | 15 |
| 2 | 9.525 | 8 | 21.00 | 174.75 | 128.25 | -14.25 | 20 | 15 |
| 3 | 9.525 | 8 | 32.00 | -8.00 | 131.16 | -16.80 | 20 | 15 |
| … | … | … | … | … | … | … | … | … |
| 28 | 9.525 | 8 | 100.49 | 154.88 | 71.97 | 70.07 | 20 | 15 |
| 29 | 9.525 | 8 | 101.76 | 214.56 | 68.14 | 70.48 | 20 | 15 |
在ABAQUS软件中运行Python语言脚本,读取data.xlsx文件中的布齿数据,即可快速形成三维PDC切削齿模型,如图 5所示。对比图 6所示在Creo软件中使用常规建模方法建立的PDC钻头模型,两者布齿相同,PDC切削齿的前后中心点坐标一致,这充分证明了该布齿方法的正确性。

|
| 图 5 ABAQUS软件中PDC钻头布齿结构 Fig.5 PDC cutter layout in ABAQUS |

|
| 图 6 Creo软件中PDC钻头布齿结构 Fig.6 PDC cutter layout in Creo |
3.2 破岩仿真模型建立
建立岩石模型,并绘制过各切削齿前中心点的样条曲线,通过旋转切削形成初始井底。使用Python语言脚本即可快速完成材料定义、网格划分、速度与载荷定义等,建立破岩仿真模型。施加20 kN的集中力模拟钻压以实现钻头钻进,定义轴向速度6.28 rad/s实现钻头旋转。岩石和切削齿材料参数如表 2所示。最终的网格划分模型如图 7所示。
| 部件名称 | 密度/(kg·m-3) | 弹性模量/GPa | 泊松比 | 内摩擦角/(°) | 剪胀角/(°) |
| 灰岩 | 2 310 | 40 | 0.25 | 44 | 10 |
| 切削齿 | 7 850 | 210 | 0.30 |

|
| 图 7 切削齿与岩石的网格划分模型 Fig.7 Cutter and rock grid division model |
3.3 仿真结果
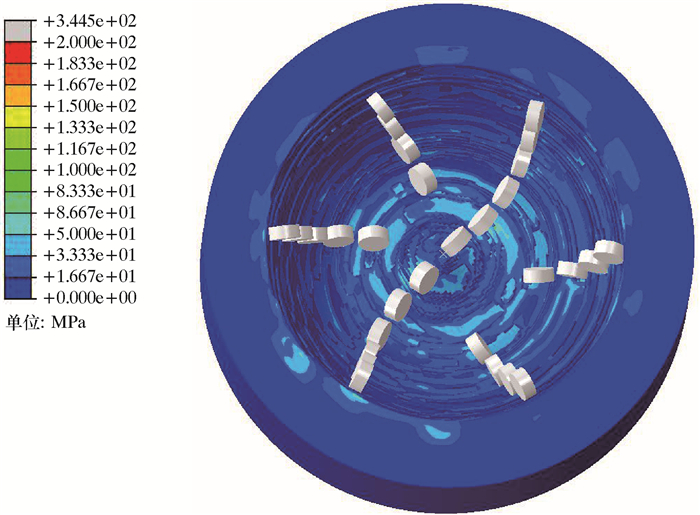
图 8为破岩过程中齿坑及应力分布图。根据齿坑形状可以观察到该布齿模型可以较好地覆盖井底,同时也可以得知井底的应力分布情况。
|
| 图 8 齿坑及应力分布 Fig.8 Cutter pit and stress distribution |
3.3.1 扭矩分析
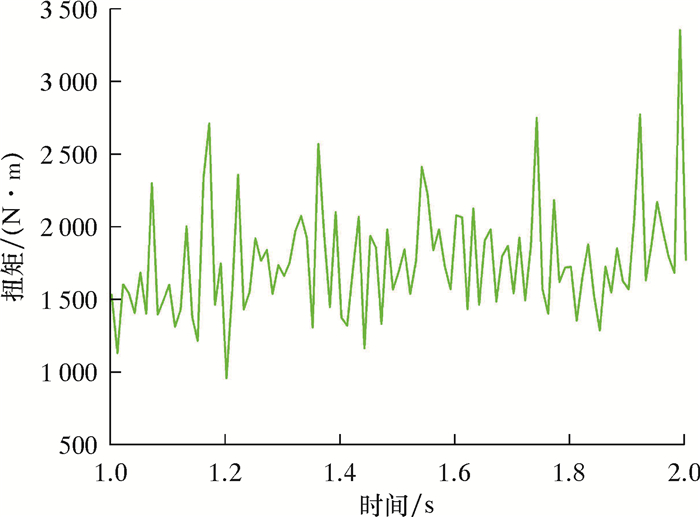
通过历程输出可以输出整个布齿模型和各切削齿的受力情况。图 9为整个布齿结构的扭矩输出。由图 9可知,扭矩在一定的数值范围内“阶跃”波动。在钻头破岩过程中,PDC切削齿对岩石单元产生挤压,切削力迅速增大,扭矩也随着增大。当岩石应力达到屈服极限时岩石单元破碎,此时切削力会产生瞬时的大幅度下降现象,而后切削齿在接触下一岩石单元时切削力会再次增大。因此,布齿模型与各切削力的受力特点皆具有明显的“阶跃”波动特征。
|
| 图 9 扭矩与时间关系曲线 Fig.9 Torque-time curve |
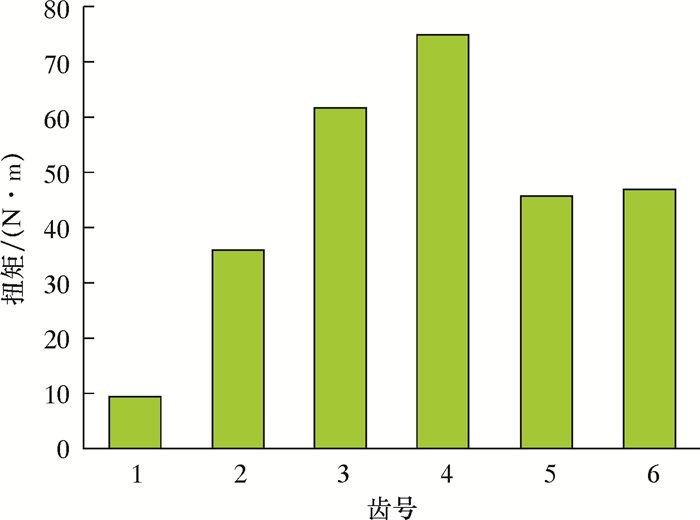
图 10为1号齿所在刀翼各切削齿的扭矩关系。由图 10可知,沿钻头包络线向两侧方向切削齿扭矩逐渐减小,4号齿扭矩最大,1号齿扭矩最小。仿真结果与彭亚洲[12]得出的试验结果很接近,这充分证明了仿真模型的正确性。
|
| 图 10 各切削齿扭矩关系 Fig.10 Correlation of torques of each cutter |
3.3.2 切削力分析
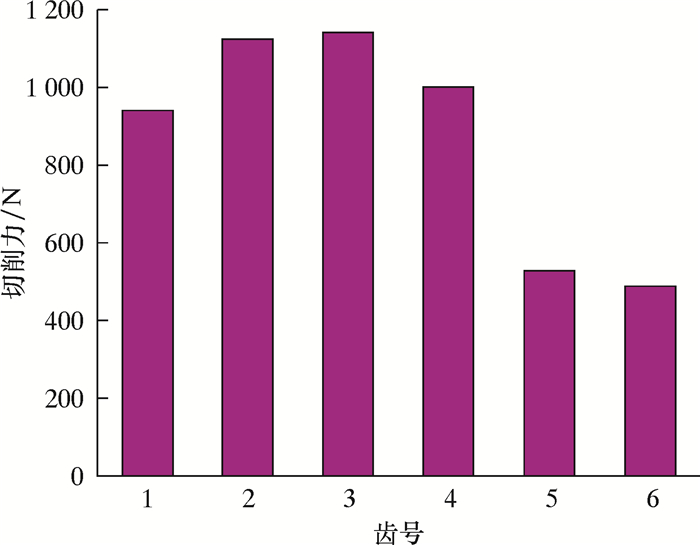
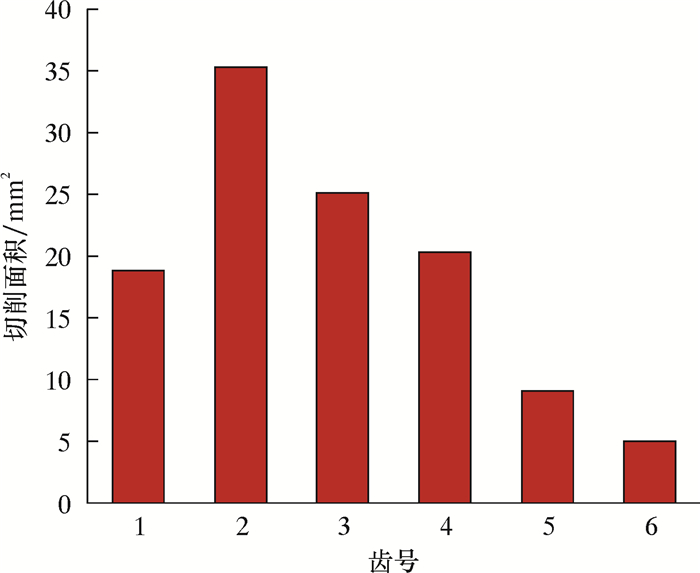
切削齿的切削力不仅受到切削速度的影响[13],也与切削面积有一定的关系。各切削齿切削力关系和切削面积关系分别如图 11和图 12所示。由图 11和图 12可知,刀翼上位于钻头底部的1~4号切削齿在破岩过程中切削面积较大,而钻头侧翼的5、6号切削齿切削面积较小,这使得钻头底部切削齿的切削力远大于侧翼切削齿的切削力。
|
| 图 11 各切削齿切削力关系 Fig.11 Correlation of cutting forces of each cutter |
|
| 图 12 各切削齿切削面积关系 Fig.12 Correlation of cutting areas of each cutter |
4 结论
(1) 提出了用Python和ABAQUS软件进行参数化布齿设计与破岩仿真的方法,采用该方法可实现PDC钻头的参数化布齿设计、破岩仿真模型的快速建立和仿真数据的输出与存储。
(2) 通过与常规建模方法建立的布齿模型进行对比分析,证明了使用该方法建立布齿模型的正确性。
(3) 对仿真结果中的扭矩进行了分析,并与前人试验结果进行对比,证明了仿真模型的正确性;通过分析各切削齿切削力和切削面积之间的关系,得出切削力受切削面积影响较大,钻头底部切削齿切削力远大于钻头侧翼的结论。
(4) 该方法可以节省大量的人工操作时间,为提高PDC钻头的布齿设计效率,缩短PDC钻头的设计研发时间提供了一种有效途径。
| [1] |
潘军, 王敏生, 光新军. PDC钻头新进展及发展思考[J]. 石油机械, 2016, 44(11): 5-13. PAN J, WANG M S, GUANG X J. New progress and future development of PDC bit[J]. China Petroleum Machinery, 2016, 44(11): 5-13. |
| [2] |
思娜, 王敏生, 李婧, 等. PDC钻头新技术及发展趋势分析[J]. 石油矿场机械, 2018, 47(2): 1-7. SI N, WANG M S, LI J, et al. Abroad PDC bit technology's research trends and development thinking[J]. Oil Field Equipment, 2018, 47(2): 1-7. |
| [3] |
杨迎新, 刘芸芸, 黄奎林. PDC钻头布齿设计中的三维齿间距计算方法[J]. 钻采工艺, 2016, 39(3): 15-18. YANG Y X, LIU Y Y, HUANG K L. Three-dimensional cutters spacing calculation method in cutters layout of PDC bit[J]. Drilling & Production Technology, 2016, 39(3): 15-18. |
| [4] |
况雨春, 王元吉, 冯明, 等. PDC钻头布齿参数的逆向设计与优化[J]. 工程设计学报, 2017, 24(5): 545-554. KUANG Y C, WANG Y J, FENG M, et al. Reverse design and optimization of PDC bit cutter parameters[J]. Chinese Journal of Engineering Design, 2017, 24(5): 545-554. |
| [5] |
牛世伟, 杨迎新, 牛永超. PDC钻头布齿计算方法的研究现状及发展[J]. 石油机械, 2015, 43(9): 6-9. NIU S W, YANG Y X, NIU Y C. Research status and development of calculation method for PDC bit tooth arrangement[J]. China Petroleum Machinery, 2015, 43(9): 6-9. |
| [6] |
张强, 李丁, 景文清, 等. PDC钻头单齿"攻击性"布齿研究及有限元分析[J]. 石油机械, 2014, 42(10): 5-8. ZHANG Q, LI D, JING W Q, et al. Research and finite element analysis on "aggressive"single-cutter placement of PDC drill bit[J]. China Petroleum Machinery, 2014, 42(10): 5-8. |
| [7] |
石志明, 杨迎新. 基于PRO/E的PDC钻头三维参数化布齿设计[J]. 河南石油, 2006, 20(3): 50-52. SHI Z M, YANG Y X. Three-dimensional parametric tooth design of PDC bit based on PRO/E[J]. Henan Petroleum, 2006, 20(3): 50-52. |
| [8] |
谢瑞敏, 王雪军. 基于Python的ABAQUS二次开发应用[J]. 中国水运(下半月), 2017, 17(10): 77-79. XIE R M, WANG X J. ABAQUS secondary development application based on Python[J]. China Water Transport, 2017, 17(10): 77-79. |
| [9] |
李树盛, 马德坤, 侯季康. PDC钻头几何学研究[J]. 西南石油学院学报, 1996, 18(2): 82-86. LI S S, MA D K, HOU J K. Study of PDC bit geometry[J]. Journal of Southwestern Petroleum Institute, 1996, 18(2): 82-86. |
| [10] |
袁小平, 刘红岩, 王志乔. 基于Drucker-Prager准则的岩石弹塑性损伤本构模型研究[J]. 岩土力学, 2012, 33(4): 1103-1108. YUAN X P, LIU H Y, WANG Z Q. Study of elastoplastic damage constitutive model of rocks based on Drucker-Prager criterion[J]. Rock and Soil Mechanics, 2012, 33(4): 1103-1108. |
| [11] |
WU A, HARELAND G, LEI L Y. Computer simulation and analysis of rock breaking process by rock bit cutters[C]//The 48th US Rock Mechanics/Geomechanics Symposium, Minneapolis, MN, USA, June 1-4, 2014.
|
| [12] |
彭亚洲. PDC全钻头破岩数值模拟方法研究[D].成都: 西南石油大学, 2015. PENG Y Z. Research on numerical simulation method on rock breaking of PDC bits[D]. Chengdu: Southwest Petroleum University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10615-1015599200.htm |
| [13] |
刘忠, 胡伟, 缪明才, 等. PDC钻头混合布齿切削试验装置[J]. 石油机械, 2019, 47(5): 44-49. LIU Z, HU W, MIAO M C, et al. Cutting test device for PDC bit with mixed cutter arrangement[J]. China Petroleum Machinery, 2019, 47(5): 44-49. |


