2. Drilling Technology Division, EXPEC Advanced Research Center
2. Drilling Technology Division, EXPEC Advanced Research Center
0 引言
随着大斜度井、水平井及水平分支井等复杂结构井的数量日益增多,如何解决定向段和水平段钻进过程中的托压问题已成为关注的焦点[1-4]。近年来,作为一种新兴的减阻工具,水力振荡器在各大油气田(川西、大庆、胜利、苏里格、涪陵及新疆等)进行了广泛的试验,尤其在沙特B区块,取得了较好的降摩减阻效果,提高了钻具的破岩效率,减少了卡钻事故的发生,为解决定向段和水平段钻进过程中的托压问题提供了可靠的技术支撑,已成为减阻技术的重要发展方向之一[5-9]。
目前,大多数学者均是基于验证水力振荡器是否具有降摩减阻、提高钻速等优点进行的研究,并未开展该工具在改变特定参数和参数间在某种最优配合条件下能否得以优化的研究[10],而这方面的研究是水力振荡器规模化应用的一个必经阶段。鉴于此,笔者基于ANSYS CFX对水力振荡器进行研究分析,仿真得到速度、压力、径向力和轴向力的分布云图;并且通过对该工具进行非定常分析(包括瞬态速度场、瞬态压力场、交界面速度、径向力及轴向力),得到上述参数和流量及时间的变化规律。所得结论可为提高水力振荡器优化设计与敏感性分析水平提供相应的理论支撑。
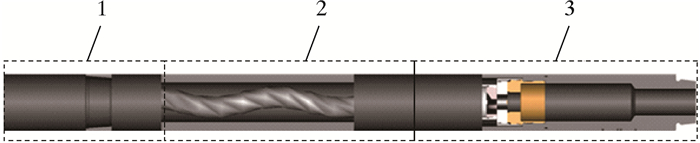
1 水力振荡器简介常用水力振荡器主要由3个部分构成:阀门部分、动力部分和配套部分(振荡/弹簧短节),其结构如图 1所示[1]。
|
| 1—振荡短节;2—动力部分;3—阀门和轴承部分。 图 1 水力振荡器结构示意图 Fig.1 Structural schematic of the hydraulic oscillator |
动力部分主要由单头螺杆马达组成,在转子的末端固定有一个动阀片,当钻井液流经液压马达时驱动马达转子转动,进而带动连接在其上的动阀片运动。由单头螺杆马达的运动特性可知,马达转子末端在平面上做往复运动,动阀片也将在平面上做往复运动。
连接在动力部分始端的是配套部分(振荡/弹簧短节),其主要功能部件为弹簧。弹簧上端与弹簧短节的壳体部分接触,下端与弹簧短节的活塞杆接触。连接在动力部分末端的是阀门系统,主要由耐磨片和定阀片构成,耐磨片固定在定阀片一端,与定阀片成为一体。装配时,定阀片有耐磨片的一端与固定在马达转子末端的动阀片紧密配合。
动力部分的螺杆马达在钻井液的推动下产生周期性转动,带动其上的动阀片产生周期性往复运动,使动阀片与阀门系统的定阀片位置相错或重合,造成上游压力周期性变化。当动阀片和定阀片处在最小重合位置时,阀门的过流面积最小,将产生最大压降。当两个阀片处在完全重合位置时,阀门的过流面积最大,将产生最小压降。过流面积的周期性变化将带来上游压力的周期性变化。
当动力部分带动阀门系统产生的周期性压力波动作用在弹簧短节中的弹簧上时,短节中的活塞杆便会产生周期性的轴向往复运动,进而带动连接在水力振荡器下端的其他钻井工具在轴向上产生往复运动。由于水力振荡器靠近钻头,故往复运动将静摩擦转换为动摩擦,周期性地产生向下的推动力,从而克服BHA的部分摩阻。
2 三维建模及网格划分采用SolidWorks三维建模软件,建立水力振荡器各部分结构三维模型,从左到右依次为进口段、静止域及旋转域。
利用ICEM-CFD对整个计算域进行网格离散,将水力振荡器划分为旋转域、静止域和进口段,分别进行网格划分,通过冻结转子法建立交界面以连通所有计算域,并进行模拟计算。其中,静止域与进口段采用六面体结构化网格划分,并进行局部加密以提高计算精度。对于结构较为复杂的旋转域,采用适应性更强的四面体非结构体网格进行离散,并对边壁区域进行局部加密,以捕捉更为细微的流动特征。采用非结构化网格的旋转域,绝大多数网格质量均在0.1以上,而采用六面体结构化网格的静止域和进口域,网格质量均在0.65以上,故网格质量满足数值计算的要求。
3 水力振荡器性能分析 3.1 定常分析 3.1.1 定常计算设置水力振荡器转速150 r/min,流量7或10 L/s,工具外径95.2或120.6 mm,适用井眼直径120.6或165.1 mm,螺杆右端压力10 MPa;钻井液密度1.2 g/cm3,塑性黏度12 Pa·s。
采用ANSYS CFX 14.5对该工具进行数值模拟,湍流模型选用RNG k-ε模型,壁面方程采用Scalable壁面函数。求解格式选用高精度求解模式,时间尺度选用自动时间尺度,收敛精度设置为10-5。进口边界条件采用压力边界条件,参考压力设置为10 MPa,出口边界条件采用流量边界条件。本文计算7与10 L/s两种流量下的工况,进口段与旋转域、旋转域与静止域间采用冻结转子方法建立交界面进行连接。
3.1.2 速度分布利用ANSYS CFX 14.5进行数值计算,并对计算结果进行速度场、压力场、径向力及轴向力分析,结果如图 2~图 7所示。
|
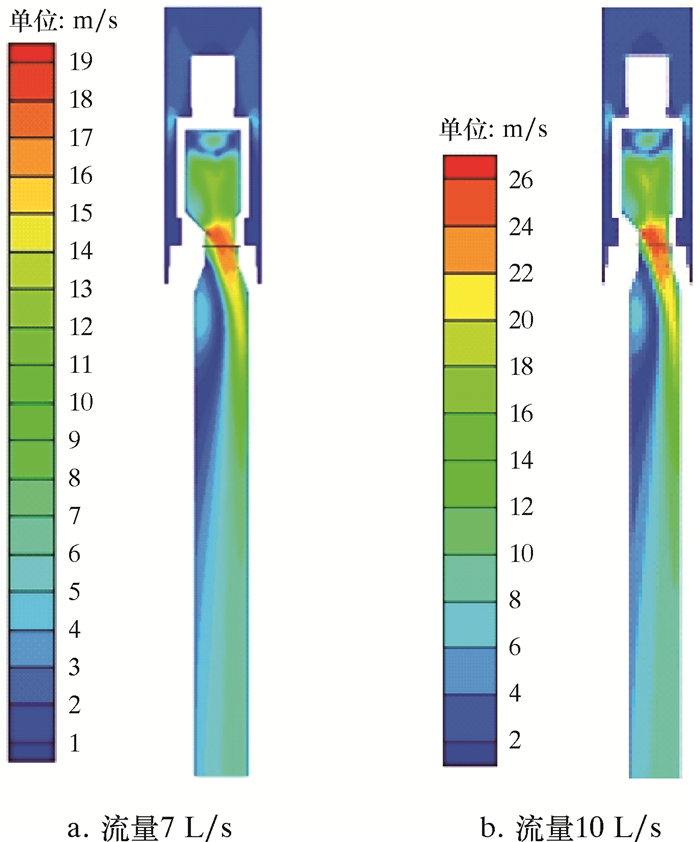
| 图 2 水力振荡器纵截面速度分布图 Fig.2 Velocity distribution of longitudinal section of the hydraulic oscillator |
|
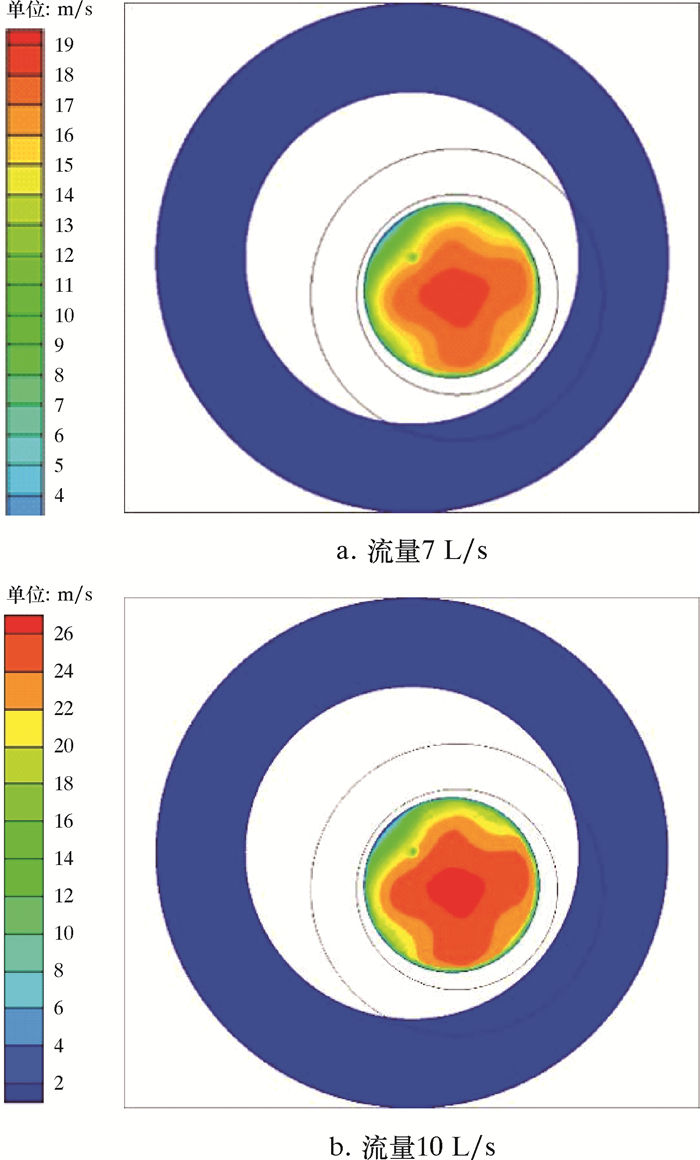
| 图 3 水力振荡器转子横截面速度分布图 Fig.3 Velocity distribution of rotor cross section of the hydraulic oscillator |
|
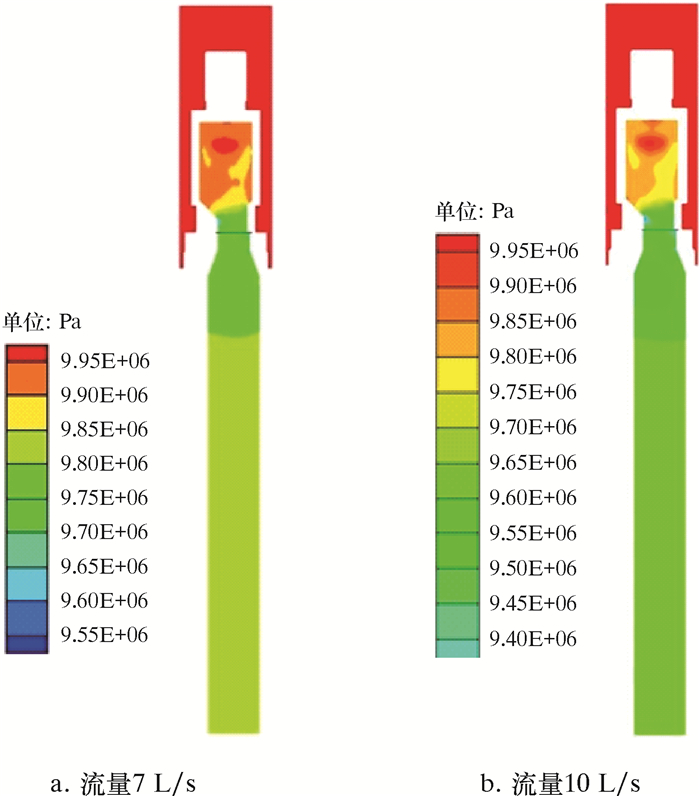
| 图 4 水力振荡器纵截面压力分布图 Fig.4 Pressure distribution of longitudinal section of the hydraulic oscillator |
|
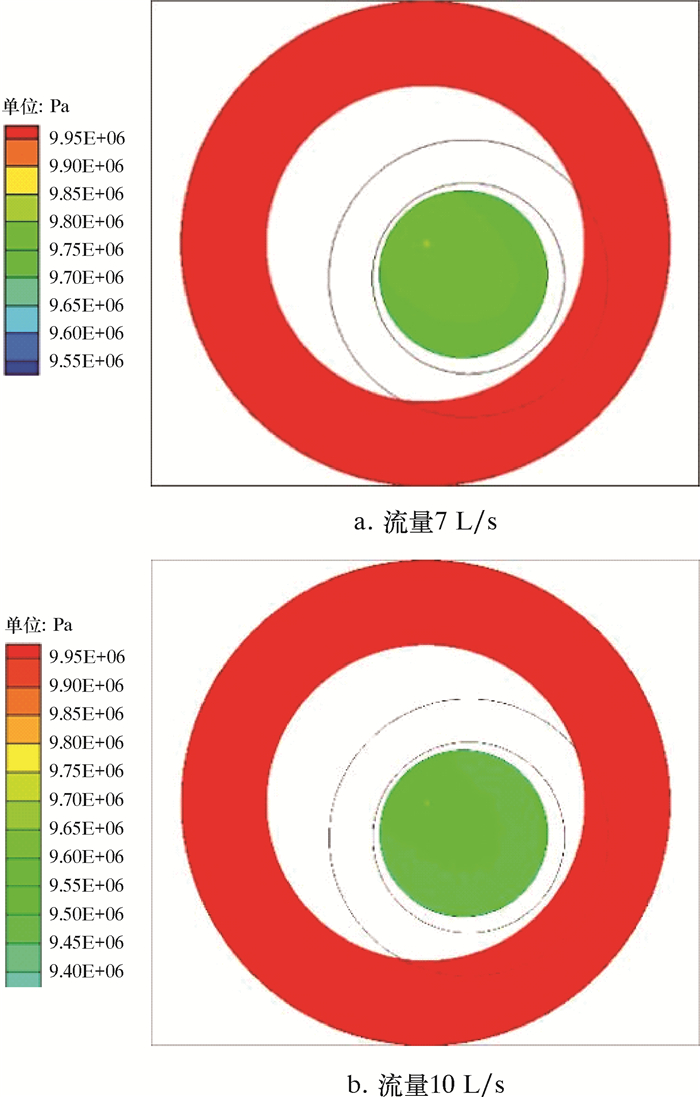
| 图 5 水力振荡器转子横截面压力分布图 Fig.5 Pressure distribution of the rotor cross section of the hydraulic oscillator |
|
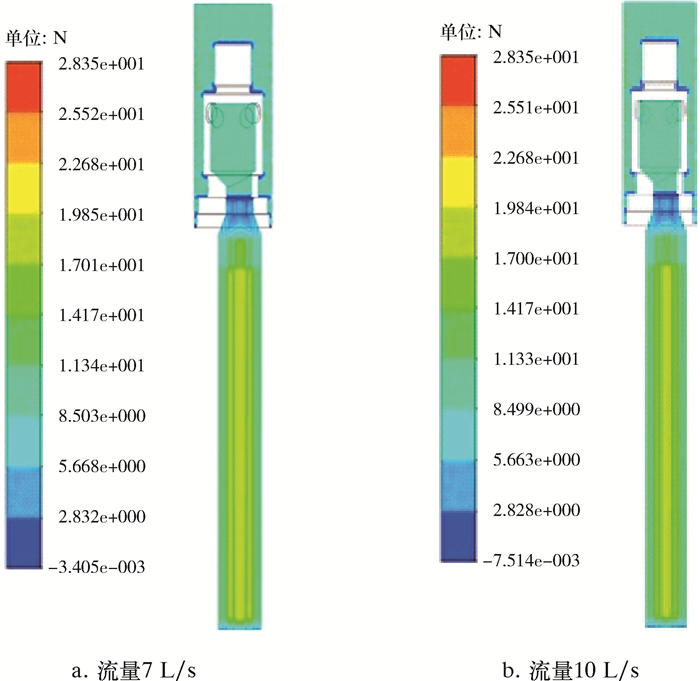
| 图 6 水力振荡器径向力分布图 Fig.6 Radial force distribution of the hydraulic oscillator |
|
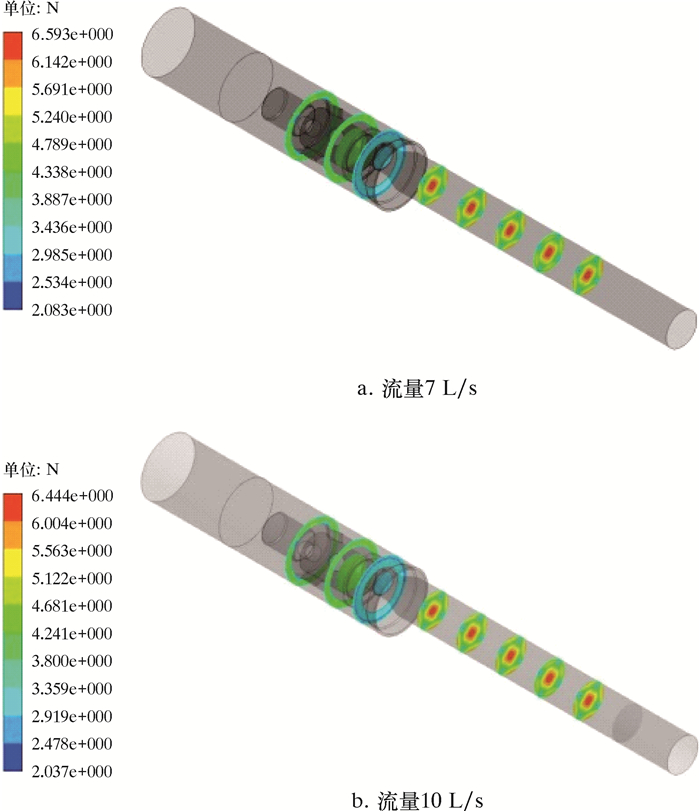
| 图 7 水力振荡器轴向力分布图 Fig.7 Axial force distribution of the hydraulic oscillator |
由图 2可知,当动阀片与定阀片交错重合时,阀门过流面积内的流体速度最大。当流体流过定阀片后,向外做放射状发展,且速度逐渐减小。由于阀门过流面积位于水力振荡器右侧,故流出段内右侧流体速度明显大于左侧。由图 3可知,当动阀片与定阀片交错重合时,在过流面积内,靠近轴心位置速度较小,远离轴心位置速度较大。在定阀片外缘与动阀片相交的圆弧段上,有一段速度最大的流体薄层。同时,流体速度较大的部分呈现出一个明显指向轴心的凸起。而在定阀片轴心位置,有一个速度小于周围区域的极小圆形范围。
3.1.3 压力分布由图 4可知,当动阀片与定阀片交错重合时,从进口段至出口段压力逐渐减小。
由图 5可知,当动阀片与定阀片交错重合时,过流面积内靠近轴心的位置压力较大,远离轴心的位置压力较小。在定阀片外缘与动阀片相交的圆弧段上,有一段压力最小的流体薄层。而在定阀片轴心位置,有一个压力大于周围区域的极小圆形范围。根据伯努利方程,压力大小和速度值成反比关系,由图 2和图 4对比可知,压力越大区域对应的速度值越小。
3.1.4 径向力分布水力振荡器定常流场径向力分布如图 6所示。由图 6可知,在交界面附近流道内径向力较小,经过静止域进口扩张段后,径向力明显增大。旋转部件运动使得流体动能增加,经过扩张段后流速降低,压力增大,流体动能重新转换为压能,导致其后流道所受径向力明显增大。
3.1.5 轴向力分布水力振荡器定常流场轴向力分布如图 7所示。由图 7可知,旋转域结构极为复杂,旋转域内轴向力分布较为复杂。在交界面附近流道内轴向力较小,经过扩张段后,轴向力明显增大。旋转部件运动使得流体动能增加,在经过扩张段后流速降低,流体动能重新转换为压能,导致其后流道所受轴向力明显增大,且定常状态下静止域轴向力分布具有很好的对称性。
3.2 非定常分析在定常计算的基础上,对水力振荡器进行非定常计算,对其内部流场的压力、径向力以及轴向力等随时间的变化规律进行分析,结果如图 8~图 25所示。
|
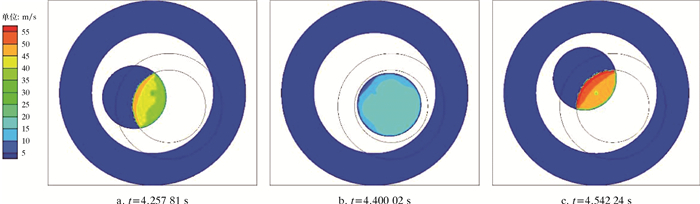
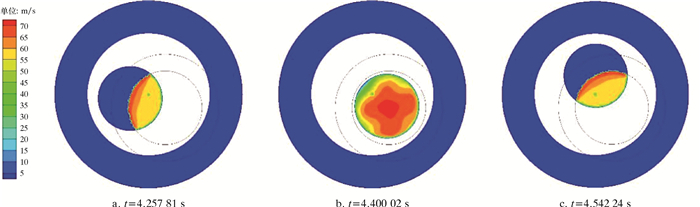
| 图 8 流量7 L/s,不同时刻转子截面速度场 Fig.8 Velocity field of the rotor cross section at different moments under the flow rate of 7 L/s |
|
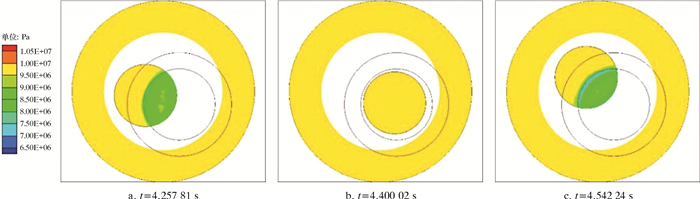
| 图 9 流量10 L/s,不同时刻转子截面速度场 Fig.9 Velocity field of the rotor cross section at different moments under the flow rate of 10 L/s |
|
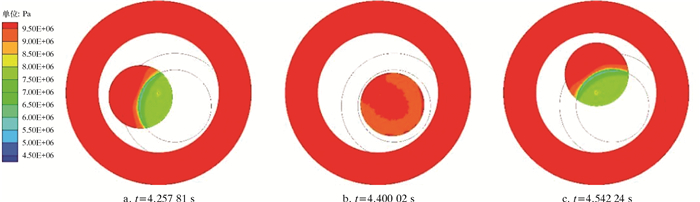
| 图 10 流量7 L/s,不同时刻转子截面压力场 Fig.10 Pressure field of the rotor cross section at different moments under the flow rate of 7 L/s |
|
| 图 11 流量10 L/s,不同时刻转子截面压力场 Fig.11 Pressure field of the rotor cross section at different moments under the flow rate of 10 L/s |
|
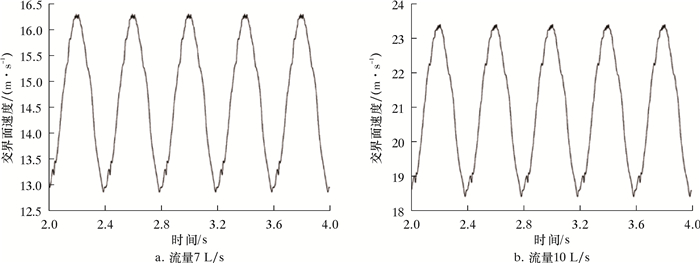
| 图 12 旋转域与静止域交界面速度随时间的变化规律 Fig.12 Velocity of the interface between the rotating domain and the stationary domain as a function of time |
|
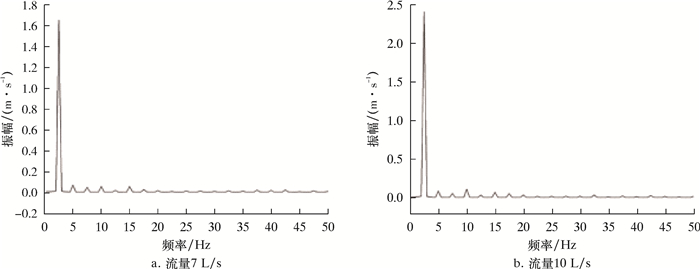
| 图 13 旋转域与静止域交界面速度脉动频谱 Fig.13 Velocity frequency pulsation spectrum at the interface between the rotation domain and the stationary domain |
|
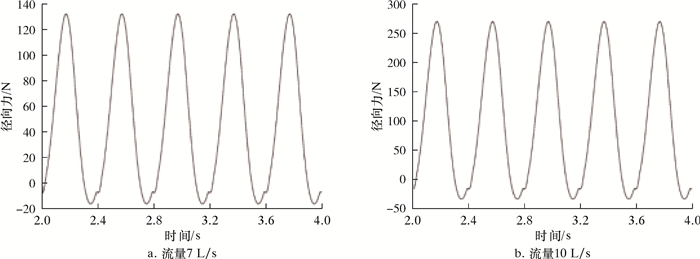
| 图 14 旋转域(Fluid1)整流域所受径向力(沿Y方向)随时间的变化规律 Fig.14 Variation of radial force (in the Y direction) on the rectification domain of the rotation domain (Fluid1) |
|
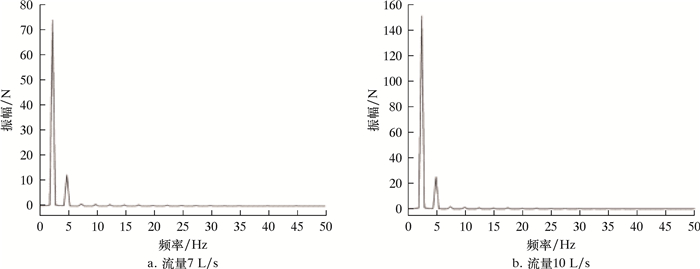
| 图 15 旋转域(Fluid1)整流域所受径向力(沿Y方向)频谱变化规律 Fig.15 Spectrum of radial force (in the Y direction) on the rectification domain of the rotation domain (Fluid1) |
|
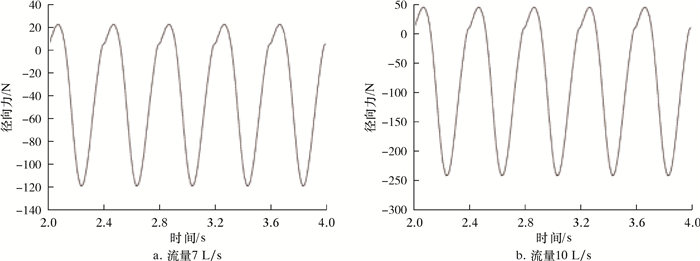
| 图 16 旋转域(Fluid1)整流域所受径向力(沿Z方向)随时间的变化规律 Fig.16 Variation of radial force (in the Z direction) on the rectification domain of the rotation domain (Fluid1) |
|
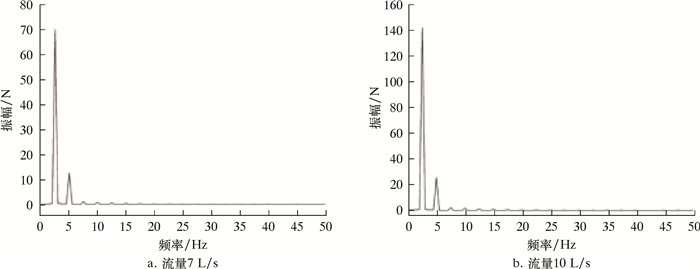
| 图 17 旋转域(Fluid1)整流域所受径向力(沿Z方向)频谱变化规律 Fig.17 Spectrum of radial force (in the Z direction) of the rectification domain of the rotation domain (Fluid1) |
|
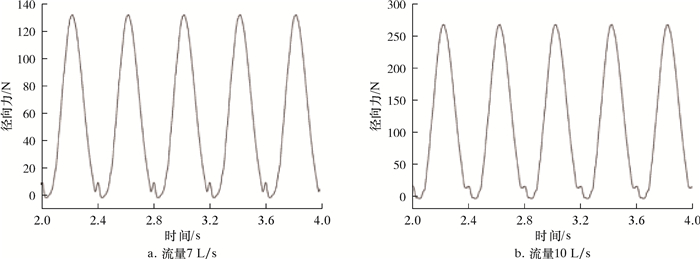
| 图 18 静止域(Fluid2)整流域所受径向力(沿Y方向)随时间的变化规律 Fig.18 Variation of radial force (in the Y direction) on the rectification domain of the static domain (Fluid2) |
|
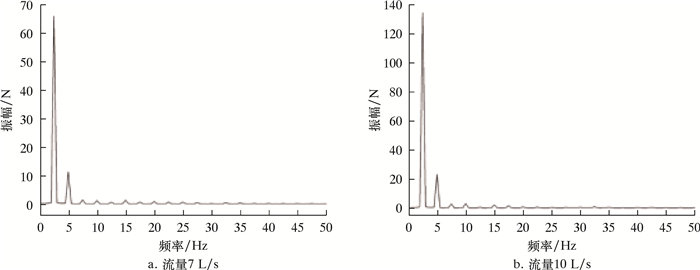
| 图 19 静止域(Fluid2)整流域所受径向力(沿Y方向)频谱变化规律 Fig.19 Spectrum of radial force (in the Y direction) of the rectification domain of the static domain (Fluid2) |
|
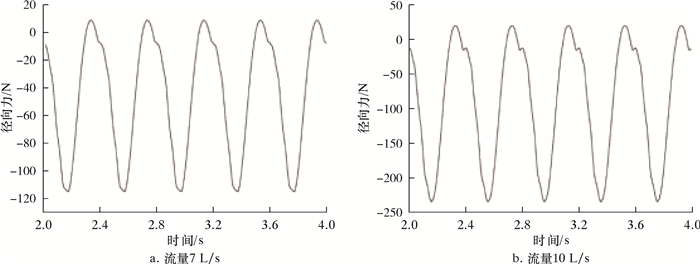
| 图 20 静止域(Fluid2)整流域所受径向力(沿Z方向)随时间的变化规律 Fig.20 Variation of radial force (in the Z direction) on the rectification domain of the static domain (Fluid2) |
|
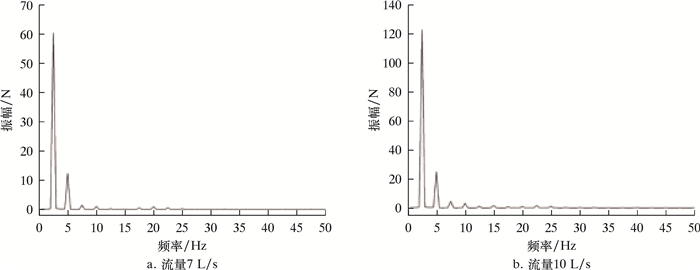
| 图 21 静止域(Fluid2)整流域所受径向力(沿Z方向)频谱变化规律 Fig.21 Spectrum of radial force (in the Z direction) in the rectification domain of the static domain (Fluid2) |
|
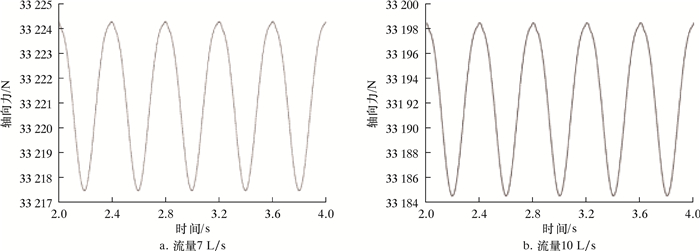
| 图 22 旋转域(Fluid1)整流域所受轴向力随时间的变化规律 Fig.22 Variation of axial force on the rectification domain of the rotation domain (Fluid1) |
|
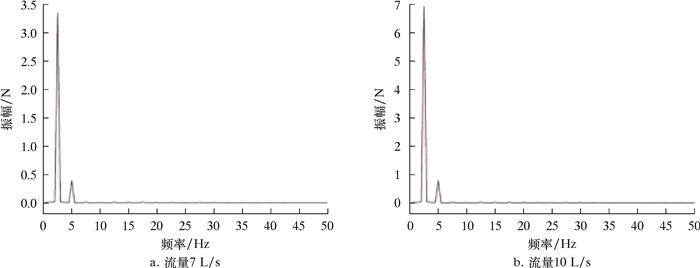
| 图 23 旋转域(Fluid1)整流域所受轴向力频谱变化规律 Fig.23 Spectrum of axial force on the rectification domain of the rotation domain (Fluid1) |
|
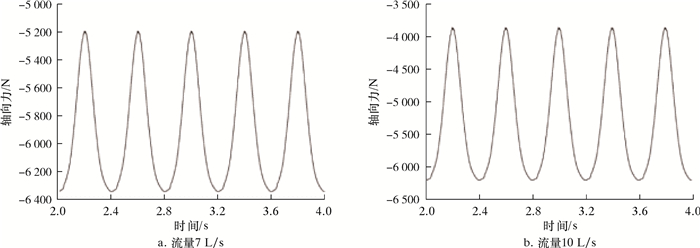
| 图 24 静止域(Fluid2)整流域所受轴向力随时间的变化规律 Fig.24 Variation of axial force on the rectification domain of the static domain (Fluid2) |
|
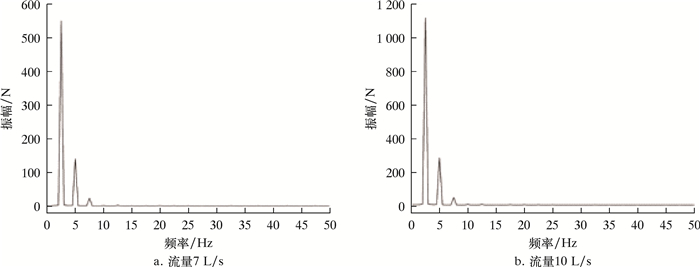
| 图 25 静止域(Fluid2)整流域所受轴向力频谱变化规律 Fig.25 Spectrum of axial force on the rectification domain of the static domain (Fluid2) |
3.2.1 非定常计算设置
将ANSYS Type改为Transient(瞬态模型),计算持续时间由最大时间步长确定,最大时间步长为2 400步。每个时间步长所计算的时间间隔由自定义函数确定。根据转速为150 r/min可得到旋转周期为0.4 s,则每计算一个时间步旋转域即转过20圈。每隔10个时间步保存一个非定常结果以便展开各瞬态分析工作。求解格式采用高精度求解模式,非稳态格式采用二阶向后欧拉格式。交界面设置由Rotor Stator改为TransientRotor Stator。其他的材料特性、计算方法、边界条件与定常计算设置完全相同。
3.2.2 瞬态速度场由图 8和图 9可知,在非定常计算的任意时刻,转子截面上速度场的分布形式相同。其中,流量为7 L/s时,非稳态速度场与稳态计算的结果在速度分布上基本相同;而流量为10 L/s时,非稳态速度场在定阀片外缘出现两处分离的局部速度极大处。沿动阀片转动方向,前端的速度极值点小于后端的速度极值点。
3.2.3 瞬态压力场对旋转域和静止域交界面截面压力场进行分析,其压力云图如图 10和图 11所示。由图 10和图 11可知,在非定常计算的任意时刻,转子截面上压力场分布形式相同。在流量确定的情况下,非稳态的计算结果与稳态的计算结果在分布上一致。
3.2.4 交界面速度水力振荡器运行过程中,旋转域和静止域的交界面面积发生周期性变化,故通过此交界面的流速也相应改变。图 12和图 13分别揭示了旋转域与静止域交界面速度随时间的变化规律和速度脉动频谱。通过交界面的流体流速呈周期性变化,且速度变化的主频为2.5 Hz,与旋转部件的转频保持一致,这说明旋转域的转动和旋转部件与静止域的主轴偏心是交界面处速度规律性变化的主要原因。
对比7和10 L/s两种流量工况,两者的速度变化主频和主要次频频率均保持一致,但大流量下交界面速度变化主频幅值更大,达到2.4 m/s,并且次频幅值也有所增大,频率为4倍转频的次频幅值增大更为明显,与旋转域具有4个进口管道结构相对应,说明旋转部件结构对流体流动状态具有规律性影响。
3.2.5 径向力对于旋转域(Fluid1),数值计算设置中,转子转速为150 r/min,旋转周期为0.4 s。图 14、图 15、图 16及图 17分别揭示了旋转域(Fluid1)整流域所受径向力(沿Y/Z方向)随时间的变化规律及频谱变化规律。在1个周期内,径向力出现1次极大值,1次极小值。Z方向的径向力与Y方向的径向力大致相等,且Y方向上力的极值点总是稍落后于Z方向出现。径向力脉动主频为2.5 Hz,与旋转域转频保持一致,且次频频率为主频的整数倍。流量为7 L/s工况下,径向力脉动的主频幅值分别为74和70 N,这表明由于动静干涉作用和交界面速度变化,引起流道中流体震荡,使得旋转域产生一定的径向振动。
对比7和10 L/s两种流量工况,旋转域所受径向力脉动的主频和主要次频频率均保持一致,但大流量下旋转域所受径向力平均值明显增大,其脉动主频幅值增长明显,达到145和140 N,近乎为7 L/s流量下主频幅值的2倍,并且次频幅值也均有所增大,这表明大流量下旋转域产生更大的径向力,并且其径向振动更加剧烈。
对于静止域(Fluid2),数值计算设置中,转子转速为150 r/min,旋转周期为0.4 s。图 18、图 19、图 20及图 21分别揭示了静止域(Fluid2)整流域所受径向力(沿Y/Z方向)随时间的变化规律及频谱变化规律。在1个周期内,径向力出现1次极大值,1次极小值。Z方向的径向力与Y方向的径向力大致相等,且Y方向上力的极值点总是稍落后于Z方向出现。径向力脉动主频为2.5 Hz,与旋转域转频保持一致,且次频频率为主频的整数倍,并且流量为7 L/s工况下径向力脉动的主频幅值分别为65和60 N,这表明由于动静干涉作用和交界面速度的变化,引起流道中流体震荡,使得静止域产生一定的径向振动。
对比7和10 L/s两种流量工况,静止域所受径向力脉动的主频和主要次频频率均保持一致,但大流量下旋转域所受径向力平均值明显增大,其脉动主频幅值增长明显,达到126和121 N,接近7 L/s流量下主频幅值的2倍,且次频幅值也均有所增大,这表明大流量下静止域产生更大的径向力并且其径向振动更加剧烈。
3.2.6 轴向力图 22、图 23、图 24及图 25分别揭示了旋转域(Fluid1)与静止域(Fluid2)所受轴向力随时间的变化规律及频谱变化规律。
其中,图 22与图 24的纵坐标为轴向力,横坐标为时间;图 23与图 25的纵坐标为振幅,横坐标为频率。在1个周期内,轴向力出现1次极大值,1次极小值,其中静止域的轴向力平均值远小于旋转域的轴向力平均值,可知全流域所受轴向力之和沿X轴正向对后接部件产生了近27 kN的推动力。轴向力脉动主频为2.5 Hz,与旋转域转频保持一致,且次频频率为主频的整数倍。7 L/s流量下,旋转域轴向力脉动的主频幅值为3.4 N,相对于其整体产生轴向力可忽略,而静止域轴向力脉动的主频幅值为550 N,其轴向振动程度较为强烈。以上分析说明,由于动静干涉作用和交界面速度变化,引起流道中流体的震荡,使得静止域产生剧烈的轴向振动。
对比7和10 L/s两种流量工况,大流量下旋转域和静止域所受轴向力平均值均明显增大。静止域所受轴向力脉动的主频和主要次频频率均保持一致,但静止域脉动主频幅值急剧增长,达到1 120 N,超出7 L/s流量下轴向力脉动主频幅值的2倍,并且次频幅值也显著增大,这表明大流量下静止域产生更大的轴向力且其轴向振动更为剧烈。
4 结论(1) 流体通过水力振荡器过程中,旋转部件的运动使得流体动能增加,在流动过程中流体的动能重新转换为压能,使得水力振荡器沿轴向正方向产生持续的轴向力而推动钻头做功。
(2) 由于动静干涉作用和交界面速度的变化所造成的流体震荡使得静止域产生剧烈的轴向和径向周期振动,大流量工况下轴向推力均值更大,轴向和径向振动也更为剧烈。
(3) 在持续轴向推力和大幅度轴向振动推动下,水力振荡器对钻柱施加周期性的轴向振动,进而产生钻压并稳定推进。
| [1] |
明瑞卿, 张时中, 王海涛, 等. 国内外水力振荡器的研究现状及展望[J]. 石油钻探技术, 2015, 43(5): 116-122. MING R Q, ZHANG S Z, WANG H T, et al. Research status and prospect of hydraulic oscillator worldwide[J]. Petroleum Drilling Techniques, 2015, 43(5): 116-122. |
| [2] |
FRIDMAN H D, LEVESQUE P. Reduction of static friction by sonic vibrations[J]. Journal of Applied Physics, 1959, 30(10): 1572-1575. DOI:10.1063/1.1735002 |
| [3] |
张辉, 吴仲华, 蔡文军. 水力振荡器的研制及现场试验[J]. 石油机械, 2014, 42(6): 12-15. ZHANG H, WU Z H, CAI W J. Development and field testing of hydraulic oscillator[J]. China Petroleum Machinery, 2014, 42(6): 12-15. DOI:10.3969/j.issn.1001-4578.2014.06.003 |
| [4] |
刘华洁, 高文金, 涂辉, 等. 一种能有效提高机械钻速的水力振荡器[J]. 石油机械, 2013, 41(7): 46-48. LIU H J, GAO W J, TU H, et al. A kind of hydraulic oscillator effectively improving ROP[J]. China Petroleum Machinery, 2013, 41(7): 46-48. DOI:10.3969/j.issn.1001-4578.2013.07.012 |
| [5] |
胥豪, 牛洪波, 唐洪林, 等. 水力振荡器在新场气田新沙21-28H井的应用[J]. 天然气工业, 2013, 33(3): 64-67. XU H, NIU H B, TANG H L, et al. Application of hydraulic oscillators to the development of Well Xinsha 21-28H in the Xinchang Gas Field, western Sichuan Basin[J]. Natural Gas Industry, 2013, 33(3): 64-67. |
| [6] |
石崇东, 党克军, 张军, 等. 水力振荡器在苏36-8-18H井的应用[J]. 石油机械, 2012, 40(3): 35-38. SHI C D, DANG K J, ZHANG J, et al. Application of the hydraulic oscillator in Well 36-8-18H of the Sulige block[J]. China Petroleum Machinery, 2012, 40(3): 35-38. |
| [7] |
谢新刚, 彭元超, 程元林, 等. 水力振荡器在储气库长水平段的应用[J]. 钻采工艺, 2014, 37(1): 99-101. XIE X G, PENG Y C, CHENG Y L, et al. Application of hydraulic oscillator in the storage of the long horizontal section[J]. Drilling & Production Technology, 2014, 37(1): 99-101. DOI:10.3969/J.ISSN.1006-768X.2014.01.29 |
| [8] |
王建龙, 王丰, 张雯琼, 等. 水力振荡器在复杂结构井中的应用[J]. 石油机械, 2015, 43(4): 54-58. WANG J L, WANG F, ZHANG W Q, et al. Application of hydraulic oscillator in complex wells[J]. China Petroleum Machinery, 2015, 43(4): 54-58. |
| [9] |
秦春, 陈小元, 李禹, 等. 水力脉冲射流钻井提速技术在江苏油田的应用[J]. 石油机械, 2015, 43(5): 17-21. QIN C, CHEN X Y, LI Y, et al. Applications of hydraulic pulse jet technology in Jiangsu Oilfield[J]. China Petroleum Machinery, 2015, 43(5): 17-21. |
| [10] |
孔令镕, 王瑜, 邹俊, 等. 水力振荡减阻钻进技术发展现状与展望[J]. 石油钻采工艺, 2019, 41(1): 23-30. KONG L R, WANG Y, ZOU J, et al. Development status and prospect of hydro-oscillation drag reduction drilling technology[J]. Oil Drilling & Production Technology, 2019, 41(1): 23-30. |



