2. 中国石化集团石油商业储备有限公司天津分公司天津实华原油商业储备基地
2. Tianjin Shihua Commercial Crude Oil Reserve Base, Tianjin Branch of Sinopec Petroleum Commercial Reserve Co., Ltd
0 引言
随着经济的发展,长距离输油管道已形成贯穿南北的管网,管线不可避免地要穿越一些地质灾害多发区,因此管道的安全面临威胁。穿越多年冻土区坡面的埋地管道不仅受到冻土冻胀和融沉的影响,还受到冻土冻融引起的土壤滑坡而产生变形。
近年来对于冻土区管道研究多集中于应力方面。A.G.RAZAQPUR等[1]首先采用有限元法对管道冻胀受力情况进行分析。B.B.RAJANI等[2]通过简单的解析法对横向滑坡下管道的力学响应进行了分析。M.J.OROURKE等[3]运用R-O模型对山体滑坡区域内发生偏移管道的力学响应进行了研究。邓道明等[4]对横向滑坡中埋地管道的位移和内力进行了计算。郝建斌等[5]推导了管道横穿滑坡状况下滑坡对管道推力的计算方法。张一楠等[6]研究了轴向、横向两种滑坡对管道应力的影响。吴亚平等[7]通过ANSYS软件研究了冻土区差异性冻胀下的管道应力与应变。张东臣等[8]分析了不同滑坡方向下管道的应力和应变分布。而关于滑坡条件下管道的应变分析研究比较少[9-10]。
本文利用ABAQUS有限元软件建立冻土区管道横向通过滑坡的模型,分析山体高度、滑坡位移和滑坡宽度对管道应变的影响规律,得到了一些有工程实用价值的结果。
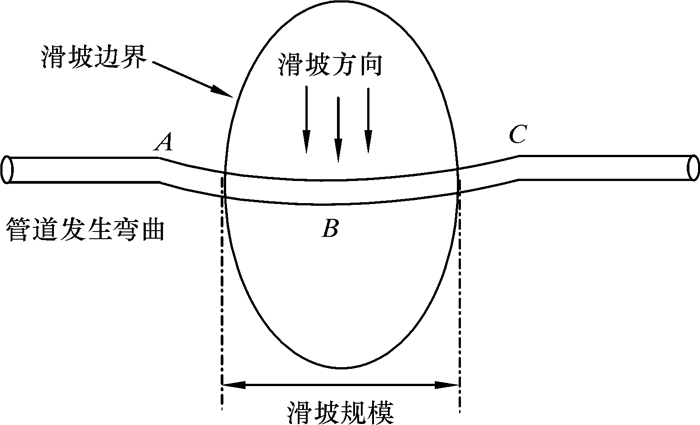
1 横向滑坡结构应力模型管道穿越不连续冻土区时,因土体性质变化,位于斜坡段的冻土区埋地管道会沿斜坡的冻融界面发生滑塌,从而形成冻融滑坡。在横向滑移模式下,管-土间作用形式复杂,管道呈现大范围弯曲变形,并可能发生塑性失稳或断裂。管道的受力和变形受滑坡规模、滑坡体土质和滑动位移等因素影响显著,常常出现受力不均的情况,并呈现不规则变形(如盆状弯曲)。横向滑坡管道受力情况如图 1所示。
|
| 图 1 横向滑坡管道受力情况 Fig.1 Diagram for stress subject to pipelines laterally crossing the landslide |
管道弯曲的微分方程为:
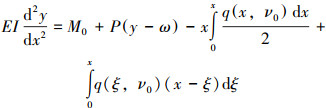
|
(1) |
式中:M0为截面处的弯矩,N·m;ω为截面处的挠度,m;q(x, ν00、q(ξ, ν0)分别为截面x和ξ处的分布密度,N/m2;E为拉伸弹性模量,Pa;I为惯性矩,m4;P为弯矩,N·m
管道最大挠度发生在x=l/2截面处,根据方程(1),x=l/2截面的挠度和弯矩分别为:

|
(2) |
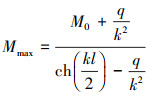
|
(3) |
其中:
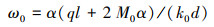
|
(4) |

|
(5) |
式中:k0为抗力系数,N/m3;d为管道直径,m;l为弯矩长度,m。
2 管-土模型的建立 2.1 有限元计算方法的选择土弹簧法、PSI单元法和接触面法是目前用ABAQUS模拟管-土相互作用时最常用的3种方法。因本文需要分析管道界面及表面的变形分布规律,所以采用接触面法进行模拟计算。接触面法是通过建立管道和土壤的实体模型,然后定义接触对属性,最后在施加的载荷条件下完成计算。
2.2 有限元模型的确立建立管-土相互作用三维有限元模型,并在实际工程的基础上分析问题。土体物理模型长40 m,宽40 m,前侧高10 m,后侧高35~55 m(每隔5 m取值)。滑坡体厚度7 m,滑坡土体宽度10~20 m。滑坡体土体采用Mohr-Coulomb模型,滑坡体下部基岩认为是弹性体材料。土体与管道界面属于有限滑动接触,摩擦因数取0.5。采用面对面的离散方式及硬接触和罚函数描述管-土间的法向与切向接触摩擦[11-13],模型采用八节点线性六面体单元(C3D8R)划分网格。相关数据如表 1所示。
| 土体 | 密度/ (kg·m-3) |
弹性模量/MPa | 泊松比 | 内摩擦角/(°) | 土体黏聚力/kPa |
| 滑坡体 | 1.834×103 | 16 | 0.2 | 18 | 100 |
| 土体基岩 | 2.000×103 | 15 | 0.3 |
建立直径813 mm、壁厚12.5 mm的管道模型,管道埋深为1.8 m,采用X65钢级管材及Ramberg-Osgood模型。管道主要性能参数:密度7 800 kg/m3,弹性模量210 GPa,泊松比0.3,输送压力10 MPa,最小屈服压力450 MPa。
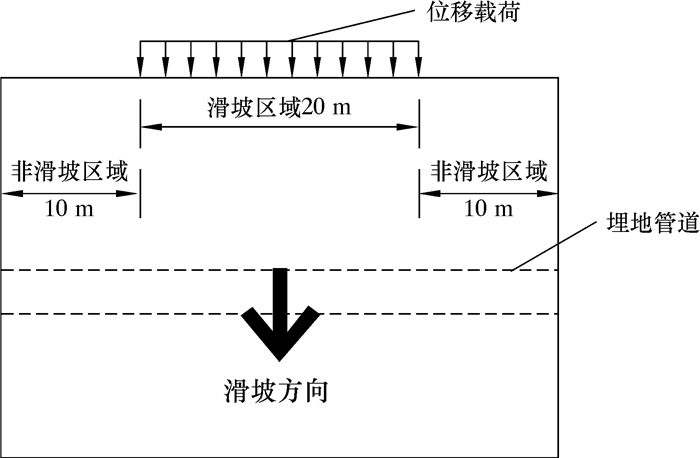
2.3 边界条件设置考虑到管道后方土体长度大于管径的5倍时,管道的极限弯曲已不明显[14],故本文建立的模型中,管道距离后端面的距离为3.5 m。管道和土体的边界条件设置如下:①对管道两端施加轴向约束;②土体基岩底面施加完全约束,土体前后两端面(非滑坡体部分)施加水平方向位移约束,土体左右两端面不约束竖直方向位移;③土体滑动可通过在土体端面施加位移载荷来体现,如图 2所示[15]。
|
| 图 2 横向滑坡平面示意图 Fig.2 Sketch of a lateral landslide |
3 模型验证
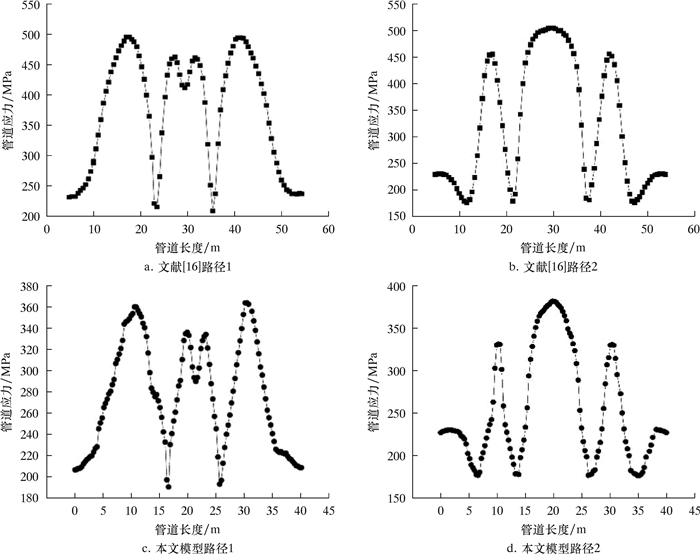
采用山体高度40 m、滑坡宽度20 m、滑坡位移2 m的有限元模型计算其应力变化,并将其与文献[16]所得到的滑坡条件下埋地管道的应力变化进行对比,结果如图 3所示。图 3中将管道内侧、外侧分别定义为路径1和路径2。从图 3可以看出,本文模型应力变化与文献[16]模型应力变化趋势一致。
|
| 图 3 模型验证示意图 Fig.3 Diagram for model verification |
4 影响管道应变的因素
以山体高度40 m时发生横向滑坡2 m的模型为例,观察横向滑坡对管道应变的影响。外侧管道应变云图如图 4所示。由图 4可以看出,滑坡灾害发生时,管道最大位移发生在管道中部,最大应变发生在滑坡与非滑坡土体交界面和管道中部。实际情况是管道应变集中会更趋于中部,这是因为土体在自身重力作用下会向管道中部堆积。

|
| 图 4 外侧管道应变云图 Fig.4 Nephogram of external pipeline strains |
4.1 山体高度与管道应变的关系
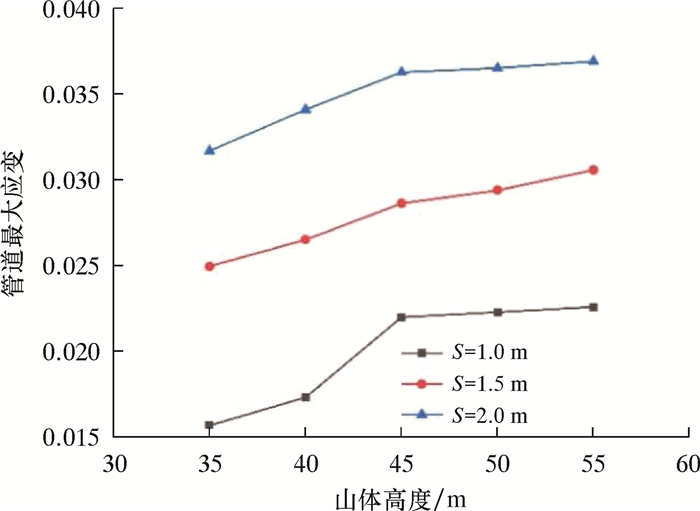
为分析山体高度对管道应变的影响[17-19],保持滑坡宽度20 m不变,设山体高度h分别为35、40、45、50和55 m,滑坡位移S分别为1.0、1.5和2.0 m,得到管道应变随山体高度的变化曲线,如图 5所示。从图 5可见:当滑坡位移相同时,管道最大应变随着山体高度的增大而增大,但是应变增量随山体高度的增加而减小;当山体高度为35~45 m时,管道应变的增大明显,山体高度为45~55 m时,管道应变增大趋于平缓;山体越高,管道屈曲变形越大,管道所受应力接近屈服强度,即超过55 m的山体发生滑坡,管道可能快速进入塑性变形;当位移为1.0 m时,管道最大应变和最小应变分别为0.022 5和0.015 6;位移为1.5 m时,管道最大应变和最小应变分别为0.031 5和0.024 9;位移为2.0 m时,管道最大应变和最小应变分别为0.036 8和0.031 6,最大应变变化量为44.0%。
|
| 图 5 管道应变随山体高度的变化曲线 Fig.5 Relationship between the pipeline strain and hill height |
4.2 滑坡位移与管道应变的关系
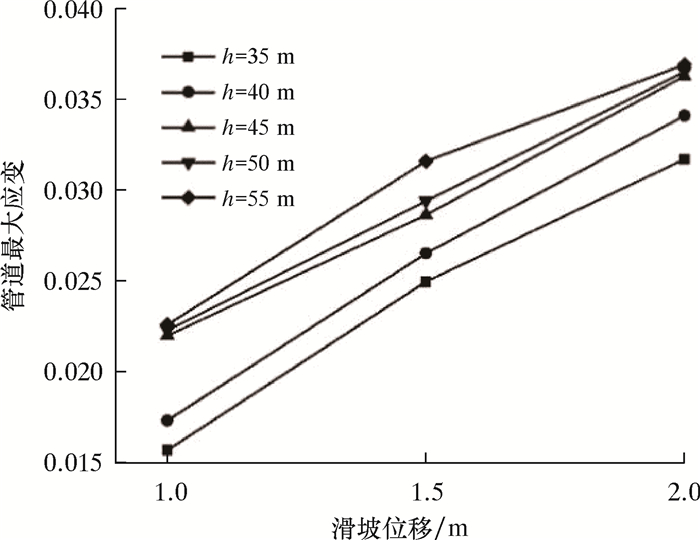
保持滑坡宽度20 m不变,设滑坡位移S分别为1.0、1.5和2.0 m,山体高度h分别为35、40、45、50和55 m,得到滑坡位移与管道应变的关系曲线,如图 6所示。从图 6可见:当山体高度不变时,管道应变都随着滑坡位移的增大而增大;滑坡位移越大,管道位移越大,应变越大。这表明滑坡发生得越剧烈,土体对管道施加的载荷越大,管道应变越大。当滑坡位移一致时,山体越高,应变越大。
|
| 图 6 滑坡位移与管道应变的关系曲线 Fig.6 Relationship between the pipeline strain and landslide mass displacement |
滑坡位移对管道应变的影响如表 2所示。从表 2可以看出,当山体高度为35 m、滑坡位移从1.0 m增加至2.0 m时,管道应变从0.015 6增长至0.031 7,应变增长1倍以上,而山体高度为55 m时,管道应变增长为64.0%,说明山体高度越低,滑坡位移对管道的影响越大,造成的破坏越大。这是因为高山体管道应变已经接近于管道的屈服极限,所以管道应变增长量才会随着山体高度的增加而减少。位移相同时,随着山体高度的增加,管道应变最大增量为44.2%,远小于位移对管道应变的影响。
| 位移/ m |
应变 | 应变增 量/% |
||||
| h=35 m | h=40 m | h=45 m | h=50 m | h=55 m | ||
| 1.0 | 0.015 64 | 0.017 28 | 0.021 95 | 0.022 25 | 0.022 55 | 44.2 |
| 1.5 | 0.024 92 | 0.026 48 | 0.028 59 | 0.029 36 | 0.031 55 | 26.6 |
| 2.0 | 0.031 66 | 0.034 06 | 0.036 24 | 0.036 49 | 0.036 88 | 16.5 |
4.3 滑坡体宽度与管道应变的关系
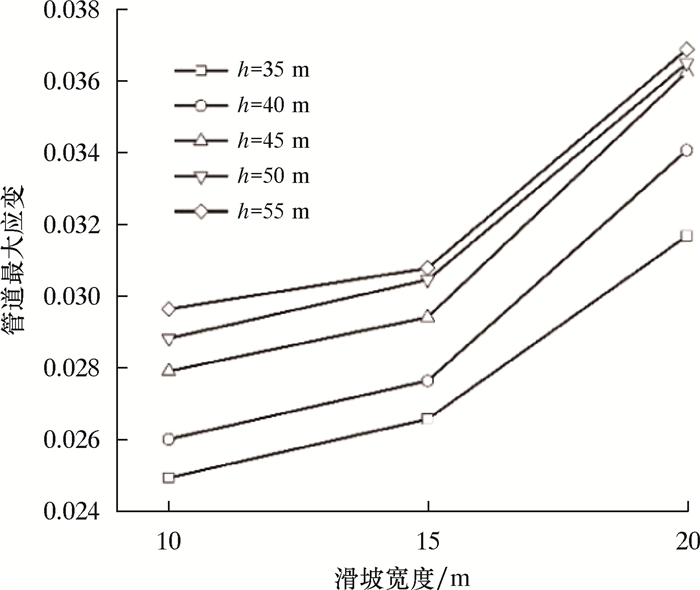
在保持滑坡位移2.0 m的条件下,研究滑坡宽度对管道应变的影响。设置滑坡宽度分别为10、15和20 m,山体高度h分别为35、40、45、50和55 m,得到管道应变与滑坡宽度的关系曲线,如图 7所示。
|
| 图 7 滑坡宽度对管道应变的影响 Fig.7 Effect of landslide mass width on pipeline strain |
从图 7可见:当山体高度一致时,管道最大应变随着滑坡宽度的增加而增大;当滑坡宽度为15~20 m时,管道最大应变突增;当滑坡宽度不变时,山体越高,应变越大;山体高度为45~55 m时,管道最大应变相差不多。这说明山体高度55 m、滑坡宽度为20 m时,管道接近屈服极限,因此应变增量不明显。
滑坡宽度对管道应变的影响如表 3所示。从表 3可见,当山体高度为35 m时,随滑坡宽度的变化,管道应变从0.024 91到0.026 55,应变增加了6.6%,而管道应变从0.026 55到0.031 66,应变增加了27.0%。滑坡宽度虽然都是5 m差距,但是应变变化量的差距高达4倍以上。这说明滑坡宽度越大,管道越容易受其影响而造成管道屈曲。与山体高度对管道应变的影响最大为18.9%相比,滑坡宽度对管道的影响小。
| 滑坡宽度/m | 应变 | 应变增 量/% |
||||
| h=35 m | h=40 m | h=45 m | h=50 m | h=55 m | ||
| 10 | 0.024 91 | 0.025 99 | 0.027 89 | 0.028 80 | 0.029 63 | 18.9 |
| 15 | 0.026 55 | 0.027 62 | 0.029 40 | 0.030 44 | 0.030 77 | 15.9 |
| 20 | 0.031 66 | 0.034 06 | 0.036 24 | 0.036 49 | 0.036 88 | 16.4 |
5 结论
(1) 冻土区山坡滑坡时,横穿管道的轴向应变主要为拉应变,最大应变在滑坡与非滑坡交界面,是危险截面。因此在滑坡发生后,要首先对管道与滑坡土体接触面进行检查和维护。
(2) 冻土区山坡埋地管道发生横向滑坡时,管道的应变随着山体高度、滑坡位移和滑坡宽度的增加而增大。冻土区管道敷设不宜超过高55 m的山体,因为该高度山体发生滑坡后,管道可能快速发生塑性变形。
(3) 山体高度对管道应变影响最大为44%。低矮山体滑波位移对管道应变影响更为明显,应变增量可高达1倍。滑坡宽度对管道应变的影响最大为27.0%。滑坡位移是影响管道应变的最主要因素。因此在面临山体滑坡时,应根据其灾害程度制定不同的应对方案。
(4) 当滑坡宽度为20 m时,管道应变突增。应每隔20 m左右设置抗滑桩,山体越高,防护措施布置应更紧密。
| [1] |
RAZAQPUR A G, WANG D. Frost-induced deformations and stresses in pipelines[J]. International Journal of Pressure Vessels & Piping, 1996, 69(2): 105-118. DOI:10.1016/0308-0161(95)00120-4 |
| [2] |
RAJANI B B, ROBERTSON P K, Morgenstern N R. Simplified design methods for pipelines subject to transverse and longitudinal soil movements[J]. Canadian Geotechnical Journal, 1995, 32(2): 309-323. DOI:10.1139/t95-032 |
| [3] |
OROURKE M J, LIU X J, FLORES-BERRONES R. Steel pipe wrinkling due to longitudinal permanent ground deformation[J]. Journal of Transportation Engineering, 1995, 121(5): 443-451. DOI:10.1061/(ASCE)0733-947X(1995)121:5(443) |
| [4] |
邓道明, 周新海, 申玉平. 横向滑坡过程中管道的内力和变形计算[J]. 油气储运, 1998, 17(7): 18-22. DENG D M, ZHOU X H, SHEN Y P. Calculation of pipeline inner force and distortion during transvers landslide body[J]. Oil and Gas Storage and Transportation, 1998, 17(7): 18-22. |
| [5] |
郝建斌, 刘建平, 荆宏远, 等. 横穿状态下滑坡对管道推力的计算[J]. 石油学报, 2012, 33(6): 1093-1097. HAO J B, LIU J P, JING H Y, et al. A calculation of landslide thrust force to transverse pipelines[J]. Acta Petrolei Sinica, 2012, 33(6): 1093-1097. |
| [6] |
张一楠, 马贵阳, 刘睿, 等. 横向冻融滑坡对埋地管道应力影响的数值模拟[J]. 辽宁石油化工大学学报, 2016, 36(2): 28-31. ZHANG Y N, MA G Y, LIU R, et al. Numerical simulation of the stress influence on buried pipelines under action of lateral landslide[J]. Journal of Liaoning Shihua University, 2016, 36(2): 28-31. DOI:10.3969/j.issn.1672-6952.2016.02.008 |
| [7] |
WU Y P, SHENG Y, WANG Y, et al. Stresses and deformations in a buried oil pipeline subject to differential frost heave in permafrost regions[J]. Cold Regions Science & Technology, 2010, 64(3): 256-261. |
| [8] |
张东臣, Быков Л И. 滑坡条件下埋地管道受力分析[J]. 石油规划设计, 2001, 12(6): 1-3. ZHANG D C, Быков Л И. The force-summing analysis of buried pipeline under landslide condition[J]. Petroleum Planning & Engineering, 2001, 12(6): 1-3. DOI:10.3969/j.issn.1004-2970.2001.06.001 |
| [9] |
齐超, 吴玉国, 王卫强, 等. 冻土参数对斜坡段埋地管道应力影响的数值模拟[J]. 辽宁石油化工大学学报, 2016, 36(2): 32-35. QI C, WU Y G, WANG W Q, et al. The numerical simulation of the frozen soil parameters on the ramp portion of buried piping stress[J]. Journal of Liaoning Shihua University, 2016, 36(2): 32-35. DOI:10.3969/j.issn.1672-6952.2016.02.009 |
| [10] |
张一楠, 马贵阳, 王锡钰, 等. 冻融滑坡作用下埋地管道的应力分析[J]. 辽宁石油化工大学学报, 2016, 36(1): 27-30. ZHANG Y N, MA G Y, WANG X Y, et al. Stress analysis of buried pipeline under the action of freezing-thawing landslide[J]. Journal of Liaoning Shihua University, 2016, 36(1): 27-30. DOI:10.3969/j.issn.1672-6952.2016.01.006 |
| [11] |
COCCHETTI G, PRISCO C D, GALLI A. Soil-pipeline interaction along unstable slopes: a coupled three-dimensional approach. Part 2: Numerical analyses[J]. Canadian Geotechnical Journal, 2009, 46(11): 1289-1304. DOI:10.1139/T09-028 |
| [12] |
黄龙, 盛煜, 胡晓莹, 等. 冻土区管土相互作用研究综述[J]. 冰川冻土, 2017, 39(1): 112-122. HUANG L, SHENG Y, HU X Y, et al. Interactions between the pipeline and soils in permafrost regions: a review[J]. Journal of Glaciology and Geocryology, 2017, 39(1): 112-122. |
| [13] |
ZHANG J M, QU G Z, JIN H J. Estimates on thermal effects of the China-Russia crude oil pipeline in Permafrost regions[J]. Cold Regions Science & Technology, 2010, 64(3): 243-247. |
| [14] |
胡生宝, 毛建, 曾跃辉. 输气管道滑坡灾害影响因素敏感性分析[J]. 成都大学学报(自然科学版), 2017, 36(4): 427-430. HU S B, MAO J, ZENG Y H. Sensitivity analysis of influencing factors of landslide in gas pipeline[J]. Journal of Chengdu University (Natural Science Edition), 2017, 36(4): 427-430. DOI:10.3969/j.issn.1004-5422.2017.04.023 |
| [15] |
刘慧.滑坡作用下埋地管线反应分析[D].大连: 大连理工大学, 2008. LIU H. Response analysis for buried pipelines subjected to the landslide[D]. Dalian: Dalian University of Technology, 2008. |
| [16] |
焦中良, 谷海威, 郭杰, 等. 滑坡条件下埋地管道的应力分析[J]. 煤气与热力, 2014, 34(12): 11-16. JIAO Z L, GU H W, GUO J, et al. Stress analysis of buried pipeline subjected to landslide[J]. Gas & Heat, 2014, 34(12): 11-16. DOI:10.3969/j.issn.1000-4416.2014.12.004 |
| [17] |
练章富, 李风雷. 滑坡带埋地管道力学强度分析[J]. 西南石油大学学报(自然科学版), 2014, 36(2): 165-170. LIAN Z F, LI F L. Analysis of mechanical strength of buried pipelines in landslide areas[J]. Journal of Southwest Petroleum University(Science & Technology Edition), 2014, 36(2): 165-170. |
| [18] |
黄坤, 卢泓方, 吴世娟, 等. 穿越滑坡体埋地输气管道应力分析[J]. 应用力学学报, 2015, 32(4): 689-693. HUANG K, LU H F, WU S J, et al. The stress analysis of buried gas pipeline crossing the landslide[J]. Chinese Journal of Applied Mechanics, 2015, 32(4): 689-693. |
| [19] |
夏梦莹, 张宏, 王宝栋, 等. 基于壳单元的连续型采空区埋地管道应变分析[J]. 油气储运, 2018, 37(3): 256-262. XIA M Y, ZHANG H, WANG B D, et al. Strain analysis of buried pipelines in continuous mining subsidence areas based on shell element[J]. Oil & Gas Storage and Transportation, 2018, 37(3): 256-262. |



