2. 四川铁投广润物流有限公司
2. Sichuan Railway Investment Guangrun Logistics Co., Ltd
0 引言
全面实现页岩气产业化可以有效缓解中国目前存在的天然气供需矛盾,对于保障国家能源安全运行具有极为重要的意义。页岩气开发主要采用水平井完井和可钻式桥塞分层大型水力加砂压裂等工艺技术[1-2],这些作业方式给页岩气井的地面返排测试带来诸多难题,如页岩气测试平台排液测试期的井口压力高、温度高、返排液量大以及返排时间长等。通过调研发现,长宁-威远页岩气测试平台所采用的波纹板分离器分离效果差,无法满足现场需要。
气液分离器作为一种操作简单、处理效率较高的分离设备而被广泛应用于国内外油气田的测试平台[3-4]。不同结构的分离设备只有在其适用的特定工况下才能达到较高的分离效果,而国内各油气田自身的物性参数与开发技术手段等均不相同,油气水的含量也有所差异。因此,为了适应不同油气田的开发,必须选用与其生产实际相符的分离设备。
多年以来,相关学者[5-9]对油水分离器的分离效率及其影响因素进行了分析,也有学者[10-18]在波纹板气液分离器的分离性能评价和优化方面取得了大量的研究成果。其多为试验验证与数值模拟两种研究方法,并将研究结果用以指导优化波纹板分离器,主要包括优化波纹板操作参数和结构参数或者改进新型材质等方面。但是很少有相关学者对波纹板分离效率的理论计算公式进行验证,以准确对波纹板分离器的分离性能进行评价和优化。为了提高波纹板分离器分离性能评价和优化方法的可靠性,本文建立了波纹板分离器分离效率的理论计算模型,并采用数值模拟方法对其进行了验证。研究结果对于满足国内页岩气测试平台的迫切需要具有重要意义。
1 波纹板分离效率理论模型页岩气测试平台排液测试期具有井口压力高、温度高、返排时间长以及返排液量大等特点,对后续分离设备具有较大影响。为了满足测试平台分离设备橇装化和高效率的要求,页岩气测试平台选用波纹板分离器对采出流体进行处理,其主要结构参数为:板间距20 mm,波高15 mm,波径100 mm,回转角64°。
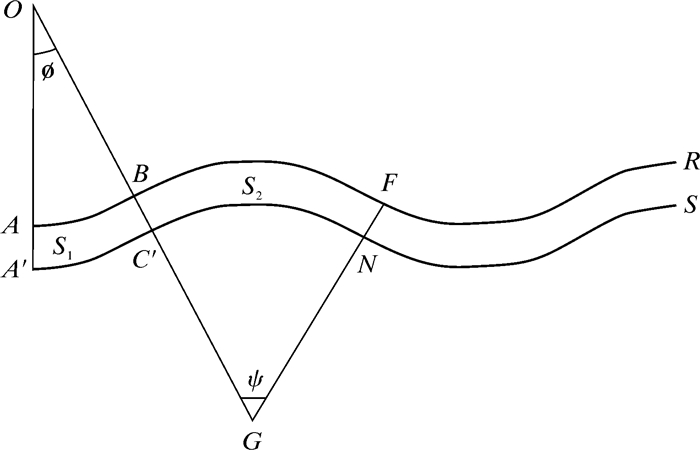
现选取一条波纹板流道界面建立数学模型,将波纹板流道内一个波段划分为两个区域,即S1和S2,如图 1所示。
|
| 图 1 波纹板流道几何形状划分示意图 Fig.1 Schematic diagram of the geometric division of corrugated plate flow passes |
随着页岩气从测试平台分离器入口到波纹板入口这一段空间的充分发展,液滴在气流中可被认为均匀分布。对于波纹板内三维、非定常的携液流动情况,可以做以下简化处理:①将波纹板内部流体视为不可压缩流体;②波纹板中各流动参数不随时间发生变化;③液滴均匀分布在气流中,波纹板入口处气液速度相等;④液滴相互之间无碰撞和聚集;⑤液滴的粒径固定,不考虑变形和自转;⑥波纹板壁面光滑,无摩擦阻力;⑦在流动过程中气液之间有速度滑移;⑧不考虑碰撞时液滴的反弹、飞溅和二次携带问题。
通过对液滴进行动力学分析,可以建立液滴的运动方程式:
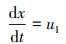
|
(1) |
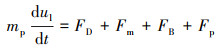
|
(2) |
式中:ul为液滴速度,m/s;mp为液滴质量,kg;FD为气流对微小液滴的拖曳力,N;Fm为附加质量力,N;FB为Basset(巴塞特)力,N;Fp为压力梯度力,N。
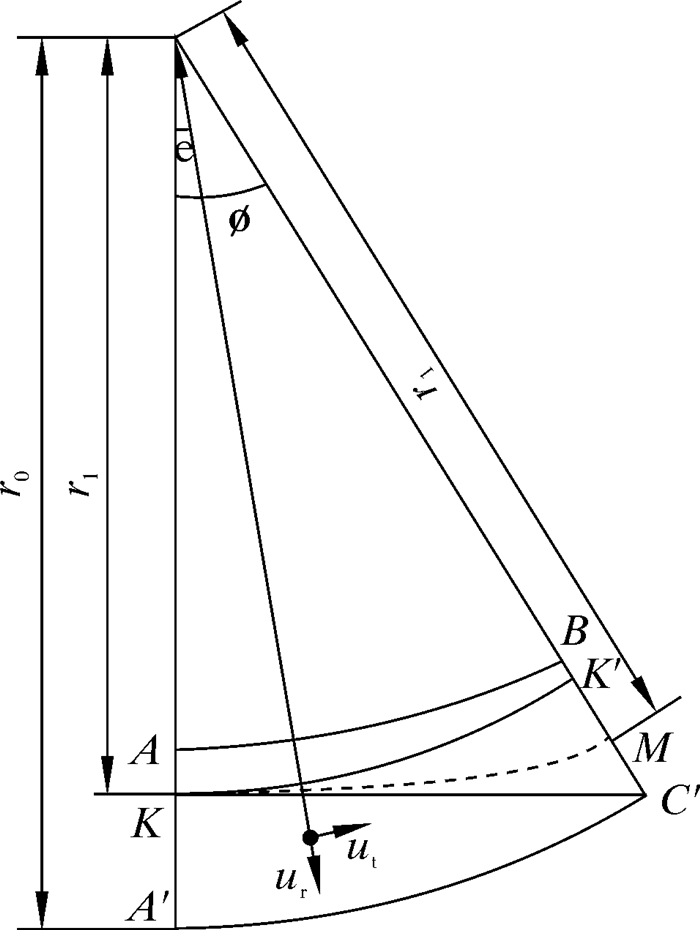
1.1 S1区域内的分离效率以弧A′C′的圆心O为坐标原点、OK为半径r1绘制与BC′段相交于K′点的圆弧,建立S1区域的角坐标系,见图 2。携液气流从波纹板入口AA′进入分离区域后,微小液滴在惯性作用下逐渐偏离气流方向,并且向弧A′C′靠近。入口截面AK段内的液滴无法在S1区域被波纹板捕集。A′K段的液滴进入波纹板后,在惯性作用下有可能撞击波纹板壁面,从而被捕集分离。
|
| 图 2 S1区域波纹板流道模型 Fig.2 Corrugated plate flow pass model of area S1 |
在S1区域中,任意一点可采用角坐标(r, θ)来描述,液滴的速度可分解为径向速度ur和切向速度ut,则可建立液滴的运动微分方程式:
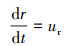
|
(3) |
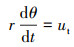
|
(4) |
式中:r为液滴到原点的距离,m。
将式(3)与式(4)合并,可得液滴的运动微分方程式:
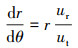
|
(5) |
携液气流在波纹板中做变向运动时流速变化迅速,故可认为其在流道内总是无径向速度,速度方向始终与其所处位置至原点O的连线相垂直。在流动过程中,分散于气相中的微小液滴在气流拖曳力的作用下做靠近外侧壁面的运动。气液两相在进入波纹板时的速度相等,因此两者在流道中的速度大小相差一个径向速度,对运动方程式(2)积分可得:
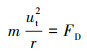
|
(6) |
液滴质量计算式为:
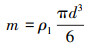
|
(7) |
式中:d为液滴直径,m。
气流对液滴的拖曳力计算式为:
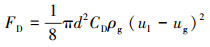
|
(8) |
式中:CD为曳力系数,无量纲;ρg为气体密度,kg/m3;ug为气流速度,m/s。
将式(6)代入式(8)可得:
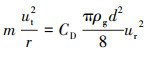
|
(9) |
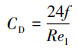
|
(10) |
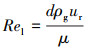
|
(11) |
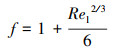
|
(12) |
式中:Rel为临界雷诺数,无量纲;f为系数,无量纲。
将式(12)与式(7)代入式(9)可得:
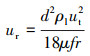
|
(13) |
式中:μ为气相黏度,Pa·s。
将式(13)代入液滴运动轨迹的微分方程式(5)后可得:
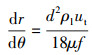
|
(14) |
在波纹板流道内的运动过程中,气相流场的速度可近似为自由涡分布,即气相的速度与其所处空间位置的圆心距成反比,即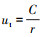
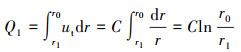
|
(15) |
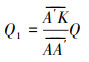
|
(16) |
式中:r0为A′点与原点O的距离,m;r1为K点与原点O的距离,m。
由式(15)和式(16)可得:
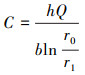
|
(17) |
式中:b为波纹板布置间距(AA′长度),m;h为波纹板圆弧段的弧高(A′K长度),m。
将式(17)与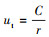
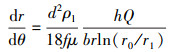
|
(18) |
对式(18)进行积分可得:
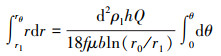
|
(19) |
将式(19)积分结果进行整理,可得在θ角度时液滴与原点的距离rθ的计算式:
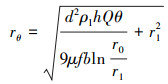
|
(20) |
式(20)表示从入口K进入的液滴经过θ角度的运动后所处的位置函数(即曲线KM),该线为气液分界线,即当分析A′K段进入的携液气流时,KM以上往内壁面方向为纯气流,KM以下往外壁面方向为气液混合部分。当携液气流从入口到达S1区域出口时,有θ=φ,此时式(20)变为:
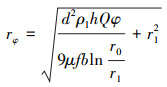
|
(21) |
对于给定直径d的微小液滴,其在S1区域中的分离效率η1的计算式为:
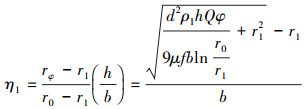
|
(22) |
若板间距b小于波纹板圆弧高h,则式(22)变为:
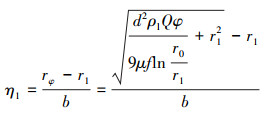
|
(23) |
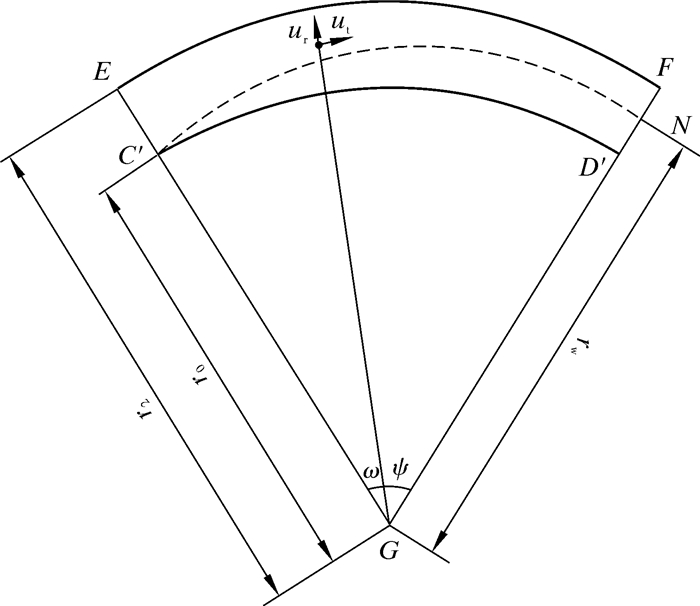
携液气流从波纹板入口进入流道后,经过S1区域分离后,部分液滴仍未被波纹板壁面所捕捉到。从S1逃逸出来后,携液气流进入S2区域继续进行惯性分离过程。与S1区域分离效率计算过程类似,对于S2区域,以弧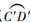
|
| 图 3 S2区域波纹板流道模型图 Fig.3 Corrugated plate flow pass model of area S2 |
在S2区域入口的所有液滴都有机会被波纹板壁面所捕捉到,故以其极限点C′来进行分析。微小液滴在S2区域内的运动微分方程与S1区域中相同。气流在S2区域内的速度呈自由涡分布,即ut=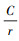
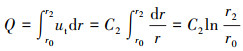
|
(24) |
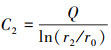
|
(25) |
式中:r2为E点与原点G的距离,m。
将式(25)代入液滴的运动方程(14)可得:
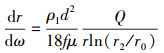
|
(26) |
将式(26)微分方程在S2区域中的运动进行积分,可得点C′处所进入液滴的位置函数方程:
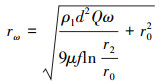
|
(27) |
式(27)表示从S2区域入口处C′点进入流场的液滴,在经过ω角度的运动后所处的位置(即曲线C′N),该曲线为S2区域内流场的纯气流与携液气流的分界线,即曲线C′N到波纹板通道内侧壁面之间的区域内流体只有气相,曲线C′N到波纹板通道外侧壁面之间的区域内气流携带有微小液滴。当液滴运动经过ψ角度后到达S2区域出口时,则有:
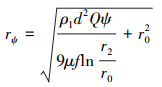
|
(28) |
对于给定直径d的微小液滴,其分离效率η2的计算式为:
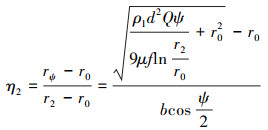
|
(29) |
通过推导出S1和S2区域的分离效率理论计算公式,可得到携液气流在两个分离区域内的运动规律,也就可得到波纹板分离器在一个波段内的分离效率,因此页岩气测试平台所使用波纹板分离器的分离效率理论计算公式为:
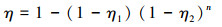
|
(30) |
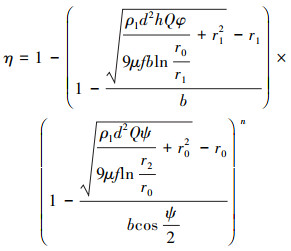
|
(31) |
式中:n为波纹板的级数。
由式(31)可见:影响波纹板分离器分离效率的结构参数主要有波纹板圆弧段的半径r0和波纹板圆弧段的弧高h等,r0越小,或h越大,则η越大;影响波纹板分离器分离效率的操作参数主要有分离器的入口流速(即流量Q)、波纹板安装间距b等,Q越大,或b越小,则η越大。
2 计算模型的建立与求解 2.1 几何模型与网格划分将波纹板流道两端水平延长,使入口处的气液能够充分发展并均匀地进入波纹板圆弧段。波纹板单通道计算区域见图 4,其用于分析各因素对分离效率的影响。
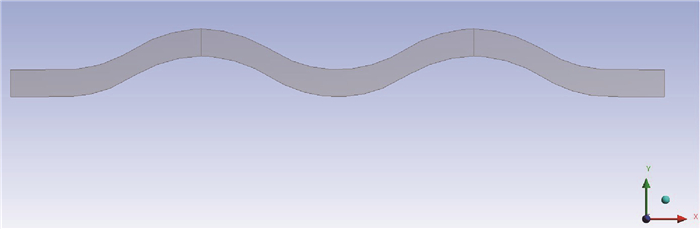
|
| 图 4 波纹板单通道计算区域示意图 Fig.4 Schematic diagram of the calculation area of the single-pass corrugated plate |
考虑每块波纹板厚度、分离器壁面以及流体的入射角度,建立一种与实际波纹板排布更为贴合的多通道模型,其计算区域见图 5。

|
| 图 5 波纹板多通道计算区域示意图 Fig.5 Schematic diagram of the calculation area of the multi-pass corrugated plate |
建立几何模型后,对于波纹板之间的流道采用非结构化网格技术进行网格划分,在波纹板的进出口处采用结构化网格划分,以达到网格规整的目的。波纹板单通道网格划分见图 6。

|
| 图 6 波纹板单通道计算区域网格划分图 Fig.6 Grid division of calculation area of the single pass of corrugated plate |
以波纹板流道入口流速3 m/s的工况为例,对波纹板流道进和地网格划分并做无关性验证,分析不同网格数量时各计算参量的差异,结果见表 1,以选择适合于波纹板流道的最佳网格划分方式。
| 网格数量 | 压降/Pa | 最大速度/(m·s-1) |
| 9 672 | 9.72 | 4.04 |
| 23 276 | 10.03 | 4.14 |
| 161 694 | 11.05 | 4.23 |
| 276 213 | 11.13 | 4.29 |
| 361 738 | 11.20 | 4.30 |
通过比较各组网格计算结果的差异,充分考虑计算机性能以及其他因素,选取网格数量161 694来对波纹板进行网格划分。
2.2 边界条件与求解方法 2.2.1 边界条件采用甲烷代替测试平台采出的页岩气,选择水作为均匀分布于气流中的离散相。气相的入口边界条件设置为速度入口,速度参数分别为2、3、4、5、6、7、8和9 m/s,气流在入口界面速度分布均匀。气相的出口边界条件设置为压力出口。选择液滴作为离散相均匀分布于气流中,液滴的入口边界条件设置为速度入口,且液滴速度与气相流速相同,均匀喷射进入波纹板流道。气液两相的入口与出口边界条件均选择“ESCAPE”类型,波纹板壁面的边界条件选择“TRAP”类型。
2.2.2 计算方法在波纹板内部流动中,携液气流作为连续相,而液滴作为离散相。为了获得精确的模拟结果,选择适用于此流场工况的RNG k-ε计算模型。对于作为离散相的液滴,选用DPM模型,初始时均匀分散于气流中的液滴从波纹板入口界面均匀喷射进入波纹板流道。
3 气相流场的模拟结果与分析为了对模拟结果进行直观分析,将波纹板流道空间划分为6个区域,如图 7所示。流体自波纹板流道入口进入第一段弯折区域A与A′,在第一段弯道区域终点处即为平缓区B与B′,在此区域流体流速变化方向发生转向,平缓区结束之后流体进入第二段弯折区域C与C′,当流体流出第二段弯道后进入波纹板的第二级波段,波纹板后续的波形流道区域均与第一级重复。气相流场模拟结果如图 8~图 12所示。
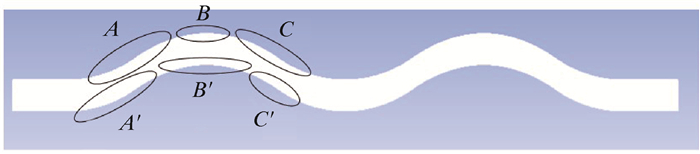
|
| 图 7 波纹板流道空间区域划分 Fig.7 Space division of the corrugated plate flow passes |
|
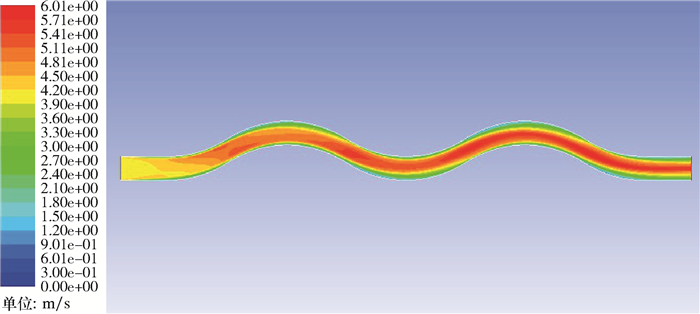
| 图 8 波纹板流道在入口流速4 m/s、板间距20 mm时的气相速度场 Fig.8 Velocity field of the gas phase in the corrugated plate flow pass at an inlet flow of 4 m/s and a plate spacing of 20 mm |
|
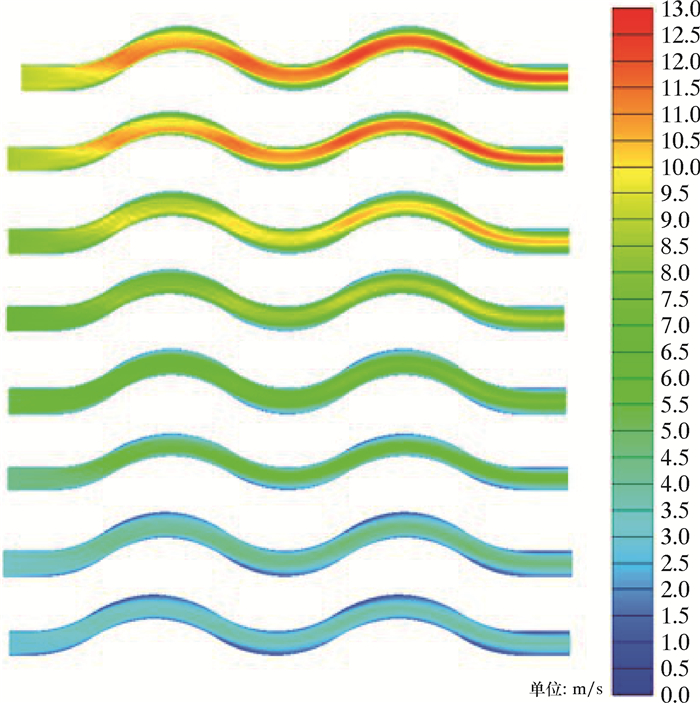
| 图 9 波纹板流道在板间距20 mm、不同入口流速时的气相速度云图(入口流速由下至上依次为2、3、4、5、6、7、8和9 m/s) Fig.9 Velocity nephogram of the gas phase in the corrugated plate flow pass at a plate spacing of 20 mm and different inlet flows(from bottom to top: 2, 3, 4, 5, 6, 7, 8 and 9 m/s) |
|
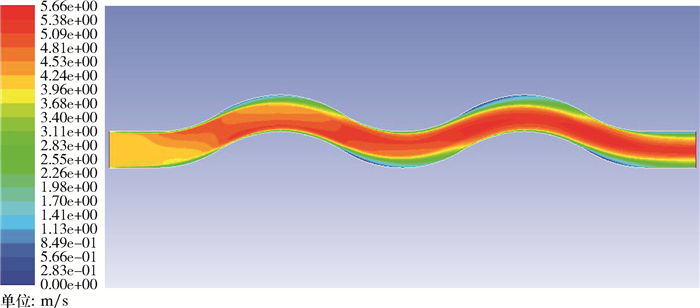
| 图 10 波纹板流道在入口流速4 m/s、板间距30 mm时的气相速度场 Fig.10 Velocity field of the gas phase in the corrugated plate flow pass at an inlet flow of 4 m/s and a plate spacing of 30 mm |

|
| 图 11 波纹板流道在入口流速4 m/s、不同板间距时的气相速度云图(波纹板间距从下至上依次为10、20和30 mm) Fig.11 Velocity nephogram of the gas phase in the corrugated plate flow mass at an inlet flow of 4 m/s and different plate spacing (the corrugated plate spacing from bottom to top is 10 mm, 20 mm and 30 mm respectively) |
|
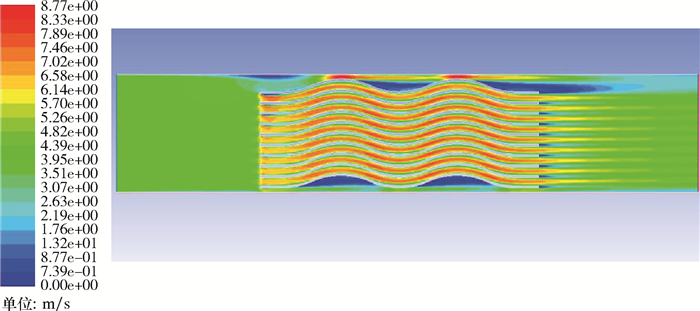
| 图 12 多流道波纹板在入口流速4 m/s时的气相速度场 Fig.12 Velocity field of the gas phase in the multi-pass corrugated plate at an inlet flow of 4 m/s |
3.1 不同入口流速时的气相流场分析
由图 8可见,气流在波纹板流道入口界面处的速度均匀分布,在A′区域壁面附近出现一个较厚的低速区,该区域的气流速度小于入口流速,而在A区域壁面附近出现一个较厚的高速区。在进入波纹板波峰段时,在B′区域入口近壁面处出现一个速度峰值,在B区域壁面附近出现一个较厚的低速区。在C、C′弯曲段区域内,靠近C壁面处的气流速度大于C′区域壁面处的气流速度。在波纹板流道的出口截面水平段靠近波纹板壁面处出现较厚的低速区,而在流道中部的气流速度逐渐呈均匀分布。
由图 9可见,不同流速条件下速度场的变化规律相似,随着波纹板入口气流速度的增加,流道内部低速区的位置未发生改变,仅速度大小发生改变,速度峰值的区域增大,速度峰值总是在流道内部各变化区域的交接处出现,且随着波纹板级数的增加,流速总体变大,波纹板弯曲流道内气流产生了一个加速效果。
3.2 不同板间距时的气相流场分析由图 10和图 8对比可见,随着波纹板间距的增加,其流道内部形成的低速区变厚,在靠近波纹板壁面处的低速区气流速度下降更明显,甚至出现气流速度为0的区域。
由图 11可见,随着波纹板间距的减小,气流在波纹板流道中的运动规律相似,但波纹板流道每个波段的加速效果明显增强,弯曲段的影响段变长,气流进入弯道前的加速点靠前,加速区域形状变狭长。
3.3 多通道内的气相流场分析由图 12可见,气流在进入波纹板时部分气流会撞击波纹板壁而分成两股流体进入同一块波纹板的两侧流道内,气流在进入波纹板每个流道时都存在一个入射角,故在波纹板流道入口界面处有一个加速效果。在上侧波纹板波峰与分离器壁面之间的流道变窄,在此区域内气流产生一个较大的加速段,波纹板波谷附近的气流存在流速为0的区域,在此区域内气流形成漩涡。在下侧波纹板与分离器壁面之间的流道内气流速度几乎无变化,在此区域的凹陷处形成漩涡。
4 液相流场的模拟结果与分析
|
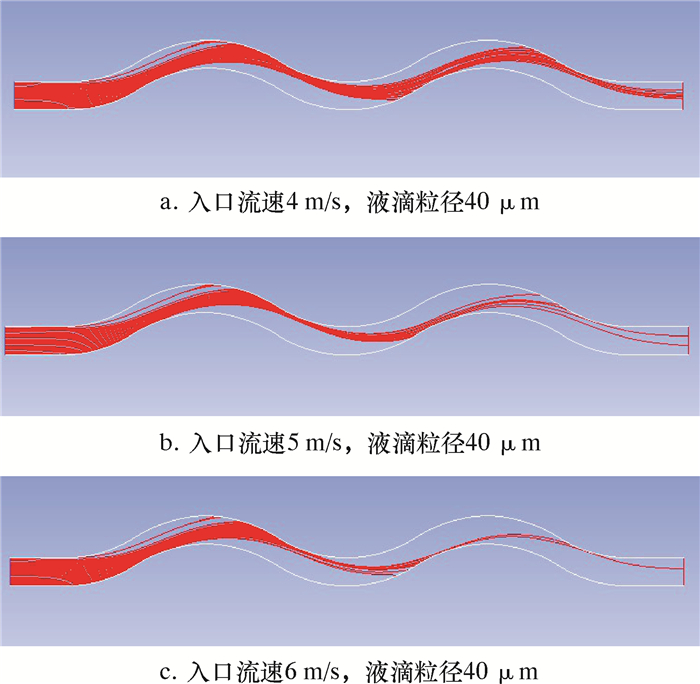
| 图 13 在不同入口流速、板间距20 mm时液滴的运动轨迹 Fig.13 Motion tracks of liquid droplets at different inlet flow and a plate spacing of 20 mm |
|
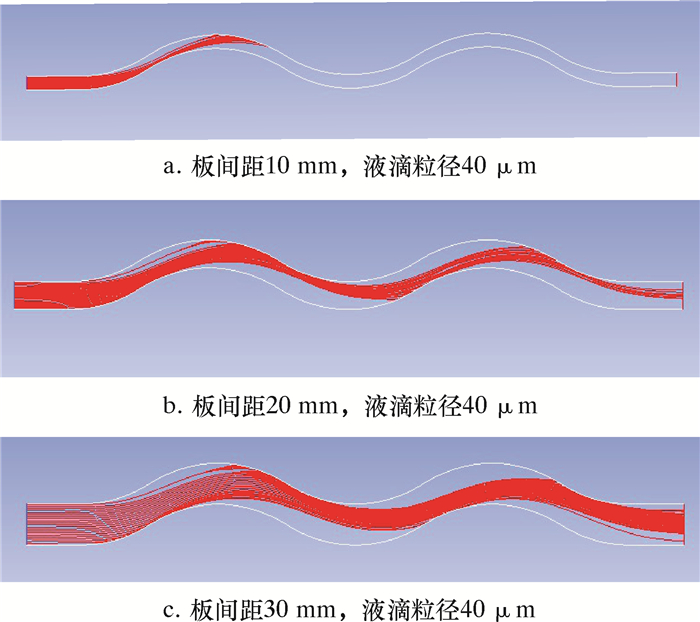
| 图 14 在不同板间距、入口流速4 m/s时液滴的运动轨迹 Fig.14 Motion tracks of liquid droplets at different plate spacing and an inlet flow of 4 m/s |
|
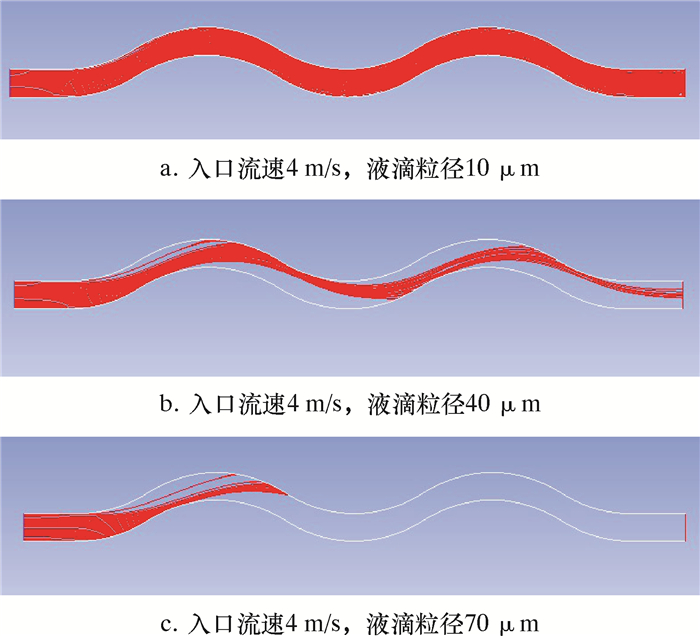
| 图 15 在不同液滴粒径、入口流速4 m/s时液滴的运动轨迹 Fig.15 Motion tracks of liquid droplets of different sizes at an inlet flow of 4 m/s |

|
| 图 16 多流道波纹板在入口流速4 m/s时液滴的运动轨迹 Fig.16 Motion tracks of liquid droplets in multi-pass corrugated plate at an inlet flow of 4 m/s |
4.1 不同入口流速时的液相运动分析
由图 13可见,波纹板流道内液滴的运动轨迹与气流的高速分布区域基本相同,表明气流的加速效果会使其对液滴的携带作用增强。随着波纹板入口流速的增加,分散于气相中的液滴由于气流的加速效果产生更大的惯性力,进而在第一个波段与波纹板壁面发生更多的碰撞。液滴在波纹板入口处均匀分布,大部分液滴在第一个波段撞击A′、B′和C区域壁面而被其吸附分离,小部分液滴进入波纹板A、B和C′区域壁面附近的低速区。这是因为在B′区域壁面和C壁面附近出现一个速度峰值,所以在波纹板流道内气流的高速区,液滴随着气流一起产生加速效应,从而获得更大的惯性而偏离主流方向;虽然在靠近A区域壁面出现一个速度峰值,但由于受波纹板入射角和壁厚的影响,液滴更易与波纹板A′区域板壁发生碰撞。
4.2 不同板间距时的液相运动分析由图 14可见,在较大板间距的流道内,由于流通截面较大,则液滴在气流的携带作用下能够在较大的空间内完成流速方向的变化,从而避免与波纹板壁面发生碰撞。
4.3 不同粒径时的液相运动分析由图 15可见,当液滴粒径增加时,由于液滴惯性变大,气流的携带作用对其流动方向变化所产生的影响减小,出现向气流高速区集中的现象,其偏离气流主流方向的效果明显增强,液滴与波纹板壁面发生碰撞的可能性也增大。
由图 15c可见,当入口流速为4 m/s、液滴粒径为70 μm时,液滴在第二波段基本无分布,与较低粒径液滴相比,其分离效果显著提高。
4.4 多通道内的液相运动分析由图 16可见,多流道波纹板内液滴的运动规律与单通道内液滴的运动规律相似,波纹板多流道内液滴的运动主要集中于流道内部的高速区,但由于多通道内各流道受其不同入射角和波纹板壁厚的影响,液滴更易与波纹板A′区域板壁发生碰撞,这也表明气流的加速效果会增强其对液滴的携带作用。由此可知,增加气流速度或减小波纹板间距可以改善波纹板的分离性能。
5 波纹板气液两相分离效率分析
|
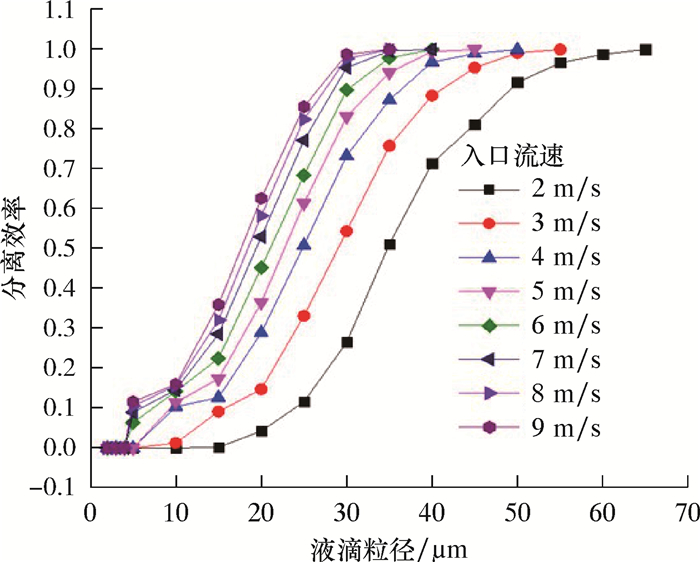
| 图 17 波纹板流道在板间距20 mm时气液两相的粒级效率曲线 Fig.17 Grade efficiency curves of the gas/liquid phases in the corrugated plate flow pass at a plate spacing of 20 mm |
|
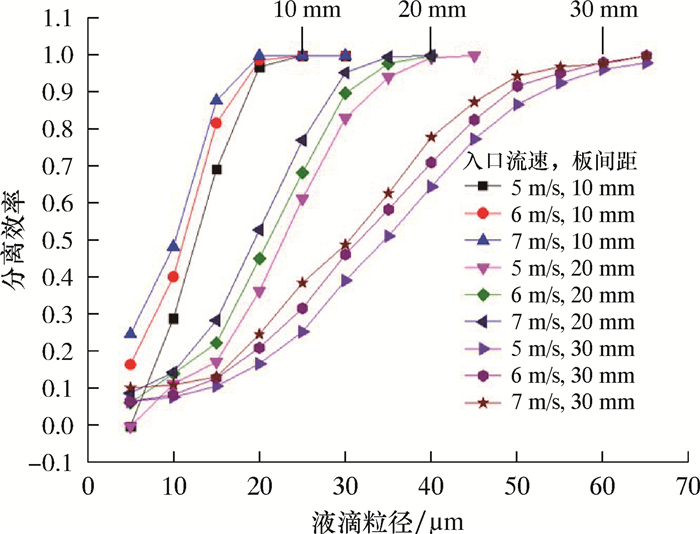
| 图 18 波纹板流道在不同板间距时气液两相的粒级效率曲线 Fig.18 Grade efficiency curves of the gas/liquid phases in the corrugated plate flow pass at different plate spacing |
|
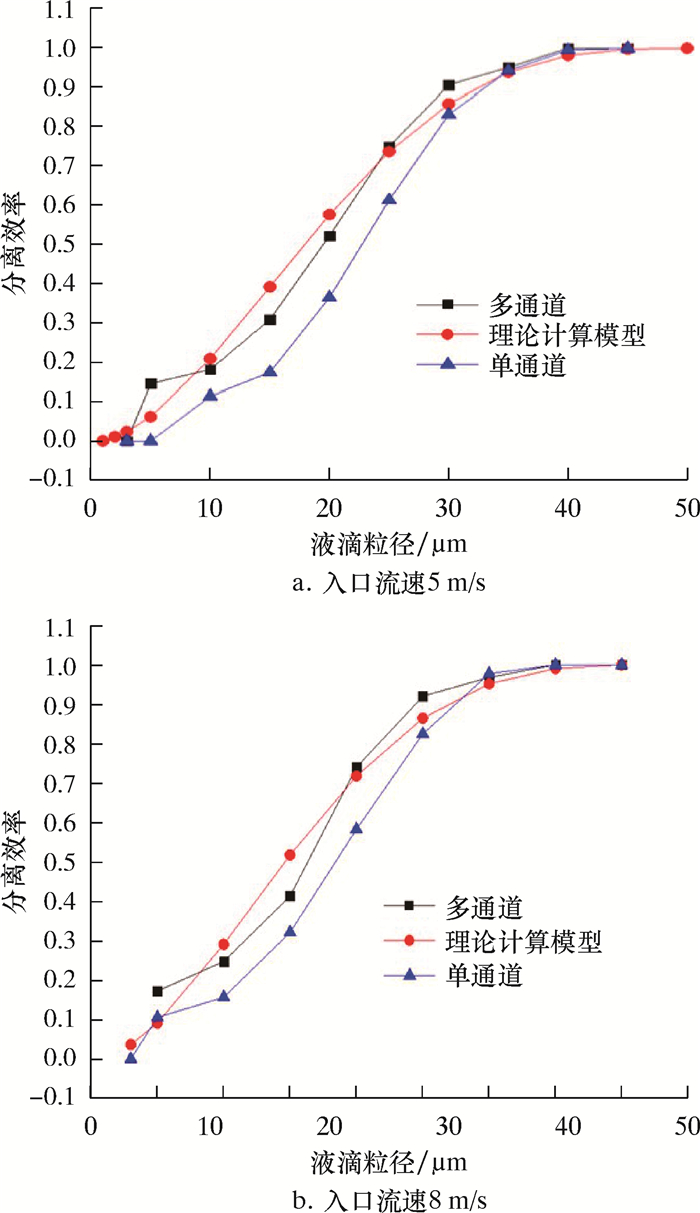
| 图 19 在板间距20 mm时波纹板分离效率理论值与数值模拟值的对比曲线 Fig.19 Comparison of theoretical value and numerical simulation value of the corrugated plate separation efficiency at a plate spacing of 20 mm |
5.1 不同入口流速时的气液分离效率分析
由图 17可见:当液滴粒径不变时,随着波纹板入口流速的增大,分离效率升高,而其流速超过波纹板极限流速时就会产生二次携带问题,波纹板的分离效率就会迅速下降;当波纹板入口流速一定时,随着液滴粒径的增大,波纹板的分离效率升高;但当液滴粒径为5~10 μm时,波纹板的分离效率曲线处于低效段,随着粒径的增加,分离效率变化不明显,波纹板入口流速的提高对分离效率的影响较小;而当液滴粒径大于10 μm时,波纹板的分离效率曲线进入敏感段,随着粒径的增加,分离效率变化较明显,最高可达90%,波纹板入口流速的提高对分离效率的影响较大,且该曲线的敏感点左移。
5.2 不同板间距时的气液分离效率分析由图 18可知:当液滴粒径小于5 μm时,波纹板的粒级效率曲线效率处于低效段,缩小波纹板间距无法显著提高其分离效率;而当液滴粒径大于5 μm时,缩小波纹板间距可以明显改善分离器性能。一方面,缩小波纹板间距可以左移分离效率曲线中的敏感点;另一方面,缩小波纹板间距还可以使分离效率曲线中的敏感段长度缩短、斜率增大,但波纹板板间距过小也会增加气流压降,增加运行能耗,使波纹板之间更易发生堵塞而不易清洗。
5.3 分离效率理论值和模拟值对比分析由图 19可见,在液滴粒径0~5 μm低效段,多通道分离效率理论计算值与其数值模拟值很接近,液滴流速与粒径的变化对分离效率的影响不明显。多流道分离效率数值模拟值总是略高于单流道分离效率数值模拟值,多流道呈现出了低效段、敏感段等分离效率变化特点,多流道与单流道数值模拟得到的敏感点几乎相同。多流道分离效率理论计算值总是略高于单流道分离效率数值模拟值,分离效率理论计算值的敏感点比其数值模拟值的敏感点略小,导致这种情况的主要原因是:在进行公式推导的过程中对于复杂流道空间进行了一定简化,对于复杂流动工况进行了一定的假设,这些条件的简化对于推导结果造成了一定的偏差。多流道分离效率数值模拟值与其理论计算值更贴近实际值,前两者之间的最大误差为10%左右。在数值模拟与理论推导的过程中均没有考虑液滴相的蒸发等现象,也没有考虑实际分离器中各部分零件对流道产生的影响,故多流道分离效率的理论计算值与数值模拟值比实际分离效率略小。
对比图 19a与图 19b可知,当入口流速增加时,波纹板分离效率也整体升高,并使分离效率曲线敏感点左移,即达到相同分离效率时的液滴粒径减小。
6 结论(1) 在一定范围内增加波纹板入口流速或减小板间距,波纹板流道内气流的加速效果明显增强。
(2) 波纹板流道内液滴的运动轨迹与气流的高速分布区域基本符合,表明气流的加速效果会使其对液滴的携带能力增强。
(3) 在一定范围内,波纹板入口流速越高、板间距越小或液滴粒径越大,波纹板流道内的液滴与其壁面发生碰撞的可能性越大。
(4) 波纹板分离器的粒级效率曲线存在一个敏感点,即当液滴粒径小于5 μm时,粒级效率曲线走势平缓;当液滴粒径为10~50 μm时,粒级效率曲线变陡峭,增加波纹板入口流速或减小板间距可使曲线敏感点左移,并可使曲线斜率增大;当液滴粒径大于50 μm时,波纹板分离效率最高可达90%。
(5) 波纹板多流道分离效率数值模拟值和理论计算值总是略高于单流道分离效率数值模拟值,前两者之间的最大误差为10%左右,从而验证了波纹板分离效率理论计算方法的可靠性。
| [1] |
荣莽, 罗君. 页岩气藏水平井分段压裂管柱技术探讨[J]. 石油机械, 2010, 38(9): 65-68. RONG M, LUO J. Discussion on the technology of staged fracturing string in horizontal well of shale gas reservoir[J]. China Petroleum Machinery, 2010, 38(9): 65-68. |
| [2] |
唐颖, 张金川, 张琴, 等. 页岩气井水力压裂技术及其应用分析[J]. 开发工程, 2010, 30(10): 33-38. TANG Y, ZHANG J C, ZHANG Q, et al. Hydraulic fracturing technology for shale gas wells and its application analysis[J]. Development Engineering, 2010, 30(10): 33-38. |
| [3] |
尤道繁, 颜大军, 郑玉龙. 试井用分离测试装置的研制[J]. 油田地面工程, 1993(1): 50-54. YOU D F, YAN D J, ZHENG Y L. Development of separation test equipment for well testing[J]. Oilfield Surface Engineering, 1993(1): 50-54. |
| [4] |
SIMMONS M J H, KOMONIBO E, AZZOPARDI B J, et al. Residence time distributions and flow behaviour within primary crude oil-water separators treating well-head fluids[J]. Chemical Engineering Research & Design, 2004, 82(10): 1383-1390. |
| [5] |
王胜, 王伟, 史仕荧, 等. 轴流式旋流油水分离器分离性能影响研究[J]. 石油机械, 2018, 46(5): 99-104. WANG S, WANG W, SHI S Y, et al. Study on the separation performance of axial-flow hydrocyclone oil-water separator[J]. China Petroleum Machinery, 2018, 46(5): 99-104. |
| [6] |
贺会群, 杨振会, 吴刚, 等. 油水旋流分离器流场模拟分析与研究[J]. 石油机械, 2005, 33(12): 1-5. HE H Q, YANG Z H, WU G, et al. Simulation analysis and research on flow field of oil-water cyclone separator[J]. China Petroleum Machinery, 2005, 33(12): 1-5. DOI:10.3969/j.issn.1001-4578.2005.12.001 |
| [7] |
曾润奇, 杨毅. 油水旋流分离器流场数值模拟研究[J]. 石油机械, 2011, 39(1): 24-27. ZENG R Q, YANG Y. Numerical simulation offlow field in oil-water cyclone separator[J]. China Petroleum Machinery, 2011, 39(1): 24-27. |
| [8] |
张瑞霞, 王继飞, 田启忠, 等. 井下旋流油水分离器仿真研究[J]. 石油机械, 2013, 41(11): 105-109. ZHANG R X, WANG J F, TIAN Q Z, et al. Research on the simulation of downhole oil-water cyclone separator[J]. China Petroleum Machinery, 2013, 41(11): 105-109. DOI:10.3969/j.issn.1001-4578.2013.11.025 |
| [9] |
张银鸽, 于萍, 刘士雷. 聚结构件倾角对分离器分离效果影响的数值模拟[J]. 石油矿场机械, 2013, 42(3): 42-45. ZHANG Y G, YU P, LIU S L. Effect of coalescence component dip angle on separation in separator[J]. Oil Field Equipment, 2013, 42(3): 42-45. DOI:10.3969/j.issn.1001-3482.2013.03.009 |
| [10] |
JAMES P W, WANG Y, AZZOPARDI B J, et al. The role of drainage channels in the performance of wave-plate mist eliminators[J]. Chemical Engineering Research & Design, 2003, 81(6): 639-648. |
| [11] |
樊水冲, 杨学忠, 郭勇. 波纹板除雾器流场与效率的数值计算[J]. 炼油与化工, 2006(2): 5-10. FAN S C, YANG X Z, GUO Y. Numerical calculation of flow field and efficiency of corrugated plate defogger[J]. Refining and Chemical Industry, 2006(2): 5-10. DOI:10.3969/j.issn.1671-4962.2006.02.003 |
| [12] |
徐淑君, 姚征, 朱懿渊. 波纹板除雾器两相流动的数值模拟与分析[J]. 上海理工大学学报, 2007, 29(3): 275-280. XU S J, YAO Z, ZHU Y Y. Numerical simulation on two phase flow in demister with corrugated baffle[J]. Journal of University of Shanghai for Science and Technology, 2007, 29(3): 275-280. DOI:10.3969/j.issn.1007-6735.2007.03.016 |
| [13] |
GALLETTI C, BRUNAZZI E, TOGNOTTI L. A numerical model for gas flow and droplet motion in wave-plate mist eliminators with drainage channels[J]. Chemical Engineering Science, 2008, 63(23): 5639-5652. DOI:10.1016/j.ces.2008.08.013 |
| [14] |
RAFEE R, RAHIMZADEH H, AHMADI G. Numerical simulations of airflow and droplet transport in a wave-plate mist eliminator[J]. Chemical Engineering Research and Design, 2010, 88(10): 1393-1404. DOI:10.1016/j.cherd.2010.03.001 |
| [15] |
VENKATESAN G, KULASEKHARAN N, INIYAN S. Design and selection of curved vane demisters using Taguchi based CFD analysis[J]. Desalination, 2014, 354: 39-52. DOI:10.1016/j.desal.2014.09.018 |
| [16] |
张立峰.波纹板内气液分离流场的数值模拟研究[D].西安: 西安石油大学, 2015. ZHANG L F. Numerical simulation of gas-liquid separation flow field in corrugated plates[D]. Xi' an: Xi' an Shiyou University, 2015. |
| [17] |
胡雪飞.波纹板气液分离器性能的实验与模拟研究[D].北京: 中国石油大学(北京), 2016. HU X F. Experimental and CFD study on performance of corrugated plate gas-liquid separator[D]. Beijing: China University of Petroleum (Beijing), 2016. |
| [18] |
曾金鹏, 李嘉.波纹板汽水分离器的数值模拟与分析[C].华中科技大学制冷空调研究生学术年会.武汉: 华中科技大学出版社, 2013. ZENG J P, LI J. Numerical simulation and analysis of corrugated separator[C]. Huazhong University of Science and Technology Refrigeration and Air Conditioning Graduate Academic Annual Meeting. Wuhan: Huazhong University of Science & Technology Press, 2013. |



