2. 中海油研究总院有限责任公司
2. CNOOC Research Institute Co., Ltd
0 引言
近年来,我国对石油能源的需求不断增长,加之陆上石油的日益短缺,使得海洋石油的开发成为必然。水下生产系统以其可靠性高、建设成本低及受灾害天气影响小等优势,成为深水油气田开发的必然选择[1-3]。在水下生产系统开发过程中,与其相关的水下装备(如采油树、水下管汇、PLET和吸力锚基础等)下放安装作业时所处工况恶劣,尤其在水下结构物穿越飞溅区阶段存在着强非线性流固耦合现象,易导致结构物发生变形或弯曲等结构损坏。因此有必要在安装设计阶段,通过理论公式、水池试验及数值模拟等方法预测水下结构物在海上下放安装作业时的动力响应及运动响应[4-6]。
水下结构物结构行为及运动响应规律预测的基础是精确获取结构物水动力系数(阻力系数Cd和附加质量系数Ca)等基础数据。通过经验公式获取形状较为复杂的结构物水动力系数时难度及误差均较大,于是水动力系数的常用获取方法主要集中于水池试验及数值模拟(CFD)。S.AN等[7]设计了一套试验装置,通过开展多孔矩形板的强迫振荡试验,研究了垂直振荡时阻力系数及附加质量系数。王庆云等[8]采用基于三角形网格的面元法程序和循环水槽操纵性试验两种方法获得系列舵翼缩比模型的水动力系数,研究了不同雷诺数下舵角水动力系数的变化趋势。姚晓杰等[9]通过试验研究了波浪要素对水平固定圆柱杆件水动力系数的影响,并基于改造的莫里森方程,计算了不同波浪要素下水动力系数的取值。
水池试验的优势在于预测精度高、计算结果可靠,但其研究成本较大,试验周期较长,对于外形复杂的结构物其试验模型制作较为困难,于是大多数学者通过CFD方法开展水动力系数的研究。朱仁传等[10]以计算流体力学理论为基础,提出了流场数值模拟并直接分析求取船舶附加质量与阻尼的方法,基于FLUENT平台的二次开发,对S175的二维横剖面绕流进行了数值模拟计算。汤珂等[11]通过流体动力学软件FLUENT建立了管汇的水动力计算模型,求得管汇非惯性水动力系数,并将数值结果与DNV经验数据进行比较和结果分析,验证了方法的有效性。黄致谦等[12]将分形理论应用于垂荡板的结构设计,提出了一种具有分形特征孔的垂荡板,运用FLUENT的自定义函数并结合动网格技术对不同垂荡板模型进行数值模拟,研究了其水动力特性。戚昱等[13]通过FLUENT中的UDF技术与动网格模型,模拟水下管汇的匀速运动与加速运动,得到了管汇的水动力系数。水下结构物大多为管阀结构,但目前尚未有关于此类特征结构的水动力系数特性的研究。为此,本文采用VOF方法标记气-液两相流体,捕捉自由表面,利用重叠网格技术模拟二维简化管阀结构在自由液面位置的强迫振荡运动,通过数值计算求解气液两相流动的雷诺时均方程,系统地分析Kc数、振荡频率、管阀长度比及管阀高度比对管阀结构水动力系数的影响。所得结果对水下结构物下放安装过程中结构行为及运动规律的精准预测具有指导作用。
1 研究对象及计算模型 1.1 研究对象本文以水下管阀结构为研究对象,研究其在飞溅区做强迫振荡时的水动力系数。以实际水下管汇(见图 1)为基础,建立其内部管阀结构的二维简化模型,即忽略结构物宽度方向的影响,以减小数值模拟的计算量。

|
| 图 1 水下管汇主视图 Fig.1 Front view of subsea manifold |
二维管阀结构、空气域、水域及前景网格域等几何模型的详细尺寸如图 2所示,流体区域覆盖了结构物运动的整个区间。为消除流场壁面边界对结构物产生的池壁效应,根据无界流场概念及计算的需要,设置流场与结构物整体尺寸之比不小于10:1。在使用重叠网格模拟管阀结构强迫振荡运动时,为保证数值计算的精确度,应使前景网格与背景网格之间具有较大的重叠面积,确保两者之间的网格重叠数大于4层,故本文建模设置的前景网格尺寸为16 m×12 m。

|
| 图 2 二维管阀结构物强迫振荡数值计算模型 Fig.2 Numerical calculation model of forced oscillation of 2D pipe-valve structure |
1.2 控制方程
本文采用的控制方程为连续方程及动量方程,并通过VOF方法计算自由液面位置。对于不可压缩的气-液两相流动,两者密度均视为常数。
连续方程:

|
(1) |
动量方程:

|
(2) |
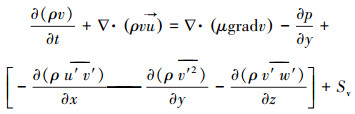
|
(3) |

|
(4) |
式中:ρ=α1ρ1+(1-α1)ρ2,为气-液两相混合物的密度;α1∈[0, 1],为水的体积分数;ρ1为水密度;α2∈ 0, 1,α2=1-α1,为空气体积分数;ρ2为空气密度;
方程(1)为时均形式的连续方程,方程(2)~方程(4)为时均形式的动量方程。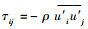
这里通过Realizable k-ε湍流模型使控制方程封闭,关于k和ε的运输方程如下:
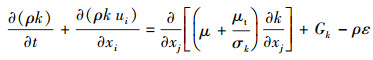
|
(5) |

|
(6) |
式中:k为湍流动能,υ为运动黏度,ε为湍动耗散率,C2=1.9、σk=1.0、σε=1.2,均为经验常数。
1.3 边界条件及数值方法因需要模拟结构物随时间变化的强迫振荡运动,故数值计算采用基于压力的瞬态求解。将水下管阀结构及流体域的左、右及下侧边界设置为无滑移壁面,流体域上侧边界设为压力出口,出口压力为标准大气压,将前景网格区域四周的边界条件设置为Overset。在流体域内,水的密度为1 025.9 kg/m3,空气密度为1.225 kg/m3,因固体运动速度较慢,于是将水及空气均视为不可压缩流体。
通过有限体积法对基于VOF方法的雷诺平均方程进行时间及空间上的离散,压力与速度的耦合采用Coupled算法。采用二阶迎风格式计算湍流动能及湍动耗散率,采用PISO算法对压力项进行离散,并且通过Geo-Reconstruct格式对自由液面进行重构。
1.4 重叠网格相比于其他动网格,重叠网格简化了网格生成过程,采用两套网格(前景网格和背景网格)可以有效避免计算过程中因网格重构产生的负体积[14]。另外,通过前景网格能够更方便地对结构物的运动进行描述,并在计算过程中始终保持较高的网格质量。重叠网格划分如图 3所示。这里两套网格的网格重叠数大于4层,且两者尺寸一致,网格划分质量较高。两套网格之间耦合关系的建立主要分为挖洞、寻点及插值3个步骤[15]。

|
| 图 3 重叠网格划分 Fig.3 Partition of overlapping grids |
2 数值计算 2.1 水下管阀结构强迫振荡运动
水下生产设备在穿越飞溅区过程中,因波浪载荷垂直作用在结构物之上,会使之发生类似于正弦函数的振荡运动。本文基于重叠网格技术与自定义运动函数程序,进行水下管阀结构在飞溅区(气-液交界面)做强迫振荡运动的数值模拟,其垂直方向上的振荡位移函数如式(7)~式(9)所示。

|
(7) |

|
(8) |

|
(9) |
式中:a为强迫振荡运动的振幅,f为振荡频率,ω为圆频率,T为振荡周期,x(t)为随时间变化的位移函数。
仿真模型参数如下:Kc=0.012 6~0.062 8,振幅a=0.02、0.04、0.06、0.08及0.10 m,频率f=2、4、6、8和10 Hz,管阀长度比为0.1、0.3、0.5和0.7,管阀高度比为1.0、1.2、1.4和1.6。
水下结构物在强迫振荡过程中所受到的水动力主要取决于Kc数及频率数β(无量纲参数),两个参数的定义如下:

|
(10) |

|
(11) |
式中:L为二维水下管阀结构的特征尺寸,这里取为管道长度10 m;υ为水的运动黏度,这里取υ=1.225×10-5 m2/s。
通过数值模拟可以获取水下管阀结构强迫振荡过程中受到的流体水动力F(t),其主要由惯性力Fa(t)以及非惯性力Fd(t)两部分构成,表达式如下所示。

|
(12) |

|
(13) |
式中:Ca为结构物附加质量系数;Cd为阻力系数;
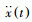

|
(14) |

|
(15) |
选择用于下文计算的合适网格尺寸,以验证所提出的数值方法的正确性。本节基于DNV经验数据中的二维矩形模型[16],详细参数如表 1所示。选择e/b=1的二维模型开展网格收敛性研究。
| 二维截面形状 | e/b | 结构物运动方向 | 附加质量系数 |
 |
2.0 | 垂直方向 | 1.36 |
| 1.0 | 1.51 | ||
| 0.5 | 1.70 |
建立最小网格尺寸l分别为0.7、0.6、0.5及0.4 m的结构物强迫振荡计算模型,其网格数量分别为4 100、5 539、7 952及12 457,计算所得的流体水动力如图 4所示。由图 4可知,网格尺寸较为粗糙时所预测的水动力幅值较大。通过式(14)可得4种不同网格尺寸下二维矩形结构附加质量系数分别为1.76、1.66、1.59及1.57。图 5为网格细化对附加质量系数预测精度的影响。由图 5可知,计算值与DNV经验值之间的误差分别为16.6%、9.93%、5.30%和3.97%,即网格尺寸越小,预测结果越精确,网格收敛性可以得到保证。本文同时考虑计算精度与计算效率的影响,选择0.5 m的网格尺寸用于下文计算。

|
| 图 4 不同网格尺寸下强迫振荡水动力预测 Fig.4 Prediction of hydrodynamic forces of forced oscillations in different grid sizes |

|
| 图 5 网格细化对附加质量系数预测精度的影响 Fig.5 Influence of grid refinement on prediction accuracy of added mass coefficient |
选择长宽之比e/b分别为2.0、1.0和0.5验证数值方法的正确性,通过编程设置结构物的运动位移函数,获取其受力时历曲线,根据式(14)得到其附加质量系数分别为1.42、1.59和1.81,计算结果略高于相应的DNV经验数据,如图 6所示,误差分别为4.41%、5.30%和6.47%,均在10%以内。由此可知,此数值计算模型具有较高的精确性及可靠性。

|
| 图 6 DNV经验数据与数值计算结果对比 Fig.6 Comparison between DNV' s empirical data and numerical calculation results |
3 结果与讨论
利用所提出的数值计算方法,改变Kc数、振荡频率、管阀长度比、管阀高度比,分别获得相应的附加质量系数与阻力系数,研究不同参数对结构物水动力系数的影响。
3.1 Kc数与振荡频率的影响设置结构物强迫振荡振幅为0.02~0.10 m,振荡频率为2~8 Hz,即Kc数为0.012 6~0.062 8。图 7与图 8分别表示不同频率下附加质量系数Ca以及阻力系数Cd随Kc数的变化关系。由图 7可知,附加质量系数Ca随着Kc数的增加而逐渐增大,且两者基本呈线性关系。随着振荡频率的增加,附加质量系数略有增加,但整体增幅很小,基本可以忽略,即结构物振荡频率与其附加质量系数两者相互独立。与附加质量系数相反(见图 8),结构物阻力系数Cd随着Kc数的增加逐渐减小,并且当Kc < 0.03时,Cd值下降较为迅速,随后降幅开始减缓,逐渐趋于稳定。同时,当Kc < 0.04时,振荡频率对Cd值影响较大,且Cd随着振荡频率的增大而增大;当Kc>0.04时,频率对Cd的影响逐渐减弱,两者基本呈独立关系。

|
| 图 7 不同振荡频率下Ca随Kc数的变化关系 Fig.7 Variation of Ca with Kc number under different oscillation frequencies |

|
| 图 8 不同振荡频率下Cd随Kc数的变化关系 Fig.8 Variation of Cd with Kc number under different oscillation frequencies |
由此可知,在结构物做强迫振荡运动时,水动力系数Ca与Cd的主要影响因素为Kc值,主要原因为Kc值与结构物-流体间的相对运动振幅联系紧密,如式(10)所示。管阀结构在强迫振荡过程中会出现漩涡脱落现象,脱落模式是影响水动力系数的主要因素,且脱落模式主要取决于Kc数与结构物的尺寸形状[17]。
3.2 管阀长度比的影响二维管阀结构示意图如图 9所示。本节保持管道长度L=10 m不变,通过改变阀门长度La,研究管阀长度比RL(La/L)的变化对水动力系数Ca和Cd的影响。不同长度比条件下附加质量系数Ca随Kc数的变化情况如图 10所示。为了保证研究结果的可靠性,这里分别在振荡频率为f=4与8 Hz下开展相关数值模拟。由图 10可知,Ca随着管阀长度比的增加而增大,主要原因是随着长度比的增加,结构物的体积逐渐增大,其周围附加的流体质量亦随之增大,从而附加质量系数逐渐增加。ZHANG S.N.等[18]研究的多体垂荡板强迫振荡运动中也出现过相同的现象,当上下两板间距离增加时,两板间所聚集的流体附加质量增加,从而结构物附加质量系数变大。不同管阀长度比下Cd随Kc数的变化关系如图 11所示。由图 11可知,与附加质量系数相反,长度比在0.1~0.7范围内,结构物的阻力系数受长度比的影响较小,两者呈相互独立关系。设置结构物强迫振荡振幅为0.02 m,振荡频率为2 Hz,仅改变管阀长度比,观察结构物周围漩涡脱落情况。在计算500时间步之后,如图 12所示,当管阀长度比在0.1~0.7范围内时,结构物形状的变化并未显著影响强迫振荡过程中的漩涡脱落模式,漩涡脱落均发生在管道左、右端尖角位置,且大小基本相同,在阀门周围并未出现明显的漩涡脱落现象。由此可知,阻力系数仅受Kc值的影响,随Kc数的增加而下降,而在同一Kc值下不同管阀长度比对阻力系数基本无影响。

|
| 图 9 二维管阀结构示意图 Fig.9 Schematic diagram of the 2D pipe-valve structure |

|
| 图 10 不同管阀长度比下Ca随Kc数的变化关系 Fig.10 Variation of Ca with Kc number at different pipe-valve length ratios |

|
| 图 11 不同管阀长度比下Cd随Kc数的变化关系 Fig.11 Variation of Cd with Kc number at different pipe-valve length ratios |

|
| 图 12 不同管阀长度比结构物周围瞬时漩涡脱落情况 Fig.12 Transient vortex shedding around structures with different pipe-valve length ratios |
3.3 管阀高度比的影响
如图 9所示,本节保持管道高度(管道直径)c=1 m不变,通过改变阀门高度Lb,研究管阀高度比RH(Lb/c)的变化对水动力系数Ca和Cd的影响。不同管阀高度比下附加质量系数Ca随Kc数的变化情况如图 13所示。不同管阀高度比下阻力系数Cd随Kc数的变化情况如图 14所示。

|
| 图 13 不同管阀高度比下Ca随Kc数的变化关系 Fig.13 Variation of Ca with Kc number at different pipe-valve height ratios |

|
| 图 14 不同管阀高度比下Cd随Kc数的变化关系 Fig.14 Variation of Cd with Kc number at different pipe-valve height ratios |
为了保证研究结果的可靠性,这里分别在振荡频率f=4与6 Hz下开展相关数值模拟。由图 13可知:Ca随着Kc数的增大而增大,但在同一Kc数下,管阀高度比对附加质量系数影响较小;当RH在1.2~1.6范围内时几乎无影响,仅在RH=1.0~1.2范围时附加质量系数有一个增大过程,但两者间增值范围分别在[0.000 7, 0.124 0]与[0.066 2, 0.133 0]内,增值较小。
阻力系数的变化情况与3.2节相同,RH在1.0~1.6范围内结构物的阻力系数受高度比的影响较小,两者成相互独立关系。同样设置强迫振荡振幅为0.02 m,振荡频率2 Hz,仅改变阀门高度,观察结构物周围的漩涡脱落情况。在计算500时间步之后,如图 15所示,当阀门高度增加时,结构物周围漩涡脱落情况并未发生显著变化,其主要集中于管道左右两侧尖角处,而在阀门周围并未出现明显的脱落现象。由此可知,在同一Kc数值下,形状上的变化(管阀高度比)对阻力系数无较大影响。

|
| 图 15 不同管阀高度比结构物周围瞬时漩涡脱落情况 Fig.15 Transient vortex shedding around structures with different pipe-valve height ratios |
4 结论
(1) 附加质量系数及阻力系数受Kc数的影响较大,前者随着Kc的增大而增大,后者与之相反。振荡频率对附加质量系数影响较小,两者基本相互独立。当Kc数 < 0.04时,振荡频率对阻力系数影响较大,阻力系数随着振荡频率的增大而增大,当Kc>0.04时,振荡频率的影响逐渐减弱。
(2) 附加质量系数随着管阀长度比的增大而逐渐增大,而管阀长度比对阻力系数的影响较小,两者基本相互独立。
(3) 管阀高度比对附加质量系数与阻力系数的影响均较小,水动力系数仅受Kc数的影响。
| [1] |
方华灿. 海洋石油工程[M]. 北京: 石油工业出版社, 2010. FANG H C. Offshore petroleum engineering[M]. Beijing: Petroleum Industry Press, 2010. |
| [2] |
白勇, 龚顺风, 白强, 等. 水下生产系统手册[M]. 哈尔滨: 哈尔滨工程大学出版社, 2012. BAI Y, GONG S F, BAI Q, et al. Manual of subsea production system[M]. Harbin: Harbin Engineering University Press, 2012. |
| [3] |
王莹莹, 王德国, 段梦兰, 等. 水下生产系统典型布局形式的适应性研究[J]. 石油机械, 2012, 40(4): 58-63, 86. WANG Y Y, WANG D G, DUAN M L, et al. Research on the adaptability of the typical layout form of the underwater production system[J]. China Petroleum Machinery, 2012, 40(4): 58-63, 86. |
| [4] |
脱浩虎, 李华, 张赢今, 等. 基于OrcaFlex的深水采油树下放安装过程仿真研究[J]. 石油机械, 2017, 45(3): 58-62. TUO H H, LI H, ZHANG Y J, et al. Simulation of running and installation of deep water X-tree based on OrcaFlex[J]. China Petroleum Machinery, 2017, 45(3): 58-62. |
| [5] |
WANG Y Y, TUO H H, LI L W, et al. Dynamic simulation of installation of the subsea cluster manifold by drilling pipe in deep water based on OrcaFlex[J]. Journal of Petroleum Science and Engineering, 2018, 163: 67-78. DOI:10.1016/j.petrol.2017.12.049 |
| [6] |
NAM B W, KIM N W, HONG S Y. Experimental and numerical study on coupled motion responses of a floating crane vessel and a lifted subsea manifold in deep water[J]. International Journal of Naval Architecture and Ocean Engineering, 2017, 9(5): 552-567. DOI:10.1016/j.ijnaoe.2017.01.002 |
| [7] |
AN S, FALTISEN O M. An experimental and numerical study of heave added mass and damping of horizontally submerged and perforated rectangular plates[J]. Journal of Fluids and Structures, 2013, 39: 87-101. |
| [8] |
王庆云, 庞永杰, 李伟坡, 等. 系列舵翼潜艇水动力系数数值计算及试验研究[J]. 舰船科学技术, 2015, 37(11): 21-26. WANG Q Y, PANG Y J, LI W P, et al. Numerical calculation and experimental study of hydrodynamic coefficients of submarine of a series of rudder and wing[J]. Ships Science and Technology, 2015, 37(11): 21-26. DOI:10.3404/j.issn.1672-7649.2015.11.004 |
| [9] |
姚晓杰, 桂福坤, 孟昂, 等. 波浪要素对水平圆柱杆件水动力系数影响研究[J]. 海洋工程, 2016, 34(1): 80-87. YAO X J, GUI F K, MENG A, et al. Experimental study on hydro-coefficients of horizontal cylinder structure in waves[J]. The Ocean Engineering, 2016, 34(1): 80-87. |
| [10] |
朱仁传, 郭海强, 缪国平, 等. 一种基于CFD理论船舶附加质量与阻尼的计算方法[J]. 上海交通大学学报, 2009, 43(2): 198-203. ZHU R C, GUO H Q, MIAO G P, et al. A computational method for evaluation of added mass and damping of ships based on CFD theory[J]. Journal of Shanghai Jiaotong University, 2009, 43(2): 198-203. DOI:10.3321/j.issn:1006-2467.2009.02.009 |
| [11] |
汤珂, 段梦兰, 张新虎, 等. 基于CFD的管汇非惯性水动力系数计算[J]. 石油矿场机械, 2014, 43(3): 34-37. TANG K, DUAN M L, ZHANG X H, et al. Numerical simulation of hydrodynamic drag coefficients using CFD[J]. Oil Field Equipment, 2014, 43(3): 34-37. DOI:10.3969/j.issn.1001-3482.2014.03.009 |
| [12] |
黄致谦, 周蕊, 丁勤卫, 等. 基于浮式风力机平台的分形特征垂荡板强迫振荡水动力特性[J]. 热能动力工程, 2018, 33(5): 133-140. HUANG Z Q, ZHOU R, DING Q W, et al. Hydrodynamic characteristics for forced oscillation of heave plate based on fractal characteristics of floating offshore wind turbine platforms[J]. Journal of Engineering for Thermal Energy and Power, 2018, 33(5): 133-140. |
| [13] |
戚昱, 罗晓兰, 张德华, 等. 管汇下放过程中的水动力系数计算[J]. 石油机械, 2018, 46(8): 43-47. QI Y, LUO X L, ZHANG D H, et al. Calculation of hydrodynamic coefficients in the process of manifold deploying[J]. China Petroleum Machinery, 2018, 46(8): 43-47. |
| [14] |
MA Z H, LING Q, MARTÍNEZ-FERRER P J, et al. An overset mesh based multiphase flow solver for water entry problems[J]. Computers & Fluids, 2018, 172: 689-705. |
| [15] |
江维青, 杨爱明. 重叠网格隐式挖洞方法的改进与应用[J]. 复旦学报(自然科学版), 2018, 57(5): 580-586, 595. JIANG W Q, YANG A M. Enhancement and application of implicit hole cutting method for overset grids[J]. Journal of Fudan University (Natural Science), 2018, 57(5): 580-586, 595. |
| [16] |
ANON. Modelling and analysis of marine operations: DNV-RP-H103[S]. Norway: DetNorske Veritas, 2011.
|
| [17] |
LI J X, LIU S X, ZHAO M, et al. Experimental investigation of the hydrodynamic characteristics of heave plates using forced oscillation[J]. Ocean Engineering, 2013, 66: 82-91. DOI:10.1016/j.oceaneng.2013.04.012 |
| [18] |
ZHANG S N, ISHIHARA T. Numerical study of hydrodynamic coefficients of multiple heave plates by large eddy simulations with volume of fluid method[J]. Ocean Engineering, 2018, 163: 583-598. DOI:10.1016/j.oceaneng.2018.03.060 |



