0 引言
在石油钻井工程中,需要对钻井工具的性能进行测试,但是钻井工具工艺复杂且造价昂贵,而且目前我国对动态偏置指向式旋转导向钻井工具的研究尚有很大的探索空间,没有能与国外三大油服公司相媲美的成熟技术。笔者所研究的是基于指向式旋转导向钻井工具试验台的加载系统控制,旨在测试配套的指向式旋转导向钻井工具的可靠性、及时发现其设计缺陷并攻克其核心技术[1-2]。模拟加载装置的控制系统是本文主要的研究对象。一般传统的控制方式是在理想的情况下需要用户提供准确的数学模型,但是实际情况中由于工作环境和其他因素的影响,被控对象都会表现出一定的偏差,所以常规的控制方式并不能满足此种情况下的建模[3]。
针对数学模型的不确定性以及建模困难这一难题,笔者提出了模糊自适应PID控制方法,运用模糊化、解模糊等一系列方法和专家经验设计模糊自适应PID控制器,然后通过计算仿真所得的曲线判断系统的动态性能和稳定性。所得结论可为旋转导向钻井工具的性能研究提供参考。
1 试验台的机械装置及工作原理 1.1 结构指向式旋转导向钻井工具性能测试试验台结构如图 1所示。
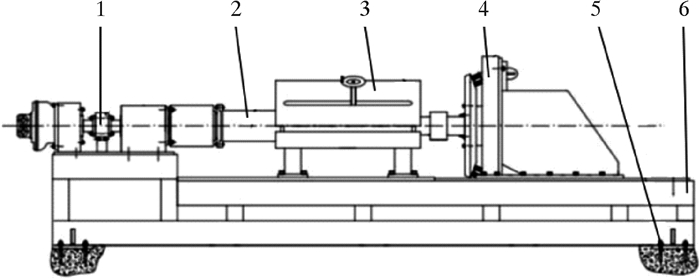
|
| 1—旋转装置;2—指向式旋转导向钻井工具;3—钻井工具夹持装置;4—模拟加载装置;5—膨胀螺栓;6—架体。 图 1 指向式旋转导向钻井工具性能测试试验台 Fig.1 A test bench for performance testing of the point-the-bit type rotary steering drilling tools |
旋转装置架体是本试验装置的主要驱动部位,由液压马达驱动,模拟在实际钻井工作中钻杆为钻井工具提供的转速。夹持装置用来夹持钻井工具,由手轮、导轨和支撑头组成,固定在两侧的支撑架上。模拟加载装置由液压缸、磁力变矩器及轴向力传感器等组成,用来模拟在实际钻井工作中钻头受到岩石的反作用力[4]。
模拟加载装置结构如图 2所示,主要包括轴向液压缸、磁力变矩器及液压比例控制阀等。
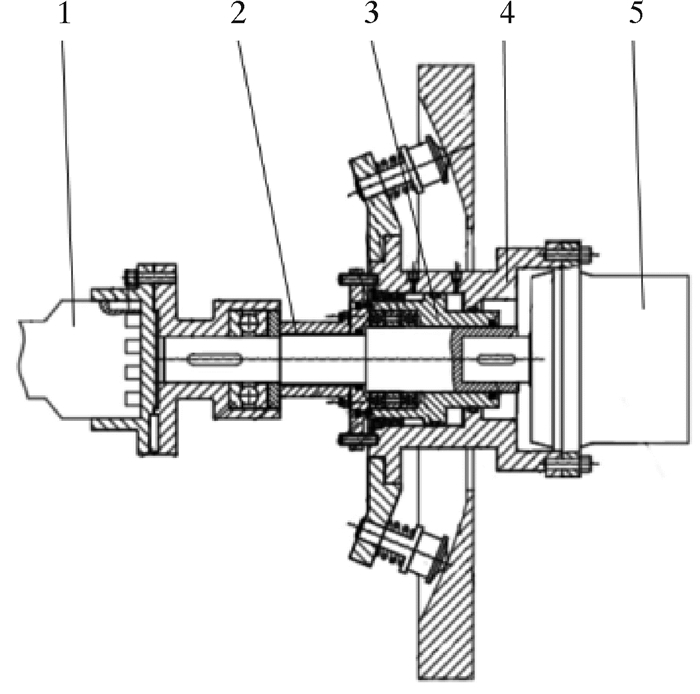
|
| 1—钻头;2—轴向压力传感器;3—油缸空心轴;4—油缸体;5—磁粉制动器。 图 2 模拟加载装置结构图 Fig.2 Structure chart of the simulation loading device |
1.2 工作原理
根据实际钻井工作中钻头的受力情况,由作用力与反作用力原理知,钻井工具主要受旋转时岩石对其产生的扭矩和钻杆对其施加的轴向压力。试验台的扭矩加载采用磁粉制动器模拟钻井工具在实际旋转钻井工作中的旋转载荷,扭矩的大小通过调节磁粉制动器的输出载荷来改变,对应地在旋转导向钻井工具的钻头部位安装有扭矩载荷传感器,可实时检测磁粉制动器加载力矩的大小,从而准确模拟钻头在钻进过程中所受的破岩扭矩。试验台的钻压加载采用单作用活塞液压缸来实现,利用液压力模拟钻井工具在钻井过程中钻柱施加的钻压,而钻压的大小由电液比例控制阀来调节,电磁铁受到不同电压的作用使阀芯具有不同的液压力,从而实现无级调速,模拟钻头在一定范围内钻压的变化情况。
2 模拟加载系统的数学模型 2.1 液压缸的数学模型试验台的模拟加载系统可以准确地模拟钻井工作中岩石对其产生的反向作用力,用轴向液压缸来模拟其对钻井工具施加的力,能够为动态指向式旋转导向钻井工具提供近似钻井状况的轴向载荷。该装置由油缸体和油缸空心轴以及密封件组成,可实现模拟钻压的均匀加载和卸载。采用液压缸进行轴向力加载能够达到实际的钻井载荷,而且液压加载能够更为精确地控制加载力的大小。液压缸在工程上可以认为是二阶环节和一节环节的组合[5],其传递函数为:
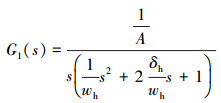
|
(1) |
式中:A为有杆腔面积,m2;Δh为阻尼比;wh为无阻尼固有频率,Hz。
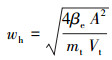
|
(2) |
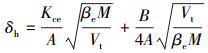
|
(3) |
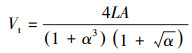
|
(4) |
将本装置试验台所选用的液压缸及相关油液参数[6]带入式(2)、式(3)和式(4)中进行计算。其中液压缸内径D为80 mm,活塞杆直径d为56 mm,有杆腔面积A=2.57×10-3 m2,综合黏性阻尼系数B=0.06 (N·m·s)/rad,面积比α=2,行程L=350 mm,负载质量mt=8 000 kg,油液密度ρ=900 kg/m3,油液弹性模量E=1.4 GPa,油液动力黏度为1×10-5 m2/s,油液作用力总体积Vt=3.26×10-3 m3,体积弹性模量βe=700 MPa,总流量-压力系数Kce=2.34×10-10 m3· s·Pa -1。
2.2 磁粉制动器的数学模型加载系统中的制动扭矩由磁粉制动器中的磁粉磁化后形成磁链之间的相互作用提供,此外还有磁链与定子、转子之间的摩擦力。
在不考虑磁粉黏滞阻力和转动离心力产生的附加扭矩的情况下,磁粉制动器的数学模型为[7-8]:
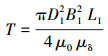
|
(5) |
式中:B1为磁感应强度,T;D1为定子外径,m;L1为宽度,m;μ0为气隙磁导率,H/m;μδ为磁粉磁导率,H/m。
在制动器磁路中,由磁场欧姆定律可得:
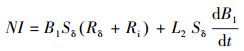
|
(6) |
式中:N为激励磁线圈匝数,匝;I为激励磁线圈电流,A;Rδ为间隙及磁粉总磁阻,H-1;Ri为铁磁阻,H-1;L2为电感量,H;Sδ为空隙中磁粉与磁路相正交的面积,m2。
将式(5)和式(6)进行拉普拉斯变化并联立可得:
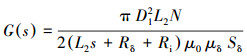
|
(7) |
上式可看作典型的一阶惯性系统,由于磁粉制动器在工作时存在延迟,磁粉制动器的传递函数为:
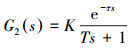
|
(8) |
由于在实际情况中磁阻存在磁滞、磁导率具有时变性及反复加载导致的滑差速度等都会使磁粉制动器不能有一个确定的数学模型,所以加载电流和制动扭矩之间具有较强的非线性。
2.3 电液比例压力阀建模试验台液压控制系统的固有频率高,钻头所受到的轴向压力由比例溢流阀所控制。比例溢流阀可简化为一个典型的二阶振荡环节[9],其传递函数为:
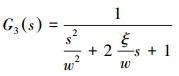
|
(9) |
式中:ξ为系统阻尼比;w为阀体本身固有频率,Hz。
比例溢流阀中电磁铁的推力可以随着输入电压的大小变化产生连续变化的液压力,实现无级调节[10],可使试验台能够按照要求准确地对钻井工具加载。
3 模糊自适应PID控制器的原理及设计 3.1 模糊自适应PID控制器原理笔者采用模糊自适应PID控制方法,不需要在控制过程中表达各种变量和评价标准,也不需要高精度的数学模型。该方法以PID算法为主体,以误差e和误差变化率ec作为系统的两个输入,结合使用条件和建立的操作规则,利用模糊数学基本方法表示,进而进行一系列的模糊化、模糊推理和解模糊操作,控制器原理如图 3所示。系统工作的实际响应情况基于预先设置在计算机信息库中的模糊控制规则自动执行PID参数,最后利用模糊自适应PID控制器计算出输入和输出之间的关系进行最佳调整[11]。
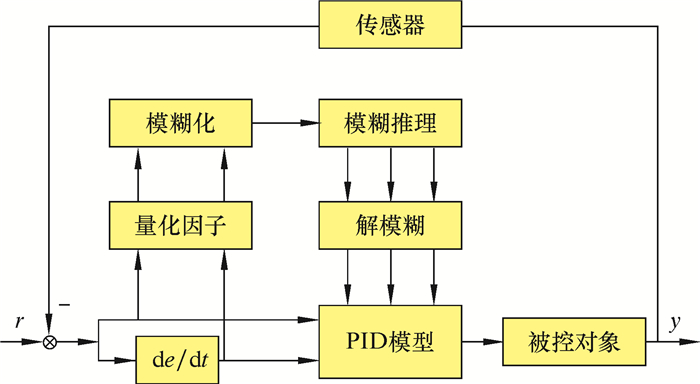
|
| 图 3 模糊自适应PID控制器原理示意图 Fig.3 Schematic diagram of the fuzzy self-adaptive PID controller |
3.2 模糊控制规则库和隶属函数的设计
首先利用FISEditor创建Mamdani推理的模糊控制器,其结构为两输入(e,ec)和三输出(ΔKp,ΔKi,ΔKd)模式,输入量(e,ec)的论域值设为(-6,6),相同于输出量(ΔKp,ΔKi,ΔKd)的模糊论域为(-6,6),语言变量均为{NB, NM, NS, ZO, PB, PM, PS}。隶属函数则选择一般的三角形隶属度函数(trimf),其中设第一条隶属曲线负大(ZB)模糊矢量用Z-型隶属度函数(zmf),最后一条隶属曲线正大(PB)模糊矢量用S-型隶属度函数(smf)。输入量和输出量的隶属度函数相同[12-13]。
模糊控制规则的建立和选取是控制系统中最重要、最关键的环节,其设计原则如表 1所示[14]。
| 语言变量 | NB | NM | NS | ZO | PS | PM | PB |
| NB | PB/NB/PS | PB/NB/NS | PM/NM/NB | PM/NM/NB | PS/NS/NB | ZO/ZO/NM | ZO/ZO/PS |
| NM | PB/NB/PS | PB/NB/NS | PM/NM/NB | PS/NS/NM | PS/NS/NM | ZO/ZO/NS | NS/ZO/ZO |
| NS | PM/NB/ZO | PM/NM/NS | PM/NS/NM | PS/NS/NM | ZO/ZO/NS | NS/PS/NS | NS/PS/ZO |
| ZO | PM/NM/ZO | PM/NM/NS | PS/NS/NS | ZO/ZO/NS | NS/PS/NS | NM/PM/NS | NM/PM/ZO |
| PS | PS/NM/ZO | PS/NS/ZO | ZO/ZO/ZO | NS/PS/ZO | NS/PS/ZO | NM/PM/ZO | NM/PB/ZO |
| PM | PS/ZO/PB | ZO/ZO/PS | NS/PS/PS | NM/PS/PS | NM/PM/PS | NM/PB/PS | NB/PB/PB |
| PB | ZO/ZO/PB | ZO/ZO/PM | NM/PS/PM | NM/PM/PM | NM/PM/PS | NB/PB/PS | NB/PB/PB |
Kp的作用是保证系统的响应速度,Kp越大,系统的响应速度越快,调节精度越精准,但是Kp不宜过大。若系统误差|e|较大时,则Kp应选较大值,Ki一般选0,Kd一般选较小值。
Ki的作用是消除系统的稳态误差,Ki越大,系统的稳态误差消失得越快;Ki越小,误差消失的时间越慢,调节精度也会受到影响。系统误差|e|和其变化|ec|为正常大小时,Kp应选较小值,可保证系统的响应速度不受影响,避免产生较大的超调量,Ki和Kd取值适中。
Kd的作用是改善系统的动态特性,控制偏差向任何方向变化,可提前预报偏差的变化趋势,Kd过大时会使系统的调节时间延长,并且系统容易受到干扰。系统的|e|较小时,Ki和Kd取值应适中,可保证系统的控制精度,加强系统的抗干扰能力。
4 试验台模拟加载控制系统的仿真及分析笔者利用Matlab软件中Simulink模块建立所设计的控制方法与常规PID控制方法的仿真结构。首先把根据模糊推理控制建立的规则输入到模糊控制系统中建立隶属函数,将模糊推理系统[15]fuzzpid.fis输出到Matlab工作空间中使其生效;然后在Simulink模块中建立相关框图并将其并联在一起。无PID调节、常规PID控制及模糊自适应PID控制下旋转导向钻井工具试验台仿真结构框图如图 4所示。
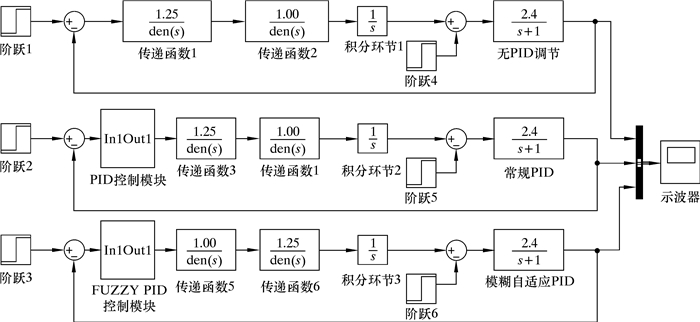
|
| 图 4 系统Simulink仿真结构框图 Fig.4 Block diagram of the Simulink module structure of the system |
利用临界比例度法在线整定PID参数,所得的参数作为模糊自适应PID控制的初值。系统在工作时,根据模糊推理方法和相关规则进行在线自动校正,即可得模糊PID控制器的量化因子Ke=2,Kec=0.5,比例因子Kp=1.9,Ki=0.01,Kd=0.5。运行所搭建的Simulink系统模型进行仿真,其仿真曲线由示波器输出,如图 5所示。由图 5可知:无PID调节的仿真曲线在0~2 s之间响应速度快于常规PID控制,但是在响应时间t=2.0 s处存在超调,超调量为38%,并且系统反复震荡,响应时间长,在t=10.0 s时才达到稳态;常规PID控制的仿真曲线虽然在t=5.8 s时达到稳态,但是超调量也较大,超调量达20%;模糊自适应PID控制的曲线反应最快,响应时间明显加快,在t=4.0 s处达到稳态,在t=2.0 s处存在超调,超调量为5%,明显低于其他两条仿真曲线,并且系统波动很小,说明其自适应能力较强。由此说明应用模糊自适应PID控制的系统更稳定,而且接受控制信号的反应更快[16]。
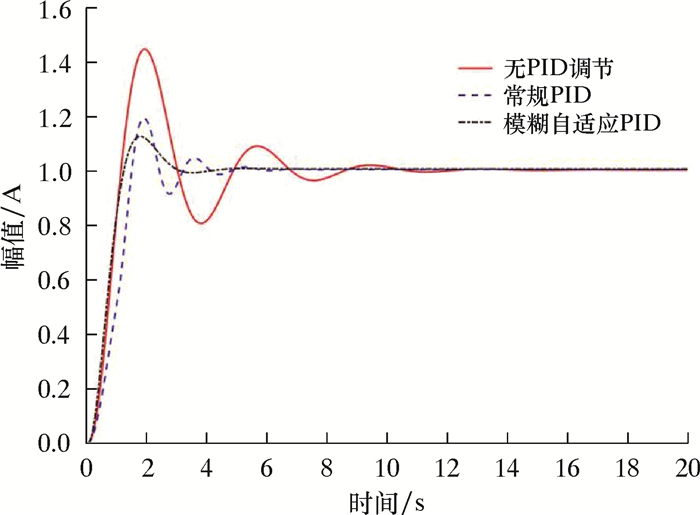
|
| 图 5 系统未加入扰动时的仿真结果 Fig.5 System simulation results without disturbance |
为了测试系统在受到扰动后的抗干扰能力,笔者在系统响应时间t=9.0 s处加入阶跃响应,则旋转导向钻井工具试验台受到干扰后的仿真波形如图 6所示。
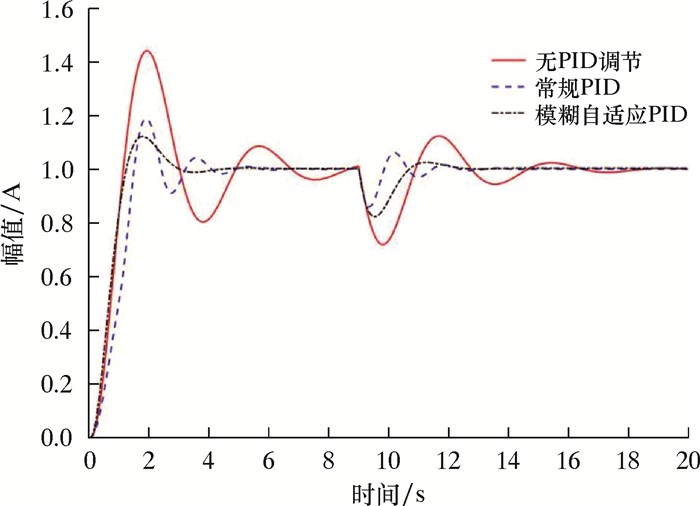
|
| 图 6 系统在加入扰动后的仿真结果 Fig.6 System simulation results with disturbance |
由图 6可以看出:在t=9.0 s处加入干扰后,无PID调节的仿真曲线波动很大并且重新恢复稳态的时间较长;常规PID控制恢复稳态的时间比无PID调节的快,反应最快,但是仍然存在较大的波动;模糊自适应PID受到干扰后能快速恢复稳态而且振荡很小。由此说明模糊自适应PID控制具有很好的鲁棒性,可实现对旋转导向钻井工具试验台加载系统的精确控制,满足控制系统研究的要求。
5 结论(1) 模糊自适应PID控制方式优于常规PID控制方式,前者响应速度快、超调量更小、系统更稳定而且振荡更小。
(2) 在系统加入扰动时,模糊自适应PID控制方式可以迅速恢复稳态、震荡小,说明其鲁棒性较好,保持自身稳定性比常规PID控制方式强。
(3) 设计的模糊自适应PID控制方式提高了指向式旋转导向钻井工具试验台控制的灵敏度,满足对试验台较高控制精度的要求,具有较强的实用性
| [1] |
王植锐, 王俊良. 国外旋转导向技术的发展及国内现状[J]. 钻采工艺, 2018, 41(2): 37-41. WANG Z R, WANG J L. Development of rotary steering technology in foreign countries and its status quo in China[J]. Drilling & Production Technology, 2018, 41(2): 37-41. DOI:10.3969/J.ISSN.1006-768X.2018.02.11 |
| [2] |
姜伟, 蒋世全, 付鑫生, 等. 旋转导向钻井技术应用研究及其进展[J]. 天然气工业, 2013, 33(4): 75-79. JIANG W, JIANG S Q, FU X S, et al. Application of rotary steering drilling technology and its research progress[J]. Natural Gas Industry, 2013, 33(4): 75-79. |
| [3] |
李浩, 马新华, 施卫东, 等. 自适应模糊PID控制在水泵试验台流量调节中的应用[J]. 水电能源科学, 2011, 29(9): 147-149. LI H, MA X H, SHI W D, et al. Application of self-adaptive fuzzy PID control to discharge regulation of water pump test-bed[J]. Water Resources and Power, 2011, 29(9): 147-149. DOI:10.3969/j.issn.1000-7709.2011.09.041 |
| [4] |
刘英海.井下闭环可控弯接头性能试验台设计与研究[D].西安: 西安石油大学, 2016. LIU Y H. Design and research of performance test bench for closed loop controllable bending joints[D]. Xi' an: Xi' an Shiyou University, 2016. |
| [5] |
张兵, 邓子龙. 基于Simulink的比例阀控液压缸的建模与仿真[J]. 机械制造与自动化, 2016, 45(3): 105-108. ZHANG B, DENG Z L. Simulink based modeling and simulation of the proportional valve controlled cylinder hydraulic system[J]. Machine Buiding & Automation, 2016, 45(3): 105-108. DOI:10.3969/j.issn.1671-5276.2016.03.032 |
| [6] |
韩晨升, 温少飞, 赖成. 基于SIMULINK的阀控液压缸运行稳定性建模与仿真分析[J]. 锻压技术, 2017, 42(1): 82-85, 91. HAN C S, WEN S F, LAI C. Modeling and simulation analysis on operation stability of valve controlled hydraulic cylinder based on SIMULINK[J]. Forging & Stamping Technology, 2017, 42(1): 82-85, 91. |
| [7] |
薛超, 白国振. 模糊自适应PID控制器在磁粉制动器加载系统中的应用研究[J]. 机电工程, 2016, 33(2): 217-220. XUE C, BAI G Z. Application and research of self-adaptive fuzzy PID controller in magnetic powder brake loading system[J]. Journal of Mechanical & Electrical, 2016, 33(2): 217-220. |
| [8] |
王力, 钱林方, 高强, 等. 磁粉制动器的建模与辨识研究[J]. 电气自动化, 2010, 32(5): 55-58. WANG L, QIAN L F, GAO Q, et al. Research on modeling and identification of magnetic particle brake[J]. Electrical Automation, 2010, 32(5): 55-58. DOI:10.3969/j.issn.1000-3886.2010.05.018 |
| [9] |
温彬, 解宁, 郭津津. 基于AMESim的电液比例压力阀建模与仿真[J]. 重型机械, 2014(6): 65-69. WEN B, XIE N, GUO J J. Modeling and simulation of electro-hydraulic proportional pressure valve based on AMESim[J]. Heavy Machinery, 2014(6): 65-69. DOI:10.3969/j.issn.1001-196X.2014.06.016 |
| [10] |
张震, 潘尚峰, 邓剑, 等. 车床动力卡盘电液比例扭矩加载系统的建模与分析[J]. 机床与液压, 2018, 46(9): 137-140. ZHANG Z, PAN S F, DENG J, et al. Modeling and analysis of electro-hydraulic proportional torque loading system on lathe' s power chuck[J]. Machine Tool & Hydraulics, 2018, 46(9): 137-140. DOI:10.3969/j.issn.1001-3881.2018.09.031 |
| [11] |
王安, 杨青青, 闫文宇. 模糊自整定PID控制器的设计与仿真[J]. 计算机仿真, 2012, 29(12): 224-228. WANG A, YANG Q Q, YAN W Y. Design and simulation of fuzzy self-tuning PID controller[J]. Computer Simulation, 2012, 29(12): 224-228. DOI:10.3969/j.issn.1006-9348.2012.12.053 |
| [12] |
周海涛, 周建华, 杭小宇. 基于自适应模糊PID控制方法的研究[J]. 机械工程与自动化, 2014(3): 139-141. ZHOU H T, ZHOU J H, HANG X Y. A control method based on adaptive fuzzy PID controller[J]. Mechanical Engineering and Automation, 2014(3): 139-141. DOI:10.3969/j.issn.1672-6413.2014.03.058 |
| [13] |
郭成林, 蒋日鹏, 李晓谦, 等. 基于Fuzzy-PID的大规格铸锭结晶器液位控制[J]. 机械工程学报, 2018, 54(22): 212-217. GUO C L, JIANG R P, LI X Q, et al. Mold level control of large size ingot based on fuzzy self-tuning PID[J]. Journal of Mechanical Engineering, 2018, 54(22): 212-217. |
| [14] |
马克, 米林, 谭伟, 等. 基于FPGA的汽车主动悬架模糊自适应PID控制器设计[J]. 机床与液压, 2018, 46(14): 95-99, 148. MA K, MI L, TAN W, et al. Design of adaptive fuzzy-PID controller of automobile active suspension based on FPGA[J]. Machine Tool & Hydraulics, 2018, 46(14): 95-99, 148. DOI:10.3969/j.issn.1001-3881.2018.14.027 |
| [15] |
RAJESH K S, DASH S S. Load frequency control of autonomous power system using adaptive fuzzy based PID controller optimized on improved sine cosine algorithm[J]. Journal of Ambient Intelligence and Humanized Computing, 2019, 10(6): 2361-2373. DOI:10.1007/s12652-018-0834-z |
| [16] |
李耀东, 程为彬, 汤楠, 等. 旋转导向钻井工具智能PID控制[J]. 石油机械, 2010, 38(8): 13-16, 104. LI Y D, CHENG W B, TANG N, et al. The intelligent PID control of the rotary navigational drilling tool[J]. China Petroleum Machinery, 2010, 38(8): 13-16, 104. |



