2. 中石油气举试验基地多相流研究室
2. Multiphase Flow Laboratory of Gas Lift Innovation Centre, CNPC
0 引言
在开发新油田和调整老油田时,都会使井眼发生碰撞的可能性增加。井眼一旦发生碰撞,将导致套管破损、钻井液泄漏,甚至停工停产[1-2]。为了减少井眼相碰带来的巨额经济损失,采用了井眼轨道设计、随钻测量和防碰扫描等技术,但这些技术均存在一定的不足[3-7]。
美国Western Atlas International公司开发的TOMEXTM系统[8],采用钻头破岩产生的震动作为震源,在硬岩钻进方面发挥着不错的作用,但在软岩层产生的震源强度不足。Tempress科技公司研制的水力脉冲钻井系统[9],在斜井和大位移井中能产生足够的能量,但增加了井下施工的复杂性。刘刚和董照显等[10-11]设计的机械式井下震源能产生合适的震源强度,但由于操作费时且繁琐,限制了它的适用范围。
本文设计了一种能产生强冲击且操作便捷的机械式井下震源发生器,它在正常作业时能利用钻井液对冲击装置蓄能且不产生误震,需要停钻测井时可通过简单操作得到高效冲击功。笔者基于流体力学理论,建立了井下震源发生器的动力学模型,通过MATLAB GUI数值模拟程序,研究了井下震源发生器设计参数对其输出性能的影响。所得结论可为井下震源发生器的现场应用提供指导。
1 井下震源发生器技术分析井下震源发生器的基本工作原理是通过液压装置蓄能,利用弹簧力驱使冲锤冲击铁砧而产生较大震击力。其结构如图 1所示,主要部件包括活塞、冲锤、弹簧、铁砧和液压延时装置等。其中铁砧横断面如图 2所示。

|
| 1—上接头;2—外筒;3—活塞;4—连接器;5—固定套筒;6—弹簧;7—弹簧套筒;8—冲击锤;9—钢球;10—止推套筒;11—铁砧及其外花键套筒;12—液压延时装置;13—内花键套筒;14—下接头。 图 1 井下震源发生器结构示意图 Fig.1 Structure diagram of the downhole seismic generator |

|
| 图 2 铁砧横断面 Fig.2 Cross section of the anvil |
正常钻进时,井下震源发生器不会产生震击作用,只是作为钻具的一部分传递扭矩和钻压。钻井液推动活塞并带动冲锤沿轴向向上运动压缩弹簧,当弹簧压缩蓄能,而冲击锤和活塞组合处于钢球卡点处时,钢球部分伸出卡住冲击锤的弧形下端。为防止即拉即震或误震,设计了液压延时装置。该装置工作时,高压钻井液通过单向阀进入液压腔中,当停泵微提钻杆,铁砧受下接头所连接动力钻具的重力和摩擦力等作用而压缩液压腔,迫使钻井液通过细缝挤出,起到延时作用。
待延时结束后,止推套筒也相应下行一小段距离,钢球在弹簧力的作用下退缩到外筒和固定套筒之间的腔体中,即卡点消失。弹簧能量释放迫使冲击锤和活塞组合迅速下行冲击铁砧,实现一次有效震击。
2 动力学分析与模型建立 2.1 动力学理论基础在研究井下震源发生器冲锤动力时,需要以流体连续性方程和能量守恒为基础来进行理论分析,同时要考虑压力损失和摩擦阻力等影响因素。
2.1.1 连续性方程连续性方程是流体力学中的一个基本方程,它是质量守恒定律在流体力学中的具体表现。对于不可压缩流体,其密度为定值时,连续性方程的表达式为:
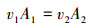
|
(1) |
式中:A1、A2分别表示不同过流面横截面积,m2;v1、v2分别表示不同过流面的平均流速,m/s。
2.1.2 伯努利方程伯努利方程是流体运动时能量守恒和转化规律的具体表达,是流体力学中最重要的方程之一,其表达式为:
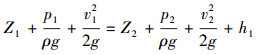
|
(2) |
式中:Z1、Z2分别表示不同过流面的高度,m;p1、p2分别表示不同过流面的压力,Pa;h1为水头损失,m;ρ为流体密度,kg/m3;g为重力加速度,m/s2。
2.1.3 水垫阻力当冲锤高速向下运动时,腔内流体对其产生较大的水垫阻力,其计算公式为[12]:
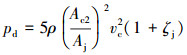
|
(3) |
式中:pd为水垫阻力,Pa;Aj为节流环面积,m2;Ac2为冲锤下端面面积,m2;vc为冲锤运动速度,m/s;ζj为节流环处的局部损失数。
2.1.4 压力损失压力损失一般包括沿程水头损失和局部水头损失,其通用表达式如下:
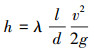
|
(4) |
式中:λ为水头损失系数;d为管道内径,m;l为当量长度,m;v为平均流速,m/s。
2.1.5 机械摩擦力冲锤和冲锤流道之间的摩擦力主要为滑动摩擦力,即机械摩擦力Ff,其经验估算公式为[13]:
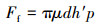
|
(5) |
式中:μ为接触面摩擦因数;h′为冲锤有效宽度,m;p为冲锤的工作压力,Pa。
2.2 冲锤动力学模型的建立根据井下震源发生器的基本工作原理,以震源发生器垂直状态建立动力学模型,主要研究冲锤下行冲击阶段的动力性能。建立的冲锤动力学模型如图 3所示。

|
| 图 3 冲锤动力学模型 Fig.3 Dynamic model of the hammer |
2.2.1 受力情况分析
由图 3可知,冲锤受力主要有重力G、下端面压力p1、上端面弹簧力F、水力阻力Fs和机械摩擦力Ff。重力表达式为:
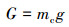
|
(6) |
式中:mc为冲锤组合质量,kg。
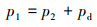
|
(7) |
式中:p2为背压。
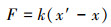
|
(8) |
式中:k为弹簧刚度系数,N/mm;x′为冲锤总行程,m;x为冲锤任意时刻的位移量,m。
流体流动时具有黏滞性,冲锤与钻井液有相对运动,存在水力阻力:
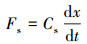
|
(9) |
式中:Cs为流体阻力系数。
2.2.2 运动微分方程加速度微分方程为:
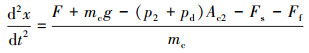
|
(10) |
速度微分方程为:
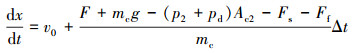
|
(11) |
位移微分方程为:
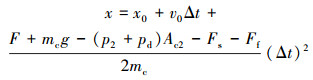
|
(12) |
式中:v0为冲锤的初始速度,m/s;x0为冲锤的初始位移,m。
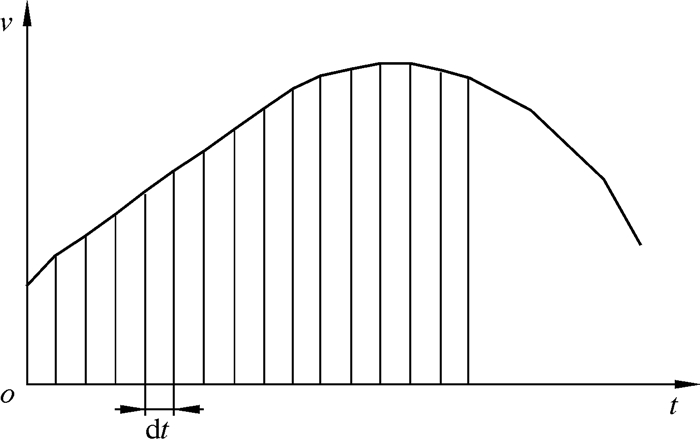
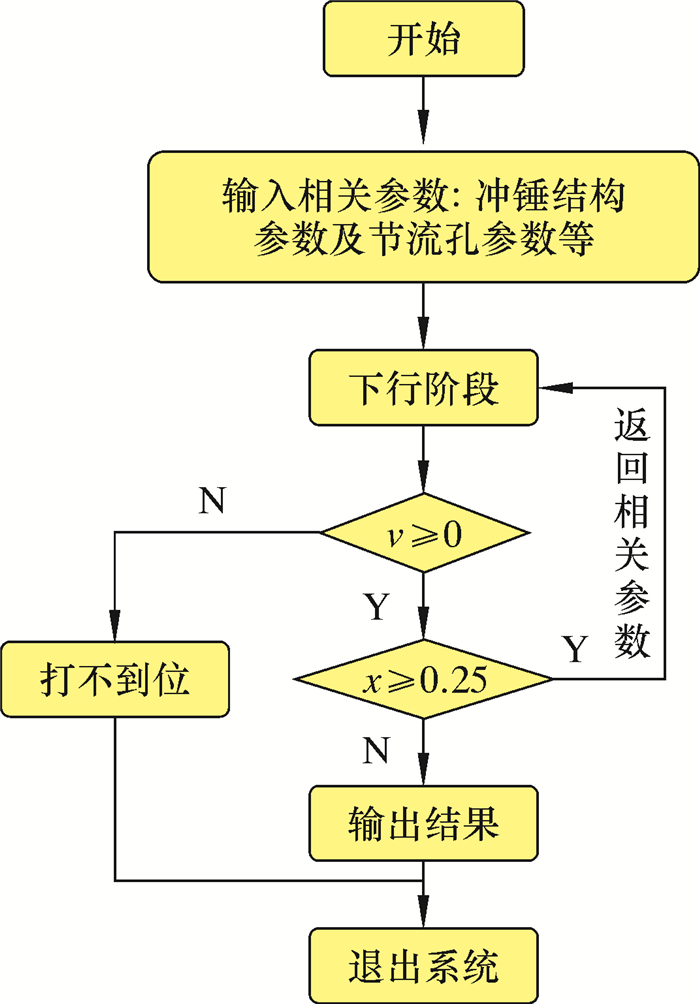
3 数值模拟程序开发利用有限差分原理(见图 4),对冲锤在下行阶段的动力学方程进行迭代计算,求得冲锤在时间微段内的加速度、速度和位移,再根据这些参数反求水垫阻力和水力阻力等,并将这些参数作为下一时间微段的起始状态参数,如此循环计算,直至计算出最终结果。以冲锤速度方向判断冲锤运动能否冲击铁砧,以冲锤流道长度来限制冲锤的位移。仿真软件的程序流程如图 5所示。
|
| 图 4 有限元差分原理图 Fig.4 Schematic diagram of the finite difference method |
|
| 图 5 冲锤下行阶段程序流程图 Fig.5 Flow diagram of the hammer during the impacting process |
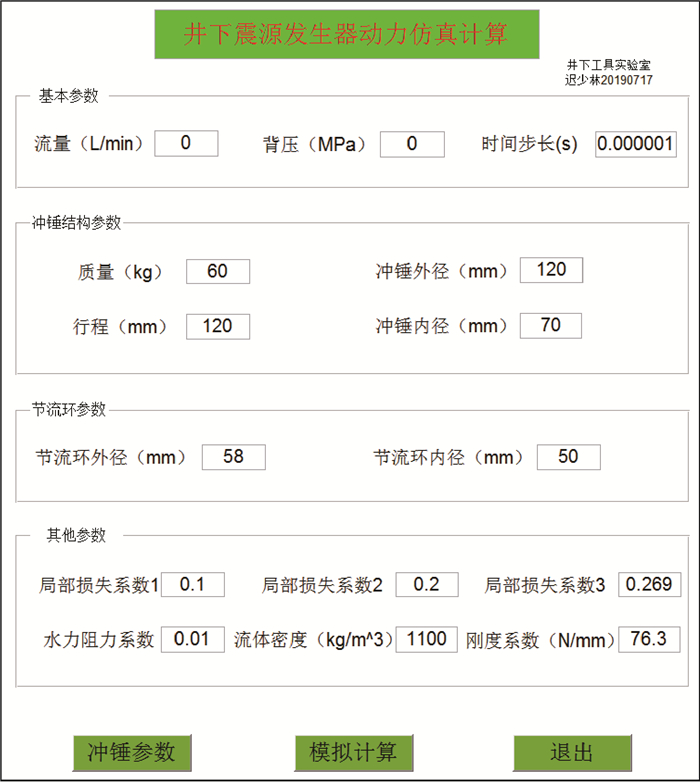
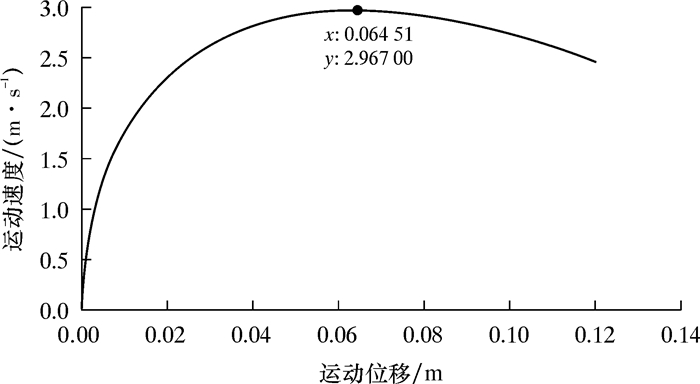
利用MATLAB的计算能力和绘图能力,进行数值模拟程序的编制[14-15]。程序中冲锤仿真的计算界面如图 6所示。图 6中设置了基本的结构参数和水力参数的输入项,如流量、背压及冲锤结构等,通过对这些参数的不同设计组合,并根据设计目标进行参数优化,研究井下震源发生器动力性能输出规律。其中冲锤性能输出界面如图 7所示。冲锤位移-速度曲线如图 8所示。
|
| 图 6 冲锤仿真的计算界面 Fig.6 Hammer simulation calculation interface |

|
| 图 7 冲锤性能输出界面 Fig.7 Hammer performance output interface |
|
| 图 8 冲锤位移-速度曲线 Fig.8 Displacement-velocity curve of the hammer |
4 井下震源发生器性能研究
影响井下震源发生器输出性能的因素较多,这里主要对弹簧刚度、节流面积、冲锤质量和钻井液密度等进行研究。以冲锤最佳输出性能,即最大冲击功及最大冲击效率等为优化目标,进行井下震源发生器的动力性能研究。
4.1 弹簧刚度对冲锤输出性能的影响弹簧是井下震源发生器的主动力蓄能装置,有必要研究不同弹簧刚度对冲锤动力性能的影响。冲锤欲获得最大输出性能,则应该在弹簧变形范围内运动,故以弹簧实际行程为运动行程。弹簧相关参数如表 1所示。
| 弹簧最小变 形量/mm |
弹簧最大变 形量/mm |
实际行 程/mm |
弹簧刚度/ (N·mm-1) |
| 21.01 | 147.08 | 126.07 | 38.07 |
| 17.90 | 138.72 | 120.82 | 44.70 |
| 16.34 | 138.91 | 122.57 | 48.95 |
| 14.60 | 135.01 | 120.41 | 54.81 |
| 13.68 | 136.83 | 123.15 | 58.47 |
| 12.31 | 132.38 | 120.07 | 64.96 |
| 11.40 | 132.55 | 121.15 | 70.16 |
| 10.49 | 131.13 | 120.64 | 76.26 |
| 9.58 | 131.70 | 122.12 | 83.52 |
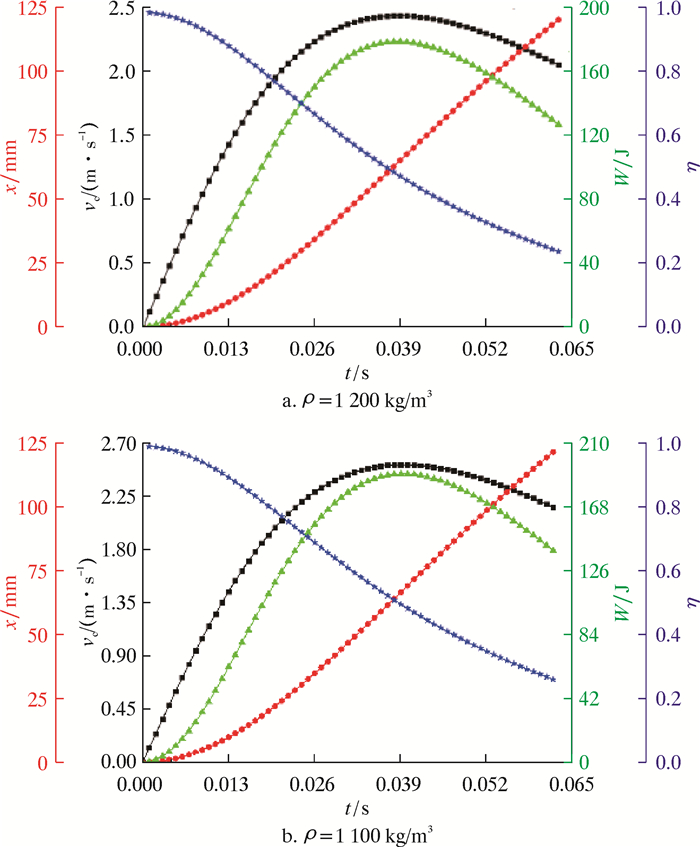
当钻井液密度ρ分别为1 200和1 100 kg/m3,质量M=60 kg, 节流面积A=1 990.51 mm2时,可以求出不同弹簧刚度时冲锤的输出性能值,这里以弹簧刚度K=48.95 N/mm为例,计算冲锤的各项输出性能值,即冲锤的速度vc、位移x、冲击功W和冲击效率η。通过origin绘图软件对冲锤的输出性能数据进行处理,结果如图 9所示。
|
| 图 9 不同钻井液密度下冲锤输出性能随时间的变化规律 Fig.9 Law of change of the hammer output performance with time at different drilling fluid densities |
从图 9可以看出:在冲锤运动行程内,随着时间的变化,冲锤的速度变化趋势是先增后减,这是由于弹簧力逐渐减小,而流体阻力相对增加,导致冲锤加速度逐渐变小;冲锤位移呈关于时间的二次函数关系递增,即认为每一个微小时间段内加速度恒定,符合匀加速运动规律;冲锤冲击功变化趋势先增后减,与冲锤速度变化趋势相似,这是由于冲锤冲击功与速度的平方呈正相关,冲锤前期冲击功曲线凹下去呈现二次函数形态,之后冲锤冲击功与冲锤速度呈现相同的下降趋势;冲锤冲击效率呈递减趋势,这是由于弹簧的弹性势能和冲锤的重力势能不只是转化为冲锤的动能,还转化为其他形式的能量,导致冲锤的动能增加量相对势能减少量降低,而斜率的绝对值变化先增加后减小,是由于阻力在冲锤运动的前期阻碍能力逐渐增加之后趋于稳定,而冲锤冲击效率后期递减缓慢也验证了这一点。
从图 9还可以看出:冲锤在钻井液密度分别为1 100和1 200 kg/m3时各输出性能值的变化规律相似;钻井液密度较低时,冲锤的输出性能更好,即最大速度增加2.88%,最大冲击功提高5.85%,最大速度对应的冲击效率提高4.58%,但达到最大速度时所对应的位移相应增加1.73%,而冲锤总行程123 mm,达到最大速度时实际行程不足70 mm,故增加的位移可忽略影响。
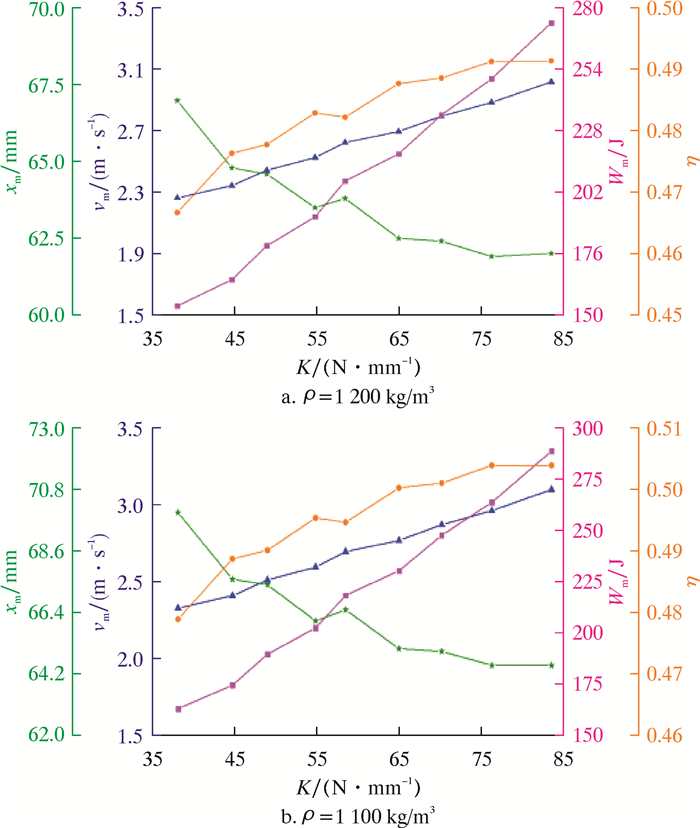
取不同弹簧刚度值修正各参数,求得冲锤各项输出性能值,结果如图 10所示。图 10中vm表示冲锤最大速度,xm表示冲锤最大速度对应的位移,Wm表示最大冲击功。
|
| 图 10 不同钻井液密度下冲锤输出性能随弹簧刚度的变化规律 Fig.10 Law of change of the hammer output performance with spring stiffness at different drilling fluid densities |
从图 10可以看出:随着冲锤弹簧刚度的增加,冲锤的最大速度呈现递增趋势,而冲锤位移则随着冲锤弹簧刚度的增加呈下降趋势,弹簧刚度越大,达到最大速度的位移越小,冲锤的冲击功和冲击效率均呈递增趋势;当弹簧刚度K=58.47 N/mm时,冲锤速度和冲击功的增量较为明显,而冲击效率降低,这是由于冲锤运动行程加长,阻力做负功,冲锤的动能增加量相对势能减少量降低;冲锤的位移较大与弹簧的选型有关,弹簧刚度受到弹簧设计参数约束,弹簧刚度不能一直增大,如弹簧刚度越大,弹簧外径、长度也随之增加,而井下震源发生器的内径是受限制的,故只能尽可能地选择较大刚度的弹簧,以满足震击需求。
从图 10还可以看出:冲锤在不同钻井液密度下工作时,随着弹簧刚度的增大,各输出性能值的变化规律基本相同,冲锤任一输出性能的增长趋势都是缓急交错式增长;当钻井液密度较小时,冲锤的输出性能较好,以弹簧刚度K=54.81 N/mm时为例,最大速度增加2.79%,最大冲击功提高5.66%,最大速度时对应的冲击效率提高2.59%,但达到最大速度所对应的位移相应增加4.09%,而冲锤总行程120 mm,达到最大速度时实际行程不足70 mm,故增加的位移可以忽略不计。因此,工具在相对较低的钻井液密度下,可以获得更佳的冲锤输出性能。
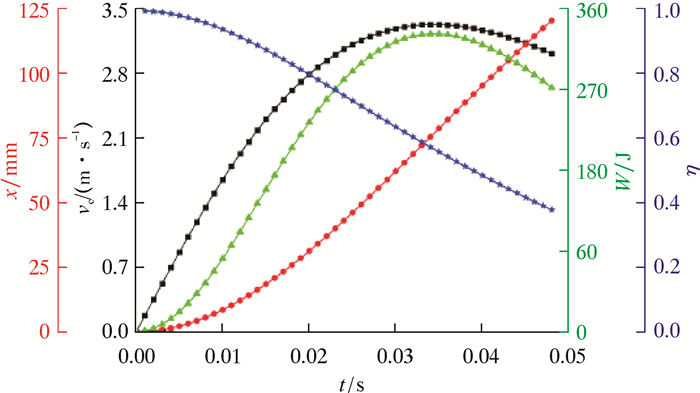
4.2 节流面积对冲锤输出性能的影响节流孔产生的阻力对冲锤性能影响较大,当钻井液密度ρ=1 100 kg/m3,质量M=60 kg,弹簧刚度K=76.26 N/mm时,以节流面积A=2 442.06 mm2为例,计算出冲锤的各项输出性能值,结果如图 11所示。
|
| 图 11 冲锤输出性能随时间的变化规律 Fig.11 Law of change of the hammer output performance with time |
从图 11可以看出:在冲锤运动行程内,随着时间的变化,冲锤的速度变化趋势是先增后减,这是由于弹簧势能逐渐减少,而流体阻力相对增加,导致冲锤加速度从正转负;冲锤位移呈现关于时间的二次函数关系递增,这是若干个匀加速运动叠加所得;冲锤冲击功变化趋势先增后减,与冲锤速度变化趋势相似,这是由于冲锤冲击功与速度的平方呈正相关;冲锤冲击效率呈递减趋势,这是因为冲锤总势能不只是转化为冲锤的动能,还转化为其他形式的能量;而斜率绝对值变化先增加后减小,反映阻力在冲锤运动过程中阻碍能力逐渐增加之后趋于平稳。
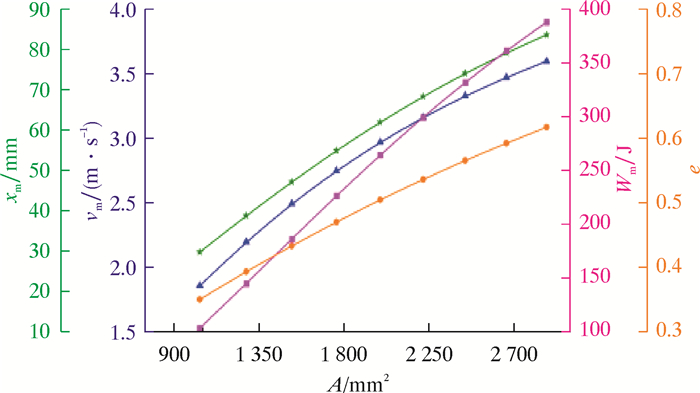
取不同节流面积并修正各参数,求得冲锤各项输出性能值,结果如图 12所示。图 12中e表示能量利用率。
|
| 图 12 冲锤输出性能随节流面积的变化规律 Fig.12 Law of change of the hammer output performance with throttling area |
从图 12可以看出:随着节流面积的增加,冲锤的各项输出性能呈现递增趋势,且增长速率逐渐缓慢,这是因为节流面积变大,对冲锤的阻力变小,冲锤动能相对增加;冲锤位移的增加是因为阻力随着节流面积的增大而减小,从而加速度减少为负的时间延长,达到最大速度的时间也会延长,则位移增加。为了满足冲锤的震击强度要求,铁砧上所开节流孔不能一直增大,因此只能在满足强度要求的情况下,适当增加节流面积,以获得更大的震击力。
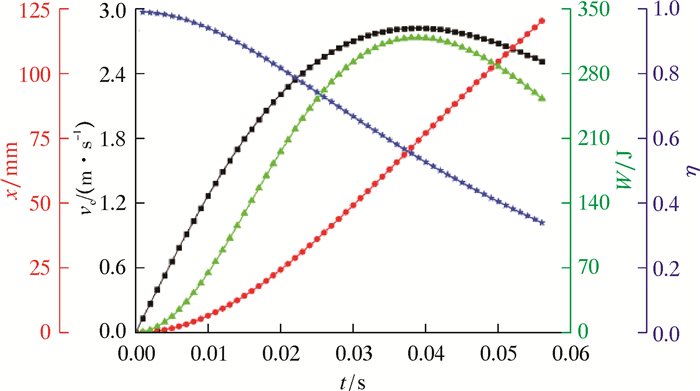
4.3 冲锤质量对冲锤输出性能的影响冲锤质量对冲锤冲击功也有较大影响,当钻井液密度ρ=1 100 kg/m3,节流面积A=1 990.51 mm2,弹簧刚度K=76.26 N/mm时,以冲锤质量M=80 kg为例,计算出冲锤的各项输出性能值,结果如图 13所示。
|
| 图 13 冲锤输出性能随时间的变化规律 Fig.13 Law of change of the hammer output performance with time |
从图 13可以看出:在冲锤运动行程内,随着时间的变化,冲锤各项输出性能变化规律与不同节流面积条件下相似,即速度和冲锤冲击功变化趋势是先增后减;冲锤位移呈现关于时间的二次函数关系递增;冲锤冲击效率呈递减趋势。
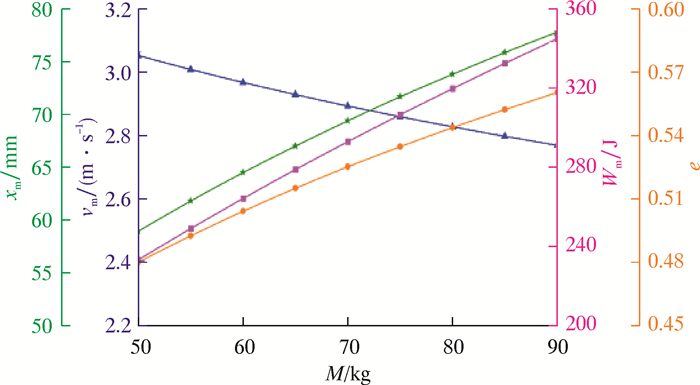
取不同冲锤质量并修正各参数,求得冲锤各项输出性能值,结果如图 14所示。
|
| 图 14 冲锤输出性能随冲锤质量的变化规律 Fig.14 Law of change of the hammer output performance with mass of hammer |
从图 14可以看出:随着冲锤质量的增加,冲锤的最大速度呈现下降趋势,这是由于冲锤合外力变化不明显,冲锤质量增加相对突出,从而使得加速度变小;冲锤的冲击功呈现递增趋势,是由于冲击功与冲锤质量和冲锤速度的乘积正相关,冲锤质量增加量相对于冲锤速度减少量更大,使得冲击功呈增长趋势;冲击效率呈现递增趋势并趋于平缓,这是因为冲锤总势能转化为冲锤动能的量随着冲锤质量的增加而提高,但冲锤质量增加量相对于冲锤速度减少量变化并不明显,使得冲击功增量相对减少。
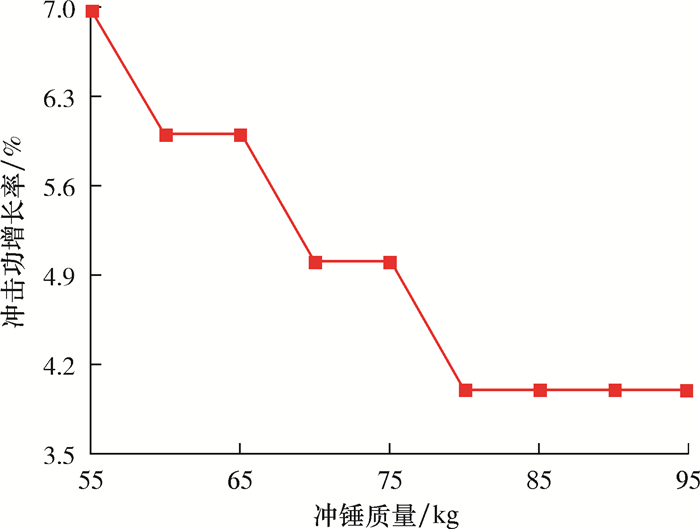
冲锤冲击功增长率随质量的变化规律如图 15所示。从图 15可以看出:前期冲击功相对增长最大7%,之后增长只有4%。因此,冲击效率增量趋于缓慢,冲锤位移的增加是因为弹簧势能不变的情况下,随着冲锤质量的增加,冲锤要获得更高的动能则需要重力做更多的功,而这需要增加位移量;冲锤冲击功后期增长缓慢,意味着冲锤质量对冲击功影响不明显,这为冲锤质量的选择提供了依据,即可以选择较小的冲锤质量。
|
| 图 15 冲锤冲击功增长率随质量的变化规律 Fig.15 Law of change of the hammer' s impact energy increase rate with mass of hammer |
根据不同参数条件下冲锤输出性能的变化规律,可以认为钻井液密度ρ=1 100 kg/m3,弹簧刚度K=76.26 N/mm,冲锤质量M=80 kg,节流面积A=2 875.19 mm2时,冲锤的输出性能最好。
5 结论(1) 冲锤在运动过程中冲击速度和冲击功呈先增后减趋势变化,存在最大值,且在钻井液密度较小时,冲锤输出性能较好。
(2) 弹簧刚度越大,冲锤冲击速度、冲击功和冲击效率越大,而冲锤位移越小,但弹簧刚度受设计参数约束,只能尽可能取较大值。
(3) 随着节流面积的增大,冲锤各输出性能都呈现递增趋势,即冲锤冲击速度、冲击功、冲击效率和冲锤位移都在增加,但受到铁砧强度影响,节流面积只能尽可能取较大值。
(4) 冲锤质量不断增加,冲锤冲击功、冲击效率和冲锤位移也在增加,但冲击速度在减小,冲击功后期增长缓慢且趋于平稳。
| [1] |
夏磊. 侧钻井过程中的井眼防碰计算及应用[J]. 中国石油大学胜利学院学报, 2013, 27(1): 18-21. XIA L. Calculation and application of borehole collision prevention during side drilling[J]. Journal of Shengli College China University of Petroleum, 2013, 27(1): 18-21. |
| [2] |
刘茂森, 付建红, 白璟. 页岩气"井工厂"水平井组防碰技术研究[J]. 石油机械, 2016, 44(6): 14-18, 23. LIU M S, FU J H, BAI J. Anti-collision technology of horizontal well groups in shale gas "well factory"[J]. China Petroleum Machinery, 2016, 44(6): 14-18, 23. |
| [3] |
CLARK B, PHILLIPS W J, POEDJONO B. Anti-collision method for drilling wells: 20100271232[P]. 2008-06-24.
|
| [4] |
SHARMA N, MCDONALD M. Optimizing directional drilling while minimizing the risk of well collision in offshore drilling[R]. SPE 124246, 2009.
|
| [5] |
POEDJONO B, VAN C P. Anti-collision risk managementfor real-world well placement[R]. SPE 121094, 2009.
|
| [6] |
吕海川, 朱伟伦, 贾衡天, 等. 随钻VSP测量中地震波场的数值模拟[J]. 石油机械, 2017, 45(2): 10-12, 44. LV H C, ZHU W L, JIA H T, et al. Numerical simulation of seismic wave field in VSP-WD[J]. China Petroleum Machinery, 2017, 45(2): 10-12, 44. |
| [7] |
唐洪林, 杨春旭, 仲俊霖, 等. 长水平段水平井钻井技术在ZC1井的应用[J]. 石油机械, 2017, 45(1): 23-29. TANG H L, YANG C X, ZHONG J L, et al. Applicati-on of long lateral section horizontal well drilling technology in Well ZC1[J]. China Petroleum Machinery, 2017, 45(1): 23-29. |
| [8] |
RECTOR J W, MARION B P. The use of drill-bit energy as a down-hole seismic source[J]. Geophysics, 1991, 56(5): 628-634. |
| [9] |
王敏生, 王智锋, 李作会, 等. 水力脉冲式钻井工具的研制与应用[J]. 石油机械, 2006, 34(5): 27-28. WANG M S, WANG Z F, LI Z H, et al. Development and application of hydraulic pulse drilling[J]. China Petroleum Machinery, 2006, 34(5): 27-28. |
| [10] |
刘刚, 于长广, 何保生, 等. 机械式井下震源设计及试验研究[J]. 石油机械, 2013, 41(11): 17-20. LIU G, YU C G, HE B S, et al. Design and experimental study of mechanical downhole seismic source[J]. China Petroleum Machinery, 2013, 41(11): 17-20. |
| [11] |
董照显.用于丛式井防碰监测的井下震源设计[D].青岛: 中国石油大学(华东), 2013. DONG Z X. The downhole seismic source design for anticollision monitoring in cluster wells[D]. Qingdao: China University of Petroleum (Huadong), 2013. |
| [12] |
叶晓平, 李博, 刘晓阳, 等. 差动式双作用液动冲击器冲锤动力学方程的研究和应用[J]. 地质与勘探, 2018, 54(4): 801-809. YE X P, LI B, LIU X Y, et al. Research and application of differential double-acting hydraulic hammer dynamics equations[J]. Geology and Exploration, 2018, 54(4): 801-809. |
| [13] |
林建亚, 何存兴. 液压元件[M]. 北京: 机械工业出版社, 1988. LIN J Y, HE C Y. Hydraulic component[M]. Beijing: China Machine Press, 1988. |
| [14] |
ESPINOSA H G, JAMES D A, KELLY S, et al. Sports monitoring data and video interface using a gui auto generation Matlab tool[J]. Procedia Engineering, 2013, 60: 243-248. |
| [15] |
徐兴平, 王西录, 冯帆, 等. 基于深海铺管船托管架系统调整的软件开发[J]. 石油机械, 2019, 47(6): 67-72. XU X P, WANG X L, FENG F, et al. Software development for adjustment of stinger system on deepwater pipe-laying ship[J]. China Petroleum Machinery, 2019, 47(6): 67-72. |


