0 引言
向深层进军是油气勘探开发的发展方向,超深、特深水平井定向钻井技术是实现深层油气高效勘探开发的重要技术手段。超深、特深定向/水平井在常规滑动导向过程中工具面调控效率偏低,工程经验依赖性较强,是制约定向钻井效率提高的关键因素。以顺北油田为例,该油田储层埋藏深度多在7 500 m以上,以定向/水平井为主要开发方式[1-2]。由于摩阻扭矩大,井超深、钻具柔性强及影响因素多(钻进参数、钻具结构、井身结构、井眼轨迹),所以工具面可控性差,工具面调控效率低,部分井工具面调控时间超过2 h,严重影响了定向钻井工程效率及质量,而明确常规导向钻井过程中扭矩传递规律对提高工具面调控效率具有重要的工程意义。
智能化、自动化钻井是油气井工程领域当前的发展方向,而自动滑动定向钻井是自动化钻井的重要组成部分。由于钻井工程的复杂性及参数的不确定性,自动化控制钻井实现的技术难度较大。国内对自动滑动钻井控制技术的研究较少,且研究水平与国外存在一定差距。国外研制的Slider和ROCKIT等[3-5]钻柱自动扭摆系统已实现商业化应用,取得了良好的提速效果。明确钻柱扭矩的传递规律是实现钻柱自动扭摆、工具面自动调控的核心理论基础之一。为此,本文将滑动导向钻井钻具系统视为扭转弹性系统并进行简化处理,以该系统为控制对象进行了动力学建模,通过转换计算,给出了井口钻具转角到井底工具面角的传递函数,分析了不同因素对扭矩传递的影响规律,以期为提高特深定向/水平井工具面调控效率提供指导,为自动化钻井技术研究打下理论基础。
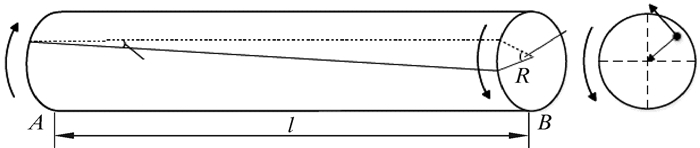
1 基础数学模型 1.1 钻具系统模型将钻具系统视为扭转弹性系统,其简化模型如图 1所示。由剪切胡克定律可知,各点的切应力为τρ=Kρ,并且满足力矩微分假设条件,即:
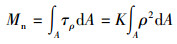
|
(1) |
|
| 图 1 钻具系统简化模型示意图 Fig.1 Simplified model of drilling tool system |
若令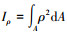
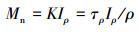
|
(2) |
即:
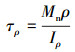
|
(3) |
对于内径为d、外径为D的钻杆,其极惯性矩表达式为:
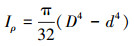
|
(4) |
深井内的钻具系统转角较小,此时有:
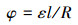
|
(5) |
由剪切胡克定律可知
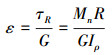
|
(6) |
联立式(5)和式(6)可得:
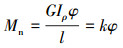
|
(7) |
若将钻具系统视为扭转弹性系统,则其弹性刚度为:
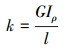
|
(8) |
式中:τp为任一点切应力,Pa;K为假设弹性刚度,N/(°);ρ为任一点在横截面上的半径,m;Mn为扭转力矩,N·m;Iρ为极惯性矩,m4;d为钻杆内径,m;φ为钻柱系统两端相对转角,(°);ε为切应变,无量纲;l为施加力矩两端长度,m;R为钻柱系统当量半径,m;τR为半径为R处的切应力,Pa;G为弹性模量,Pa;k为钻杆系统扭转弹性刚度,N/(°)。
1.2 摩阻/扭矩计算模型钻具系统的摩阻/扭矩沿井筒的分布规律对滑动导向过程中的扭矩传递规律至关重要。在钻具系统动力学建模过程中,将钻具系统视为阻尼系统,阻尼系数确定的关键在于钻具系统内的摩阻系数。目前摩阻扭矩计算模型主要分为软杆模型和钢杆模型,超深、特深定向/水平井通常具有井超深和钻具尺寸较小等工程特征,因此采用软杆模型进行分析更符合工程实际[6-10]。
软杆计算模型的假设条件为:①管柱类似于软绳,其刚性很小,可以忽略;②管柱与井眼轴线形状完全一致,且与井壁连续接触;③井壁为近似刚性;④忽略管柱和井眼局部形状(如钻杆接头、扶正器和井径扩大等)对摩阻扭矩的影响;⑤忽略钻柱动态因素的影响。
对钻杆微单元体进行受力分析,如图 2所示。图 2中,1平面为管柱微元所在的斜平面,2平面为过微元中点切线方向的铅垂面。以微元中点为原点,分别以中点的切线、主法线和副法线方向为3个坐标轴的方向建立微元随动坐标系(et,en,eb)。
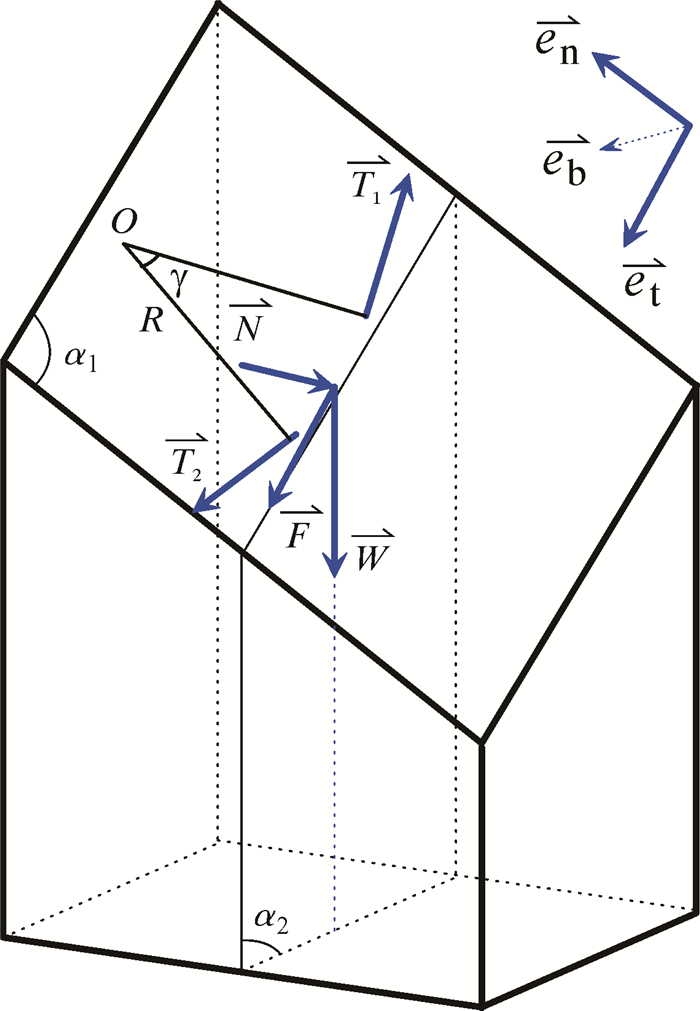
|
| 图 2 管柱微元受力分析 Fig.2 Infinitesimal drill string stress analysis |
将重力向随动坐标系3个坐标轴方向上分解,则有:
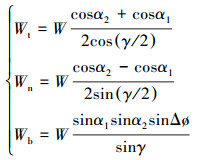
|
(9) |
解上述方程组并化简得:
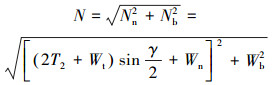
|
(10) |
根据接触正压力计算公式,推算各段摩阻扭矩,具体表达如下:
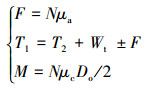
|
(11) |
其中:
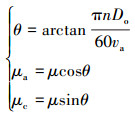
|
(12) |
式中:下标t, n, b表示3个方向;F为微元摩阻力,N;W为正压力,N;θ为传递角度,(°);M为微元摩扭矩,N·m;N为微元接触正压力,N;μ为摩擦因数;μa为微元轴向摩阻系数分量;μc为微元切向摩阻系数分量;T1为微元上端轴向力,N;T2为微元下端轴向力,N;Do为管柱外径,m;n为微元转速,r/min;va为微元轴向速度,m/s。
根据钻具软杆模型可以获取钻具在井筒内摩阻扭矩的分布规律,从而确定钻具系统动力学模型内的阻尼系数。
1.3 动力学模型假设滑动钻进过程中钻压保持稳定,此时钻头上的反扭矩假定为恒定值,将钻具与井壁间的摩擦视为黏性摩擦,则滑动过程中的动力学模型可视为如图 3所示。图 3中c为阻尼系数。
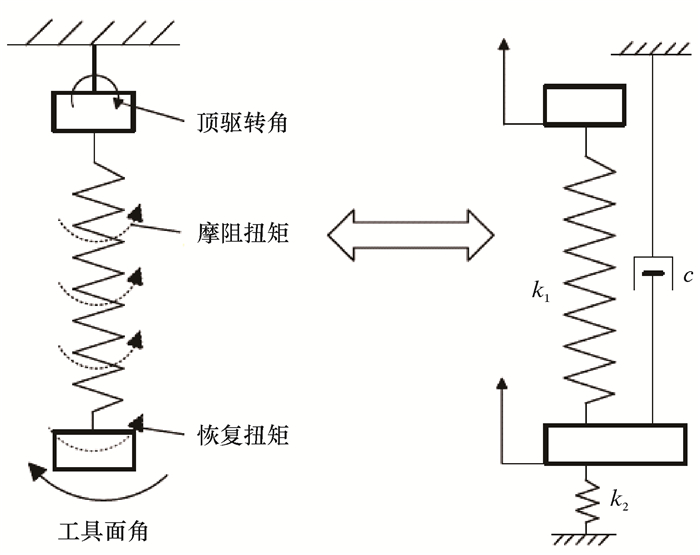
|
| 图 3 常规导向过程中钻具动力学模型示意图 Fig.3 Diagram of dynamic model for drilling tools during conventional steering |
将其初步简单视为双自由度平动系统(根据钻具结构和弹性刚度增加该系统的自由度),则该系统的动力学方程为[11-13]:
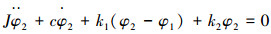
|
(13) |
式中:φ2为井口钻具转动角度,(°);φ1为井底工具面转动角度,(°);k1为上部钻具系统弹性刚度,kN/(°);k2为下部钻具系统弹性刚度,kN/(°);J为钻柱系统等效转动惯量。
将公式(13)进行拉普拉斯变换,则井口钻具转角到井底工具面角的传递函数为[14-15]:
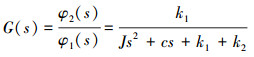
|
(14) |
设
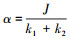
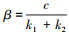
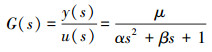
|
(15) |
本文主要分析井口钻具扭转角度、钻具结构尺寸、井深及井眼轨迹等对井口钻具扭矩到井底钻具传递规律的影响。
模型参数设置:井深9 000 m,套管内摩阻系数0.25,裸眼内摩阻系数0.30,井身结构如表 1所示,井眼轨迹如表 2所示。
| 开钻顺序 | 钻头直径/mm | 井深/m | 套管外径/mm | 套管下深/m |
| 0 | 660.4 | 50 | 508.0 | 50 |
| 1 | 444.5 | 1 500 | 339.7 | 1 498 |
| 2 | 311.2 | 5 000 | 250.8 | 4 998 |
| 3 | 215.9 | 8 500 | 177.8 | 8 498 |
| 4 | 149.2 | 9 000 |
| 井深/ m |
井斜/ (°) |
方位角/ (°) |
垂深/ m |
南北位 移/m |
东西位 移/m |
每30 m狗 腿度/(°) |
| 0 | 0 | 0 | 0.00 | 0.00 | 0.00 | 0 |
| 8 850 | 0 | 0 | 8 850.00 | 0.00 | 0.00 | 0 |
| 9 000 | 90 | 0 | 8 945.49 | 95.49 | 0.00 | 18 |
| 9 200 | 90 | 0 | 8 945.49 | 295.49 | 0.00 | 0 |
钻具组合设置为外径127.0和139.7 mm两种:①ø149.2 mm钻头+ø120.0 mm单弯螺杆+单流阀+ø88.9 mm无磁承压钻杆1根+ø120.0 mm MWD短节+ø88.9 mm HWDP+ø88.9 mm DP+ø127.0 mm DP;②ø149.2 mm钻头+ø120.0 mm单弯螺杆+单流阀+ø88.9 mm无磁承压钻杆1根+ø120.0 mm MWD短节+ø88.9 mm HWDP+ø88.9 mm DP+ø139.7 mm DP。
2.1 井口钻具扭转角度按照上述模型参数,设置井口钻具扭转角度分别为180°、360°、540°和720°,分析不同井口钻具扭转角度下井底工具面的动态变化规律,如图 4和表 3所示。
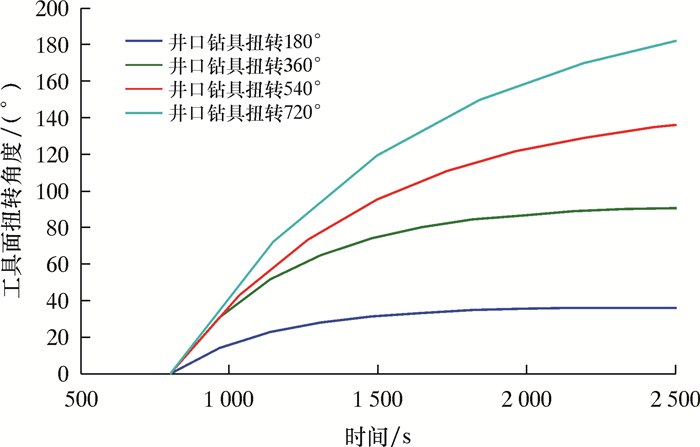
|
| 图 4 不同井口钻具扭转角度下工具面动态变化曲线 Fig.4 Tool face performance variation curve at different torsional angles of wellhead drilling tools |
| 井口扭转 角度/(°) |
达到稳态 时间/s |
工具面变化 角度/(°) |
传递效率/% |
| 180 | 864 | 36.36 | 20.2 |
| 360 | 903 | 92.16 | 25.6 |
| 540 | 956 | 147.96 | 27.4 |
| 720 | 1 127 | 208.08 | 28.9 |
从图 4及表 3可见:井口钻具扭转角度越大,井底工具面达到稳态所需的时间越长,但总体上影响不大,基本在15~20 min之间;井口钻具扭转角度越大,扭矩传递效率越高。这是因为扭矩从井口到井底的传递过程是扭转能量的传递过程,在传递过程中存在能量损耗,能量损耗基本一定,此时从井口输入的扭转能量越高,则扭矩传递效率越高。
2.2 钻具结构尺寸按照上述模型参数,分析了井口钻具扭转角度360°时,两种不同尺寸钻具组合的井底工具面的动态变化规律,如图 5及表 4所示。从图 5及表 4可见:钻具尺寸越大,井底工具面达到稳态所需的时间越短;钻具尺寸越大,扭矩传递效率也越高。这是由于钻具外径越大,钻具扭转刚度越大,在扭转能量传递过程中沿程能量损失较少,同时传递速度也越快。
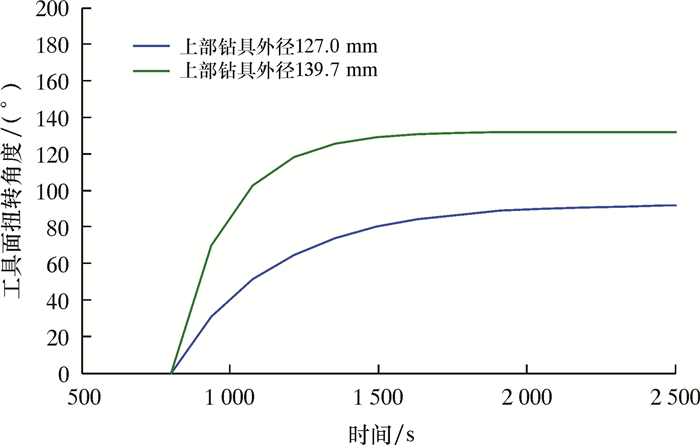
|
| 图 5 不同尺寸钻具工具面动态变化曲线 Fig.5 Tool face performance variation curve for different sizes of drilling tools |
| 钻具外 径/mm |
达到稳态 时间/s |
工具面变化 角度/(°) |
传递效率/% |
| 127.0 | 903 | 92.16 | 25.6 |
| 139.7 | 675 | 132.12 | 36.7 |
2.3 井深
按照上述模型参数,设不同井深时的水平段长度和狗腿度等井眼轨迹参数均相同,井口钻具扭转角度为360°,分析井深3 000、6 000和9 000 m时井底工具面的动态变化规律,如图 6和表 5所示。
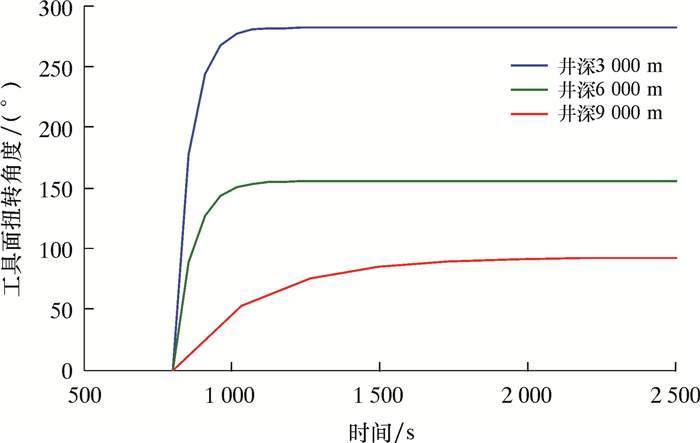
|
| 图 6 不同井深条件下工具面动态变化曲线 Fig.6 Tool face performance variation curve at different well depths |
| 井深/m | 达到稳态时间/s | 工具面变化角度/(°) | 传递效率/% |
| 3 000 | 211 | 281.88 | 78.3 |
| 6 000 | 431 | 155.52 | 43.2 |
| 9 000 | 903 | 92.16 | 25.6 |
从图 6及表 5可见:井深越深,井底工具面达到稳态所需的时间越长,且对工具面达到稳态的时间影响越显著;在造斜段及水平段轨迹参数相同的条件下,井深9 000 m时,井底工具面达到稳态的时间比井深3 000 m慢了约12 min;井深越深,扭矩传递效率越低,因此,井深越深,工具面调控难度越大。
2.4 井眼轨迹按照上述模型参数,分析了4种不同井眼轨迹的井底工具面的动态变化规律,如图 7和表 6所示。井口钻具扭转角度均为360°,4种不同井眼轨迹条件下工具面变化数据如表 7所示。

|
| 图 7 不同井眼轨迹条件下工具面动态变化曲线 Fig.7 Tool surface performance variation curve at different wellbore trajectories |
| 井眼 轨迹 |
井深/ m |
井斜/ (°) |
方位 角/(°) |
垂深/ m |
南北位 移/m |
东西位 移/m |
每30 m狗 腿度/(°) |
| 0 | 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | |
| ① | 8 950 | 0 | 0.01 | 8 950.00 | 0.00 | 0.00 | 0 |
| 9 000 | 30 | 0.00 | 8 997.75 | 12.79 | 0.00 | 18 | |
| 0 | 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | |
| 0 | 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | |
| ② | 8 900 | 0 | 0.00 | 8 900.00 | 0.00 | 0.00 | 0 |
| 9 000 | 60 | 0.00 | 8 982.70 | 47.75 | 0.00 | 18 | |
| ③ | 0 | 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0 |
| 8 850 | 0 | 0.00 | 8 850.00 | 0.00 | 0.00 | 0 | |
| 9 000 | 90 | 0.00 | 8 945.49 | 95.49 | 0.01 | 18 | |
| 9 600 | 90 | 0.00 | 8 945.49 | 695.49 | 0.06 | 0 | |
| 0 | 0 | 0.00 | 0.00 | 0.00 | 0.00 | 0 | |
| ④ | 8 850 | 0 | 0.00 | 8 850.00 | 0.00 | 0.00 | 0 |
| 9 000 | 90 | 0.00 | 8 945.49 | 95.49 | 0.00 | 18 | |
| 9 200 | 90 | 0.00 | 8 945.49 | 295.49 | 0.00 | 0 |
| 井眼轨 迹序号 |
达到稳态 时间/s |
工具面变化 角度/(°) |
传递效率/% |
| ① | 548 | 45.7 | 164.52 |
| ② | 763 | 34.1 | 122.76 |
| ③ | 903 | 25.6 | 92.16 |
| ④ | 1 347 | 21.3 | 76.68 |
如图 7和表 7所示,对比第一种及第二种井眼轨迹可知,在相同井深条件下,井斜角越大,井底工具面达到稳态所需的时间越长,并且井口到井底扭矩的传递效率越低。这是因为井斜角越大,沿程摩阻扭矩及能量损耗越大,所以扭矩传递效率越低,传递时间越长。
对比第三种及第四种井眼轨迹可知,水平段长度越长,井底工具面达到稳态所需的时间越长,井口到井底扭矩的传递效率越低,而且水平段长度对扭矩传递影响较为显著。这是因为水平段越长,沿程摩阻扭矩及能量损耗越大,所以扭矩传递效率越低,传递时间越长。
通过上述分析,钻柱扭转弹性刚度和黏滞阻尼系数对钻柱扭矩传递规律影响显著。为此,提出了提高工具面调控效率的工程建议。
(1) 提高钻柱扭转弹性刚度。调整钻具组合结构,尽量采用大尺寸钻具;采用大扭矩螺杆钻具,钻柱系统稳定性好。
(2) 降低黏滞阻尼系数。改善钻井液润滑性能,减小摩擦因数;强化钻进参数,保证井眼清洁度。
3 模型优化 3.1 工程实例井简介以特深定向井顺北Y1井为工程实例,对比分析评价模型的精度及合理性,为模型优化指明方向。顺北Y1井是部署在顺北油气田特深层的重点探井,该井在四开进行定向施工,井眼直径为215.9 mm,井身结构如表 8所示。所用钻具组合为:ø215.9 mm钻头(PDC)+直螺杆+单流阀+ø158.8 mm无磁钻铤1根+ø214.0 mm螺旋扶正器+ø158.8 mm钻铤1根+ø214.0 mm螺旋扶正器+ø158.8 mm钻铤18根+ø158.8 mm随钻震击器+ø158.8 mm钻铤2根+旁通阀+ø127.0 mm加重钻杆15根+ø127.0 mm钻杆+ø139.7 mm钻杆。
| 开钻顺序 | 钻头直径/mm | 井深/m | 套管外径/mm | 套管下深/m |
| 0 | 914.4 | 20 | 720.0 | 20 |
| 1 | 660.4 | 600 | 508.0 | 599 |
| 2 | 444.5 | 5 417 | 339.7 | 5 415 |
| 3 | 311.2 | 7 610 | 250.8+244.5 | 7 611 |
| 4 | 215.9 | 8 400 | — | — |
3.2 结果对比分析
记录顺北Y1井两处井深的实测工具面动态变化情况,并与模型计算结果进行对比分析。所选两处井深的井眼轨迹参数如表 9所示。
| 井深/ m |
井斜/ (°) |
方位角/ (°) |
垂深/ m |
南北位 移/m |
东西位 移/m |
每30 m狗 腿度/(°) |
| 8 161.19 | 81.5 | 284.1 | 7 906.13 | 122.10 | -349.64 | 1.619 |
| 8 328.15 | 82.5 | 285.6 | 7 931.37 | 163.81 | -509.29 | 1.054 |
顺北Y1井两处实测工具面动态变化情况与模型计算结果对比如图 8所示。
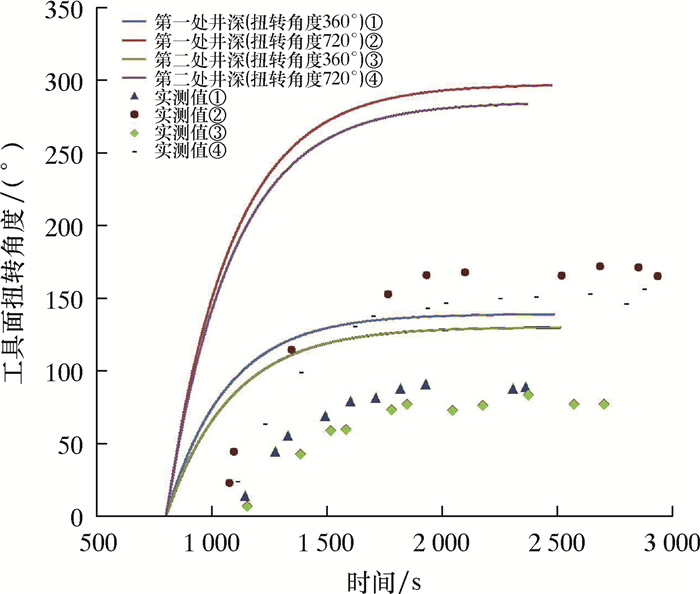
|
| 图 8 模型计算结果与实测数据对比 Fig.8 Comparison of model calculation results with measured data |
从图 8可见,实测数据与模型计算结果变动趋势基本一致,但在扭矩传递效率、延迟时间和工具面达到稳态时所需的时间等方面均存在一定偏差,具体如下。
(1) 模型计算的扭矩传递效率较实测数据偏高,实测扭矩传递效率为模型计算结果的50%~60%。
(2) 模型计算的工具面到达稳态的时间较实测数据偏长,偏长幅度为200~300 s。
(3) 工程实际应用中,在井口钻具转动后,井底工具面变化存在一定的延迟时间。以顺北Y1井为例,该井的延迟时间为5~10 min,但在模型计算结果中,延迟时间为1~3 min,与工程实际应用存在差异。
分析模型计算结果存在偏差的原因主要有以下几个方面。
(1) 模型中仅将全井钻具系统设为双自由度系统,而工程实际应用中钻具系统为多自由度弹性系统,模型过于简单。
(2) 模型中的阻尼系数偏小,导致延迟时间与工程实际应用差异较大。模型中将阻尼系数进行了统一处理,而工程实际应用中各井段的阻尼系数均存在差异,需分段细化处理。
针对模型结果与工程实际应用的差异,从以下几个方面开展了模型优化。
(1) 将全井钻柱细化处理,分段确定弹性刚度,将模型假设为4~6个自由度的钻柱动力学模型。
(2) 分段细化处理摩阻系数及阻尼系数,利用工程数据进行反系数修正,以提高计算精度。
模型优化前、后计算结果如表 10所示。
| 序号 | 传递效率 | 稳态时间/s | |||||
| 优化前 | 优化后 | 实测数据 | 优化前 | 优化后 | 实测数据 | ||
| ① | 0.387 | 0.253 | 0.203 | 663 | 523 | 412 | |
| ② | 0.413 | 0.302 | 0.201 | 736 | 563 | 467 | |
| ③ | 0.362 | 0.256 | 0.193 | 718 | 643 | 534 | |
| ④ | 0.396 | 0.289 | 0.211 | 753 | 614 | 486 | |
4 结论
(1) 根据常规导向钻井工程特点,建立滑动导向过程中钻具动力学计算模型,得到了钻具井口扭转角度与井底工具面扭转角度间的函数关系,分析了多种因素对钻具扭矩传递的影响规律,明确了影响钻柱扭矩传递效率的关键因素——钻柱扭转弹性刚度和黏滞阻尼系数,给出了提高工具面调控效率的工程建议。
(2) 模型与工程实际应用的对比分析结果指明了模型优化方向,优化后的模型计算精度在70%以上,影响规律趋势与工程实际应用很接近。针对现有模型的计算偏差,需从钻压影响规律和阻尼系数细化处理等方面进一步攻关。
| [1] |
管志川, 陈庭根. 钻井工程理论与技术[M]. 2版. 东营: 中国石油大学出版社, 2017. GUAN Z C, CHEN T G. Drilling engineering theory and technology[M]. 2nd ed. Dongying: China University of Petroleum (Huadong) Press, 2017. |
| [2] |
赵志国, 白彬珍, 何世明, 等. 顺北油田超深井优快钻井技术[J]. 石油钻探技术, 2017, 45(6): 8-13. ZHAO Z G, BAI B Z, HE S M, et al. Optimization of fast drilling technology for ultra-deep wells in the Shunbei Oilfield[J]. Petroleum Drilling Techniques, 2017, 45(6): 8-13. |
| [3] |
徐文, 刘新立, 马瑞, 等. 基于顶部驱动的滑动钻井导向控制技术[J]. 石油机械, 2013, 41(3): 27-30. XU W, LIU X L, MA R, et al. Top drive-based steering control technology for slide drilling[J]. China Petroleum Machinery, 2013, 41(3): 27-30. DOI:10.3969/j.issn.1001-4578.2013.03.006 |
| [4] |
易先中, 吉源强, 盛拥军, 等. 自动滑动钻井控制系统的研究进展[J]. 石油机械, 2013, 41(9): 12-15. YI X Z, JI Y Q, SHENG Y J, et al. Research progress in automatic slide drilling control system[J]. China Petroleum Machinery, 2013, 41(9): 12-15. DOI:10.3969/j.issn.1001-4578.2013.09.003 |
| [5] |
武广瑷, 何保生, 邓果, 等. 工具面动态控制钻井系统的室内研究[J]. 石油机械, 2014, 42(9): 15-18. WU G A, HE B S, DENG G, et al. Laboratory study on tool face dynamic control drilling system[J]. China Petroleum Machinery, 2014, 42(9): 15-18. DOI:10.3969/j.issn.1001-4578.2014.09.004 |
| [6] |
SALAR B, HANI Q. Reservoir candidate screening is critical to ensure successful application of under balanced drilling technology-case study[R]. SPE 105448, 2007.
|
| [7] |
SPOONER M, MAGEE K, OTTO M, et al.The application of high temperature polymer drilling fluid on smackover operations in Mississippi[C]//AADE 2004 Drilling Fluids Conference, held at the Radisson Astrodome in Houston, Texas, April 6-7, 2004.
|
| [8] |
AI-SAEEDI M J, AI-KHAYAT B, AI-ENEZI, et al. Successful HPHT application of potassium formate/manganese tetra-oxide fluid helps improve drilling characteristics and imaging log quality[R].SPE 132151, 2010.
|
| [9] |
李乾, 纪国栋, 张辉, 等. 滑动钻进中顶驱扭摆减阻控制技术研究[J]. 石油机械, 2018, 46(5): 1-6. LI Q, JI G D, ZHANG H, et al. Drag reduction control for torsion and osciuation in top drive system slide drilling[J]. China Petroleum Machinery, 2018, 46(5): 1-6. |
| [10] |
王秀亭, 汪海阁, 陈祖锡, 等. 大位移井摩阻和扭矩分析及其对钻深的影响[J]. 石油机械, 2005, 33(12): 6-9. WANG X T, WANG H G, CHEN Z X, et al. Analysis on friction drag and torque from extend reach wells and influence on well drilling depth[J]. China Petroleum Machinery, 2005, 33(12): 6-9. DOI:10.3969/j.issn.1001-4578.2005.12.002 |
| [11] |
钟晓宇, 刘佳鹏, 陆秋海, 等. 一种滑动导向钻井工具面自适应控制方法[J]. 自动化学报, 2019, 45(6): 1044-1054. ZHONG X Y, LIU J P, LU Q H, et al. An adaptive toolface control method for slide steering drilling[J]. Acta Automatica Sinica, 2019, 45(6): 1044-1054. |
| [12] |
MAIDLA E, HACI M. Understanding torque: the key to slide-drilling directional wells[C]//IADC/SPE Drilling Conference, March 2-4, 2004, Dallas, Texas, USA.DOI: http:Ⅱdx.doi.org/10.2118/87162-MS.
|
| [13] |
葛一楠, 唐毅谦, 喻晓红, 等. 自动控制原理[M]. 北京: 清华大学出版社, 2016: 169-170. GE Y N, TANG Y Q, YU X H, et al. Automatic control theory[M]. Beijing: Tsinghua University Press, 2016: 169-170. |
| [14] |
韩正之, 陈彭年, 陈树中. 自适应控制[M]. 北京: 清华大学出版社, 2014: 257-258. HAN Z Z, CHEN P N, CHEN S Z. A textbook for Adaptive control[M]. Beijing: Tsinghua University Press, 2014: 257-258. |
| [15] |
CHENG Z B, JIANG W, REN G X, et al. A multibody dynamical model for full hole drillstring dynamics[J]. Applied Mechanics and Materials, 2013, 378: 91-96. DOI:10.4028/www.scientific.net/AMM.378.91 |


