2. 西南石油大学油气藏地质及开发工程国家重点实验室;
3. 西南油气田四川长宁天然气开发有限责任公司;
4. 中国石油西南油气田公司工程技术研究所
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploration, Southwest Petroleum University;
3. Southwest Oil and Gas Field Sichuan Changning Natural Gas Development Co., Ltd.;
4. Engineering and Technology Research Institute of PetroChina Southwest Oil and Gas Field Company
0 引言
水力压裂是地层气开采过程中广泛运用的方法,利用水力压裂在页岩层中开采页岩气也为全球的天然气产业注入了新的活力。但相较于其他的地层气藏,低渗透性的页岩层大大加剧了开采的难度,因此需要高压力、大排量的工况来实现页岩气的压裂[1-4]。由于开采环境的严峻和较大的施工排量,相较于其他地层气的开采,页岩气套管在压裂施工时的损坏率更高[5]。因此,针对页岩气开采的特殊施工情况,有必要开展压裂工况对页岩气套管应力分布影响的研究。
中国在页岩气资源潜力评价和勘探开发先导性试验上取得了重要进展,正在寻求实现页岩气资源的有效开发。但与北美相比, 中国页岩气形成与发展具有明显的特殊性, 许多地质与开发难题亟待解决[6-8]。蒋廷学等[9]对深层页岩气水平井体积压裂技术做了相关研究,提出了针对性与现场可操作性均强的深层页岩气水平井体积压裂技术方案。中国地质大学的裴森龙[10]针对龙马溪组页岩气开采中使用的多级压裂技术开展了适应性研究,选出了一套适用于我国川南龙马溪组页岩的压裂方法,认为龙马溪组页岩可以采用固井滑套多级压裂技术+混合压裂液体系+树脂包层低密度陶粒支撑剂进行压裂作业。何启平等[11]结合威远-长宁地区返排液成分分析,初步认为影响返排液回用的主要因素是返排液中的离子种类和含量,通过室内研究提出了采用稀释法和抗盐降阻剂等方法,实践验证表明,可根据返排液水质特点、工艺需求和成本核算形成不同处理方案。刘飞等[12]针对页岩气井钻井过程中套管磨损可能导致套管抗内压强度和抗挤强度降低的问题, 建立了钻杆与套管磨损的计算模型,分析了页岩气井钻井过程中套管磨损机理, 研究了套管钢级、井眼曲率、钻井时间和钻杆拉力等因素对套管磨损的影响。国内外学者对页岩气水泥环完整性的问题做了大量研究,建立了井底工况下的界面裂缝扩展数学模型,推导出了高压压裂液促使界面裂缝扩展长度的理论公式[13-16]。徐华翔[17]针对目前关于页岩气水泥石固井没有考虑射孔这一因素的影响, 进行了压裂条件下页岩气固井水泥石力学性能研究, 并在此基础上给出了页岩气固井水泥石性能的优选建议。田中兰等[18]针对页岩气水平井的特点, 以提高钻井质量(DQ)为核心, 从设计和施工工艺等方面提出了井筒完整性控制对策:①修订页岩气井套管设计计算方法和校核标准;②优化井身结构和全井眼轨迹设计;③提高钻井质量;④优化水泥石性能并校核压裂过程中水泥石的密封完整性等。
近年来,国内外多数专家开始使用有限元软件对套管损伤进行机理研究。但是,专门针对页岩气套管损伤的相关研究工作还比较少,针对不同压裂工况对页岩气套管应力分布的影响研究更是少见。本文采用有限元仿真方法,借助ANSYS有限元仿真模拟软件,对不同压裂工况下的页岩气套管应力分布开展了研究,得到了地层岩石弹性模量、水平地应力和井口施工压力对页岩气套管应力分布的影响规律。研究结果可为页岩气的开采工作和页岩气套管的损坏防治提供一定的指导。
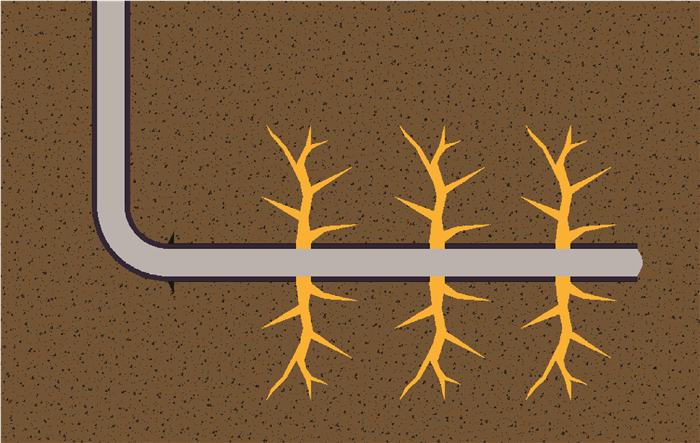
1 模型建立 1.1 物理模型 1.1.1 模型假设水平井压裂示意图如图 1所示。页岩气产层通常水平分布在地下的某一深度,为具有一定厚度的页岩层,也因其水平分布的特征,页岩气开采施工中大量使用到了水平井技术。页岩气井采用水泥环套管固井,在井眼与套管的环空中注入水泥浆,待其凝固后将套管和地层紧紧地结合在一起。参考此种固井形式,本文在模拟中建立套管-水泥环-地层模型。因压裂施工发生在页岩气井的水平井段,此井段受力最为复杂,所以主要研究水平井段套管在压裂工况下的应力分布。施工中,水平井的长度远远大于井眼直径,根据弹塑性力学的相关理论,可以将这个三维的受力问题看作一个平面问题,即只关注平行于套管某个径向截面方向应力的分布情况,而垂直于这个面的其他力都忽略不计。在考察数值计算结果时,只截取套管模型的中间截面观察应力分布情况。
|
| 图 1 水平井压裂示意图 Fig.1 Schematic diagram of horizontal well fracturing |
建立一段0.5 m长的套管-水泥环-地层模型,如图 2所示,取套管轴向的中间截面作为研究对象,考察其应力分布的特征。为了使套管的应力分析更加可靠合理,需要简化力学模型,做如下基本假设:

|
| 图 2 套管-水泥环-地层模型 Fig.2 Casing-cement sheath-formation model |
(1) 套管-水泥环-地层紧密接触,没有缝隙;
(2) 套管、水泥环、井眼均为理想的圆形;
(3) 套管、水泥环、地层均为各向同性的弹性材料;
(4) 不考虑温度变化对套管的影响;
(5) 模型中的接触不考虑相对位移和摩擦。
1.1.2 模型尺寸选用压裂施工中水平井段常用的套管尺寸建立模型,根据圣维南原理,取井径尺寸的5倍以上设置为地层尺寸,以此来消除边界效应对模型中套管受力的影响。模型长0.5 m,其余尺寸参数如下。
地层尺寸(长×宽):1 200 mm×1 200 mm;
水泥环外径:125.9 mm;
套管外径:139.7 mm;
套管内径:118.62 mm。
1.2 有限元模型 1.2.1 材料设置参考重庆礁石坝地区龙马溪组3 000 m深处页岩层岩石力学性能,确定地层材料的弹性模量和泊松比,该区域的岩石性能具有高弹性模量、低泊松比的特征。套管的材料选用P110钢级,参考此级别钢材力学性能设置套管材料参数。水泥环力学性能设定参考页岩气开采固井中常用的水泥性能。具体材料相关力学参数见表 1。
| 材料 | 密度/(kg·m-3) | 弹性模量/GPa | 泊松比 |
| 地层 | 2 600 | 38.37 | 0.218 |
| 水泥环 | 1 950 | 7.00 | 0.200 |
| 套管 | 7 850 | 210.00 | 0.300 |
1.2.2 网格化
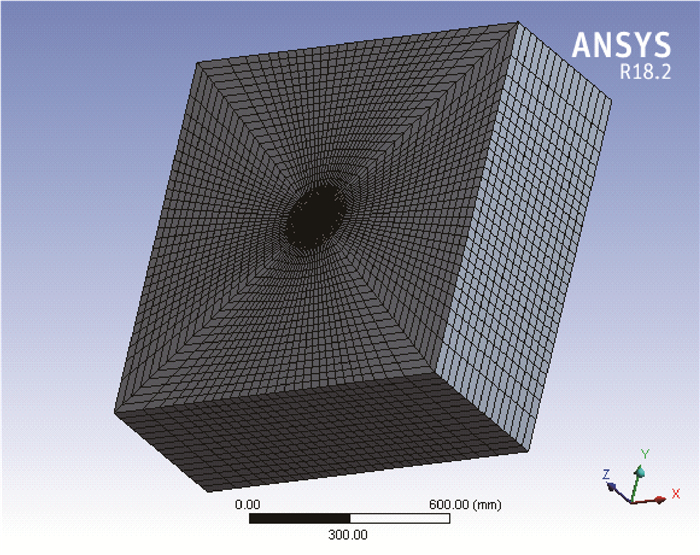
对已经建立的套管-水泥环-地层几何模型进行有限元网格划分,在划分网格时,注意采用“外疏内密”的方法。另外,在几何体模型轴线方向的一个面上采用映射控制来划分网格,这样得到的网格大小均匀、形状合理,对提高计算求解的效率和准确性有益。网格单元采用六面体单元类型,划分时,地层的网格尺寸大小设置为20 mm,水泥环的网格尺寸大小设置为5 mm,套管的网格尺寸大小设置为2 mm。网格划分出来的节点总数为1 671 330个,单元总数为366 683个。网格划分结果如图 3所示。
|
| 图 3 网格划分结果 Fig.3 Meshing result |
1.2.3 边界条件
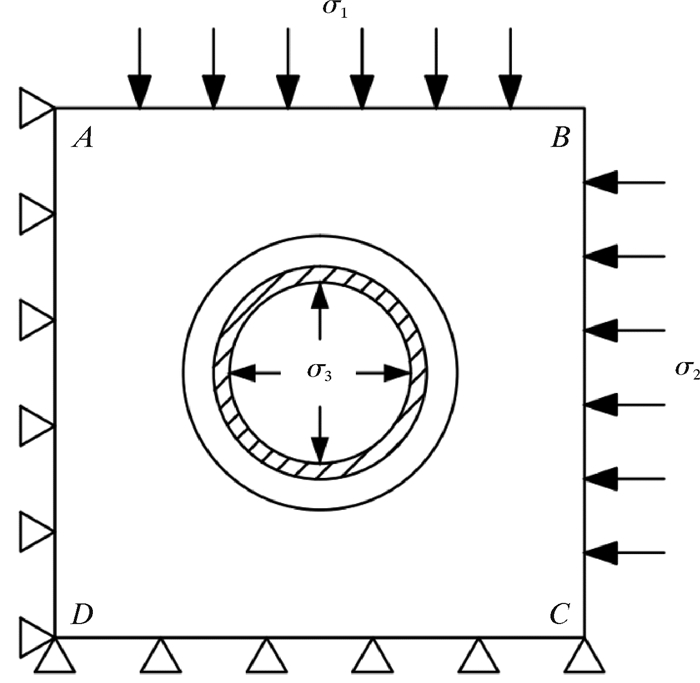
页岩气井水平段套管在地层中主要承受来自地层中地应力的挤压作用,参考龙马溪组页岩气产层地应力场测量数据的平均值,取垂向地应力σ1= 53.68 MPa、水平地应力σ2 =48.63 MPa。参考龙马溪组页岩气井的实际钻井工况,其井口施工压力p=75 MPa,根据计算可得压裂施工时地层中压裂区域的套管内壁压力σ3= 111.38 MPa。如图 4所示,建立模型受力的边界条件,图中的AD边和DC边设置为全约束,AB边设置来自于上覆地层挤压的垂向地应力σ1,BC边设置为水平挤压的水平地应力σ2,套管内壁受到法向压力σ3。
|
| 图 4 模型受力边界条件 Fig.4 Boundary conditions of the model |
1.2.4 不同地应力场模型
页岩气开采工作中,由于不同的井处于不同的地理位置,所以每一口井所处的地下应力环境具有一定差异。其中页岩气井的水平段套管受力情况最为复杂,尤其在压裂工况下会受到垂向地应力、水平地应力和管内压裂液压力3种力的挤压。对于地层应力状况的分析不需要考虑管内压力的变化,因此只讨论垂向地应力和水平地应力的差异。除了地应力本身的原始差异外,压裂施工也会人为改变压裂区域内的地应力分布。为了研究地应力场对套管应力分布的影响,建立多组不同的地应力场对同一套管-水泥环-地层模型进行加载,计算仿真出套管上的应力分布情况。考虑到水平段套管所处的深度不变,设置几组不同地应力场中每组的垂向地应力为固定值,同时考虑到控制变量的研究方法,设定每组地应力场中的套管内压力也为固定值。只改变水平地应力,建立几组不同的地应力场,地应力场相关参数如表 2所示。
| 地层 | 垂向应力/MPa | 水平应力/MPa | 泊松比 | 密度/ (kg·m-3) |
| 应力场1 | 50.17 | 20 | 0.3 | 2 600 |
| 应力场2 | 50.17 | 30 | 0.3 | 2 600 |
| 应力场3 | 50.17 | 40 | 0.3 | 2 600 |
| 应力场4 | 50.17 | 50 | 0.3 | 2 600 |
| 应力场5 | 50.17 | 60 | 0.3 | 2 600 |
| 应力场6 | 50.17 | 70 | 0.3 | 2 600 |
| 应力场7 | 50.17 | 80 | 0.3 | 2 600 |
| 应力场8 | 50.17 | 90 | 0.3 | 2 600 |
1.2.5 不同岩石弹性模量模型
压裂施工时,利用高压向地层中注入大量的压裂液将页岩气产层的岩石压碎。岩石受到水力压裂的作用挤压破碎后,其力学性能会产生一定的变化。根据相关的试验结果,岩石通过压裂破碎在其内部产生大量的网状裂缝,此时岩石的弹性模量有所下降,在承受较大地应力作用时岩石的变形也更加剧烈。
由于水平井压裂施工时采用了分段压裂技术,其结果是同一个区域可能会实施重复压裂,每一次压裂都会降低岩石的力学性能,从而多级压裂会导致岩石力学性能的急剧下降。为了实现对压裂后岩石力学性能下降的模拟,本文假定几组地层的岩石力学性能参数,如表 3所示。
| 参数名称 | 弹性模量/GPa | 泊松比 | 密度/(kg·m-3) |
| 地层1 | 38.37 | 0.3 | 2 600 |
| 地层2 | 30.00 | 0.3 | 2 600 |
| 地层3 | 25.00 | 0.3 | 2 600 |
| 地层4 | 20.00 | 0.3 | 2 600 |
| 地层5 | 15.00 | 0.3 | 2 600 |
| 地层6 | 10.00 | 0.3 | 2 600 |
| 地层7 | 5.00 | 0.3 | 2 600 |
| 地层8 | 2.50 | 0.3 | 2 600 |
1.2.6 不同井口施工压力模型
页岩气井的压裂施工通常会使用较大的压力对岩石进行破碎,此压力下的压裂液在对岩石进行破碎的同时,也对压裂段的套管产生了巨大的压力。页岩气井压裂施工时,井口的施工压力范围通常为65~81 MPa。为研究井口施工压力对套管应力分布的影响,以常用施工压力范围为基础建立几组不同的井口施工压力模型。由于液注压力的存在,井下套管内压力会有所增大,所以在本次模拟过程中,井口施工压力取值分别为65、70、75、80、85和90 MPa。
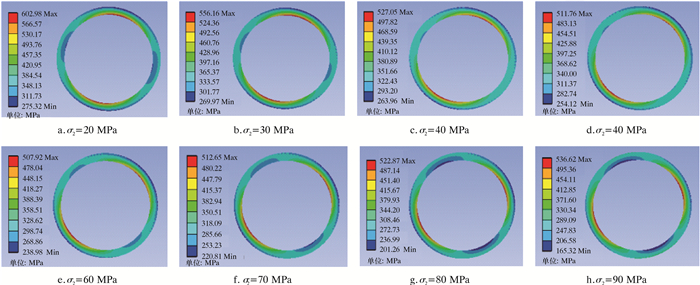
2 算例分析 2.1 地应力场对套管应力的影响水平地应力与垂向地应力的差异越大,加载到套管上的应力不均匀度也就越大。图 5是压裂工况下页岩气井水平段套管在不同水平地应力下的应力分布云图。从图 5可以看出,随着水平地应力的变化,页岩气套管的应力呈现出了一定程度的变化。取水平地应力为横坐标,套管截面上的最大等效应力为纵坐标,绘制套管最大等级应力随水平地应力的变化曲线,如图 6所示。
|
| 图 5 不同水平地应力下的套管应力云图 Fig.5 Casing stress distribution under different horizontal in-situ stresses |
|
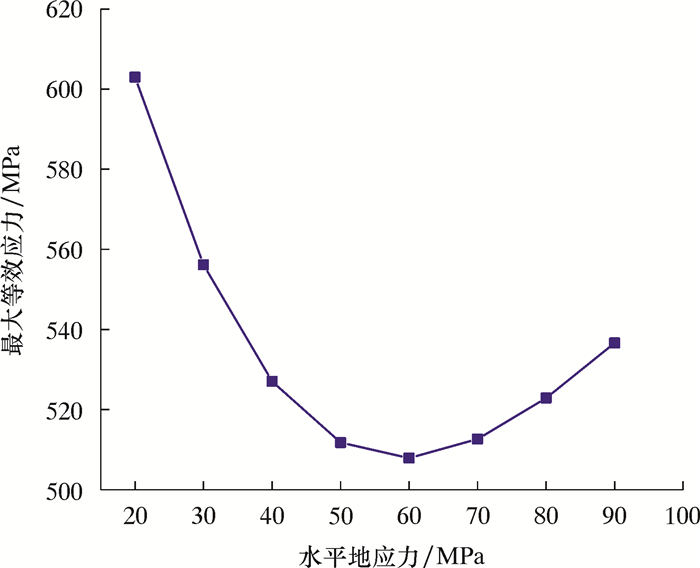
| 图 6 最大等效应力随水平地应力的变化曲线 Fig.6 Effect of the horizontal in-situ stress on the maximum equivalent stress |
从图 6可以看出,在一定的垂向地应力50.17 MPa下,套管受到的水平地应力为60.00 MPa时,其套管最大等效应力最小,为507.92 MPa;当水平地应力为20.00 MPa时,套管最大等效应力为602.98 MPa;当水平地应力为90.00 MPa时,套管最大等效应力为536.62 MPa。这说明在页岩气井压裂工况下,垂向地应力与水平地应力相差越大,对套管损坏的影响作用越大。因此上述两种力分别来自于两个不同的方向,从垂向和水平两个方向对套管进行挤压,挤压力越大,套管的变形越明显。但当两种地应力差值较大的时候,通过有限元仿真的结果可以发现,套管在垂直方向和水平方向的变形程度会有所差异。地应力的差异越大,套管两个方向变形大小的差异也越大。当套管在垂直方向和水平方向两个方向变形差异较大时,原本截面形状为圆形的套管会变形成为椭圆形,几何形状改变明显,此种变形导致了套管上产生较大的应力集中。
因此,在页岩气井的钻井过程中,应优化设计井眼轨迹,提前避开地下页岩气产层中垂向地应力与水平地应力差值较大的区域,从而降低套管损坏的风险。
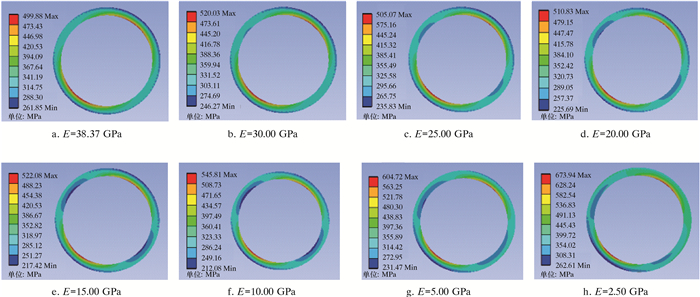
2.2 岩石弹性模量E对套管应力的影响不同岩石弹性模量下的套管应力云图如图 7所示。从图 7可以看出,随着页岩气产层中岩石弹性模量的逐渐降低,套管上的最大等效应力呈现出了上升的趋势。
|
| 图 7 不同岩石弹性模量下的套管应力云图 Fig.7 Casing stress distribution under different rock elastic modulus |
取岩石弹性模量为横坐标,套管截面上的最大等效应力为纵坐标,绘制套管应力随岩石弹性模量的变化曲线,如图 8所示。

|
| 图 8 最大等效应力随岩石弹性模量的变化曲线 Fig.8 Effect of the rock elastic modulus on the maximum equivalent stress |
从图 8可以看出,当地层岩石的弹性模量越低时,套管上的等效应力值也越大。这是因为岩石弹性模量反映了岩石抵抗挤压变形的能力,弹性模量越低,在相同地应力情况下地层的变形程度也越高。地层的变形会改变井眼的几何形状,使页岩气井水平段的套管也发生变形,从而致使套管上产生较大的应力集中。
38.37 GPa是地层原始的岩石弹性模量数据,当地层未进行压裂时,套管的最大等效应力为499.88 MPa,远小于套管的屈服强度。随着页岩气井压裂施工的进行,岩石弹性模量开始逐渐降低。当岩石弹性模模量下降为15.00 GPa时,套管最大等效应力为522.08 MPa,与地层未进行压裂时相比,套管的最大等效应力增加了22.00 MPa。对于此工况下的套管而言,岩石弹性量下降值在15.00 GPa以内时,套管最大等效应力和套管应力分布都发生了一定改变,但影响不大。然而分段压裂技术容易在同一区域对页岩进行重复压裂,多次的压裂会使岩石的弹性模量急剧下降。当岩石弹性模量继续降低时,对套管应力的影响越来越大,尤其当岩石弹性模量下降到10.00 GPa以下后,套管变形增大的趋势陡然加剧。这说明页岩气井经历多次压裂,地层岩石弹性模量下降,对套管应力有非常大的影响,即对多次重复压裂容易造成套管损坏。因此,在页岩气井压裂施工中,应避免对同一区域的多次重复压裂,在射孔时可适当加大孔段之间的距离,以防止施工时压裂区域重叠。
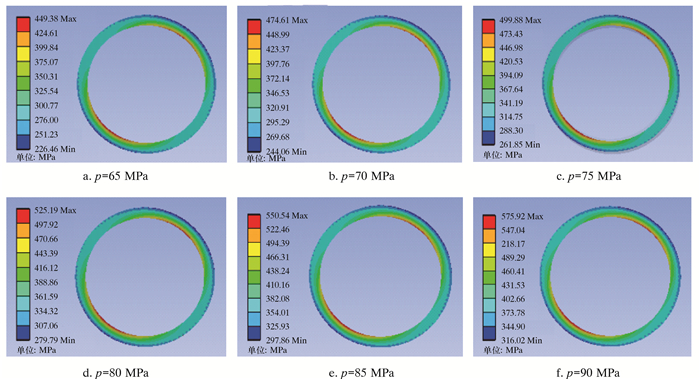
2.3 井口施工压力对套管应力的影响不同井口施工压力下的套管应力云图如图 9所示。从图 9可以看出,随着井口施工压力的逐渐增大,套管上的最大等效应力有上升的趋势。取井口施工压力为横坐标,套管截面上的最大等效应力为纵坐标,绘制套管应力随井口施工压力的变化曲线,如图 10所示。
|
| 图 9 不同井口施工压力下的套管应力云图 Fig.9 Casing stress distribution under different wellhead construction pressures |
|
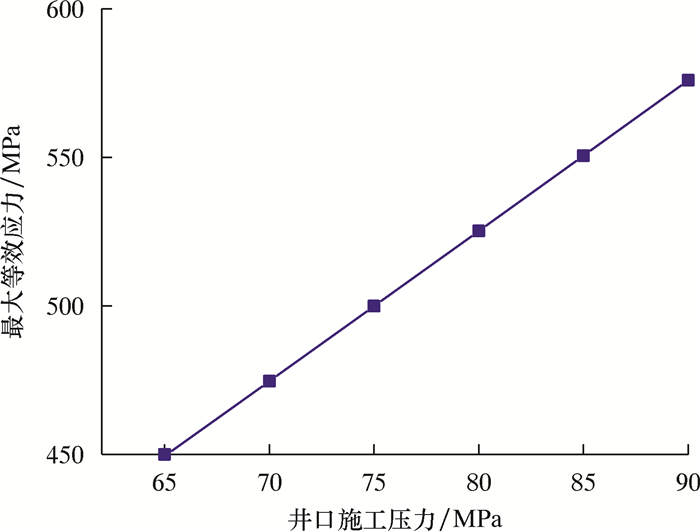
| 图 10 最大等效应力随井口施工压力的变化曲线 Fig.10 Effect of wellhead pressure on the maximum equivalent stress |
页岩气压裂具有压力大、排量高的特点,巨大的施工压力加载到套管内壁上,会使套管在内壁上产生较大的应力集中。从图 10可以看出,随着井口施工压力增加,套管应力也呈现增加趋势,二者几乎都呈线性增长关系。当井口施工压力为65.00 MPa时,施加在套管内壁的压力为101.38 MPa,套管最大应力为449.38 MPa;当井口施工压力为90.00 MPa时,施加在套管内壁的压力为126.38 MPa,套管最大应力为575.92 MPa。井口施工压力的增大对套管应力产生了明显的影响,即井口施工压力越大,套管内壁的等效应力值越大。因此在页岩气井压裂时,合理地预算井口施工压力对减小和预防套管损坏有重要意义。
3 结论与建议(1) 垂向地应力与水平地应力的差异对套管上的应力有显著影响,即差异越大,套管内壁上的等效应力值越大。因此建议通过优化井眼轨迹,适当避开页岩气产层中地应力差异较大的区域。
(2) 岩石弹性模量的下降会导致套管应力上升,当岩石弹性模量下降超过10 GPa后,套管应力值会大幅度上升。应在压裂施工中避免对同一区域的重复压裂,防止岩石弹性模量急剧下降,从而防止套管损坏。
(3) 套管内壁上的最大等效应力值随井口施工压力的增大而呈线性增加。因此在页岩气井压裂施工时,合理预算井口施工压力对减小和预防套管损坏有重要意义。
| [1] |
姜瑞忠, 蒋廷学, 汪永利. 水力压裂技术的近期发展及展望[J]. 石油钻采工艺, 2004, 26(4): 52-57. JIANG R Z, JIANG T X, WANG Y L. Recent development and prospect of hydraulic fracturing technology[J]. Oil Drilling & Production Technology, 2004, 26(4): 52-57. DOI:10.3969/j.issn.1000-7393.2004.04.016 |
| [2] |
陈升, 范明涛, 李军, 等. 体积压裂过程套管力学行为研究[J]. 石油机械, 2019, 47(1): 1-7. CHEN S, FAN M T, LI J, et al. Study on the mechanical behavior of casing during stimulated reservoir volume fracturing[J]. China Petroleum Machinery, 2019, 47(1): 1-7. |
| [3] |
薛承瑾. 页岩气压裂技术现状及发展建议[J]. 石油钻探技术, 2011, 39(3): 24-29. XUE C J. Current situation and development suggestions of shale gas fracturing technology[J]. Petroleum Drilling Techniques, 2011, 39(3): 24-29. DOI:10.3969/j.issn.1001-0890.2011.03.004 |
| [4] |
张树立, 李心成. 适合中国大型页岩气压裂成套装备的解决方案[J]. 石油机械, 2018, 46(12): 60-67. ZHANG S L, LI X C. The solution of massive hydraulic fracturing of shale gas in China[J]. China Petroleum Machinery, 2018, 46(12): 60-67. |
| [5] |
付盼, 廖明豪, 田中兰, 等. 页岩气水平井压裂中地层滑移数值模拟研究[J]. 石油机械, 2019, 47(4): 73-79. FU P, LIAO M H, TIAN Z L, et al. Numerical simulation of formation slippage in shale gas horizontal well fracturing[J]. China Petroleum Machinery, 2019, 47(4): 73-79. |
| [6] |
董大忠, 邹才能, 杨桦, 等. 中国页岩气勘探开发进展与发展前景[J]. 石油学报, 2012, 33(增刊1): 107-114. DONG D Z, ZOU C N, YANG H, et al. China's shale gas exploration and development progress and development prospects[J]. Acta Petrolei Sinica, 2012, 33(S1): 107-114. DOI:10.7623/syxb2012S1013 |
| [7] |
李明飞, 徐绯, 窦益华, 等. 压裂工况下重复射孔套管强度安全性分析[J]. 石油机械, 2018, 46(9): 92-99. LI M F, XU F, DOU Y H, et al. Safety analysis of reperforated casing under fracturing conditions[J]. China Petroleum Machinery, 2018, 46(9): 92-99. |
| [8] |
吴奇, 胥云, 刘玉章, 等. 美国页岩气体积改造技术现状及对我国的启示[J]. 石油钻采工艺, 2011, 33(2): 1-7. WU Q, XU Y, LIU Y Z, et al. The status quo of shale gas volume reconstruction technology in the United States and its enlightenment to China[J]. Oil Drilling & Production Technology, 2011, 33(2): 1-7. DOI:10.3969/j.issn.1000-7393.2011.02.001 |
| [9] |
蒋廷学, 卞晓冰, 王海涛, 等. 深层页岩气水平井体积压裂技术[J]. 天然气工业, 2017, 37(1): 90-96. JIANG T X, BIAN X B, WANG H T, et al. Volume fracturing of horizontal wells in deep shale gas[J]. Natural Gas Industry, 2017, 37(1): 90-96. |
| [10] |
裴森龙.多级压裂技术在龙马溪组页岩中的适应性研究[D].北京: 中国地质大学(北京), 2013. PEI S L. Study on the adaptability of multistage fracturing technology in Longmaxi Formation shale[D]. Beijing: China University of Geosciences (Beijing), 2013. http://cdmd.cnki.com.cn/Article/CDMD-11415-1013270200.htm |
| [11] |
何启平, 尹丛彬, 李嘉, 等. 威远-长宁地区页岩气压裂返排液回用技术研究与应用[J]. 钻采工艺, 2016, 39(1): 118-121. HE Q P, YIN C B, LI J, et al. Research and application of shale gas fracturing flowback recovery technology in Weiyuan-Changning area[J]. Drilling & Production Technology, 2016, 39(1): 118-121. DOI:10.3969/J.ISSN.1006-768X.2016.01.35 |
| [12] |
刘飞, 方春飞, 夏成宇, 等. 页岩气井钻井过程中套管磨损的计算分析[J]. 中国科技论文, 2016, 11(15): 1699-1702. LIU F, FANG C F, XIA C Y, et al. Calculation and analysis of casing wear during drilling in shale gas wells[J]. Chinese Sciential and Technical Theses, 2016, 11(15): 1699-1702. DOI:10.3969/j.issn.2095-2783.2016.15.004 |
| [13] |
WANG W, TALEGHANI A D. Three-dimensional analysis of cement sheath integrity around wellbores[J]. Journal of Petroleum Science and Engineering, 2014, 121: 38-51. DOI:10.1016/j.petrol.2014.05.024 |
| [14] |
LECANPION B, BUNGER A, KEAR J, et al. Interface debonding driven by fluid injection in a cased and cemented wellbore:modeling and experiments[J]. International Journal of Green-house Gas Control, 2013, 18: 208-223. DOI:10.1016/j.ijggc.2013.07.012 |
| [15] |
BATCHELOR G K. An introduction to fluid dynamics[M]. Cambridge: Cambridge University Press, 1967.
|
| [16] |
ADACHI J I, DETOURNAY E. Self-similar solution of a plane-strain fracture driven by a power-law fluid[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2002, 26(6): 579-604. DOI:10.1002/nag.213 |
| [17] |
徐华翔.页岩气层固井水泥石力学性能有限元模拟研究[D].东营: 中国石油大学(华东), 2014. XU H X. Finite element simulation of mechanical properties of cementing cement in shale gas layer[D]. Dongying: China University of Petroleum (Huadong), 2014. http://cdmd.cnki.com.cn/Article/CDMD-10425-1016711763.htm |
| [18] |
田中兰, 石林, 乔磊. 页岩气水平井井筒完整性问题及对策[J]. 天然气工业, 2015, 35(9): 70-76. TIAN Z L, SHI L, QIAO L. Wellbore integrity of horizontal shale gas wells and countermeasures[J]. Natural Gas Industry, 2015, 35(9): 70-76. DOI:10.3787/j.issn.1000-0976.2015.09.010 |


