2. 江苏大学能源与动力工程学院;
3. 惠生工程(中国)有限公司
2. School of Energy and Power Engineering, Jiangsu University;
3. Wison Engineering(China) Ltd.
0 引言
在诸多原油破乳脱水方法中,电脱水因其高效、环保等优点而被广泛使用,其脱水机理是原油乳化液中的小水滴在电场作用下发生变形和聚并,此时相互碰撞的小水滴会合并成大水滴,并在重力作用下沉降,实现油和水的分离[1-2]。然而,三次采油技术的广泛应用,使原油在电脱水过程中出现脱水效率下降及脱水电场不稳定等问题,影响了原油的电脱水效率和原油外输品质[3-4]。近年来,脉冲电脱水技术以其高效低耗的显著优点得到了广泛关注,但是其破乳机理仍有待深入研究[5]。
国内外相关学者通过试验和数值模拟等方法,对乳状液中水滴的电流体动力学行为进行了一系列研究。樊玉新等[6]通过显微试验,研究了高频脉冲电场下无机盐质量浓度和种类对水滴极化变形的影响规律。梁猛等[7]对匀强电场作用下液滴的变形和破裂行为进行模拟,研究了分散相液滴变形过程中电荷密度、电场强度和电场力的分布规律。王贞涛等[8]通过VOF方法,采用漏电介质模型计算了不同操作参数下悬浮在另外一种不相溶黏性液体中的单液滴变形以及内部流动情况。陈庆国等[9]基于相场方法对均匀与非均匀电场下液滴的变形进行模拟,研究了液滴电荷密度和电场力的分布以及液滴的聚结情况,并通过试验研究了在均匀场与非均匀场中液滴的变形以及运动行为。任瑞娟等[10]通过建立不同电场波形条件下单液滴变形的模型,研究了电场波形对液滴变形的影响。彭烨等[11]运用电流体动力学(EHD)理论,建立在脉冲电场中液滴的电介质物理学模型,得到液滴内外极化电场分布和极化电场力,分析了液滴内外速度场和流动应力。
然而,相关研究工作仍处于起步阶段,对脉冲电场作用下液滴的极化作用机制研究仍较为匮乏。基于此,本文采用基于Cahn-Hilliard方程的相场方法的数值模拟方法,在脉冲电场下建立分散相液滴的行为模型,通过流场和电场的耦合作用,从微观角度研究了液滴极化变形的影响因素和行为规律。研究结果可为脉冲电场静电破乳机理的深入研究提供理论依据。
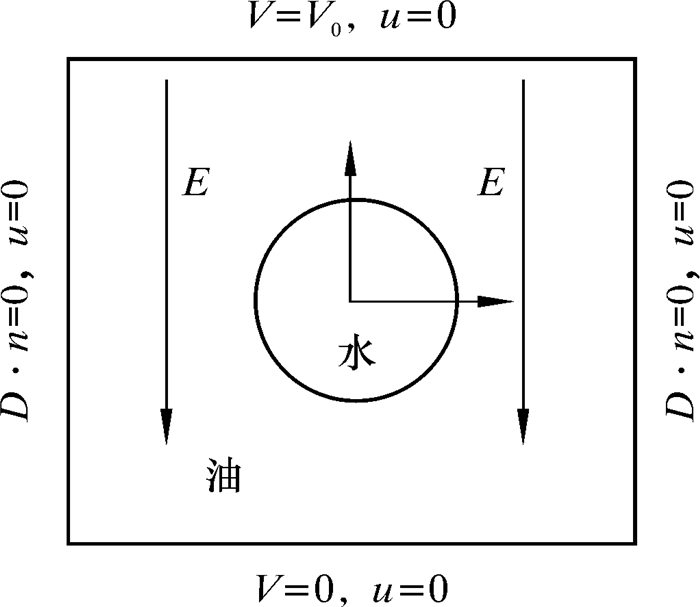
1 数学模型 1.1 物理问题描述基于实验室微型静电聚结器,将几何模型简化为图 1所示的二维模型。图 1中水滴为球形,直径为d,置于电极板中心位置,连续相液体介质为油。上电极板施加如图 2所示的占空比为0.5的脉冲直流电压,下电极板接地,满足边界无滑移条件,左侧为流体进口边界,右侧为流体出口边界。流域几何尺寸设为6 mm×8 mm。图 1中,V为电压,u为主流流速,D为电位移,n为法向向量,E为电场强度。
|
| 图 1 单液滴二维模型示意图 Fig.1 Schematic diagram of the two- dimensional model of a droplet |

|
| 图 2 电场波形 Fig.2 Electric field waveform |
1.2 数值模拟方法
本文基于多物理场耦合软件COMSOL Multphysics、采用二维平面模型,研究脉冲电场作用下液滴极化变形的行为规律。在进行数值模拟时,为研究相场条件下的液滴变形,需要在所建立的二维物理模型上绘制网格,采用三角形单元网格,并对油水界面处进行局部加密。一般来说,为提高模拟的精确性,须绘制较多网格,但过多的网格数量会更加耗时、耗力,影响数值模拟的研究进程,若绘制较少网格,则会对数值模拟结果造成较大误差,故在模拟之前,需进行网格无关性验证,以确定网格的适当数量。
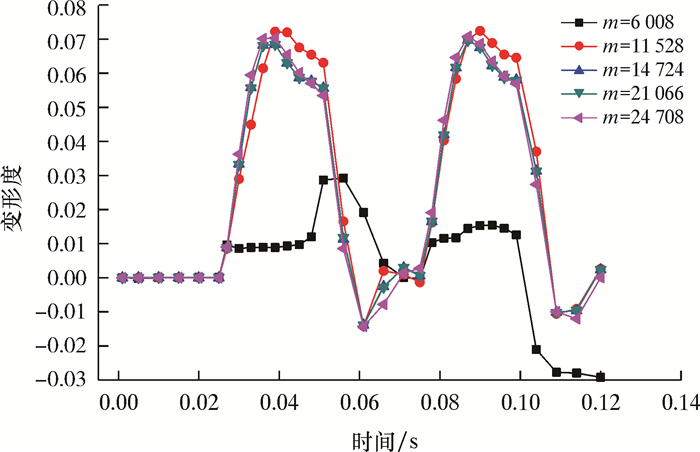
不同网格数对应的液滴变形度曲线如图 3所示。对同一参数模型绘制不同数量的网格,分别得到了网格数m为6 008、11 528、14 724、21 006和24 708的模型,并进行模拟分析。模型参数为:电场强度600 V/mm,液滴粒径1.2 mm,界面张力0.025 N/m,连续相黏度200 mPa·s。
|
| 图 3 不同网格数对应的液滴变形度曲线 Fig.3 Droplet deformation curve corresponding to different grid numbers |
由图 3可知:网格数为6 008时,对应变形度曲线变化不稳定,且与其他四组网格数对应的变形度曲线相差较大;网格数为11 528、14 724、21 066、24 708所对应的变形度曲线接近重合,最高误差不超过0.01,即当网格数超过11 528时,液滴变形度不再随网格的增加而改变。考虑到模拟的准确性与节省时间问题,液滴变形部分模拟网格数采用14 724。物性参数和模拟工况分别见表 1和表 2。
| 液相 | 密度/ (kg·m-3) | 黏度/ (mPa·s) | 相对介电常数 |
| 分散相液滴 | 998 | 1.14 | 80.00 |
| 连续相油相 | 922 | 200.00 | 2.62 |
| 电场强度/ (V·mm-1) | 界面张力/ (N·m-1) | 电场频率/Hz | 液滴直径/mm |
| 400~1 000 | 0.025 | 20 | 1.1 |
| 600 | 0.020~0.035 | 20 | 1.2 |
| 600 | 0.025 | 10~50 | 1.2 |
| 800 | 0.025 | 20 | 1.1~1.6 |
1.3 液滴变形模型验证
图 4a表示在试验条件下脉冲电场中的单液滴变形过程,经历了拉伸和压缩的一个周期变化,最终恢复成原状。试验中采用的各项参数为:液滴直径2 mm,界面张力20 N/m,电压幅值8 kV,电场频率1 Hz[12]。图 4b是在相同条件下采用上述模拟方法得到的液滴变形图,液滴变形量和试验结果与图 4a基本一致。

|
| 图 4 单液滴变形过程的模拟结果与试验结果对比 Fig.4 Comparison of simulation results and experimental results of single droplet deformation process |
为了定量地描述各参数对液滴变形的影响,定义变形度D如下:
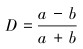
|
(1) |
式中:a和b分别为液滴纵向轴长和横向轴长。
定义液滴变形度相对误差表达式为:
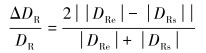
|
(2) |
式中:ΔDR为试验和模拟所得的液滴变形度之差;DR为试验和模拟所得的液滴变形度的平均值;DRe和DRs分别为液滴变形度的试验结果和模拟结果。
表 3给出了液滴变形度试验结果和模拟结果对比。由表 3可知,试验结果和模拟结果一致性良好,最大误差为2.92%,验证了模拟结果的准确性。
| 时间/s | 0 | 0.250 5 | 0.501 0 | 0.751 5 | 1.00 2 |
| 变形度试验值 | 0 | 0.139 1 | 0.147 5 | 0 | 0 |
| 变形度模拟值 | 0 | 0.142 9 | 0.142 9 | 0 | 0 |
| 相对误差 | 0 | 0.027 3 | -0.029 2 | 0 | 0 |
2 结果分析与讨论 2.1 电场强度对液滴变形的影响
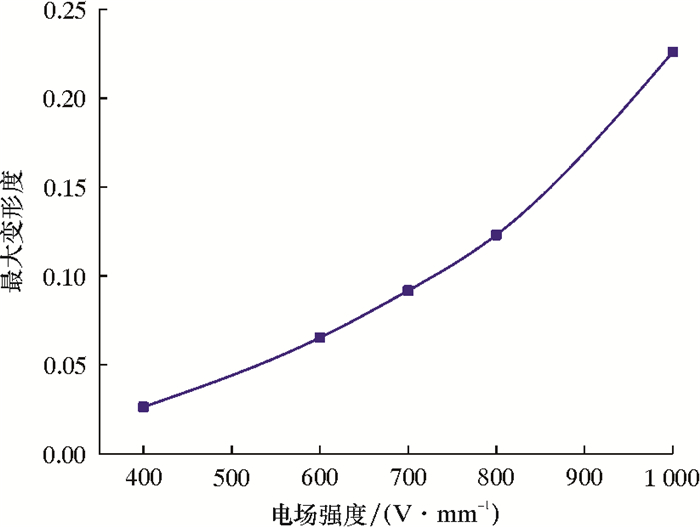
电场强度对液滴变形度影响的趋势如图 5所示。由图 5可知:分散相液滴的变形度受电场强度影响显著;随着电场强度的增大,液滴的极化程度增大,且增大的趋势近似呈指数。
|
| 图 5 电场强度对液滴变形度影响的趋势 Fig.5 Trend of effect of electric field strength on droplet deformation |
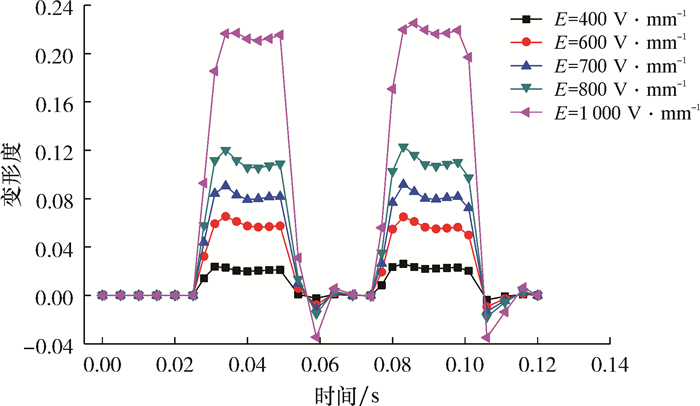
不同电场强度下液滴变形度的变化规律如图 6所示。由图 6可知,液滴振荡变形的幅值随着电场强度的增大而增大,且液滴变形度的变化周期与脉冲电场的变化周期相同。这是由于电场力与电场强度的平方成正比,故电场力随电场的周期变化呈现周期变化,而电场力又是液滴变形的驱动力;电场力越大,克服液滴内外压差及界面张力的拉伸驱动力越大,则液滴变形度越大。值得注意的是,当电场强度增大至800和1 000 V/mm时,液滴变形度出现负值,且电场强度越大,负值越大。其原因是在直流脉冲电场下,液滴的变形度曲线发生了过冲现象,而且随着电场强度幅值的增加,上升沿的过冲现象逐渐减弱,下降沿的过冲现象逐渐增强。
|
| 图 6 不同电场强度下液滴变形度的变化规律 Fig.6 Deformation of droplet at different electric field strengths |
2.2 界面张力对液滴变形的影响
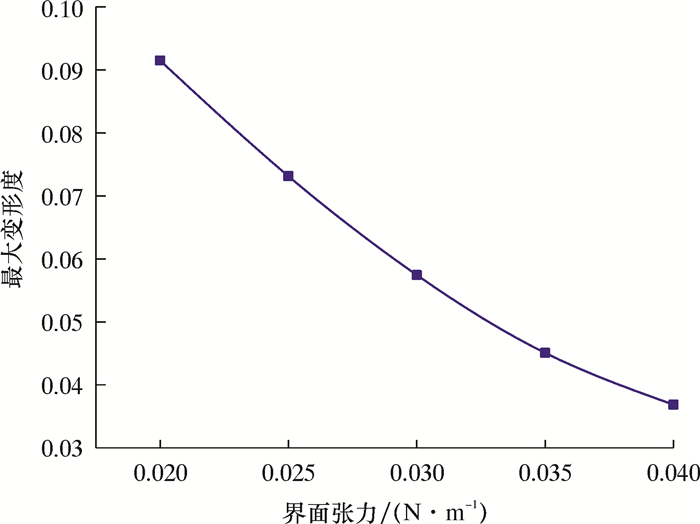
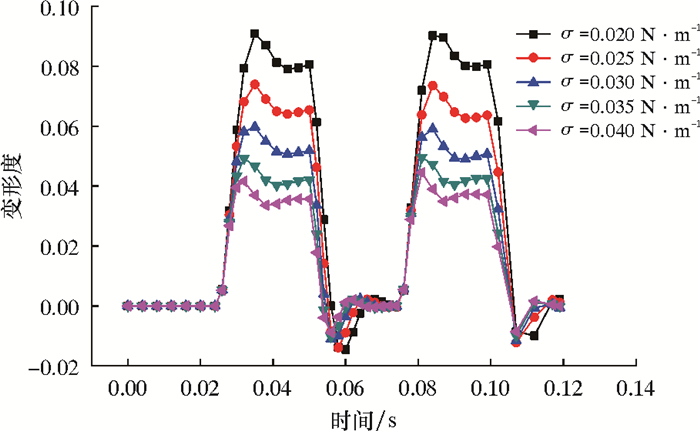
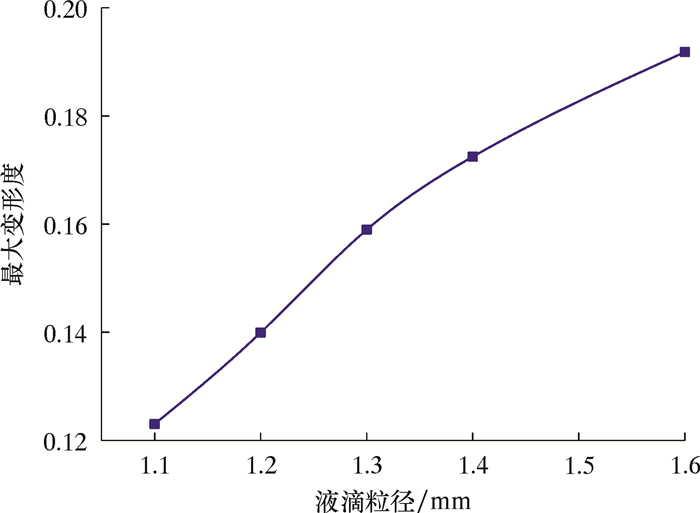
液滴的界面张力对液滴极化变形的影响显著,如图 7所示,随着界面张力由0.020 N/m增大至0.040 N/m,液滴的变形度由9.22%骤减至3.86%。由拉普拉斯方程(见式3)可知,弯曲液面的附加压力Δp与液体界面张力σ成正比,与曲率半径r成反比。液滴界面张力是克服电场力使液滴保持原状的作用力,当液滴界面张力减小时,液滴抵抗电场极化变形的能力大幅降低,其极化变形程度以及随脉冲电场的振荡幅度显著增大。不同界面张力下液滴变形度的变化规律如图 8所示。
|
| 图 7 界面张力对液滴变形度影响 Fig.7 Effect of interfacial tension on droplet deformation |
|
| 图 8 不同界面张力下液滴变形度的变化规律 Fig.8 Variation of droplet deformation under different interfacial tension |
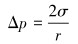
|
(3) |
脉冲电场同一周期内经历脉冲导通期和休止期,电场频率f对液滴的极化变形特性也存在显著影响[13]。电场频率对液滴变形度的影响如图 9所示。由图 9可知,随着电场频率由10 Hz增大至50 Hz,液滴的最大变形度由7.32%小幅增大至7.57%。这是因为随着电场频率增加,乳状液容性负载变化,液滴受到的偶极聚结力小幅增大。不同电场频率下液滴变形度的变化规律如图 10所示。
|
| 图 9 电场频率对液滴变形度的影响 Fig.9 Effect of electric field frequency on droplet deformation |
|
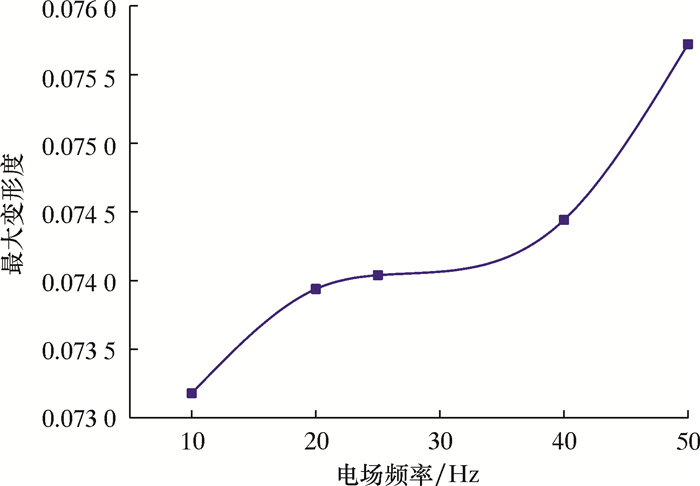
| 图 10 不同电场频率下液滴变形度的变化规律 Fig.10 Variation of droplet deformation under different electric field frequencies |
由图 10可知,随电场频率的增大,液滴的变形周期明显缩短,且变形周期与脉冲电场的变化周期一致。虽然液滴在单个周期内受力时间缩短,但分散相液滴及连续相油相的动力黏度较低,同时液滴的界面张力较小,故液滴可在短时间内达到最大变形度,导致液滴的变形周期明显缩短。
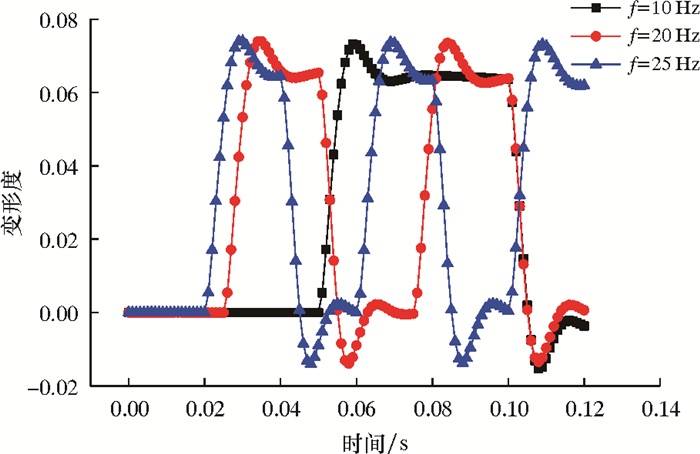
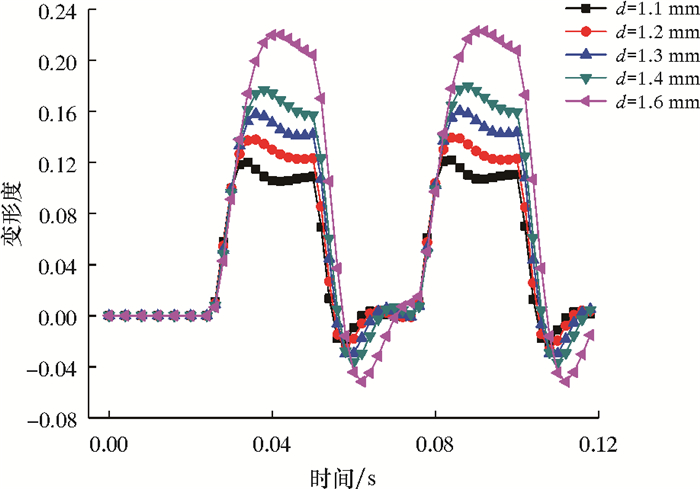
2.4 液滴粒径对液滴变形的影响在静电聚结器中,液滴尺寸对液滴沉降速度具有重要影响。液滴粒径对变形度的影响如图 11所示。不同液滴粒径下液滴变形度的变化规律如图 12所示。由图 11和图 12可知,随着液滴粒径的增大,液滴的变形度及液滴振荡幅度明显变大。其原因在于,随液滴粒径的增加,液滴两端的感生电荷增多、电场作用力增大,而由拉普拉斯方程(式3)可知,液滴粒径的增加会导致液滴内外压差降低。上述两个因素的共同作用,导致液滴的变形度及振荡幅度随液滴粒径的增加而增大。
|
| 图 11 液滴粒径对变形度的影响 Fig.11 Effect of droplet size on deformation |
|
| 图 12 不同液滴粒径下液滴变形度的变化规律 Fig.12 Variation of droplet deformation under different droplet sizes |
3 结论
(1) 随着电场强度的增加,液滴振荡变形的幅值增大,液滴变形度曲线上升沿的过冲现象逐渐减弱,下降沿的过冲现象逐渐增强。
(2) 随着液滴界面张力的减小,液滴抵抗电场极化变形的能力大幅降低,其极化变形程度以及随脉冲电场的振荡幅度显著增大。
(3) 随着电场频率增加,乳状液容性负载变化,液滴受到的偶极聚结力小幅增大,极化变形程度提高,液滴变形周期缩短。
(4) 随着液滴粒径的增大,施加于液滴两端的电场力增大,液滴内外压差减小,液滴的变形度及振荡幅度增大。
| [1] |
李梦坤.特高含水原油体系特性研究[D].大庆: 大庆石油学院, 2005. LI M T. Study on characteristics of super high water cut crude oil system[D]. Daqing: Daqing Petroleum Institute, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10220-2005154538.htm |
| [2] |
ARYAFARD E, FARSI M, RAHIMPOUR M R, et al. Modeling electrostatic separation for dehydration and desalination of crude oil in an industrial two-stage desalting plant[J]. Journal of the Taiwan Institute of Chemical Engineers, 2016, 58: 141-147. DOI:10.1016/j.jtice.2015.06.028 |
| [3] |
ABULLAH M M S, AL-LOHEDAN H A, ATTAH A M. Synthesis and application of amphiphilic ionic liquid based on acrylate copolymers as demulsifier and oil spill dispersant[J]. Journal of Molecular Liquids, 2016, 219: 54-62. DOI:10.1016/j.molliq.2016.03.011 |
| [4] |
魏炳和. 实施技术改造, 降低外输原油含水[J]. 今日科苑, 2008(14): 78. WEI B H. Implement technical transformation to reduce water cut of crude oil transported abroad[J]. Modern Science, 2008(14): 78. |
| [5] |
赵忠杰. 高频脉冲电脱水技术应用研究[J]. 石油工程建设, 2009, 35(增刊1): 143-145. ZHAO Z J. Application research of electric dehydration technique using high frequency pulses[J]. Petroleum Engineering Construction, 2009, 35(S1): 143-145. |
| [6] |
樊玉新, 李彬, 孙治谦, 等. 无机盐浓度及种类对电脱水过程水滴极化的影响[J]. 化工学报, 2016, 67(8): 3297-3303. FAN Y X, LI B, SUN Z Q, et al. Effect of salt concentration and type on polarization and deformation of water droplet during electric dehydration[J]. CIESC Journal, 2016, 67(8): 3297-3303. |
| [7] |
梁猛, 李青, 王奎升, 等. 匀强电场作用下分散相液滴的变形和破裂[J]. 化工学报, 2014, 65(3): 843-848. LIANG M, LI Q, WANG K S, et al. Deformation and breakup of dispersed phase droplets in uniform electric field[J]. CIESC Journal, 2014, 65(3): 843-848. DOI:10.3969/j.issn.0438-1157.2014.03.011 |
| [8] |
王贞涛, 董庆铭, 张永辉, 等. 静电场中液滴变形及内部流动的研究[J]. 高校化学工程学报, 2015(5): 1098-1105. WANG Z T, DONG Q M, ZHANG Y H, et al. Droplet deformation and its internal flow in electrostatic field[J]. Journal of Chemical Engineering of Chinese Universities, 2015(5): 1098-1105. DOI:10.3969/j.issn.1003-9015.2015.05.011 |
| [9] |
陈庆国, 宋春辉, 梁雯, 等. 非均匀和均匀电场下液滴的形变及运动行为[J]. 高电压技术, 2016, 42(3): 949-958. CHEN Q G, SONG C H, LIANG W, et al. Deformation and motion behavior of water droplet under uniform and non-uniform electric field[J]. High Voltage Engineering, 2016, 42(3): 949-958. |
| [10] |
任瑞娟, 李彬, 孙治谦, 等. 不同电场波形下液滴极化变形规律研究[J]. 化学工程, 2018, 46(7): 51-56. REN R J, LI B, SUN Z Q, et al. Investigation on the law of droplet polarization and deformation under different electrical waveforms[J]. Chemical Engineering, 2018, 46(7): 51-56. DOI:10.3969/j.issn.1005-9954.2018.07.011 |
| [11] |
彭烨, 刘涛, 龚海峰, 等. 基于EHD理论的油包水液滴在脉冲电场作用下的振动变形研究[J]. 石油学报(石油加工), 2017, 33(6): 1146-1151. PENG Y, LIU T, GONG H F, et al. Research on vibrating deformation of water droplets in oil subjected to pulsed electric field by electro-hydrodynamic (EHD) theory[J]. Acta Petrolei Sinica (Petroleum Processing Section), 2017, 33(6): 1146-1151. DOI:10.3969/j.issn.1001-8719.2017.06.014 |
| [12] |
EOW J S, GHADIRI M. Drop-drop coalescence in an electric field:the effects of applied electric field and electrode geometry[J]. Colloids and Surfaces a:Physicochemical and Engineering Aspects, 2003, 219(1/2/3): 253-279. |
| [13] |
AKBARIAN K N, FARSI M, RAHIMPOUR M R. Effect of current frequency on crude oil dehydration in an industrial electrostatic coalescer[J]. Journal of the Taiwan Institute of Chemical Engineers, 2016, 67: 1-10. DOI:10.1016/j.jtice.2016.06.021 |



