0 引言
连续管技术作为石油工业的一项新兴技术,具有安全、高效、环保等特点,在油气井开发领域得到了广泛应用,需求日益增加。随着我国油气井开发的逐步深入,连续管作业深度不断加深,管径不断增大,对井口注入头的性能提出了更高要求。目前ZR450型注入头已经成为各连续管作业机的主流配置,ZR680和ZR900型注入头将成为需求趋势[1]。为满足大规格注入头的提升力需求,目前通用的做法有两种,一是增大单夹持块上的夹紧力,二是增加注入头夹持长度和夹持区域内夹持块数量。这两种做法都存在弊端,前者会引起单位长度内连续管受力增大,可能造成连续管受损甚至挤毁;后者会导致注入头尺寸和质量增大,增加转运和安装难度。注入头主要通过夹持块与连续管之间的摩擦力驱动连续管起/下井,夹持块与连续管之间的正压力需要达到井下载荷的5倍以上,因此夹持块性能对注入头整体可靠性具有至关重要的影响。
在连续管夹持块性能研究方面,杨高等[2]研究了不同结构夹持块的夹持性能,发现四瓣式夹持块具有最优的夹持效率;李现东和车传睿等[3-4]研究了圆周包角、圆弧直径和内压对夹持块性能的影响,并进行了参数优选;张宏等[5]研究了注入头夹持区域内各夹持块受力均匀性,并对夹持块径向间隙和沟槽参数进行了优化;马卫国等[6]研究了振动对夹持块夹持力的影响。
上述研究中,大都是以特定外径值的连续管为研究对象,忽略了连续管的外径偏差。根据API标准,连续管外径偏差范围为±0.25 mm,同种规格的每一盘连续管,甚至是同一盘连续管不同位置的外径都可能存在差异。因此研究夹持块性能,必须考虑其对连续管外径偏差的适应性。本文基于接触力学基本理论,建立了夹持块夹持力学模型,在考虑夹持块对连续管外径适应性的基础上综合评估夹持块性能,并在此基础上提出了一种高性能弹性夹持块。研究结果对夹持块和注入头的设计开发有一定的指导意义。
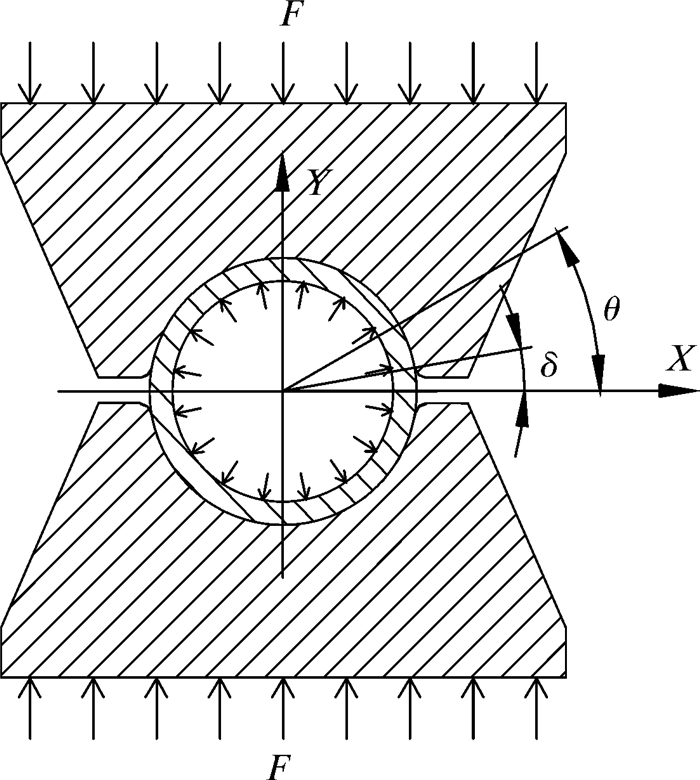
1 力学模型 1.1 受力分析夹持块夹持状态下力学模型如图 1所示。图 1中F为夹紧力,δ为夹持块圆弧起始角,θ为接触单元在圆弧上的周向角度。
|
| 图 1 夹持块力学模型 Fig.1 Mechanical model of the gripper block |
受表面形状、摩擦和大变形等因素的影响,夹持块的夹持行为具有明显的非线性特征。基于有限元思想和虚功原理,系统平衡方程可以表示为:
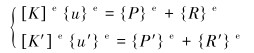
|
(1) |
式中:[K]e、[K]′ e分别为夹持块和连续管单元刚度矩阵;{u}e、{u}′e分别为夹持块和连续管单元的位移向量;{P}e、{P}′e分别为夹持块和连续管单元所受的外载荷向量;{R}e、{R}′e分别为夹持块和连续管之间的接触力向量。
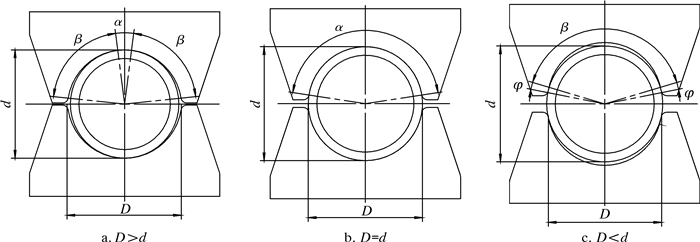
夹持块和连续管之间无法做到“完美匹配”,夹持块与连续管之间的接触状态如图 2所示。图 2中D为夹持块圆弧直径,d为连续管外径。
|
| 图 2 夹持块与连续管接触状态图 Fig.2 Contact state diagram of gripper block and coiled tubing |
根据夹持块受力和运动趋势,初始状态下夹持块与连续管的接触行为可分为α、β和φ三个区域,其中α区域处于连续接触状态,β区域处于分离状态,φ区域处于滑动接触状态。采用增量法求解夹持块与连续管接触行为,则接触平衡条件如下。
区域α内,接触平衡条件为:
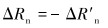
|
(2) |
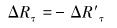
|
(3) |
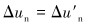
|
(4) |
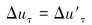
|
(5) |
区域β内,接触平衡条件为:
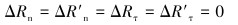
|
(6) |
区域φ内,接触平衡条件为:
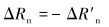
|
(7) |
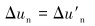
|
(8) |
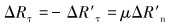
|
(9) |
式中:ΔRn、ΔR′n分别是夹持块和连续管表面增加的正向压力,ΔRτ、ΔR′τ分别是夹持块和连续管表面增加的切向力,Δun、Δu′n分别是夹持块和连续管正向位移增量,Δuτ=Δu′τ分别是夹持块和连续管法向位移增量,μ为摩擦因数。
需要指出的是,随着外载荷的变化,夹持块与连续管会产生弹塑性变形,它们之间的接触区域和接触形式会不断发生变化,需要根据表面节点位置和受力不断调整节点接触状态。
β区域内的节点对,设u为初始位移,Δu为初始位移增量,在经历Δt的时间增量后,如Δun-Δu′n<u,则节点对保持分离状态,如Δun-Δu′n≥u,则节点对进入接触状态;α区域的节点对,在经历Δt的时间增量后,如果Rn<0,则判定节点对分离;如Rn≥0,且Rτ≤μRn,则节点对依然处于连续接触;如Rn≥0,且Rτ>μRn,则节点对进入滑动接触;
φ区域的节点对,在经历Δt的时间增量后,如Rn<0,则判定节点对分离;如Rn≥0,且RτΔu>0,则判定节点对处于连续接触,如Rn≥0,且RτΔu≤0,则判定节点对进入滑动接触。
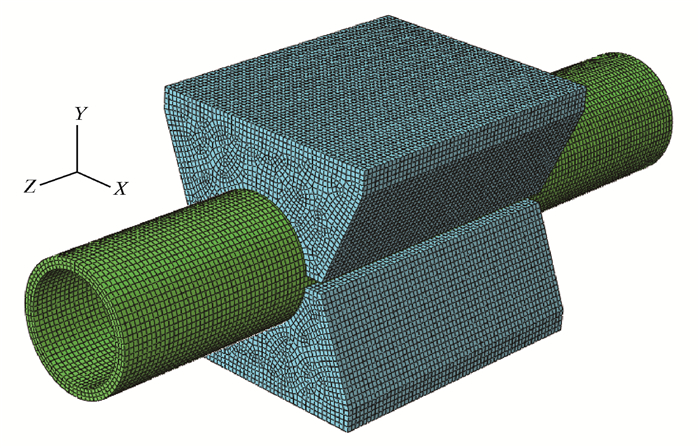
1.2 有限元模型选取基准外径为50.8 mm的夹持块和连续管作为分析对象,并建立了有限元模型,如图 3所示。夹持块和连续管材料的弹性模量为210 GPa,泊松比为0.3,连续管壁厚为4.8 mm,钢级QT80,屈服强度为550 MPa,夹持块圆弧起始角δ=5°。
|
| 图 3 夹持块和连续管有限元模型 Fig.3 Finite element model of gripper block and coiled tubing |
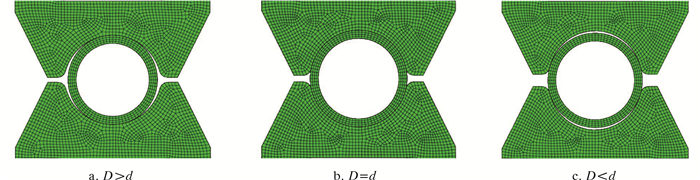
根据API标准,基准外径为50.8 mm的连续管实际外径为50.6~51.1 mm。在设计过程中,夹持块圆弧直径大都是在连续管实际外径范围内进行选择,即D和d之间的偏差为±0.5 mm,不同尺寸偏差的夹持块和连续管有限元模型如图 4所示。
|
| 图 4 不同尺寸偏差的夹持块和连续管有限元模型 Fig.4 Finite element model of gripper block and coiled tubing with different dimensional deviation |
2 夹持块性能分析 2.1 常规夹持块性能分析
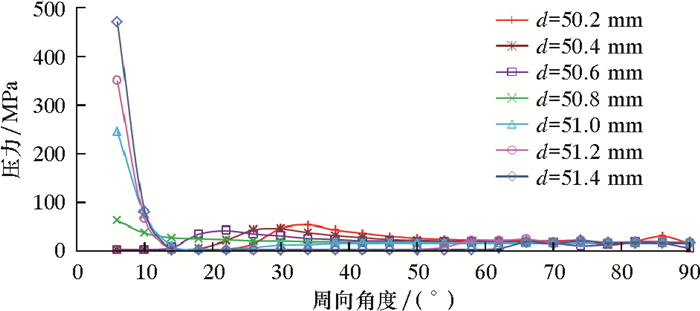
采用有限元法对系统力学模型进行求解,考虑到夹持块、连续管结构和受力的对称性,提取夹持块¼圆弧区域(0≤θ≤90°)内的接触压力,如图 5所示。从图 5可看出:D与d越接近,压力分布越均匀;当D<d时,夹持块开口区域表面压力集中明显,峰值随连续管外径增大而急剧增大,最大压力达到245~472 MPa。
|
| 图 5 夹持块表面压力分布曲线 Fig.5 Surface pressure distribution curve of the gripper block |
在应用中受连续管直线度和夹持块尺寸偏差的影响,这种压力集中会更加严重,且由于夹持块开口区域处于滑动接触状态,压力集中可能导致严重的粘着磨损,影响连续管和夹持块的使用寿命[7]。因此,尽管夹持块和连续管采用过盈配合可有效增大夹持块提升能力,但可能造成连续管受损,目前D大都比d大0.3 mm左右,本文也主要研究D>d时的夹持性能。
分析夹持块性能,需要综合评估夹持块圆弧表面压力总值[8]以及其在夹持状态下对连续管的挤毁作用,因此引入反映夹持块表面正压力Fn以及连续管应力关系的无量纲效率系数ε,定义如下:
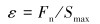
|
(10) |
式中:Smax为连续管的最大Mises应力。
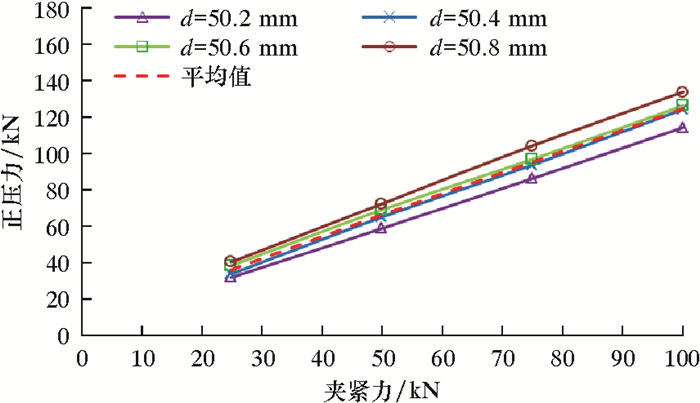
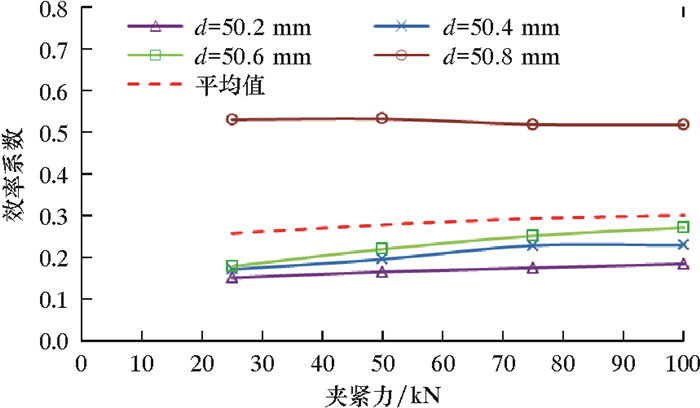
ε越大,表明Fn越大,对连续管损伤越小,夹持性能越好。连续管实际外径存在一个范围,考虑夹持块对连续管外径偏差的适应性,在分析中引入平均值作为对比依据。图 6和图 7分别为夹持块表面正压力曲线和效率系数曲线。
|
| 图 6 夹持块表面正压力曲线 Fig.6 Surface normal pressure curve of the gripper block |
|
| 图 7 夹持块效率系数曲线 Fig.7 Efficiency coefficient curve of the gripper block |
从图 6和图 7可看出:夹持块与连续管直径差值越小,夹持块正压力总值越大,且正压力总值随夹紧力增大而呈线性增长,夹紧力由25 kN增大至100 kN时,平均正压力总值从35 kN增大至124 kN;当夹持块与连续管直径完全一致时,夹持块性能较好,且夹紧力对其性能的影响不大,ε=0.51~0.53;而当夹持块与连续管直径不一致时,夹持块性能大幅度降低,且降幅随夹紧力增大而减小,当d=50.2~51.4 mm时,ε=0.26~0.30。
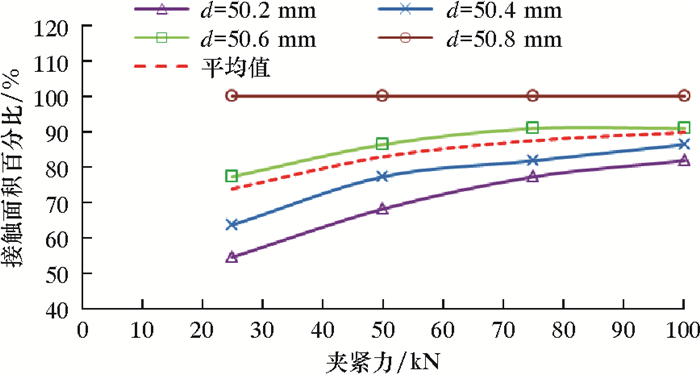
图 8是不同夹紧力下夹持块与连续管的接触面积。从图 8可看出:夹持块与连续管之间的接触面积随其直径差值增大而减小;随着夹紧压力增大,连续管变形量增大,其与连续管之间的平均接触面积增大,夹紧压力由25 kN增大至100 kN时,其平均接触面积由圆弧表面积的74%增大至90%。
|
| 图 8 不同夹紧力下夹持块与连续管的接触面积 Fig.8 Contact area of the gripper block and the coiled tubing |
2.2 夹持块结构优化
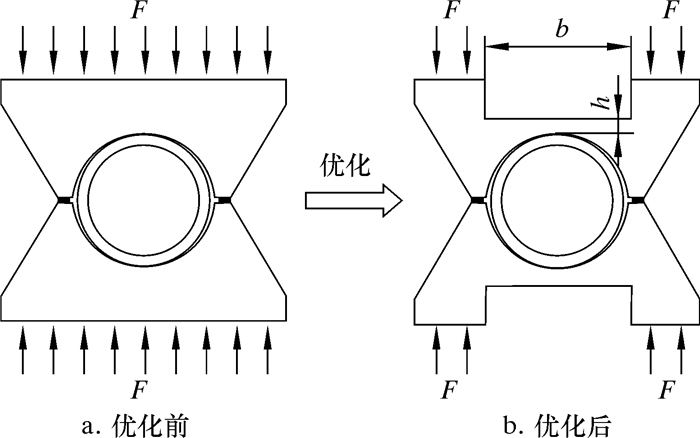
由分析可知,夹持块与连续管尺寸偏差对其夹持性能有重要影响,而常规刚性夹持块对连续管外径偏差适应性相对较差,因此将夹持块优化为弓形弹簧结构,并将夹紧力施加在两侧台肩上,弹性夹持块与常规夹持块力学模型对比如图 9所示。图 9中b和h分别为弹性夹持块沟槽宽度和最小厚度。
|
| 图 9 优化前、后模型对比 Fig.9 Comparison of models before and after optimization |
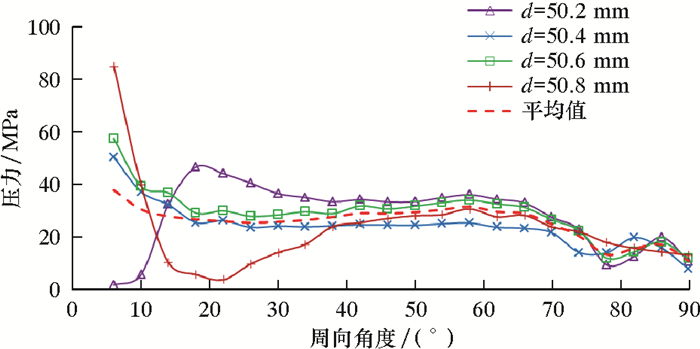
图 10是弹性夹持块表面压力分布情况。从图 10可以看出,在100 kN的夹紧压力下,夹持块与连续管在整个圆弧表面均发生接触,平均压力为11~38 MPa,分布均匀性优于常规夹持块。
|
| 图 10 弹性夹持块表面压力分布情况 Fig.10 Surface pressure distribution of the elastic gripper block |
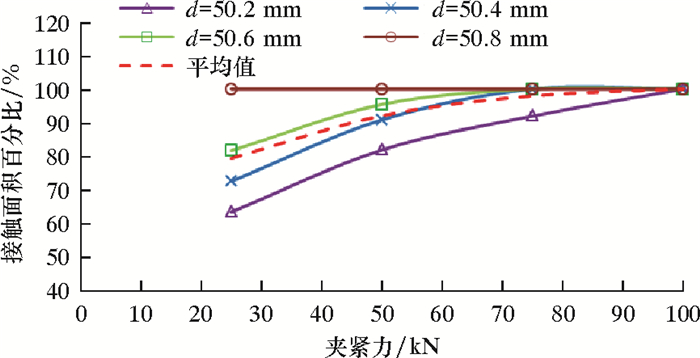
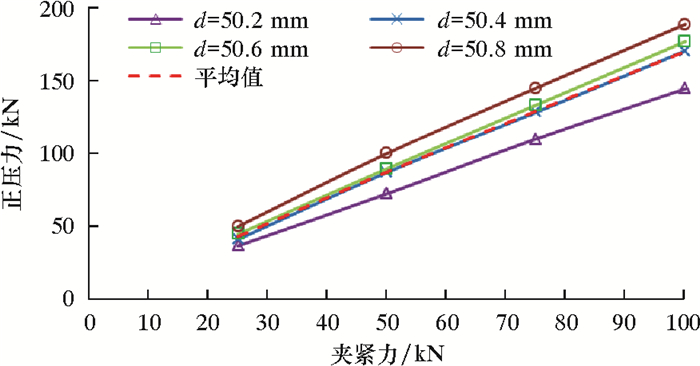
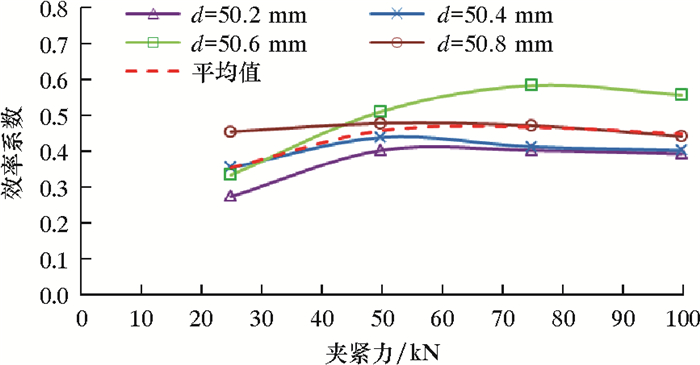
图 11为不同夹紧力下弹性夹持块与连续管的接触面积。从图 11可以看出:当夹持块圆弧直径与连续管不一致时,在夹紧力的作用下,夹持块和连续管同时发生适应性变形;在25~100 kN夹紧力范围内,平均接触面积为80%~100%,比常规刚性夹持块接触面积增大了6%~10%。图 12是弹性夹持块正压力总值。从图 12可以看出,在25~100 kN夹紧力下,夹持块平均正压力总值为42~170 kN,比常规夹持块增大了20%~37%。图 13是弹性夹持块效率系数曲线。从图 13可以看出,夹持块整体性能较为稳定,平均效率系数为0.35~0.47, 比常规夹持块提高了35%~57%。
|
| 图 11 不同夹紧力下弹性夹持块与连续管接触面积 Fig.11 Contact area of elastic gripper block and coiled tubing |
|
| 图 12 弹性夹持块正压力总值 Fig.12 Total normal pressure of the elastic gripper block |
|
| 图 13 弹性夹持块效率系数曲线 Fig.13 Efficiency coefficient curve of the elastic gripper block |
2.3 参数敏感性分析
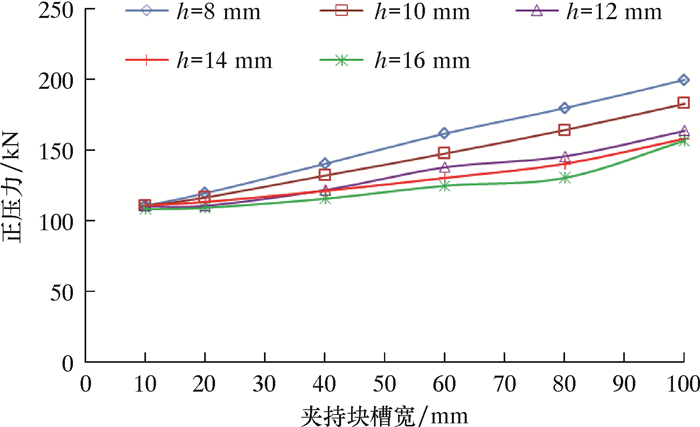
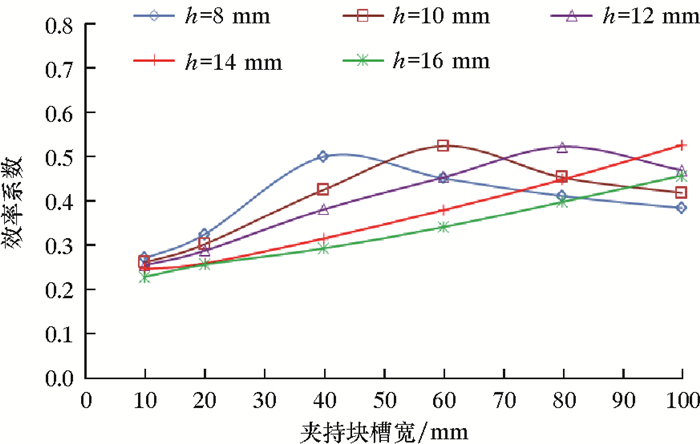
图 14是夹持块槽宽和底部壁厚对夹持块正压力的影响曲线。从图 14可以看出,槽宽越宽,底部壁厚越小,夹持块弹性越好,正压力越大。图 15是槽宽和底部壁厚对夹持块效率的影响曲线。从图 15可以看出:当壁厚一定时,存在一个最优槽宽,小于该槽宽时,夹持块效率随槽宽增大而增大,大于该槽宽时,效率随槽宽增大而减小;槽宽最优值随夹持块底部壁厚的增大而增大。综合考虑夹持块表面压力值和夹持块结构尺寸,建议槽宽取为40~60 mm,底部壁厚取为8~10 mm。
|
| 图 14 槽宽和底部壁厚对夹持块正压力的影响曲线 Fig.14 Effect of groove width and bottom wall thickness on the gripping pressure |
|
| 图 15 槽宽和底部壁厚对夹持块效率的影响曲线 Fig.15 Effect of groove width and bottom wall thickness on the efficiency of the gripper block |
3 试验验证
在理论分析的基础上,开展了常规夹持块和弹性夹持块的对比试验。考虑到普通连续管表面粗糙度、直线度和椭圆度难以控制,且对摩擦因数存在较大影响,在试验中用不锈钢管替代连续管。由于连续管应力测量难度较大,所以用当量摩擦因数作为对比依据。
表 1为对比试验结果。从表 1可以看出:在夹持块圆弧直径不变的情况下,连续管外径越小,夹持块效率越低,连续管外径由50.8 mm减小至50.4 mm时,弹性夹持块效率降低了7%,常规夹持块效率降低了14%;弹性结构可以有效提升夹持块效率,在本试验中,弹性夹持块效率平均值比常规夹持块提升了23%~31%。
| d/mm | 夹持块类型 | 当量摩擦因数 | 平均值 | |||
| F=20 kN | F=40 kN | F=60 kN | F=80 kN | |||
| 50.8 | 弹性 | 0.63 | 0.60 | 0.54 | 0.52 | 0.573 |
| 50.8 | 常规 | 0.52 | 0.47 | 0.44 | 0.43 | 0.465 |
| 50.4 | 弹性 | 0.61 | 0.51 | 0.51 | 0.51 | 0.535 |
| 50.4 | 常规 | 0.42 | 0.40 | 0.41 | 0.40 | 0.408 |
4 结论
(1) 当夹持块直径小于连续管外径时,在夹持块开口区域存在压力集中现象,可能出现严重的粘着磨损,影响夹持块和连续管的使用寿命。
(2) 常规夹持块管径适应性较差,当夹持块与连续管圆弧直径不一致时,其效率急剧下降。
(3) 和常规夹持块相比,弹性夹持块具有接触面积大、压力总值大、对连续管损伤小以及管径适应性强等优势,可以有效提升夹持块综合性能。
(4) 弹性夹持块沟槽和底部壁厚具有一个最优值,基于本文所选用的分析参数,建议槽宽取值40~60 mm,底部壁厚取值8~10 mm。
| [1] |
贺会群, 熊革, 刘寿军, 等. 我国连续管钻井技术的十年攻关与实践[J]. 石油机械, 2019, 47(7): 1-8. HE H Q, XIONG G, LIU S J, et al. Ten years of key problems tackling and practice of coiled tubing drilling technology in China[J]. China Petroleum Machinery, 2019, 47(7): 1-8. |
| [2] |
杨高, 刘菲, 唐纯静, 等. 连续管注入头夹持块的夹持性能研究[J]. 石油机械, 2012, 40(11): 10-14. YANG G, LIU F, TANG C J, et al. Research on the gripping performance of CT clamping block on injector head[J]. China Petroleum Machinery, 2012, 40(11): 10-14. |
| [3] |
李现东, 文涛. 连续管注入头夹持块结构优化研究[J]. 石油机械, 2012, 40(11): 48-52. LI X D, WEN T. Structural optimization of CT clamping block on injector head[J]. China Petroleum Machinery, 2012, 40(11): 48-52. |
| [4] |
车传睿, 李德忠, 顾国利, 等. 连续管作业注入头夹持机理研究[J]. 石油机械, 2012, 40(11): 43-47. CHE C R, LI D Z, GU G L, et al. Research on the clamping mechanism of CT injector head[J]. China Petroleum Machinery, 2012, 40(11): 43-47. |
| [5] |
张宏, 贺会群, 李远舟, 等. 连续管钻机注入头夹紧系统载荷均布设计方法[J]. 石油机械, 2015, 43(2): 1-4. ZHANG H, HE H Q, LI Y Z, et al. Design for even load distribution of grip system for injection head ofcoiled tubing drilling rig[J]. China Petroleum Machinery, 2015, 43(2): 1-4. |
| [6] |
马卫国, 卢雷, 王刚, 等. 基于AMESim的连续管注入头夹持力动态特性研究[J]. 石油机械, 2018, 46(5): 65-70. MA W G, LU L, WANG G, et al. AMESim-based study on dynamic behavior of gripping force of coiled tubing injector head[J]. China Petroleum Machinery, 2018, 46(5): 65-70. |
| [7] |
BURWELL J T, STRANG C D. On the empirical law of adhesive wear[J]. Journal of Applied Physics, 1952, 23(1): 18-28. |
| [8] |
胡志强, 杨高, 刘菲, 等. 连续管夹持力学特性研究[J]. 石油机械, 2016, 44(11): 89-93. HU Z Q, YANG G, LIU F, et al. Study on the mechanical properties of coiled tubbing under clamping state[J]. China Petroleum Machinery, 2016, 44(11): 89-93. |


